Impact of Dataset Size on the Signature-Based Calibration of a Hydrological Model
Abstract
1. Introduction
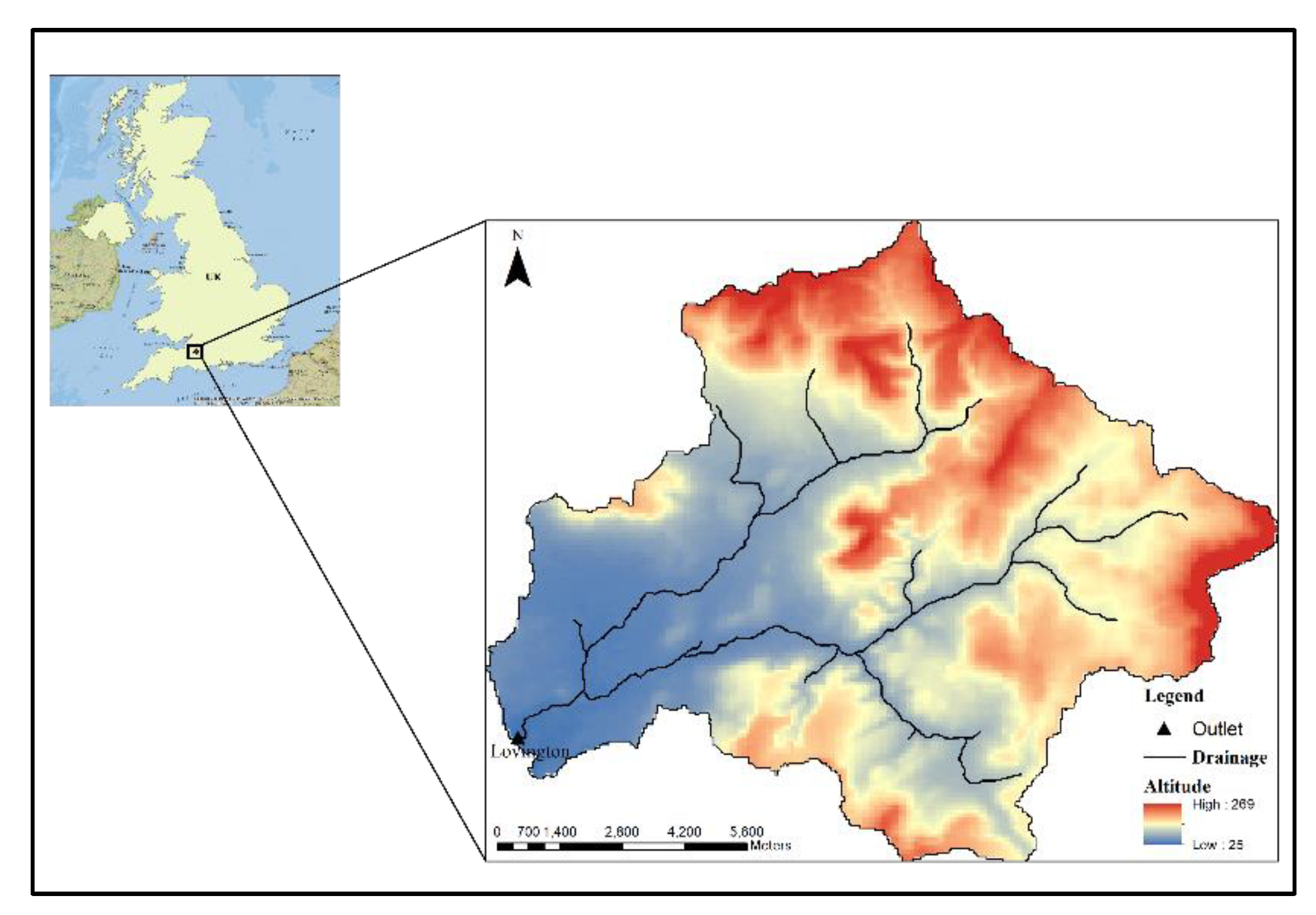
2. Study Area and Datasets
3. Methodology
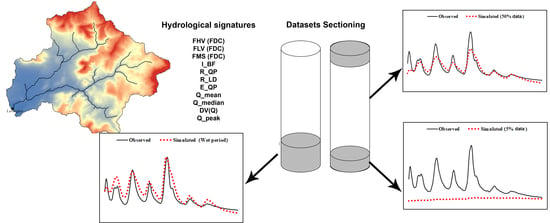
3.1. Selection of Hydrological Signatures
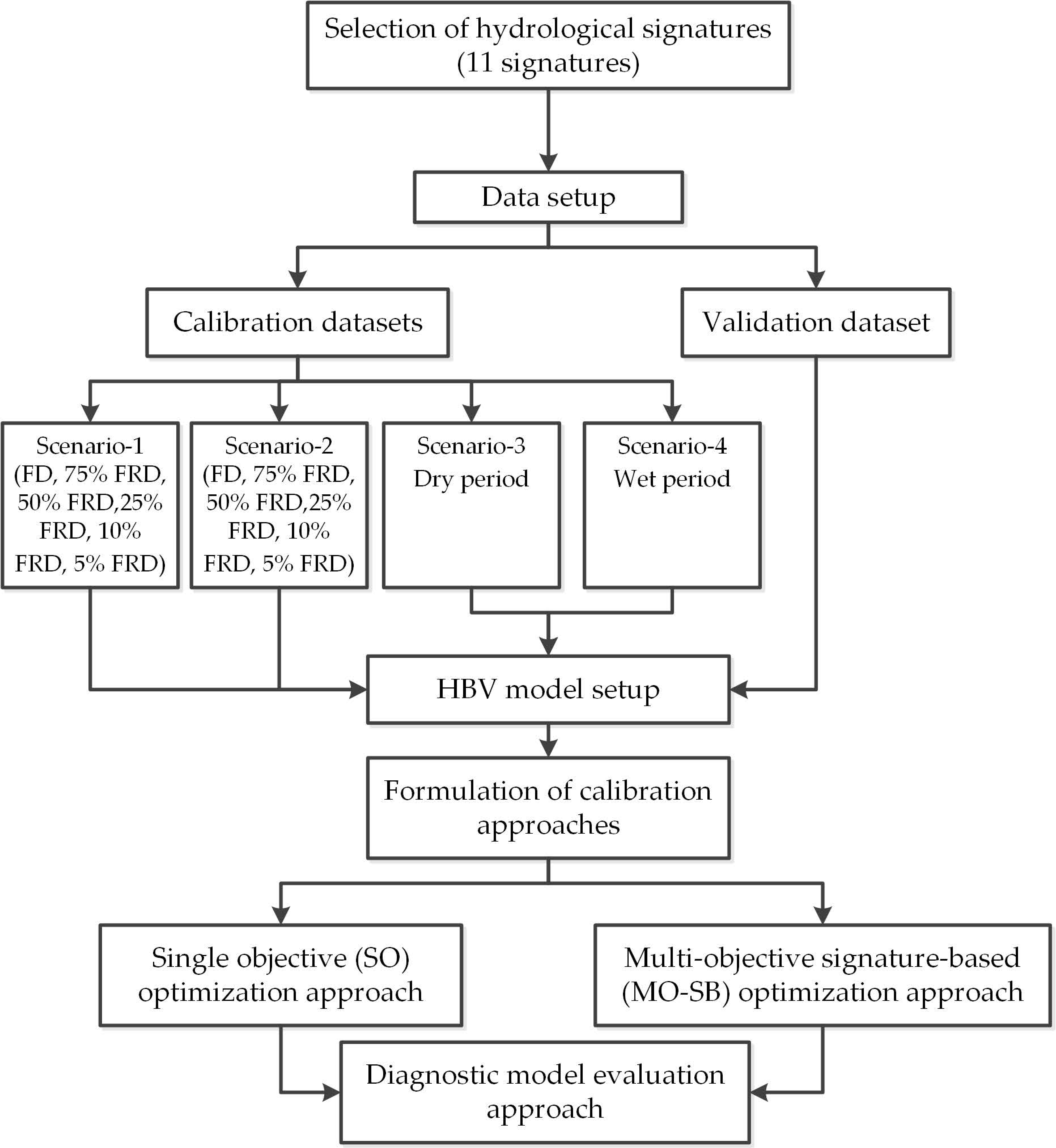
3.2. Data Setup
- Select a long-period dataset as an FD for model calibration (benchmark dataset) (Table 2);
- Select an additional dataset for model validation (Table 2);
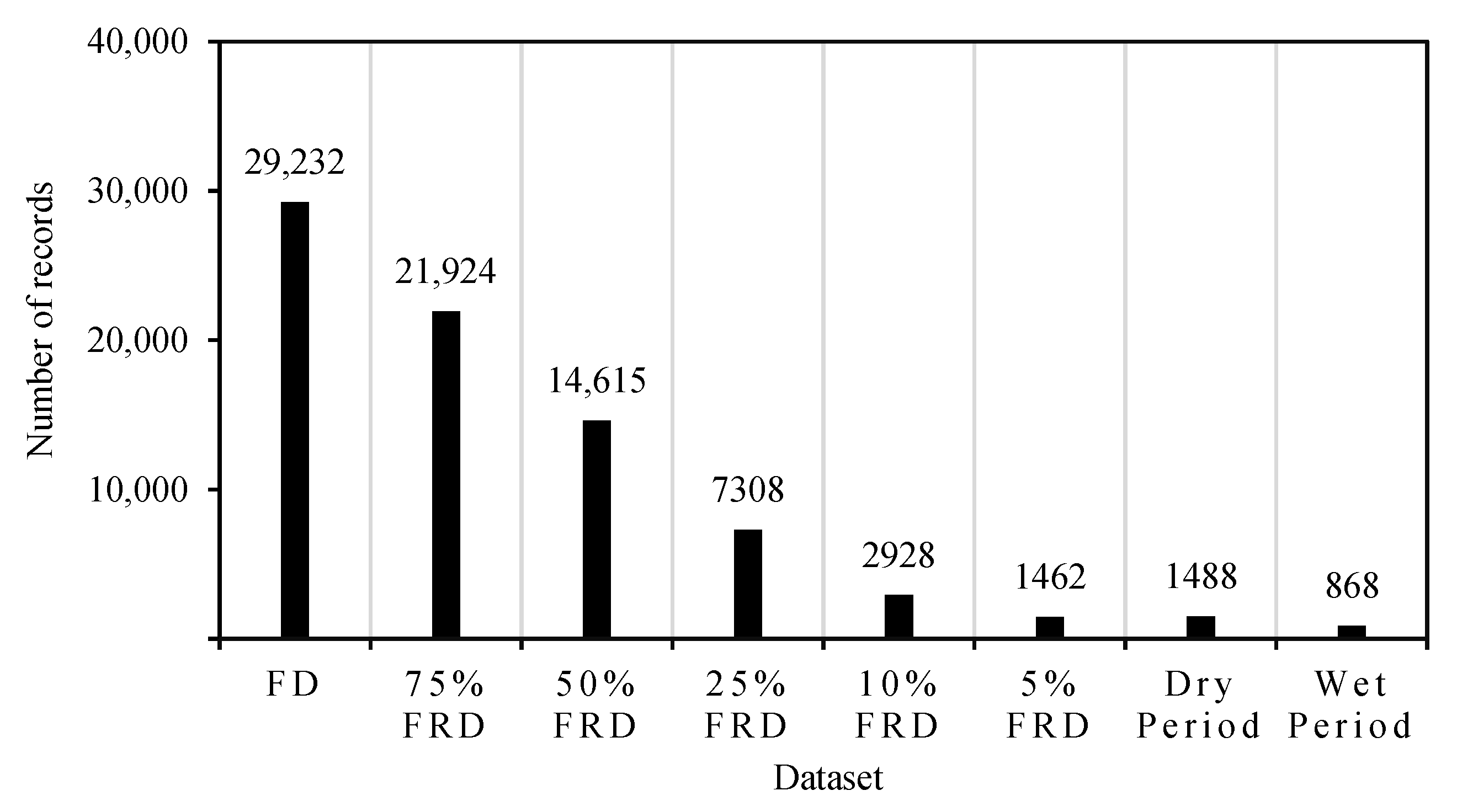
- Divide the FD into partial datasets progressively decreasing in size, from long-term- to short-term data using four scenarios (Table 2):
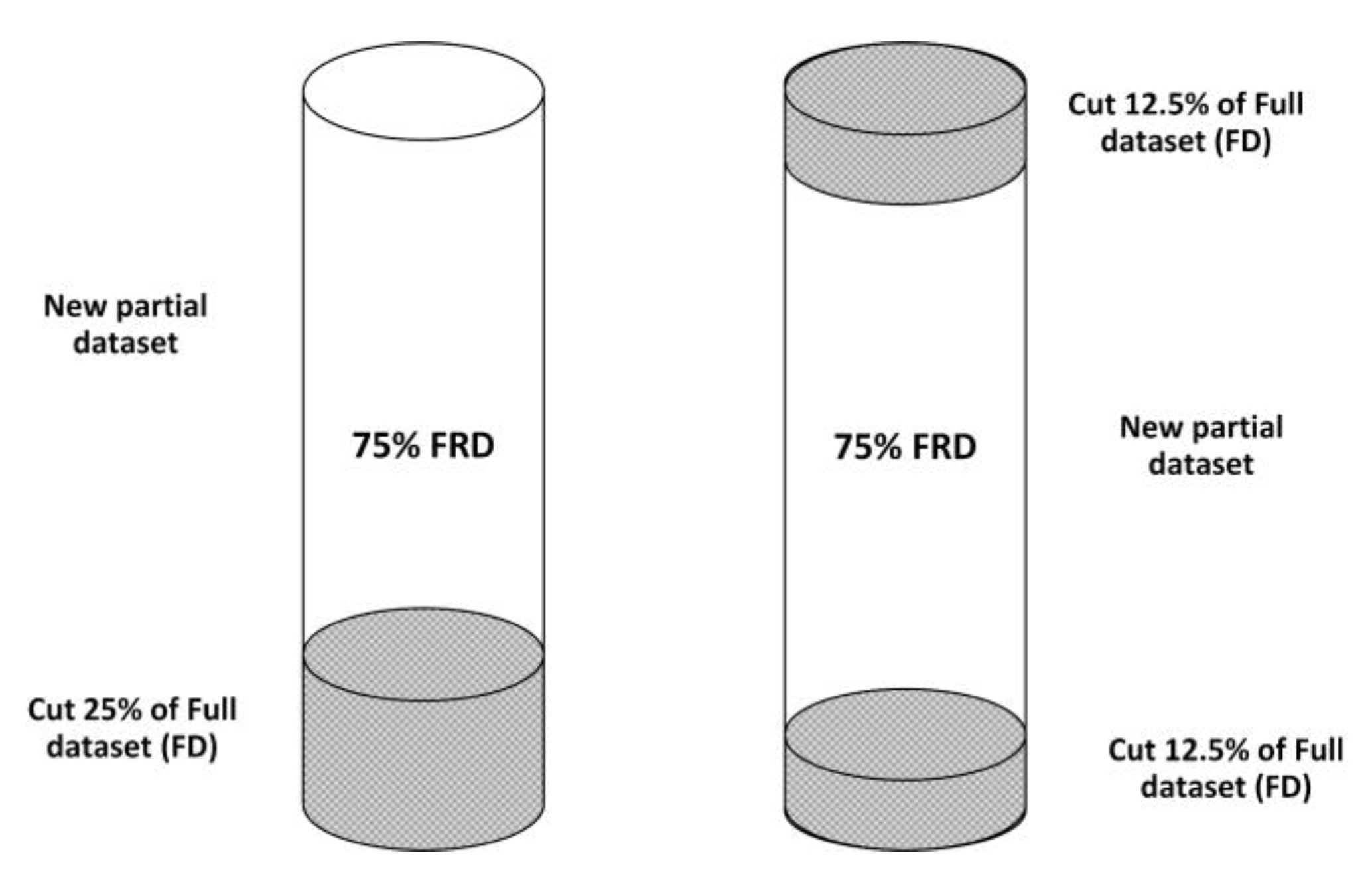
- Scenario 1: Each new data subset is composed by removing a certain amount of data (a certain percentage, e.g., remove 25% of the total data) from the end of the FD (Figure 3);
- Scenario 2: The new data subset is created by removing an equal amount of data from both the start and end of the FD (Figure 3);
- Scenario 3: A section of the FD represents a short continuous dry period (no precipitation);
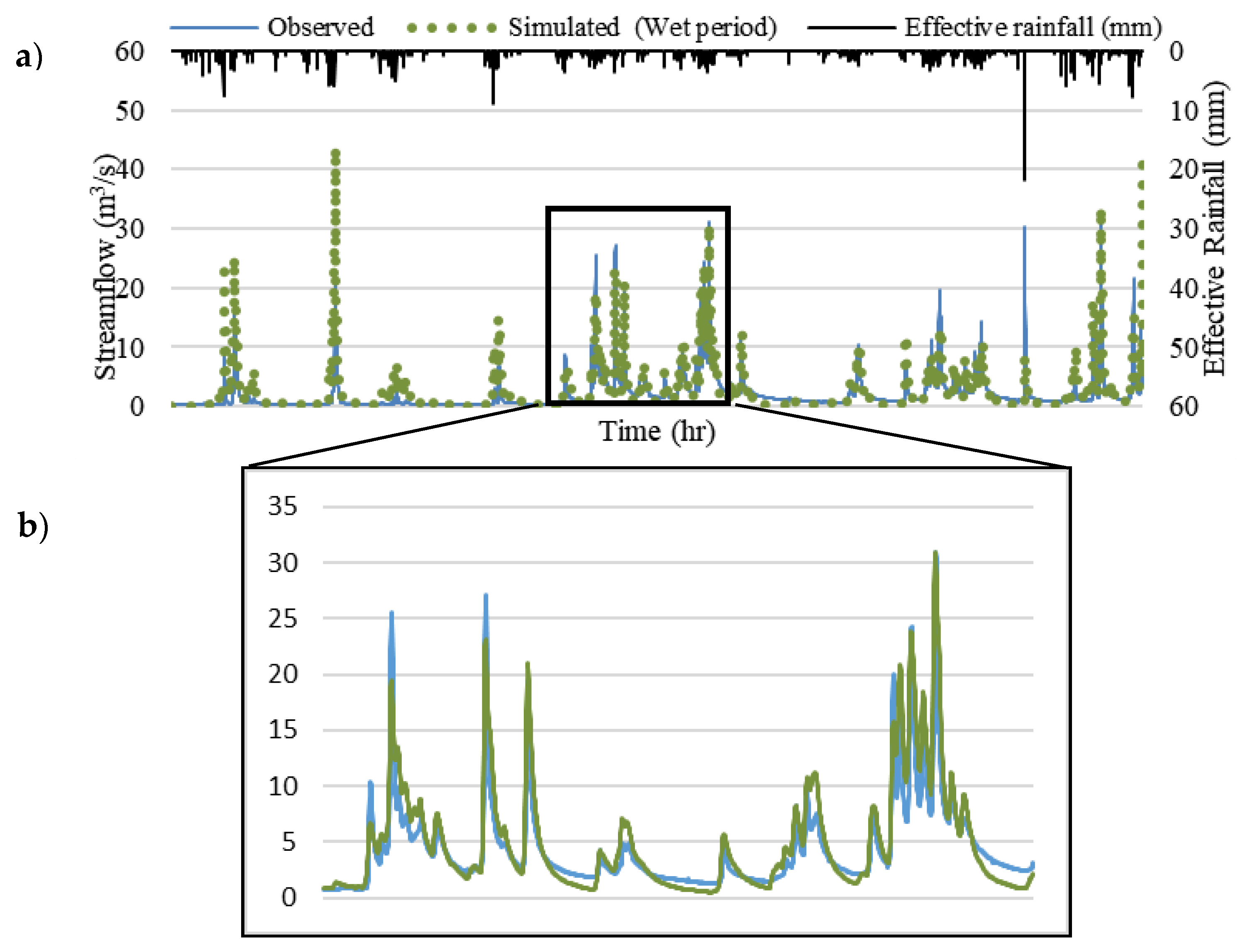
- Scenario 4: A section of the FD represents a short continuous wet period (frequent and intensive precipitation).
3.3. HBV Model Setup
3.4. Model Calibration Approaches
3.4.1. Formulation of SO Optimization Approach
3.4.2. Formulation of MO-SB Optimization Approach
- 10% acceptability threshold and BC, MO-BC (10%);
- 10% acceptability threshold and UC, MO-UC (10%);
- 20% acceptability threshold and BC, MO-BC (20%);
- 20% acceptability threshold and UC, MO-UC (20%);
3.5. The Diagnostic Model Evaluation Approach
4. Results
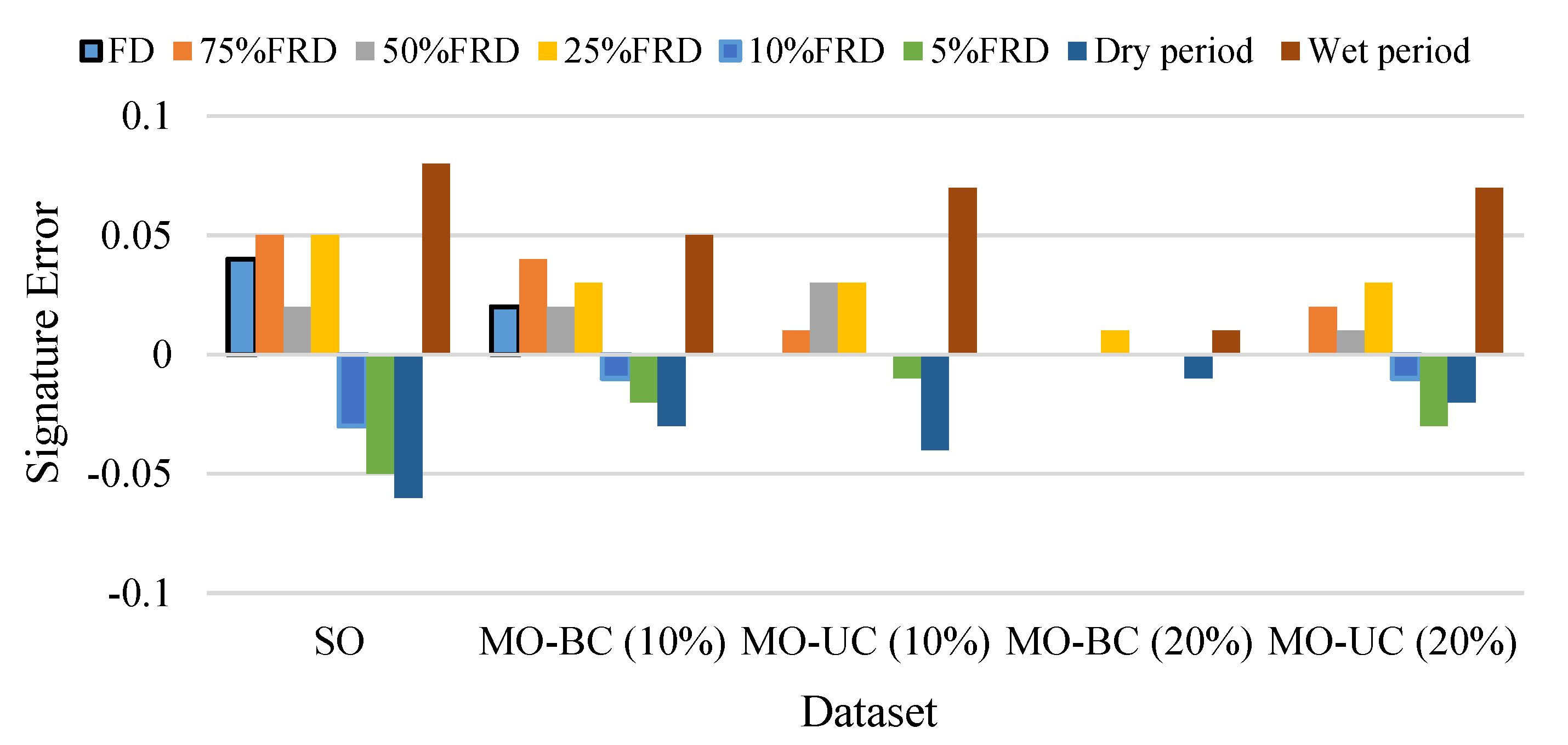
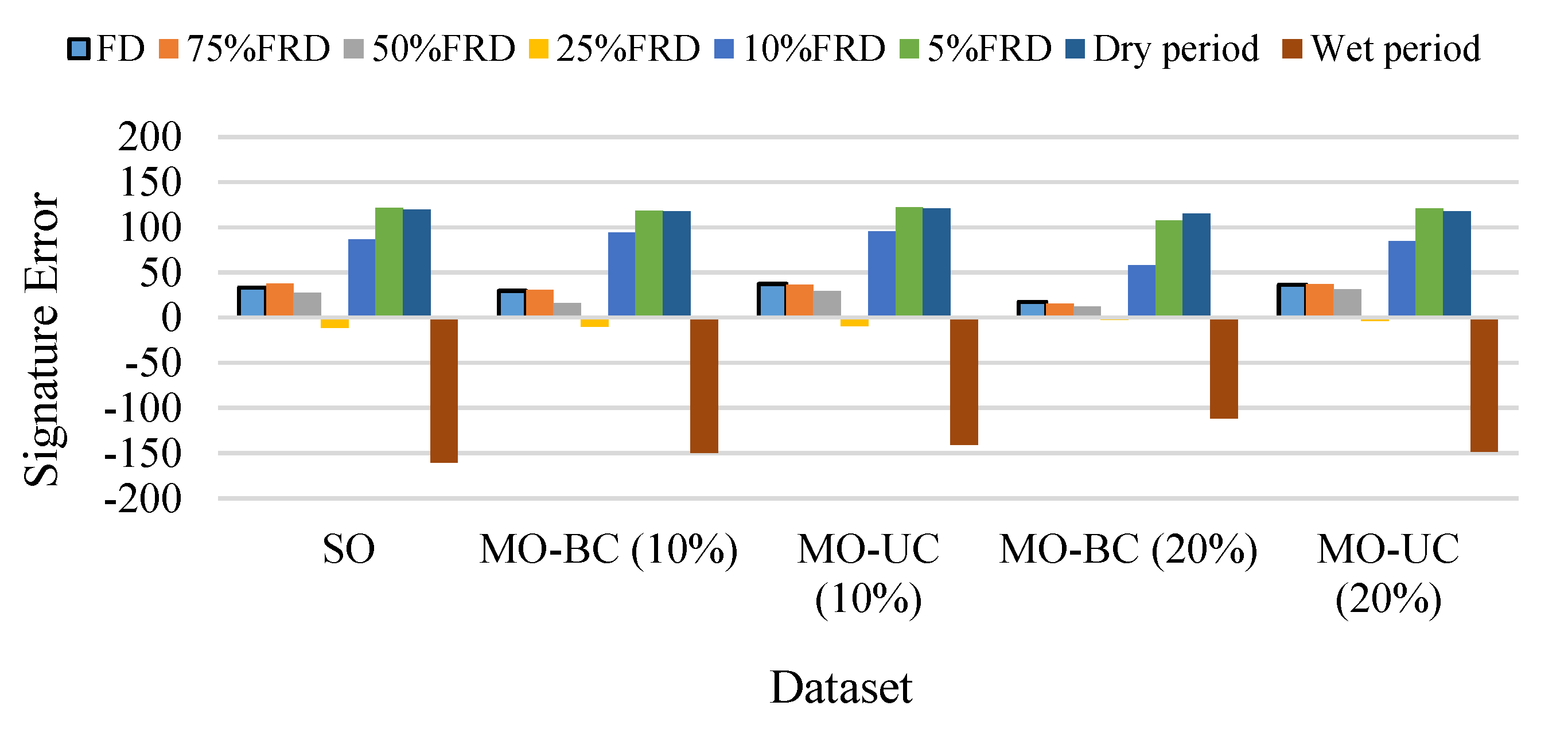
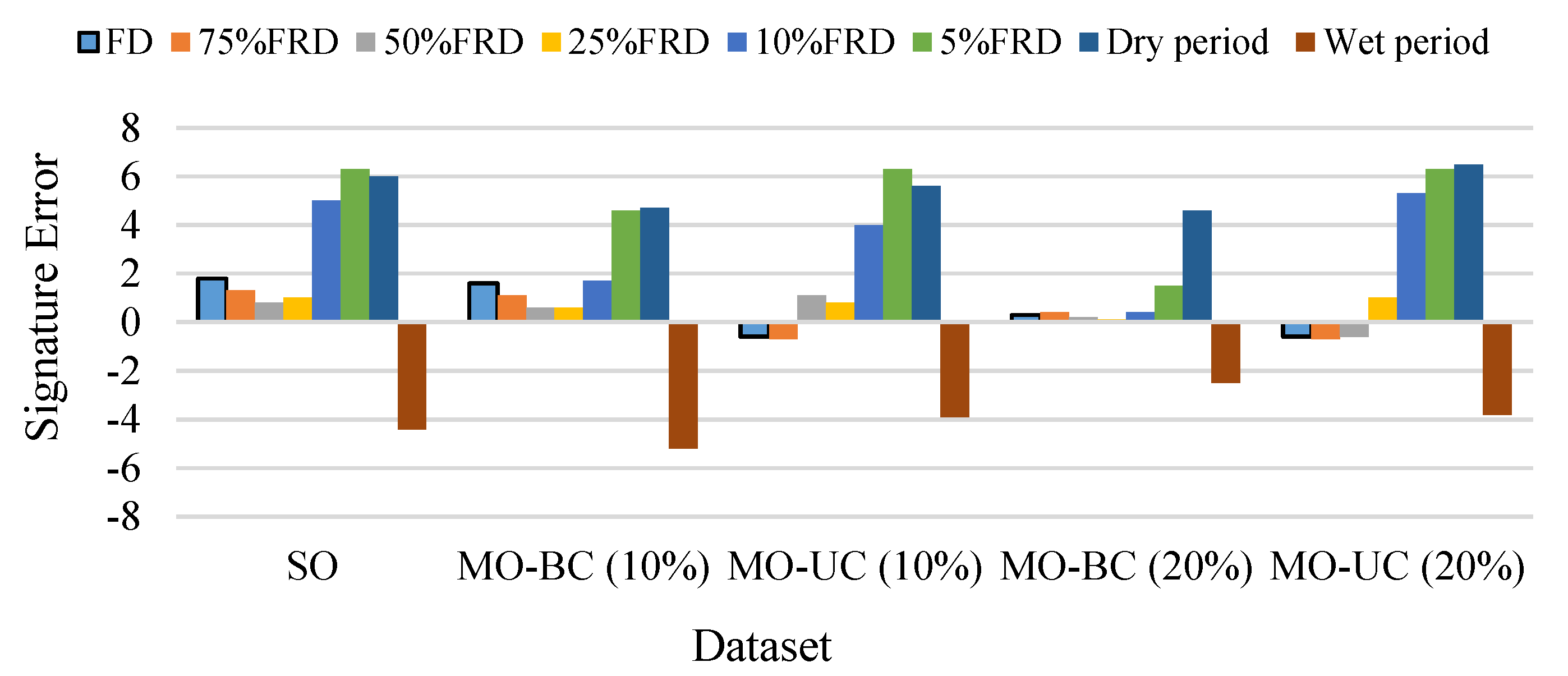
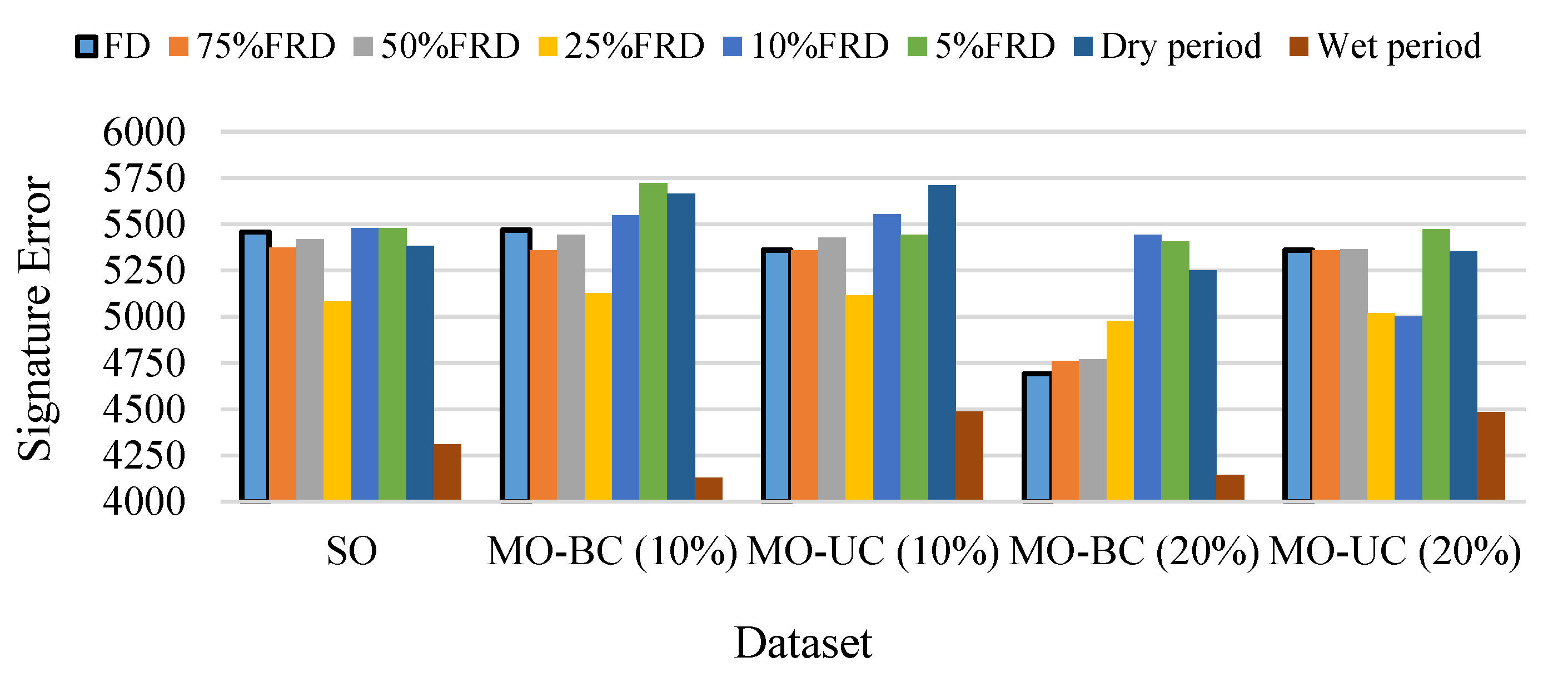
4.1. Diagnostic Evaluation of the SO Optimization Approach
4.1.1. General Characterization of Results
4.1.2. General Characterization of Results
4.2. Diagnostic Evaluation of the MO-SB Optimization Approach
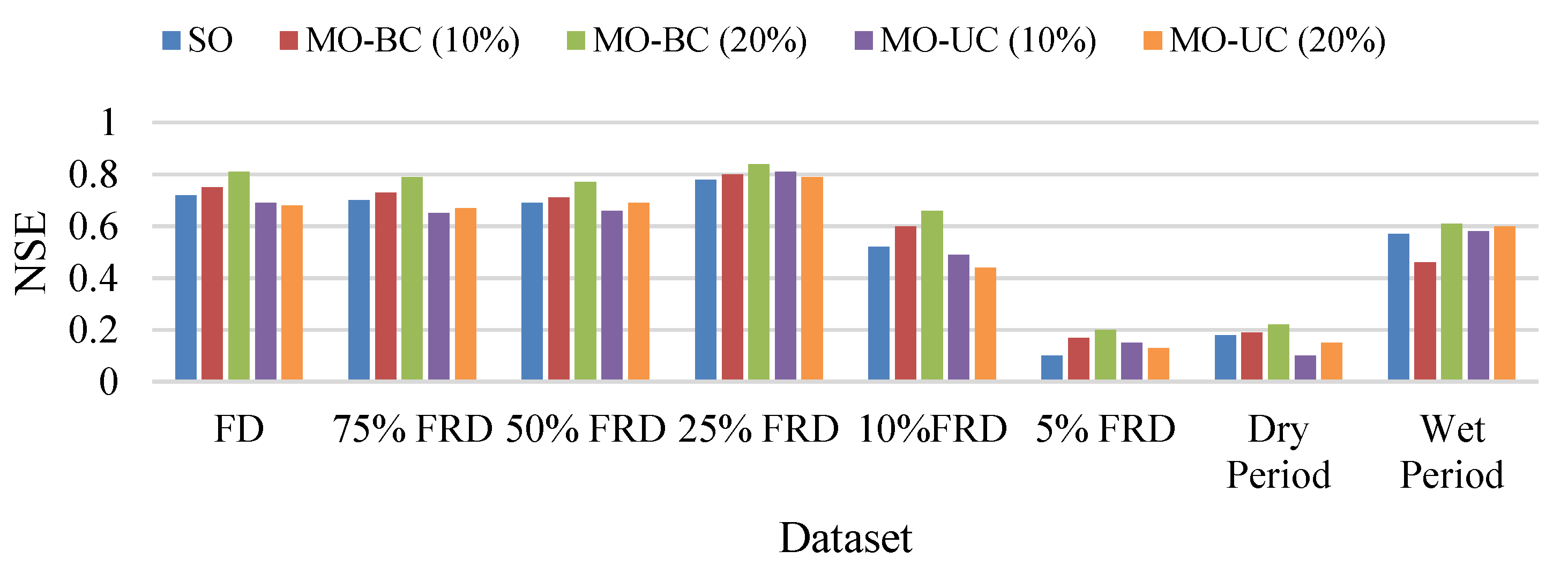
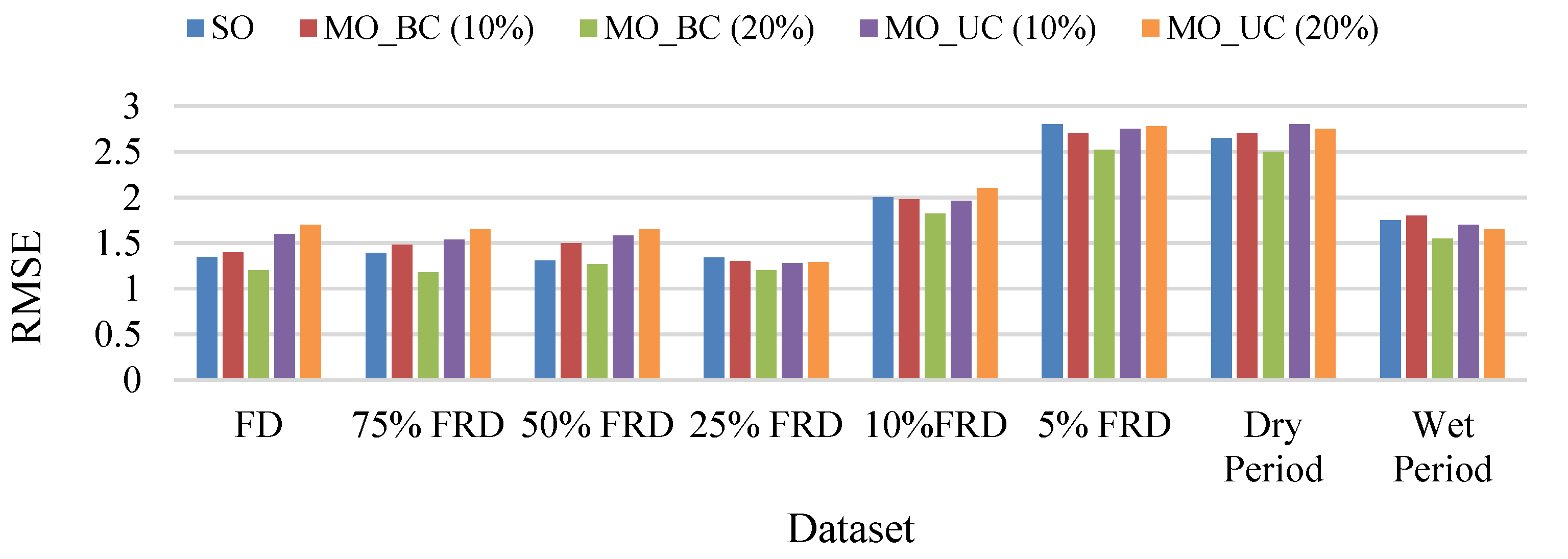
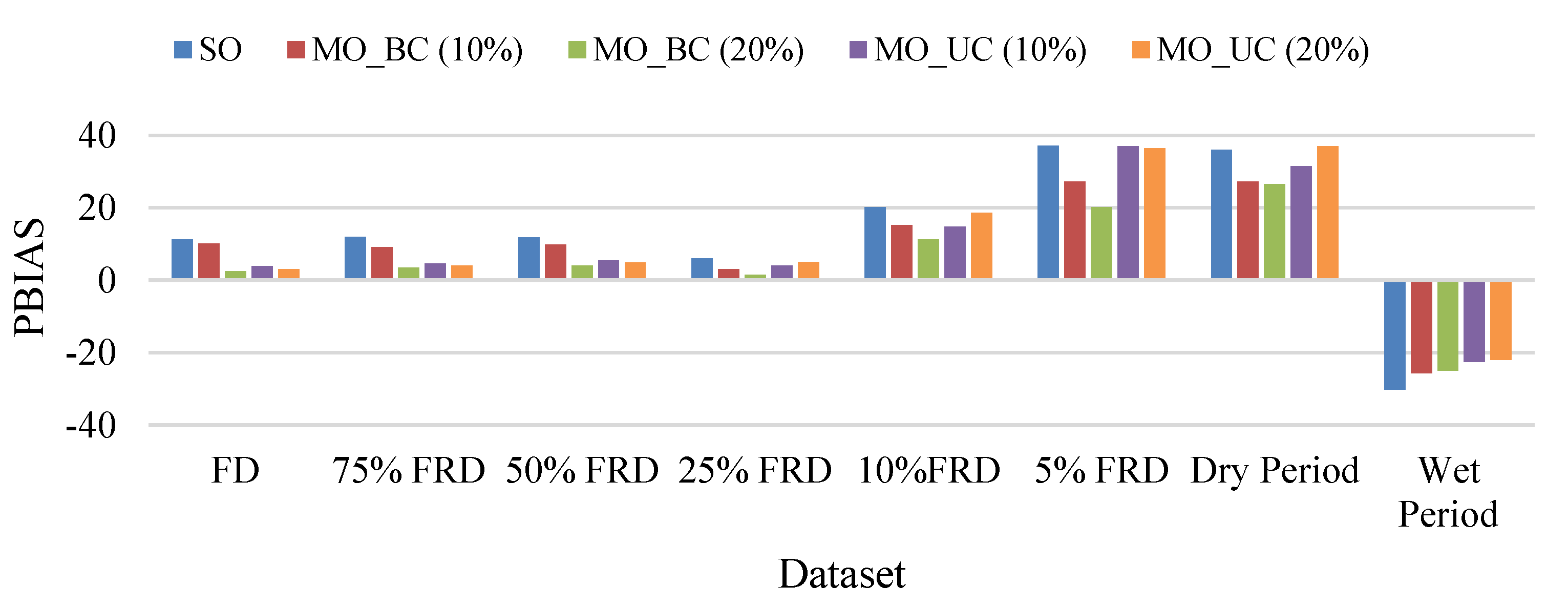
4.2.1. Performance Evaluation of MO-SB
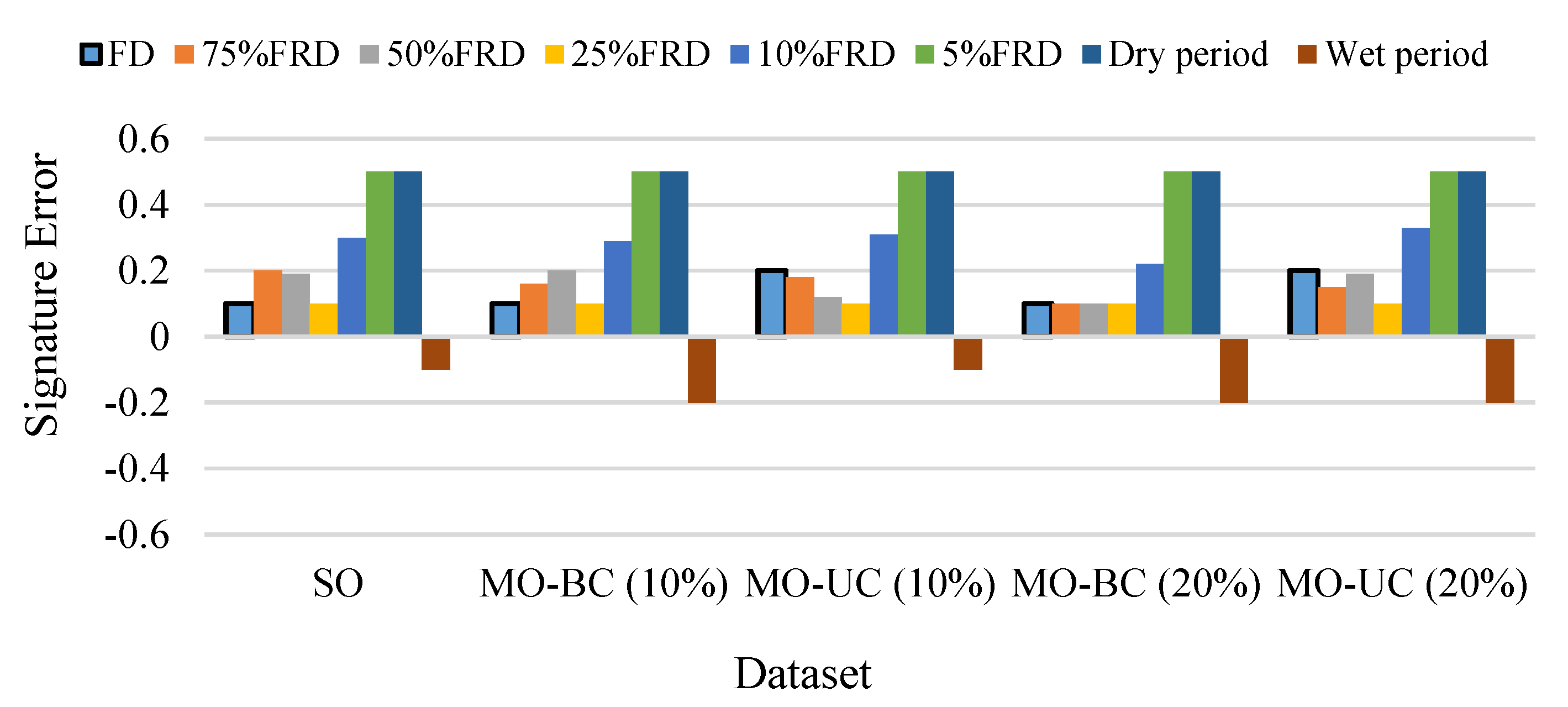
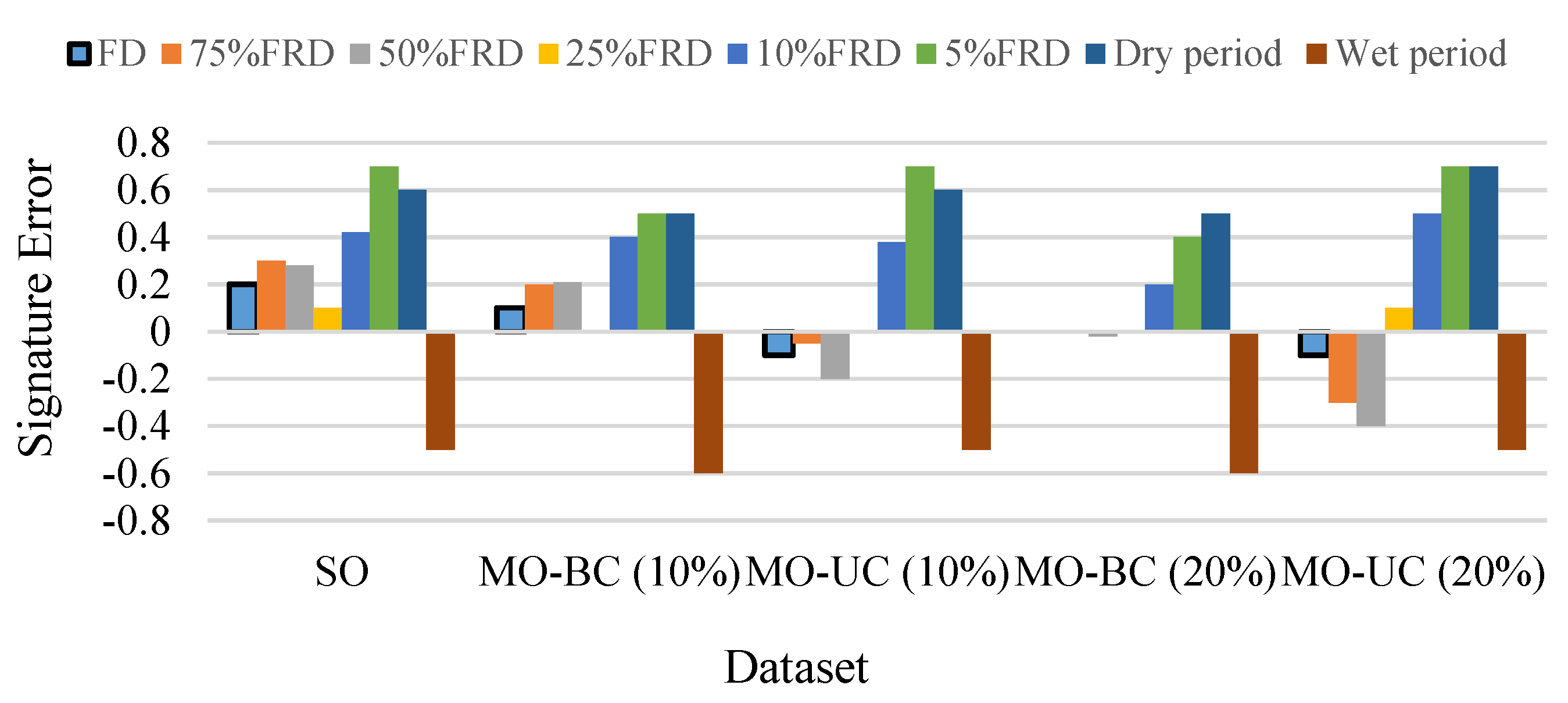
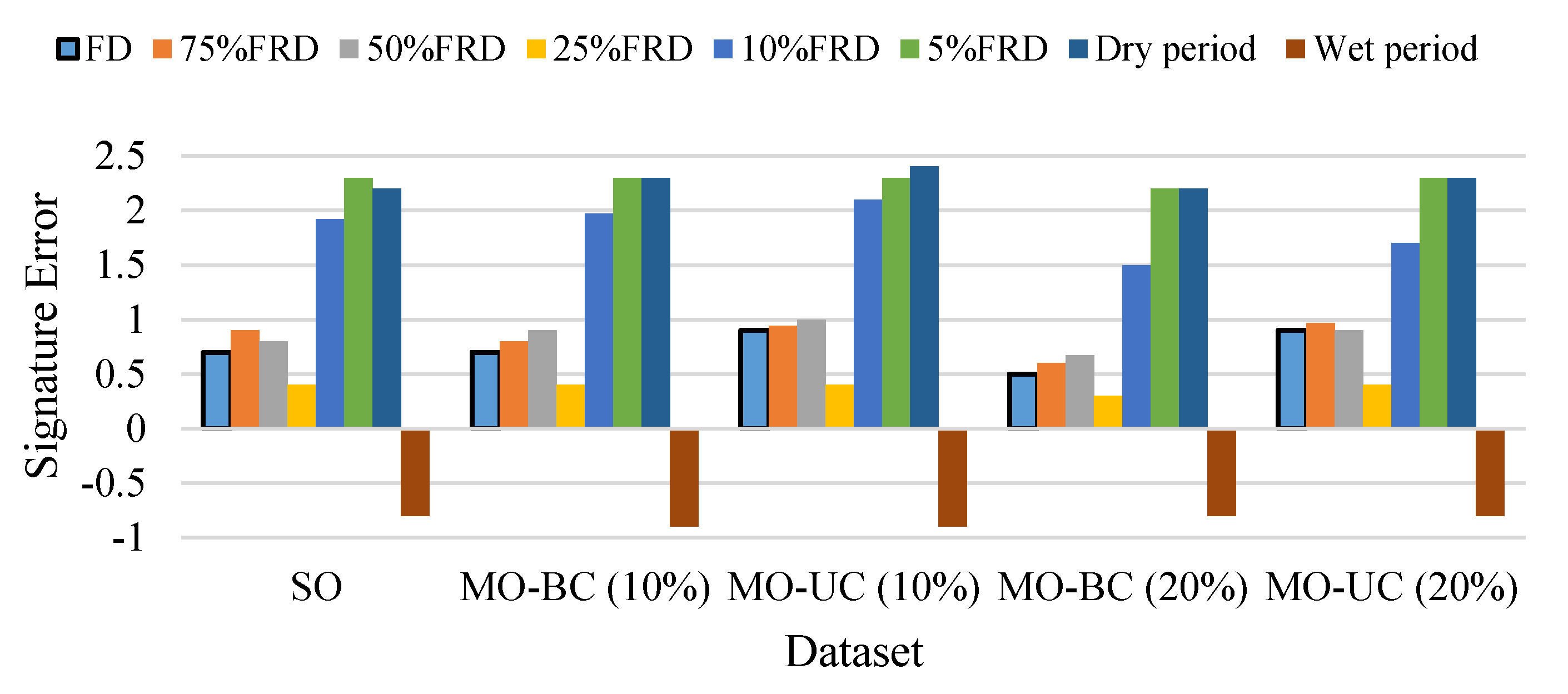
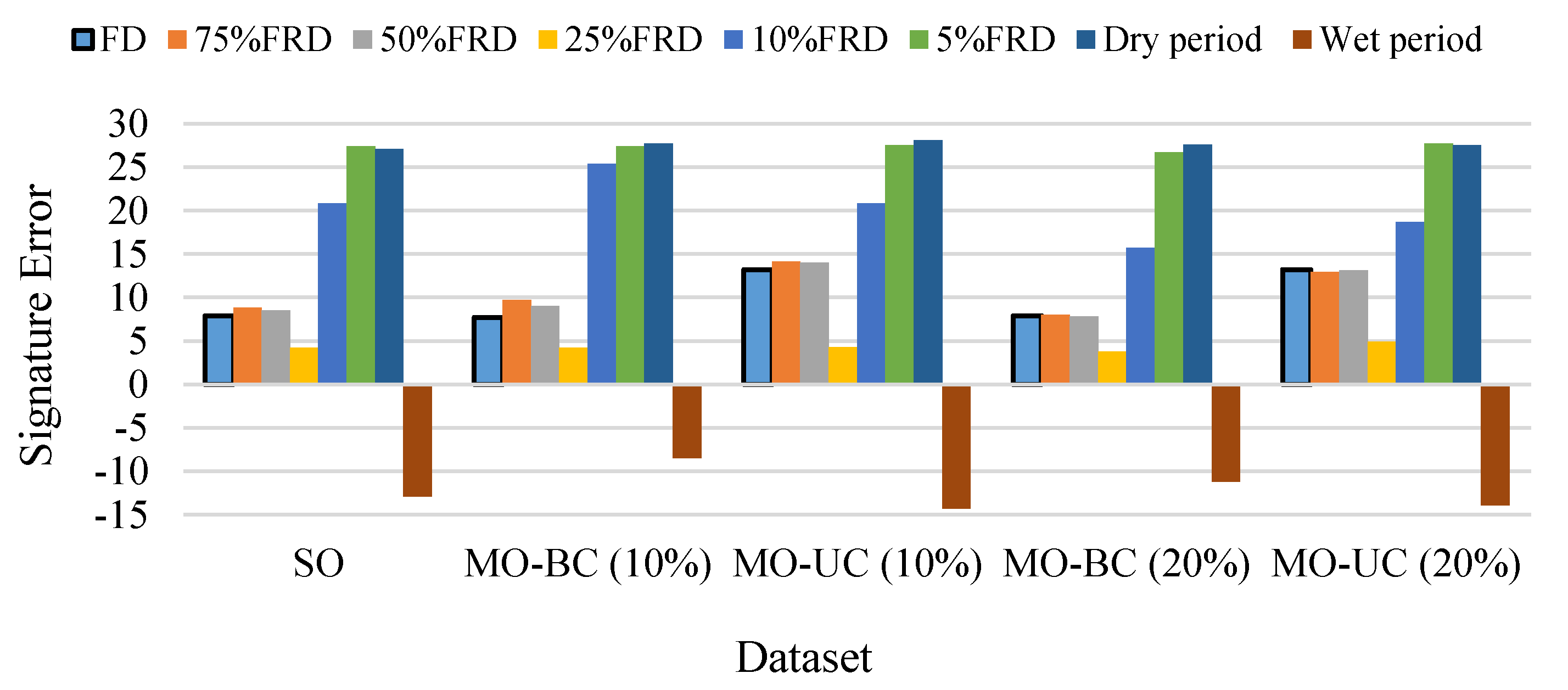
4.2.2. Behavioral Consistency Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Dibike, Y.B.; Kukuric, N. Calage automatique de modèles d’écoulement souterrain utilisant des techniques d’optimisation globales. Hydrol. Sci. J. 1999, 44, 879–894. [Google Scholar] [CrossRef]
- Lawrence, D.; Haddeland, I.; Langsholt, E. Calibration of HBV Hydrological Models Using PEST Parameter Estimation; Norwegian Water Resources and Energy Directorate: Oslo, Norway, 2009; ISBN 9788241006807.
- Patil, S.D.; Stieglitz, M. Comparing spatial and temporal transferability of hydrological model parameters. J. Hydrol. 2015, 525, 409–417. [Google Scholar] [CrossRef]
- Wöhling, T.; Samaniego, L.; Kumar, R. Evaluating multiple performance criteria to calibrate the distributed hydrological model of the upper Neckar catchment. Environ. Earth Sci. 2013, 69, 453–468. [Google Scholar] [CrossRef]
- Fenicia, F.; Solomatine, D.P.; Savenije, H.H.G.; Matgen, P. Soft combination of local models in a multi-objective framework. Hydrol. Earth Syst. Sci. 2007, 11, 1797–1809. [Google Scholar] [CrossRef]
- Sahraei, S.; Asadzadeh, M.; Unduche, F. Signature-based multi-modelling and multi-objective calibration of hydrologic models: Application in flood forecasting for Canadian Prairies. J. Hydrol. 2020, 588, 125095. [Google Scholar] [CrossRef]
- Reed, P.M.; Hadka, D.; Herman, J.D.; Kasprzyk, J.R.; Kollat, J.B. Evolutionary multiobjective optimization in water resources: The past, present, and future. Adv. Water Resour. 2013, 51, 438–456. [Google Scholar] [CrossRef]
- Zhou, A.; Qu, B.Y.; Li, H.; Zhao, S.Z.; Suganthan, P.N.; Zhangd, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Koutsoyiannis, D. Une décennie d’approches de calage multi-objectifs en modélisation hydrologique: Une revue. Hydrol. Sci. J. 2010, 55, 58–78. [Google Scholar] [CrossRef]
- Kollat, J.B.; Reed, P.M.; Wagener, T. When are multiobjective calibration trade-offs in hydrologic models meaningful? Water Resour. Res. 2012, 48, 3520. [Google Scholar] [CrossRef]
- Asadzadeh, M.; Tolson, B.A.; Burn, D.H. A new selection metric for multiobjective hydrologic model calibration. Water Resour. Res. 2014, 50, 7082–7099. [Google Scholar] [CrossRef]
- Euser, T.; Winsemius, H.C.; Hrachowitz, M.; Fenicia, F.; Uhlenbrook, S.; Savenije, H.H.G. A framework to assess the realism of model structures using hydrological signatures. Hydrol. Earth Syst. Sci. 2013, 17, 1893–1912. [Google Scholar] [CrossRef]
- Martinez, G.F.; Gupta, H.V. Hydrologic consistency as a basis for assessing complexity of monthly water balance models for the continental United States. Water Resour. Res. 2011, 47, W12540. [Google Scholar] [CrossRef]
- van Werkhoven, K.; Wagener, T.; Reed, P.; Tang, Y. Sensitivity-guided reduction of parametric dimensionality for multi-objective calibration of watershed models. Adv. Water Resour. 2009, 32, 1154–1169. [Google Scholar] [CrossRef]
- Pokhrel, P.; Yilmaz, K.K.; Gupta, H.V. Multiple-criteria calibration of a distributed watershed model using spatial regularization and response signatures. J. Hydrol. 2012, 418–419, 49–60. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. Smart low flow signature metrics for an improved overall performance evaluation of hydrological models. J. Hydrol. 2014, 510, 447–458. [Google Scholar] [CrossRef]
- Asadzadeh, M.; Leon, L.; McCrimmon, C.; Yang, W.; Liu, Y.; Wong, I.; Fong, P.; Bowen, G. Watershed derived nutrients for Lake Ontario inflows: Model calibration considering typical land operations in Southern Ontario. J. Great Lakes Res. 2015, 41, 1037–1051. [Google Scholar] [CrossRef]
- Chilkoti, V.; Bolisetti, T.; Balachandar, R. Multi-objective autocalibration of SWAT model for improved low flow performance for a small snowfed catchment. Hydrol. Sci. J. 2018, 63, 1482–1501. [Google Scholar] [CrossRef]
- Sawicz, K.; Wagener, T.; Sivapalan, M.; Troch, P.A.; Carrillo, G. Catchment classification: Empirical analysis of hydrologic similarity based on catchment function in the eastern USA. Hydrol. Earth Syst. Sci. 2011, 15, 2895–2911. [Google Scholar] [CrossRef]
- Seibert, J.; McDonnell, J.J. On the dialog between experimentalist and modeler in catchment hydrology: Use of soft data for multicriteria model calibration. Water Resour. Res. 2002, 38, 1241–1252. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Fovet, O.; Ruiz, L.; Euser, T.; Gharari, S.; Nijzink, R.; Freer, J.; Savenije, H.H.G.; Gascuel-Odoux, C. Process consistency in models: The importance of system signatures, expert knowledge, and process complexity. Water Resour. Res. 2014, 50, 7445–7469. [Google Scholar] [CrossRef]
- McMillan, H.K.; Clark, M.P.; Bowden, W.B.; Duncan, M.; Woods, R.A. Hydrological field data from a modeller’s perspective: Part 1. Diagnostic tests for model structure. Hydrol. Process. 2011, 25, 511–522. [Google Scholar] [CrossRef]
- Clark, M.P.; McMillan, H.K.; Collins, D.B.G.; Kavetski, D.; Woods, R.A. Hydrological field data from a modeller’s perspective: Part 2: Process-based evaluation of model hypotheses. Hydrol. Process. 2011, 25, 523–543. [Google Scholar] [CrossRef]
- Reusser, D.E.; Zehe, E. Inferring model structural deficits by analyzing temporal dynamics of model performance and parameter sensitivity. Water Resour. Res. 2011, 47, W07550. [Google Scholar] [CrossRef]
- Wagener, T.; Montanari, A. Convergence of approaches toward reducing uncertainty in predictions in ungauged basins. Water Resour. Res. 2011, 47, 453–460. [Google Scholar] [CrossRef]
- Westerberg, I.K.; Guerrero, J.L.; Younger, P.M.; Beven, K.J.; Seibert, J.; Halldin, S.; Freer, J.E.; Xu, C.Y. Calibration of hydrological models using flow-duration curves. Hydrol. Earth Syst. Sci. 2011, 15, 2205–2227. [Google Scholar] [CrossRef]
- Schaefli, B. Snow hydrology signatures for model identification within a limits-of-acceptability approach. Hydrol. Process. 2016, 30, 4019–4035. [Google Scholar] [CrossRef]
- Shafii, M.; Tolson, B.A. Optimizing hydrological consistency by incorporating hydrological signatures into model calibration objectives. Water Resour. Res. 2015, 51, 3796–3814. [Google Scholar] [CrossRef]
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Automatic calibration of conceptual rainfall-runoff models: Sensitivity to calibration data. J. Hydrol. 1996, 181, 23–48. [Google Scholar] [CrossRef]
- Kim, U.; Kaluarachchi, J.J. Hydrologic model calibration using discontinuous data: An example from the upper Blue Nile River Basin of Ethiopia. Hydrol. Process. 2009, 23, 3705–3717. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y.; Wang, G.; Cui, X.; Yu, J.; Zuo, D.; Xu, Z. Physically based distributed hydrological model calibration based on a short period of streamflow data: Case studies in four Chinese basins. Hydrol. Earth Syst. Sci. 2017, 21, 251–265. [Google Scholar] [CrossRef]
- McIntyre, N.R.; Wheater, H.S. Calibration of an in-river phosphorus model: Prior evaluation of data needs and model uncertainty. J. Hydrol. 2004, 290, 100–116. [Google Scholar] [CrossRef]
- Tan, S.B.; Chua, L.H.; Shuy, E.B.; Lo, E.Y.-M.; Lim, L.W. Performances of Rainfall-Runoff Models Calibrated over Single and Continuous Storm Flow Events. J. Hydrol. Eng. 2008, 13, 597–607. [Google Scholar] [CrossRef]
- Sorooshian, S.; Gupta, V.K.; Fulton, J.L. Evaluation of Maximum Likelihood Parameter estimation techniques for conceptual rainfall-runoff models: Influence of calibration data variability and length on model credibility. Water Resour. Res. 1983, 19, 251–259. [Google Scholar] [CrossRef]
- Li, C.Z.; Wang, H.; Liu, J.; Yan, D.H.; Yu, F.L.; Zhang, L. Effect of calibration data series length on performance and optimal parameters of hydrological model. Water Sci. Eng. 2010, 3, 378–393. [Google Scholar]
- Tada, T.; Beven, K.J. Hydrological model calibration using a short period of observations. Hydrol. Process. 2012, 26, 883–892. [Google Scholar] [CrossRef]
- Perrin, C.; Oudin, L.; Andreassian, V.; Rojas-Serna, C.; Michel, C.; Mathevet, T. Impact of limited streamflow data on the efficiency and the parameters of rainfall-runoff models. Hydrol. Sci. J. 2007, 52, 131–151. [Google Scholar] [CrossRef]
- Reynolds, J.E.; Halldin, S.; Seibert, J.; Xu, C.Y.; Grabs, T. Robustness of flood-model calibration using single and multiple events. Hydrol. Sci. J. 2020, 65, 842–853. [Google Scholar] [CrossRef]
- Seibert, J.; McDonnell, J.J. Gauging the Ungauged Basin: Relative Value of Soft and Hard Data. J. Hydrol. Eng. 2015, 20, A4014004. [Google Scholar] [CrossRef]
- Brath, A.; Montanari, A.; Toth, E. Analysis of the effects of different scenarios of historical data availability on the calibration of a spatially-distributed hydrological model. J. Hydrol. 2004, 291, 232–253. [Google Scholar] [CrossRef]
- Seibert, J.; Beven, K.J. Gauging the ungauged basin: How many discharge measurements are needed? Hydrol. Earth Syst. Sci. 2009, 13, 883–892. [Google Scholar] [CrossRef]
- Pool, S.; Viviroli, D.; Seibert, J. Prediction of hydrographs and flow-duration curves in almost ungauged catchments: Which runoff measurements are most informative for model calibration? J. Hydrol. 2017, 554, 613–622. [Google Scholar] [CrossRef]
- Gharari, S.; Shafiei, M.; Hrachowitz, M.; Kumar, R.; Fenicia, F.; Gupta, H.V.; Savenije, H.H.G. A constraint-based search algorithm for parameter identification of environmental models. Hydrol. Earth Syst. Sci. 2014, 18, 4861–4870. [Google Scholar] [CrossRef]
- Bell, V.A.; Moore, R.J. The sensitivity of catchment runoff models to rainfall data at different spatial scales. Hydrol. Earth Syst. Sci. 2000, 4, 653–667. [Google Scholar] [CrossRef]
- Shrestha, D.L.; Solomatine, D.P. Data-driven approaches for estimating uncertainty in rainfall-runoff modelling. Int. J. River Basin Manag. 2008, 6, 109–122. [Google Scholar] [CrossRef]
- Westerberg, I.K.; McMillan, H.K. Uncertainty in hydrological signatures. Hydrol. Earth Syst. Sci. 2015, 19, 3951–3968. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration—Guidelines for computing crop water requirements. In FAO Irrigation and Drainage; FAO: Rome, Italy, 1998. [Google Scholar]
- Yadav, M.; Wagener, T.; Gupta, H. Regionalization of constraints on expected watershed response behavior for improved predictions in ungauged basins. Adv. Water Resour. 2007, 30, 1756–1774. [Google Scholar] [CrossRef]
- Mcmillan, H.; Westerberg, I.; Branger, F. Five guidelines for selecting hydrological signatures. Hydrol. Process. 2017, 31, 4757–4761. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A process-based diagnostic approach to model evaluation Application to the NWS distributed hydrologic model. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Shamir, E.; Imam, B.; Gupta, H.V.; Sorooshian, S. Application of temporal streamflow descriptors in hydrologic model parameter estimation. Water Resour. Res. 2005, 41, 1–16. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M.; Limbrunner, J.F. Climate elasticity of streamflow in the United States. Water Resour. Res. 2001, 37, 1771–1781. [Google Scholar] [CrossRef]
- Donnelly, C.; Andersson, J.C.M.; Arheimer, B. Using flow signatures and catchment similarities to evaluate the E-HYPE multi-basin model across Europe. Hydrol. Sci. J. 2016, 61, 255–273. [Google Scholar] [CrossRef]
- Westerberg, I.K.; Wagener, T.; Coxon, G.; McMillan, H.K.; Castellarin, A.; Montanari, A.; Freer, J. Uncertainty in hydrological signatures for gauged and ungauged catchments. Water Resour. Res. 2016, 52, 1847–1865. [Google Scholar] [CrossRef]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments; Report RHO 7; Swedish Meteorological and Hydrological Institute: Norrkoping, Sweden, 1976; 134p.
- Lindström, G.; Bergström, S. Improving the HBV and PULSE-models by use of temperature anomalies. Vannet i Norden 1992, 25, 16–23. [Google Scholar]
- Seibert, J. Estimation of Parameter Uncertainty in the HBV Model. Nord. Hydrol. 1997, 28, 247–262. [Google Scholar] [CrossRef]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Dai, X.; Yuan, X.; Zhang, Z. A self-adaptive multi-objective harmony search algorithm based on harmony memory variance. Appl. Soft Comput. J. 2015, 35, 541–557. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Wang, H.; Jiao, L.; Yao, X. Two_Arch2: An Improved Two-Archive Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2014, 19, 524–541. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. A limits of acceptability approach to model evaluation and uncertainty estimation in flood frequency estimation by continuous simulation: Skalka catchment, Czech Republic. Water Resour. Res. 2009, 45, W00B16. [Google Scholar] [CrossRef]
- Komuro, R.; Ford, E.D.; Reynolds, J.H. The use of multi-criteria assessment in developing a process model. Ecol. Modell. 2006, 197, 320–330. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.H.; Wang, D.; Zhang, X. Multi-period calibration of a semi-distributed hydrological model based on hydroclimatic clustering. Adv. Water Resour. 2011, 34, 1292–1303. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Madsen, H. Automatic calibration of a conceptual rainfall-runoff model using multiple objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S. Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods. Water Resour. Res. 2000, 36, 3663–3674. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Dogulu, N.; López López, P.; Solomatine, D.P.; Weerts, A.H.; Shrestha, D.L. Estimation of predictive hydrologic uncertainty using the quantile regression and UNEEC methods and their comparison on contrasting catchments. Hydrol. Earth Syst. Sci. 2015, 19, 3181–3201. [Google Scholar] [CrossRef]




| Symbol | Hydrological Signature | Equation | Comments | References |
|---|---|---|---|---|
| High-flow segment volume of the flow duration curve | are the indices of high flows; their probability of exceedance is <0.02 | [51] | ||
| Low-flow segment volume of the flow duration curve | are the indices of low flows; their probability of exceedance is between 0.7 and 1.0 (L is the minimum flow index) | [51] | ||
| Medium-flow segment of the flow duration curve | and are the lowest and highest flow exceedance probabilities within the mid-segment of FDC (0.2 and 0.7, respectively, in this study) | [51] | ||
| Baseflow index | is the filtered surface runoff at t time-step, is the total flow (original streamflow) at t time-step, is the baseflow at t time-step, is the filter parameter (0.925), is the baseflow index, and is the total time steps of the study period | [20,52] | ||
| Runoff ratio | is the runoff ratio, is the long-term average streamflow, and is the long-term precipitation | [20,49,51] | ||
| Rising limb density | is rising limbs(number of peaks of the hydrograph) and is the total time that the hydrograph is rising | [13,20,49,53] | ||
| Stream flow elasticity | is the proportional change in the streamflow, is the proportional change in precipitation, and are streamflow and precipitation, respectively, at t time-step, and and are the mean of streamflow and precipitation, respectively, in the long-term | [20,54] | ||
| Mean discharge | is the streamflow at t time-step and is total time steps of the study period | [29,55,56] | ||
| Median discharge | [29] | |||
| Discharge variance | is the streamflow at t time-step, is the mean of the streamflow, and is the total time steps of the study period | [29] | ||
| Peak discharge | is the peak of the streamflow data | [29] |
| Dataset | Date (from–to) | Number of Data Records |
|---|---|---|
| FD | 1 September 1993 00:00–31 December 1996 23:00 | 29,232 |
| Validation dataset | 1 June 1997 01:00–30 June 1998 23:00 | 9478 |
| Scenario 1 | ||
| 75% FRD | 1 September 1993 00:00–2 March 1996 11:00 | 21,924 |
| 50% FRD | 1 September 1993 00:00–2 May 1995 22:00 | 14,615 |
| 25% FRD | 1 September 1993 00:00–2 July 1994 11:00 | 7308 |
| 10% FRD | 1 September 1993 00:00–31 December 1993 23:00 | 2928 |
| 5% FRD | 1 September 1993 00:00–31 October 1993 21:00 | 1462 |
| Scenario 2 | ||
| 75% FRD | 31 January 1994 05:00–1 August 1996 17:00 | 21,924 |
| 50% FRD | 2 July 1994 10:00–2 March 1996 11:00 | 14,615 |
| 25% FRD | 1 December 1994 15:00–2 October 1995 05:00 | 7308 |
| 10% FRD | 2 March 1995 22:00–2 July 1995 21:00 | 2928 |
| 5% FRD | 2 April 1995 08:00–2 June 1995 10:00 | 1462 |
| Scenario 3 | ||
| Dry-period dataset | 1 June 1994 00:00–1 August 1994 23:00 | 1488 |
| Scenario 4 | ||
| Wet-period dataset | 27 December 1994 10:00–1 February 1995 13:00 | 868 |
| Parameter | Explanation | Unit |
|---|---|---|
| Precipitation Routine | ||
| LTT | Lower temperature threshold | °C |
| UTT | Upper temperature threshold | °C |
| RFCF | Rainfall corrector factor | — |
| SFCF | Snowfall corrector factor | — |
| Snow Routine | ||
| CFMAX | Day degree factor | mm °C−1 h−1 |
| TTM | The temperature threshold for melting | °C |
| CFR | Refreezing factor | — |
| CWH | Water holding capacity | — |
| Soil and Evaporation Routine | ||
| FC | Maximum soil moisture | Mm |
| ETF | Total potential evapotranspiration | mm h−1 |
| LP | Soil moisture threshold for evaporation reduction (wilting point) | — |
| E_CORR | Evapotranspiration corrector factor | — |
| BETA | Shape coefficient | — |
| C_FLUX | Capillary flux in the root zone | mm h−1 |
| Response Routine | ||
| K | Upper zone recession coefficient | h−1 |
| K1 | Lower zone recession coefficient | h−1 |
| PERC | Maximum percolation rate from the upper to the lower tank | mm h−1 |
| ALPHA | Response box parameter | — |
| Routing Routine | ||
| MAXBAS | Routing, length of weighting function | H |
| Symbol | Description | Formula | Optimal Value | References |
|---|---|---|---|---|
| NSE | Nash–Sutcliffe efficiency | 1 | [17,49,67,68] | |
| RMSE | Root mean square error | 0 | [15,49,69,70] | |
| PBIAS | Percent bias (relative volume error) | 0 | [17,67,71] |
| Dataset | NSE | RMSE | PBIAS | |||
|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | Calibration | Validation | |
| Scenario 1 | ||||||
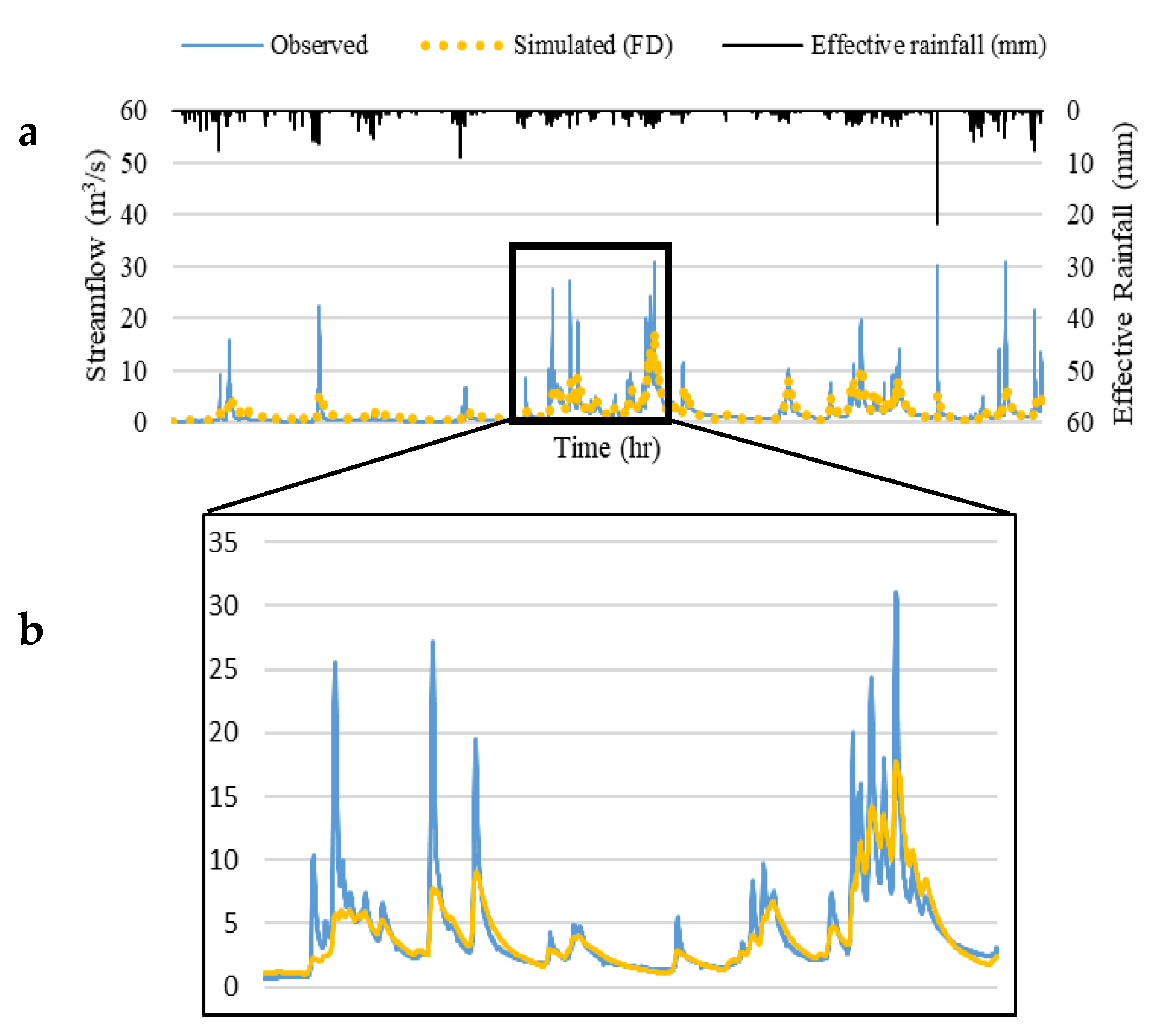
| FD | 0.87 | 0.77 | 1.14 | 1.7 | 9.16 | 10.2 |
| 75% FRD | 0.87 | 0.77 | 1.25 | 1.6 | 8.9 | 10.73 |
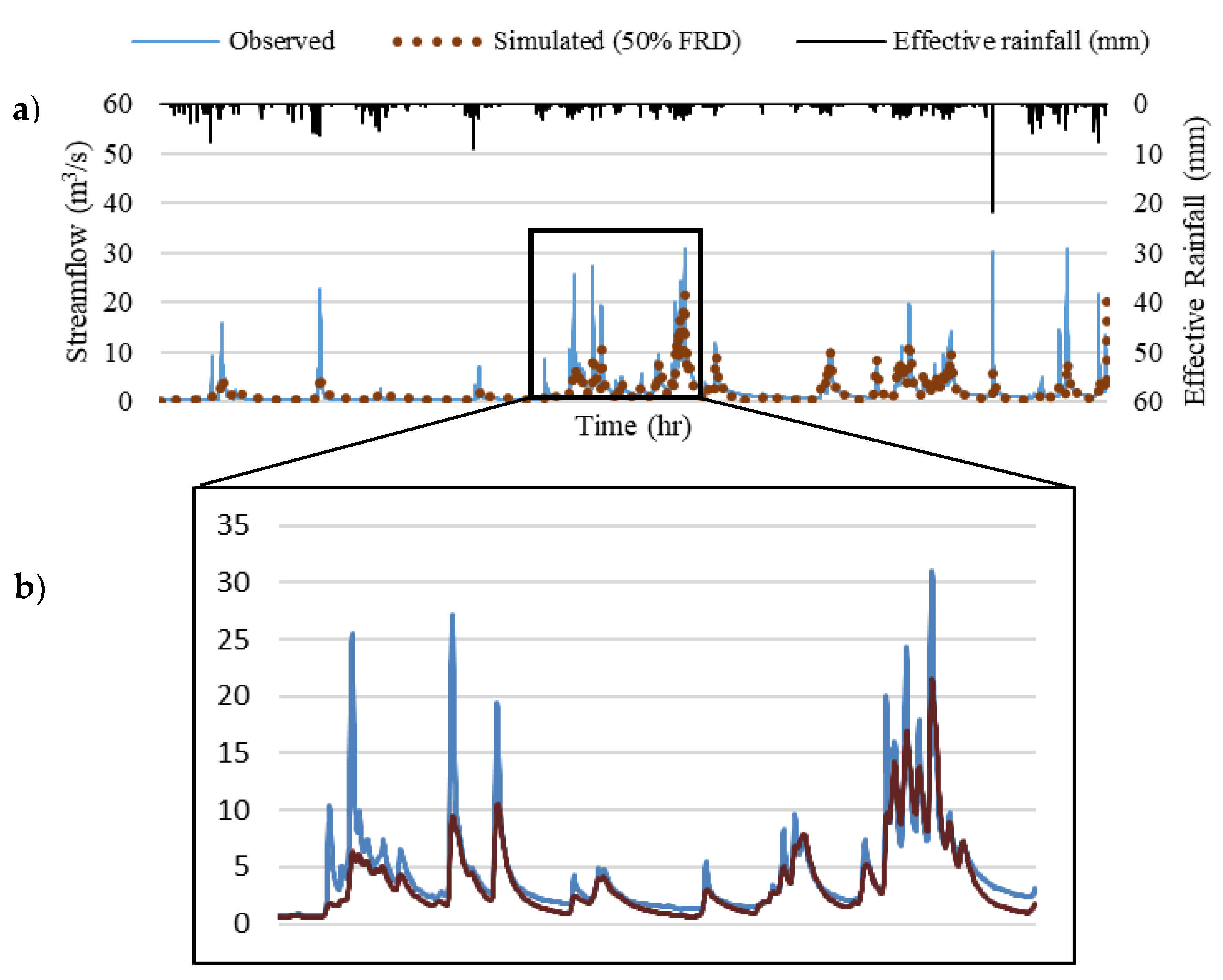
| 50% FRD | 0.89 | 0.81 | 1.31 | 1.52 | 8.42 | 9.61 |
| 25% FRD | 0.89 | 0.85 | 1.28 | 1.5 | 8.81 | −3.16 |
| 10% FRD | 0.94 | 0.82 | 1.14 | 1.51 | 10.03 | −7.78 |
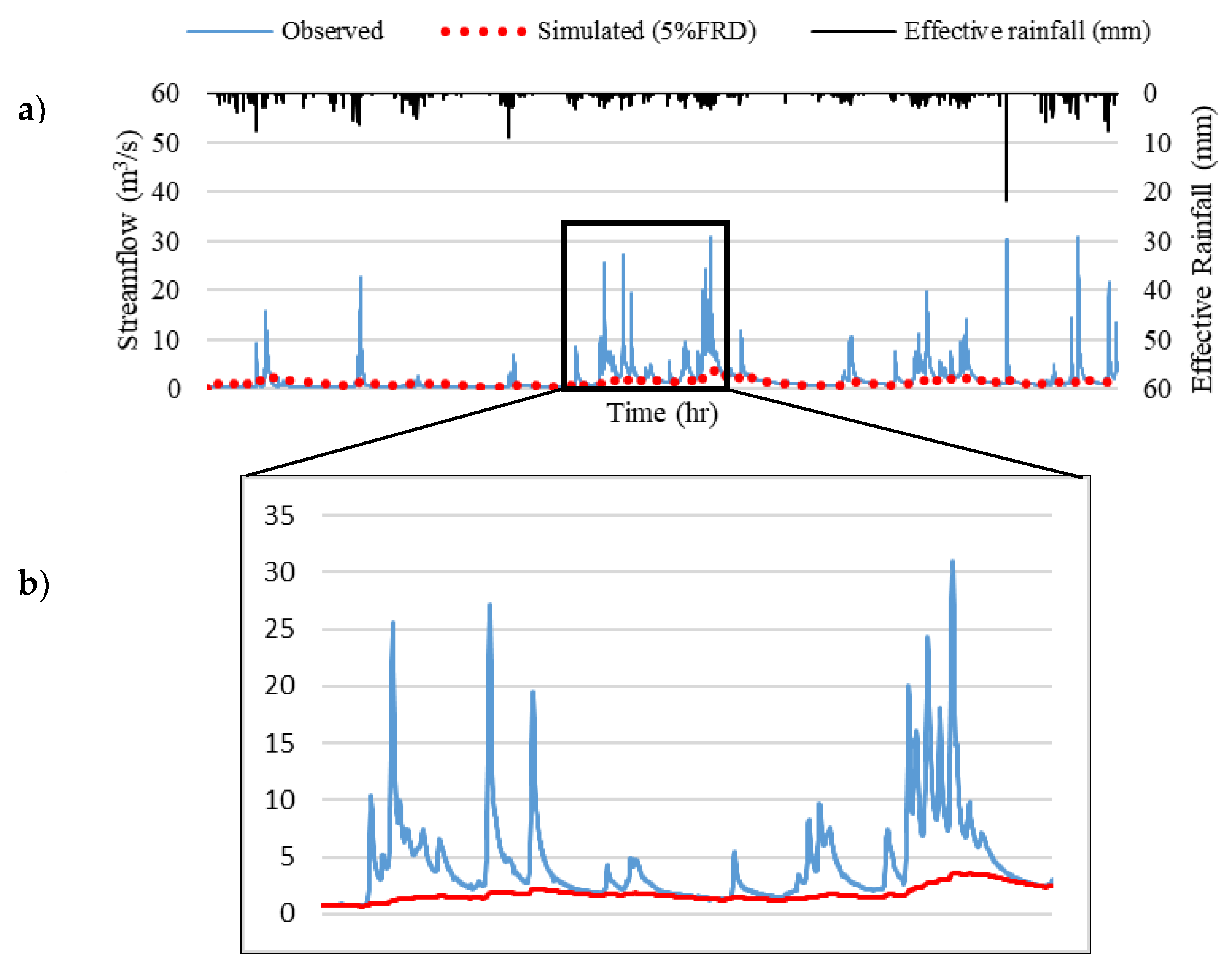
| 5% FRD | 0.96 | 0.01 | 0.96 | 5.65 | 1.2 | −106.47 |
| Scenario 2 | ||||||
| FD | 0.87 | 0.7 | 1.12 | 1.35 | 7.5 | 11.2 |
| 75% FRD | 0.87 | 0.72 | 1.09 | 1.3 | 7.33 | 10.24 |
| 50% FRD | 0.9 | 0.69 | 1.02 | 1.8 | 7.63 | 15.98 |
| 25% FRD | 0.84 | 0.78 | 1.3 | 1.34 | 15.44 | 5.96 |
| 10% FRD | 0.86 | 0.69 | 0.41 | 1.6 | 6.92 | −22.64 |
| 5% FRD | 0.52 | 0.1 | 0.25 | 2.8 | −0.24 | −37.1 |
| Scenario 3 | ||||||
| Dry-period dataset | 0.72 | 0.18 | 0.1 | 2.65 | 6.58 | −36 |
| Scenario 4 | ||||||
| Wet-period dataset | 0.86 | 0.57 | 2 | 1.75 | 6.19 | 25.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, S.A.; Solomatine, D.P.; Hrachowitz, M.; Hamouda, M.A. Impact of Dataset Size on the Signature-Based Calibration of a Hydrological Model. Water 2021, 13, 970. https://doi.org/10.3390/w13070970
Mohammed SA, Solomatine DP, Hrachowitz M, Hamouda MA. Impact of Dataset Size on the Signature-Based Calibration of a Hydrological Model. Water. 2021; 13(7):970. https://doi.org/10.3390/w13070970
Chicago/Turabian StyleMohammed, Safa A., Dimitri P. Solomatine, Markus Hrachowitz, and Mohamed A. Hamouda. 2021. "Impact of Dataset Size on the Signature-Based Calibration of a Hydrological Model" Water 13, no. 7: 970. https://doi.org/10.3390/w13070970
APA StyleMohammed, S. A., Solomatine, D. P., Hrachowitz, M., & Hamouda, M. A. (2021). Impact of Dataset Size on the Signature-Based Calibration of a Hydrological Model. Water, 13(7), 970. https://doi.org/10.3390/w13070970