Vine-Copula-Based Quantile Regression for Cascade Reservoirs Management
Abstract
1. Introduction
2. Materials and Methods
2.1. Copulas
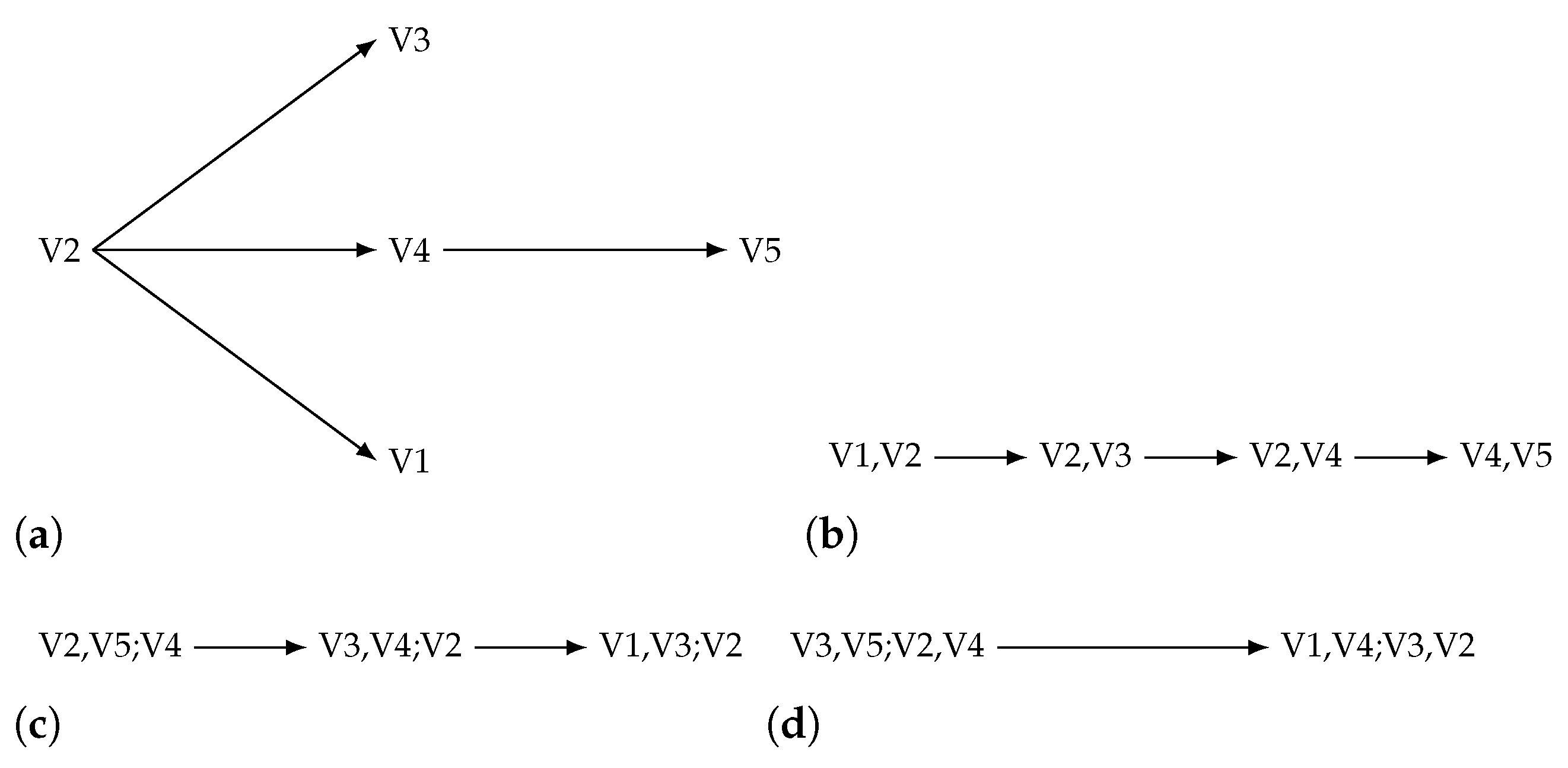
2.2. R-Vines
- .
- is a tree with nodes and a set of edges denoted .
- For , is a tree with nodes and edge set .
2.3. R-Vine Copulas
- Selection of vine R (structure), i.e., selection of unconditioned and conditioned pairs to be used.
- Choice of a family of bivariate copula for each pair selected in the previous step.
- Estimation of the corresponding parameter(s) for each copula.
2.4. Quantile Regression
3. Results
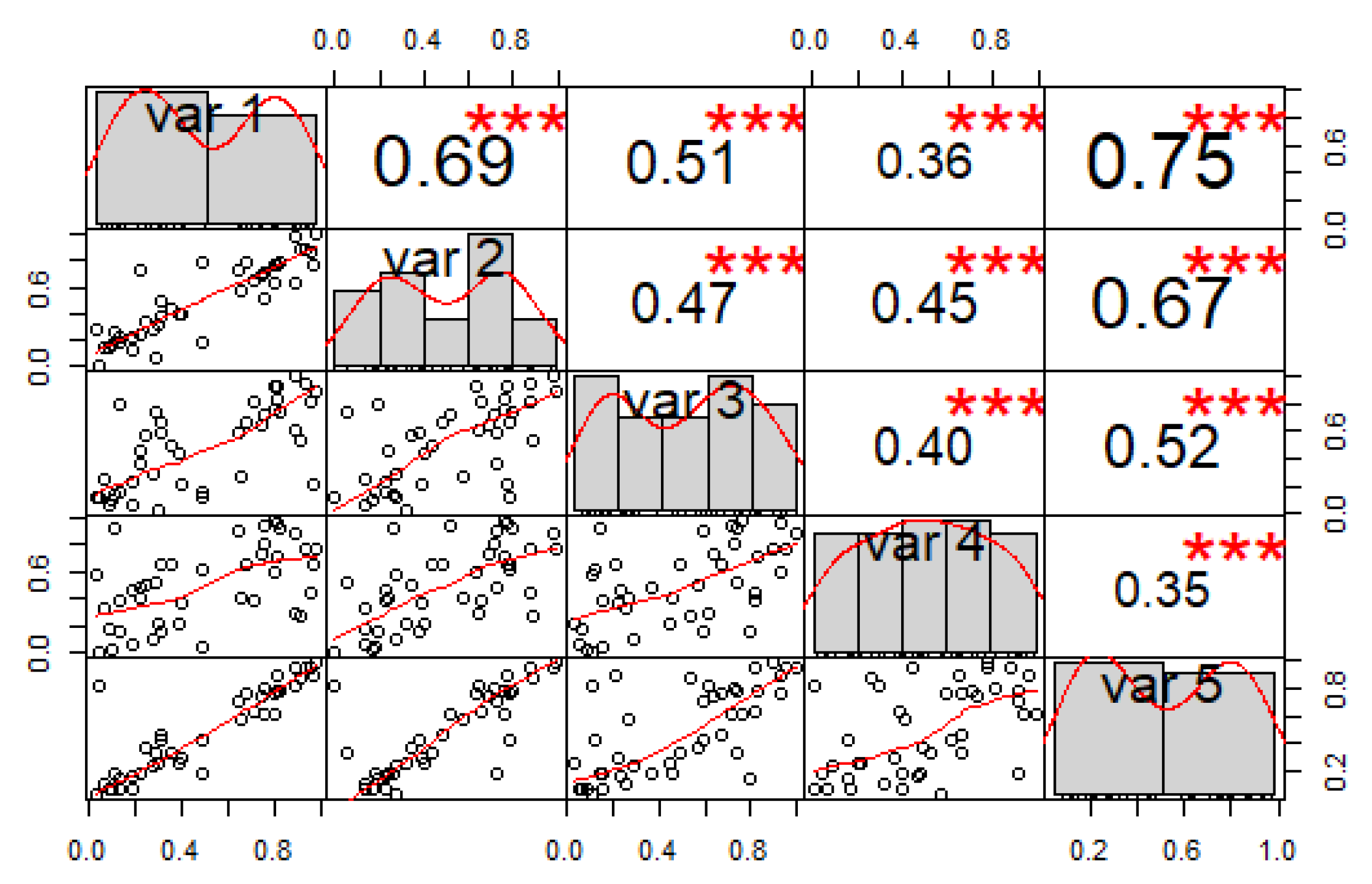
3.1. Data
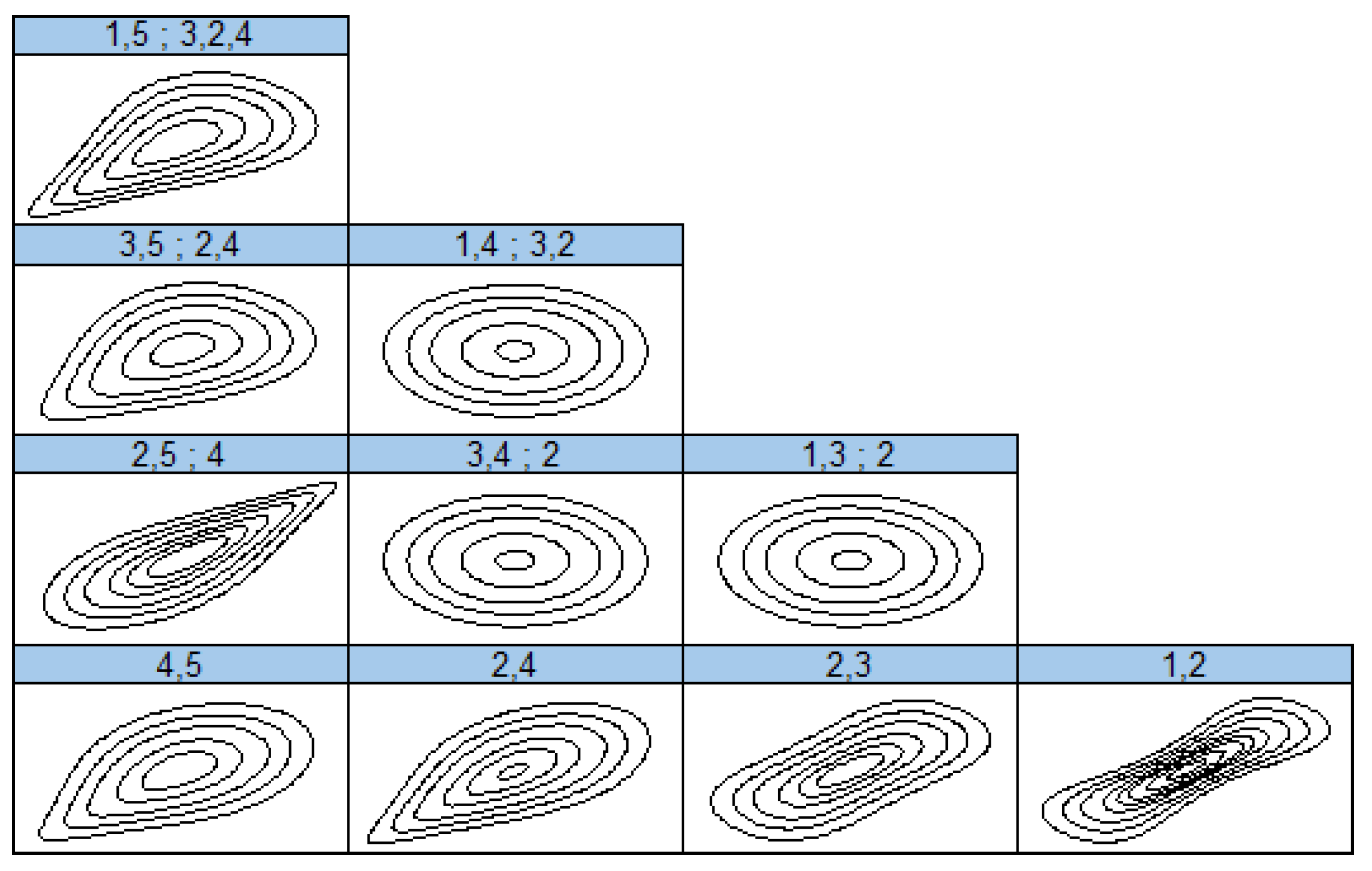
3.2. The New R-Vine
3.3. Quantile Regression
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
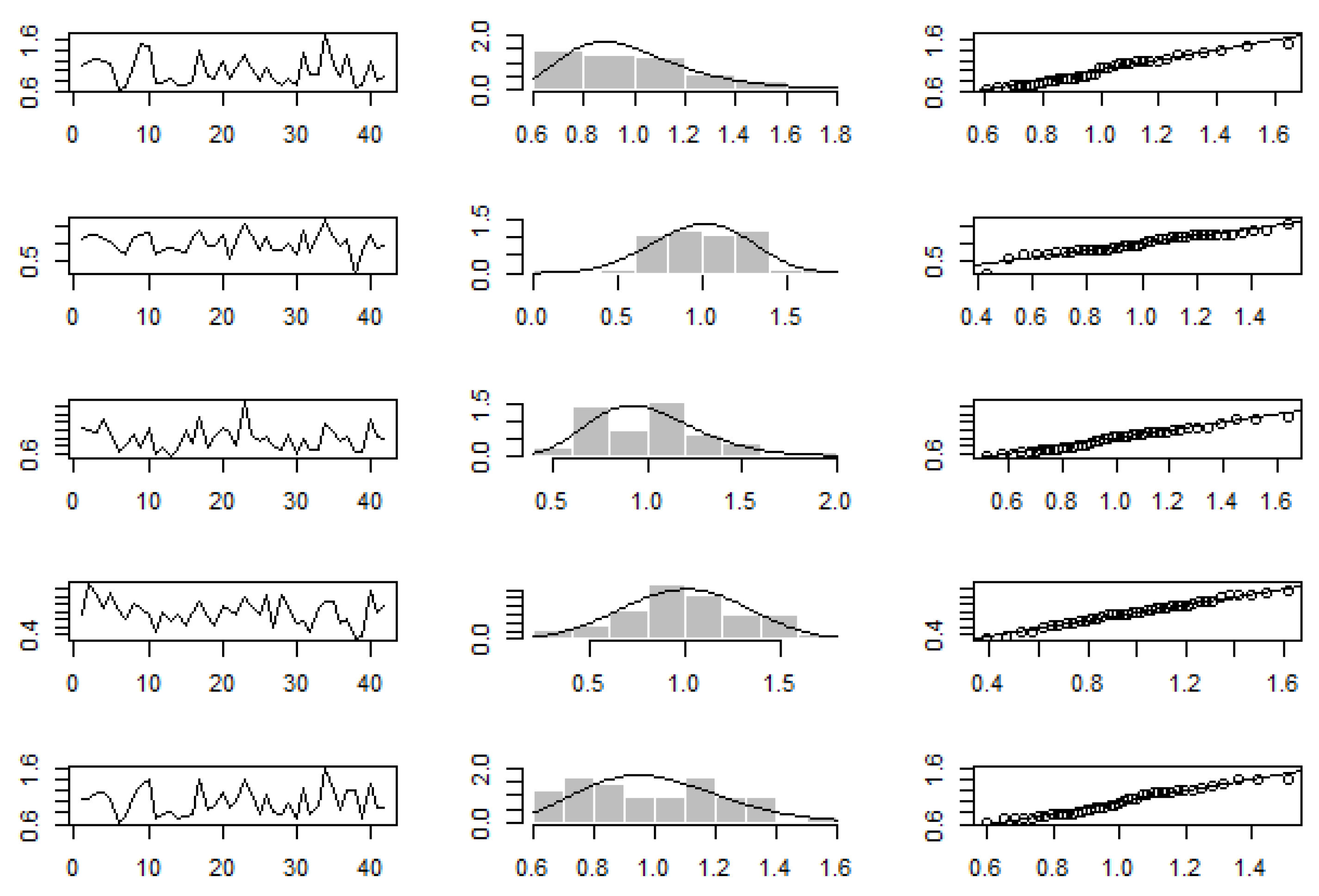
Appendix B
References
- Oliveira, R.; Loucks, D.P. Operating rules for multireservoir systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Young, G.K. Finding reservoir operating rules. J. Hydraul. Div. 1967, 93, 297–322. [Google Scholar] [CrossRef]
- Celeste, A.B.; Billib, M. Evaluation of stochastic reservoir operation optimization models. Adv. Water Resour. 2009, 32, 1429–1443. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Wang, X.; Lei, X.; Liu, P.; Feng, M.; Khu, S.T.; Wang, H. A novel method for deriving reservoir operating rules based on flood classification-aggregation-decomposition. J. Hydrol. 2019, 568, 722–734. [Google Scholar] [CrossRef]
- Li, L.; Liu, P.; Rheinheimer, D.E.; Deng, C.; Zhou, Y. Identifying explicit formulation of operating rules for multi-reservoir systems using genetic programming. Water Resour. Manag. 2014, 28, 1545–1565. [Google Scholar] [CrossRef]
- Liu, P.; Guo, S.; Xu, X.; Chen, J. Derivation of aggregation-based joint operating rule curves for cascade hydropower reservoirs. Water Resour. Manag. 2011, 25, 3177–3200. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G. A generalized Pareto intensity-duration model of storm rainfall exploiting 2-copulas. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G. Copula based multisite model for daily precipitation simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef]
- Samaniego, L.; Bárdossy, A.; Kumar, R. Streamflow prediction in ungauged catchments using copula-based dissimilarity measures. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- De Luca, D.L.; Biondi, D. Bivariate return period for design hyetograph and relationship with t-year design flood peak. Water 2017, 9, 673. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Vines: A new graphical model for dependent random variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Joe, H.; Kurowicka, D. Dependence Modeling: Vine Copula Handbook; World Scientific: Vancouver, BC, Canada, 2011. [Google Scholar]
- Brechmann, E.C.; Hendrich, K.; Czado, C. Conditional copula simulation for systemic risk stress testing. Insur. Math. Econ. 2013, 53, 722–732. [Google Scholar] [CrossRef]
- Krouthén, J. Extreme Joint Dependencies with Copulas. A New Approach for the Structure of C-Vines. Master’s Thesis, Department of Mathematics, Uppsala University, Uppsala, Sweden, 2015. [Google Scholar]
- Geidosch, M.; Fischer, M. Application of vine copulas to credit portfolio risk modeling. J. Risk Financ. Manag. 2016, 9, 4. [Google Scholar] [CrossRef]
- Bevacqua, E.; Maraun, D.; Hobæk Haff, I.; Widmann, M.; Vrac, M. Multivariate statistical modelling of compound events via pair-copula constructions: Analysis of floods in Ravenna (Italy). Hydrol. Earth Syst. Sci. 2017, 21, 2701–2723. [Google Scholar] [CrossRef]
- Fink, H.; Klimova, Y.; Czado, C.; Stöber, J. Regime switching vine copula models for global equity and volatility indices. Econometrics 2017, 5, 3. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y. Copula-based daily rainfall disaggregation model. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Erhardt, T.M.; Czado, C.; Schepsmeier, U. R-vine models for spatial time series with an application to daily mean temperature. Biometrics 2015, 71, 323–332. [Google Scholar] [CrossRef] [PubMed]
- Vernieuwe, H.; Vandenberghe, S.; De Baets, B.; Verhoest, N. A continuous rainfall model based on vine copulas. Hydrol. Earth Syst. Sci. 2015, 19, 2685–2699. [Google Scholar] [CrossRef]
- Musafer, G.N.; Thompson, M.H. Non-linear optimal multivariate spatial design using spatial vine copulas. Stoch. Environ. Res. Risk Assess. 2017, 31, 551–570. [Google Scholar] [CrossRef]
- Pereira, G.; Veiga, A. PAR (p)-vine copula based model for stochastic streamflow scenario generation. Stoch. Environ. Res. Risk Assess. 2018, 32, 833–842. [Google Scholar] [CrossRef]
- Gómez, M.; Ausín, M.C.; Domínguez, M.C. Vine copula models for predicting water flow discharge at King George Island, Antarctica. Stoch. Environ. Res. Risk Assess. 2018, 32, 2787–2807. [Google Scholar] [CrossRef]
- Avila, L.; Miriam, R.; Kaviski, E. Probabilistic long-term reservoir operation employing copulas and implicit stochastic optimization. Stoch. Environ. Res. Risk Assess. 2020, 34, 931–947. [Google Scholar] [CrossRef]
- Nápoles, O.M. Bayesian Belief Nets and Vines in Aviation Safety and other Applications. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2009. [Google Scholar]
- Pereira, G.; Veiga, A.; Erhardt, T.; Czado, C. Spatial R-vine copula for streamflow scenario simulation. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar]
- Hernandez, J.A. Vine Copula Modelling of Dependence and Portfolio Optimization with Application to Mining and Energy Stock Return Series from the Australian Market. Ph.D. Thesis, Edith Cowan University, Perth, Australia, 2015. [Google Scholar]
- Cooke, R.M.; Joe, H.; Chang, B. Vine regression. In Resources for the Future Discussion Paper; RFF: Washington, DC, USA, 2015; pp. 15–52. [Google Scholar]
- Kraus, D.; Czado, C. D-vine copula based quantile regression. Comput. Stat. Data Anal. 2017, 110, 1–18. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Portland, OR, USA, 2007. [Google Scholar]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Dißmann, J.F. Statistical Inference for Regular Vines and Application. Diploma Thesis, Zentrum Mathematik, Technische Universita¨t Mu¨nchen, Mu¨nchen, Germany, 2010. [Google Scholar]
- Bedford, T.; Cooke, R.M. Probability density decomposition for conditionally dependent random variables modeled by vines. Ann. Math. Artif. Intell. 2001, 32, 245–268. [Google Scholar] [CrossRef]
- Joe, H. Families of m-Variate Distributions with Given Margins and m (m-1)/2 Bivariate Dependence Parameters; Lecture Notes-Monograph Series; Institute of Mathematical Statistics: Hayward, ON, Canada, 1996; pp. 120–141. [Google Scholar]
- Czado, C. Analyzing Dependent Data with Vine Copulas; Lecture Notes in Statistics; Springer: Garching, Germany, 2019. [Google Scholar]
- Dissmann, J.; Brechmann, E.C.; Czado, C.; Kurowicka, D. Selecting and estimating regular vine copulae and application to financial returns. Comput. Stat. Data Anal. 2013, 59, 52–69. [Google Scholar] [CrossRef]
- Czado, C.; Jeske, S.; Hofmann, M. Selection strategies for regular vine copulae. J. Société Française Stat. 2013, 154, 174–191. [Google Scholar]
- Singh, V.P. Entropy Theory and Its Application in Environmental and Water Engineering; John Wiley & Sons: Carrllton, TX, USA, 2013. [Google Scholar]
- Alina, B. Copula Modeling for World’s Biggest Competitors. Master’s Thesis, Amsterdam School of Economics, Universiteit Van Amsterdam, Amsterdam, The Netherlands, 2018. [Google Scholar]
- Chang, B.; Joe, H. Prediction based on conditional distributions of vine copulas. Comput. Stat. Data Anal. 2019, 139, 45–63. [Google Scholar] [CrossRef]
- El Adlouni, S. Quantile regression C-vine copula model for spatial extremes. Nat. Hazards 2018, 94, 299–317. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on a multivariate transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]
- Schepsmeier, U. Efficient information based goodness-of-fit tests for vine copula models with fixed margins: A comprehensive review. J. Multivar. Anal. 2015, 138, 34–52. [Google Scholar] [CrossRef]
- Newton, B.; Burrell, B.C. The April–May 2008 flood event in the Saint John River Basin: Causes, assessment and damages. Can. Water Resour. J./Rev. Can. Des Ressour. Hydr. 2016, 41, 118–128. [Google Scholar] [CrossRef]
- El-Jabi, N.; Rousselle, J. Hydrologie Fondamentale; Éditions de l’École Polytechnique de Montréal: Montréal, QC, Canada, 1987. [Google Scholar]
- Mediero, L.; Jiménez-Álvarez, A.; Garrote, L. Design flood hydrographs from the relationship between flood peak and volume. Hydrol. Earth Syst. Sci. 2010, 14, 2495. [Google Scholar] [CrossRef]
- Pramanik, N.; Panda, R.K.; Sen, D. Development of design flood hydrographs using probability density functions. Hydrol. Process. Int. J. 2010, 24, 415–428. [Google Scholar] [CrossRef]
- Langat, P.K.; Kumar, L.; Koech, R. Identification of the most suitable probability distribution models for maximum, minimum, and mean streamflow. Water 2019, 11, 734. [Google Scholar] [CrossRef]
- Perreault, L.; Bobée, B. Loi Généralisée des Valeurs Extrêmes: Propriétés Mathématiques et Statistiques: Estimation des Paramètres et des Quantiles XT de période de Retour T; Number R350; INRS-Eau: Québec, QC, Canada, 1992. [Google Scholar]
- Vuong, Q.H. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 1989, 57, 307–333. [Google Scholar] [CrossRef]
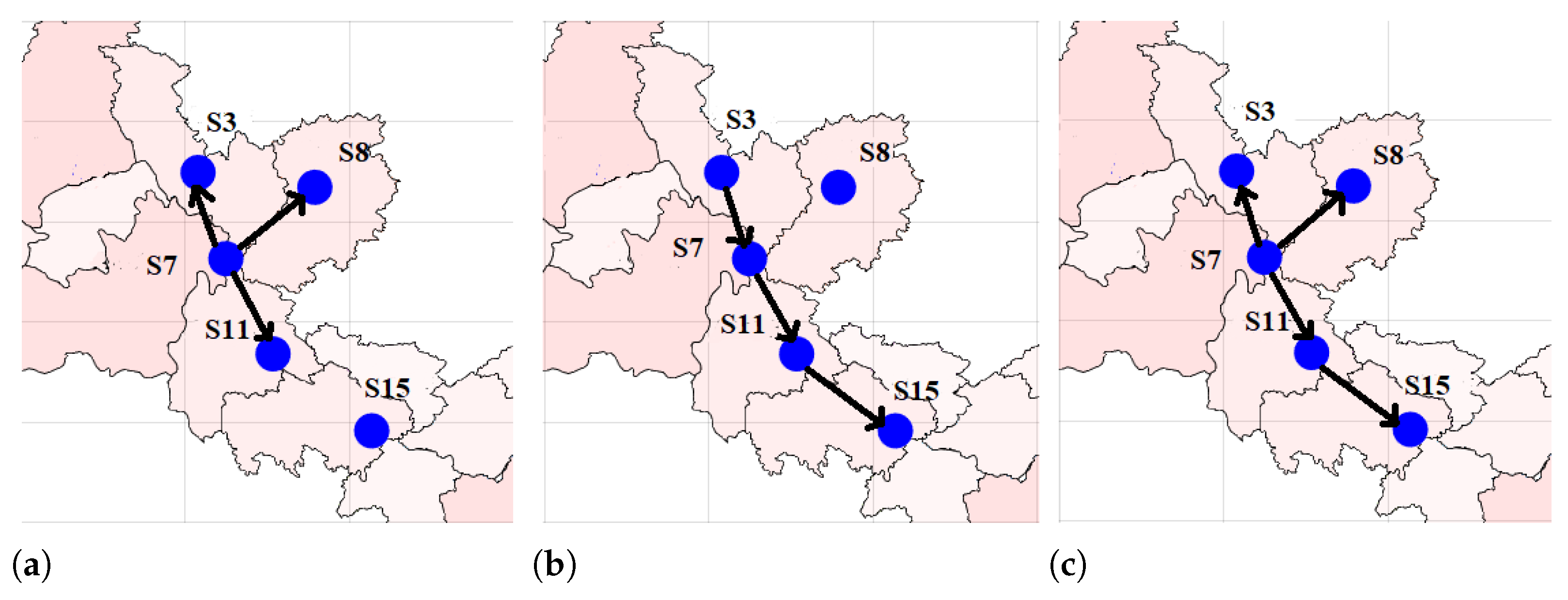
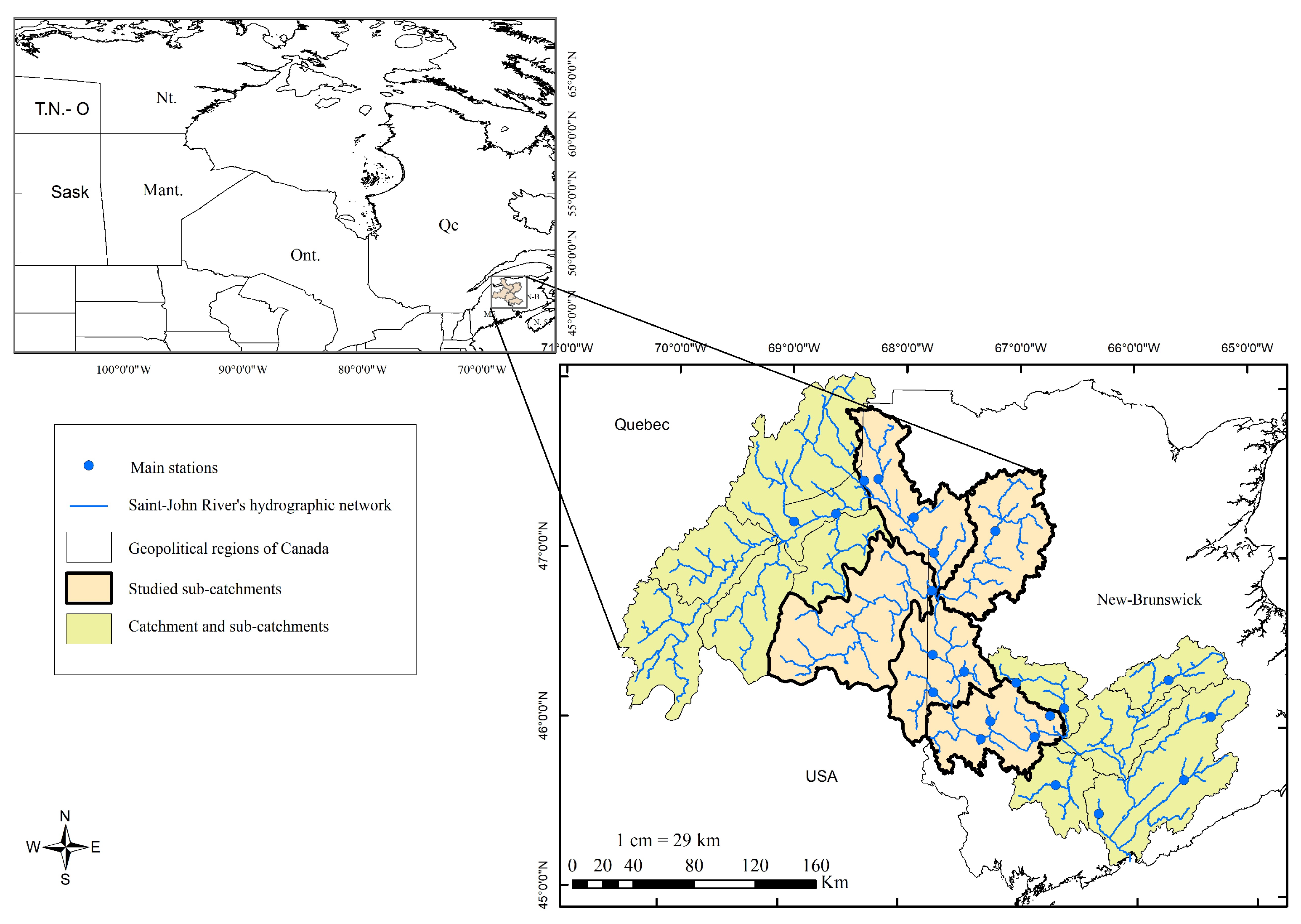
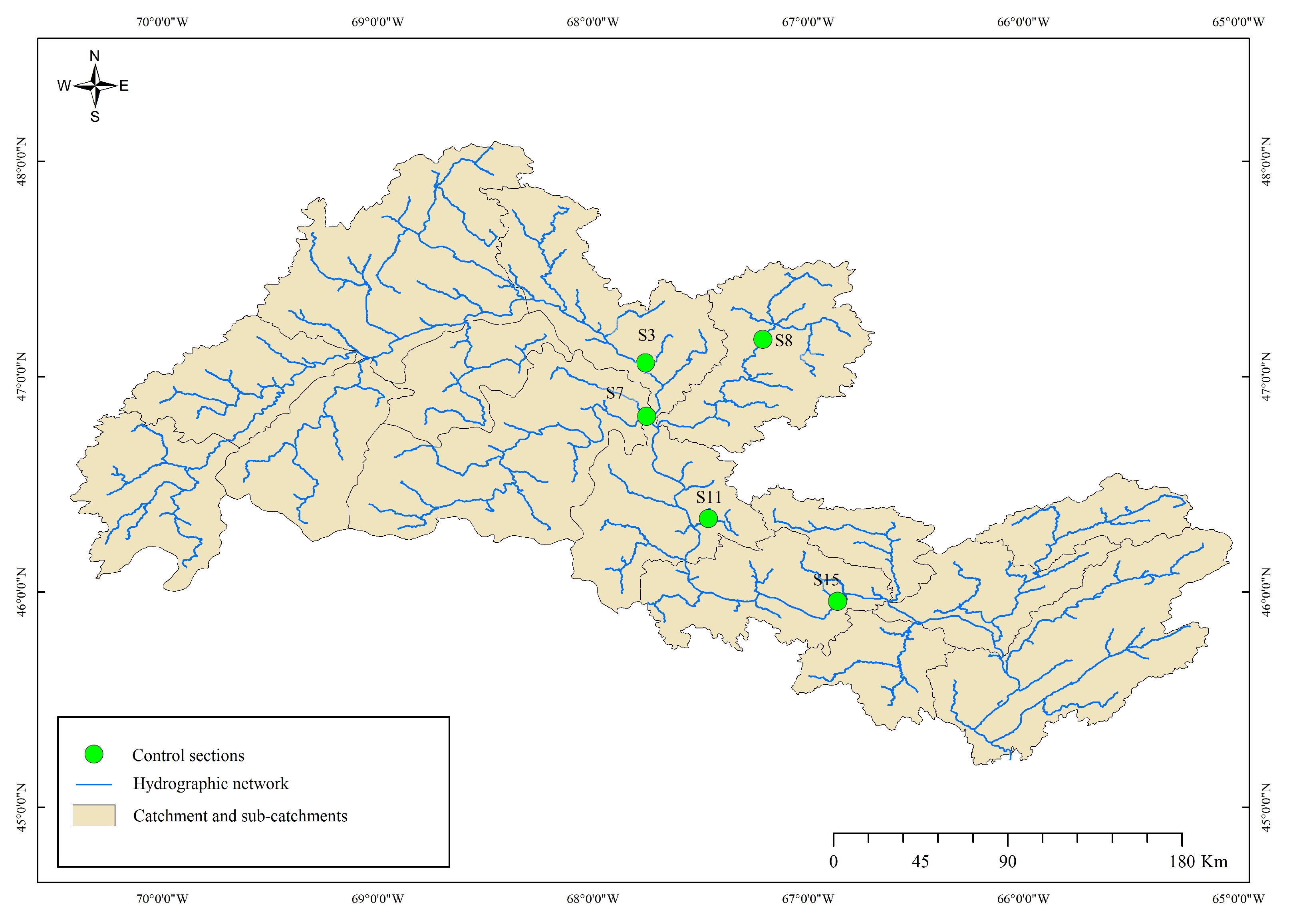
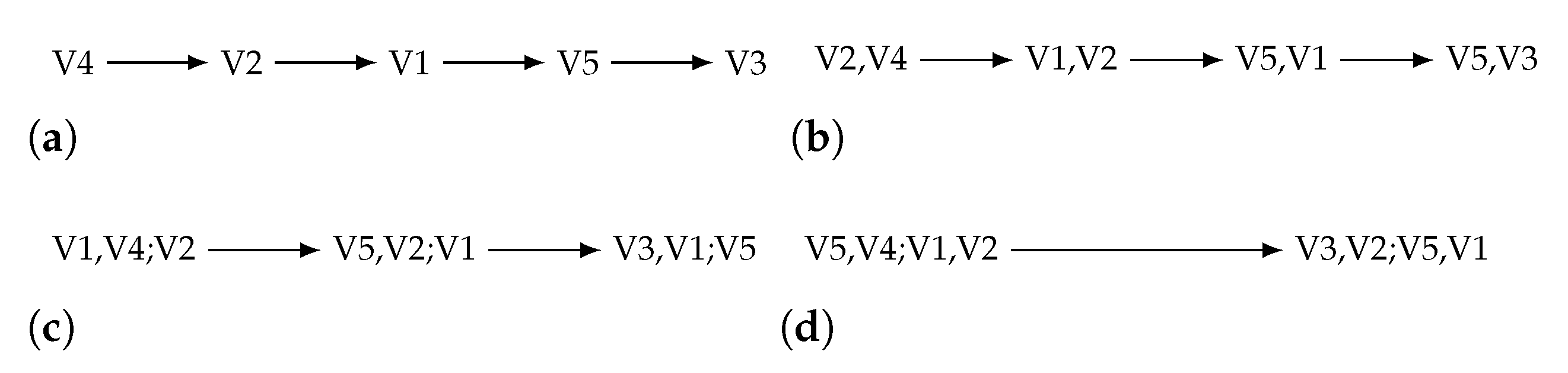
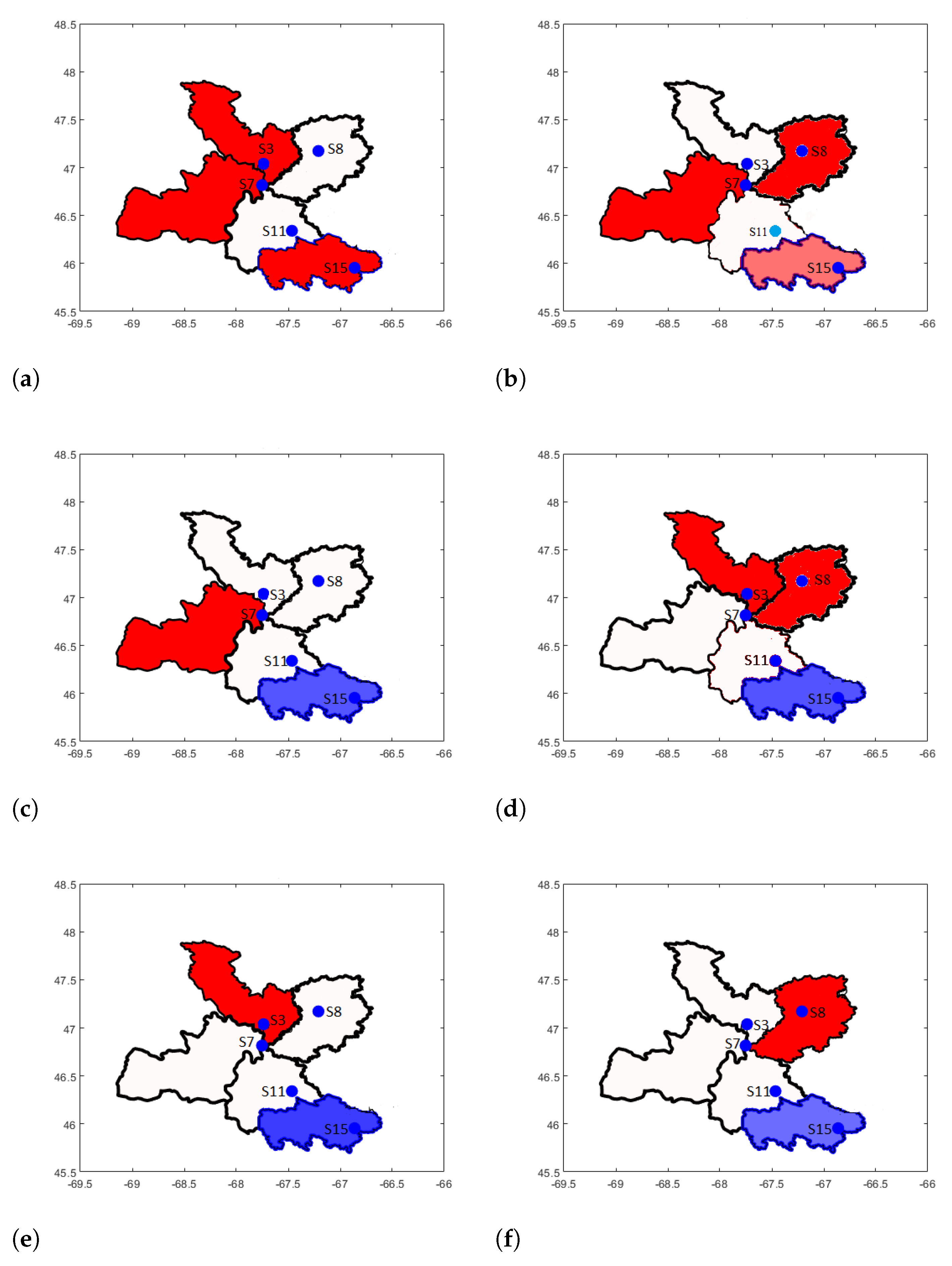
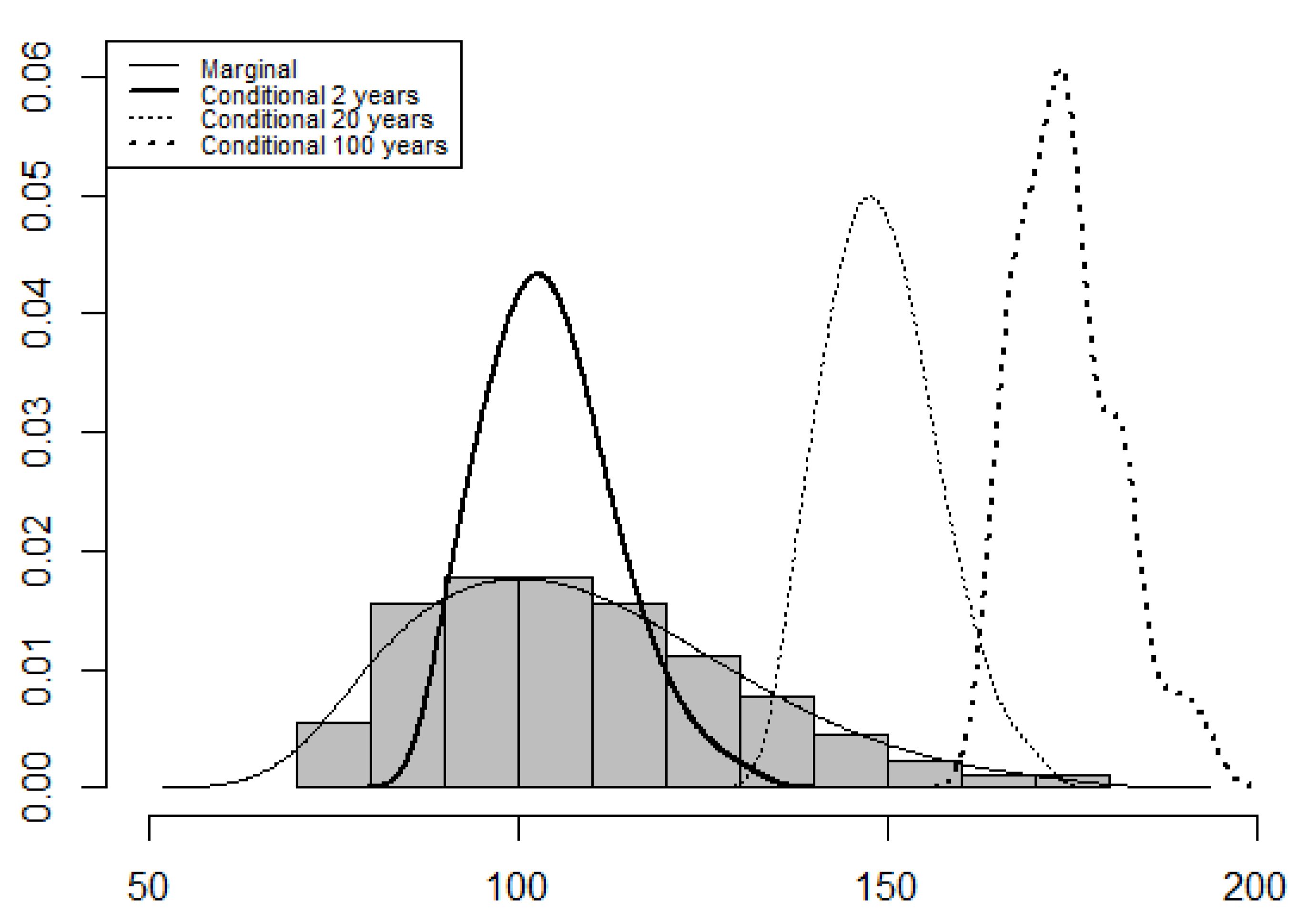
| Station | Code | Name | River | Drainage Area (km) |
|---|---|---|---|---|
| S3 | FX01AF002 | Grand Falls | Saint John | 21,900 |
| S7 | FX01AG003 | Tinker | Aroostook | 6060 |
| S8 | FX01AH002 | Riley Brook | Tobique | 2230 |
| S11 | FX01AJ010 | Coldstream | Becaguimec stream | 350 |
| S15 | FX01AK010 | Mactaquac Generating Station | Saint John | 39,900 |
| Variable | Station | Distribution | Parameter 1 | Parameter 2 | Box-Ljung Test |
|---|---|---|---|---|---|
| 3 | Gumbel | 0.2054731 | 0.8775550 | 0.5819 | |
| 7 | Weibull | 3.956469 | 1.100047 | 0.2502 | |
| Volume | 8 | Gamma | 12.26178 | 12.26174 | 0.6783 |
| 11 | Weibull | 3.498557 | 1.111809 | 0.864 | |
| 15 | Gamma | 18.47347 | 18.47331 | 0.778 | |
| 3 | Gumbel | 0.2391086 | 0.8574496 | 0.6619 | |
| 7 | Gumbel | 0.2508672 | 0.8574092 | 0.2957 | |
| Peak flow | 8 | Gumbel | 0.2432496 | 0.8625942 | 0.3618 |
| 11 | Gumbel | 0.2801832 | 0.8363660 | 0.365 | |
| 15 | Gumbel | 0.2201248 | 0.8738290 | 0.2701 |
| Tree | Edge | Copula | Volume Parameter | K-Tau | Copula | Peak Flow Parameter | K-Tau |
|---|---|---|---|---|---|---|---|
| 1 | 4,5 | Sur Gumbel | 1.45 | 0.31 | Sur Gumbel | 1.42 | 0.30 |
| 2,4 | Sur Gumbel | 1.65 | 0.39 | Sur Gumbel | 1.58 | 0.37 | |
| 2,3 | Frank | 5.38 | 0.48 | Gumbel | 1.50 | 0.34 | |
| 1,2 | Frank | 11.21 | 0.70 | Gumbel | 2.12 | 0.53 | |
| 2 | 2,5;4 | Gumbel | 2.13 | 0.53 | Gumbel | 3.34 | 0.70 |
| 3,4;2 | I | - | 0.00 | I | - | 0.00 | |
| 1,3;2 | I | - | 0.00 | I | - | 0.00 | |
| 3 | 3,5;2,4 | Clayton | 0.67 | 0.25 | I | - | 0.00 |
| 1,4;3,2 | I | - | 0.00 | I | - | 0.00 | |
| 4 | 1,5;3,2,4 | Clayton | 1.18 | 0.37 | Gumbel | 1.53 | 0.35 |
| R-N Vine | Volume K-Tau Vine | All-G Vine | R-N Vine | Peak Flow K-Tau Vine | All-G Vine | |
|---|---|---|---|---|---|---|
| MLE | 86.17 | 97.2 | 87.98 | 81.1 | 87.13 | 84.22 |
| AIC | −158.34 | −182.41 | −155.96 | −150.2 | −166.26 | −148.43 |
| BIC | −146.18 | −171.98 | −138.58 | −139.78 | −159.31 | −131.06 |
| Parameters | 7 | 6 | 10 | 6 | 4 | 10 |
| Plain V | −1.59 | −0.30 | −1.48 | −0.78 | ||
| Akaike V | −1.73 | 0.20 | −1.97 | 0.22 | ||
| Schwarz V | −1.86 | 0.63 | −2.39 | 1.09 | ||
| Plain P | 0.11 | 0.77 | 0.14 | 0.44 | ||
| Akaike P | 0.08 | 0.84 | 0.05 | 0.83 | ||
| Schwarz P | 0.06 | 0.53 | 0.02 | 0.28 |
| Scenarios | S 3 | S 7 | S 8 | S 11 | S15 (1000 m) | M. Index | O. Index |
|---|---|---|---|---|---|---|---|
| Scenario 5 | 300.91 | 1.77 | 1.81 | ||||
| Scenario 8 | 166.32 | 0.98 | 1.00 | ||||
| Scenario 7 | 153.73 | 0.90 | 0.92 | ||||
| Scenario 4 | 148.81 | 0.87 | 0.90 | ||||
| Scenario 2 | 145.54 | 0.86 | 0.88 | ||||
| Scenario 6 | 145.22 | 0.85 | 0.87 | ||||
| Scenario 1 | 141.78 | 0.83 | 0.85 | ||||
| Scenario 3 | 139.56 | 0.82 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Hannoun, W.; El Adlouni, S.-E.; Zoglat, A. Vine-Copula-Based Quantile Regression for Cascade Reservoirs Management. Water 2021, 13, 964. https://doi.org/10.3390/w13070964
El Hannoun W, El Adlouni S-E, Zoglat A. Vine-Copula-Based Quantile Regression for Cascade Reservoirs Management. Water. 2021; 13(7):964. https://doi.org/10.3390/w13070964
Chicago/Turabian StyleEl Hannoun, Wafaa, Salah-Eddine El Adlouni, and Abdelhak Zoglat. 2021. "Vine-Copula-Based Quantile Regression for Cascade Reservoirs Management" Water 13, no. 7: 964. https://doi.org/10.3390/w13070964
APA StyleEl Hannoun, W., El Adlouni, S.-E., & Zoglat, A. (2021). Vine-Copula-Based Quantile Regression for Cascade Reservoirs Management. Water, 13(7), 964. https://doi.org/10.3390/w13070964






