Hydroclimatic Variability and Land Cover Transformations in the Central Italian Alps
Abstract
1. Introduction
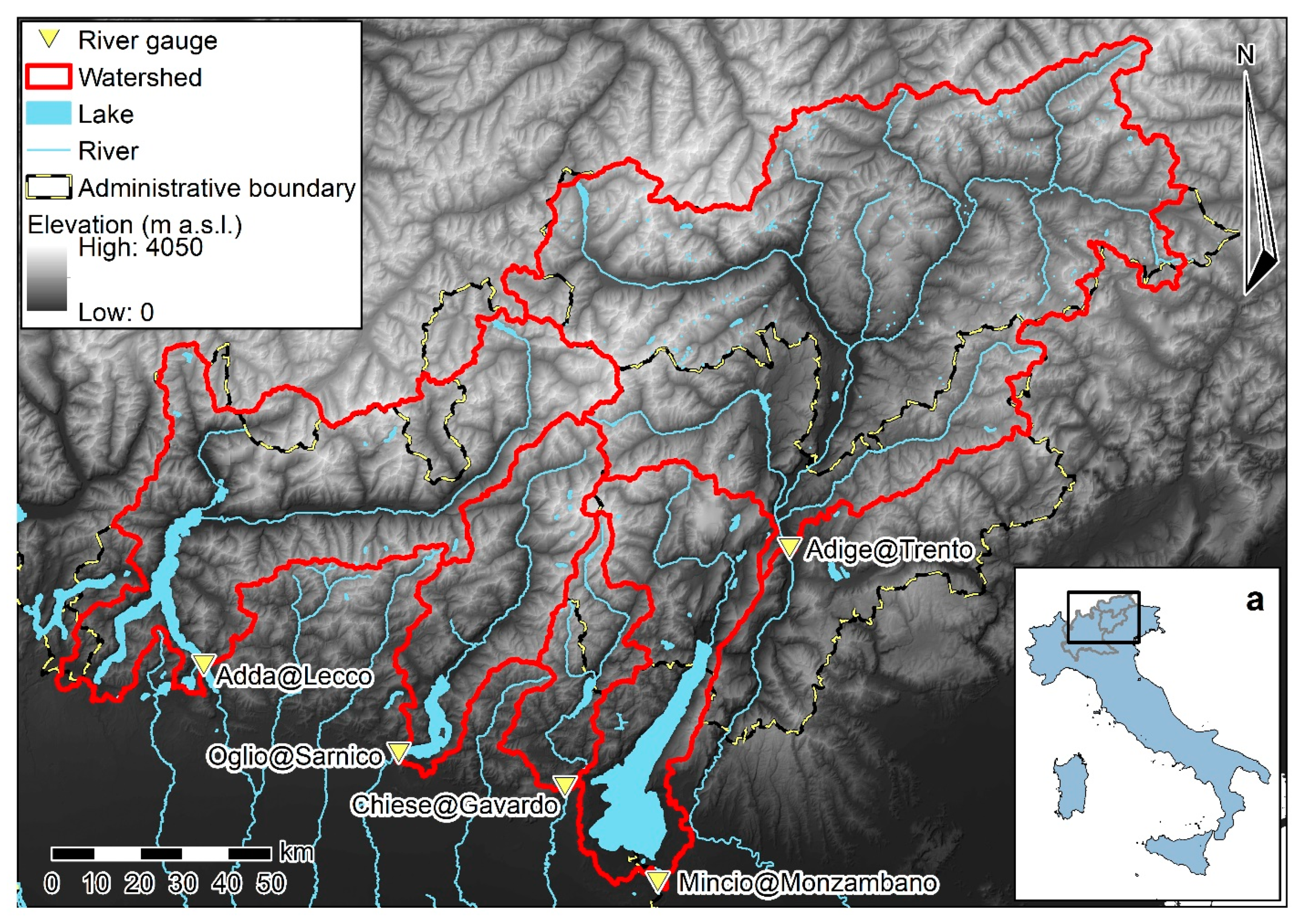
2. Study Watersheds and Data Collection
2.1. Streamflow Data
2.2. Precipitation Data
2.3. Land Cover Data
3. Trend Analysis Methodology
4. Results and Discussion
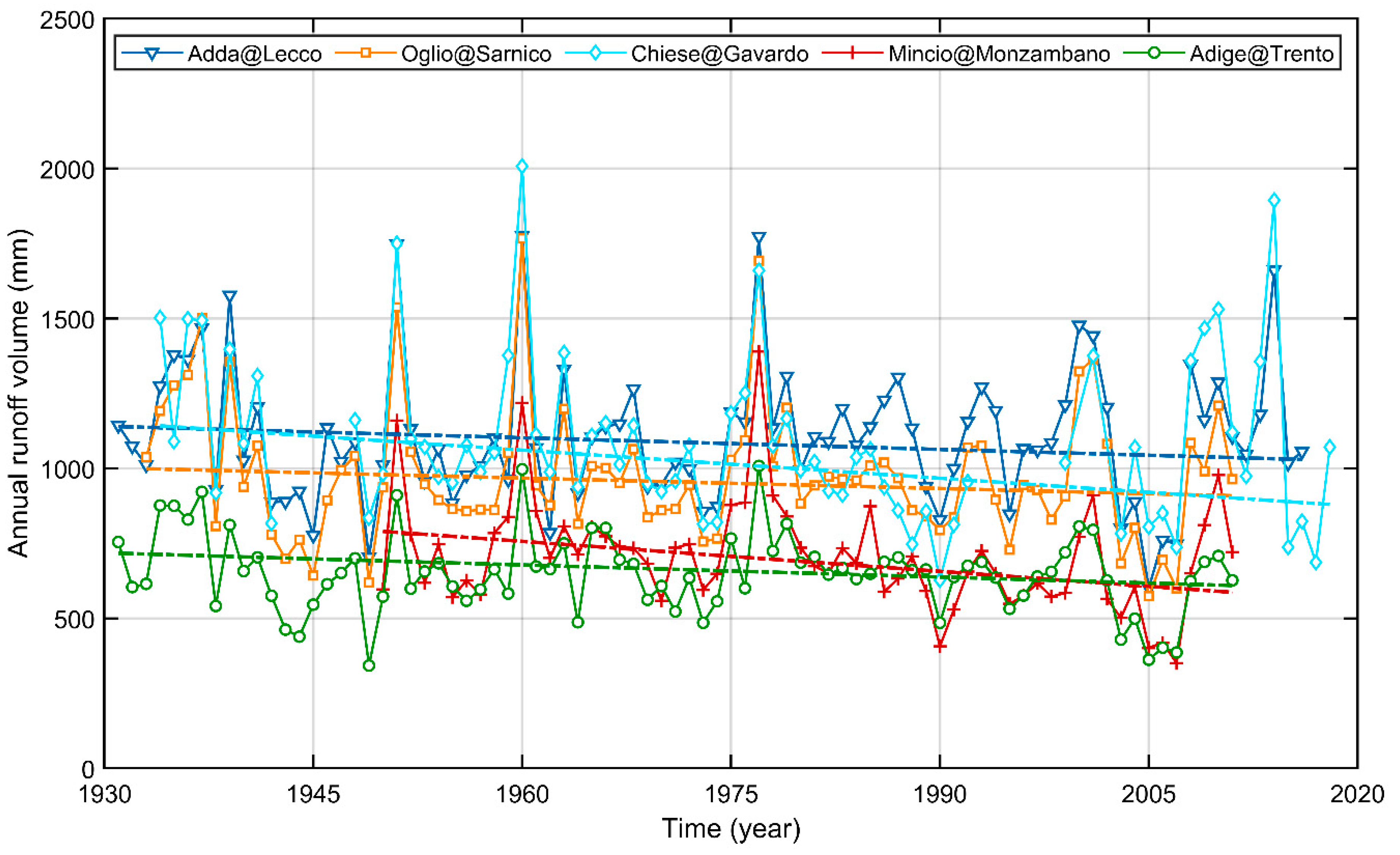
4.1. Runoff Volume Series Analysis
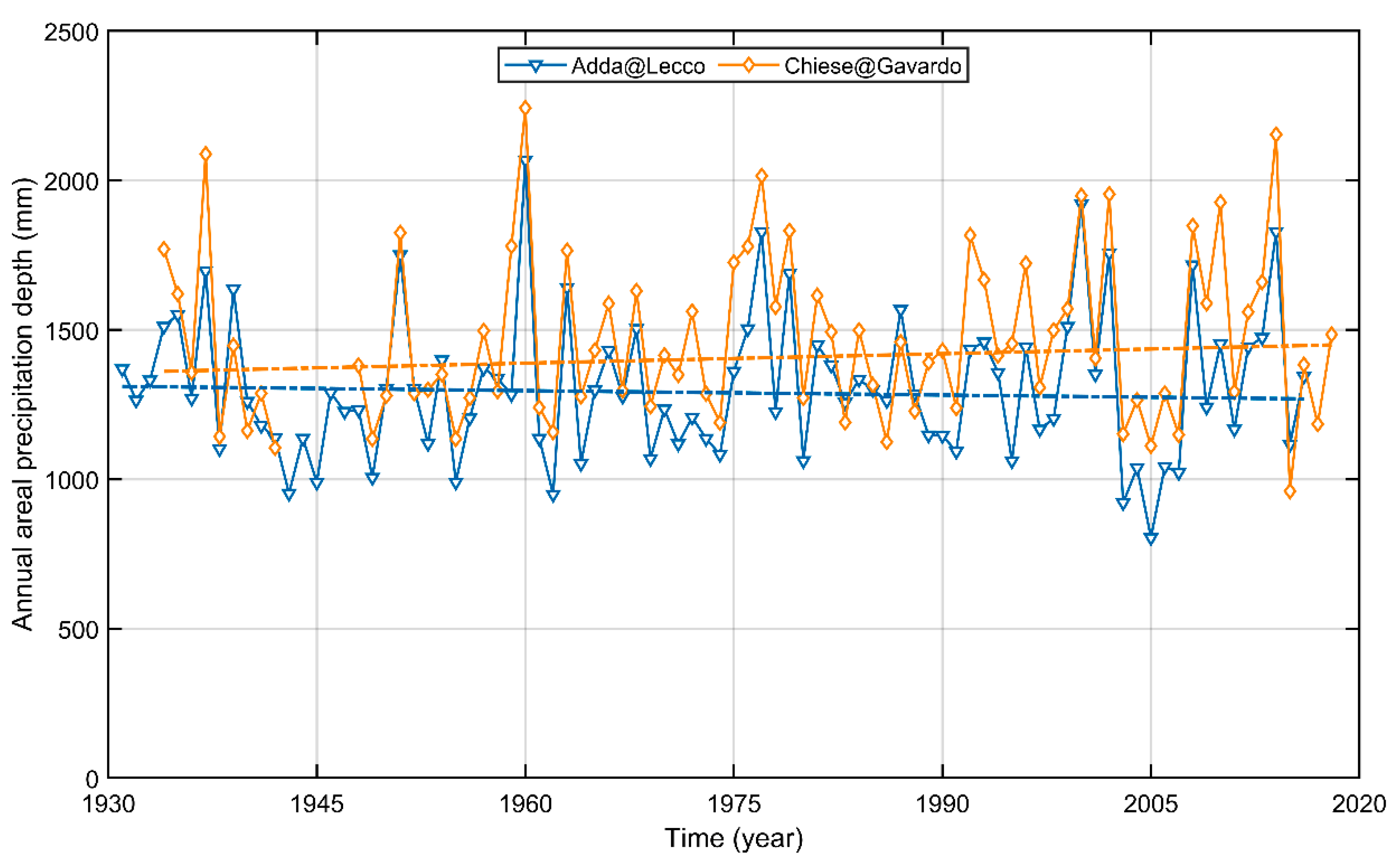
4.2. Precipitation Series Analysis
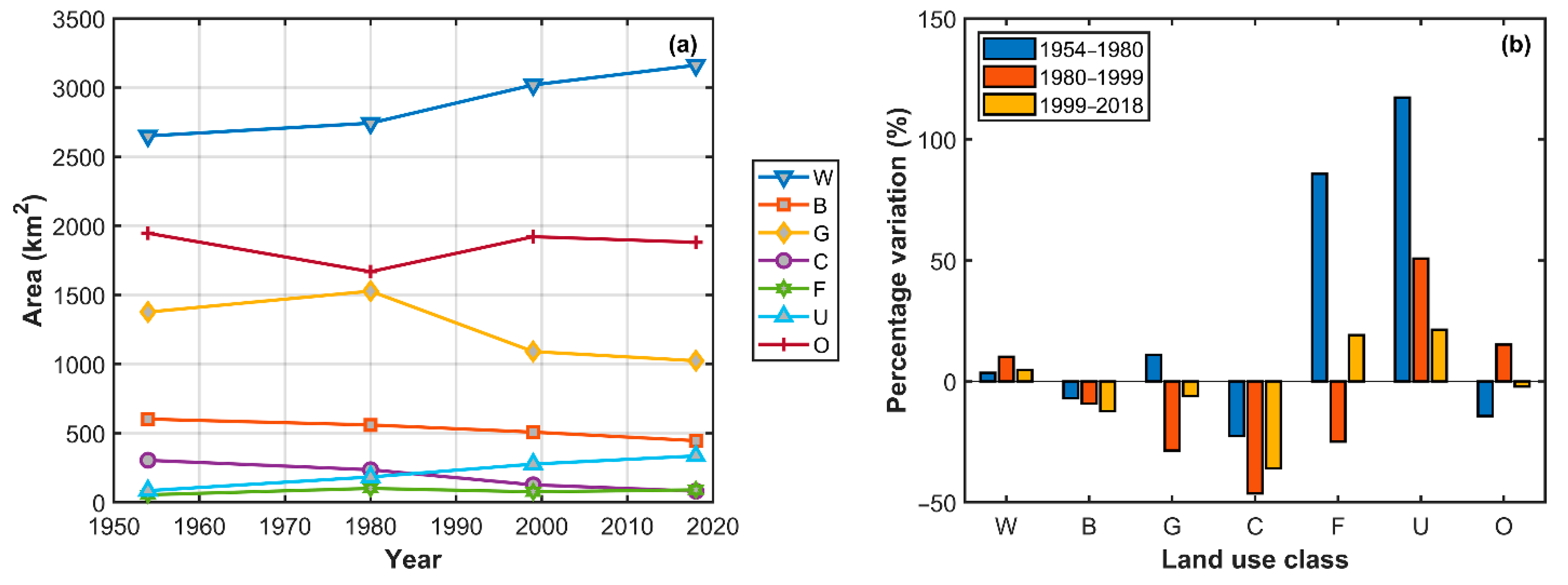
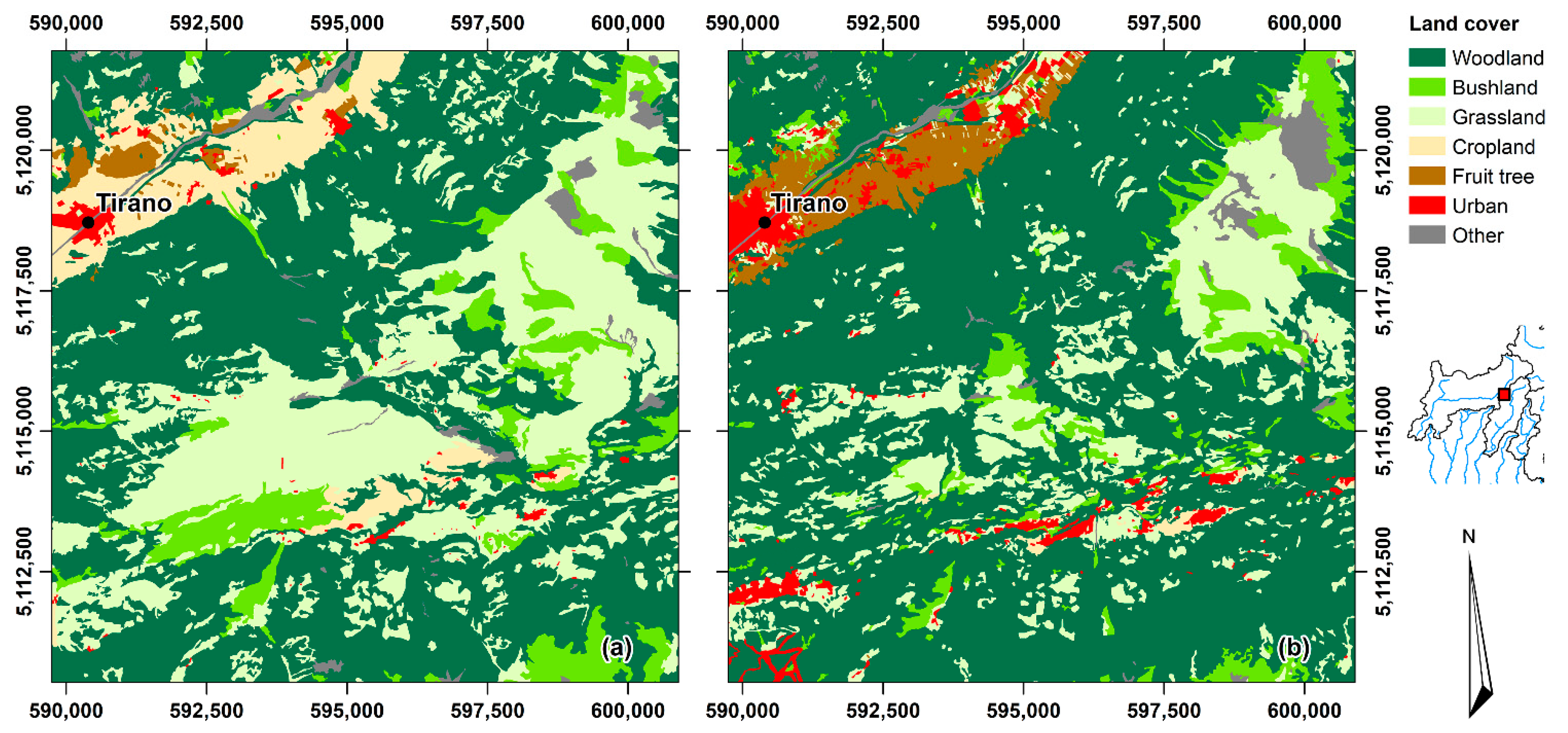
4.3. Land Cover Transformation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Bates, B.C.; Kundzewicz, Z.W.; Wu, S.; Palutikof, J.P. Climate Change and Water. Technical Paper VI of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2008; p. 210. [Google Scholar]
- Hartmann, D.L.; Klein Tank, A.M.G.; Rusticucci, M.; Alexander, L.V.; Brönnimann, S.; Charabi, Y.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and Surface. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 159–254. [Google Scholar]
- Labat, D.; Godderis, Y.; Probst, J.L.; Guyot, J.L. Evidence for global runoff increase related to climate warming. Adv. Water Resour. 2004, 27, 631–642. [Google Scholar] [CrossRef]
- Milliman, J.D.; Farnsworth, K.L.; Jones, P.D.; Xu, K.H.; Smith, L.C. Climatic and anthropogenic factors affecting river discharge to the global ocean, 1951–2000. Global Planet. Chang. 2008, 62, 187–194. [Google Scholar] [CrossRef]
- Dai, A.; Qian, T.T.; Trenberth, K.E.; Milliman, J.D. Changes in continental freshwater discharge from 1948 to 2004. Int. J. Climatol. 2009, 22, 2773–2792. [Google Scholar] [CrossRef]
- Stahl, K.; Hisdal, H.; Hannaford, J.; Tallaksen, L.; Van Lanen, H.; Sauquet, E.; Demuth, S.; Fendekova, M.; Jordar, J. Streamflow trends in Europe: Evidence from a dataset of near-natural catchments. Hydrol. Earth Syst. Sci. 2010, 14, 2367–2382. [Google Scholar] [CrossRef]
- Stahl, K.; Tallaksen, L.M.; Hannaford, J.; Van Lanen, H.A.J. Filling the white space on maps of European runoff trends: Estimates from a multi-model ensemble. Hydrol. Earth Syst. Sci. 2012, 16, 2035–2047. [Google Scholar] [CrossRef]
- Su, L.; Miao, C.; Kong, D.; Duan, Q.; Lei, X.; Hou, Q.; Li, H. Long-term trends in global river flow and the causal relationships between river flow and ocean signals. J. Hydrol. 2018, 563, 818–833. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing climate shifts timing of European floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef]
- Brunetti, M.; Lentini, G.; Maugeri, M.; Nanni, T.; Auer, I.; Böhm, R.; Schöner, W. Climate variability and change in the Greater Alpine Region over the last two centuries based on multi-variable analysis. Int. J. Climatol. 2009, 29, 2197–2225. [Google Scholar] [CrossRef]
- Montanari, A. Hydrology of the Po River: Looking for changing patterns in river discharge. Hydrol. Earth Syst. Sci. 2012, 16, 3739–3747. [Google Scholar] [CrossRef]
- Zanchettin, D.; Traverso, P.; Tomasino, M. Po river discharge: A preliminary analysis of a 200-year time series. Clim. Chang. 2008, 88, 411–433. [Google Scholar] [CrossRef]
- Crespi, A.; Brunetti, M.; Maugeri, M.; Ranzi, R.; Tomirotti, M. 1845–2016 gridded dataset of monthly precipitation over the upper Adda river basin: A comparison with runoff series. Adv. Sci. Res. 2018, 15, 173–181. [Google Scholar] [CrossRef]
- Ranzi, R.; Michailidi, E.M.; Tomirotti, M.; Crespi, A.; Brunetti, M.; Maugeri, M. A multi-century meteo-hydrological analysis for the Adda river basin (central Alps). Part II: Daily runoff (1845–2016) at different scales. Int. J. Climatol. 2021, 41, 181–199. [Google Scholar] [CrossRef]
- Ranzi, R.; Caronna, P.; Tomirotti, M. Impact of climatic and land use changes on river flows in the Southern Alps. In Sustainable Water Resources Planning and Management under Climate Change; Kolokytha, E., Oishi, S., Teegavarapu, R.S.V., Eds.; Springer: Singapore, 2017; pp. 61–83. [Google Scholar]
- Crespi, A.; Brunetti, M.; Ranzi, R.; Tomirotti, M.; Maugeri, M. A multi-century meteo-hydrological analysis for the Adda river basin (central Alps). part I: Gridded monthly precipitation (1800–2016) records. Int. J. Climatol. 2021, 41, 162–180. [Google Scholar] [CrossRef]
- Regione Lombardia, 2002. Regolamento per la gestione coordinata del Lago d’Idro e dei serbatoi dell’Alto Chiese. Edizione 21 Marzo 2002. Deliberazione di Giunta Regionale n° VII/9297 del 7 Giugno 2002. (In Italian). Available online: www.consultazioniburl.servizirl.it (accessed on 1 February 2021).
- Lombardini, E. Della Natura dei Laghi e Delle Opere Intese a Regolarne il Deflusso, 2nd ed.; Tipografia Degli Ingegneri: Milan, Italy, 1866; p. 165. (In Italian) [Google Scholar]
- Fantoli, G. Il lago di Como e l’Adda Emissario Nella Condizione Idraulica Odierna e Nella Divisata Regolazione Del Deflusso Mediante Opere Mobile di Trattenuta e di Scarico; Hoepli: Milan, Italy, 1921; p. 306. (In Italian) [Google Scholar]
- Citrini, D. Le Piene del Lario e dell’Adda nel Regime Regolato; Consorzio dell’Adda: Milan, Italy, 1978; p. 40. (In Italian) [Google Scholar]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis, I; Koninklijke Nederlandse Akademie van Wetenschappen 53: Amsterdam, The Netherlands, 1950; pp. 386–392. [Google Scholar]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis, II; Koninklijke Nederlandse Akademie van Wetenschappen 53: Amsterdam, The Netherlands, 1950; pp. 521–525. [Google Scholar]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis, III; Koninklijke Nederlandse Akademie van Wetenschappen Series A 53: Amsterdam, The Netherlands, 1950; pp. 1397–1412. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Regression problems. In Nonparametric Statistical Methods, 3rd ed.; Hollander, M., Wolfe, D.A., Chicken, E., Eds.; Wiley & Sons: New York, NY, USA, 2014; pp. 451–494. [Google Scholar]
- Hettmansperger, T.P.; McKean, J.W. A robust alternative based on ranks to least squares in analyzing linear models. Technometrics 1977, 19, 275–284. [Google Scholar] [CrossRef]
- Wilcox, R.R. Fundamentals of Modern Statistical Methods, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Kendall, M.G. A new measure of the rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrics 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Sen, P.K. On a class of rank order tests for the parallelism of several regression lines. Ann. Math. Stat. 1969, 40, 1668–1683. [Google Scholar] [CrossRef]
- Adichie, J.N. Testing parallelism of regression lines against ordered alternatives. Commun. Stat. Theory 1976, 5, 985–997. [Google Scholar] [CrossRef]
- Adichie, J.N. Rank tests in linear model. In Handbook of Statistics 4: Nonparametric Methods; Krishnaiah, P.R., Sen, P.K., Eds.; North Holland: Amsterdam, The Netherlands, 1984; pp. 229–257. [Google Scholar]
- Auer, I.; Böhm, R.; Jurkovic, A.; Lipa, W.; Orlik, A.; Potzmann, R.; Schoener, W.; Ungersboeck, M.; Matulla, C.; Briffa, K.; et al. HISTALP—historical instrumental climatological surface time series of the Greater Alpine Region. Int. J. Climatol. 2007, 27, 17–46. [Google Scholar] [CrossRef]
- FAO. State of the World’s Forests, 2011; Food and Agriculture Organization of the United Nations: Rome, Italy, 2011. [Google Scholar]
- FAO. State of the World’s Forests, 2018; Food and Agriculture Organization of the United Nations: Rome, Italy, 2018. [Google Scholar]
- Gurtz, J.; Baltensweiler, A.; Lang, H. Spatially distributed hydrotope-based modelling of evapotranspiration and runoff in mountainous basins. Hydrol. Process. 1999, 13, 2751–2768. [Google Scholar] [CrossRef]
- Zierl, B.; Bugmann, H. Global change impacts on hydrological processes in Alpine catchments. Water Resour. Res. 2005, 41, W02028. [Google Scholar] [CrossRef]
- Moisello, U. Idrologia Tecnica; La Goliardica Pavese: Pavia, Italy, 1999. (In Italian) [Google Scholar]
| Watershed | Outlet | A | Zx | Zm | Zn | Hm | Dm | Observation Period | Sample Size nk | |
|---|---|---|---|---|---|---|---|---|---|---|
| (km2) | (m a.s.l.) | (m a.s.l.) | (m a.s.l.) | (mm) | (mm) | P | R | |||
| Adige | Trento | 9763 | 3899 | 1735 | 186 | 950 | 708 | 1862–2011 | - | 150 |
| Mincio | Monzambano | 2350 | 3556 | 966 | 60 | 1180 | 709 | 1950–2011 | - | 62 |
| Chiese | Gavardo | 934 | 3462 | 1230 | 198 | 1460 | 1090 | 1934–2018 | 80 | 72 |
| Oglio | Sarnico | 1840 | 3554 | 1429 | 154 | 1260 | 980 | 1933–2011 | - | 79 |
| Adda | Lecco | 4508 | 4050 | 1569 | 197 | 1330 | 1150 | 1845–2016 | 172 | 172 |
| Watershed | mk | mkl | mku | α0k | τk | αtk | ρk | αrk | mp | αp | αpk |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (mm/year) | (mm/year) | (mm/year) | (%) | - | (%) | - | (%) | (mm/year) | (%) | (%) | |
| Adige | −1.34 | −1.75 | −0.98 | <0.1 | −0.30 | <0.1 | −0.46 | <0.1 | −1.45 | 54.8 | 66.2 |
| Mincio | −3.33 | −5.00 | −1.28 | 0.5 | −0.24 | 0.6 | −0.32 | 1.0 | 15.8 | ||
| Chiese | −3.12 | −5.02 | −1.10 | 0.8 | −0.21 | 0.8 | −0.28 | 1.6 | 16.2 | ||
| Oglio | −1.16 | −2.91 | 0.56 | 32.2 | −0.08 | 32.4 | −0.11 | 32.8 | 71.3 | ||
| Adda | −1.29 | −1.85 | −0.70 | <0.1 | −0.19 | <0.1 | −0.27 | <0.1 | 62.2 |
| Watershed | mk | mkl | mku | α0k | τk | αtk | ρk | αrk | mp | αp | αpk |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (mm/year) | (mm/year) | (mm/year) | (%) | - | (%) | - | (%) | (mm/year) | (%) | (%) | |
| Chiese | 1.05 | −0.94 | 3.09 | 40.8 | 0.06 | 41.1 | 0.09 | 41.6 | −0.25 | 22.1 | 40.8 |
| Adda | −0.49 | −1.09 | 0.15 | 21.0 | −0.06 | 21.0 | −0.09 | 21.5 | 21.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balistrocchi, M.; Tomirotti, M.; Muraca, A.; Ranzi, R. Hydroclimatic Variability and Land Cover Transformations in the Central Italian Alps. Water 2021, 13, 963. https://doi.org/10.3390/w13070963
Balistrocchi M, Tomirotti M, Muraca A, Ranzi R. Hydroclimatic Variability and Land Cover Transformations in the Central Italian Alps. Water. 2021; 13(7):963. https://doi.org/10.3390/w13070963
Chicago/Turabian StyleBalistrocchi, Matteo, Massimo Tomirotti, Alessandro Muraca, and Roberto Ranzi. 2021. "Hydroclimatic Variability and Land Cover Transformations in the Central Italian Alps" Water 13, no. 7: 963. https://doi.org/10.3390/w13070963
APA StyleBalistrocchi, M., Tomirotti, M., Muraca, A., & Ranzi, R. (2021). Hydroclimatic Variability and Land Cover Transformations in the Central Italian Alps. Water, 13(7), 963. https://doi.org/10.3390/w13070963







