Prediction of River Stage Using Multistep-Ahead Machine Learning Techniques for a Tidal River of Taiwan
Abstract
1. Introduction
- This study contributes to improving forecasting performance by revealing the optimal combinations of input variables, such as rainfall, water level, and tidal stage.
- This is the first study to propose a direct multistep forecasting model based on LGBMR with Bayesian optimization for flood forecasting with a lead time of 1–6 h.
- The present study comprehensively assessed and compared the performance of four models (SVR, RFR, MLPR, and LGBMR) for forecasting the water level in a tidal river.
2. Methodology
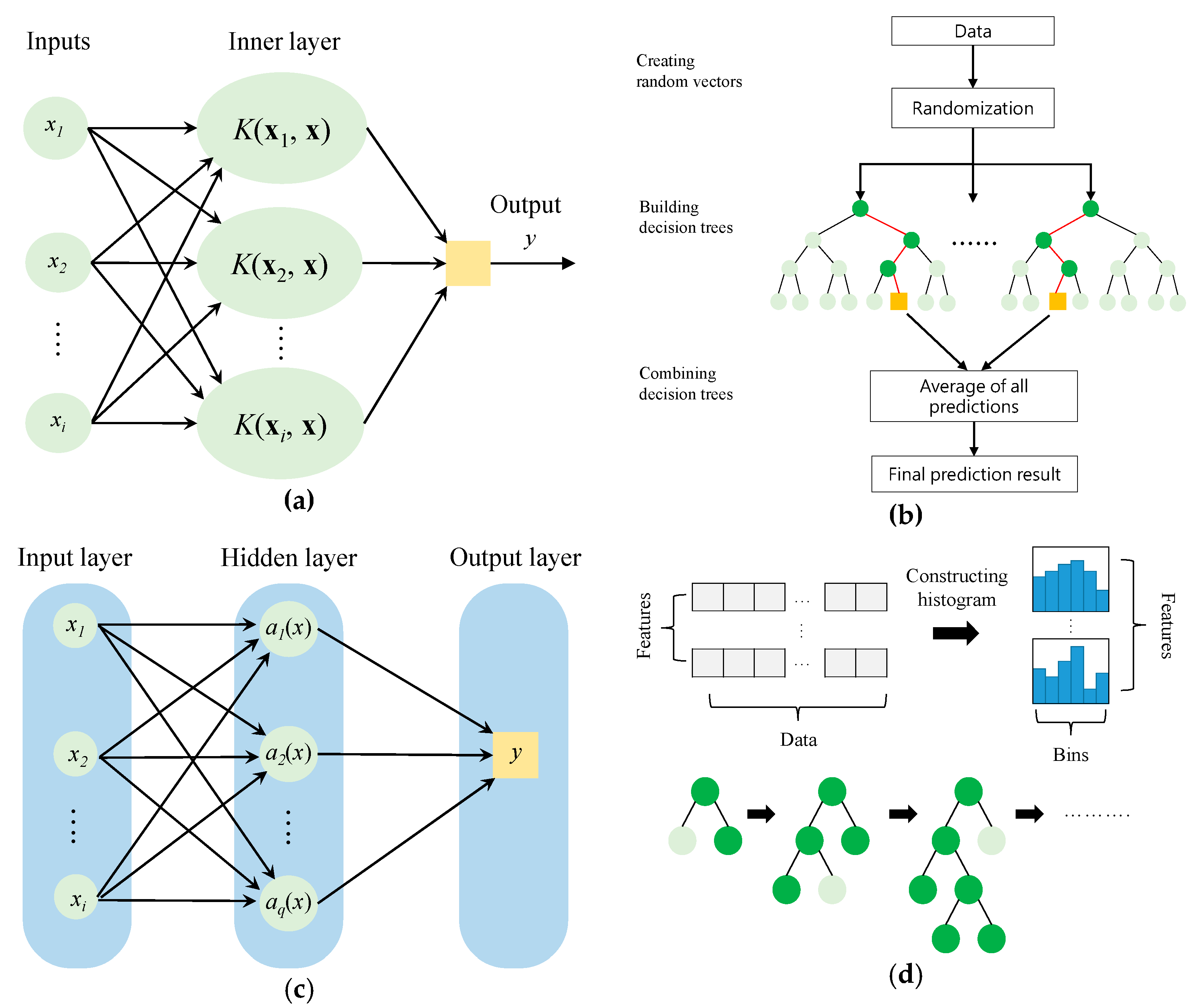
2.1. Data-Driven Model for River Stage Forecasting
2.2. SVR
2.3. RFR
- On the basis of the bootstrap method, a subset of samples is randomly produced with replacements from the original dataset.
- These bootstrap samples are employed to construct regression trees. The optimal split criterion is used to split each node of the regression trees into two descendant nodes. The process on each descendant node is continued recursively until a termination criterion is fulfilled.
- Each regression tree provides a predicted result. Once all of the regression trees have reached their maximum size, the final prediction is determined as the average of the results from all of the regression trees:in which tr is the number of trees, is the maximum size of the trees, and denotes the prediction of each regression tree. Detailed descriptions of RFR have been provided in previous studies [55,56].
2.4. MLPR
2.5. LGBMR
2.6. Bayesian Optimization and Cross-Validation
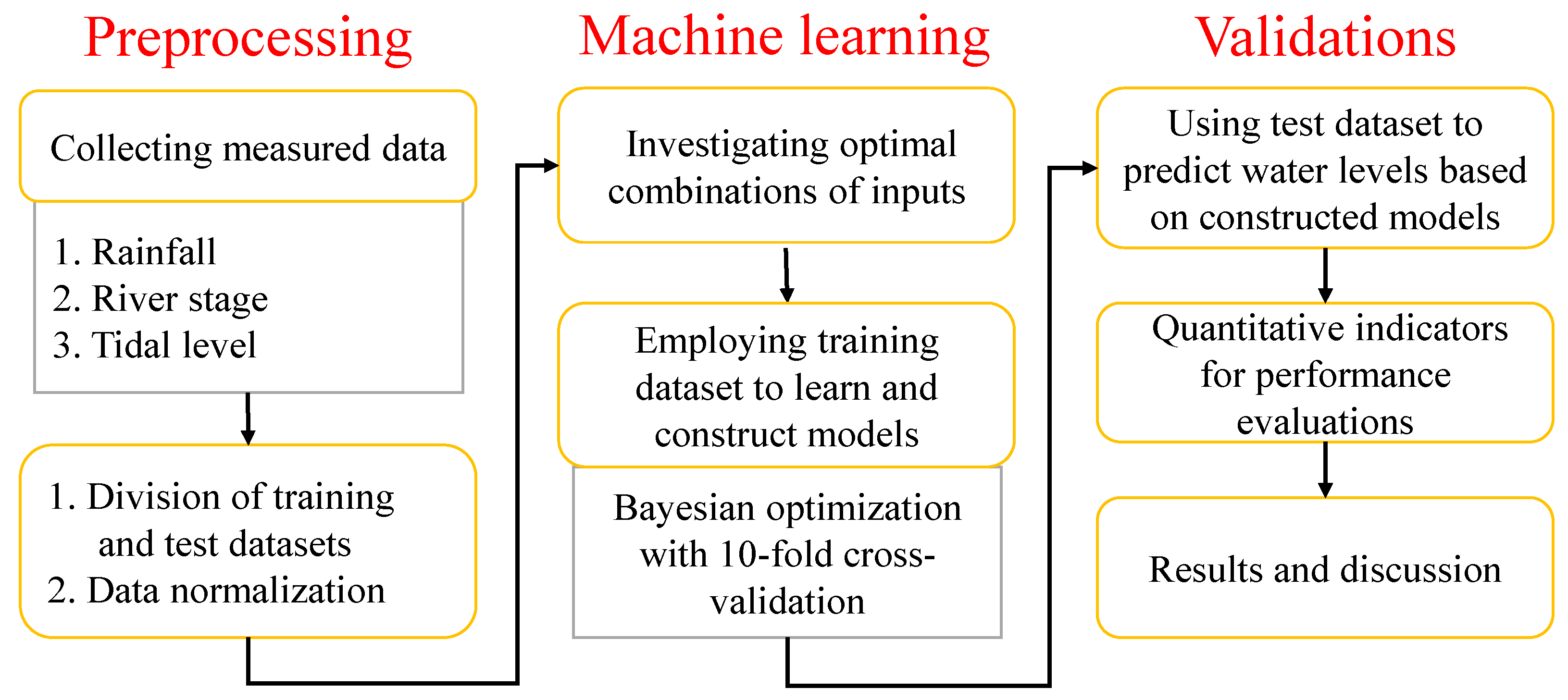
- The objective function was defined, and the interval range of the parameters was set.
- During the training process of the four models, the indicator of the mean square error was used to evaluate the result of each parameter combination.
- The optimal combination of parameters could be determined through 10-fold cross-validation.
- With these optimal parameters, the model was finally constructed, and the test dataset was used for river stage prediction.
2.7. Performance Evaluation Criteria
- Nash–Sutcliffe efficiency (NSE)
- Coefficient of determination (R2)
- Mean absolute error (MAE)
- Root mean square error (RMSE)where and are, respectively, the measured and predicted river stages and and are, respectively, the mean of the measured and predicted river stages.
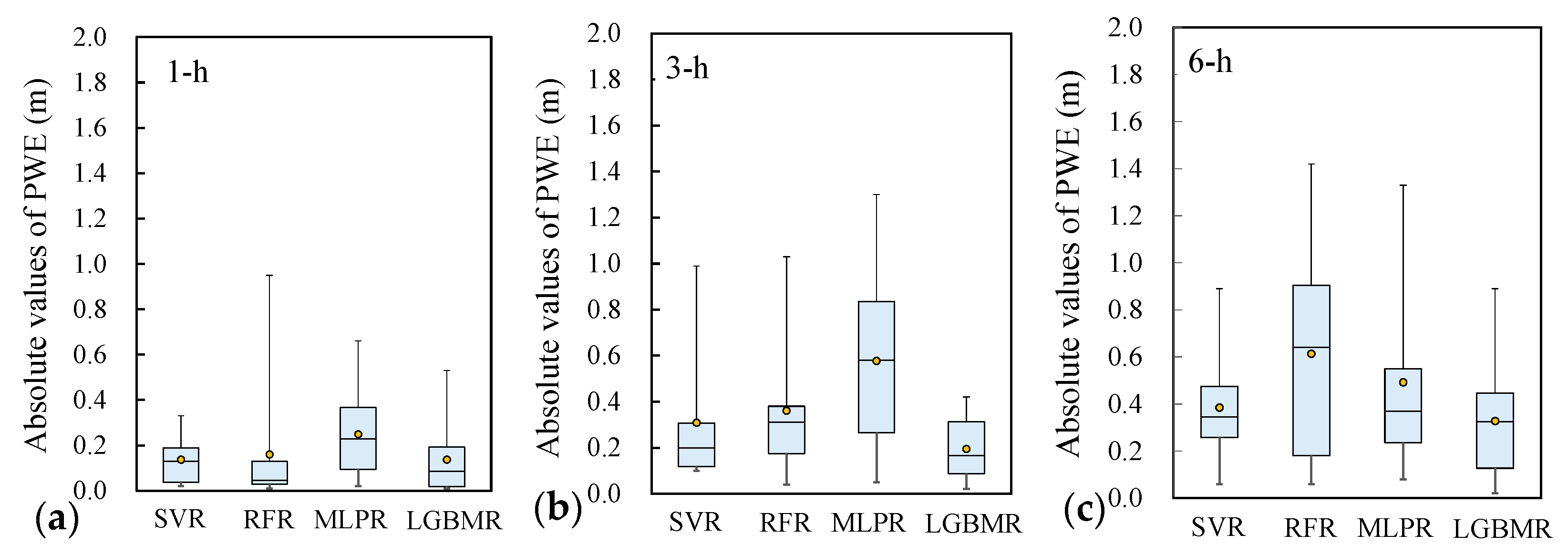
- Peak water-level error (PWE)
- Error of time-to-peak water level (ETP)where and are, respectively, the measured and predicted peak river stages and and denote the measured and predicted time to the peak river stage, respectively. The closer the values of PWE and ETP are to 0, the higher the accuracy of the model is.
2.8. Flowchart for Training and Validation
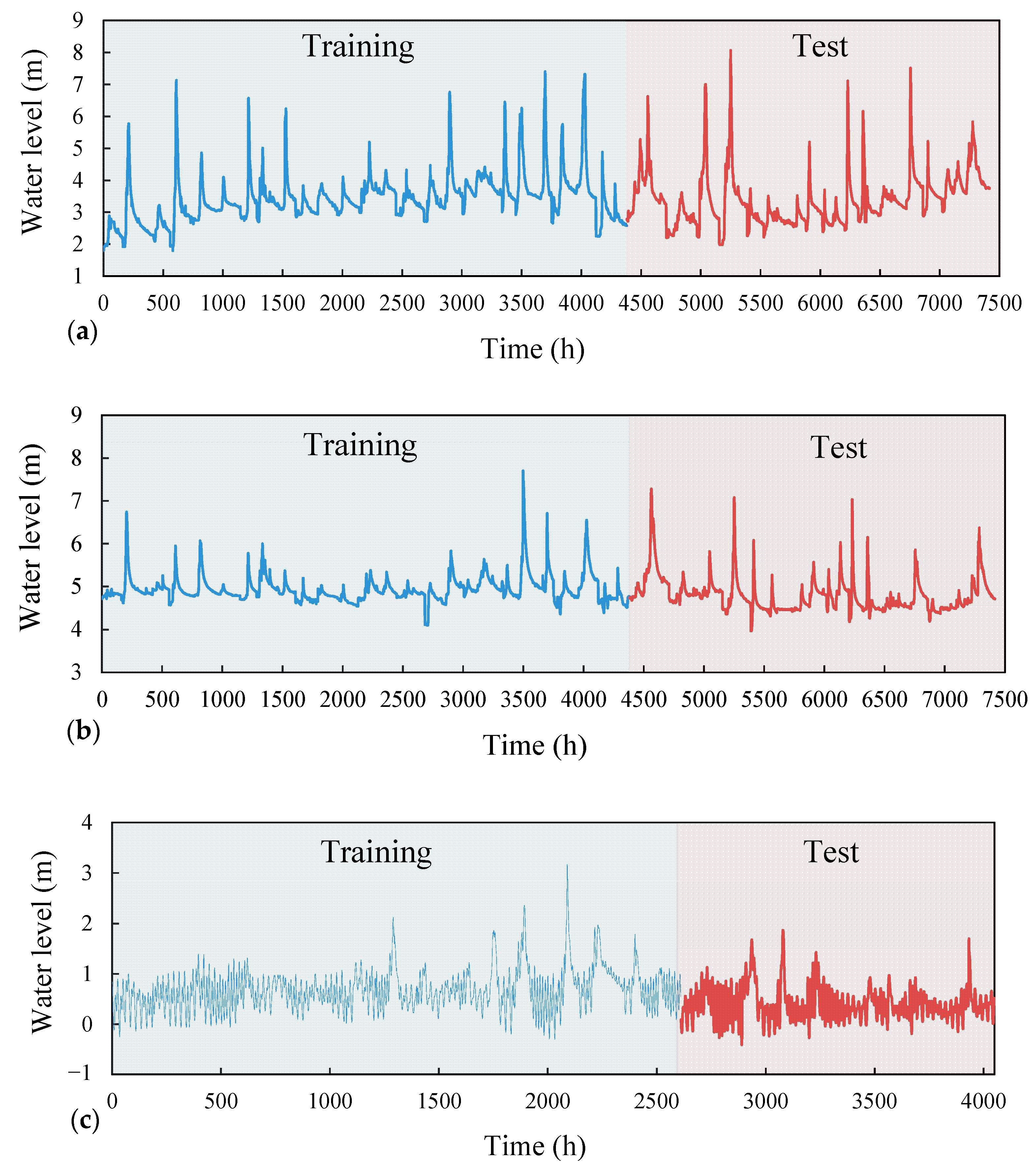
3. Study Area and Data
4. Results and Discussion
4.1. Analysis for Combinations of Input Variables
4.2. Analysis of Model Training Results
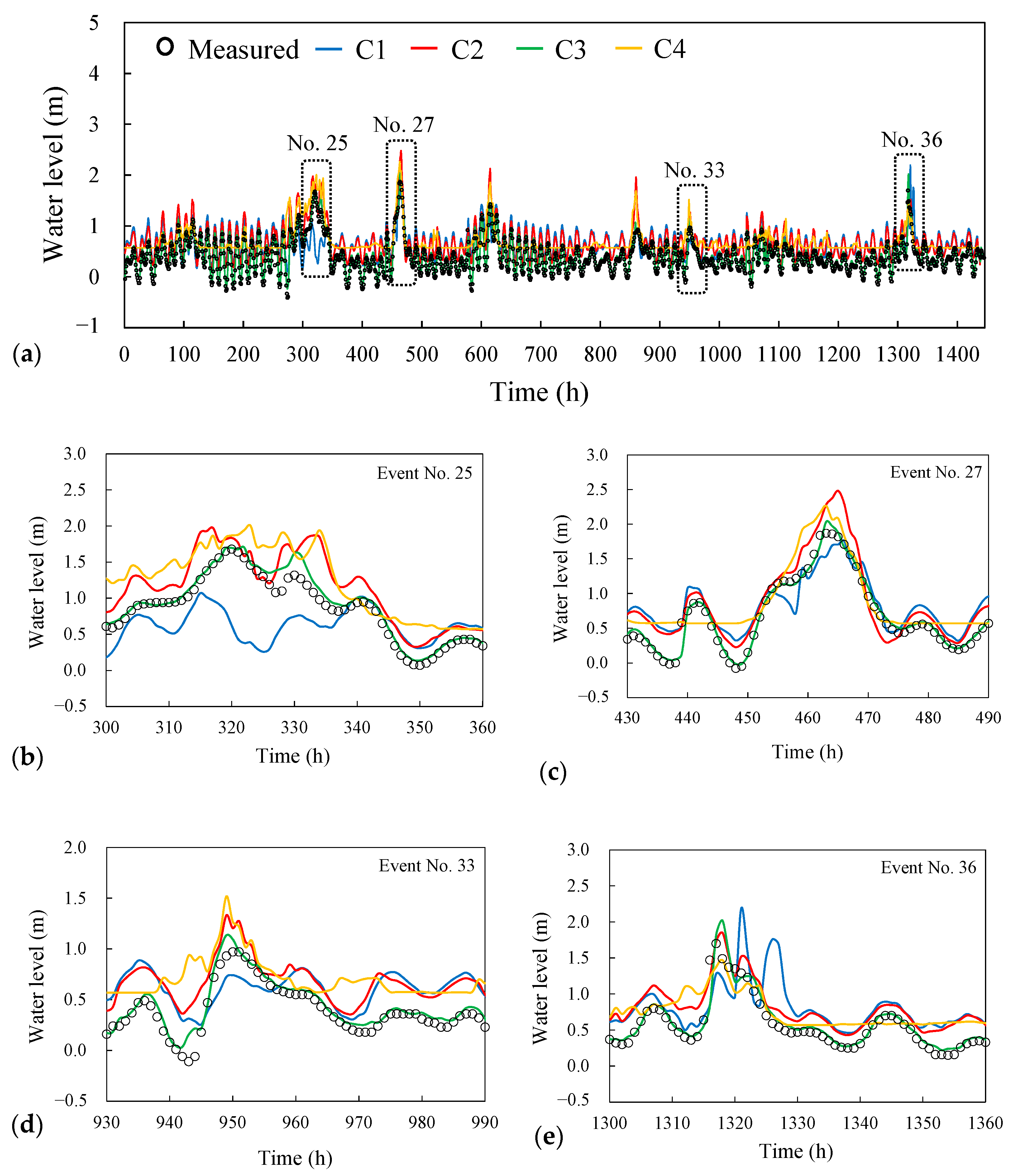
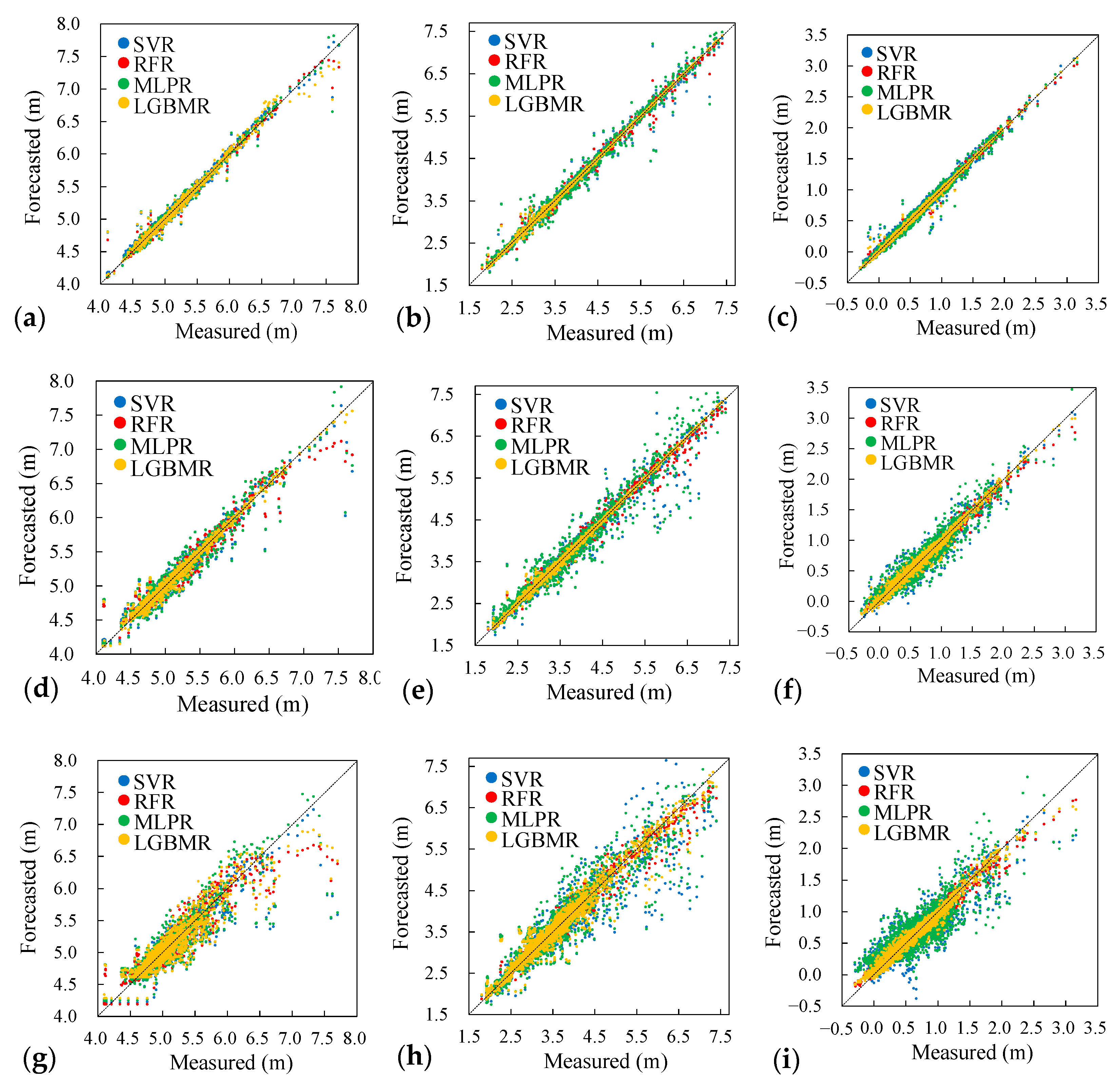
4.3. Results of Model Validation
4.4. Performance Evaluation of River Stage Forecasting
5. Conclusions
- The optimal combination of input variables was determined using the SVR model with four designed combinations. The results indicate that the combination of rainfall, river stage, and tidal level as the input variables can improve the river stage prediction accuracy in a tidal reach.
- The results of the quantitative analysis of model training and validation were used to compare the forecasting performance of the four models. The results demonstrated that the LGBMR model produced more satisfactory river stage forecasting at a lead time of up to 6 h. The average PWE and ETP values obtained using LGBMR were 0.22 m and 2 h, respectively, indicating an acceptable accuracy in river stage forecasting.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Water Resources Agency (WRA). Hydrological Yearbook of Taiwan; Total Report 00-H-30-47, Ministry of Economic Affairs; Water Resources Agency: Taipei, Taiwan, 2019. Available online: https://gweb.wra.gov.tw/wrhygis/ (accessed on 31 December 2020).
- Hsu, W.K.; Huang, P.C.; Chang, C.C.; Chen, C.W.; Hung, D.M.; Chiang, W.L. An integrated flood risk assessment model for property insurance industry in Taiwan. Nat. Hazards 2011, 58, 1295–1309. [Google Scholar] [CrossRef]
- Li, H.C.; Hsieh, L.S.; Chen, L.C.; Lin, L.Y.; Li, W.S. Disaster investigation and analysis of Typhoon Morakot. J. Chin. Inst. 2014, 37, 558–569. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. HEC-RAS. River Analysis System; Hydraulic Reference Manual; Hydrologic Engineering Center: Davis, CA, USA, 2020; Available online: https://www.hec.usace.army.mil/software/hec-ras/documentation.aspx (accessed on 31 December 2020).
- Deltares. SOBEK. Hydrodynamics, Rainfall Runoff and Real Time Control; User Manual. Deltares: Delft, The Netherlands, 2019. Available online: https://content.oss.deltares.nl/delft3d/manuals/SOBEK_User_Manual.pdf (accessed on 31 December 2020).
- Liu, P.C.; Shih, D.S.; Chou, C.Y.; Chen, C.H.; Wang, Y.C. Development of a parallel computing watershed model for flood forecasts. Procedia Eng. 2016, 154, 1043–1049. [Google Scholar] [CrossRef][Green Version]
- Liu, W.C.; Chen, W.B.; Hsu, M.H.; Fu, J.C. Dynamic routing modeling for flash flood forecast in river system. Nat. Hazards 2010, 52, 519–537. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C. Modeling the influence of river cross-section data on a river stage using a two-dimensional/three-dimensional hydrodynamic model. Water 2017, 9, 203. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinform. 2008, 10, 3–22. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Maity, R.; Bhagwat, P.P.; Bhatnagar, A. Potential of support vector regression for prediction of monthly streamflow using endogenous property. Hydrol. Process. 2010, 24, 917–923. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Predicting typhoon-induced storm surge tide with a two-dimensional hydrodynamic model and artificial neural network model. Nat. Hazards Earth Syst. Sci. 2012, 12, 3799–3809. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Comparison of ANN approach with 2D and 3D hydrodynamic models for simulating estuary water stage. Adv. Eng. Softw. 2012, 45, 69–79. [Google Scholar] [CrossRef]
- Lin, G.F.; Lin, H.Y.; Chou, Y.C. Development of a real-time regional-inundation forecasting model for the inundation warning system. J. Hydroinform. 2013, 15, 1391–1407. [Google Scholar] [CrossRef]
- Wu, M.C.; Lin, G.F.; Lin, H.Y. Improving the forecasts of extreme streamflow by support vector regression with the data extracted by self-organizing map. Hydrol. Process. 2014, 28, 386–397. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Mahjouri, N. Integrating support vector regression and a geomorphologic artificial neural network for daily rainfall-runoff modeling. Appl. Soft Comput. J. 2016, 38, 329–345. [Google Scholar] [CrossRef]
- Jhong, B.C.; Wang, J.H.; Lin, G.F. An integrated two-stage support vector machine approach to forecast inundation maps during typhoons. J. Hydrol. 2017, 547, 236–252. [Google Scholar] [CrossRef]
- Seo, Y.; Choi, Y.; Choi, J. River stage modeling by combining maximal overlap discrete wavelet transform, support vector machines and genetic algorithm. Water 2017, 9, 525. [Google Scholar]
- Jhong, Y.D.; Chen, C.S.; Lin, H.P.; Chen, S.T. Physical hybrid neural network model to forecast typhoon floods. Water 2018, 10, 632. [Google Scholar] [CrossRef]
- Muñoz, P.; Orellana-Alvear, J.; Willems, P.; Célleri, R. Flash-flood forecasting in an Andean mountain catchment-development of a step-wise methodology based on the random forest algorithm. Water 2018, 10, 1519. [Google Scholar] [CrossRef]
- Wu, J.; Liu, H.; Wei, G.; Song, T.; Zhang, C.; Zhou, H. Flash flood forecasting using support vector regression model in a small mountainous catchment. Water 2019, 11, 1327. [Google Scholar] [CrossRef]
- Kim, H.I.; Han, K.Y. Inundation map prediction with rainfall return period and machine learning. Water 2020, 12, 1552. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Chen, S.T. Real-time probabilistic flood forecasting using multiple machine learning methods. Water 2020, 12, 787. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Artificial neural network modeling of dissolved oxygen in reservoir. Environ. Monit. Assess. 2014, 186, 1203–1217. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.F.; Chen, G.R.; Huang, P.Y. Effective typhoon characteristics and their effects on hourly reservoir inflow forecasting. Adv. Water Resour. 2010, 33, 887–898. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Huu, Q.N.; Li, M.J. Forecasting time series water levels on Mekong River using machine learning models. In Proceedings of the 7th International Conference on Knowledge and Systems Engineering, Ho Chi Minh City, Vietnam, 8–10 October 2015; pp. 292–297. [Google Scholar]
- Li, B.; Yang, G.; Wan, R.; Dai, X.; Zhang, Y. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47, 69–83. [Google Scholar] [CrossRef]
- Panagoulia, D.; Tsekouras, G.J.; Kousiouris, G. A multi-stage methodology for selecting input variables in ANN forecasting of river flows. Glob. Nest J. 2017, 19, 49–57. [Google Scholar]
- Yang, T.; Asanjan, A.A.; Welles, E.; Gao, X.; Sorooshian, S.; Liu, X. Developing reservoir monthly inflow forecasts using artificial intelligence and climate phenomenon information. Water Resour. Res. 2017, 53, 2786–2812. [Google Scholar] [CrossRef]
- Pini, M.; Scalvini, A.; Liaqat, M.U.; Ranzi, R.; Serina, I.; Mehmood, T. Evaluation of machine learning techniques for inflow prediction in Lake Como, Italy. Procedia Comput. Sci. 2020, 176, 918–927. [Google Scholar] [CrossRef]
- Ebrahimi, E.; Shourian, M. River flow prediction using dynamic method for selecting and prioritizing k-nearest neighbors based on data features. J. Hydrol. Eng. 2020, 25, 04020010. [Google Scholar] [CrossRef]
- Maspo, N.A.; Bin Harun, A.N.; Goto, M.; Cheros, F.; Haron, N.A.; Mohd Nawi, M.N. Evaluation of Machine Learning approach in flood prediction scenarios and its input parameters: A systematic review. IOP Conf. Ser. Earth Environ. Sci. 2020, 479, 012038. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Jin, Q.; Fan, X.; Liu, J.; Xue, Z.; Jian, H. Using eXtreme gradient BOOSTing to predict changes in tropical cyclone intensity over the Western North Pacific. Atmosphere 2019, 10, 341. [Google Scholar] [CrossRef]
- Tama, B.A.; Rhee, K.H. An in-depth experimental study of anomaly detection using gradient boosted machine. Neural Comput. Appl. 2019, 31, 955–965. [Google Scholar] [CrossRef]
- Sun, R.; Wang, G.Y.; Zhang, W.Y.; Hsu, L.T.; Ochieng, W.Y. A gradient boosting decision tree based GPS signal reception classification algorithm. Appl. Soft Comput. 2020, 86, 105942. [Google Scholar] [CrossRef]
- Lucas, A.; Pegios, K.; Kotsakis, E.; Clarke, D. Price forecasting for the balancing energy market using machine-learning regression. Energies 2020, 13, 5420. [Google Scholar] [CrossRef]
- Tang, M.; Zhao, Q.; Ding, S.X.; Wu, H.; Li, L.; Long, W.; Huang, B. An improved lightGBM algorithm for online fault detection of wind turbine gearboxes. Energies 2020, 13, 807. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, T.E. Application of improved LightGBM model in blood glucose prediction. Appl. Sci. 2020, 10, 3227. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3146–3154. [Google Scholar]
- Gao, X.; Luo, H.; Wang, Q.; Zhao, F.; Ye, L.; Zhang, Y. A human activity recognition algorithm based on stacking denoising autoencoder and lightGBM. Sensors 2019, 19, 947. [Google Scholar] [CrossRef]
- Qadeer, K.; Jeon, M. Prediction of PM10 concentration in South Korea using gradient tree boosting models. In Proceedings of the 3rd International Conference on Vision, Image and Signal Processing, Vancouver, BC, Canada, 26–28 August 2019; pp. 1–6. [Google Scholar]
- Bontempi, G.; Ben Taieb, S.; Le Borgne, Y.A. Machine learning strategies for time series forecasting. Lect. Notes Bus. Inf. Process. 2013, 138, 62–77. [Google Scholar]
- Wang, J.H.; Lin, G.F.; Chang, M.J.; Huang, I.H.; Chen, Y.R. Real-time water-level forecasting using dilated causal convolutional neural networks. Water Resour. Manag. 2019, 33, 3759–3780. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, S.T.; Chang, I.F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inform. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Liong, S.Y.; Chandrasekaran, S. Flood stage forecasting with support vector machines. J. Am. Water Resour. Assoc. 2007, 38, 173–186. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Li, Y.S. River stage prediction based on a distributed support vector regression. J. Hydrol. 2008, 358, 96–111. [Google Scholar] [CrossRef]
- Gunn, S.R. Support Vector Machines for Classification and Regression; Technical Report; University of Southampton: Southampton, UK, 1998. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intern. Syst. Technol. 2001, 2, 1–27. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Choi, C.; Kim, J.; Han, H.; Han, D.; Kim, H.S. Development of water level prediction models using machine learning in wetlands: A case study of Upo Wetland in South Korea. Water 2020, 12, 93. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Janitza, S.; Kruppa, J.; König, I.R. Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics. Wiley Interdisc. Rev. Data Min. Knowl. Discov. 2012, 2, 493–507. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Khan, M.S.; Coulibaly, P. Application of support vector machine in lake water level prediction. J. Hydrol. Eng. 2006, 11, 199–205. [Google Scholar] [CrossRef]
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study among machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 3904. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; MacMillan: New York, NY, USA, 1994. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design; PWS Publishing: Boston, MA, USA, 1996. [Google Scholar]
- Govindaraju, R.S.; Rao, A.R. Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar]
- Ju, Y.; Sun, G.; Chen, Q.; Zhang, M.; Zhu, H.; Rehman, M.U. A model combining convolutional neural network and lightgbm algorithm for ultra-short-term wind power forecasting. IEEE Access 2019, 7, 28309–28318. [Google Scholar] [CrossRef]
- Kopsiaftis, G.; Protopapadakis, E.; Voulodimos, A.; Doulamis, N.; Mantoglou, A. Gaussian process regression tuned by Bayesian optimization for seawater intrusion prediction. Comput. Intell. Neurosci. 2019, 2019, 2859429. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2960–2968. [Google Scholar]
- Su, B.; Wang, Y. Genetic algorithm based feature selection and parameter optimization for support vector regression applied to semantic textual similarity. J. Shanghai Jiaotong Univ. 2015, 20, 143–148. [Google Scholar] [CrossRef]
- Patel, S.S.; Ramachandran, P. A comparison of machine learning techniques for modeling river flow time series: The case of upper Cauvery River Basin. Water Resour. Manag. 2015, 29, 589–602. [Google Scholar] [CrossRef]
- Lin, G.F.; Chou, Y.C.; Wu, M.C. Typhoon flood forecasting using integrated two-stage support vector machine approach. J. Hydrol. 2013, 486, 334–342. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of long short-term memory (LSTM) neural network for flood forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Liu, M.; Huang, Y.; Li, Z.; Tong, B.; Liu, Z.; Sun, M.; Jiang, F.; Zhang, H. The applicability of LSTM-KNN model for real-time flood forecasting in different climate zones in China. Water 2020, 12, 440. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep learning convolutional neural network in rainfall-runoff modelling. J. Hydroinform. 2020, 22, 541–561. [Google Scholar] [CrossRef]






| No. | Events | Date | Duration (h) | Maximum Water Level (m) | ||
|---|---|---|---|---|---|---|
| Lanyan | Simon | Kavalan | ||||
| 1 | Typhoon Mindulle | 30 June 2004 | 162 | 2.87 | 4.94 | - |
| 2 | Typhoon Aere | 23 August 2004 | 258 | 5.77 | 6.72 | - |
| 3 | Storm | 28 May 2005 | 138 | 3.20 | 5.26 | - |
| 4 | Typhoon Haitang | 16 July 2005 | 210 | 7.11 | 5.92 | - |
| 5 | Typhoon Matsa | 3 August 2005 | 378 | 4.80 | 6.05 | - |
| 6 | Typhoon Talim | 29 August 2005 | 138 | 6.56 | 5.78 | - |
| 7 | Typhoon Damrey | 21 September 2005 | 186 | 4.92 | 6.00 | - |
| 8 | Typhoon Longwang | 30 September 2005 | 138 | 6.21 | 5.36 | - |
| 9 | Typhoon Chanchu | 15 May 2006 | 186 | 3.82 | 5.20 | 0.98 |
| 10 | Storm | 9 June 2006 | 162 | 3.90 | 5.03 | 1.06 |
| 11 | Typhoon Saomai | 7 August 2006 | 186 | 4.11 | 5.04 | 1.39 |
| 12 | Typhoon Shanshan | 7 September 2006 | 306 | 5.20 | 5.38 | 1.30 |
| 13 | Storm | 5 June 2007 | 234 | 4.32 | 5.14 | 1.07 |
| 14 | Typhoon Wutip | 6 August 2007 | 138 | 4.47 | 5.07 | 1.28 |
| 15 | Typhoon Sepat | 15 August 2007 | 186 | 6.73 | 5.83 | 2.12 |
| 16 | Typhoon Wipha | 17 September 2007 | 330 | 4.42 | 5.64 | 1.23 |
| 17 | Typhoon Fung-Wong | 27 July 2008 | 114 | 6.39 | 5.50 | 1.87 |
| 18 | Typhoon Sinlaku | 12 September 2008 | 210 | 6.14 | 7.54 | 2.33 |
| 19 | Typhoon Jangmi | 27 September 2008 | 90 | 7.40 | 6.60 | 3.11 |
| 20 | Typhoon Morakot | 4 August 2009 | 210 | 5.75 | 5.33 | 1.96 |
| 21 | Typhoon Parma | 3 October 2009 | 162 | 7.21 | 6.51 | - |
| 22 | Typhoon Fanapi | 17 September 2010 | 258 | 4.88 | 5.36 | 1.79 |
| 23 | Typhoon Megi | 27 October 2010 | 330 | 6.62 | 7.24 | - |
| 24 | Typhoon Nanmadol | 3 September 2011 | 258 | 3.60 | 5.34 | 1.13 |
| 25 | Storm | 7 October 2011 | 186 | 6.98 | 5.76 | 1.64 |
| 26 | Typhoon Saola | 7 August 2012 | 234 | 8.06 | 7.08 | - |
| 27 | Typhoon Soulik | 17 July 2013 | 138 | 3.70 | 6.08 | 1.86 |
| 28 | Typhoon Trami | 3 September 2013 | 354 | 3.51 | 5.20 | 1.43 |
| 29 | Typhoon Matmo | 27 July 2014 | 138 | 5.20 | 5.56 | - |
| 30 | Storm | 28 September 2014 | 186 | 3.70 | 5.96 | - |
| 31 | Typhoon Soudelor | 11 August 2015 | 114 | 7.11 | 7.01 | - |
| 32 | Typhoon Dujuan | 29 September 2015 | 54 | 6.11 | 6.15 | - |
| 33 | Storm | 17 May 2016 | 114 | 3.77 | 4.68 | 0.97 |
| 34 | Typhoon Nepartak | 16 July 2016 | 234 | 3.77 | 4.87 | 0.93 |
| 35 | Typhoon Megi | 1 October 2016 | 138 | 7.51 | 5.86 | - |
| 36 | Typhoon Nesat | 3 August 2017 | 162 | 5.22 | 4.71 | 1.70 |
| 37 | Storm | 19 October 2017 | 402 | 5.83 | 6.20 | - |
| Characteristic | Training Data Sets | Test Data Sets | ||||
|---|---|---|---|---|---|---|
| Lanyan | Simon | Kavalan | Lanyan | Simon | Kavalan | |
| Maximum Water Level (m) | 7.40 | 7.70 | 3.16 | 8.06 | 7.28 | 1.87 |
| Minimum Water Level (m) | 1.80 | 4.10 | −0.30 | 1.98 | 3.96 | −0.41 |
| Mean Water Level (m) | 3.42 | 4.94 | 0.68 | 3.39 | 4.80 | 0.39 |
| Combinations of Inputs | Input Vectors | Output Variables | ||
|---|---|---|---|---|
| Rainfall | River Stage | Tidal Level | ||
| C1 | - | - | ||
| C2 | - | |||
| C3 | ||||
| C4 | - | - | ||
| Combinations of Inputs | R2 | MAE (m) | RMSE (m) | NSE |
|---|---|---|---|---|
| C1 | 0.587 | 0.171 | 0.263 | 0.579 |
| C2 | 0.711 | 0.142 | 0.219 | 0.708 |
| C3 | 0.980 | 0.040 | 0.056 | 0.981 |
| C4 | 0.359 | 0.256 | 0.325 | 0.359 |
| Events | C1 | C2 | C3 | C4 | ||||
|---|---|---|---|---|---|---|---|---|
| ETP (h) | PWE (m) | ETP (h) | PWE (m) | ETP (h) | PWE (m) | ETP (h) | PWE (m) | |
| No. 25 (Storm) | −6 | −0.61 | −3 | 0.29 | 0 | −0.05 | 3 | 0.32 |
| No. 27 (Typhoon Soulik) | 3 | −0.18 | 2 | 0.62 | 0 | 0.17 | 0 | 0.40 |
| No. 33 (Storm) | −1 | −0.23 | −1 | 0.36 | −1 | 0.16 | −1 | 0.54 |
| No. 36 (Typhoon Nesat) | 4 | 0.48 | 1 | 0.15 | 1 | 0.30 | 1 | −0.23 |
| Stations | Lead Times (h) | SVR | RFR | MLPR | LGBMR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| C | γ | |||||||||
| Lanyan | 1 | 50.0 | 0.005 | 7 | 215 | 6 | tanh | 5 | 881 | 6 |
| 3 | 49.6 | 0.02 | 3 | 296 | 6 | tanh | 4 | 900 | 98 | |
| 6 | 42.9 | 0.005 | 3 | 298 | 6 | tanh | 16 | 895 | 6 | |
| Simon | 1 | 44.8 | 0.005 | 6 | 300 | 6 | tanh | 19 | 106 | 5 |
| 3 | 34.0 | 0.007 | 17 | 144 | 6 | tanh | 3 | 214 | 25 | |
| 6 | 24.7 | 0.005 | 36 | 295 | 6 | tanh | 3 | 107 | 6 | |
| Kavalan | 1 | 50.0 | 0.005 | 3 | 298 | 12 | ReLU | 4 | 895 | 100 |
| 3 | 44.3 | 0.007 | 4 | 298 | 12 | ReLU | 7 | 105 | 97 | |
| 6 | 27.7 | 0.011 | 3 | 297 | 12 | ReLU | 20 | 900 | 100 | |
| Stations | Models | R2 | MAE (m) | RMSE (m) | NSE | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-h | 2-h | 3-h | 4-h | 5-h | 6-h | 1-h | 2-h | 3-h | 4-h | 5-h | 6-h | 1-h | 2-h | 3-h | 4-h | 5-h | 6-h | 1-h | 2-h | 3-h | 4-h | 5-h | 6-h | ||
| Lanyan | SVR | 0.98 | 0.98 | 0.98 | 0.94 | 0.92 | 0.90 | 0.03 | 0.05 | 0.06 | 0.08 | 0.11 | 0.12 | 0.08 | 0.12 | 0.13 | 0.18 | 0.23 | 0.25 | 0.99 | 0.98 | 0.97 | 0.94 | 0.91 | 0.89 |
| RFR | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.02 | 0.02 | 0.03 | 0.03 | 0.04 | 0.04 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | |
| MLPR | 0.98 | 0.98 | 0.96 | 0.94 | 0.90 | 0.90 | 0.03 | 0.05 | 0.08 | 0.08 | 0.12 | 0.12 | 0.08 | 0.11 | 0.17 | 0.18 | 0.24 | 0.24 | 0.99 | 0.98 | 0.95 | 0.95 | 0.90 | 0.89 | |
| LGBMR | 0.98 | 0.98 | 0.98 | 0.98 | 0.96 | 0.96 | 0.01 | 0.02 | 0.02 | 0.06 | 0.07 | 0.09 | 0.03 | 0.03 | 0.04 | 0.10 | 0.12 | 0.16 | 0.99 | 0.99 | 0.99 | 0.98 | 0.97 | 0.96 | |
| Simon | SVR | 0.98 | 0.98 | 0.96 | 0.92 | 0.90 | 0.85 | 0.02 | 0.03 | 0.04 | 0.05 | 0.05 | 0.06 | 0.04 | 0.05 | 0.07 | 0.09 | 0.11 | 0.13 | 0.99 | 0.98 | 0.95 | 0.92 | 0.89 | 0.85 |
| RFR | 0.98 | 0.98 | 0.98 | 0.96 | 0.94 | 0.92 | 0.01 | 0.01 | 0.02 | 0.03 | 0.04 | 0.04 | 0.02 | 0.03 | 0.05 | 0.06 | 0.08 | 0.10 | 0.99 | 0.99 | 0.98 | 0.97 | 0.94 | 0.91 | |
| MLPR | 0.98 | 0.98 | 0.94 | 0.92 | 0.88 | 0.85 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.03 | 0.05 | 0.07 | 0.09 | 0.11 | 0.13 | 0.99 | 0.98 | 0.96 | 0.92 | 0.89 | 0.84 | |
| LGBMR | 0.98 | 0.98 | 0.98 | 0.96 | 0.96 | 0.88 | 0.01 | 0.02 | 0.02 | 0.03 | 0.03 | 0.06 | 0.03 | 0.04 | 0.04 | 0.05 | 0.06 | 0.11 | 0.98 | 0.98 | 0.98 | 0.97 | 0.96 | 0.88 | |
| Kavalan | SVR | 0.98 | 0.96 | 0.92 | 0.90 | 0.85 | 0.77 | 0.04 | 0.06 | 0.08 | 0.10 | 0.12 | 0.14 | 0.06 | 0.08 | 0.11 | 0.13 | 0.16 | 0.19 | 0.98 | 0.96 | 0.92 | 0.89 | 0.84 | 0.77 |
| RFR | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.96 | 0.01 | 0.03 | 0.04 | 0.05 | 0.05 | 0.06 | 0.02 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.99 | 0.99 | 0.98 | 0.97 | 0.97 | 0.96 | |
| MLPR | 0.98 | 0.96 | 0.90 | 0.83 | 0.83 | 0.72 | 0.03 | 0.06 | 0.09 | 0.12 | 0.12 | 0.16 | 0.05 | 0.09 | 0.13 | 0.16 | 0.16 | 0.22 | 0.99 | 0.96 | 0.90 | 0.83 | 0.81 | 0.72 | |
| LGBMR | 0.98 | 0.98 | 0.98 | 0.96 | 0.96 | 0.96 | 0.01 | 0.03 | 0.04 | 0.05 | 0.05 | 0.05 | 0.02 | 0.05 | 0.05 | 0.06 | 0.07 | 0.07 | 0.99 | 0.98 | 0.98 | 0.97 | 0.97 | 0.97 | |
| Stations | Events | SVR | RFR | MLPR | LGBMR | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ETP (h) | PWE (m) | ETP (h) | PWE (m) | ETP (h) | PWE (m) | ETP (h) | PWE (m) | ||||||||||||||||||
| 1-h | 3-h | 6-h | 1-h | 3-h | 6-h | 1-h | 3-h | 6-h | 1-h | 3-h | 6-h | 1-h | 3-h | 6-h | 1-h | 3-h | 6-h | 1-h | 3-h | 6-h | 1-h | 3-h | 6-h | ||
| Lanyan | No. 23 (Typhoon Megi) | 1 | 1 | 5 | 0.19 | 0.11 | 0.41 | 1 | 4 | 3 | 0.09 | 0.20 | −0.21 | 1 | 3 | 7 | 0.29 | 0.60 | 1.33 | 1 | 0 | 3 | 0.02 | 0.17 | 0.89 |
| No. 26 (Typhoon Saola) | 0 | 2 | 5 | 0.02 | −0.12 | −0.06 | −1 | 1 | 3 | −0.95 | −1.03 | −1.42 | 1 | 2 | 6 | 0.42 | 0.94 | 0.08 | 1 | 1 | 3 | −0.53 | −0.41 | −0.56 | |
| No. 31 (Typhoon Soudelor) | 0 | 0 | 7 | 0.33 | −0.17 | 0.89 | 1 | 2 | 6 | −0.22 | −0.38 | −1.13 | 0 | 1 | 3 | 0.66 | 1.30 | 1.28 | −1 | 1 | 4 | 0.26 | 0.42 | 0.29 | |
| No. 35 (Typhoon Megi) | 1 | 0 | 3 | −0.04 | −0.42 | 0.31 | 0 | 3 | 3 | −0.35 | −0.87 | −1.15 | 1 | 1 | 3 | 0.45 | 0.80 | 0.53 | 0 | 2 | 3 | −0.31 | −0.30 | −0.40 | |
| Simon | No. 23 (Typhoon Megi) | 1 | 3 | 5 | −0.09 | −0.24 | −0.28 | 0 | 3 | 5 | −0.03 | −0.38 | −0.72 | −1 | 1 | 4 | −0.02 | 0.05 | −0.19 | −2 | −1 | 2 | 0.01 | 0.04 | −0.43 |
| No. 26 (Typhoon Saola) | 0 | 1 | 4 | 0.03 | 0.14 | −0.29 | 1 | 2 | 4 | −0.04 | −0.36 | −0.56 | 0 | 2 | 4 | 0.16 | 0.13 | 0.09 | 0 | 1 | 3 | 0.06 | −0.16 | −0.36 | |
| No. 31 (Typhoon Soudelor) | 2 | 3 | 5 | −0.19 | −0.27 | −0.63 | 2 | 3 | 6 | −0.03 | −0.26 | −0.77 | 2 | 3 | 6 | 0.26 | 0.29 | −0.35 | 0 | 1 | 5 | 0.17 | 0.02 | 0.08 | |
| No. 37 (Storm) | 1 | 2 | 5 | 0.10 | 0.10 | −0.43 | 2 | 1 | 4 | −0.04 | 0.30 | −0.36 | 1 | 2 | 5 | 0.11 | 0.19 | −0.50 | −1 | 0 | 3 | −0.01 | 0.35 | 0.02 | |
| Kavalan | No. 25 (Storm) | −1 | 2 | 9 | 0.02 | 0.11 | 0.14 | 0 | 4 | 9 | −0.05 | 0.32 | 0.83 | 1 | 5 | 9 | −0.02 | 0.69 | 0.61 | 1 | 2 | 9 | −0.01 | 0.12 | 0.50 |
| No. 27 (Typhoon Soulik) | 0 | 2 | 4 | 0.16 | 0.23 | 0.19 | 1 | 3 | 4 | 0.10 | 0.09 | 0.06 | 0 | 3 | 4 | 0.20 | 0.56 | 0.31 | 1 | 2 | 4 | 0.14 | 0.10 | 0.09 | |
| No. 33 (Storm) | −2 | 0 | 2 | 0.16 | 0.80 | 0.61 | 0 | 4 | 4 | 0.01 | 0.10 | 0.09 | −3 | 0 | 2 | 0.05 | 0.41 | 0.25 | 0 | 0 | 4 | 0.02 | 0.05 | 0.18 | |
| No. 36 (Typhoon Nesat) | 1 | 3 | 5 | 0.32 | 0.99 | 0.38 | 1 | 4 | 6 | 0.01 | −0.04 | −0.06 | 0 | 3 | 5 | 0.35 | 0.97 | 0.39 | 0 | 2 | 6 | 0.11 | 0.20 | 0.14 | |
| Process | Models | Consumed CPU Time (sec) |
|---|---|---|
| Training (10-fold cross-validation) (1–6 h lead times) | SVR | 192 |
| RFR | 1080 | |
| MLPR | 1873 | |
| LGBMR | 156 | |
| Validation (1–6 h lead times) | SVR | 0.38 |
| RFR | 0.06 | |
| MLPR | 0.01 | |
| LGBMR | 0.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.-D.; Chen, W.-B.; Yeh, S.-H.; Chang, C.-H.; Chen, H. Prediction of River Stage Using Multistep-Ahead Machine Learning Techniques for a Tidal River of Taiwan. Water 2021, 13, 920. https://doi.org/10.3390/w13070920
Guo W-D, Chen W-B, Yeh S-H, Chang C-H, Chen H. Prediction of River Stage Using Multistep-Ahead Machine Learning Techniques for a Tidal River of Taiwan. Water. 2021; 13(7):920. https://doi.org/10.3390/w13070920
Chicago/Turabian StyleGuo, Wen-Dar, Wei-Bo Chen, Sen-Hai Yeh, Chih-Hsin Chang, and Hongey Chen. 2021. "Prediction of River Stage Using Multistep-Ahead Machine Learning Techniques for a Tidal River of Taiwan" Water 13, no. 7: 920. https://doi.org/10.3390/w13070920
APA StyleGuo, W.-D., Chen, W.-B., Yeh, S.-H., Chang, C.-H., & Chen, H. (2021). Prediction of River Stage Using Multistep-Ahead Machine Learning Techniques for a Tidal River of Taiwan. Water, 13(7), 920. https://doi.org/10.3390/w13070920








