Actual Evapotranspiration Estimates in Arid Cold Regions Using Machine Learning Algorithms with In Situ and Remote Sensing Data
Abstract
1. Introduction
2. Materials and Methods
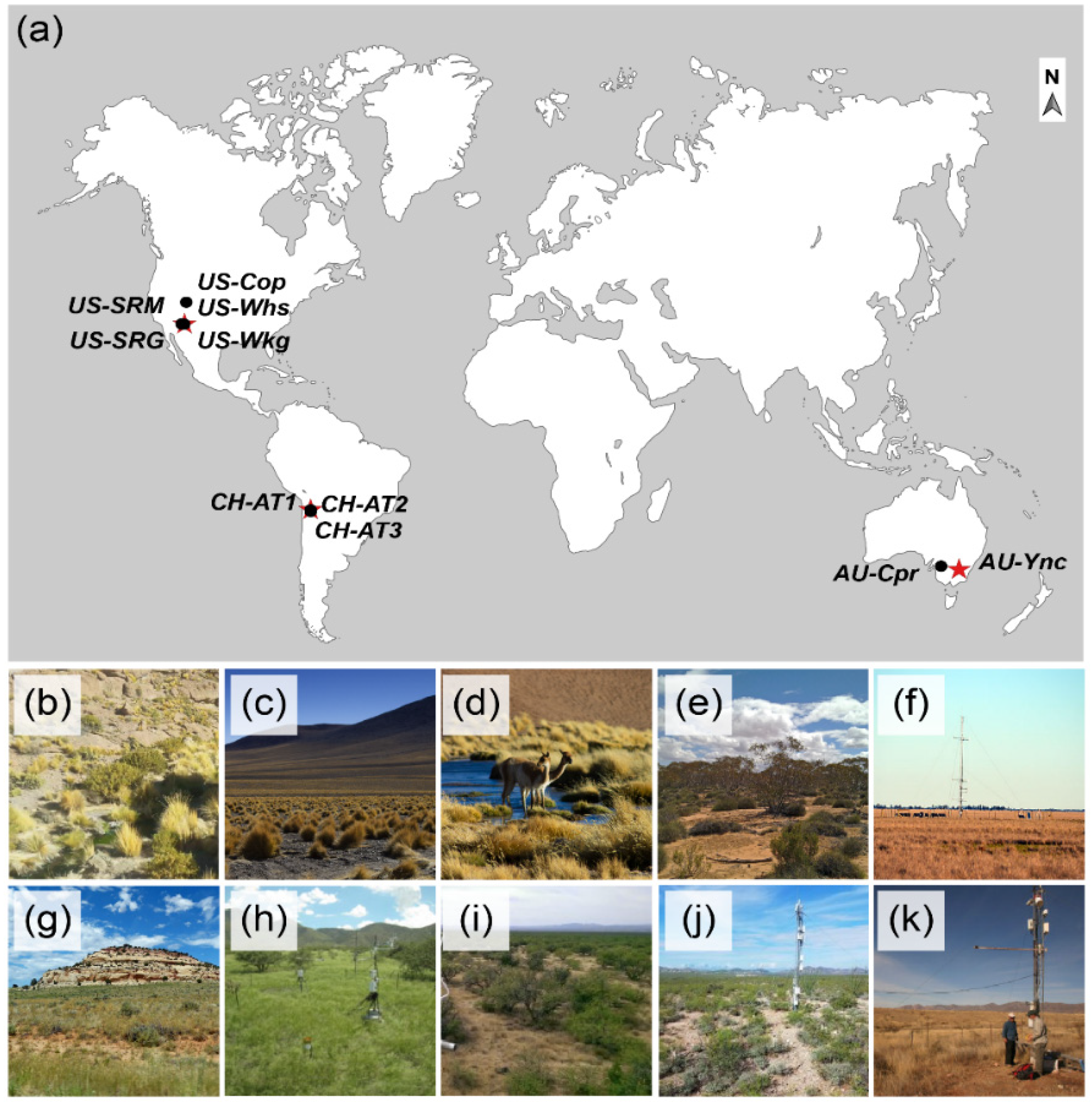
2.1. Study Sites
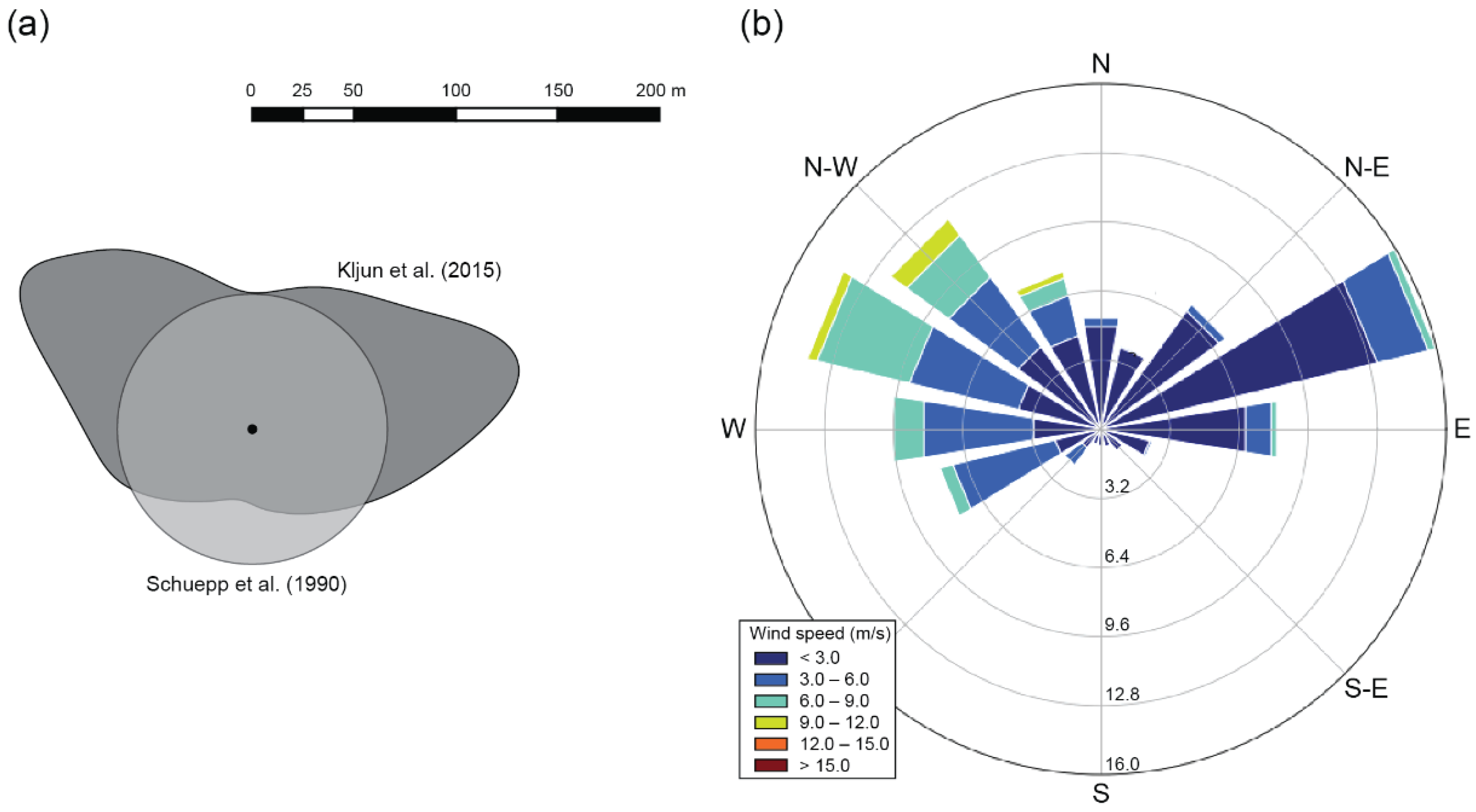
2.2. ETa Fluxes and Meteorological Data
2.3. Remote Sensing and Vegetation Indices
2.3.1. Normalized Difference Vegetation Index (NDVI)
2.3.2. Soil-Adjusted Vegetation Index (SAVI)
2.3.3. Enhance Vegetation Index (EVI)
2.3.4. Normalized Difference Water Index (NDWI)
2.3.5. Normalized Difference Greenness Index (NDGI)
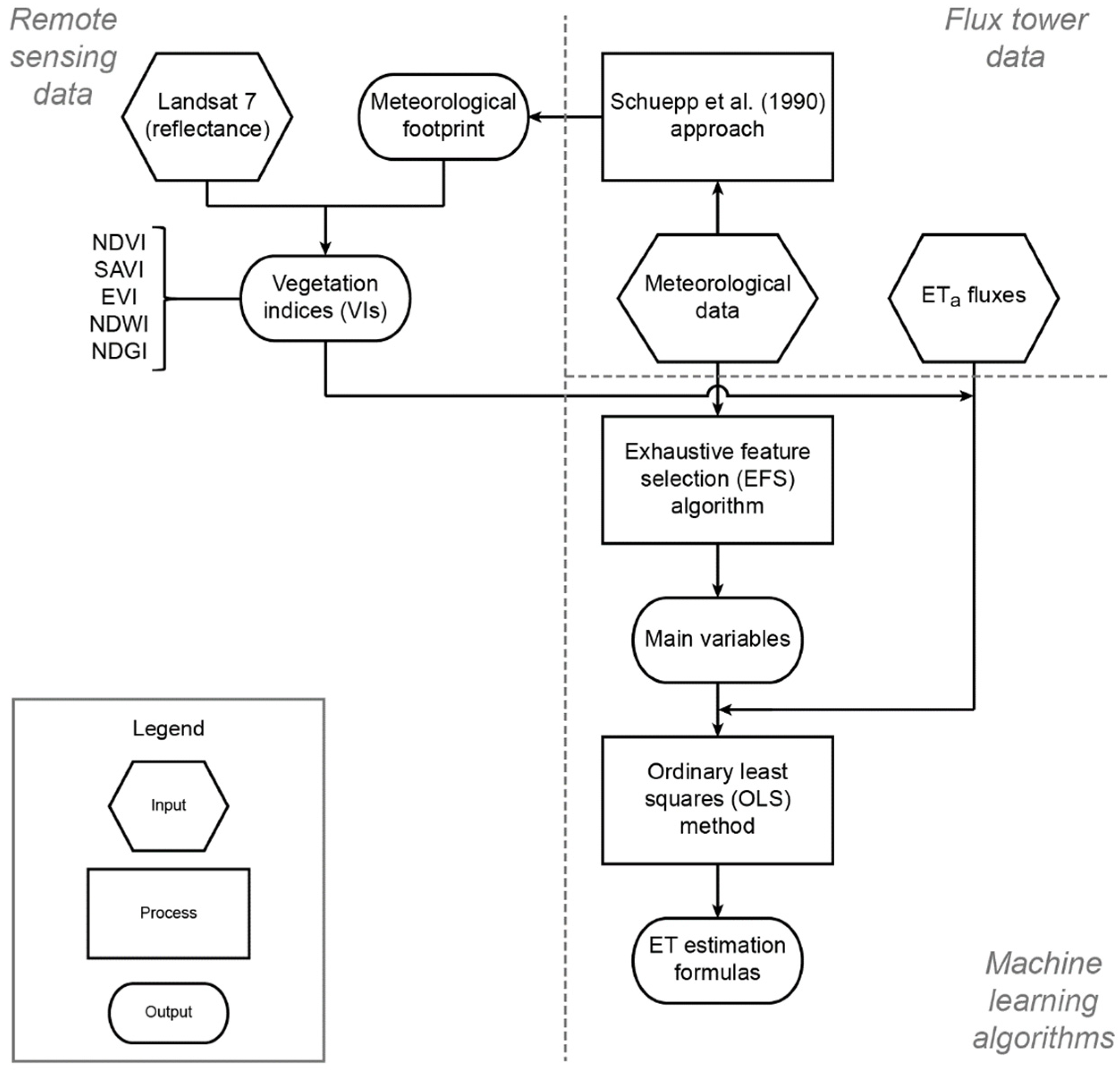
2.4. Determination of Main Variables and ETa Estimates Using Machine Learning
3. Results
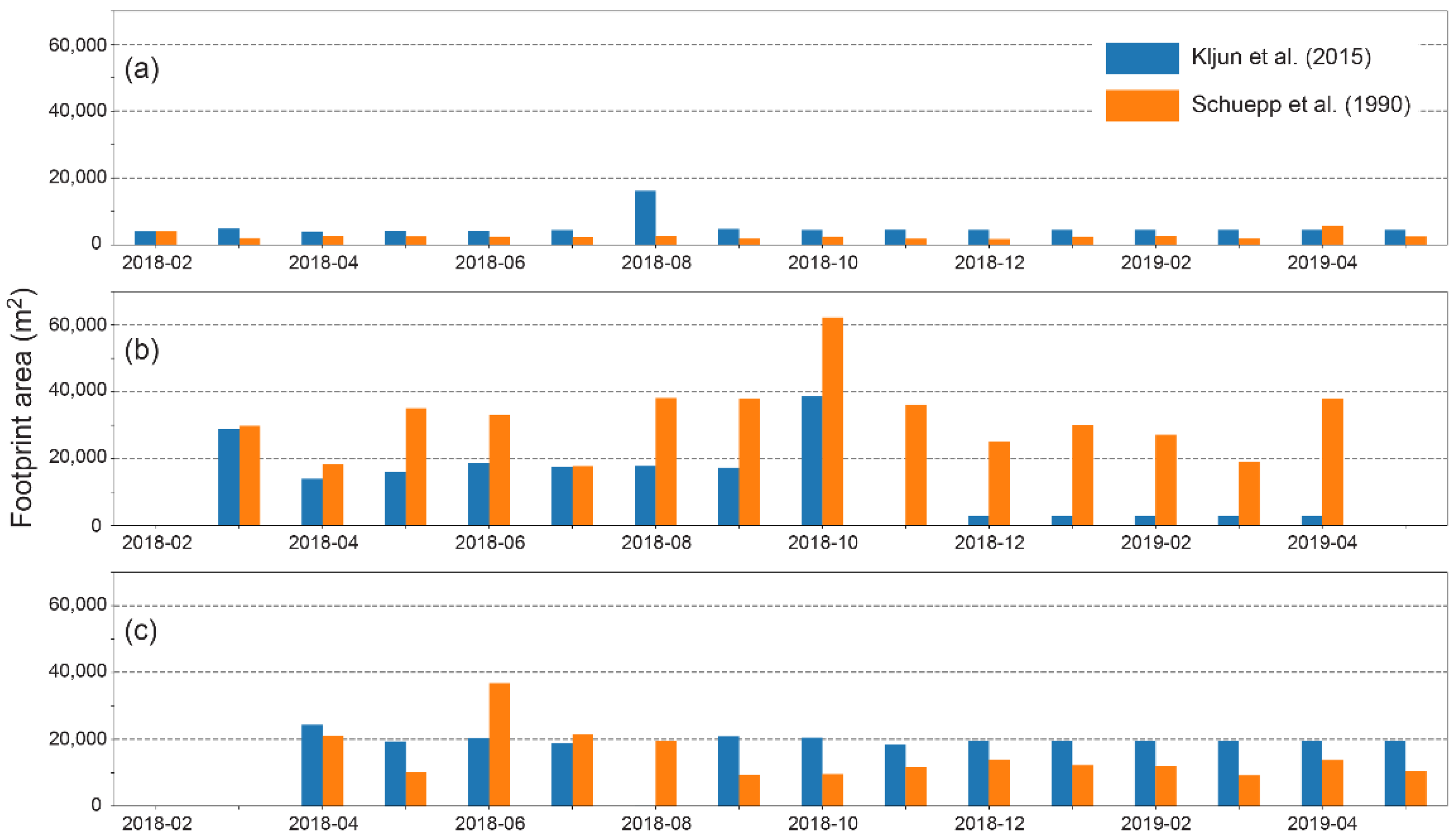
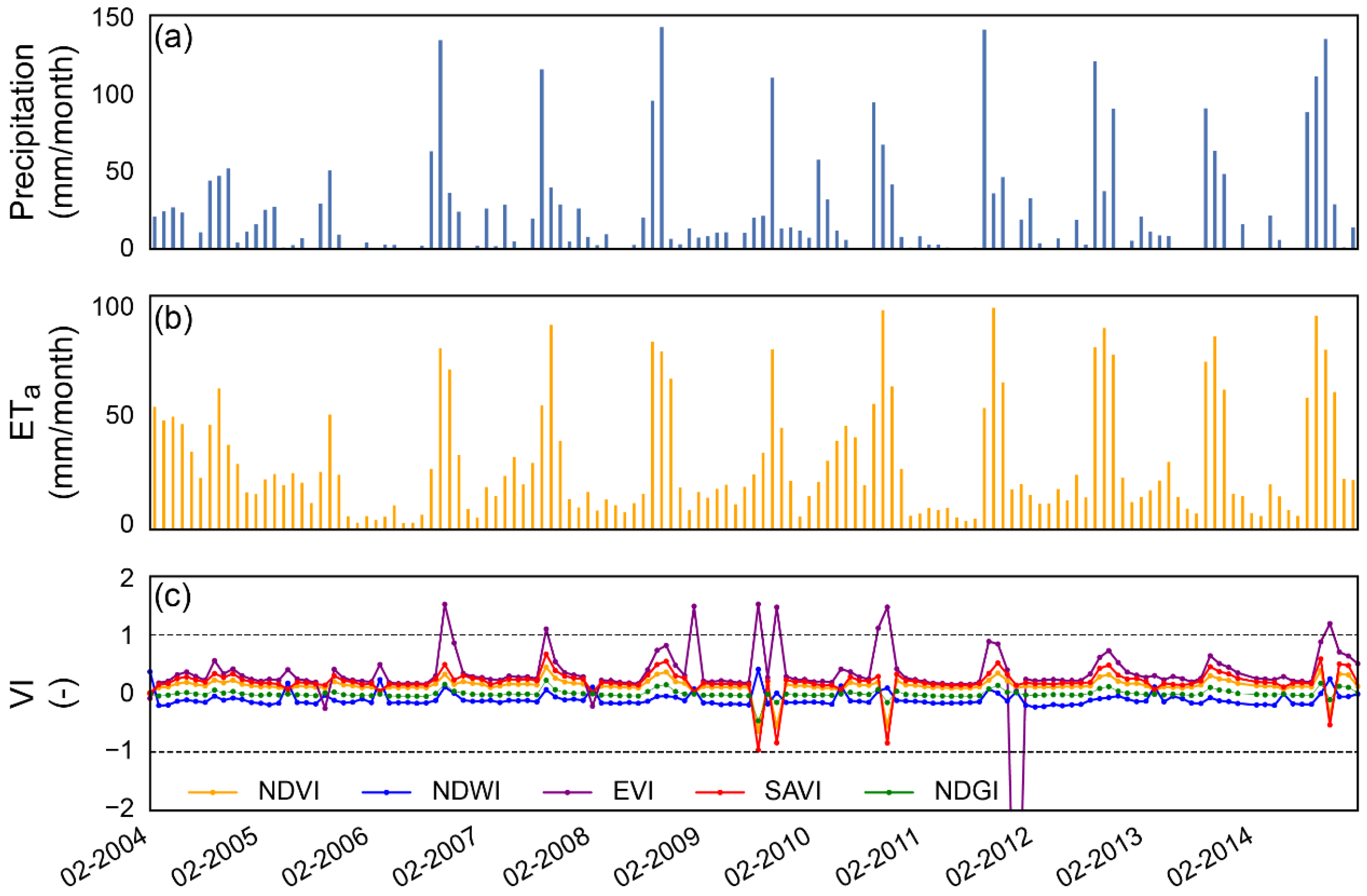
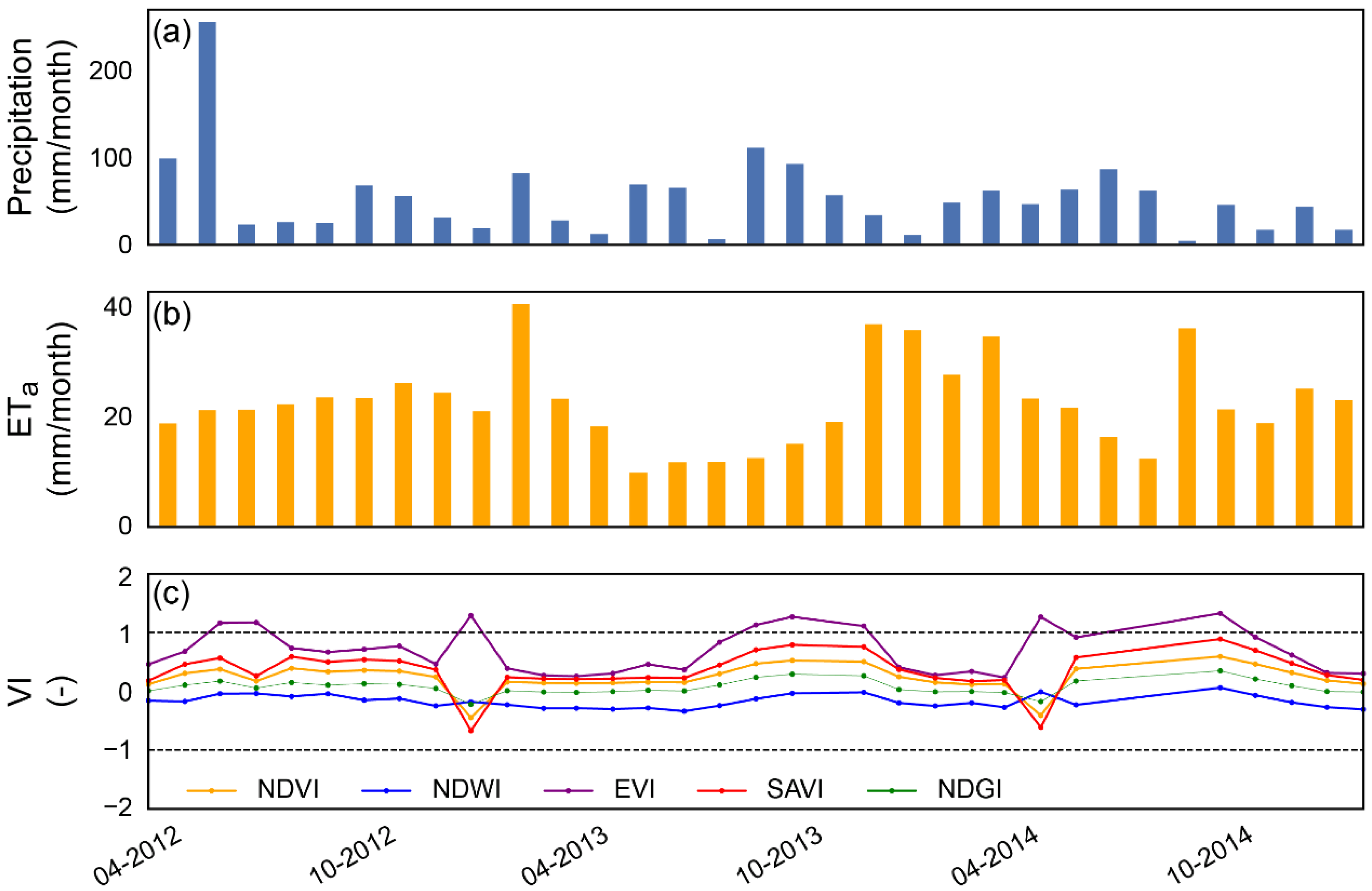
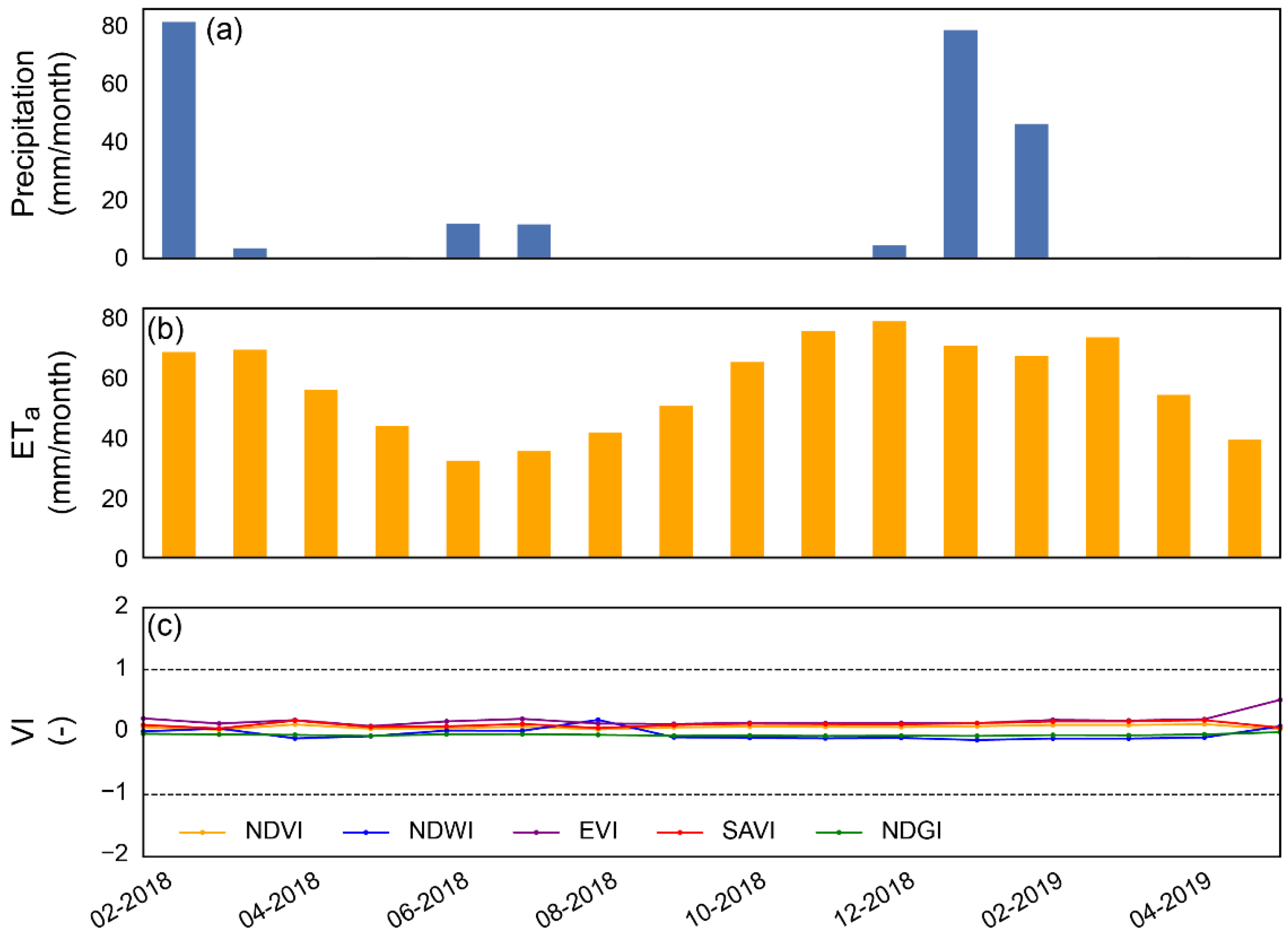
3.1. Remote Sensing Information
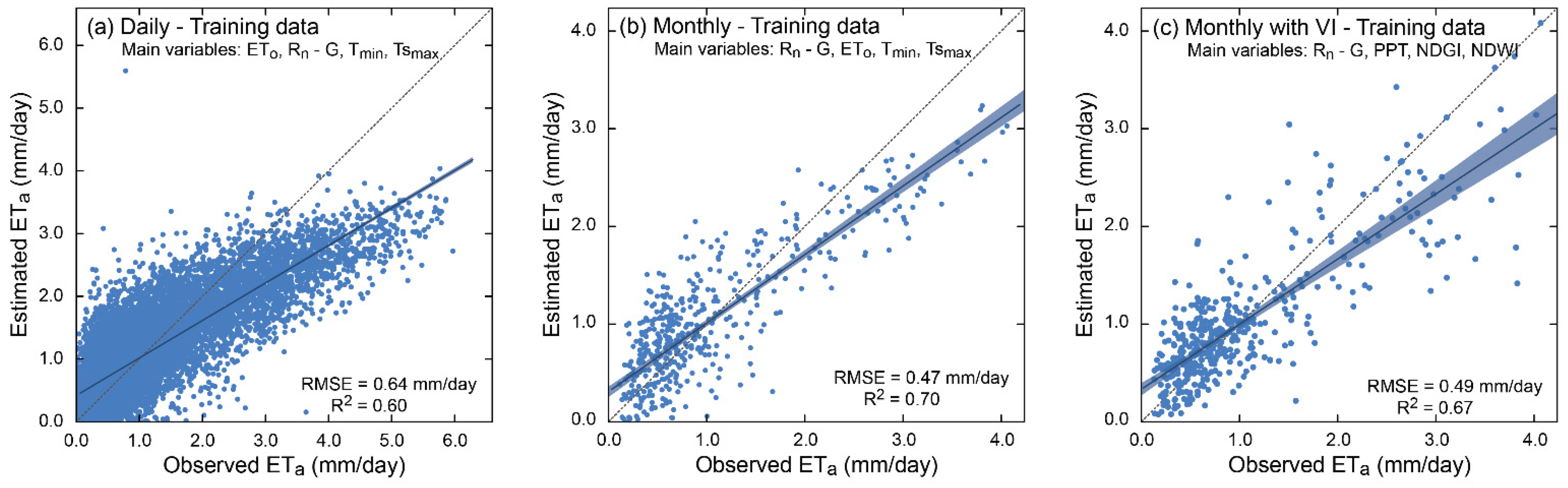
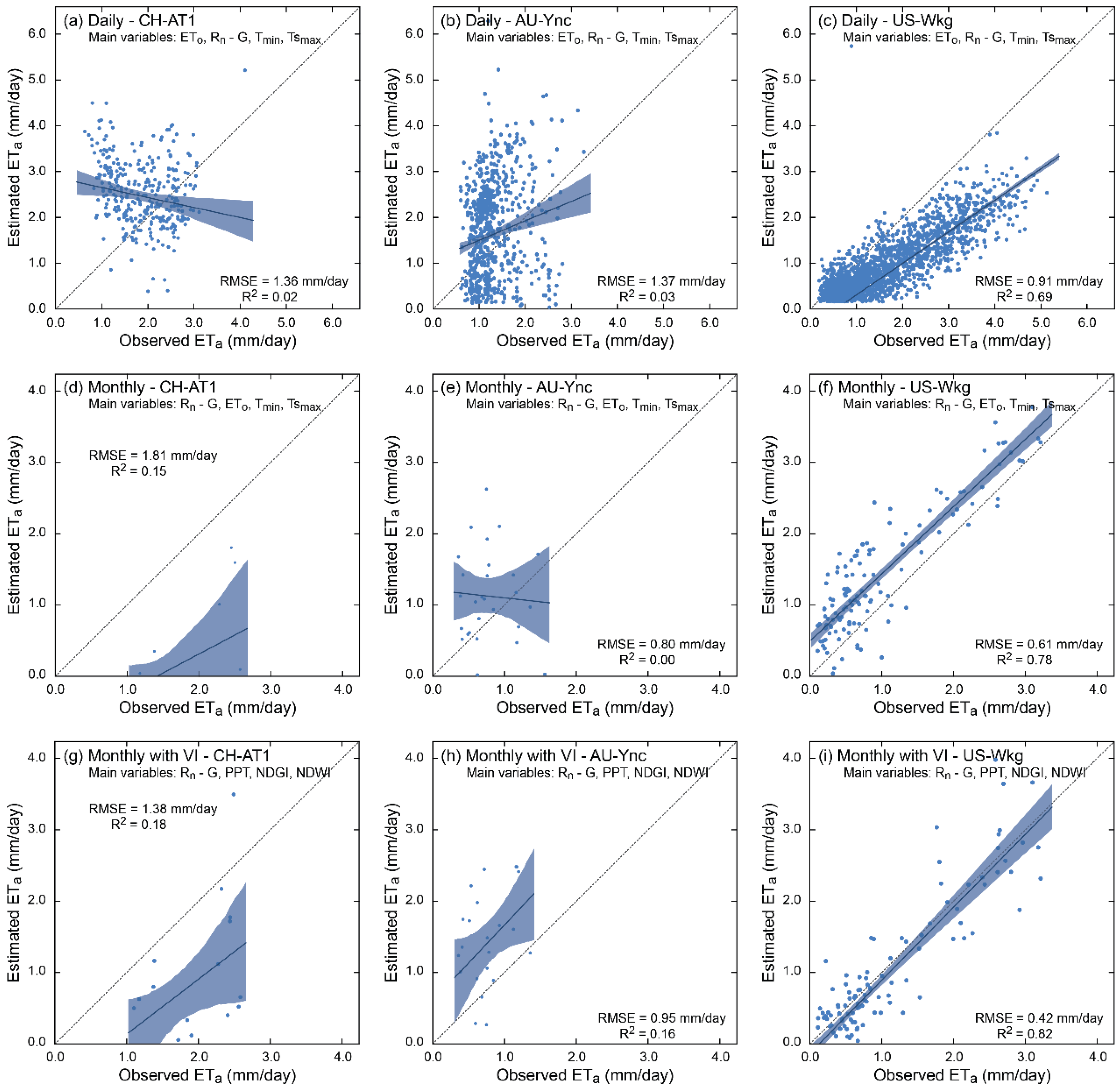
3.2. ETa Estimation Formulae
3.3. Variables Controlling ETa
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Sites Description
Appendix A.1. CH-AT1
Appendix A.2. CH-AT2
Appendix A.3. CH-AT3
Appendix A.4. AU-Cpr
Appendix A.5. AU-Ync
Appendix A.6. US-Cop
Appendix A.7. US-SRG
Appendix A.8. US-SRM
Appendix A.9. UC-Whs
Appendix A.10. US-Wkg
References
- Gaur, M.K.; Squires, V.R. Geographic Extent and Characteristics of the World’s Arid Zones and Their Peoples. In Climate Variability Impacts on Land Use and Livelihoods in Drylands; Gaur, M.K., Squires, V.R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–20. ISBN 978-3-319-56681-8. [Google Scholar]
- Nagler, P.L.; Scott, R.L.; Westenburg, C.; Cleverly, J.R.; Glenn, E.P.; Huete, A.R. Evapotranspiration on Western U.S. Rivers Estimated Using the Enhanced Vegetation Index from MODIS and Data from Eddy Covariance and Bowen Ratio Flux Towers. Remote Sens. Environ. 2005, 97, 337–351. [Google Scholar] [CrossRef]
- Bunting, D.P.; Kurc, S.A.; Glenn, E.P.; Nagler, P.L.; Scott, R.L. Insights for Empirically Modeling Evapotranspiration Influenced by Riparian and Upland Vegetation in Semiarid Regions. J. Arid Environ. 2014, 111, 42–52. [Google Scholar] [CrossRef]
- Carter, C.; Liang, S. Comprehensive Evaluation of Empirical Algorithms for Estimating Land Surface Evapotranspiration. Agric. For. Meteorol. 2018, 256–257, 334–345. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 Dataset and the ONEFlux Processing Pipeline for Eddy Covariance Data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- FLUXNET2015 Dataset. Available online: https://fluxnet.org/data/fluxnet2015-dataset/ (accessed on 2 March 2021).
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration Information Reporting: I. Factors Governing Measurement Accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Mata-González, R.; McLendon, T.; Martin, D.W. The Inappropriate Use of Crop Transpiration Coefficients (Kc) to Estimate Evapotranspiration in Arid Ecosystems: A Review. Arid Land Res. Manag. 2005, 19, 285–295. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Deng, J.; Wang, K.; Malik, A.; Maroufpoor, S. Modeling Long-Term Dynamics of Crop Evapotranspiration Using Deep Learning in a Semi-Arid Environment. Agric. Water Manag. 2020, 241, 106334. [Google Scholar] [CrossRef]
- Mulovhedzi, N.E.; Araya, N.A.; Mengistu, M.G.; Fessehazion, M.K.; du Plooy, C.P.; Araya, H.T.; van der Laan, M. Estimating Evapotranspiration and Determining Crop Coefficients of Irrigated Sweet Potato (Ipomoea Batatas) Grown in a Semi-Arid Climate. Agric. Water Manag. 2020, 233, 106099. [Google Scholar] [CrossRef]
- Glenn, E.P.; Nagler, P.L.; Huete, A.R. Vegetation Index Methods for Estimating Evapotranspiration by Remote Sensing. Surv. Geophys. 2010, 31, 531–555. [Google Scholar] [CrossRef]
- El Masri, B.; Rahman, A.F.; Dragoni, D. Evaluating a New Algorithm for Satellite-Based Evapotranspiration for North American Ecosystems: Model Development and Validation. Agric. For. Meteorol. 2019, 268, 234–248. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of Variable-Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef]
- Billah, M.M.; Goodall, J.L.; Narayan, U.; Reager, J.T.; Lakshmi, V.; Famiglietti, J.S. A Methodology for Evaluating Evapotranspiration Estimates at the Watershed-Scale Using GRACE. J. Hydrol. 2015, 523, 574–586. [Google Scholar] [CrossRef]
- Hu, G.; Jia, L.; Menenti, M. Comparison of MOD16 and LSA-SAF MSG Evapotranspiration Products over Europe for 2011. Remote Sens. Environ. 2015, 156, 510–526. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H. Evaluating the Feasibility of 1016Using Sentinel-2 and Sentinel-3 Satellites for High-Resolution Evapotranspiration Estimations. Remote Sens. Environ. 2019, 221, 157–172. [Google Scholar] [CrossRef]
- DHI-GRAS. User Manual for SEN-ET SNAP Plugin; DHI GRAS: Horsholm, Dnemark, 2020; Available online: https://www.esa-sen4et.org/static/media/sen-et-user-manual-v1.1.0.5d1ac526.pdf (accessed on 22 March 2021).
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring Daily Evapotranspiration over Two California Vineyards Using Landsat 8 in a Multi-Sensor Data Fusion Approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef]
- Yebra, M.; Van Dijk, A.; Leuning, R.; Huete, A.; Guerschman, J.P. Evaluation of Optical Remote Sensing to Estimate Actual Evapotranspiration and Canopy Conductance. Remote Sens. Environ. 2013, 129, 250–261. [Google Scholar] [CrossRef]
- Huete, A.R. Vegetation Indices, Remote Sensing and Forest Monitoring. Geogr. Compass 2012, 6, 513–532. [Google Scholar] [CrossRef]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation Index-Based Crop Coefficients to Estimate Evapotranspiration by Remote Sensing in Agricultural and Natural Ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B.K.; Rover, J. On the Terminology of the Spectral Vegetation Index (NIR − SWIR)/(NIR + SWIR). Int. J. Remote Sens. 2011, 32, 6901–6909. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J.; Hao, X.; Zhu, Q. Sensitivity Studies of the Moisture Effects on MODIS SWIR Reflectance and Vegetation Water Indices. Int. J. Remote Sens. 2008, 29, 7065–7075. [Google Scholar] [CrossRef]
- Sriwongsitanon, N.; Gao, H.; Savenije, H.H.G.; Maekan, E.; Saengsawang, S.; Thianpopirug, S. Comparing the Normalized Difference Infrared Index (NDII) with Root Zone Storage in a Lumped Conceptual Model. Hydrol. Earth Syst. Sci. 2016, 20, 3361–3377. [Google Scholar] [CrossRef]
- Groeneveld, D.P.; Baugh, W.M.; Sanderson, J.S.; Cooper, D.J. Annual Groundwater Evapotranspiration Mapped from Single Satellite Scenes. J. Hydrol. 2007, 344, 146–156. [Google Scholar] [CrossRef]
- Nagler, P.L.; Glenn, E.P.; Nguyen, U.; Scott, R.L.; Doody, T. Estimating Riparian and Agricultural Actual Evapotranspiration by Reference Evapotranspiration and MODIS Enhanced Vegetation Index. Remote Sens. 2013, 5, 3849–3871. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration Evaluation Models Based on Machine Learning Algorithms—A Comparative Study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Torres, A.F.; Walker, W.R.; McKee, M. Forecasting Daily Potential Evapotranspiration Using Machine Learning and Limited Climatic Data. Agric. Water Manag. 2011, 98, 553–562. [Google Scholar] [CrossRef]
- Zhao, W.L.; Gentine, P.; Reichstein, M.; Zhang, Y.; Zhou, S.; Wen, Y.; Lin, C.; Li, X.; Qiu, G.Y. Physics-Constrained Machine Learning of Evapotranspiration. Geophys. Res. Lett. 2019, 46, 14496–14507. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; Fang, B.; Konings, A.G.; Aires, F.; Green, J.K.; Kolassa, J.; Miralles, D.; Prigent, C.; Gentine, P. Water, Energy, and Carbon with Artificial Neural Networks (WECANN): A Statistically Based Estimate of Global Surface Turbulent Fluxes and Gross Primary Productivity Using Solar-Induced Fluorescence. Biogeosciences 2017, 14, 4101–4124. [Google Scholar] [CrossRef]
- Chaney, N.W.; Herman, J.D.; Ek, M.B.; Wood, E.F. Deriving Global Parameter Estimates for the Noah Land Surface Model Using FLUXNET and Machine Learning. J. Geophys. Res. Atmos. 2016, 121, 13218–13235. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Bondeau, A. Towards Global Empirical Upscaling of FLUXNET Eddy Covariance Observations: Validation of a Model Tree Ensemble Approach Using a Biosphere Model. Biogeosciences 2009, 6, 2001–2013. [Google Scholar] [CrossRef]
- Ke, Y.; Im, J.; Park, S.; Gong, H. Downscaling of MODIS One Kilometer Evapotranspiration Using Landsat-8 Data and Machine Learning Approaches. Remote Sens. 2016, 8, 215. [Google Scholar] [CrossRef]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting Carbon Dioxide and Energy Fluxes across Global FLUXNET Sites with Regression Algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef]
- Yang, F.; White, M.A.; Michaelis, A.R.; Ichii, K.; Hashimoto, H.; Votava, P.; Zhu, A.; Nemani, R.R. Prediction of Continental-Scale Evapotranspiration by Combining MODIS and AmeriFlux Data Through Support Vector Machine. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3452–3461. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Kumari, N.; Dharpure, J.K.; Mokhtar, A.; Alsafadi, K.; Kumar, M.; Mehdinejadiani, B.; Ramezani Etedali, H.; Brouziyne, Y.; Towfiqul Islam, A.R.M.; et al. Prediction of Combined Terrestrial Evapotranspiration Index (CTEI) over Large River Basin Based on Machine Learning Approaches. Water 2021, 13, 547. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger Climate Classification Updated. Meteorol. Z. 2006, 259–263. [Google Scholar] [CrossRef]
- Beringer, J.; Walker, J. FLUXNET2015 AU-Ync Jaxa. Available online: https://fluxnet.org/doi/FLUXNET2015/AU-Ync (accessed on 11 February 2021).
- Bowling, D. FLUXNET2015 US-Cop Corral Pocket. Available online: https://fluxnet.org/doi/FLUXNET2015/US-Cop (accessed on 11 February 2021).
- Meyer, W.; Cale, P.; Koerber, G.; Ewenz, C.; Sun, Q. FLUXNET2015 AU-Cpr Calperum. Available online: https://fluxnet.org/doi/FLUXNET2015/AU-Cpr (accessed on 11 February 2021).
- Scott, R. FLUXNET2015 US-SRG Santa Rita Grassland. Available online: https://fluxnet.org/doi/FLUXNET2015/US-SRG (accessed on 11 February 2021).
- Scott, R. FLUXNET2015 US-SRM Santa Rita Mesquite. Available online: https://fluxnet.org/doi/FLUXNET2015/US-SRM (accessed on 11 February 2021).
- Scott, R. FLUXNET2015 US-Whs Walnut Gulch Lucky Hills Shrub. Available online: https://fluxnet.org/doi/FLUXNET2015/US-Whs (accessed on 11 February 2021).
- Scott, R. FLUXNET2015 US-Wkg Walnut Gulch Kendall Grasslands. Available online: https://fluxnet.org/doi/FLUXNET2015/US-Wkg (accessed on 11 February 2021).
- Suárez, F.; Lobos, F.; de la Fuente, A.; Vilà-Guerau de Arellano, J.; Prieto, A.; Meruane, C.; Hartogensis, O. E-DATA: A Comprehensive Field Campaign to Investigate Evaporation Enhanced by Advection in the Hyper-Arid Altiplano. Water 2020, 12, 745. [Google Scholar] [CrossRef]
- Scott, R.L.; Biederman, J.A.; Hamerlynck, E.P.; Barron-Gafford, G.A. The Carbon Balance Pivot Point of Southwestern U.S. Semiarid Ecosystems: Insights from the 21st Century Drought. J. Geophys. Res. Biogeosci. 2015, 120, 2612–2624. [Google Scholar] [CrossRef]
- TERN Monitoring Sites—Calperum. Available online: http://www.ozflux.org.au/monitoringsites/calperum/calperum_pictures.html (accessed on 11 February 2021).
- TERN Monitoring Sites—Yanco. Available online: http://www.ozflux.org.au/monitoringsites/yanco/yanco_pictures.html (accessed on 11 February 2021).
- Zhou, S.; Yu, B.; Zhang, Y.; Huang, Y.; Wang, G. Partitioning Evapotranspiration Based on the Concept of Underlying Water Use Efficiency. Water Resour. Res. 2016, 52, 1160–1175. [Google Scholar] [CrossRef]
- Mosre, J.; Suarez, F. Dataset of Actual Evapotranspiration Estimates in Arid Cold Regions Using Machine Learning Algorithms with In-Situ and Remote Sensing Data. 2021. Available online: https://repositorio.uc.cl/xmlui/bitstream/handle/11534/29294/Thesis_Josefina%20Mosre_Final.pdf (accessed on 11 February 2021).
- Scott, R. US-SRG Site. Available online: https://ameriflux.lbl.gov/sites/siteinfo/US-SRG (accessed on 11 February 2021).
- Scott, R. US-SRM Site. Available online: https://ameriflux.lbl.gov/sites/siteinfo/US-SRM#image-gallery (accessed on 11 February 2021).
- Scott, R. US-Whs: Walnut Gulch Lucky Hills Shrub. Available online: https://ameriflux.lbl.gov/sites/siteinfo/US-Whs#image-gallery (accessed on 11 February 2021).
- Schuepp, P.H.; Leclerc, M.Y.; MacPherson, J.I.; Desjardins, R.L. Footprint Prediction of Scalar Fluxes from Analytical Solutions of the Diffusion Equation. Bound. Layer Meteorol. 1990, 50, 355–373. [Google Scholar] [CrossRef]
- Leclerc, M.Y.; Foken, T. Footprints in Micrometeorology and Ecology; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-54544-3. [Google Scholar]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A Simple Two-Dimensional Parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Riad, P.; Graefe, S.; Hussein, H.; Buerkert, A. Landscape Transformation Processes in Two Large and Two Small Cities in Egypt and Jordan over the Last Five Decades Using Remote Sensing Data. Landsc. Urban Plan. 2020, 197, 103766. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Nagler, P.L.; Morino, K.; Murray, R.S.; Osterberg, J.; Glenn, E.P. An Empirical Algorithm for Estimating Agricultural and Riparian Evapotranspiration Using MODIS Enhanced Vegetation Index and Ground Measurements of ET. I. Description of Method. Remote Sens. 2009, 1, 1273–1297. [Google Scholar] [CrossRef]
- Kumari, N.; Saco, P.M.; Rodriguez, J.F.; Johnstone, S.A.; Srivastava, A.; Chun, K.P.; Yetemen, O. The Grass Is Not Always Greener on the Other Side: Seasonal Reversal of Vegetation Greenness in Aspect-Driven Semiarid Ecosystems. Geophys. Res. Lett. 2020, 47, e2020GL088918. [Google Scholar] [CrossRef]
- Odi-Lara, M.; Campos, I.; Neale, C.M.U.; Ortega-Farías, S.; Poblete-Echeverría, C.; Balbontín, C.; Calera, A. Estimating Evapotranspiration of an Apple Orchard Using a Remote Sensing-Based Soil Water Balance. Remote Sens. 2016, 8, 253. [Google Scholar] [CrossRef]
- Jovanovic, N.; Garcia, C.L.; Bugan, R.D.H.; Teich, I.; Rodriguez, C.M.G. Validation of Remotely-Sensed Evapotranspiration and NDWI Using Ground Measurements at Riverlands, South Africa. Water 2014, 40, 211–220. [Google Scholar] [CrossRef]
- Yang, W.; Kobayashi, H.; Wang, C.; Shen, M.; Chen, J.; Matsushita, B.; Tang, Y.; Kim, Y.; Bret-Harte, M.S.; Zona, D.; et al. A Semi-Analytical Snow-Free Vegetation Index for Improving Estimation of Plant Phenology in Tundra and Grassland Ecosystems. Remote Sens. Environ. 2019, 228, 31–44. [Google Scholar] [CrossRef]
- Yıldırım, A.A.; Özdoğan, C.; Watson, D.; Yıldırım, A.A.; Özdoğan, C.; Watson, D. Parallel Data Reduction Techniques for Big Datasets. Available online: https://www.igi-global.com/gateway/chapter/85450 (accessed on 11 February 2021).
- Wang, L.; Wang, Y.; Chang, Q. Feature Selection Methods for Big Data Bioinformatics: A Survey from the Search Perspective. Methods 2016, 111, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Stoyan, G.; Baran, A. Elementary Numerical Mathematics for Programmers and Engineers; Springer International Publishing: Basel, Switzerland, 2016; ISBN 978-3-319-44659-2. [Google Scholar]
- Wang, K.; Dickinson, R.E.; Wild, M.; Liang, S. Evidence for Decadal Variation in Global Terrestrial Evapotranspiration between 1982 and 2002: 1. Model Development. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Jarchow, C.J.; Nagler, P.L.; Glenn, E.P.; Ramírez-Hernández, J.; Rodríguez-Burgueño, J.E. Evapotranspiration by Remote Sensing: An Analysis of the Colorado River Delta before and after the Minute 319 Pulse Flow to Mexico. Ecol. Eng. 2017, 106, 725–732. [Google Scholar] [CrossRef]
- Adnan, S.; Ullah, K.; Khan, A.H.; Gao, S. Meteorological Impacts on Evapotranspiration in Different Climatic Zones of Pakistan. J. Arid Land 2017, 9, 938–952. [Google Scholar] [CrossRef]
- Eslamian, S.; Khordadi, M.J.; Abedi-Koupai, J. Effects of Variations in Climatic Parameters on Evapotranspiration in the Arid and Semi-Arid Regions. Glob. Planet. Chang. 2011, 78, 188–194. [Google Scholar] [CrossRef]
- Mokhtari, M.H.; Ahmad, B.; Hoveidi, H.; Busu, I. Sensitivity Analysis of METRIC–Based Evapotranspiration Algorithm. Int. J. Environ. Res. 2013, 7, 407–422. [Google Scholar] [CrossRef]
- Wang, K.; Wang, P.; Li, Z.; Cribb, M.; Sparrow, M. A Simple Method to Estimate Actual Evapotranspiration from a Combination of Net Radiation, Vegetation Index, and Temperature. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Badgley, G.; Fisher, J.B.; Jiménez, C.; Tu, K.P.; Vinukollu, R. On Uncertainty in Global Terrestrial Evapotranspiration Estimates from Choice of Input Forcing Datasets. J. Hydrometeorol. 2015, 16, 1449–1455. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. An Improved Method for Estimating Global Evapotranspiration Based on Satellite Determination of Surface Net Radiation, Vegetation Index, Temperature, and Soil Moisture. J. Hydrometeorol. 2008, 9, 712–727. [Google Scholar] [CrossRef]
- Irmak, S.; Istanbulluoglu, E.; Irmak, A. An Evaluation of Evapotranspiration Model Complexity against Performance in Comparison with Bowen Ratio Energy Balance Measurements. Trans. ASABE 2008, 51, 1295–1310. [Google Scholar] [CrossRef]
- Lobos-Roco, F.; Hartogensis, O.; Vilà-Guerau de Arellano, J.; de la Fuente, A.; Muñoz, R.; Rutllant, J.; Suárez, F. Local Evaporation Controlled by Regional Atmospheric Circulation in the Altiplano of the Atacama Desert. Atmos. Chem. Phys. Discuss. 2021, 1–38. [Google Scholar] [CrossRef]
- Seevers, P.M.; Ottmann, R.W. Evapotranspiration Estimation Using a Normalized Difference Vegetation Index Transformation of Satellite Data. Hydrol. Sci. J. 1994, 39, 333–345. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Jarchow, C.J.; Didan, K.; Barreto-Muñoz, A.; Nagler, P.L.; Glenn, E.P. Application and Comparison of the MODIS-Derived Enhanced Vegetation Index to VIIRS, Landsat 5 TM and Landsat 8 OLI Platforms: A Case Study in the Arid Colorado River Delta, Mexico. Sensors 2018, 18, 1546. [Google Scholar] [CrossRef]
- Scott, R.L.; Jenerette, G.D.; Potts, D.L.; Huxman, T.E. Effects of Seasonal Drought on Net Carbon Dioxide Exchange from a Woody-Plant-Encroached Semiarid Grassland. J. Geophys. Res. Biogeosci. 2009, 114. [Google Scholar] [CrossRef]
- Scott, R.L.; Hamerlynck, E.P.; Jenerette, G.D.; Moran, M.S.; Barron-Gafford, G.A. Carbon Dioxide Exchange in a Semidesert Grassland through Drought-Induced Vegetation Change. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Meyer, W.S.; Kondrlovà, E.; Koerber, G.R. Evaporation of Perennial Semi-Arid Woodland in Southeastern Australia Is Adapted for Irregular but Common Dry Periods. Hydrol. Processes 2015, 29, 3714–3726. [Google Scholar] [CrossRef]
- Restrepo-Coupe, N.; Huete, A.; Davies, K.; Cleverly, J.; Beringer, J.; Eamus, D.; van Gorsel, E.; Hutley, L.B.; Meyer, W.S. MODIS Vegetation Products as Proxies of Photosynthetic Potential along a Gradient of Meteorologically and Biologically Driven Ecosystem Productivity. Biogeosciences 2016, 13, 5587–5608. [Google Scholar] [CrossRef]
- Centro de Ciencias del Clima y la Resiliencia Explorador Climático. Available online: http://explorador.cr2.cl/ (accessed on 11 February 2021).
- Yee, M.S.; Pauwels, V.R.N.; Daly, E.; Beringer, J.; Rüdiger, C.; McCabe, M.F.; Walker, J.P. A Comparison of Optical and Microwave Scintillometers with Eddy Covariance Derived Surface Heat Fluxes. Agric. For. Meteorol. 2015, 213, 226–239. [Google Scholar] [CrossRef]
| Site | Location | Elevation (m ASL) | IGBP Land Cover Classification | |||
|---|---|---|---|---|---|---|
| Latitude (°) | Longitude (°) | Mean Annual Precipitation (mm) | Mean Annual Temperature (°C) | |||
| CH-AT1 | 22.02 S | 68.05 W | 4182 | Barren or sparsely vegetated | 78 | 5.8 |
| CH-AT2 | 22.01 S | 68.05 W | 4330 | Barren or sparsely vegetated | 78 | 5.8 |
| CH-AT3 | 22.52 S | 68.02 W | 4255 | Barren or sparsely vegetated | 106 | 1.7 |
| AU-Cpr | 34.00 S | 140.59 E | 166 | Open shrubland | 250 | 18 |
| AU-Ync | 34.99 S | 146.29 E | 125 | Grassland | 419 | 17.3 |
| US-Cop | 38.09 N | 109.39 W | 1520 | Grassland | 216 | 12 |
| US-SRG | 31.79 N | 110.83 W | 1290 | Grassland | 377 | 19 |
| US-SRM | 31.82 N | 110.87 W | 1116 | Open shrubland | 377 | 19 |
| US-Whs | 31.74 N | 110.05 W | 1370 | Grassland | 285 | 17.6 |
| US-Wkg | 31.74 N | 109.94 W | 1530 | Grassland | 294 | 17.3 |
| Site | Time Period | Sensor Height (m) | Dominant Vegetation Type | Vegetation Height (m) | |
|---|---|---|---|---|---|
| Start Date | End Date | ||||
| CH-AT1 | 18-01-2018 | 29-05-2019 | 2.11 | Oxychloe andina and grass Deyeuxia sp. | 0.7 |
| CH-AT2 | 22-02-2018 | 25-04-2019 | 2.11 | Festuca genera | 0.2 |
| CH-AT3 | 19-04-2018 | 28-05-2019 | 2.49 | Oxychloe andina, Festuca and Deyeuxia genera grass | 0.2 |
| AU-Cpr | 01-01-2010 | 31-12-2014 | 20 | Several species of Eucalyptus | 4.0 |
| AU-Ync | 01-01-2012 | 31-12-2014 | 8 | perennial tussock grasses | 0.3 |
| US-Cop | 01-01-2001 | 31-12-2007 | 1.85 | Hilaria jamesii, Stipa hymenoides bunchgrasses and Coleogyne ramosissima shrub | 0.3 |
| US-SRG | 01-01-2008 | 31-12-2014 | 14 | South African warm-season bunchgrass, Eragrostis lehmanniana, and Prosopis velutina | 0.3 |
| US-SRM | 01-01-2004 | 31-12-2014 | 8 | Prosopis velutina and native and nonnative perennial grasses, subshrubs, and scattered succulents | 1.5 |
| US-Whs | 01-01-2007 | 31-12-2014 | 5 | Parthenium incanum, Acacia constricta, Larrea tridentata, and Flourensia cernua | 4.3 |
| US-Wkg | 01-01-2004 | 31-12-2014 | 5 | Eragrostis lehmanniana, Bouteloua eripoda, and Aristida spp. | 0.3 |
| Variable | Symbol | Units | Variable | Symbol | Units |
|---|---|---|---|---|---|
| Available energy | Rn − G | MJ m−2 d−1 | Volumetric water content | WVC | cm3 cm−3 |
| Precipitation | PPT | mm | Water vapor deficit | VPD | kPa |
| Mean temperature | T | °C | Wind speed | WS | m s−1 |
| Minimum temperature | Tmin | °C | Reference evapotranspiration | ETo | mm |
| Maximum temperature | Tmax | °C | Normalized difference vegetation index | NDVI | - |
| Soil temperature | Ts | °C | Soil-adjusted vegetation index | SAVI | - |
| Minimum soil temperature | Tsmin | °C | Enhanced vegetation index | EVI | - |
| Maximum soil temperature | Tsmax | °C | Normalized difference water index | NDWI | |
| Relative humidity | RH | - | Normalized difference greenness index | NDGI | - |
| Site | Footprint Model, R2 and RMSE | NDVI | SAVI | EVI | NDWI | NDGI |
|---|---|---|---|---|---|---|
| CH-AT1 | Kljun mean | 0.09 | 0.14 | 0.20 | −0.03 | −0.04 |
| Schuepp mean | 0.08 | 0.12 | 0.19 | −0.03 | −0.04 | |
| R2 | 0.91 | 0.92 | 0.94 | 0.88 | 0.84 | |
| RMSE | 0.01 | 0.02 | 0.03 | 0.03 | 0.01 | |
| CH-AT2 | Kljun mean | 0.04 | 0.07 | 0.08 | 0.00 | −0.06 |
| Schuepp mean | 0.05 | 0.07 | 0.09 | 0.01 | −0.06 | |
| R2 | 0.96 | 0.96 | 0.95 | 0.99 | 0.93 | |
| RMSE | 0.00 | 0.01 | 0.01 | 0.01 | 0.00 | |
| CH-AT3 | Kljun mean | 0.15 | 0.22 | 0.27 | 0.16 | 0.00 |
| Schuepp mean | 0.22 | 0.33 | 0.41 | 0.25 | 0.05 | |
| R2 | 0.99 | 0.99 | 0.99 | 0.87 | 0.99 | |
| RMSE | 0.09 | 0.14 | 0.17 | 0.10 | 0.06 |
| Site | ETa Estimate Formula | R2 | Notes |
|---|---|---|---|
| Global | 0.60 | Daily | |
| 0.70 | Monthly | ||
| 0.67 | Monthly with VI | ||
| CH-AT1 | 0.90 | Daily | |
| 0.99 | Monthly | ||
| 0.97 | Monthly with VI | ||
| CH-AT2 | 0.25 | Daily | |
| 0.83 | Monthly | ||
| 0.83 | Monthly with VI | ||
| CH-AT3 | 0.82 | Daily | |
| 0.98 | Monthly | ||
| 0.99 | Monthly with VI | ||
| AU-Cpr | 0.58 | Daily | |
| 0.45 | Monthly | ||
| 0.34 | Monthly with VI | ||
| AU-Ync | 0.30 | Daily | |
| 0.55 | Monthly | ||
| 0.67 | Monthly with VI | ||
| US-Cop | 0.33 | Daily | |
| 0.55 | Monthly | ||
| 0.21 | Monthly with VI | ||
| US-SRG | 0.78 | Daily | |
| 0.89 | Monthly | ||
| 0.85 | Monthly with VI | ||
| US-SRM | 0.76 | Daily | |
| 0.89 | Monthly | ||
| 0.90 | Monthly with VI | ||
| US-Whs | 0.77 | Daily | |
| 0.91 | Monthly | ||
| 0.90 | Monthly with VI | ||
| US-Wkg | 0.71 | Daily | |
| 0.90 | Monthly | ||
| 0.89 | Monthly with VI |
| Variable | Daily | Monthly | Monthly with VI | Variable | Daily | Monthly | Monthly with VI |
|---|---|---|---|---|---|---|---|
| Rn − G | 8 | 7 | 4 | Tsmax | 3 | 1 | 1 |
| VPD | 3 | 3 | 5 | PPT | 0 | 3 | 4 |
| VWC | 6 | 2 | 2 | ETo | 6 | 4 | 3 |
| RH | 1 | 2 | 2 | WS | 1 | 3 | 1 |
| T | 5 | 5 | 4 | NDVI | - | - | 0 |
| Tmin | 2 | 2 | 1 | NDWI | - | - | 8 |
| Tmax | 1 | 1 | 0 | SAVI | - | - | 0 |
| Ts | 3 | 6 | 3 | EVI | - | - | 0 |
| Tsmin | 1 | 1 | 0 | NDGI | - | - | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mosre, J.; Suárez, F. Actual Evapotranspiration Estimates in Arid Cold Regions Using Machine Learning Algorithms with In Situ and Remote Sensing Data. Water 2021, 13, 870. https://doi.org/10.3390/w13060870
Mosre J, Suárez F. Actual Evapotranspiration Estimates in Arid Cold Regions Using Machine Learning Algorithms with In Situ and Remote Sensing Data. Water. 2021; 13(6):870. https://doi.org/10.3390/w13060870
Chicago/Turabian StyleMosre, Josefina, and Francisco Suárez. 2021. "Actual Evapotranspiration Estimates in Arid Cold Regions Using Machine Learning Algorithms with In Situ and Remote Sensing Data" Water 13, no. 6: 870. https://doi.org/10.3390/w13060870
APA StyleMosre, J., & Suárez, F. (2021). Actual Evapotranspiration Estimates in Arid Cold Regions Using Machine Learning Algorithms with In Situ and Remote Sensing Data. Water, 13(6), 870. https://doi.org/10.3390/w13060870






