Effect of a Submerged Vane-Field on the Flow Pattern of a Movable Bed Channel with a 90° Lateral Diversion
Abstract
1. Introduction
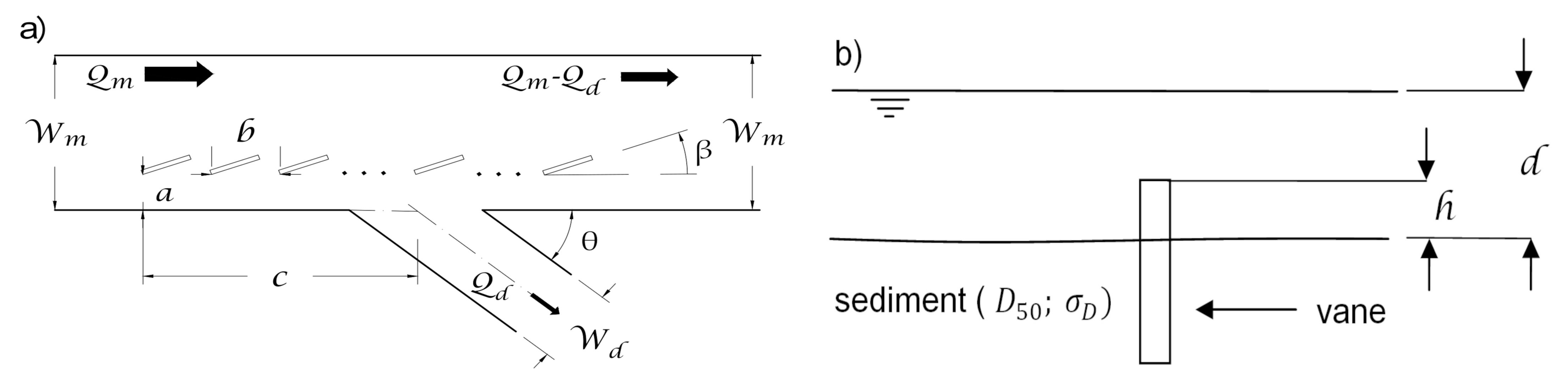
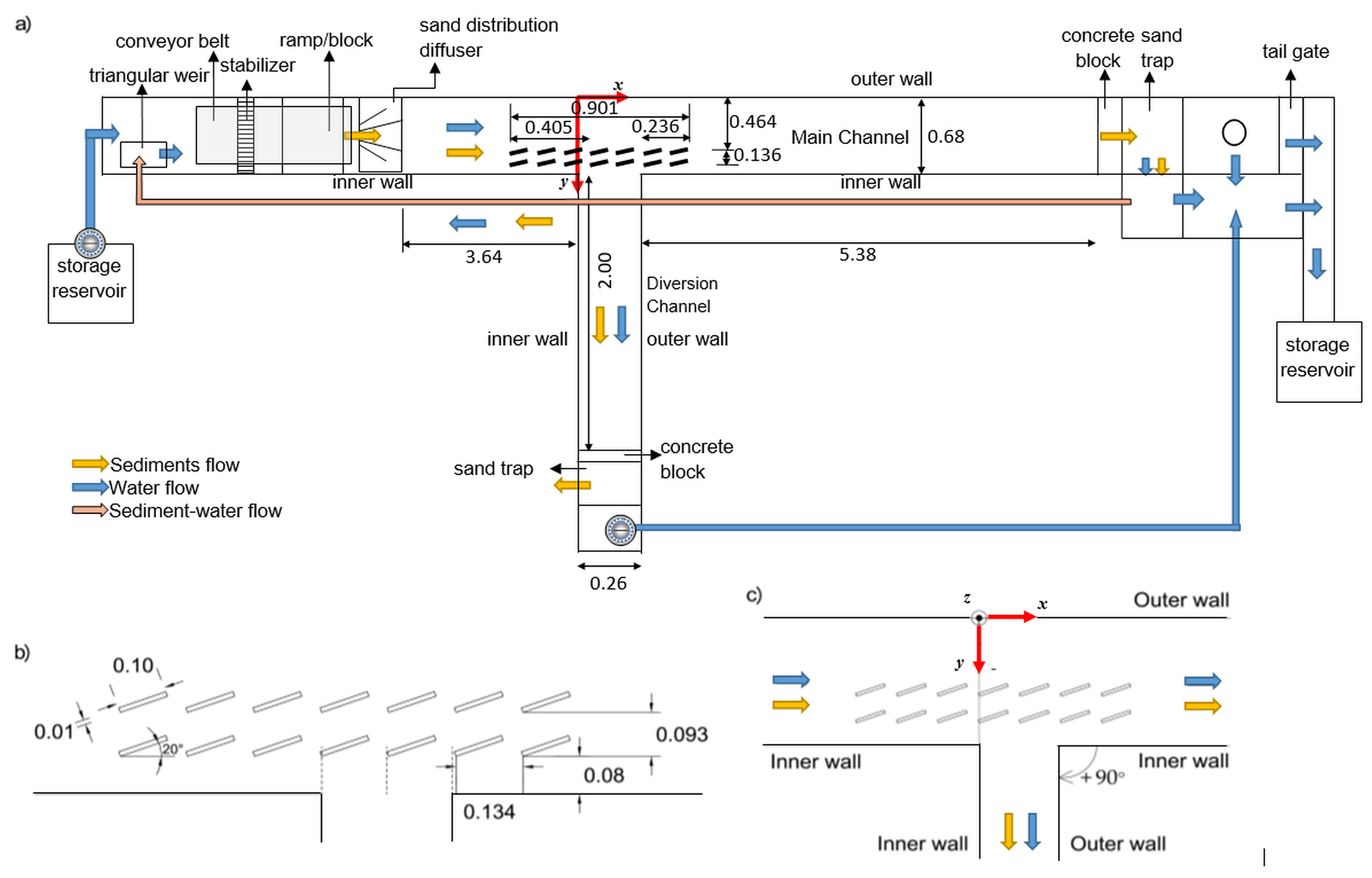
2. Experimental Set-up and Procedure, and Data Processing
2.1. Experimental Set-Up and Procedure
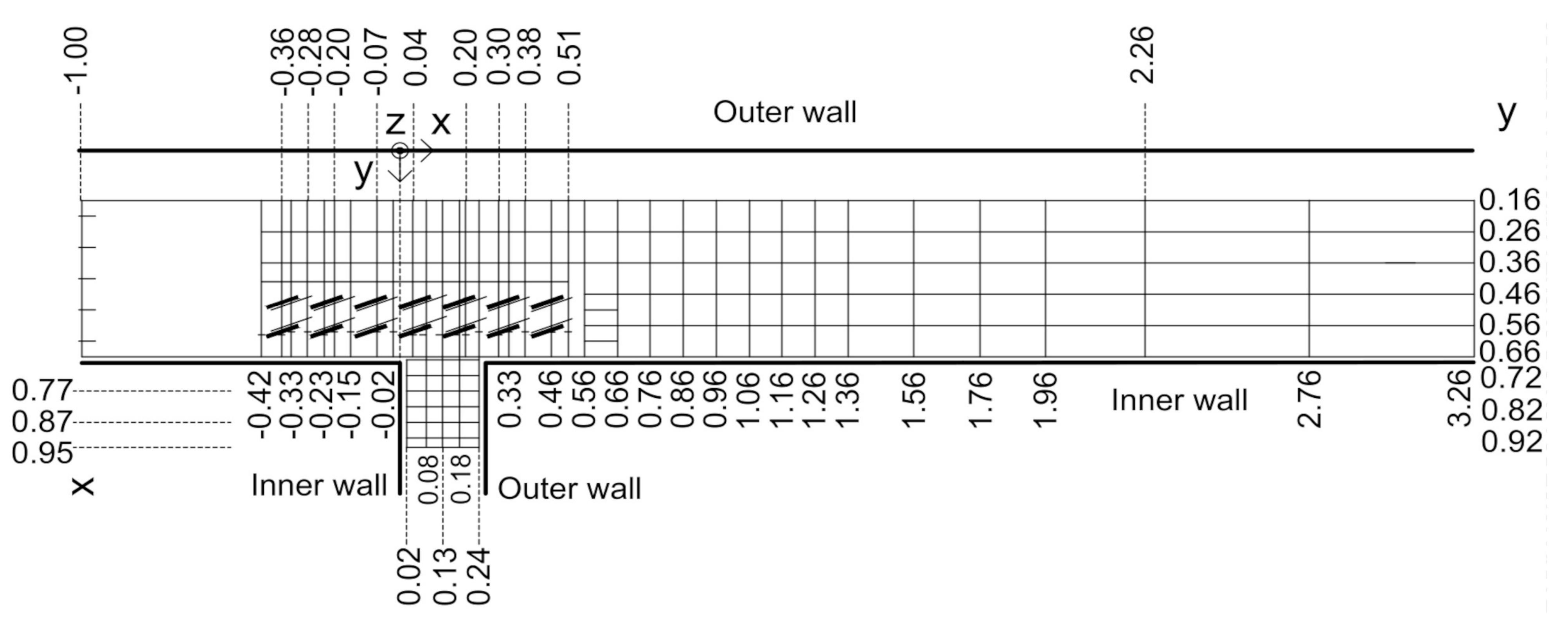
2.2. Data Processing
3. Results and Discussion
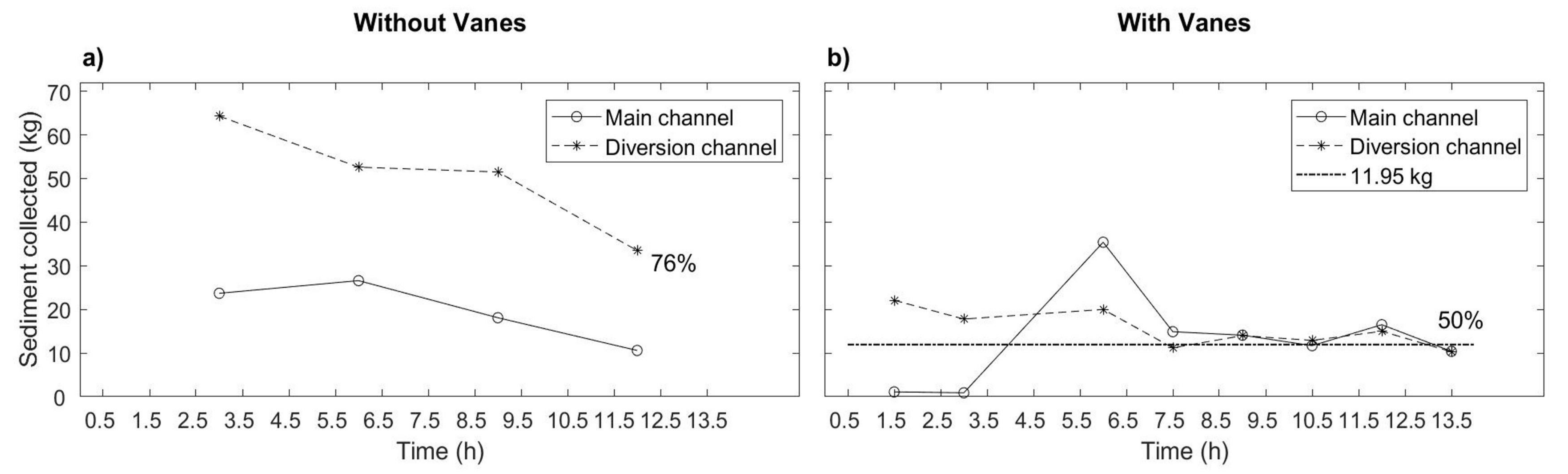
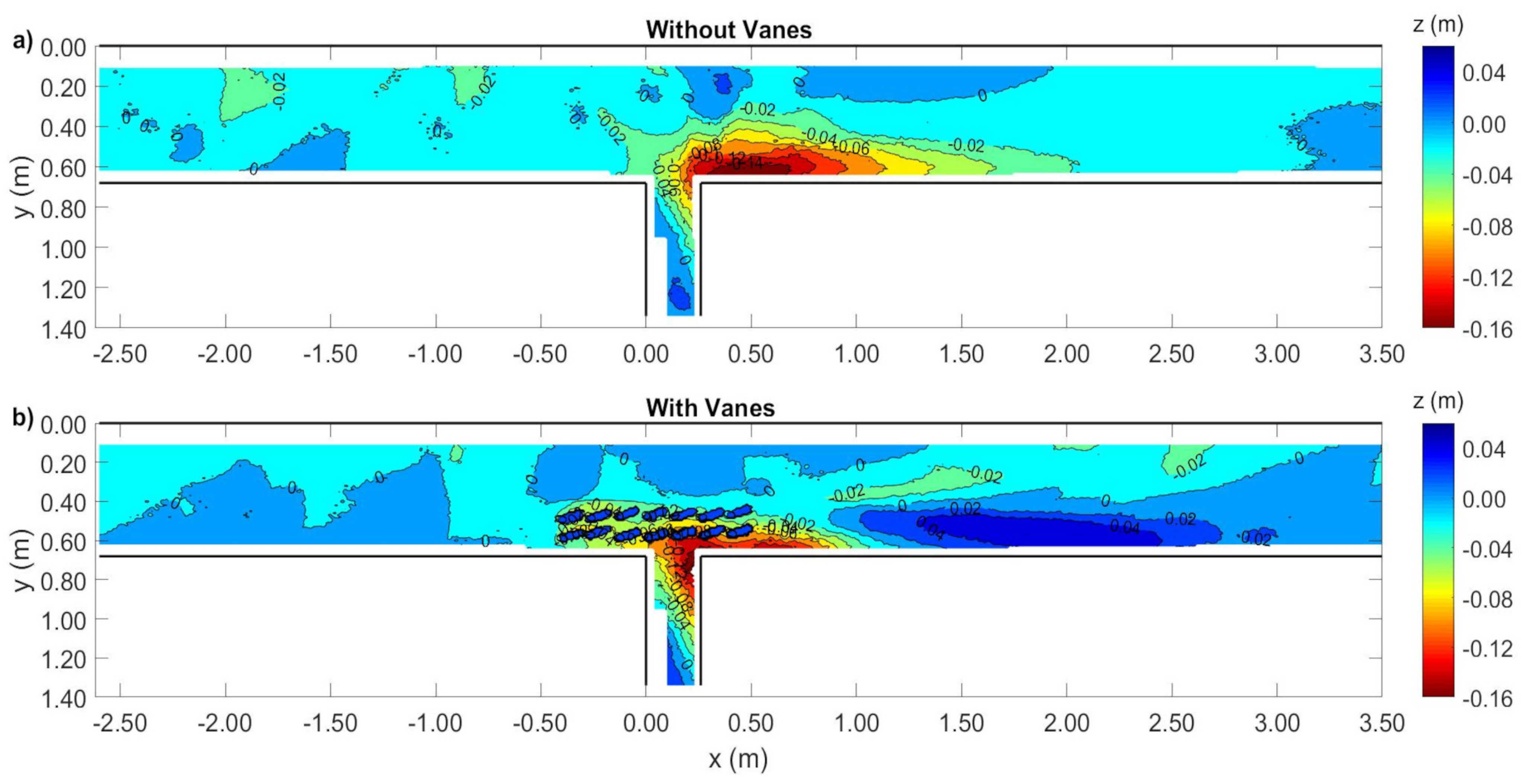
3.1. Bed Morphology
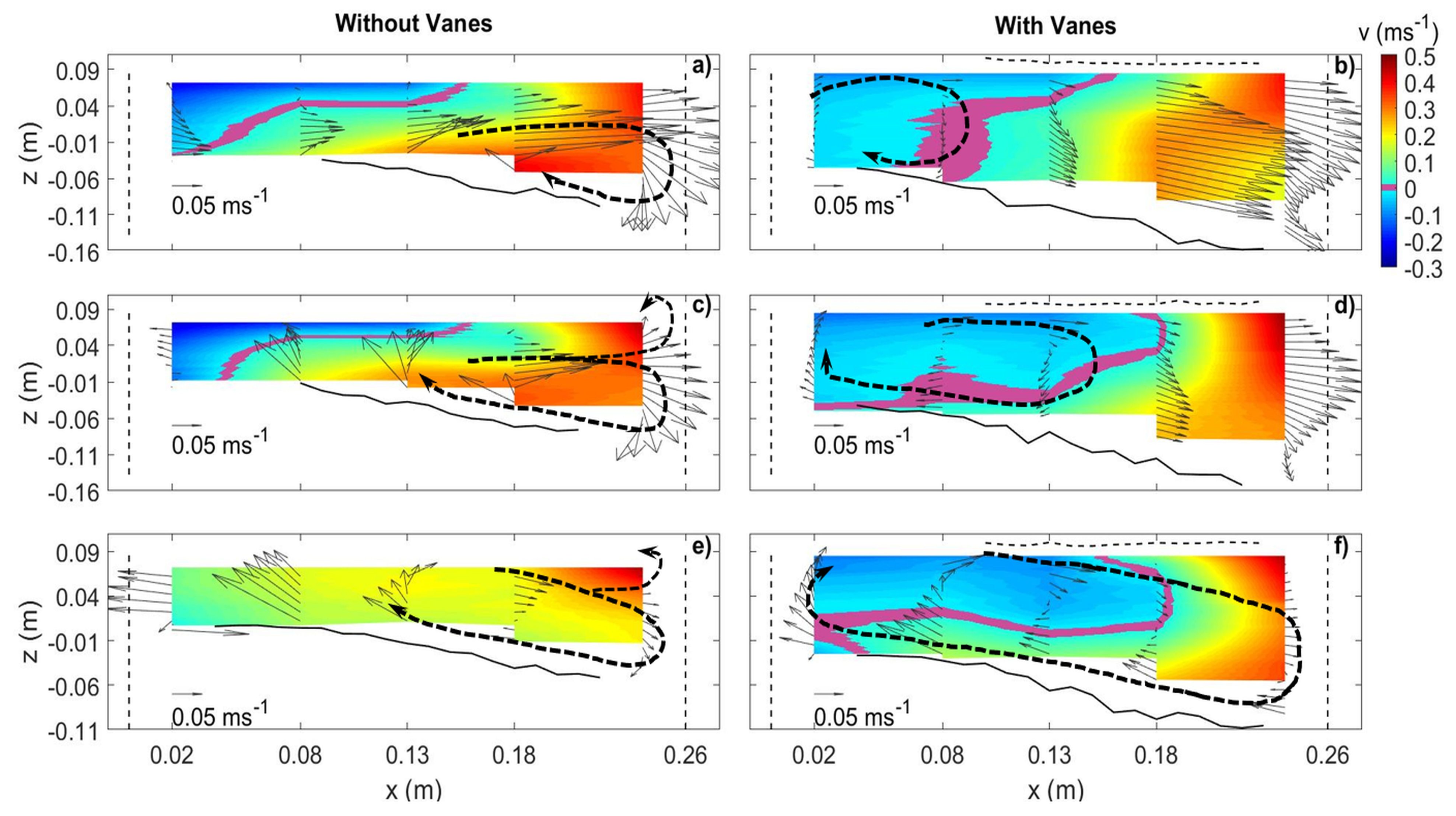
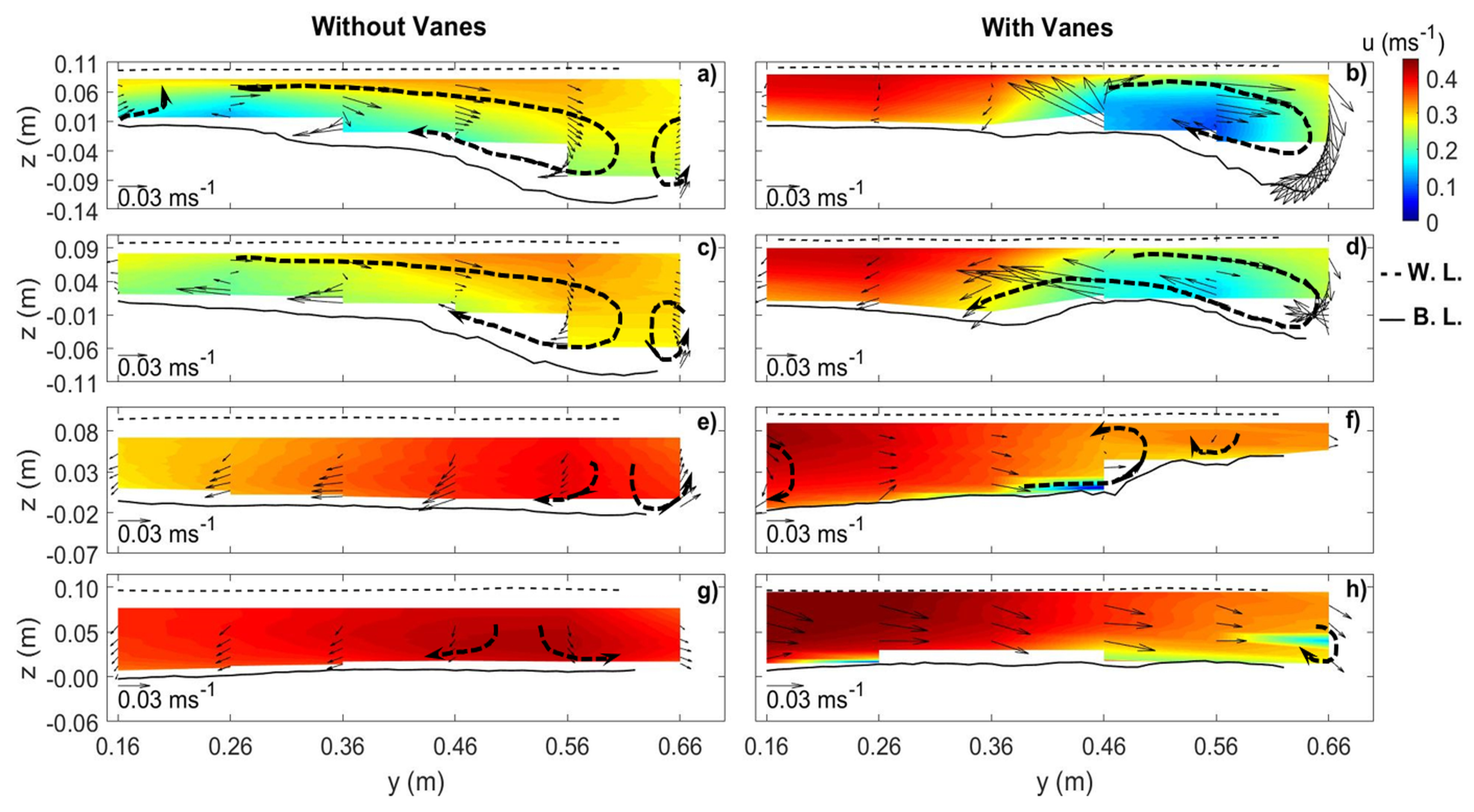
3.2. Average Flow Field
3.2.1. Data Presentation
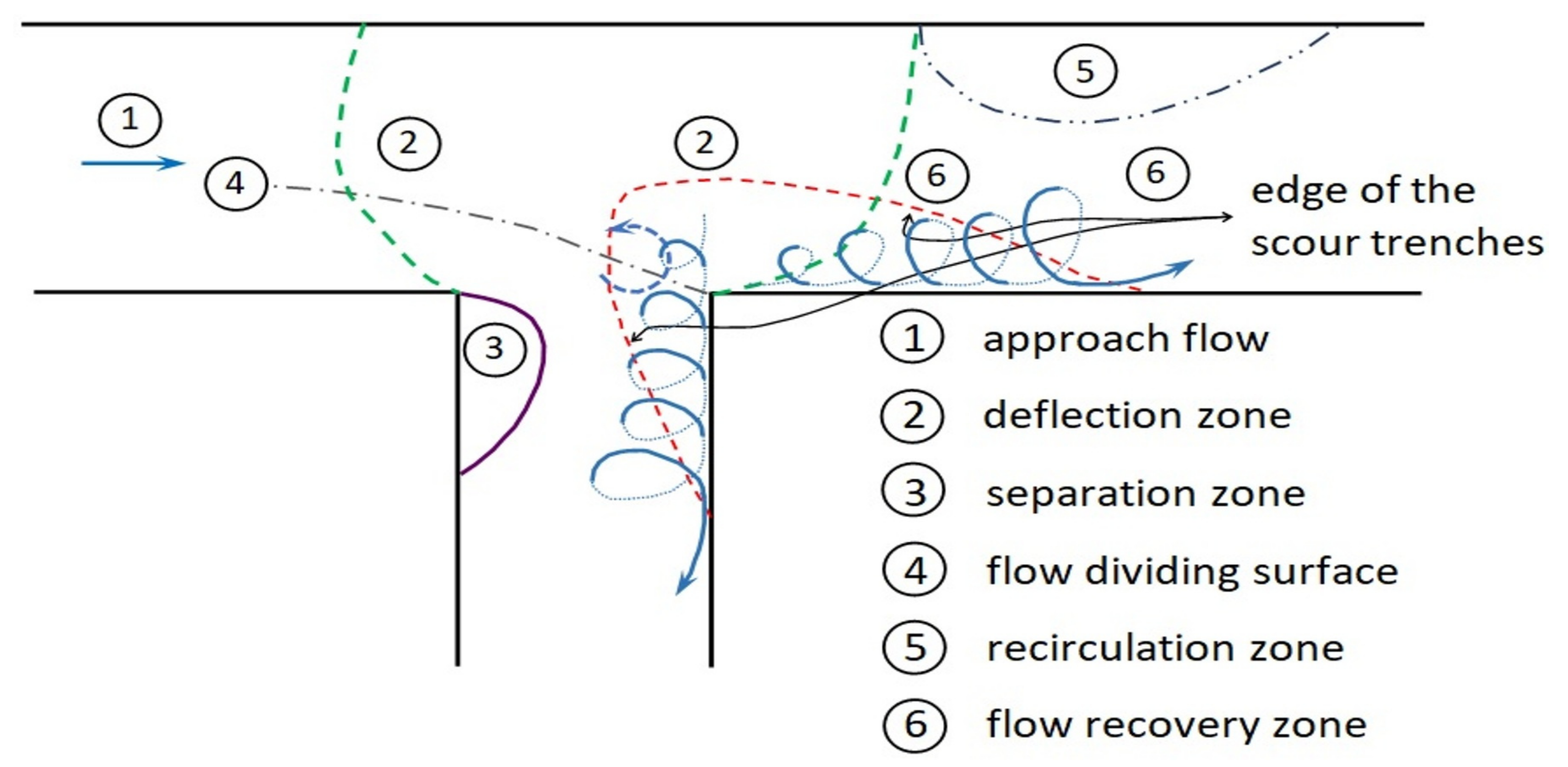
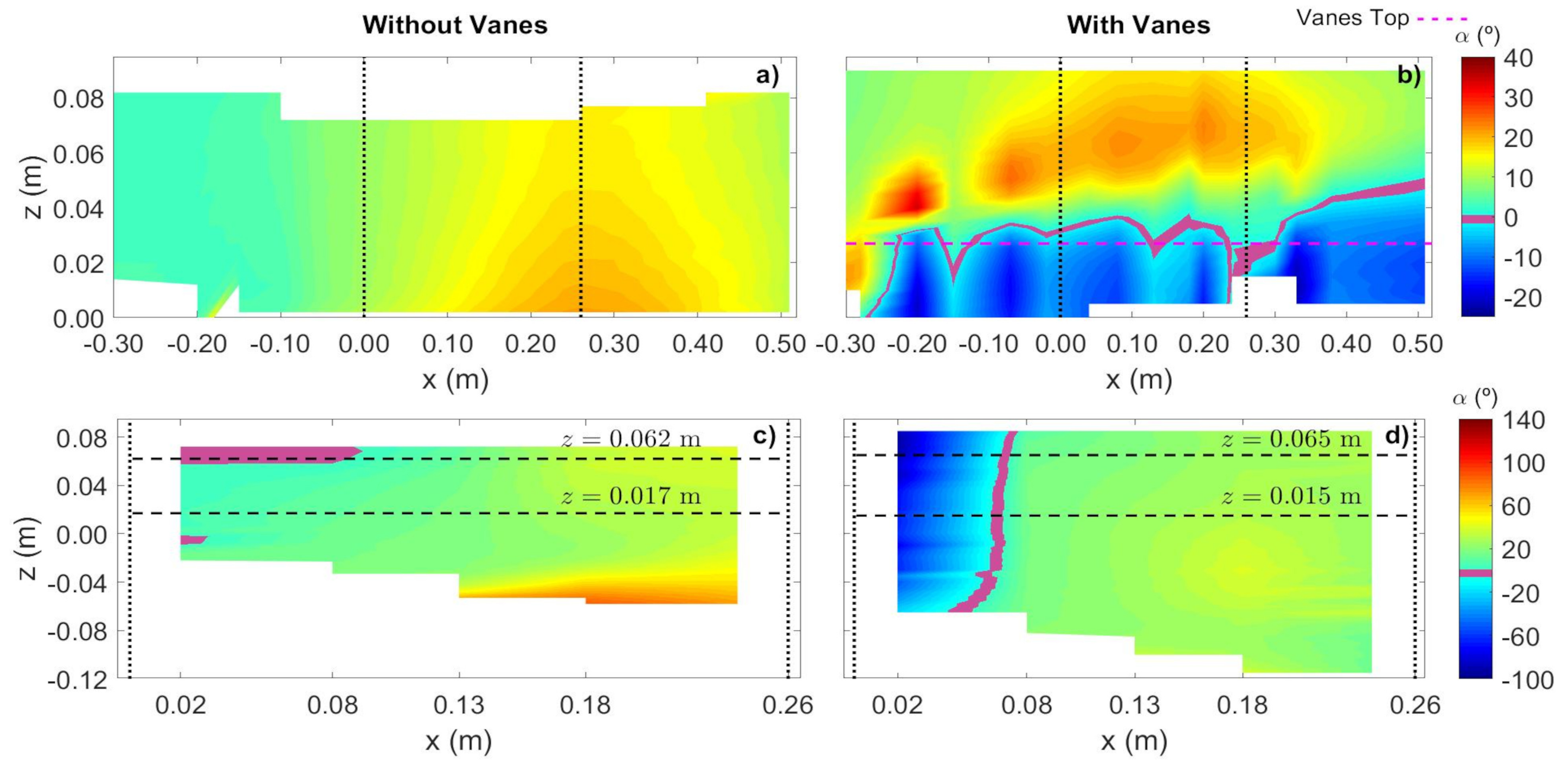
3.2.2. Approach Flow Zone ( m)
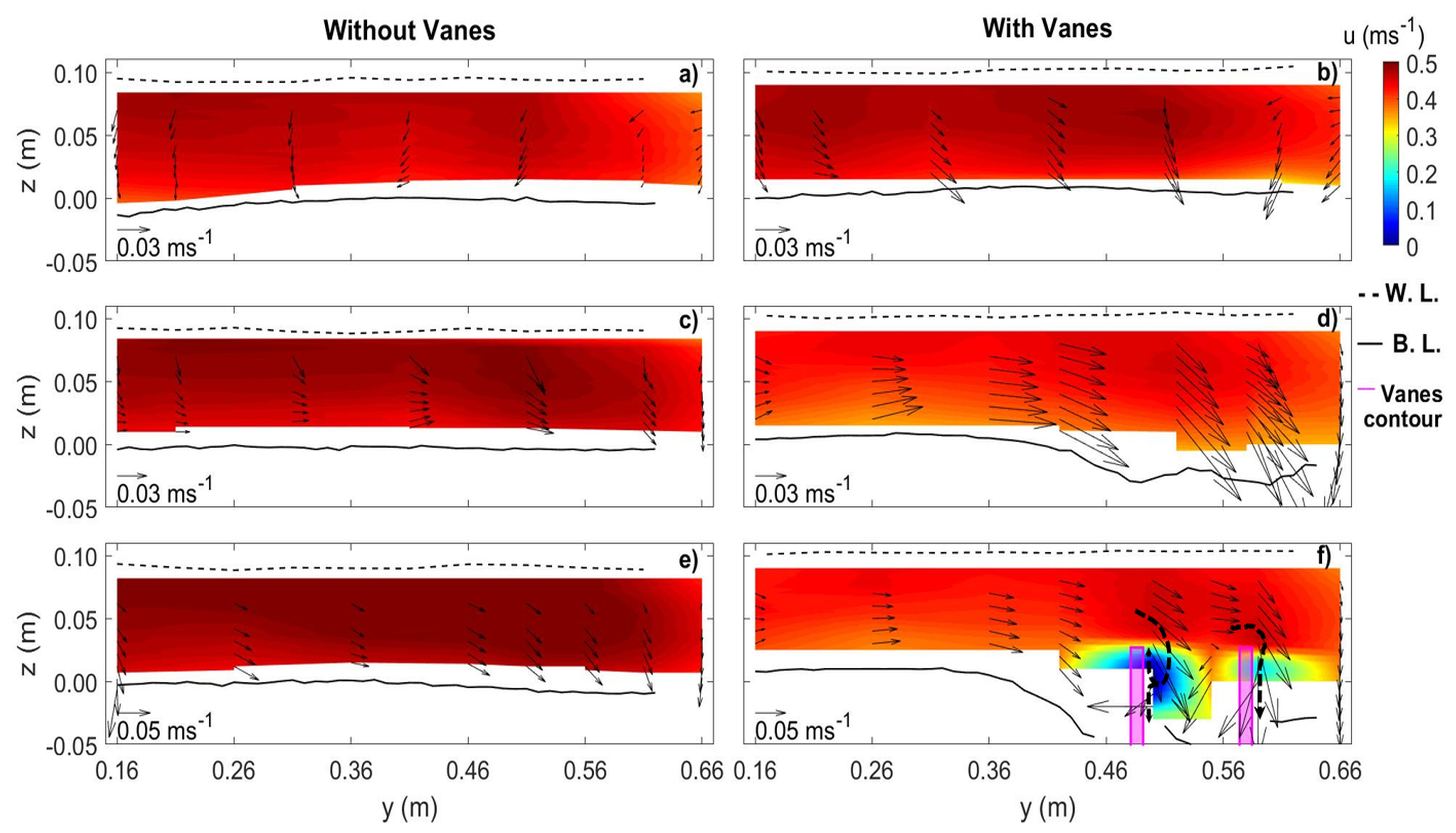
3.2.3. Flow Deflection Zone in the Main Channel ( m 0.70 m)
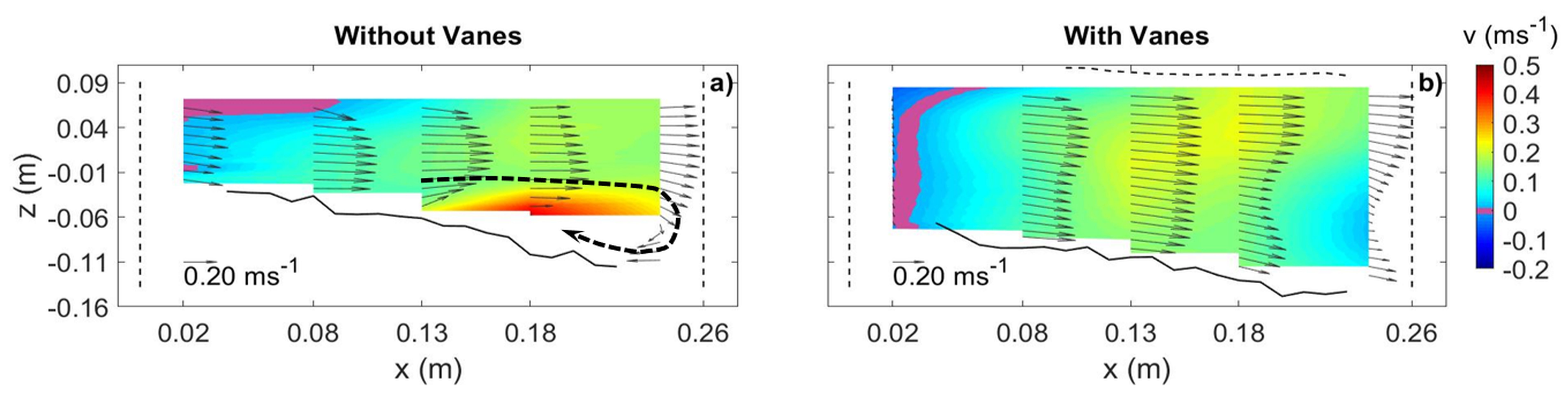
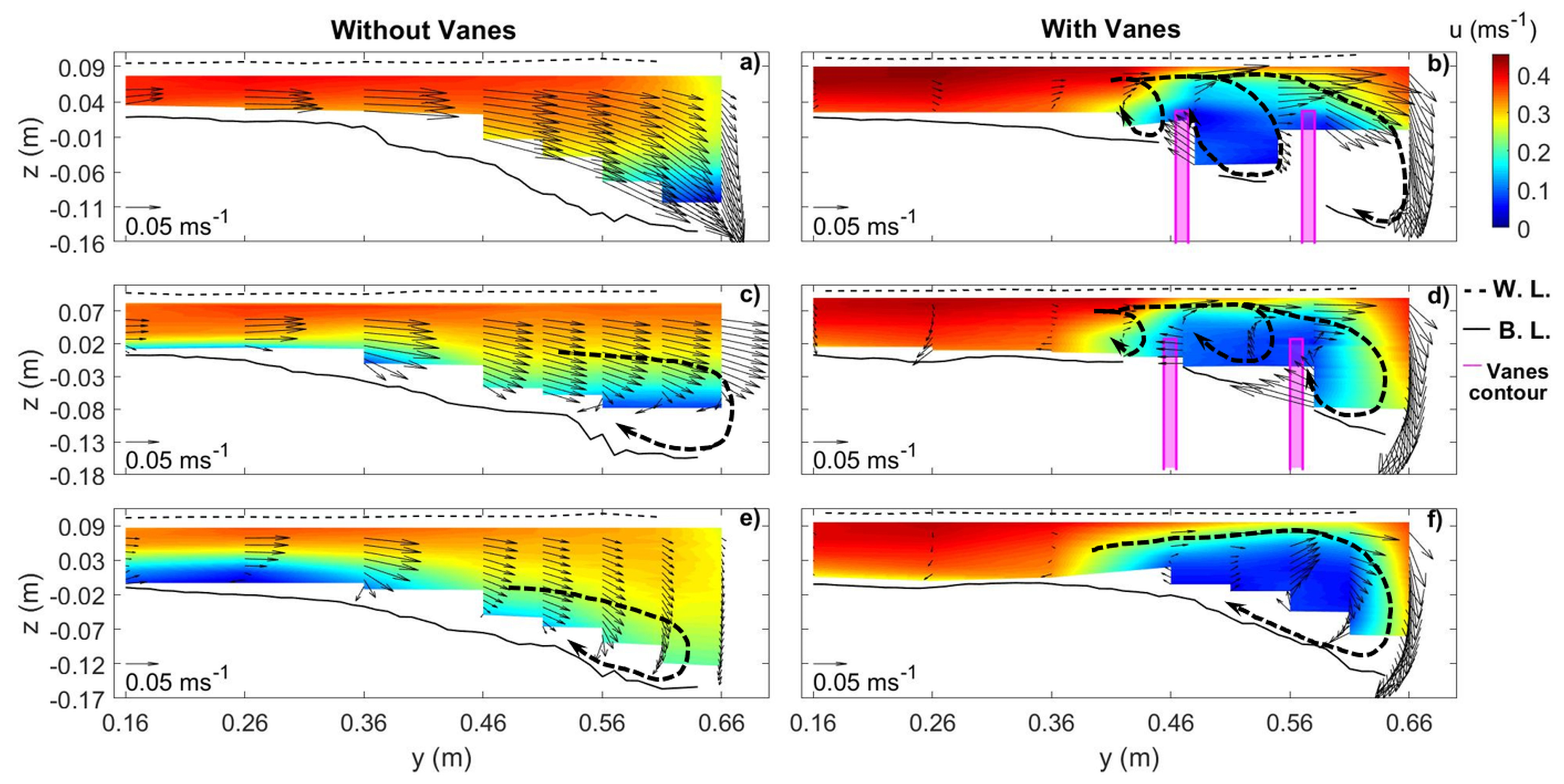
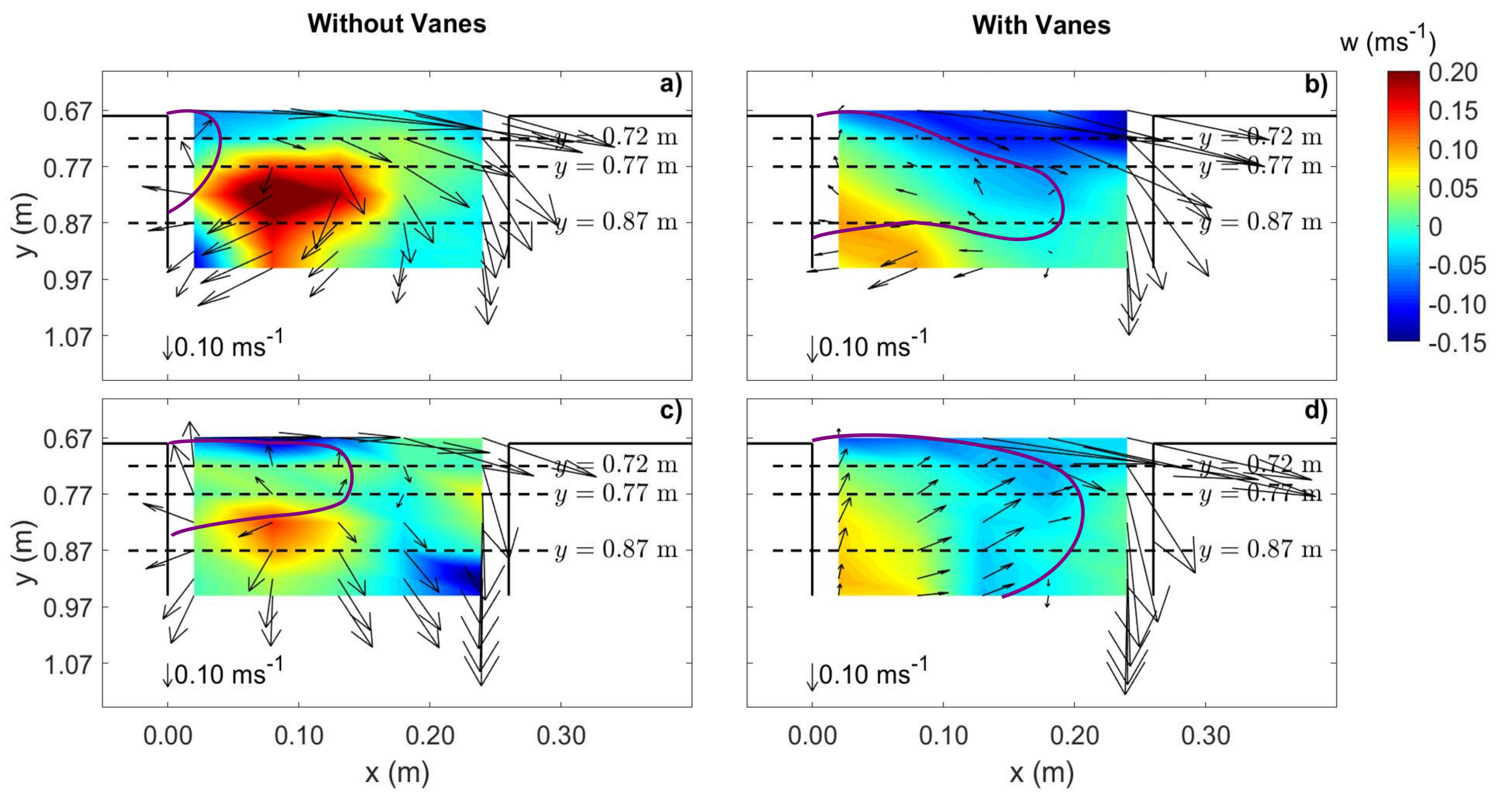
3.2.4. Diversion Entrance Zone (0.67 m 0.95 m)
3.2.5. Flow Recovery Zone ( 0.70 m)
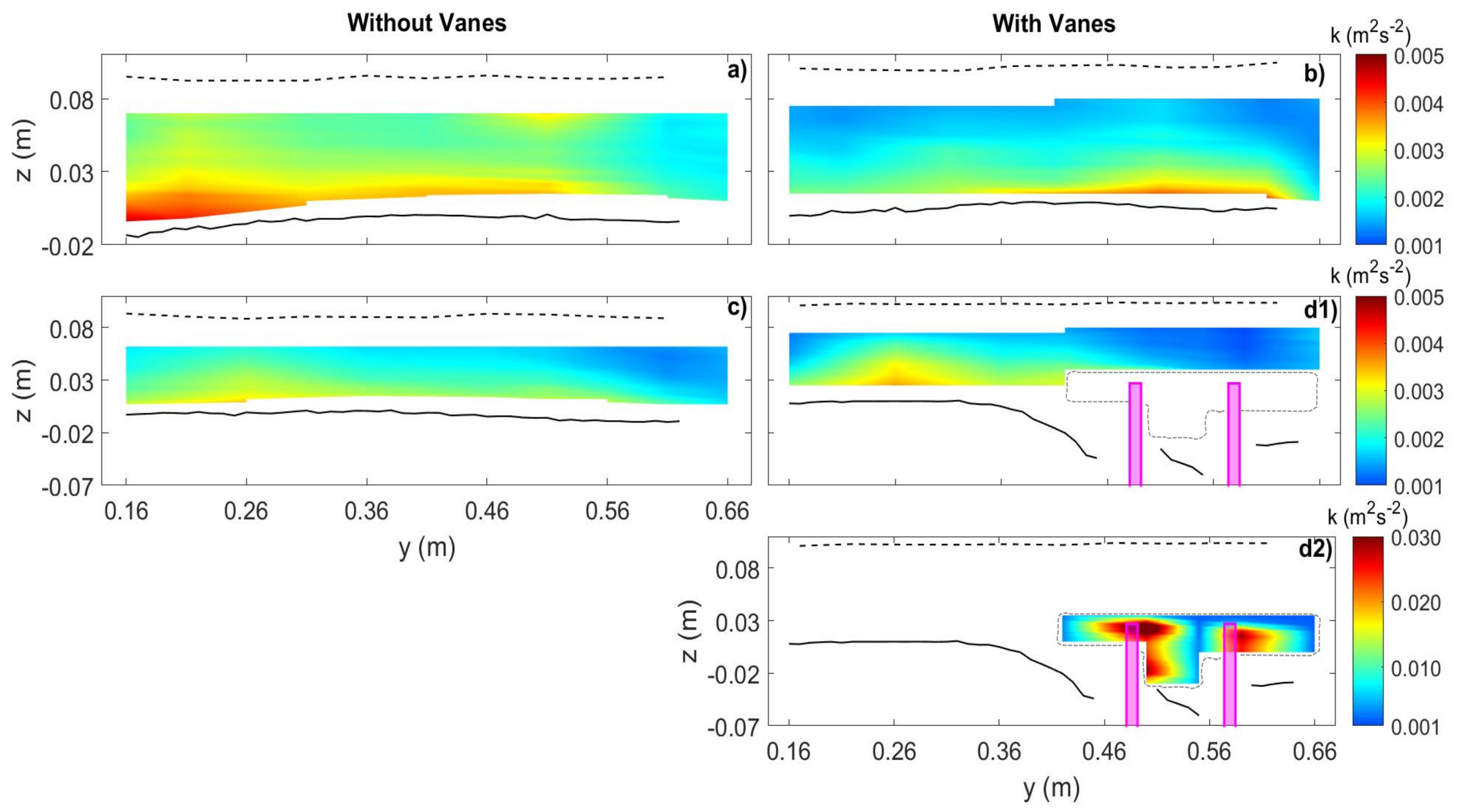
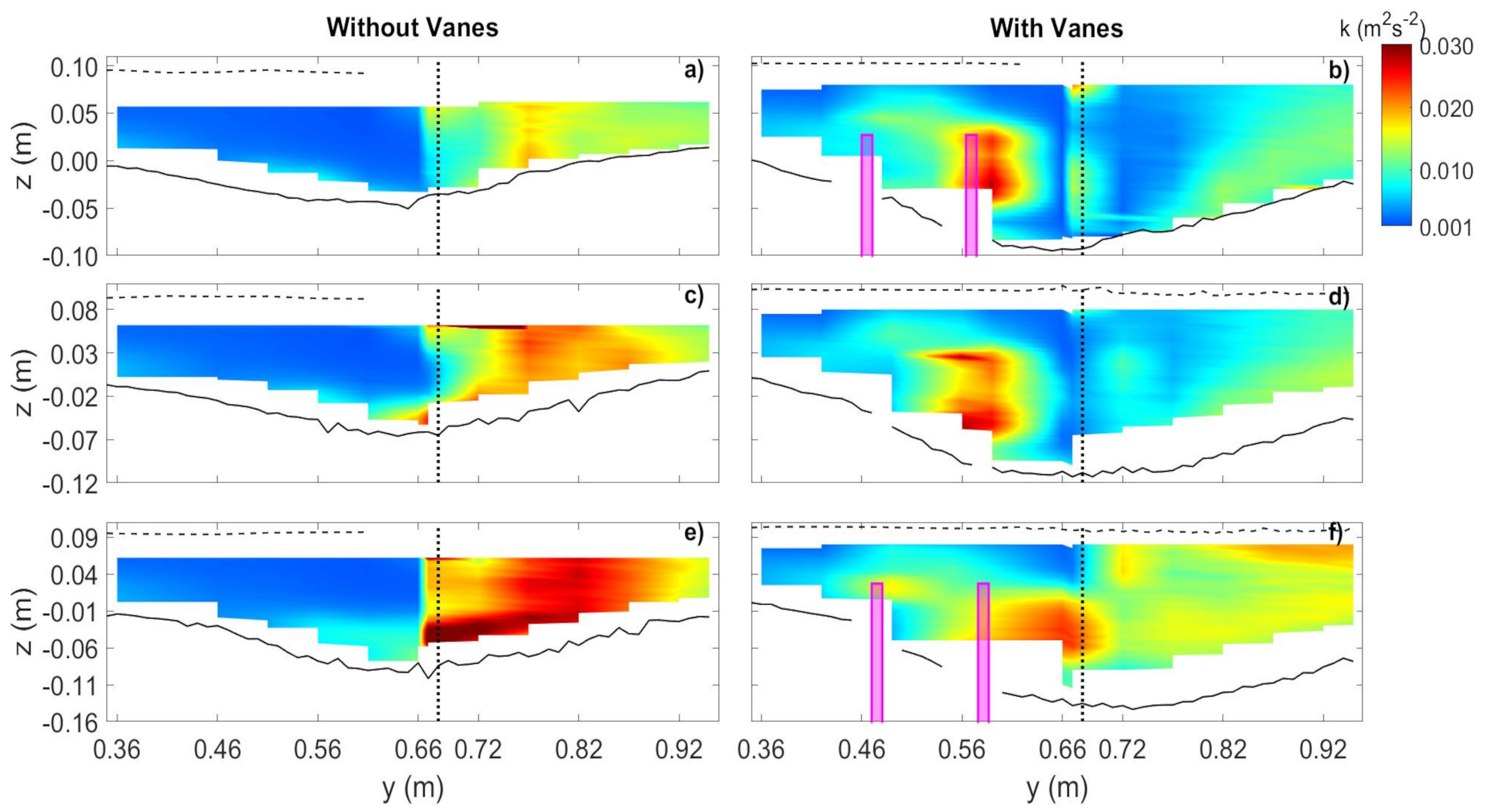
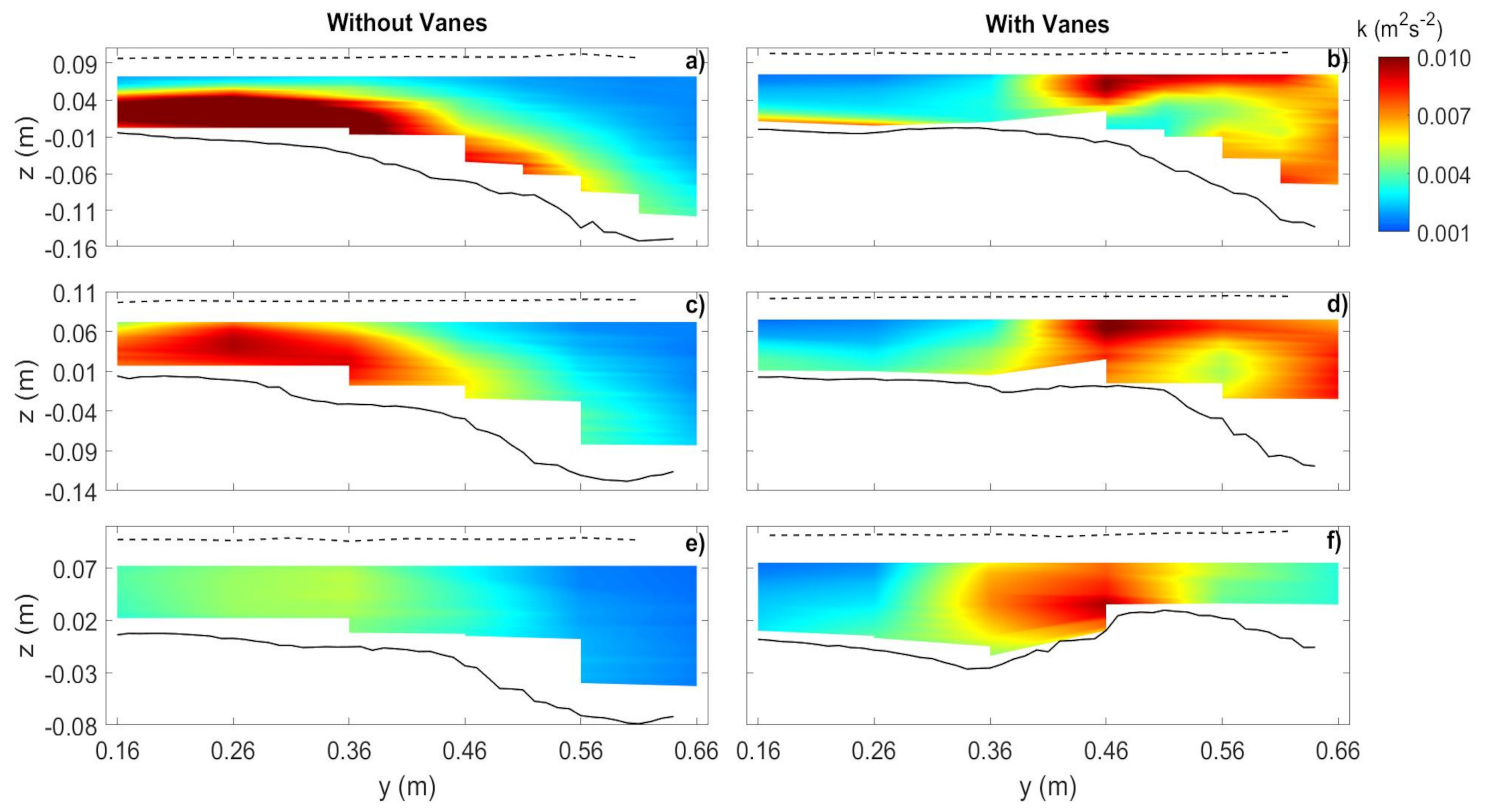
3.3. Turbulent Kinetic Energy
4. Conclusions
- (i)
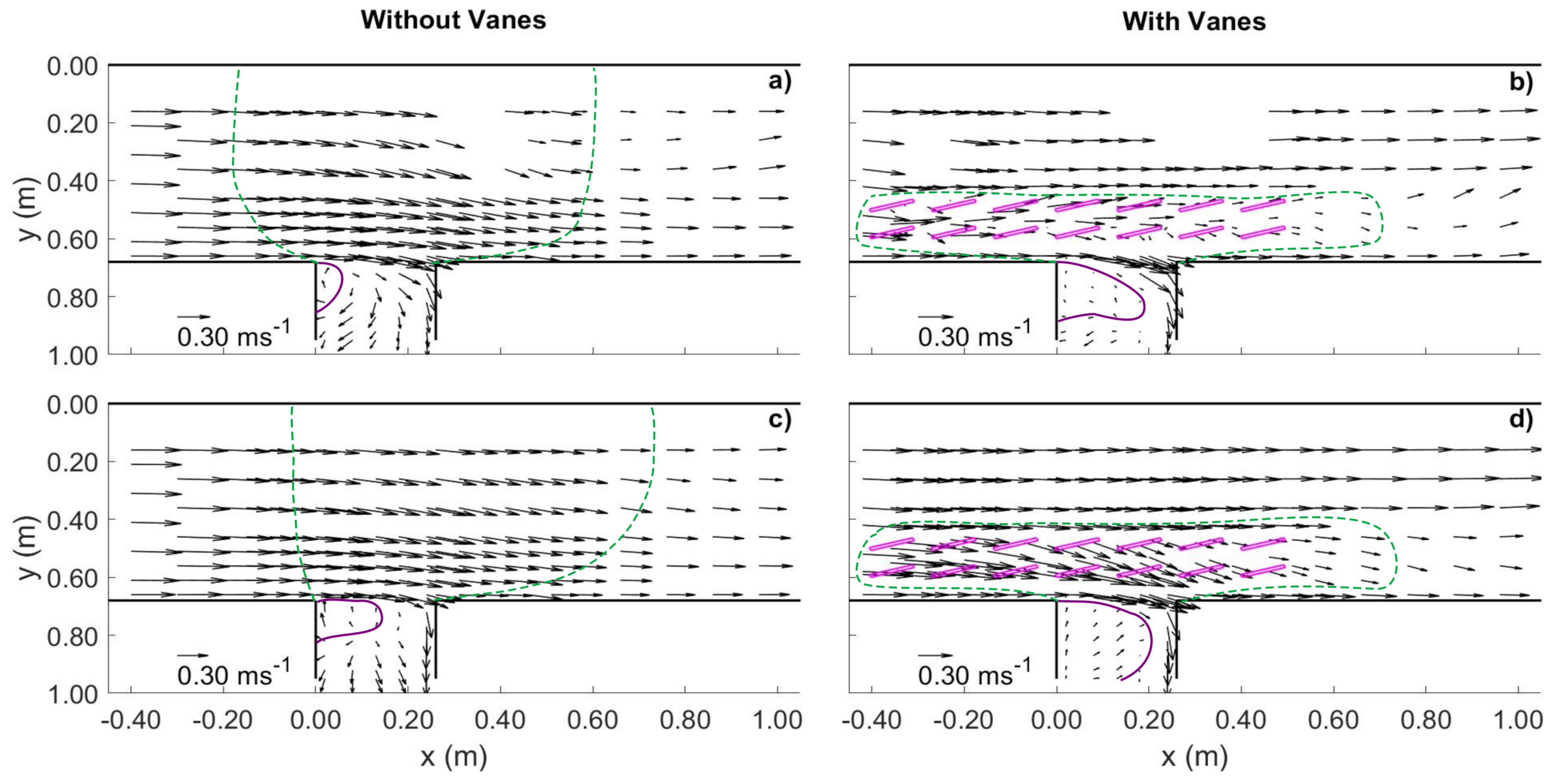
- The vanes altered their near velocity field by creating tip vortices around them. The combination of the vane-induced circulation and the streamwise velocity caused a longitudinal vortex all along the vane-field, right from the most upstream vanes, which persisted downstream of the diversion, for a distance of between eight to ten times the flow depth.
- (ii)
- The longitudinal vortex was not identified in front of the diversion entrance in the absence of the vanes. In this case, the main channel vortex initiated downstream of the diversion due to the impact of the deflected flow on the inner lateral wall of the main channel.
- (iii)
- The flow deflection towards the diversion channel was enhanced above the vanes in the presence of the vane-field.
- (iv)
- The scoured trench inside the diversion was slightly deeper in the presence of vanes, whereas the bed material excavated along the vane-field originated a sediment deposition further downstream.
- (v)
- The vanes also originated downflows along their downstream faces which caused scour in the experiment with vanes.
- (vi)
- The vanes increased the dimensions of the separation zone identified inside the diversion channel relative to the vanes-free case, slightly decreasing the conveyance at equal flow levels.
- (vii)
- The increase of the size of the separation zone in the case of vane-field was accompanied by the decrease of the velocity magnitude as well as of the flow turbulent kinetic energy inside that zone.
- (viii)
- A rising flow zone, characterized by high turbulent kinetic energy, was observed, supposedly for the first time, side by side, underneath or immediately downstream of the separation zone, in both experiments, though it was clearly more pronounced in the experiment without vanes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bertoldi, W.; Miori, S.; Salvaro, M.; Zanoni, L.; Tubino, M. Morphological description of river bifurcations in gravel-bed braided networks. In Proceedings of the International Conference on Fluvial Hydraulics, River Flow 2006, Lisbon, Portugal, 6–8 September 2006; Ferreira, R.M.L., Alves, E., Leal, J., Cardoso, A.H., Eds.; Taylor & Francis: London, UK, 2006; pp. 1311–1318. [Google Scholar]
- Nakato, T.; Kennedy, J.F. Pump-station intake-shoaling control with submerged vanes. J. Hydraul. Eng. 1990, 116, 119–128. [Google Scholar] [CrossRef]
- Sruthi, T.K.; Ranjith, K.B.; Chandra, V. Control of sediment entry into an intake canal by using submerged vanes. In Proceedings of the International Conference on Applied Physics and Engineering, Penang, Malaysia, 2–3 November 2016; Mohd, M.J., Mohd, A., Mohd, N.A., Eds.; American Institute of Physics: Melville, NY, USA, 2017. [Google Scholar]
- Wang, Y.; Odgaard, A.J.; Melville, B.W.; Jain, S.C. Sediment Control at Water Intakes. J. Hydraul. Eng. 1996, 122, 353–356. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Spoljaric, A. Sediment Control by Submerged Vanes. J. Hydraul. Eng. 1986, 112, 1164–1180. [Google Scholar] [CrossRef]
- Barkdoll, B.D.; Ettema, R.; Odgaard, A.J. Sediment control at lateral diversions: Limits and enhancements to vane use. J. Hydraul. Eng. 1999, 125, 862–870. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Kennedy, J.F. River-Bend Bank Protection by Submerged Vanes. J. Hydraul. Eng. 1983, 109, 1161–1173. [Google Scholar] [CrossRef]
- Herrero, A.; Bateman, A.; Medina, V. Water flow and sediment transport in a 90∘ channel diversion: An experimental study. J. Hydraul. Res. 2015, 53, 253–263. [Google Scholar] [CrossRef]
- Alomari, N.K.; Yusuf, B.; Mohammad, T.A.; Ghazalib, A.H. Experimental investigation of scour at a channel junctions of different diversion angles and bed width ratios. Catena 2018, 166, 10–20. [Google Scholar]
- Karami, H.; Farzin, S.; Sadrabadi, M.T.; Moazeni, H. Simulation of flow pattern at rectangular lateral intake with different dike and submerged vane scenarios. Water Sci. Eng. 2017, 10, 246–255. [Google Scholar] [CrossRef]
- Sarhadi, A.; Jabbari, E. Investigating Effect of Different Parameters of the Submerged Vanes on the Lateral Intake Discharge Located in the 180 Degree Bend Using the Numerical Model. Civ. Eng. J. 2017, 3, 1176–1187. [Google Scholar] [CrossRef]
- Michell, F.; Ettema, R.; Muste, M. Case Study: Sediment Control at Water Intake for Large Thermal-Power Station on a Small River. J. Hydraul. Eng. 2006, 132, 440–449. [Google Scholar] [CrossRef]
- Nakato, T.; Ogden, F.L. Sediment Control at Water Intakes along Sand-Bed Rivers. J. Hydraul. Eng. 1998, 124, 589–596. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Wang, Y. Sediment Management with Submerged Vanes. II: Applications. J. Hydraul. Eng. 1991, 117, 284–302. [Google Scholar] [CrossRef]
- Firozjae, M.R.; Neyshabouri, S.A.; Sola, S.A.; Mohajeri, S.H. Numerical Simulation on the Performance Improvement of a Lateral Intake Using Submerged Vanes. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 167–177. [Google Scholar] [CrossRef]
- Moghadam, M.K.; Amini, A.; Keshavarzi, A. Intake design attributes and submerged vanes effects on sedimentation and shear stress. Water Environ. J. 2020, 4, 374–380. [Google Scholar] [CrossRef]
- Guillén-Ludeña, S.; Franca, M.; Cardoso, A.H.; Schleiss, A.J. Evolution of the hydromorphodynamics of mountain river confluences for varying discharge ratios and junction angles. Geomorphology 2015, 255, 1–15. [Google Scholar] [CrossRef]
- Bombar, G.; Cardoso, A.H. Effect of the sediment discharge on the equilibrium bed morphology of movable bed open-channel confluences. Geomorphology 2020, 367, 107329. [Google Scholar] [CrossRef]
- Chanson, H. Acoustic doppler velocimetry (adv) in the field and in laboratory: Practical experiences. In International Meeting on Measurements and Hydraulics of Sewers, Hydraulic Model Report No. CH70/08; Division of Civil Engineering, The University of Queensland: Brisbane, Australia, 2008. [Google Scholar]
- Goring, D.; Nikora, V. Despiking acoustic doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]
- Ramamurthy, A.S.; Qu, J.; Vo, D. Numerical and experimental study of dividing open-channel flows. J. Hydraul. Eng. 2007, 133, 1135–1144. [Google Scholar] [CrossRef]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 2000. [Google Scholar]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; IAHR Monograph Series; Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Sharma, H.; Ahmad, Z. Turbulence characteristics of flow past submerged vanes. Int. J. Sediment Res. 2020, 35, 42–56. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baltazar, J.; Alves, E.; Bombar, G.; Cardoso, A.H. Effect of a Submerged Vane-Field on the Flow Pattern of a Movable Bed Channel with a 90° Lateral Diversion. Water 2021, 13, 828. https://doi.org/10.3390/w13060828
Baltazar J, Alves E, Bombar G, Cardoso AH. Effect of a Submerged Vane-Field on the Flow Pattern of a Movable Bed Channel with a 90° Lateral Diversion. Water. 2021; 13(6):828. https://doi.org/10.3390/w13060828
Chicago/Turabian StyleBaltazar, Joana, Elsa Alves, Gökçen Bombar, and António Heleno Cardoso. 2021. "Effect of a Submerged Vane-Field on the Flow Pattern of a Movable Bed Channel with a 90° Lateral Diversion" Water 13, no. 6: 828. https://doi.org/10.3390/w13060828
APA StyleBaltazar, J., Alves, E., Bombar, G., & Cardoso, A. H. (2021). Effect of a Submerged Vane-Field on the Flow Pattern of a Movable Bed Channel with a 90° Lateral Diversion. Water, 13(6), 828. https://doi.org/10.3390/w13060828







