Unravelling the Importance of Uncertainties in Global-Scale Coastal Flood Risk Assessments under Sea Level Rise
Abstract
1. Introduction
2. Materials and Methods
2.1. DIVA Modelling Framework
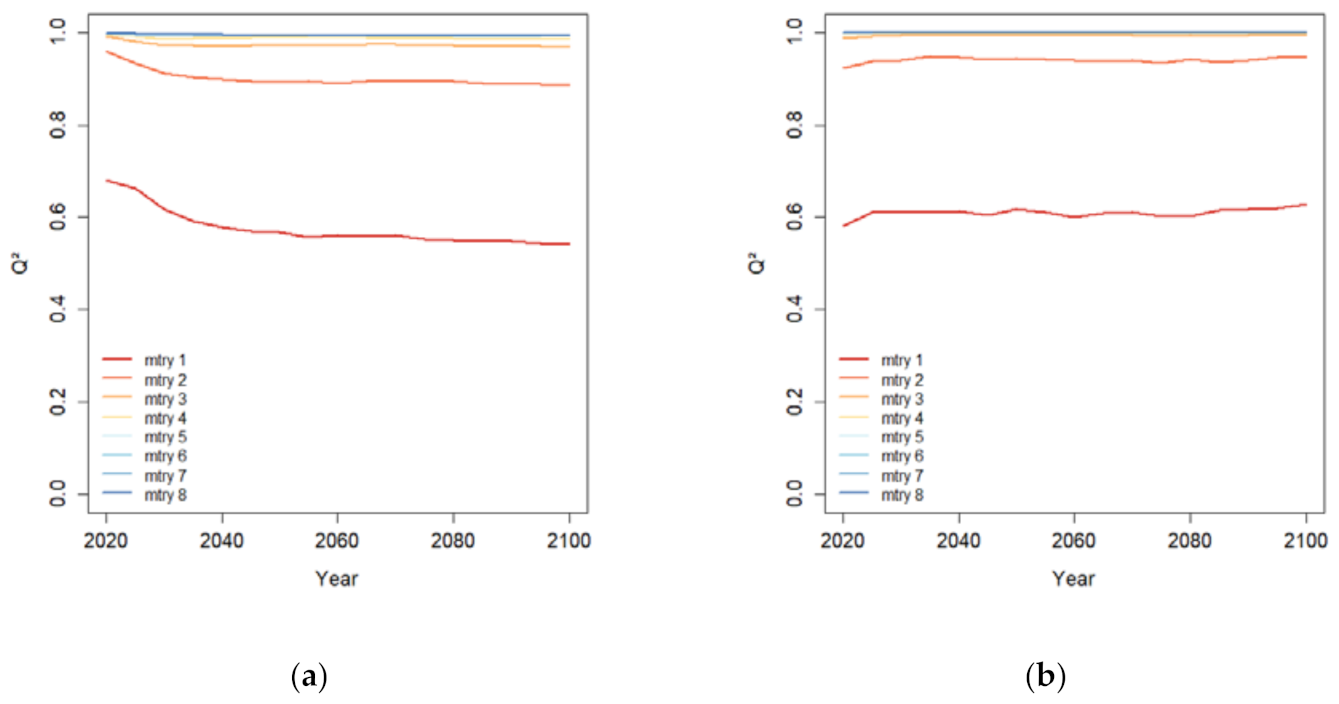
2.2. Global Sensitivity Analysis
2.3. Uncertain Variables and Values Considered
2.4. Likelihoods of Variables Values
- The r-largest annual value rGEV = 5 is chosen as of higher likelihood based on the conclusions of [20];
- A preference is given to the original parametrization of the Logistic depth-damage curves by using a half-damage depth of 1.0 m;
- In light of recent observations by [39], subsidence in delta regions is considered a more plausible scenario;
- Likelihood weights are assigned to combinations of RCP/SSPs; this is further detailed below;
- No preference is given, neither for global population distribution, nor for the Assets-to-GDP ratio, in the absence of evidence favoring one scenario over another.
2.5. Dependence between Uncertain Variables
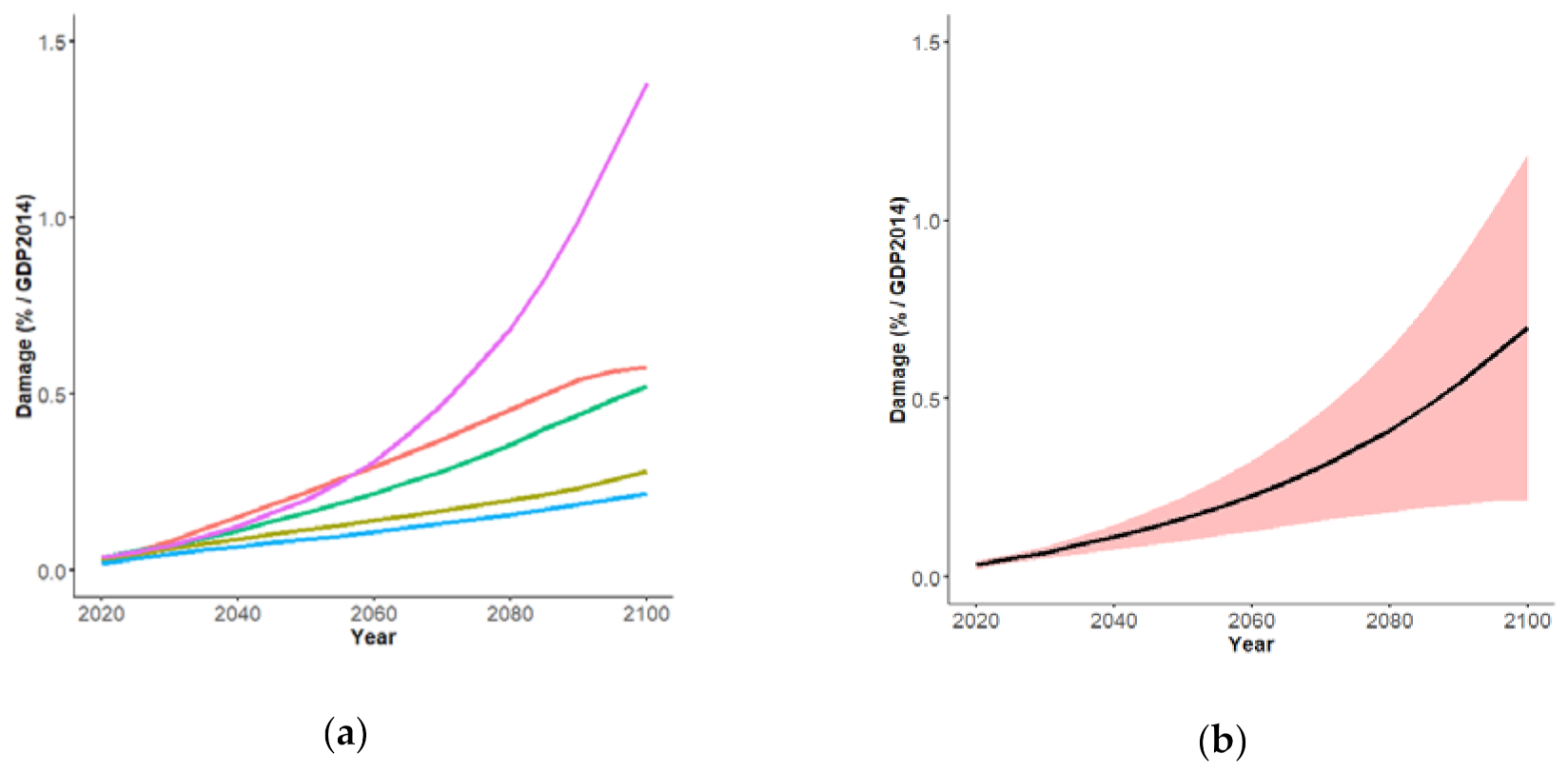
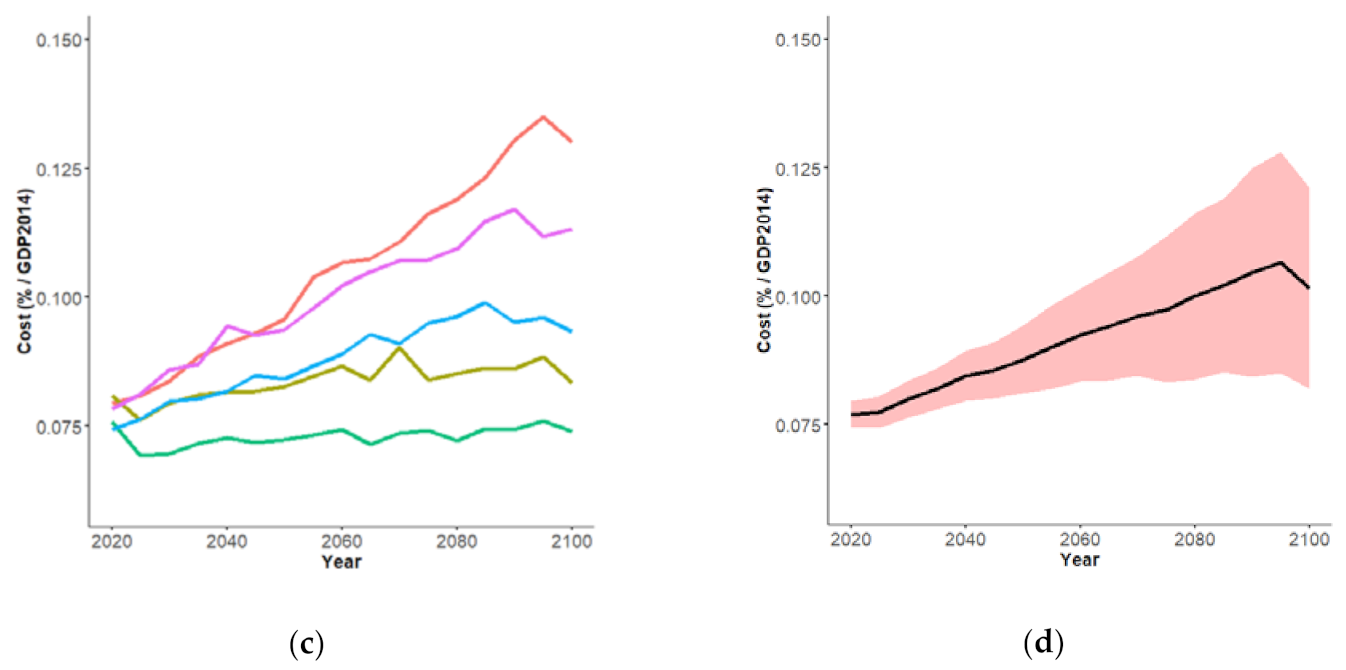
3. Results
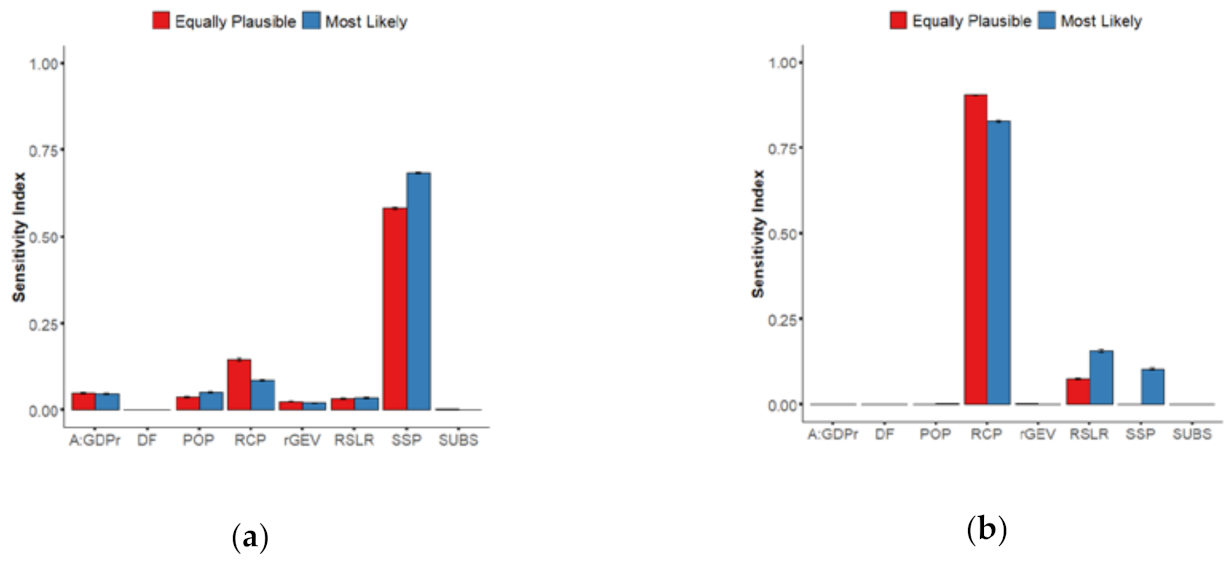
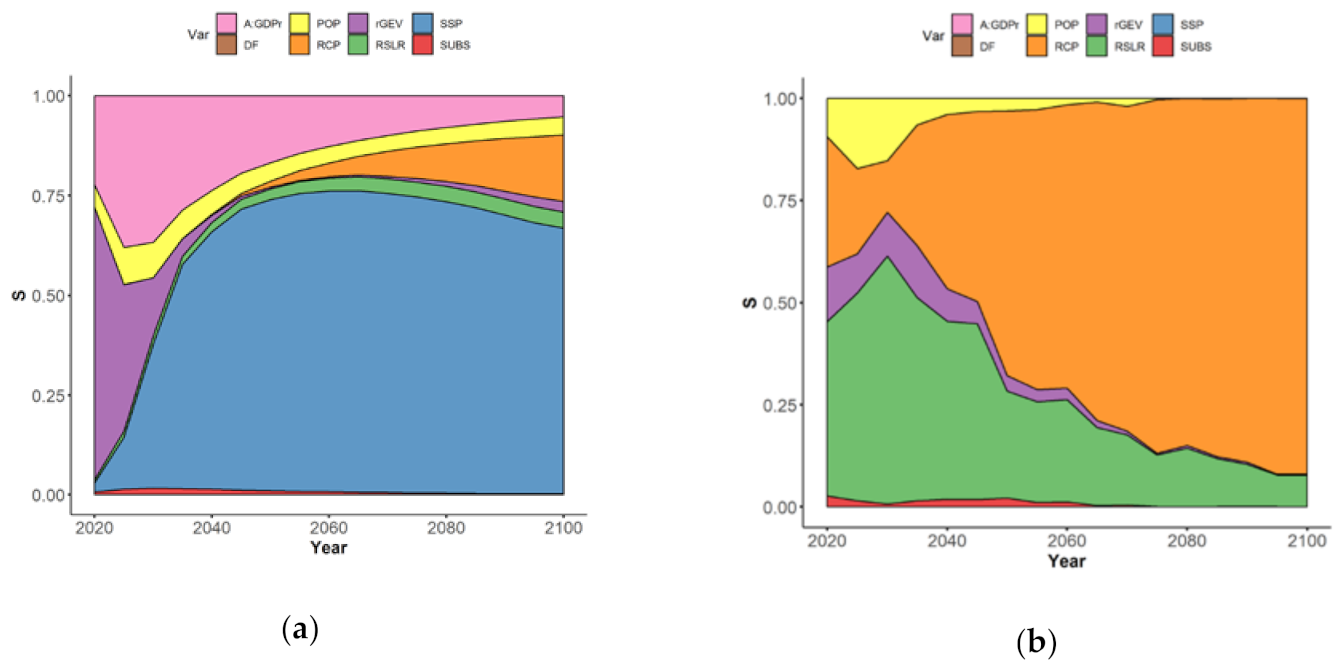
3.1. Equally Plausible Values
- In the short term (before 2030–2040, leftmost part of Figure 3a), the uncertainty is mainly controlled by two sources of uncertainty, namely the value of the Assets-to-GDP ratio (rose-colored envelope), the rGEV parameter of the extreme value analysis (purple-colored envelope) with sensitivity indices of ~25%, and ~75% respectively;
- After this date, the time evolution of their influence differs: Figure 3a shows the rapidly decreasing rGEV influence to low value <1% by 2050, whereas the influence of A:GDPr decreases less abruptly, down to values of ~10% by 2050; This decrease is relative to the total uncertainty, which is increasing rapidly after 2040; hence, this decrease simply reflects the growing importance of other sources of uncertainties after 2050;
- The importance of SSP scenarios (blue-colored envelope) rapidly increases over time: the sensitivity index reaches large values above 50% after 2030, until driving the whole uncertainty by 2100 with a contribution >50%; again, the slow decrease of the relative contribution of SSP to EAD uncertainty after 2050 is due to RCP becoming a significant source of uncertainty. This large impact of SSP is expected because different SSPs have large impacts in the development of the global floodplains;
- The importance of RCP scenarios (in orange) is only slowly increasing over time reaching a low index value >5% by 2065–2070; this late emergence of RCP scenarios as a source of uncertainty in EAD is consistent with the projected times of divergence of sea-level projections: until about 2050, sea-level projections are almost the same whatever the RCP scenario due to their high dependence on past greenhouse gas emissions [40];
- The role of the choice in the population database (in yellow) and of RSLR (in green) remain moderate with a sensitivity index of 5–8%, and the role of subsidence in delta regions is minor (in red).
- In the short term (leftmost part of Figure 3b), the uncertainty related to RSLR (in green) dominates (with an index of >40%);
- The three other most important uncertainties are the population database (in yellow), the extreme modelling parameter (in purple), and the RCP scenario (in blue);
- Over time, the importance of RCP rapidly exceeds the one of RSLR, and reaches >60% by 2050, whereas the one of RSLR drops down to <25% after this date;
- The sensitivity index of POP and of rGEV rapidly decreases down to low value <5% by 2040.
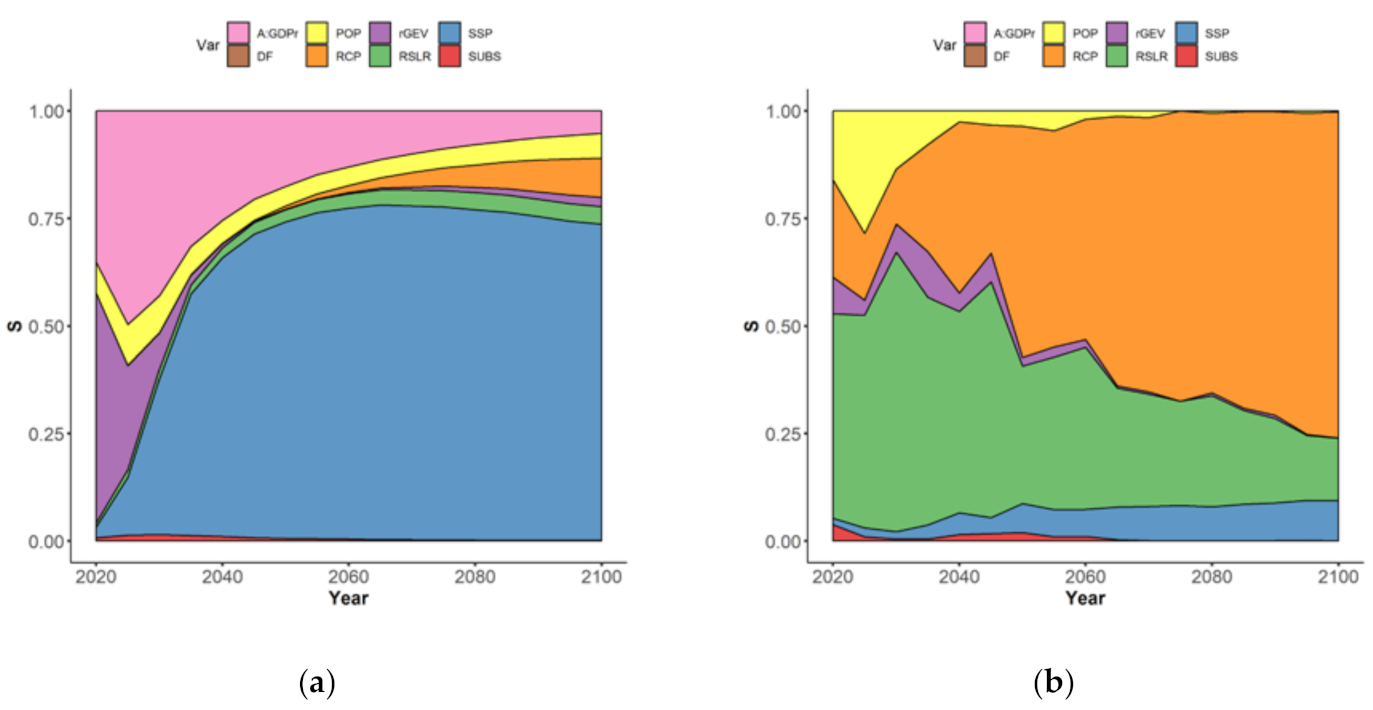
3.2. With Most Likely Values
4. Discussion and Conclusion
4.1. Summary and Implications
4.2. Residual Uncertainties
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Random Forest Regression
Appendix B. Filtering Algorithm for Estimating the Sensitivity Indices
- Random sampling of the uncertainty input space. No particular algorithm is here required, and dependencies can here be taken into account using appropriate random sampling scheme;
- Partition of the input parameter space into clusters. This can be done in different manners, for instance using an equi-probable partitioning [30]. Alternatives can focus on clustering techniques; for instance K-means algorithm with a fixed number of samples, or a simple systematic regular partition. In the present study, the partition corresponds, by construction, to the selection of a given modelling scenario;
- Computation of the local conditional variance, i.e., for each cluster. This provides a quantification of the evolution of the local variance in the domain of variation of the input parameters;
- Estimation of the local Sobol’ indices, i.e., (Y). Depending on the value at which the parameter is fixed, the local variance reduction can be high or low;
- The Sobol’ indices are then obtained by computation of the expectation values of the local Sobol’ Indices as described by Equation (1).
Appendix C. Projections of Extreme Sea Levels
Appendix D. Coastal Flood Risk in DIVA
References
- IPCC. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Nicolai, M., Okem, A., Petzold, J., et al., Eds.; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Nicholls, R.J.; Cazenave, A. Sea-Level Rise and Its Impact on Coastal Zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
- Hinkel, J.; Lincke, D.; Vafeidis, A.T.; Perrette, M.; Nicholls, R.J.; Tol, R.S.J.; Marzeion, B.; Fettweis, X.; Ionescu, C.; Levermann, A. Coastal flood damage and adaptation costs under 21st century sea-level rise. Proc. Natl. Acad. Sci. USA 2014, 111, 3292–3297. [Google Scholar] [CrossRef] [PubMed]
- Jevrejeva, S.; Jackson, L.P.; Grinsted, A.; Lincke, D.; Marzeion, B. Flood damage costs under the sea level rise with warming of 1.5 °C and 2 °C. Environ. Res. Lett. 2018, 13, 074014. [Google Scholar] [CrossRef]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Tiggeloven, T.; De Moel, H.; Winsemius, H.C.; Eilander, D.; Erkens, D.; Erkens, G.; Gebremedhin, E.; Diaz Loaiza, A.; Kuzma, S.; Luo, T.; et al. Global-scale benefit–cost analysis of coastal flood adaptation to different flood risk drivers using structural measures. Nat. Hazards Earth Syst. Sci. 2020, 20, 1025–1044. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Bianchi, A.; Dottori, F.; Feyen, L. Climatic and socioeconomic controls of future coastal flood risk in Europe. Nat. Clim. Chang. 2018, 8, 776–780. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dessai, S. Robust adaptation to climate change. Weather 2010, 65, 180–185. [Google Scholar] [CrossRef]
- Stephens, S.A.; Bell, R.G.; Lawrence, J. Applying Principles of Uncertainty within Coastal Hazard Assessments to Better Support Coastal Adaptation. J. Mar. Sci. Eng. 2017, 5, 40. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Bouziotas, D.; Giardino, A.; Bouwer, L.M.; Mentaschi, L.; Voukouvalas, E.; Feyen, L. Understanding epistemic uncertainty in large-scale coastal flood risk assessment for present and future climates. Nat. Hazards Earth Syst. Sci. 2018, 18, 2127–2142. [Google Scholar] [CrossRef]
- Wolff, C.; Vafeidis, A.T.; Lincke, D.; Marasmi, C.; Hinkel, J. Effects of Scale and Input Data on Assessing the Future Impacts of Coastal Flooding: An Application of DIVA for the Emilia-Romagna Coast. Front. Mar. Sci. 2016, 3, 41. [Google Scholar] [CrossRef]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; Wiley: West Sussex, England, 2007. [Google Scholar]
- Le Cozannet, G.; Rohmer, J.; Cazenave, A.; Idier, D.; van de Wal, R.; de Winter, R.; Pedreros, R.; Balouin, Y.; Vinchon, C.; Oliveros, C. Evaluating uncertainties of future marine flooding occurrence as sea-level rises. Environ. Model. Softw. 2015, 73, 44–56. [Google Scholar] [CrossRef]
- Wong, T.E.; Keller, K. Deep Uncertainty Surrounding Coastal Flood Risk Projections: A Case Study for New Orleans. Earths Futur. 2017, 5, 1015–1026. [Google Scholar] [CrossRef]
- Anderson, B.; Borgonovo, E.; Galeotti, M.; Roson, R. Uncertainty in Climate Change Modeling: Can Global Sensitivity Analysis Be of Help? Risk Anal. 2013, 34, 271–293. [Google Scholar] [CrossRef] [PubMed]
- Hinkel, J.; Klein, R.J. Integrating knowledge to assess coastal vulnerability to sea-level rise: The development of the DIVA tool. Glob. Environ. Chang. 2009, 19, 384–395. [Google Scholar] [CrossRef]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.L.T.; Lamarque, J.F.; Matsumoto, K.; Montzka, S.A.; Raper, S.C.B.; Riahi, K.; et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Chang. 2011, 109, 213–241. [Google Scholar] [CrossRef]
- Riahi, K.; Van Vuuren, D.; Kriegler, E.; Edmonds, J.; O’Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.V.; Dellink, R.B.; Fricko, O.; et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Chang. 2017, 42, 153–168. [Google Scholar] [CrossRef]
- Wahl, T.; Haigh, I.D.; Nicholls, R.J.; Arns, A.; Dangendorf, S.; Hinkel, J.; Slangen, A.B.A. Understanding extreme sea levels for broad-scale coastal impact and adaptation analysis. Nat. Commun. 2017, 8, 16075. [Google Scholar] [CrossRef]
- Ward, P.J.; Brenden, J.; Frederiek Sperna, W.; Arno, B.; van Rens, B.; Marc, F.P.B.; Willem, L.; Hessel, C.W. Assessing flood risk at the global scale: Model setup, results, and sensitivity. Environ. Res. Lett. 2013, 8, 044019. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Frederikse, T.; Kopp, R.E.; Le Cozannet, G.; Jackson, L.P.; Van De Wal, R.S.W. Probabilistic Sea Level Projections at the Coast by 2100. Surv. Geophys. 2019, 40, 1673–1696. [Google Scholar] [CrossRef]
- Oppenheimer, M.; Glavovic, B.C.; Hinkel, J.; van de Wal, R.; Magnan, A.K.; Abd-Elgawad, A.; Cai, R.; Cifuentes-Jara, M.; DeConto, R.M.; Ghosh, T.; et al. Low Lying Isl. Sea Level Rise and Implications for Low-Lying Islands. Coasts Communities 2019, 321–445, in press. [Google Scholar]
- Brown, S.; Nicholls, R.J.; Hanson, S.; Brundrit, G.; Dearing, J.A.; Dickson, M.E.; Gallop, S.L.; Gao, S.; Haigh, I.D.; Hinkel, J.; et al. Shifting perspectives on coastal impacts and adaptation. Nat. Clim. Chang. 2014, 4, 752–755. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Mentaschi, L.; Hinkel, J.; Ward, P.J.; Mongelli, I.; Ciscar, J.-C.; Feyen, L. Economic motivation for raising coastal flood defenses in Europe. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Vafeidis, A.T.; Nicholls, R.J.; Mc Fadden, L.; Tol, R.S.J.; Hinkel, J.; Spencer, T.; Grashoff, P.S.; Boot, G.; Klein, R.J.T. A New Global Coastal Database for Impact and Vulnerability Analysis to Sea-Level Rise. J. Coast. Res. 2008, 244, 917–924. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.B. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Da Veiga, S.; Wahl, F.; Gamboa, F. Local Polynomial Estimation for Sensitivity Analysis on Models with Correlated Inputs. Technometrics 2009, 51, 452–463. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Li, C.; Mahadevan, S. An efficient modularized sample-based method to estimate the first-order Sobol’ index. Reliab. Eng. Syst. Saf. 2016, 153, 110–121. [Google Scholar] [CrossRef]
- Muis, S.; Verlaan, M.; Winsemius, H.C.; Aerts, J.C.; Ward, P.J. A global reanalysis of storm surges and extreme sea levels. Nature Commun. 2016, 7, 1–12. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modelling of Extreme Values; Springer: London, UK, 2001; Volume 208, p. 208. [Google Scholar]
- Lichter, M.; Vafeidis, A.T.; Nicholls, R.J. Exploring Data-Related Uncertainties in Analyses of Land Area and Population in the “Low-Elevation Coastal Zone” (LECZ). J. Coast. Res. 2010, 27, 757. [Google Scholar] [CrossRef]
- McGrath, H.; El Ezz, A.A.; Nastev, M. Probabilistic depth–damage curves for assessment of flood-induced building losses. Nat. Hazards 2019, 97, 1–14. [Google Scholar] [CrossRef]
- Prahl, B.F.; Boettle, M.; Costa, L.; Kropp, J.P.; Rybski, D. Damage and protection cost curves for coastal floods within the 600 largest European cities. Sci. Data 2018, 5, 180034. [Google Scholar] [CrossRef] [PubMed]
- Santamaría-Gómez, A.; Gravelle, M.; Dangendorf, S.; Marcos, M.; Spada, G.; Wöppelmann, G. Uncertainty of the 20th century sea-level rise due to vertical land motion errors. Earth Planet. Sci. Lett. 2017, 473, 24–32. [Google Scholar] [CrossRef]
- Peltier, W. Global Glacial Isostasy and the Surface of the Ice-Age Earth: The ICE-5G (VM2) Model and GRACE. Annu. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Kwakkel, J.H.; Walker, W.E.; Marchau, V.A. Classifying and communicating uncertainties in model-based policy analysis. Int. J. Technol. Policy Manag. 2010, 10, 299. [Google Scholar] [CrossRef]
- Karegar, M.A.; Larson, K.M.; Kusche, J.; Dixon, T.H. Novel Quantification of Shallow Sediment Compaction by GPS Interferometric Reflectometry and Implications for Flood Susceptibility. Geophys. Res. Lett. 2020, 47, 087807. [Google Scholar] [CrossRef]
- Hinkel, J.; Church, J.A.; Gregory, J.M.; Lambert, E.; Le Cozannet, G.; Lowe, J.; McInnes, K.L.; Nicholls, R.J.; Van Der Pol, T.D.; Van De Wal, R. Meeting User Needs for Sea Level Rise Information: A Decision Analysis Perspective. Earths Futur. 2019, 7, 320–337. [Google Scholar] [CrossRef]
- Kulp, S.A.; Strauss, B.H. New elevation data triple estimates of global vulnerability to sea-level rise and coastal flooding. Nat. Commun. 2019, 10, 1–12. [Google Scholar] [CrossRef]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote. Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Raucoules, D.; Le Cozannet, G.; Wöppelmann, G.; de Michele, M.; Gravelle, M.; Daag, A.; Marcos, M. High nonlinear urban ground motion in Manila (Philippines) from 1993 to 2010 observed by DInSAR: Implications for sea-level measurement. Remote. Sens. Environ. 2013, 139, 386–397. [Google Scholar] [CrossRef]
- Ng, A.H.-M.; Ge, L.; Li, X.; Abidin, H.Z.; Andreas, H.; Zhang, K. Mapping land subsidence in Jakarta, Indonesia using persistent scatterer interferometry (PSI) technique with ALOS PALSAR. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 232–242. [Google Scholar] [CrossRef]
- Wang, J.; Gao, W.; Xu, S.; Yu, L. Evaluation of the combined risk of sea level rise, land subsidence, and storm surges on the coastal areas of Shanghai, China. Clim. Chang. 2012, 115, 537–558. [Google Scholar] [CrossRef]
- Wolff, C.; Nikoletopoulos, T.; Hinkel, J.; Vafeidis, A. What Plausible Urban Coastal Futures May Look Like? Spatially Explicit Urbanization Projections for 10 Mediterranean Countries; EGU General Assembly: Vienna, Austria, 2019. [Google Scholar] [CrossRef]
- Breilh, J.F.; Chaumillon, E.; Bertin, X.; Gravelle, M. Assessment of static flood modeling techniques: Application to contrasting marshes flooded during Xynthia (western France). Nat. Hazards Earth Syst. Sci. 2013, 13, 1595–1612. [Google Scholar] [CrossRef]
- Vafeidis, A.T.; Schuerch, M.; Wolff, C.; Spencer, T.; Merkens, J.L.; Hinkel, J.; Lincke, D.; Brown, S.; Nicholls, R.J. Water-level attenuation in global-scale assessments of exposure to coastal flooding: A sensitivity analysis. Nat. Hazards Earth Syst. Sci. 2019, 19, 973–984. [Google Scholar] [CrossRef]
- Galasso, C.; Pregnolato, M.; Parisi, F. A model taxonomy for flood fragility and vulnerability assessment of buildings. Int. J. Disaster Risk Reduct. 2021, 53, 101985. [Google Scholar] [CrossRef]
- Lambert, E.; Rohmer, J.; Le Cozannet, G.; Van De Wal, R.S.W. Adaptation time to magnified flood hazards underestimated when derived from tide gauge records. Environ. Res. Lett. 2020, 15, 074015. [Google Scholar] [CrossRef]
- Arns, A.; Wahl, T.; Wolff, C.; Vafeidis, A.T.; Haigh, I.D.; Woodworth, P.; Niehüser, S.; Jensen, J. Non-linear interaction modulates global extreme sea levels, coastal flood exposure, and impacts. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Haigh, I.D.; Pickering, M.D.; Green, J.A.M.; Arbic, B.K.; Arns, A.; Dangendorf, S.; Hill, D.F.; Horsburgh, K.; Howard, T.; Idier, D.; et al. The Tides They Are A-Changin’: A Comprehensive Review of Past and Future Nonastronomical Changes in Tides, Their Driving Mechanisms, and Future Implications. Rev. Geophys. 2020, 58, 000636. [Google Scholar] [CrossRef]
- Chen, C.; Liu, W.; Wang, G. Understanding the Uncertainty in the 21st Century Dynamic Sea Level Projections: The Role of the AMOC. Geophys. Res. Lett. 2019, 46, 210–217. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
| Modelling Uncertainty | Values | Number of Values |
|---|---|---|
| Socio-economic development (SSP) | SSP1-5 | 5 |
| Greenhouse gas concentrations (RCP) | RCP2.6, 4.5, 8.5 | 3 |
| Global population distribution (POP) | GPW4 or Landscan | 2 |
| Magnitude of the Regional Sea-Level Rise (RSLR) | Median value, 5th and 95th percentile given RCP scenario | 3 |
| Logistic depth-damage curves (DF) | Half-damage depth 1 or 1.5 m | 2 |
| r-largest annual value (rGEV) | Number of r largest values used to fit GEV: 1, 2 or 5 | 3 |
| Subsidence in delta region (SUBS) | Included or not | 2 |
| Assets-to-GDP ratio (A:GDPr) | Value of 2.8 or 3.8 | 2 |
| Uncertain Variable | Most Likely Value | Likelihood Weight |
|---|---|---|
| Logistic depth-damage curves | Half-damage depth at 1.0 m | 0.75 |
| Extreme value modelling | rGEV = 5 | 0.66 |
| Subsidence in delta region | Included | 0.75 |
| Socio-economic & Greenhouse Gas concentrations | See Table 3 | See Table 3 |
| RCP2.6 | RCP4.5 | RCP8.5 | |
|---|---|---|---|
| SSP1 | 0.18 | 0.34 | 0.48 |
| SSP2 | 0.09 | 0.12 | 0.79 |
| SSP3 | <0.01 | 0.11 | 0.89 |
| SSP4 | 0.12 | 0.18 | 0.70 |
| SSP5 | 0.05 | 0.085 | 0.865 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rohmer, J.; Lincke, D.; Hinkel, J.; Le Cozannet, G.; Lambert, E.; Vafeidis, A.T. Unravelling the Importance of Uncertainties in Global-Scale Coastal Flood Risk Assessments under Sea Level Rise. Water 2021, 13, 774. https://doi.org/10.3390/w13060774
Rohmer J, Lincke D, Hinkel J, Le Cozannet G, Lambert E, Vafeidis AT. Unravelling the Importance of Uncertainties in Global-Scale Coastal Flood Risk Assessments under Sea Level Rise. Water. 2021; 13(6):774. https://doi.org/10.3390/w13060774
Chicago/Turabian StyleRohmer, Jeremy, Daniel Lincke, Jochen Hinkel, Gonéri Le Cozannet, Erwin Lambert, and Athanasios T. Vafeidis. 2021. "Unravelling the Importance of Uncertainties in Global-Scale Coastal Flood Risk Assessments under Sea Level Rise" Water 13, no. 6: 774. https://doi.org/10.3390/w13060774
APA StyleRohmer, J., Lincke, D., Hinkel, J., Le Cozannet, G., Lambert, E., & Vafeidis, A. T. (2021). Unravelling the Importance of Uncertainties in Global-Scale Coastal Flood Risk Assessments under Sea Level Rise. Water, 13(6), 774. https://doi.org/10.3390/w13060774








