Distributed-Framework Basin Modeling System: II. Hydrologic Modeling System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Digital Basin Generation Model
2.1.1. Runoff Concentration on Underlying Surface for Other Models
- Input the raster DEM data for analysis.
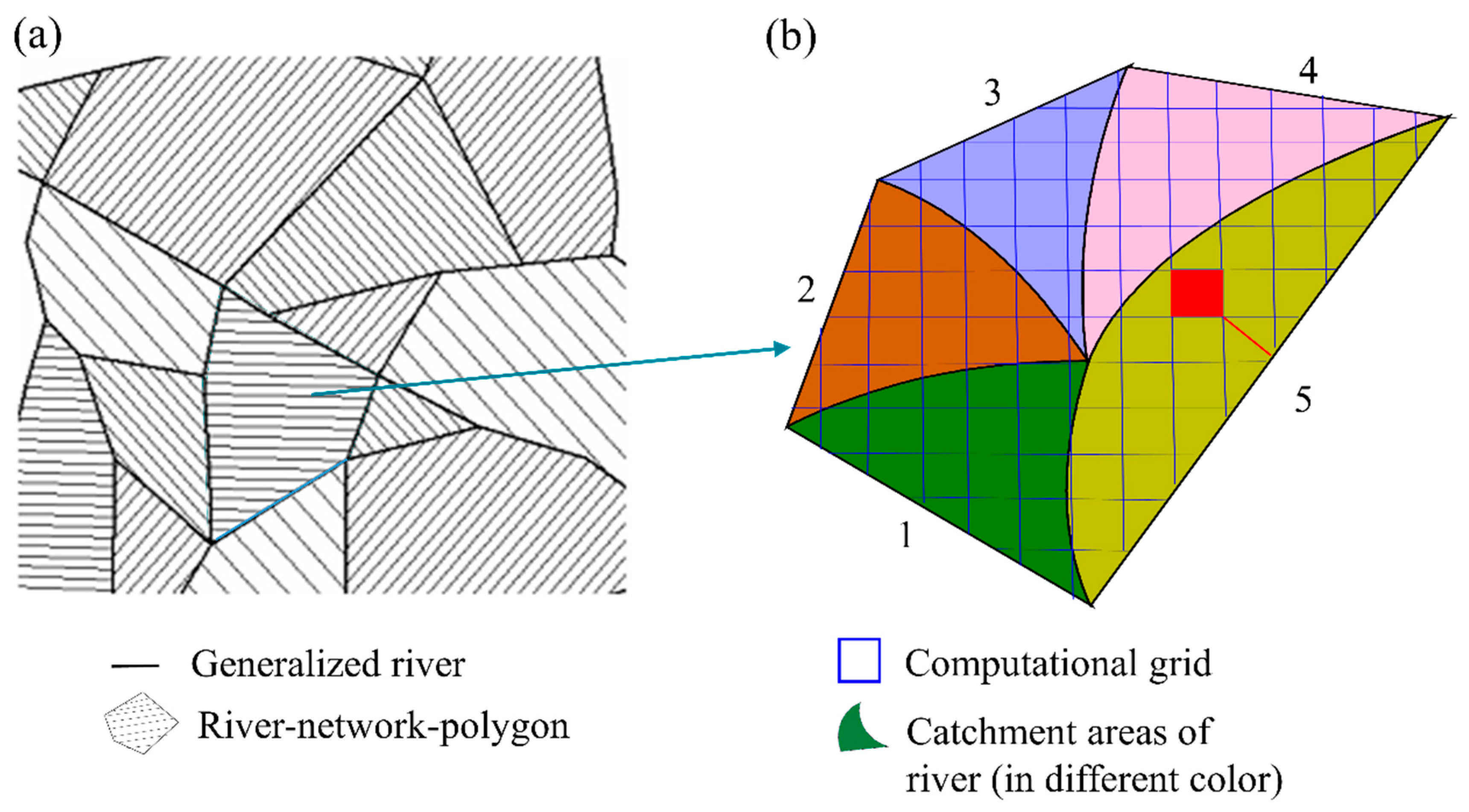
- Calculate the gradients between a cell and all lower neighboring cells to identify the steepest downslope for every cell and accumulate catchment area downslope along the runoff concentration paths connecting adjacent cells.
- Determine the sub-watershed area and watershed dividing line based on the area threshold and runoff concentration path.
- Generate the drainage, channel, and river network based on the runoff concentration path.
- Calculate the geographic and hydrologic parameters for the sub-watershed, such as slope, slope orientation, and area.
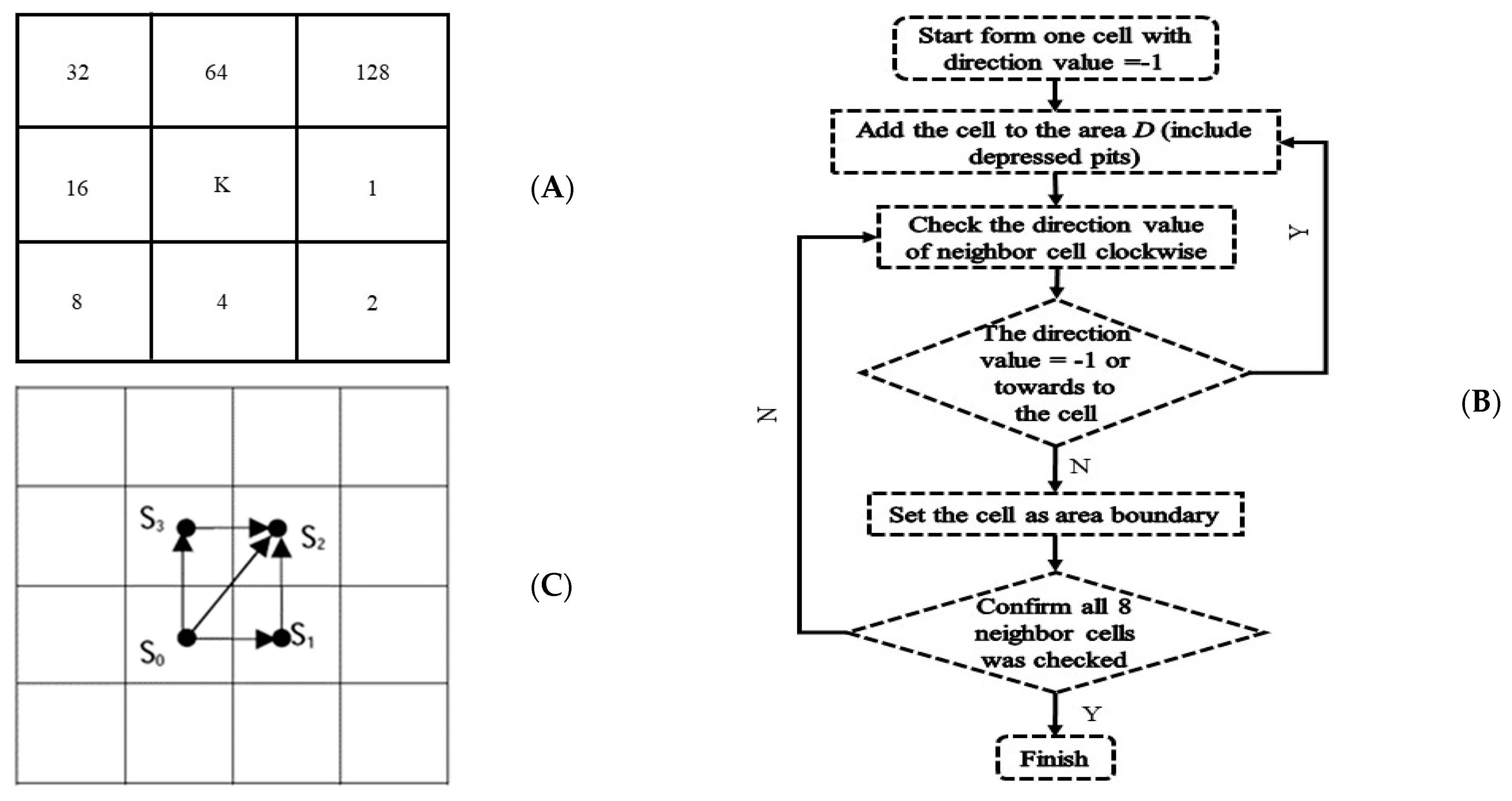
2.1.2. Runoff Concentration in DFBMS
- We assigned 0 to the runoff concentration direction of invalid cells with DEM value equal to –9999.
- For cells at the boundary, 3 treatment methods were adopted for different situations: (a) The runoff concentration direction was set to be out of the domain when the maximum slope of the cell was smaller or equal to 0, (b) the runoff concentration direction was set to the maximum slope direction when there was only one maximum slope larger than zero, and (c) the runoff concentration direction was established based on Figure 2B when there was more than 1 slope larger than 0.
- For other cells, the slopes of cell K and 8 neighboring cells were calculated first, then 4 treatment methods were adopted for different situations: (a) −1 was assigned to the cell to indicate the runoff concentration direction was undetermined when the maximum slope of the cell was smaller than zero (depressed pit cell), (b) the runoff concentration direction was set to the maximum slope direction when there was only 1 slope larger than 0; (c) the runoff concentration direction was set based on Figure 2B when there was more than one positive slope larger than zero, and (d) −1 was assigned to the cell to indicate the runoff concentration direction was undetermined when there was more than 1 slope equal to 0 ( for some neighboring cells).
- We started from the cell with runoff concentration direction value equal to −1 and checked whether the values of the 8 neighboring cells equaled −1 or not. After that, we generated the runoff concentration path with the area accumulation method, which is shown in Figure 2B.
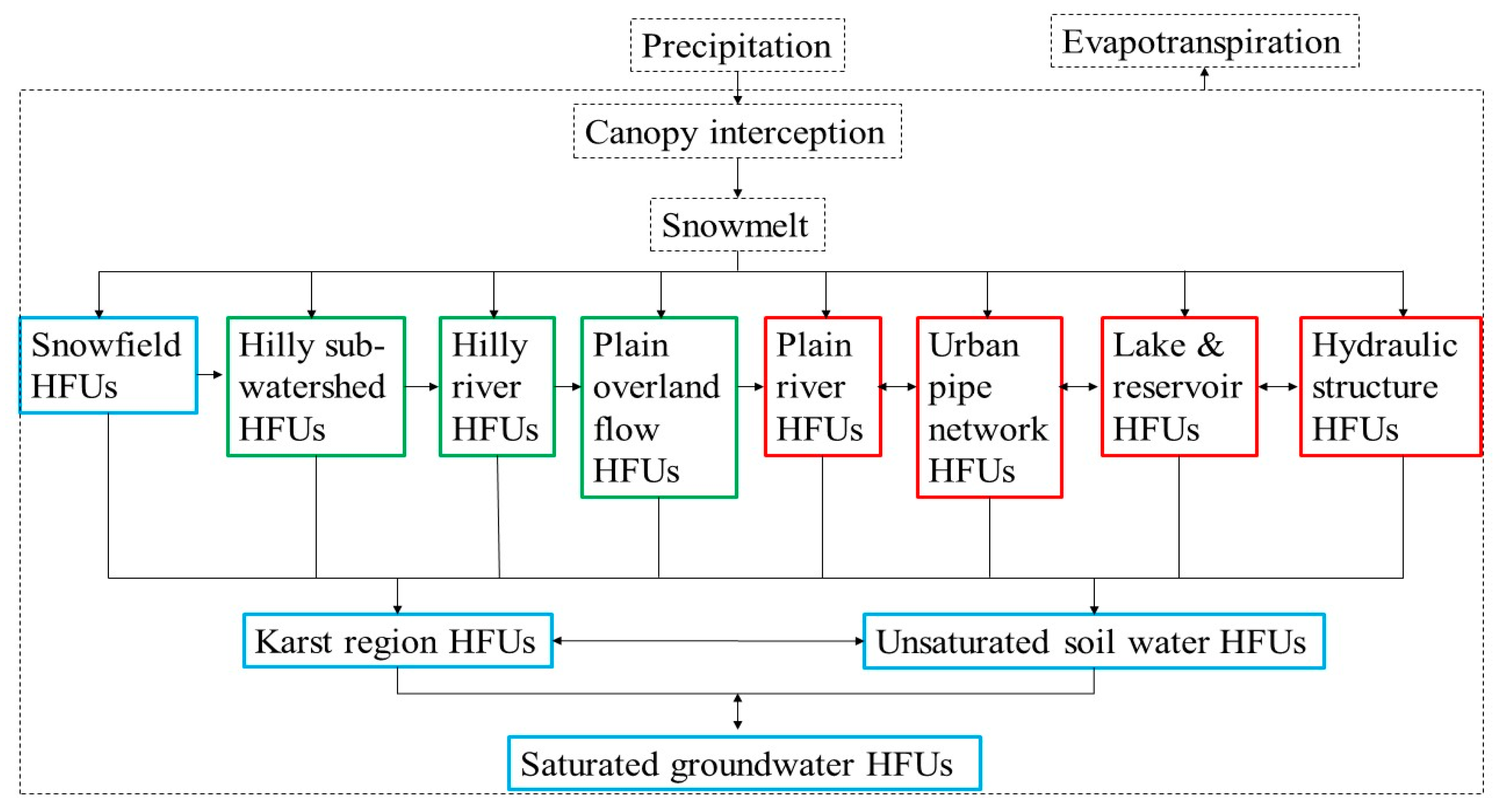
2.2. Primary HFUs of DF-HMS
2.2.1. Hilly Sub-Watershed HFUs
2.2.2. Hilly River HFUs
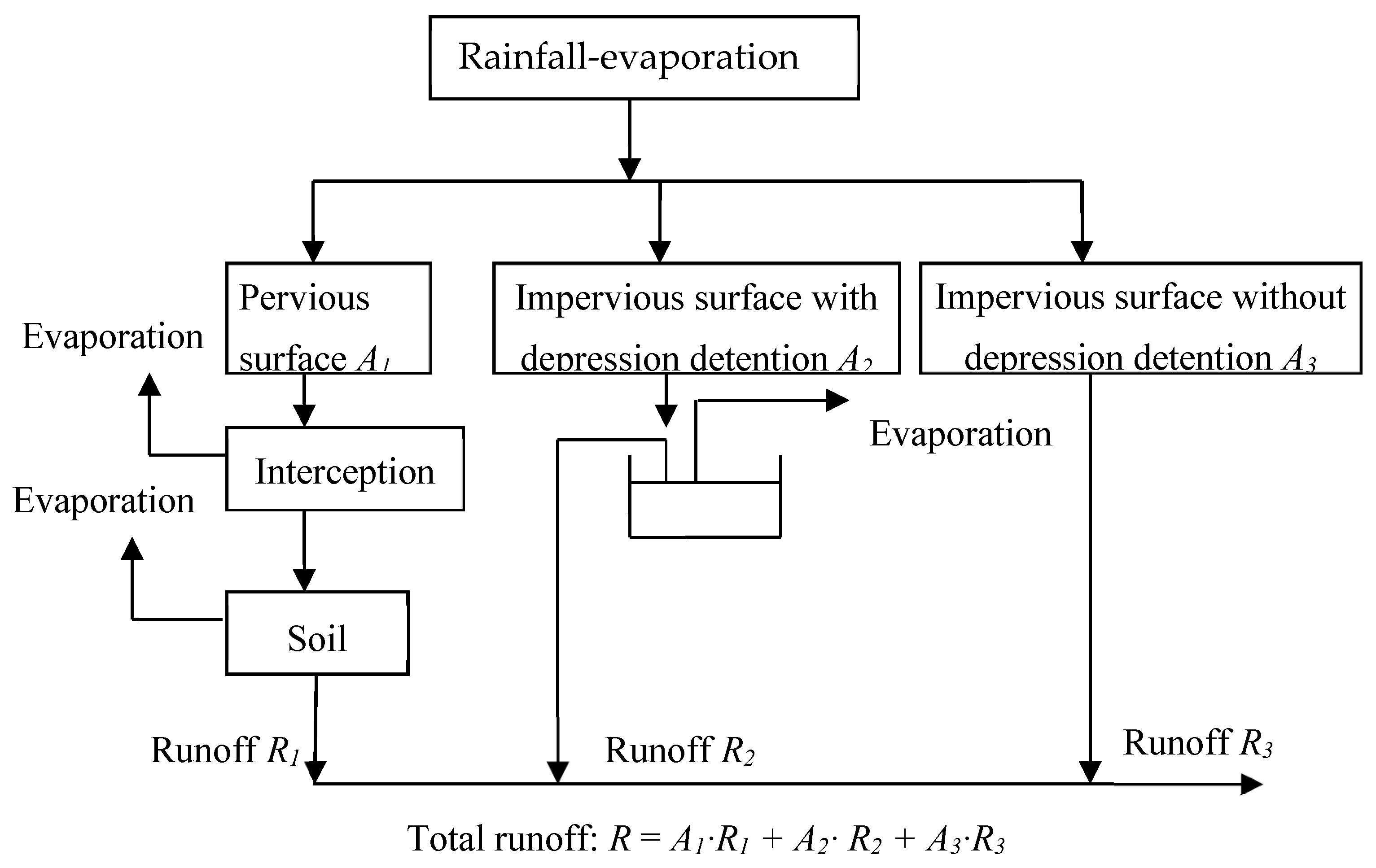
2.2.3. Plain Overland Runoff Flow HFUs
- (a)
- The delta plain is characterized by low elevation and flat topography, which leads to a slow confluence process and jacking influence between river flow and overland flow.
- (b)
- The delta plain maintains a shallow groundwater table, which causes more significant transformation between atmosphere water, surface water, soil water, and groundwater.
- (c)
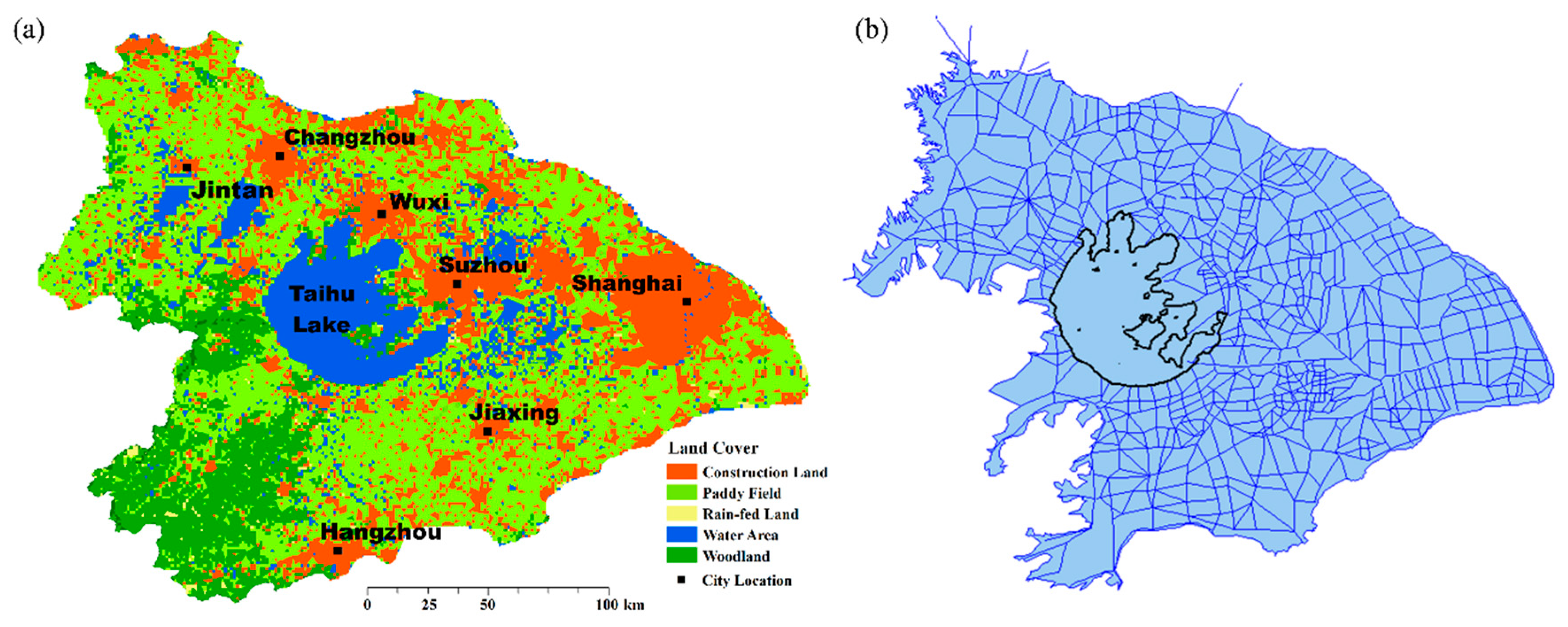
- The underlying surface in the delta plain is more variable than in the hilly area, especially for specific land-use types. For example, paddy fields present different kinds of underlying surfaces in the growing and dormant periods, which means different rainfall-runoff mechanisms. Figure 4a shows an example of the land cover in the Taihu basin.
- (d)
- Extensive river networks are characterized by cyclic structure and uncertain catchment boundaries in the delta plain, which is far different from process of the dendritic river systems in the hilly area. The flow of the river here does not always converge from the upstream to the downstream section, but rather moves in various directions. This open system with several outlets is hard to study by limited technology and conditions because it is difficult to measure flow and direction data of enough river control sections for model validation. Figure 4b shows an example of the plain river network in the Taihu basin.
- (e)
- Human activities in small hydraulic engineering projects such as polder embankments and water gates increase the complexity of the confluence process.
- i.
- Modeling in the water area
- ii.
- Modeling in rain-fed land
- iii.
- Modeling in the paddy field
- iv.
- Modeling in construction land
2.2.4. Distributed Overland Flow Concentration Model in the Delta Plain
2.3. Typical HFUs in Hydraulic Modeling System
- (1).
- The plain river HFU, which is a confluence/routing hydrological feature unit. It includes rivers characterized by low flow rate, jacking influence between main streams and tributaries, and even reciprocating flow existing in the littoral region. Both the mean water level and discharge process and the distribution of water level and flow velocity in the river are sometimes considered. Therefore, the dynamical method was applied to deal with these confluence processes. The river flow model includes one-dimensional and two-dimensional models to simulate for single channels and the river network as well as the coupling process between different models.
- (2).
- The lake and reservoir HFU, which is also a confluence hydrological feature unit. Lakes and reservoirs usually maintain a certain level of water, and water moves inside flood districts and polders after a dam breaks or a gate opens. Once the water flow exists, it will follow the same rule of confluence that was classified as the same HFU in the DFBMS. According to the accuracy requirement, the confluence simulation for this kind of HFU can be divided into three types: Zero-dimensional, two-dimensional, and three-dimensional models. However, the three-dimensional model is not commonly used at the basin scale.
- (3).
- The hydraulic structure HFU, which is part of the confluence hydrological feature unit. It includes hydraulic structures such as gates, dams, reservoirs, and flood area entrance gates. This kind of HFUs is commonly applied in flood control/forecasting and water resource scheduling. Models for these HFUs focus on simulating the flow control and scheduling process.
2.4. Uncommon HFUs in Distributed-Framework Professional Model System
3. Case Study
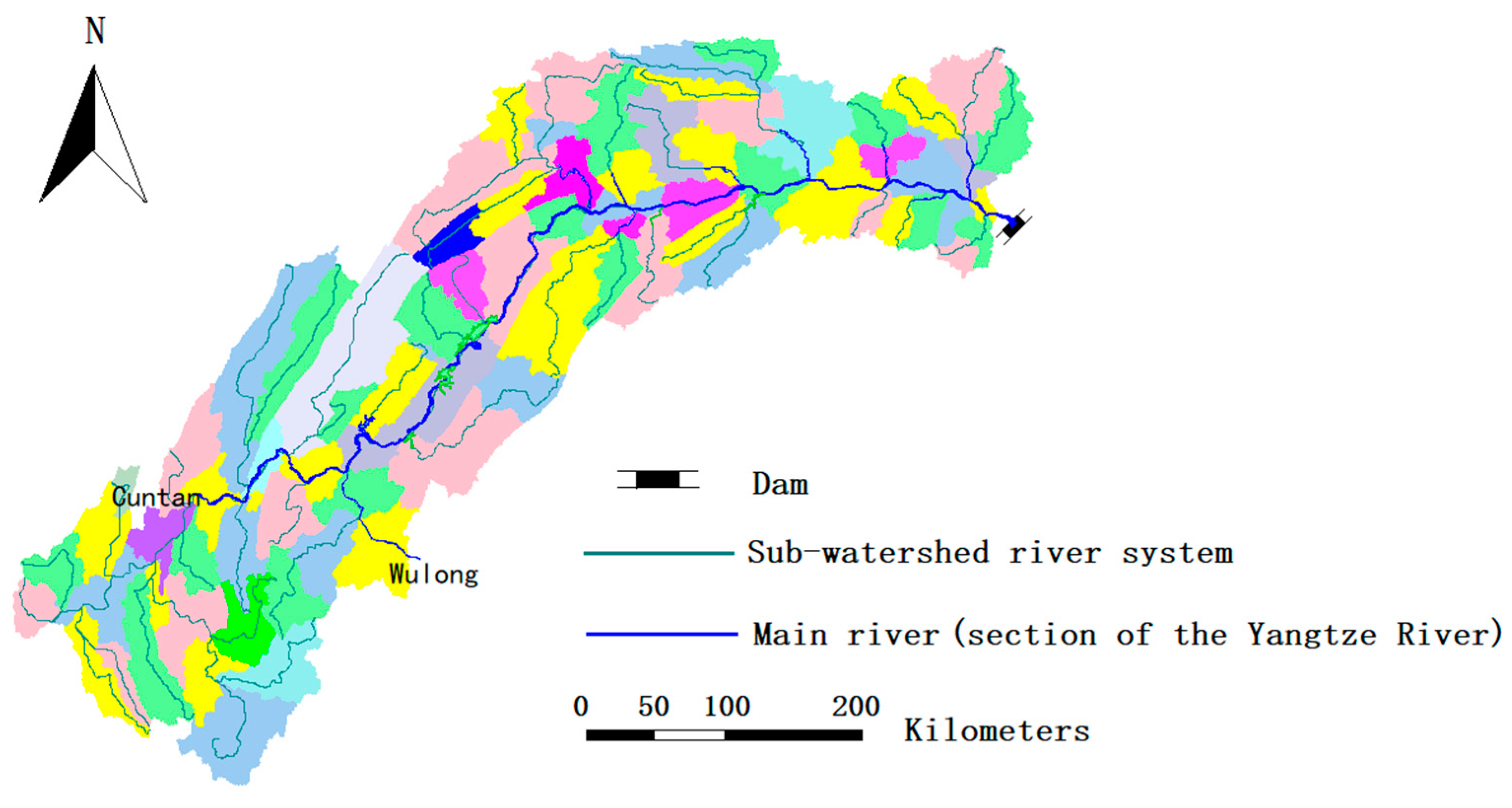
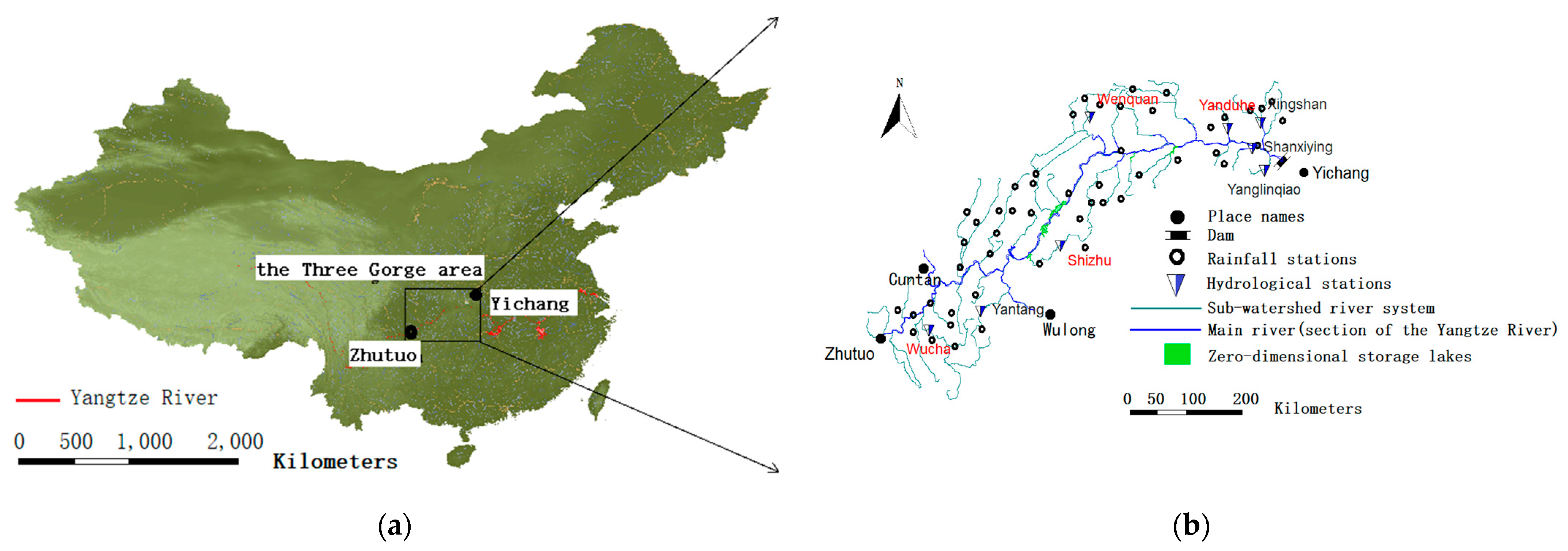
3.1. Study Area and Corresponding Hydrological Characteristic Unit
3.2. Methodology
3.3. Model Calibration and Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beven, K.J. A discussion of distributed hydrological modelling. Distributed Hydrological Modelling; Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 1990; Volume 22, pp. 255–278. [Google Scholar] [CrossRef]
- Wurbs, R.A. Dissemination of generalized water resources models in the United States. Water Int. 1998, 23, 190–198. [Google Scholar] [CrossRef]
- Singh, V.P.; Woolhiser, D.A. Mathematical modeling of watershed hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef] [Green Version]
- Pechlivanidis, I.; Jackson, B.; Mcintyre, N.; Wheater, H. Catchment scale hydrological modelling—A review of model types, calibration approaches and uncertainty analysis methods in the context of recent developments in technology and applications. Glob. NEST Int. J. 2011, 13, 193–214. [Google Scholar]
- Rafaeli Neto, S.L.; Schatz Sa, E.A.; Debastiani, A.B.; Padilha, V.L.; Antunes, T.A. Efficacy of Rainfall-Runoff Models in Loose Coupling Spacial Decision Support Systems Modelbase. Water Resour. Manag. 2019, 33, 1–16. [Google Scholar]
- Yu, Z. Assessing the response of subgrid hydrologic processes to atmospheric forcing with a hydrologic model system. Glob. Planet. Chang. 2000, 25, 1–17. [Google Scholar] [CrossRef]
- Wang, C.; Hua, W.; Chen, G.; Fang, X.; Li, X. Distributed-Framework Basin Modeling System: I. Overview and Model Coupling. Water 2021, 13, 678. [Google Scholar] [CrossRef]
- Mohamad, B.; Zhang, X.N. GIS-based hydrological modelling: A comparative study of HEC-HMS and the Xinanjiang model. In Proceedings of the Twelfth International Water Technology Conference-Hydrological Sciences for Managing Water Resources in the Asian Developing World, IWTC12, Alexandria, Egypt, 1 January 2006; pp. 124–133. [Google Scholar]
- Ahirwar, A.; Jain, M.K.; Perumal, M. Performance of the Xinanjiang Model. Hydrol. Modeling Water Sci. Technol. Libr. 2018, 81, 715–731. [Google Scholar]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.J.; Participants, D. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Smith, M.B.; Seo, D.J.; Koren, V.I.; Reed, S.M.; Zhang, Z.; Duan, Q.; Cong, S. The distributed model intercomparison project (DMIP): Motivation and experiment design. J. Hydrol. 2004, 298, 4–26. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J.; Schofield, N.; Tagg, A.F. Testing a physically based flood forecasting model (TOPMODEL) for three UK catchments. J. Hydrol. 1984, 69, 119–143. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A review on hydrological models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments; Report RH07; SMHI: Norrköping, Sweden, 1976; p. 134.
- Abbott, M.B.; Bathrust, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological Systèm-Systeme Hydrologique Européen, “SHE”, 2: Structure of a physically-based distributed modeling system. J. Hydrol. 1986b, 87, 61–77. [Google Scholar] [CrossRef]
- Shi, P.; Chen, C.; Srinivasan, R.; Zhang, X.; Cai, T.; Fang, X. Evaluating the swat model for hydrological modeling in the xixian watershed and a comparison with the xaj model. Water Resour. Manag. 2011, 25, 2595–2612. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [CrossRef] [Green Version]
- Zhao, R.J.; Zhang, Y.L.; Fang, L.R.; Liu, X.R.; Zhang, Q.S. The Xinanjiang Model. Hydrol. Forecast. Proc. Oxf. Symp. IASH 1980, 129, 351–356. [Google Scholar]
- Kuok, O.; Chiu, P.C. Particle Swarm Optimization and Shuffle Complex Evolution for Calibrating Xinanjiang Model Parameters. Int. J. Comput. Technol. 2013, 10, 2036–2047. [Google Scholar] [CrossRef] [Green Version]
- Lü, H.; Hou, T.; Horton, R.; Zhu, Y.; Chen, X.; Jia, Y.; Wang, W.; Fu, X. The streamflow estimation using the Xinanjiang rainfall runoff model and dual state-parameter estimation method. J. Hydrol. 2013, 480, 102–114. [Google Scholar] [CrossRef]
- Li, X.; Wang, C.; Chen, G.; Fang, X.; Zhang, P.; Hua, W. Distributed-Framework Basin Modeling System: Ⅲ. Hydraulic Modeling System. Water 2021, 13, 649. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System-Système Hydrologique Européen, “SHE”,1: History and philosophy of a physically-based, distributed modeling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Law, B.E.; Falge, E. Carbon dioxide and water vapor exchange of terrestrial vegetation in response to environment. Agric. For. Meteorol. 2002, 113, 97–120. [Google Scholar] [CrossRef] [Green Version]
- Skoulikaris, C.; Anagnostopoulou, C.; Lazoglou, G. Hydrological Modeling Response to Climate Model Spatial Analysis of a South Eastern Europe International Basin. Climate 2020, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Perumal, M. Multilinear muskingum flood routing method. J. Hydrol. 1992, 133, 259–272. [Google Scholar] [CrossRef]
- Dai, C.Z. Method of Cowpilation of Annual Data of Flood and Tidal Volume by Principle of Characteristic River Length. Renmin Zhujiang 1993, 4, 15–18. (In Chinese) [Google Scholar]
- Moore, I.D.; Grayson, R.; Ladson, A. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Quinn, P.; Beven, K.; Chevallier, P.; Planchon, O. The prediction of hillslope flow paths for distributed hydrological modelling using digital terrain models. Hydrol. Process. 1991, 5, 59–79. [Google Scholar] [CrossRef]
- Tarboton, D.G. A new method for the determination of flow directions and upslope areas in grid digital elevation models. Water Resour. Res. 1997, 33, 309–319. [Google Scholar] [CrossRef] [Green Version]
- Freeman, T.G. Calculating catchment area with divergent flow based on a regular grid. Comput. Geosci. 1991, 17, 413–422. [Google Scholar] [CrossRef]
- Fairfield, J.; Leymarie, P. Drainage networks from grid digital elevation models. Water Resour. Res. 1991, 27, 709–717. [Google Scholar] [CrossRef]
- Wolock, D.M.; McCabe, G.J., Jr. Comparison of Single and Multiple Flow Direction Algorithms for Computing Topographic Parameters in TOPMODEL. Water Resour. Res. 1995, 31, 1315–1324. [Google Scholar] [CrossRef]
- Desmet, P.J.J.; Govers, G. Comparison of routing algorithms for digital elevation models and their implications for predicting ephemeral gullies. Int. J. Geogr. Inf. Syst. 1996, 10, 311–331. [Google Scholar] [CrossRef]
- Band, L.E. Topographic partition of watersheds with digital elevation models. Water Resour. Res. 1986, 22, 15–24. [Google Scholar] [CrossRef]
- Martz, L.W.; De Jong, E. CATCH: A Fortran program for measuring catchment area from digital elevation models. Comput. Geosci. 1988, 14, 627–640. [Google Scholar] [CrossRef]
- Jenson, S.K.; Domingue, J.O. Extracting topographic structure from digital elevation data for geographic information system analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- Martz, L.W.; Garbrecht, J. Numerical definition of drainage network and subcatchment areas from digital elevation models. Comput. Geosci. 1992, 18, 747–761. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H. An efficient method for identifying and filling surface depressions in digital elevation models for hydrologic analysis and modelling. Int. J. Geogr. Inf. Sci. 2006, 20, 193–213. [Google Scholar] [CrossRef]
- Wang, C.H.; Guo, L.J.; Rui, X.F.; Kong, F.Z. Study on real-time flood forecasting system for the Three Gorges Reservoir. Adv. Water Sci. 2003, 14, 677–681. [Google Scholar]
- Brassel, K.E.; Reif, D. A Procedure to Generate Thiessen Polygons. Geogr. Anal. 2010, 11, 289–303. [Google Scholar] [CrossRef]
- Singh, V.P. Computer models of watershed hydrology. Comput. Models Watershed Hydrol. 1997, 29, 88–90. [Google Scholar] [CrossRef]
- Rui, X.F. Study on WGIUH by means of geomorphologic and hydrodynamic dispersion. Adv. Water Sci. 2002, 13, 439–444. [Google Scholar]
- Ali, S.N.; Sil, B.S. Derivation of Geomorphology-based IUH Using GIS-supported GIUH Model for the Barak River Basin. In Development of Water Resources in India; Garg, V., Singh, V., Raj, V., Eds.; Water Science and Technology Library; Springer: Cham, Switzerland, 2017; p. 75. [Google Scholar] [CrossRef]
- Cheng, W.H.; Wang, C.H.; Zhu, Y. Taihu Basin Model; Hohai University Press: Nanjing, China, 2006. [Google Scholar]
- Xu, D.M.; Wang, W.C.; Cheng, C.T.; Chen, S. Comparison of three global optimization algorithms for calibration of the Xinanjiang model parameters. J. Hydroinf. 2013, 15, 174. [Google Scholar] [CrossRef] [Green Version]
- Ohta, T. A distributed snowmelt prediction model in mountain areas based on an energy balance method. Ann. Glaciol. 1994, 19, 107–113. [Google Scholar] [CrossRef] [Green Version]
- Kumar, M.; Marks, D.; Dozier, J.; Reba, M.; Winstral, A. Evaluation of distributed hydrologic impacts of temperature-index and energy-based snow models. Adv. Water Resour. 2013, 56, 77–89. [Google Scholar] [CrossRef]
- Trefry, M.G.; Muffels, C. Feflow: A finite-element groundwater flow and transport modeling tool. Ground Water 2007, 45, 525–528. [Google Scholar] [CrossRef]
- Chen, G.; Wang, C.; Fang, X.; Li, X.; Zhang, P.; Hua, W. Distributed-Framework Basin Modeling System: IV. Application in Taihu Basin. Water 2021, 13, 611. [Google Scholar] [CrossRef]
- Khan, M.H. Xinanjiang Model on Bird Creek catchment in USA. Pak. J. Agric. Res. 1993, 14, 373–382. [Google Scholar]
- Ju, Q.; Yu, Z.; Hao, Z.; Ou, G.; Zhao, J.; Liu, D. Division-based rainfall-runoff simulations with BP neural networks and Xinanjiang model. Neurocomputing 2009, 72, 2873–2883. [Google Scholar] [CrossRef]
- Zhao, R.J.; Liu, X.R. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Sorooshian, S.; Duan, Q.; Gupta, V.K. Calibration of rainfall-runoff models: Application of global optimization to the Sacramento Soil Moisture Accounting Model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]

| Modeling Systems | Classification | HFUs | Methods or Models | Conditions | Inputs | Parameters |
|---|---|---|---|---|---|---|
| All | Geographic | All | Digital Basin Generation Model | With DEM data | DEM or GIS map | This paper Section 2.1 |
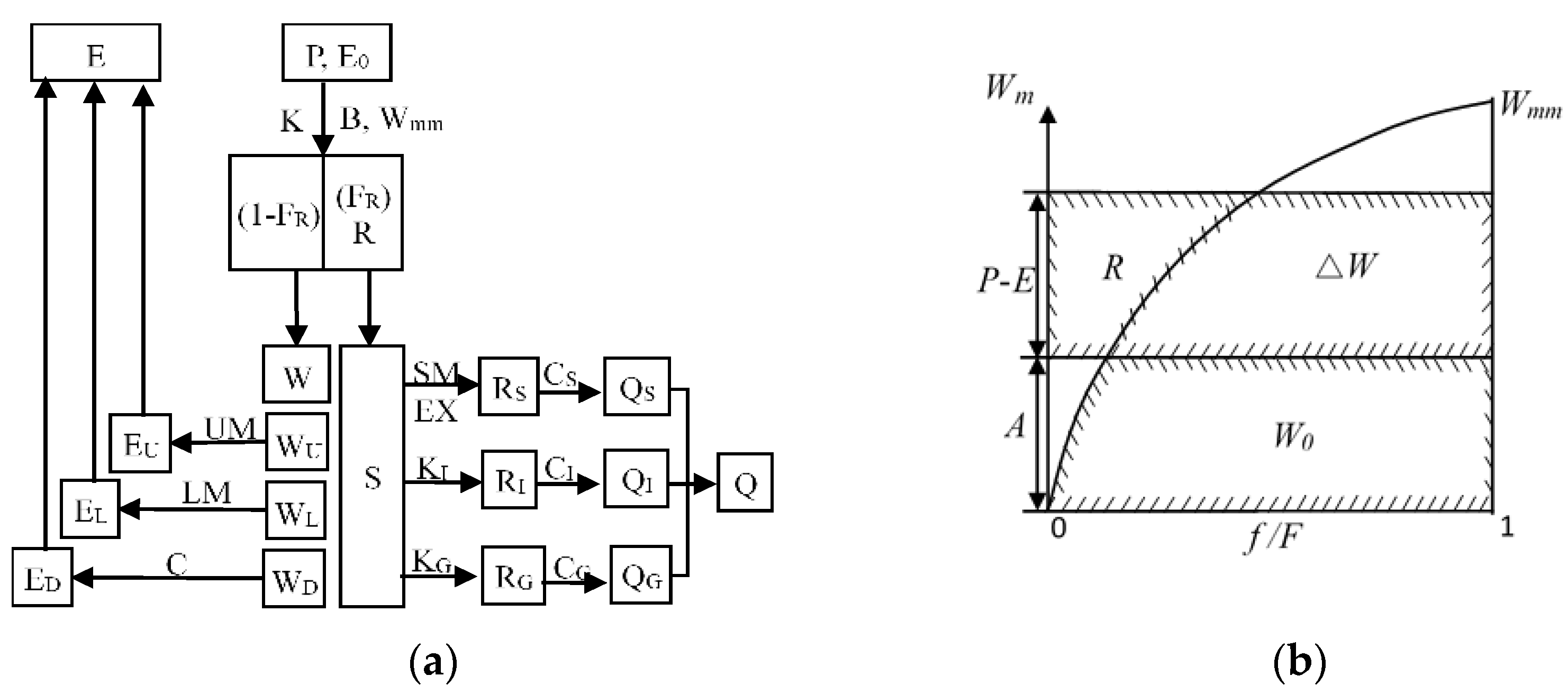
| DF-HMS | Hydrologic | Hilly sub-watershed | Xinanjiang model | Humid and semi-humid area | Measured precipitation, Pan evaporation | This paper Section 3.2 and [18] |
| DF-HMS | Hydrologic | Hilly sub-watershed | TOPMODEL | Based on digital Topography model | Topographic data, precipitation | [12] |
| DF-HMS | Hydrologic | Hilly river | Muskingum model | Confluence in river | Upstream inflow | This paper and [25] |
| DF-HMS | Hydrologic | Hilly river | Characteristic river length method | Hilly area | Inflow | [26] |
| DF-HMS | Hydrologic | Plain overland flow | Rainfall‒runoff model in delta plain | Plain area | This paper Section 2.2.3 | This paper Section 2.2.3 |
| DF-RMS | Hydraulic | Lakes & reservoirs | Zero-dimensional model | 3rd paper | 3rd paper | 3rd paper |
| Two-dimensional model | 3rd paper | 3rd paper | 3rd paper | |||
| DF-RMS | Hydraulic | Plain river | One dimensional hydrodynamic model | 3rd paper | 3rd paper | 3rd paper |
| Two-dimensional hydrodynamic model | 3rd paper | 3rd paper | 3rd paper | |||
| DF-RMS | Hydraulic | Hydraulic structures | Gate and dam simulation | 3rd paper | 3rd paper | 3rd paper |
| Other | Hydraulic | Urban pipe network | Urban pipe network model | Further paper | Further paper | Further paper |
| Number | Parameter | Definition | Range |
|---|---|---|---|
| 1 | K | Ratio of potential evapotranspiration to pan evaporation | 0.1–1.5 |
| 2 | UM | Upper layer soil water storage capacity | 5–20 mm |
| 3 | LM | Lower layer soil water storage capacity | 60–90 mm |
| 4 | C | Deep evaporation coefficient | 0.09–0.3 |
| Wmm | Maximum watershed soil water storage capacity (mm) | 70–210 | |
| B | the exponent of soil water storage capacity curve | 0.05–0.4 | |
| 5 | SM | Free water storage capacity (mm) | 1–50 |
| 6 | EX | the exponent of soil water storage capacity curve | 1.0–1.5 |
| 7 | KI | Outflow coefficient of free water storage to interflow | 0.2–0.6 |
| 8 | KG | Outflow coefficient of free water storage to Groundwater | 0.2–0.6 |
| 9 | CS | Recession constant of surface runoff | 0.01–0.4 |
| 10 | CI | Recession constant of interflow | 0.1–0.99 |
| 11 | CG | Recession constant of groundwater runoff | 0.7–0.99 |
| 12 | KE | Routing time in channel unit (h) | 0–1 |
| 13 | XE | A weight factor of Muskingum method | 0–0.5 |
| Growing Period | Duration | Resistance to Submergence Depth (Hp) (mm) | Upper (Hu) (Lower (Hd)) Limit (mm) | Water Requirement Coefficient | Daily Leakage (mm) | Period of Paddy Field |
|---|---|---|---|---|---|---|
| Soaking | 16–25 May | 40 | 10 (5) | 1.00 | 2 | Rice seedling bed |
| Seedling | 26 May–13 June | 30 | 20 (10) | 1.00 | 2 | |
| Soaking | 14–23 June | 40 | 10 (5) | 1.00 | 2 | Primary growing |
| Resume growth | 24–30 June | 50 | 30 (20) | 1.35 | 2 | |
| Tiller earlier | 1–4 July | 50 | 30 (20) | 1.30 | 2 | |
| 5–9 July | 0 | 0 (0) | 1.30 | 0 | Field drying | |
| 10–19 July | 50 | 30 (20) | 1.30 | 2 | Primary growing | |
| Tiller later | 20–23 July | 50 | 30 (20) | 1.30 | 2 | |
| 24 July–4 August | 10 | 0 (0) | 1.30 | 0 | Field drying | |
| Booting | 5–18 August | 50 | 40 (30) | 1.40 | 2 | Primary growing |
| 19–23 August | 0 | 0 (0) | 1.30 | 0 | Field drying | |
| 24 August–3 September | 50 | 40 (30) | 1.30 | 2 | Primary growing | |
| Heading | 4–16 September | 50 | 30 (20) | 1.30 | 2 | |
| Mature | 17 September–15 October | 20 | 10 (0) | 1.30 | 0.7 | |
| 16–20 October | 0 | 0 (0) | 1.05 | 0 | Mature later |
| Hydrological Station | Flood Event | Rainfall (mm) | Observed (Simulated) Flood Peak Discharge (m3/s) | Flood Peak Discharge RE (%) | RMSE (m3/s) | NSE |
|---|---|---|---|---|---|---|
| Shanxiying | 20080625 | 254.4 | 166 (166.6) | 0.36 | 14.1 | 0.9 |
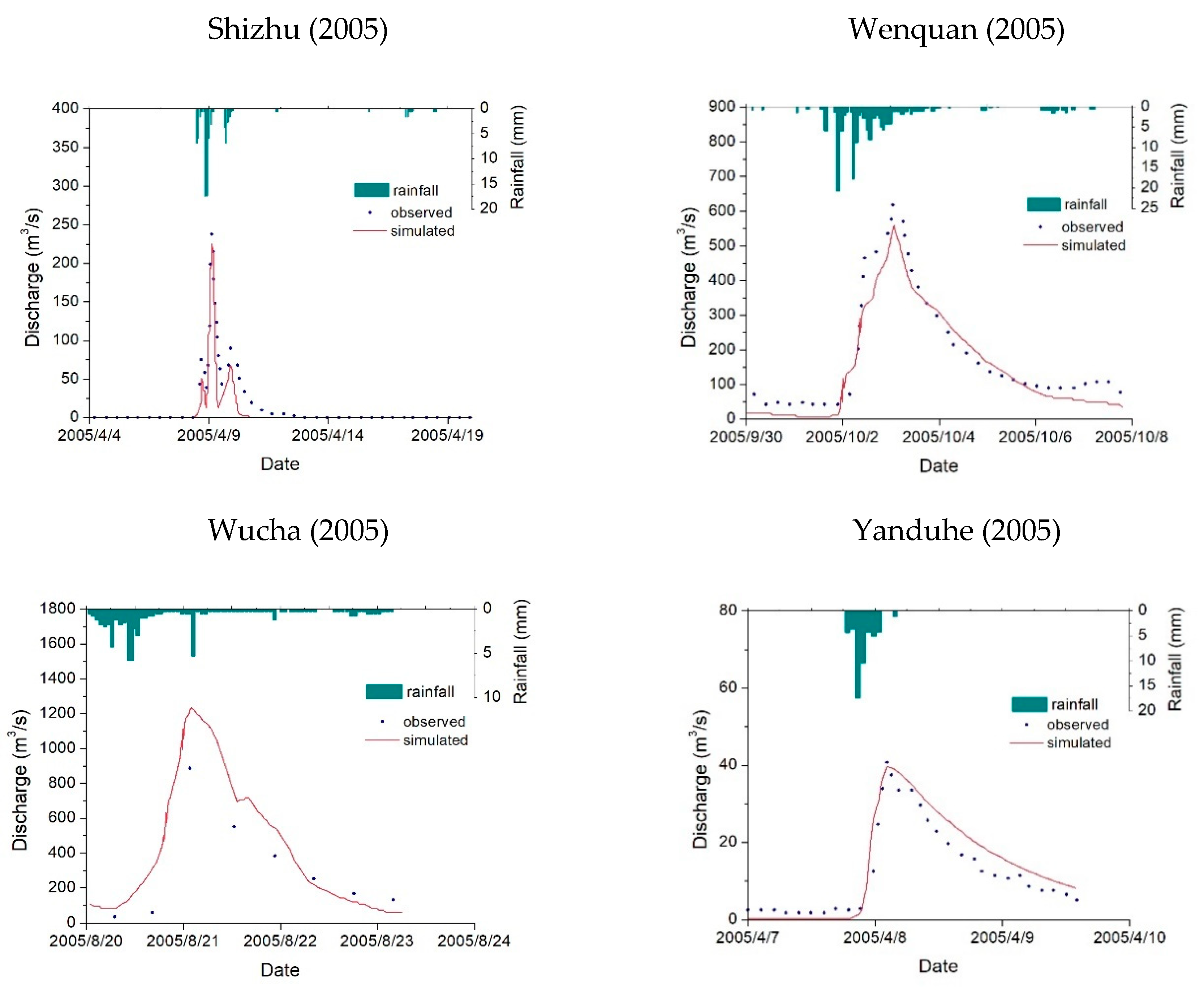
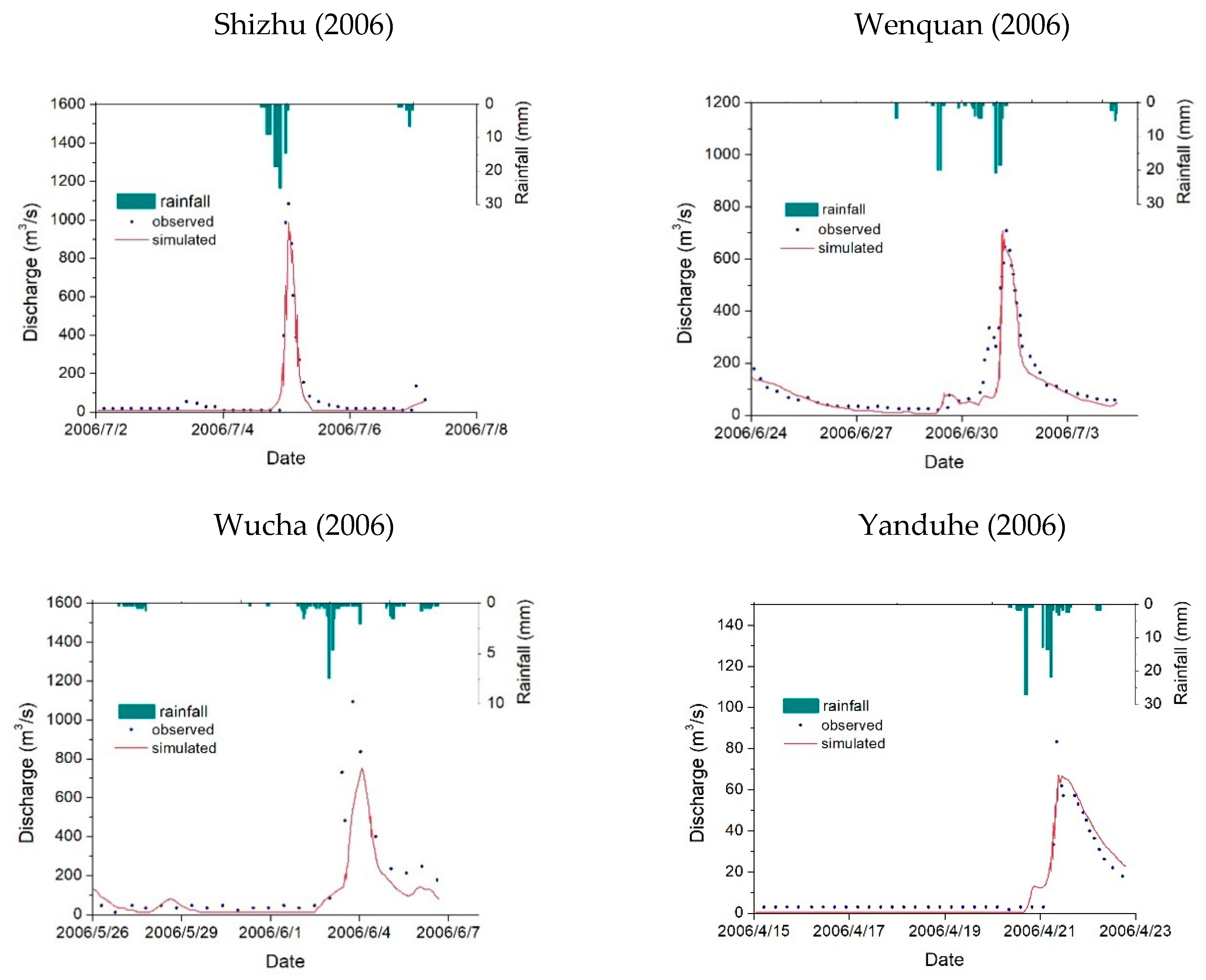
| Shizhu | 20050404 | 75.5 | 238 (243.6) | 2.4 | 16.3 | 0.8 |
| 20060703 | 107.9 | 1091 (992.5) | −9.0 | 40.7 | 0.9 | |
| Wenquan | 20040828 | 285.5 | 2033 (2077) | 2.2 | 95.9 | 0.9 |
| 20050625 | 86.8 | 410 (377.9) | −7.8 | 28.7 | 0.9 | |
| 20050930 | 154.4 | 619 (580.1) | −6.2 | 45.6 | 0.9 | |
| 20060625 | 186.3 | 710 (719.4) | 1.3 | 48.3 | 0.8 | |
| Wucha | 20040401 | 63.7 | 710 (725.6) | 2.2 | 71.4 | 0.7 |
| 20040529 | 63.2 | 2290 (2524) | 10.2 | 215.2 | 0.9 | |
| 20050820 | 49.8 | 881.4 (786.9) | −10.7 | 73.6 | 0.9 | |
| 20060530 | 56.2 | 1085 (1232) | 13.5 | 112.4 | 0.7 | |
| 20081022 | 194.8 | 2360 (2553) | 8.2 | 191.4 | 0.8 | |
| Xingshan | 20070616 | 215.6 | 624 (668.5) | 7.1 | 154.1 | 0.6 |
| 20080415 | 88.7 | 345.1(326.3) | −5.4 | 26.0 | 0.9 | |
| 20080812 | 130.2 | 580.2 (559.4) | −3.6 | 56.9 | 0.8 | |
| Yanduhe | 20050406 | 67.4 | 41 (40.9) | −0.2 | 3.6 | 0.9 |
| 20060419 | 99.9 | 83 (71.6) | −13.7 | 6.6 | 0.9 | |
| Yanglinqiao | 20060902 | 74.6 | 100 (96.3) | −3.7 | 7 | 0.9 |
| 20080415 | 99 | 107.2 (110.4) | −2.9 | 9.1 | 0.8 | |
| Yantang | 20070712 | 80.1 | 472 (462.6) | −2.0 | 36.8 | 0.9 |
| 20070726 | 73.8 | 253.5 (256.4) | 1.1 | 11.1 | 0.9 |
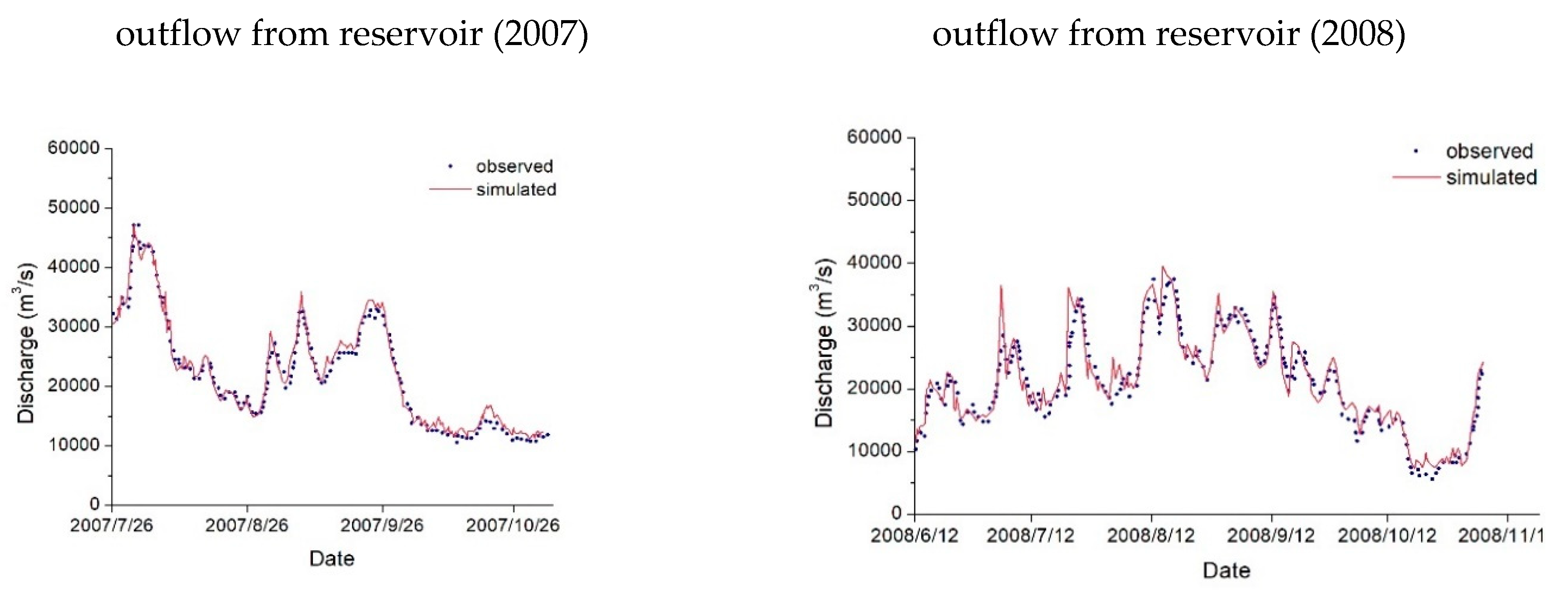
| Water Stage Gauging Station | Flood Event | Flood Peak Level (m) | NSE | ||
|---|---|---|---|---|---|
| Observed | Simulated | Error | |||
| Cuntan | 070731 | 176.8 | 177.6 | 0.8 | 0.87 |
| 070827 | 172.7 | 172.6 | −0.1 | 0.95 | |
| 070902 | 174.6 | 174.7 | 0.1 | 0.88 | |
| Changshou | 070731 | 166.4 | 165.7 | −0.7 | 0.94 |
| 070903 | 162.3 | 161.4 | −0.9 | 0.87 | |
| Qingxichang | 070731 | 159.4 | 159.4 | 0.0 | 0.97 |
| 070827 | 152.3 | 151.9 | −0.4 | 0.90 | |
| 070903 | 154.4 | 154 | −0.4 | 0.93 | |
| Zhongxian | 070731 | 152.9 | 152.5 | −0.4 | 0.91 |
| 070828 | 148 | 147.9 | −0.1 | 0.99 | |
| 070903 | 149.2 | 149.3 | 0.1 | 0.96 | |
| Wulong | 070730 | 194.5 | 194.2 | −0.3 | 0.98 |
| 070902 | 178.7 | 178.5 | −0.2 | 0.94 | |
| 070909 | 179.9 | 179.2 | −0.7 | 0.95 | |
| Wanxian | 070801 | 151.2 | 150.3 | −0.9 | 0.90 |
| 071031 | 156.1 | 156.2 | 0.1 | 1.00 | |
| Fengjie | 070801 | 149.8 | 148.8 | −1.0 | 0.84 |
| 071031 | 156 | 156 | 0.0 | 1.00 | |
| Wushan | 070801 | 148.9 | 148.2 | −0.7 | 0.82 |
| 071031 | 156.1 | 156 | −0.1 | 1.00 | |
| Badong | 070801 | 146.9 | 146.6 | −0.3 | 0.82 |
| 071031 | 156 | 155.9 | −0.1 | 1.00 | |
| Water Stage Gauging Station | Flood Event | Flood Peak Level (m) | NSE | ||
|---|---|---|---|---|---|
| Observed | Simulated | Error | |||
| Cuntan | 080724 | 173.5 | 173.4 | −0.1 | 0.90 |
| 080812 | 175.5 | 176.1 | 0.6 | 0.90 | |
| 080929 | 174.9 | 174.7 | −0.2 | 0.90 | |
| 081105 | 175.9 | 176.1 | 0.2 | 0.95 | |
| Changshou | 080424 | 157.1 | 156.9 | −0.2 | 0.94 |
| 080724 | 161.6 | 160.9 | −0.7 | 0.93 | |
| 080812 | 175.5 | 176.1 | 0.6 | 0.90 | |
| 080929 | 162.8 | 161.8 | −1.0 | 0.90 | |
| 081105 | 174.6 | 174.1 | −0.5 | 1.00 | |
| Qingxichang | 080425 | 155.0 | 155.1 | 0.1 | 0.98 |
| 080708 | 152.3 | 152.1 | −0.2 | 0.97 | |
| 080724 | 154.5 | 154.4 | −0.1 | 0.96 | |
| 081106 | 173.9 | 173.7 | −0.2 | 1.00 | |
| Zhongxian | 080425 | 154.3 | 154.4 | 0.1 | 1.00 |
| 080817 | 150.9 | 150.7 | −0.2 | 0.98 | |
| 081106 | 173.4 | 173.3 | −0.1 | 1.00 | |
| Wulong | 080724 | 181.3 | 181.4 | 0.1 | 0.95 |
| 080817 | 182.2 | 182.1 | −0.1 | 0.87 | |
| 080904 | 183.1 | 182.9 | −0.2 | 0.93 | |
| Wanxian | 080426 | 154.1 | 154.1 | 0.0 | 1.00 |
| 080817 | 149.6 | 149.1 | −0.5 | 0.95 | |
| 081104 | 172.8 | 172.8 | 0.0 | 1.00 | |
| Fengjie | 080425 | 154.0 | 153.9 | −0.1 | 1.00 |
| 081104 | 172.7 | 172.6 | −0.1 | 1.00 | |
| Wushan | 080425 | 154.0 | 153.8 | −0.2 | 0.99 |
| 081104 | 172.6 | 172.5 | −0.1 | 1.00 | |
| Badong | 080425 | 153.8 | 153.7 | −0.1 | 0.99 |
| 081104 | 172.5 | 172.3 | −0.2 | 1.00 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Hua, W.; Fang, X.; Wang, C.; Li, X. Distributed-Framework Basin Modeling System: II. Hydrologic Modeling System. Water 2021, 13, 744. https://doi.org/10.3390/w13050744
Chen G, Hua W, Fang X, Wang C, Li X. Distributed-Framework Basin Modeling System: II. Hydrologic Modeling System. Water. 2021; 13(5):744. https://doi.org/10.3390/w13050744
Chicago/Turabian StyleChen, Gang, Wenjuan Hua, Xing Fang, Chuanhai Wang, and Xiaoning Li. 2021. "Distributed-Framework Basin Modeling System: II. Hydrologic Modeling System" Water 13, no. 5: 744. https://doi.org/10.3390/w13050744
APA StyleChen, G., Hua, W., Fang, X., Wang, C., & Li, X. (2021). Distributed-Framework Basin Modeling System: II. Hydrologic Modeling System. Water, 13(5), 744. https://doi.org/10.3390/w13050744








