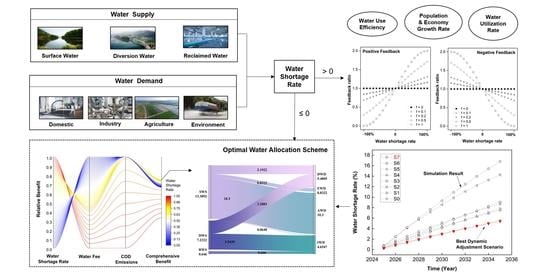
System Dynamics-Multiple Objective Optimization Model for Water Resource Management: A Case Study in Jiaxing City, China
Abstract
:1. Introduction
2. Methodology
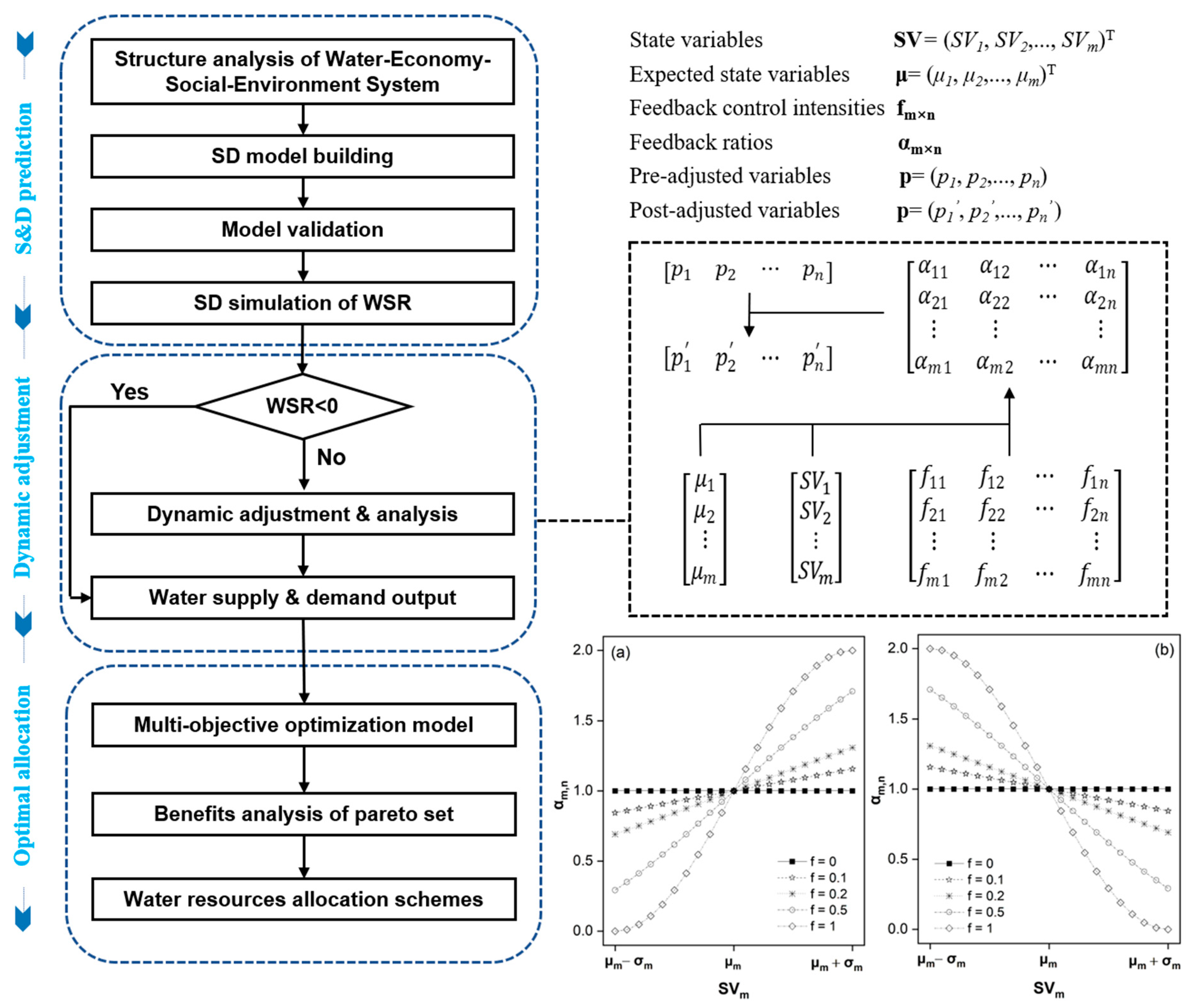
2.1. System Dynamics (SD) Model
2.2. Dynamic Adjustment Based on Feedback
2.3. Water Allocation Based on Multi-Objective Optimization
3. Case Study
3.1. Study Area
3.2. Data Sources
3.3. Parameter Selection and Scenarios in Model Application
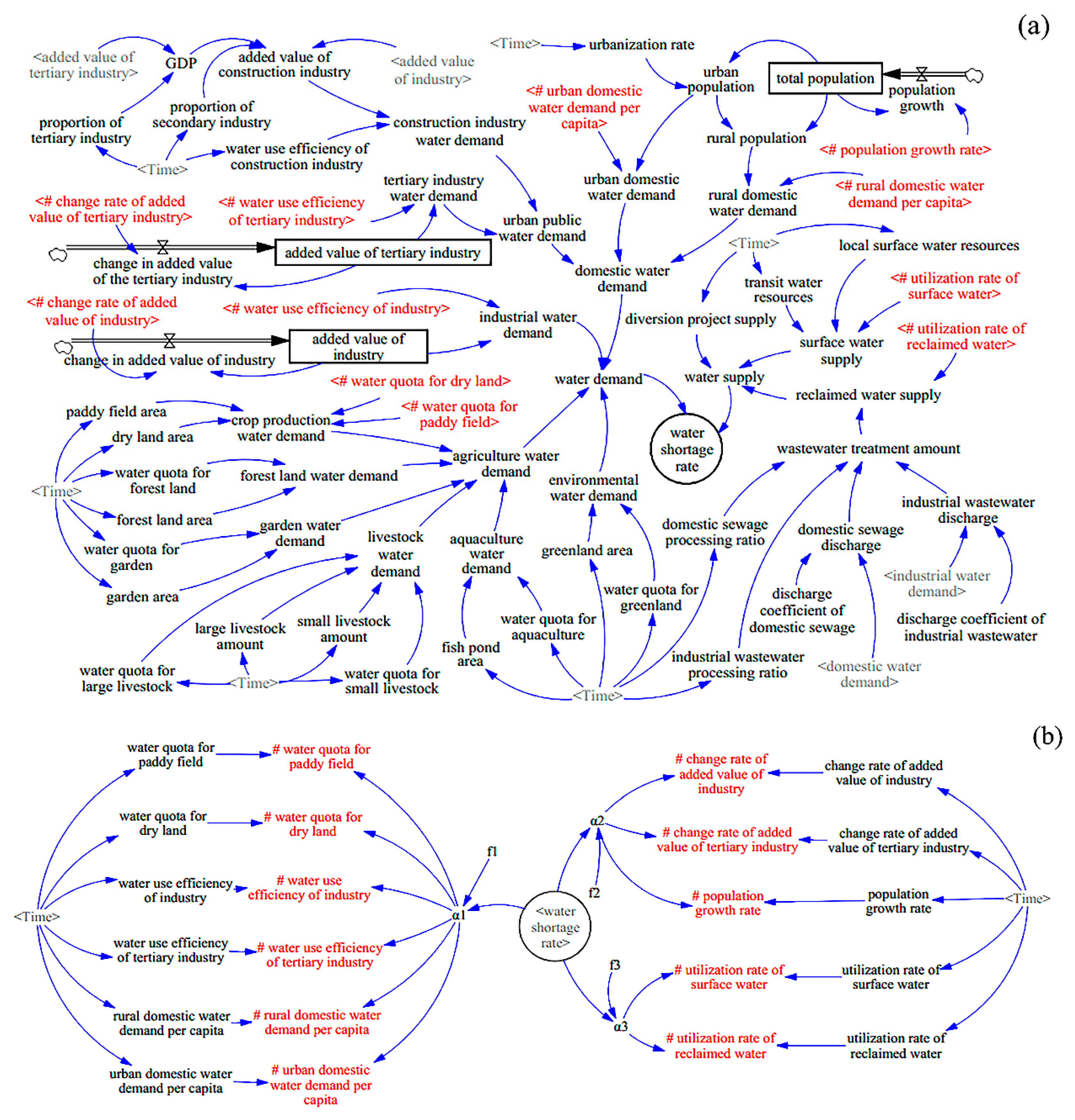
3.3.1. SD Model for Water Supply and Demand Prediction
3.3.2. Parameters for Dynamic Adjustment
3.3.3. MOO Model for Water Allocation
- (1)
- No less than 40% and no more than 60% of the domestic water would be supplied by diversion water (;
- (2)
- Diversion water was only for industrial and domestic users ();
- (3)
- Reclaimed water was only for industrial users ().
3.4. Results
3.4.1. SD Model Validation
3.4.2. Water Supply and Demand Prediction
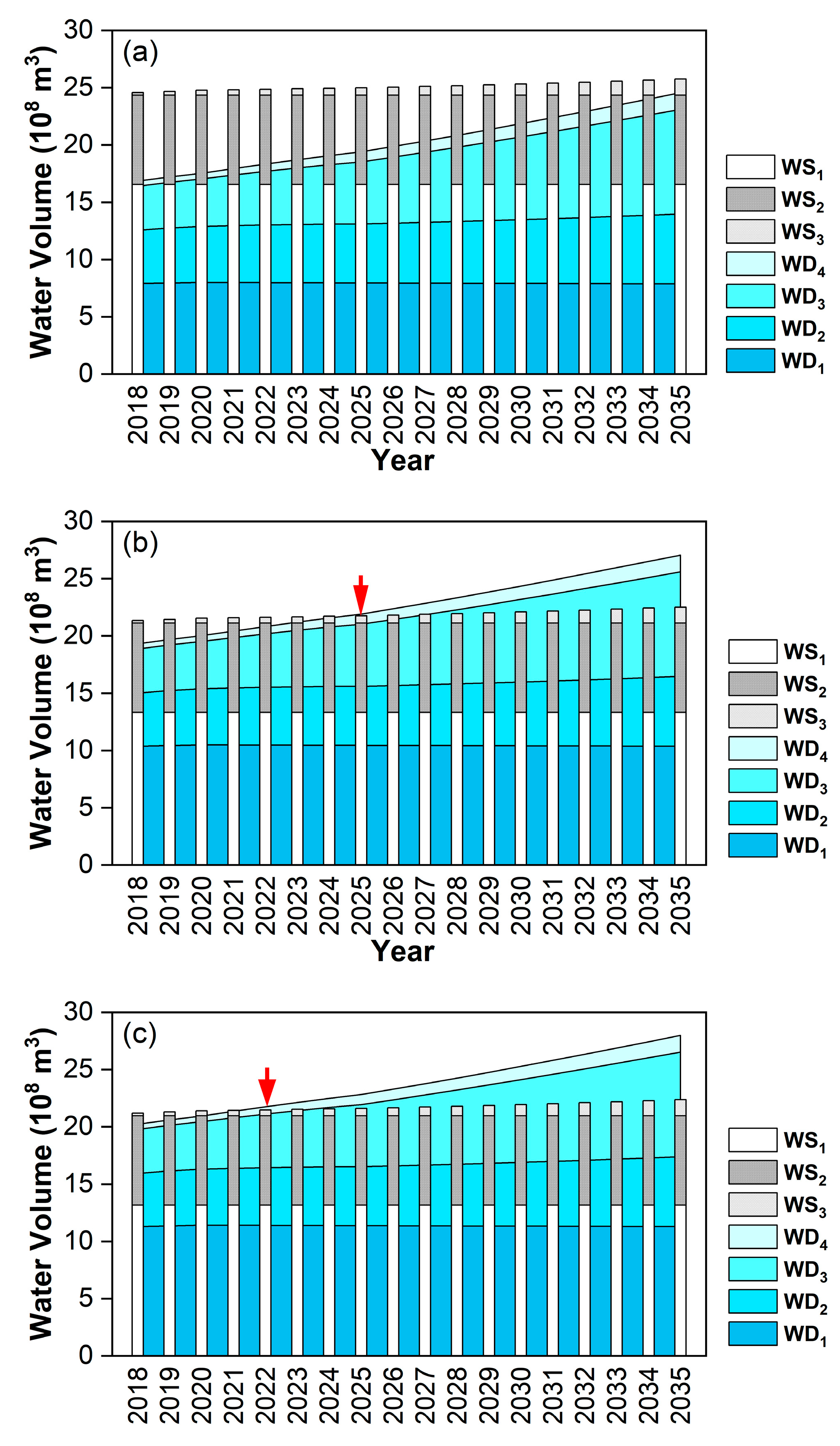
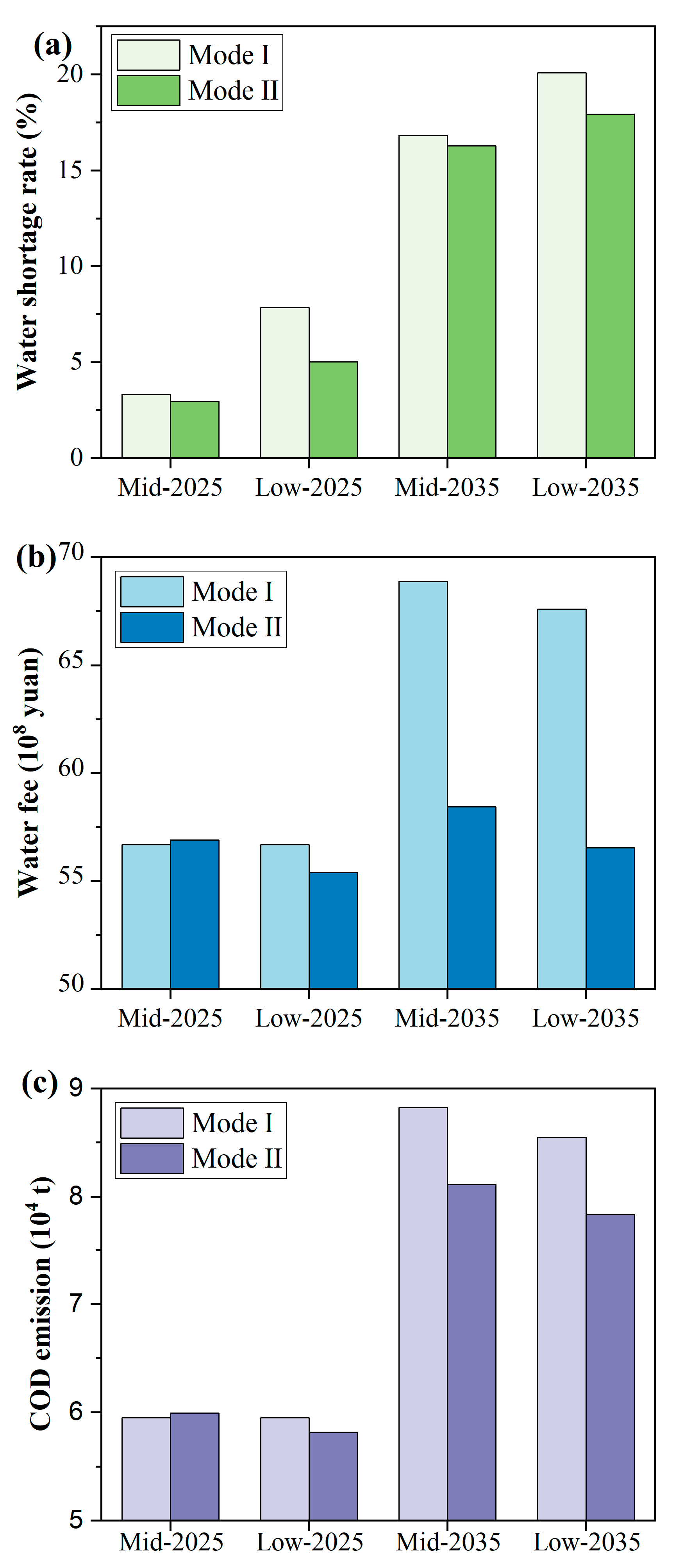
3.4.3. Dynamic Adjustment
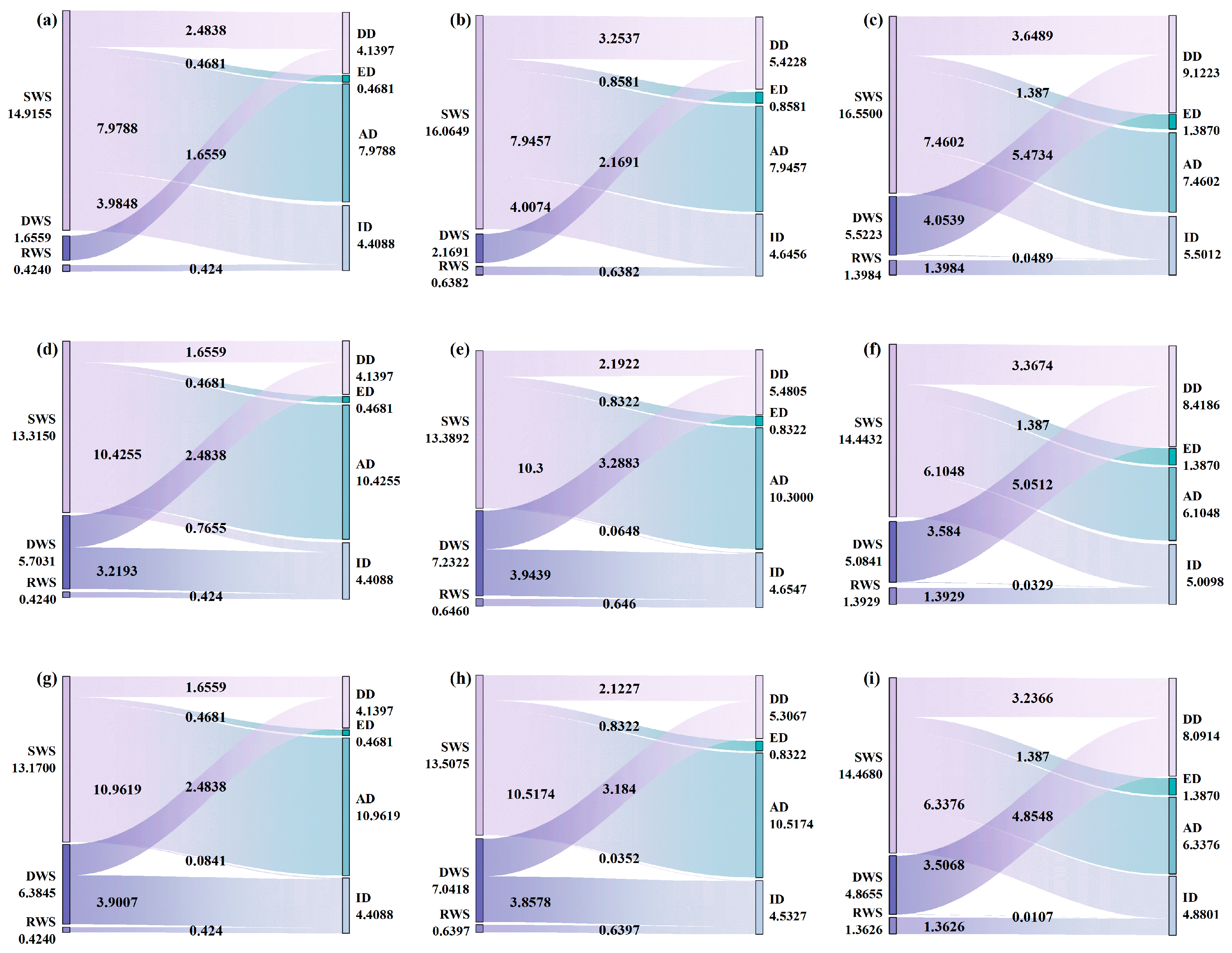
3.4.4. Optimal Allocation of Water Resources
- (i).
- High supply and low demand (High-2020, High-2025): the ratio of surface water and diversion water allocated to domestic was 3:2; most industrial water was provided by surface water and the remainder was supplied by reclaimed water; no diversion water was used.
- (ii).
- Low supply and low demand (Mid-2020, Mid-2025, Low-2020, Low-2035): agriculture and environment accounted for 82–87% of surface water, forcing domestic and industrial users to use diversion water as a supplement. To maximize economic benefits, industry was allocated a large amount of diversion water due to its high economic density [50], accounting for approximately 73–89% of the total industrial water allocation; the domestic sector uses surface water and diversion water at a ratio of 2:3.
- (iii).
- High supply and high demand (High-2035): sufficient water supply guaranteed harmonious allocation. The percentages of surface water supplied to agriculture, environment, domestic, and industry were 45.07, 0.08, 23.31, and 24.81%, respectively, meeting 40% of domestic and 70% of industrial water demands. The reclaimed water supply has risen sharply with technological advances and can satisfy a quarter of the industrial water demand.
- (iv).
- Low supply and high demand (Mid-2035, Low-2035): the high WSR led to all users tolerating a certain degree of water scarcity; however, it also intensified competition for surface water resources. Domestic water had the highest priority in water allocation; with a satisfaction degree of 100%, it was supplied by surface water and diversion water at a ratio of 2:3. Compared with other users, agriculture was in a relatively disadvantaged position, resulting in a low satisfaction degree (60%). This prevented agriculture from consuming a large portion of surface water and created an opportunity for industry to use surface water. Similar to High-2035, the share of diversion water for industry remained lower than those of inexpensive surface water and reclaimed water.
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Momblanch, A.; Connor, J.D.; Crossman, N.D.; Paredes-Arquiola, J.; Andreu, J. Using ecosystem services to represent the environment in hydro-economic models. J. Hydrol. 2016, 538, 293–303. [Google Scholar] [CrossRef]
- Burian, S.J.; Walsh, T.; Kalyanapu, A.J.; Larsen, S.G. Climate Vulnerabilities and Adaptation of Urban Water Infrastructure Systems. In Climate Vulnerability; Pielke, R.A., Ed.; Academic Press: Oxford, UK, 2013; pp. 87–107. [Google Scholar] [CrossRef]
- Mekonnen, M.M.; Hoekstra, A.Y. Four billion people facing severe water scarcity. Sci. Adv. 2016, 2, 6. [Google Scholar] [CrossRef] [Green Version]
- Roson, R.; Damania, R. The macroeconomic impact of future water scarcity An assessment of alternative scenarios. J. Pol. Model. 2017, 39, 1141–1162. [Google Scholar] [CrossRef]
- Swain, A. Water Wars. In International Encyclopedia of the Social & Behavioral Sciences (Second Edition); Wright, J.D., Ed.; Elsevier: Oxford, UK, 2015; pp. 443–447. [Google Scholar] [CrossRef]
- Frini, A.; Benamor, S. Making Decisions in a Sustainable Development Context: A State-of-the-Art Survey and Proposal of a Multi-period Single Synthesizing Criterion Approach. Comput. Econom. 2018, 52, 341–385. [Google Scholar] [CrossRef]
- Gau, H.S.; Liu, C.W. Estimation of the Effective Precipitation Recharge Coefficient in an Unconfined Aquifer Using Stochastic Analysis. Hydrol. Proc. 2000, 14, 811–830. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, X.; Bao, H.; Skitmore, M. Review of social water cycle research in a changing environment. Renew. Sustain. Energy Rev. 2016, 63, 132–140. [Google Scholar] [CrossRef] [Green Version]
- Hou, B.D.; Yang, R.X.; Zhou, Y.Y.; Xiao, W.H.; Wang, J.H.; Zhao, Y.; Zhan, X.Z. Evolution mechanisms and fundamental equations of social water cycle fluxes. Hydrol. Res. 2019, 50, 1344–1358. [Google Scholar] [CrossRef]
- Kummu, M.; Ward, P.J.; de Moel, H.; Varis, O. Is physical water scarcity a new phenomenon? Global assessment of water shortage over the last two millennia. Environ. Res. Lett. 2010, 5, 10. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y. Why an urban population continues to grow under intensifying water scarcity: An answer from generalized water resources. Urban Water J. 2018, 15, 961–965. [Google Scholar] [CrossRef]
- Sahin, O.; Bertone, E.; Beal, C.; Stewart, R.A. Evaluating a novel tiered scarcity adjusted water budget and pricing structure using a holistic systems modelling approach. J. Environ. Manag. 2018, 215, 79–90. [Google Scholar] [CrossRef] [Green Version]
- Karimlou, K.; Hassani, N.; Rashidi Mehrabadi, A.; Nazari, M.R. Developing a Model for Decision-Makers in Dynamic Modeling of Urban Water System Management. Water Resour. Manag. 2020, 34, 481–499. [Google Scholar] [CrossRef]
- Park, S.; Jeon, D.H.; Jung, S.Y. Developing efficient management strategies for a water supply system using system dynamics modelling. Civ. Eng. Environ. Syst. 2014, 31, 189–208. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, S. Application of System Dynamics to Water Security Research. Water Resour. Manag. 2014, 28, 287–300. [Google Scholar] [CrossRef]
- Abadi, L.S.K.; Shamsai, A.; Goharnejad, H. An analysis of the sustainability of basin water resources using Vensim model. KSCE J. Civ. Eng. 2015, 19, 1941–1949. [Google Scholar] [CrossRef]
- Guo, H.C.; Liu, L.; Huang, G.H.; Fuller, G.A.; Zou, R.; Yin, Y.Y. A system dynamics approach for regional environmental planning and management: A study for the Lake Erhai Basin. J. Environ. Manag. 2001, 61, 93–111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pagano, A.; Pluchinotta, I.; Giordano, R.; Vurro, M. Drinking water supply in resilient cities: Notes from L’Aquila earthquake case study. Sustain. Cities Soc. 2017, 28, 435–449. [Google Scholar] [CrossRef]
- Wang, K.; Davies, E.G.R. Municipal water planning and management with an end-use based simulation model. Environ. Model. Software 2018, 101, 204–217. [Google Scholar] [CrossRef]
- Li, K.; Ma, T.; Wei, G.; Zhang, Y.; Feng, X. Urban Industrial Water Supply and Demand: System Dynamic Model and Simulation Based on Cobb–Douglas Function. Sustainability 2019, 11, 5893. [Google Scholar] [CrossRef] [Green Version]
- Xiang, N.; Sha, J.; Yan, J.; Xu, F. Dynamic Modeling and Simulation of Water Environment Management with a Focus on Water Recycling. Water 2013, 6, 17–31. [Google Scholar] [CrossRef] [Green Version]
- Mirchi, A.; Madani, K.; Watkins, D.; Ahmad, S. Synthesis of System Dynamics Tools for Holistic Conceptualization of Water Resources Problems. Water Resour. Manag. 2012, 26, 2421–2442. [Google Scholar] [CrossRef]
- Ghasemi, A.; Saghafian, B.; Golian, S. System Dynamics Approach for Simulating Water Resources of an Urban Water System with Emphasis on Sustainability of Groundwater. Environ. Earth Sci. 2017, 76, 15. [Google Scholar] [CrossRef]
- Peng, J.; Lu, S.; Cao, Y.; Wang, X.; Hu, X.; Wang, M.; Zheng, B. A dualistic water cycle system dynamic model for sustainable water resource management through progressive operational scenario analysis. Environ. Sci. Pollut. R. 2019, 26, 16085–16096. [Google Scholar] [CrossRef] [PubMed]
- Zarghami, S.A.; Gunawan, I.; Schultmann, F. System Dynamics Modelling Process in Water Sector: A Review of Research Literature. Syst. Res. Behav. Sci. 2018, 35, 776–790. [Google Scholar] [CrossRef]
- Winz, I.; Brierley, G.; Trowsdale, S. The Use of System Dynamics Simulation in Water Resources Management. Water Resour. Manag. 2009, 23, 1301–1323. [Google Scholar] [CrossRef]
- Babel, M.S.; Das Gupta, A.; Nayak, D.K. A model for optimal allocation of water to competing demands. Water Resour. Manag. 2005, 19, 693–712. [Google Scholar] [CrossRef]
- Roozbahani, R.; Schreider, S.; Abbasi, B. Optimal water allocation through a multi-objective compromise between environmental, social, and economic preferences. Environ. Model. Softw. 2015, 64, 18–30. [Google Scholar] [CrossRef]
- Kitayama, S.; Yamazaki, K. Compromise point incorporating trade-off ratio in multi-objective optimization. Appl. Soft. Comput. 2012, 12, 1959–1964. [Google Scholar] [CrossRef]
- Hou, J.W.; Mi, W.B.; Sun, J.L. Optimal spatial allocation of water resources based on Pareto ant colony algorithm. Int. J. Geogr. Inf. Sci. 2014, 28, 213–233. [Google Scholar] [CrossRef]
- Yu, L.; Ling, M.; Chen, F.; Ding, Y.; Lv, C. Practices of groundwater over-exploitation control in Hebei Province. Water Policy 2020, 22, 591–601. [Google Scholar] [CrossRef]
- Liu, W.L.; Liu, L.N.; Tong, F. Least Squares Support Vector Machine for Ranking Solutions of Multi-Objective Water Resources Allocation Optimization Models. Water 2017, 9, 257. [Google Scholar] [CrossRef] [Green Version]
- Linneusson, G.; Ng, A.H.C.; Aslam, T. Quantitative analysis of a conceptual system dynamics maintenance performance model using multi-objective optimisation. J. Simul. 2018, 12, 171–189. [Google Scholar] [CrossRef] [Green Version]
- Aslam, T.; Ng, A.H.C. Combining system dynamics and multi-objective optimization with design space reduction. Ind. Manag. Data Syst. 2016, 116, 291–321. [Google Scholar] [CrossRef]
- Simonovic, S.P. Bringing Future Climatic Change into Water Resources Management Practice Today. Water Resour. Manag. 2017, 31, 2933–2950. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, L.; Wang, Z.; Tang, Q.; Piao, S.; Chen, D.; Xia, J.; Conradt, T.; Liu, J.; Wada, Y.; et al. Quantifying Water Scarcity in Northern China Within the Context of Climatic and Societal Changes and South-to-North Water Diversion. Earths Futur. 2020, 8. [Google Scholar] [CrossRef]
- Kattel, G.R.; Shang, W.X.; Wang, Z.J.; Langford, J. China’s South-to-North Water Diversion Project Empowers Sustainable Water Resources System in the North. Sustainability 2019, 11, 3735. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Tian, C.; Zhou, F. Research of Water Diversion and Allocation of Sanjiang Plain River Network in Ningbo City Based on Water Quantity and Quality United-control System. Water Resour. Power 2019, 37, 32–35, 48. [Google Scholar]
- Cherchi, C.; Kesaano, M.; Badruzzaman, M.; Schwab, K.; Jacangelo, J.G. Municipal reclaimed water for multi-purpose applications in the power sector: A review. J. Environ. Manag. 2019, 236, 561–570. [Google Scholar] [CrossRef]
- Yi, L.L.; Jiao, W.T.; Chen, X.N.; Chen, W.P. An overview of reclaimed water reuse in China. J. Environ. Sci. 2011, 23, 1585–1593. [Google Scholar] [CrossRef]
- Hamilton, A.J.; Boland, A.M.; Stevens, D.; Kelly, J.; Radcliffe, J.; Ziehrl, A.; Dillon, P.; Paulin, B. Position of the Australian horticultural industry with respect to the use of reclaimed water. Agric. Water Manag. 2005, 71, 181–209. [Google Scholar] [CrossRef]
- Wu, G.; Li, L.; Ahmad, S.; Chen, X.; Pan, X. A Dynamic Model for Vulnerability Assessment of Regional Water Resources in Arid Areas: A Case Study of Bayingolin, China. Water Resour. Manag. 2013, 27, 3085–3101. [Google Scholar] [CrossRef]
- Swanson, D.; Barg, S.; Tyler, S.; Venema, H.; Tomar, S.; Bhadwal, S.; Nair, S.; Roy, D.; Drexhage, J. Seven tools for creating adaptive policies. Technol. Forecast. Soc. Chang. 2010, 77, 924–939. [Google Scholar] [CrossRef]
- Dong, Q.; Zhang, X.; Chen, Y.; Fang, D. Dynamic Management of a Water Resources-Socioeconomic-Environmental System Based on Feedbacks Using System Dynamics. Water Resour. Manag. 2019, 33, 2093–2108. [Google Scholar] [CrossRef]
- Han, Y.; Huang, Y.-F.; Wang, G.-Q.; Maqsood, I. A Multi-objective Linear Programming Model with Interval Parameters for Water Resources Allocation in Dalian City. Water Resour. Manag. 2011, 25, 449–463. [Google Scholar] [CrossRef]
- Li, W.; Jiao, K.; Bao, Z.; Xie, Y.L.; Zhen, J.L.; Huang, G.H.; Fu, L.B. Chance-Constrained Dynamic Programming for Multiple Water Resources Allocation Management Associated with Risk-Aversion Analysis: A Case Study of Beijing, China. Water 2017, 9, 596. [Google Scholar] [CrossRef]
- Lin, C.; Huang, J.W.; Chen, Y.; Cui, L.Z. Thinking and methodology of multi-objective optimization. Int. J. Mach. Learn. Cybern. 2018, 9, 2117–2127. [Google Scholar] [CrossRef]
- China Water Resources Bulletin. Available online: http://www.mwr.gov.cn/sj/tjgb/szygb/201811/t20181116_1055003.html (accessed on 16 November 2018).
- Jiaxing Water Resources Bulletin. Available online: http://slj.jiaxing.gov.cn/art/2018/12/10/art_1229371997_3636668.html (accessed on 10 December 2018).
- Xiao, Y.; Hipel, K.W.; Fang, L.P. Incorporating Water Demand Management into a Cooperative Water Allocation Framework. Water Resour. Manag. 2016, 30, 2997–3012. [Google Scholar] [CrossRef]
- Guo, Z.H.; Chang, J.X.; Huang, Q.; Xu, L.; Da, C.J.; Wu, H.X. Bi-level Optimization Allocation Model of Water Resources for Different Water Industries. Water Sci. Technol. Water Suppl. 2014, 14, 470–477. [Google Scholar] [CrossRef]
- Li, Z.; Li, C.H.; Wang, X.; Peng, C.; Cai, Y.P.; Huang, W.C. A hybrid system dynamics and optimization approach for supporting sustainable water resources planning in Zhengzhou City, China. J. Hydrol. 2018, 556, 50–60. [Google Scholar] [CrossRef]
- Mancosu, N.; Snyder, R.L.; Kyriakakis, G.; Spano, D. Water Scarcity and Future Challenges for Food Production. Water 2015, 7, 975–992. [Google Scholar] [CrossRef]
- Men, B.H.; Wu, Z.J.; Liu, H.L.; Hu, Z.H.; Li, Y.S. Improved grey prediction method for optimal allocation of water resources: A case study in Beijing in China. Water Sci. Technol.-Water Suppl. 2019, 19, 1044–1054. [Google Scholar] [CrossRef]
- Magri, A.; Berezowska-Azzag, E. New tool for assessing urban water carrying capacity (WCC) in the planning of development programs in the region of Oran, Algeria. Sustain. Cities Soc. 2019, 48, 19. [Google Scholar] [CrossRef]
- Oliva, R. Structural Dominance Analysis of Large and Stochastic Models. Syst. Dynam. Rev. 2016, 32, 26–51. [Google Scholar] [CrossRef]
- Zomorodian, M.; Lai, S.H.; Homayounfar, M.; Ibrahim, S.; Fatemi, S.E.; El-Shafie, A. The State-of-the-Art System Dynamics Application in Integrated Water Resources Modeling. J. Environ. Manag. 2018, 227, 294–304. [Google Scholar] [CrossRef]
- Dai, S.S.; Li, L.H.; Xu, H.G. Simulation of Water Scarcity in a Leap-forward Developing Arid Region: A System Dynamics Model of Xinjiang Uygur Autonomous Region. Water Policy 2017, 19, 741–757. [Google Scholar] [CrossRef]
- Keshtkar, A.R.; Asefjah, B.; Afzali, A. Application of multi-criteria decision-making approach in catchment modeling and management. Desalin. Water Treat. 2018, 116, 83–95. [Google Scholar] [CrossRef]
- Ghislain, d.M. An overview of the world’s water resources problems in 2050. Ecohydrol. Hydrobiol. 2007, 7, 147–155. [Google Scholar]
- Sharawat, I.; Dahiya, R.; Dahiya, R.P.; Sreekrishnan, T.R.; Kumari, S. Policy options for managing the water resources in rapidly expanding cities: A system dynamics approach. Sustain. Wat. Resour. Manag. 2019, 5, 1201–1215. [Google Scholar] [CrossRef]
- Qaiser, K.; Ahmad, S.; Johnson, W.; Batista, J.R. Evaluating Water Conservation and Reuse Policies Using a Dynamic Water Balance Model. Environ. Manag. 2013, 51, 449–458. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, Z.; Shi, M. Where is the future for a growing metropolis in North China under water resource constraints? Sustain. Sci. 2015, 10, 113–122. [Google Scholar] [CrossRef]
- Nasiri, F.; Savage, T.; Wang, R.; Barawid, N.; Zimmerman, J.B. A system dynamics approach for urban water reuse planning: A case study from the Great Lakes region. Stoch. Environ. Res. Risk Assess. 2013, 27, 675–691. [Google Scholar] [CrossRef]
- Xie, N.M.; Wang, R.Z.; Chen, N.L. Measurement of shock effect following change of one-child policy based on grey forecasting approach. Kybernetes 2018, 47, 559–586. [Google Scholar] [CrossRef]
- Li, H.D.; Zhou, T.M.; Jia, C. The influence of the universal two-child policy on China’s future population and ageing. J. Popul. Res. 2019, 36, 183–203. [Google Scholar] [CrossRef]
- Winter, J.M.; Lopez, J.R.; Ruane, A.C.; Young, C.A.; Scanlon, B.R.; Rosenzweig, C. Representing Water Scarcity in Future Agricultural Assessments. Anthropocene 2017, 18, 15–26. [Google Scholar] [CrossRef]
- Yamout, G.; El-Fadel, M. An Optimization Approach for Multi-sectoral Water Supply Management in the Greater Beirut Area. Water Resour. Manag. 2005, 19, 791–812. [Google Scholar] [CrossRef]
- Garrone, P.; Grilli, L.; Marzano, R. Incentives to Water Conservation Under Scarcity: Comparing Price and Reward Effects Through Stated Preferences. J. Clean Prod. 2020, 244, 10. [Google Scholar] [CrossRef] [Green Version]
- Jia, X.P.; Zhang, L.X.; Li, Z.W.; Tan, R.R.; Dou, J.H.; Foo, D.C.Y.; Wang, F. Pinch Analysis for Targeting Desalinated Water Price Subsidy. J. Clean Prod. 2019, 227, 950–959. [Google Scholar] [CrossRef]
- Wichelns, D. Enhancing the Performance of Water Prices and Tariff Structures in Achieving Socially Desirable Outcomes. Int. J. Water Resour. Dev. 2013, 29, 310–326. [Google Scholar] [CrossRef]
- Macian-Sorribes, H.; Pulido-Velazquez, M.; Tilmant, A. Definition of Efficient Scarcity-Based Water Pricing Policies Through Stochastic Programming. Hydrol. Earth Syst. Sci. 2015, 19, 3925–3935. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.J.; Folmer, H.; Xue, J.H. Technical and Allocative Efficiency of Irrigation Water Use in the Guanzhong Plain, China. Food Policy 2015, 50, 43–52. [Google Scholar] [CrossRef]
| Group | Adjustable Variable (pn) |
|---|---|
| Group1 | water quota for paddy field (p1), water quota for dry land (p2), water use efficiency of industry (p3), water use efficiency of the tertiary industry (p4), rural domestic water demand per capita (p5), urban domestic water demand per capita (p6) |
| Group2 | change rate of added value of industry (p7), change rate of added value of the tertiary industry (p8), population growth rate (p9) |
| Group3 | utilization rate of surface water (p10), utilization rate of reclaimed water (p11) |
| Variables | MRE (%) | R2 | NSE |
|---|---|---|---|
| total population | −0.004 | 0.985 | 0.703 |
| added value of industry | −0.010 | 0.944 | 0.938 |
| added value of tertiary industry | −0.025 | 0.975 | 0.933 |
| agriculture water demand | 0.036 | 0.934 | 0.367 |
| industrial water demand | −0.004 | 0.688 | 0.665 |
| domestic water demand | −0.017 | 0.860 | 0.653 |
| environmental water demand | 0.000 | 1.000 | 1.000 |
| reclaimed water supply | 0.117 | 0.973 | 0.946 |
| Scenario | Dynamic Adjustment | Water Shortage Rate (%) | |||
|---|---|---|---|---|---|
| Mid-2025 | Mid-2035 | Low-2025 | Low-2035 | ||
| S0 | / | 0.67 | 16.80 | 5.33 | 20.07 |
| S1 | Group1 | 0.28 | 7.79 | 2.28 | 9.36 |
| S2 | Group2 | 0.66 | 14.25 | 5.02 | 16.39 |
| S3 | Group3 | 0.33 | 9.06 | 2.73 | 11.05 |
| S4 | Group1 + Group2 | 0.28 | 7.19 | 2.22 | 8.47 |
| S5 | Group1 + Group3 | 0.20 | 5.54 | 1.62 | 6.71 |
| S6 | Group2 + Group3 | 0.33 | 8.26 | 2.65 | 9.81 |
| S7 | Group1 + Group2 + Group3 | 0.20 | 5.41 | 1.59 | 6.28 |
| Subdivision | Directly Predicted Values | Dynamic Adjusted Values (S7, f = 1) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mid-2025 | Mid-2035 | Low-2025 | Low-2035 | Mid-2025 | Mid-2035 | Low-2025 | Low-2035 | |
| WS1 | 13.32 | 13.32 | 13.17 | 13.17 | 13.39 | 14.44 | 13.51 | 14.47 |
| WS2 | 7.80 | 7.80 | 7.80 | 7.80 | 7.80 | 7.80 | 7.80 | 7.80 |
| WS3 | 0.64 | 1.40 | 0.64 | 1.40 | 0.64 | 1.38 | 0.64 | 1.36 |
| WD1 | 10.44 | 10.36 | 11.36 | 11.29 | 10.38 | 9.54 | 11.09 | 10.24 |
| WD2 | 5.16 | 6.11 | 5.16 | 6.11 | 5.15 | 5.57 | 5.04 | 5.42 |
| WD3 | 5.42 | 9.12 | 5.42 | 9.12 | 5.41 | 8.42 | 5.31 | 8.09 |
| WD4 | 0.88 | 1.46 | 0.88 | 1.46 | 0.88 | 1.46 | 0.88 | 1.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wang, F.; Huang, K.; Zhang, H.; Yu, J.; Han, A.Y. System Dynamics-Multiple Objective Optimization Model for Water Resource Management: A Case Study in Jiaxing City, China. Water 2021, 13, 671. https://doi.org/10.3390/w13050671
Zhou X, Wang F, Huang K, Zhang H, Yu J, Han AY. System Dynamics-Multiple Objective Optimization Model for Water Resource Management: A Case Study in Jiaxing City, China. Water. 2021; 13(5):671. https://doi.org/10.3390/w13050671
Chicago/Turabian StyleZhou, Xiaoying, Feier Wang, Kuan Huang, Huichun Zhang, Jie Yu, and Alan Y. Han. 2021. "System Dynamics-Multiple Objective Optimization Model for Water Resource Management: A Case Study in Jiaxing City, China" Water 13, no. 5: 671. https://doi.org/10.3390/w13050671