Neural Network Approach to Retrieving Ocean Subsurface Temperatures from Surface Parameters Observed by Satellites
Abstract
1. Introduction
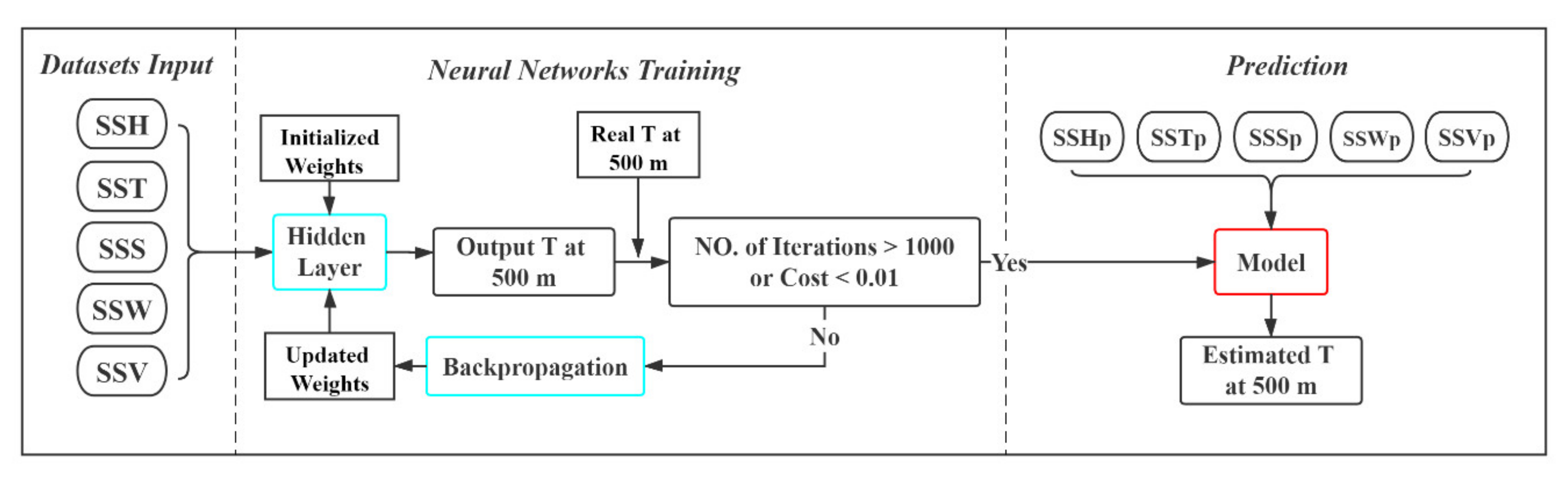
2. Study Area, Datasets and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, M.M.; Swain, D.; Weller, R.A. Estimation of ocean subsurface thermal structure from surface parameters: A neural network approach. Geophys. Res. Lett. 2004. [Google Scholar] [CrossRef]
- Chapman, C.; Charantonis, A.A. Reconstruction of subsurface velocities from satellite observations using iterative self-organizing maps. IEEE Geosci. Remote Sens. 2017, 1, 617–620. [Google Scholar] [CrossRef]
- Guinehut, S.; Dhomps, A.L.; Larnicol, G.; Le Traon, P.Y. High resolution 3-D temperature and salinity fields derived from in situ and satellite observations. Ocean. Sci. 2012, 8, 845–857. [Google Scholar] [CrossRef]
- Wang, X.D.; Han, G.J.; Li, W.; Qi, Y.Q. Reconstruction of ocean temperature profile using satellite observations. J. Trop. Oceanogr. 2011, 30, 10–17. [Google Scholar]
- Vinogradova, N.; Lee, T.; Boutin, J.; Drushka, K.; Fournier, S.; Sabia, R.; Stammer, D.; Bayler, E.; Reul, N.; Gordon, A.; et al. Satellite salinity observing system: Recent discoveries and the way forward. Front. Mar. Sci. 2019, 6, 243. [Google Scholar] [CrossRef]
- Klemas, V.; Yan, X.H. Subsurface and deeper ocean remote sensing from satellites: An overview and new results. Prog. Oceanogr. 2014, 122, 1–9. [Google Scholar] [CrossRef]
- Meehl, G.A.; Arblaster, J.M.; Fasullo, J.T.; Hu, A.; Trenberth, K.E. Model-based evidence of deep-ocean heat uptake during surface-temperature hiatus periods. Nat. Clim. Chang. 2011, 1, 360–364. [Google Scholar] [CrossRef]
- Yan, X.H.; Boyer, T.; Trenberth, K.; Karl, T.R.; Xie, S.P.; Nieves, V.; Tung, K.K.; Roemmich, D. The global warming hiatus: Slowdown or redistribution? Earth’s Future 2016, 4, 472–482. [Google Scholar] [CrossRef]
- Bindoff, N.L.; Willebrand, J.; Artale, V.; Cazenave, A.; Gregory, J.M.; Gulev, S.; Hanawa, K.; Le Quere, C.; Levitus, S.; Nojiri, Y.; et al. Observations: Oceanic Climate Change and Sea Level. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I; Cambridge University Press: Cambridge, UK, 2007; pp. 385–428. [Google Scholar]
- Balmaseda, M.A.; Trenberth, K.E.; Källén, E. Distinctive climate signals in reanalysis of global ocean heat content. Geophys. Res. Lett. 2013, 40, 1754–1759. [Google Scholar] [CrossRef]
- Song, Y.T.; Colberg, F. Deep ocean warming assessed fromaltimeters, gravity recovery and climate experiment, in situ measurements, and a non-Boussinesq ocean general circulation model. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Chen, X.; Tung, K.K. Varying planetary heat sink led to global-warming slowdown and acceleration. Science 2014, 345, 897–903. [Google Scholar] [CrossRef] [PubMed]
- Drijfhout, S.S.; Blaker, A.T.; Josey, S.A.; Nurser, A.J.G.; Sinha, B.; Balmaseda, M.A. Surface warming hiatus caused by increased heat uptake across multiple ocean basins. Geophys. Res. Lett. 2014, 41, 7868–7874. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Locarnini, R.A.; Garcia, H.E.; Mishonov, A.V. Global ocean heat content 1955–2008 in light of recently revealed instrumentation problems. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Baranova, O.K.; Garcia, H.E.; Locarnini, R.A.; Zweng, M.M. World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- Lyman, J.M.; Good, S.A.; Gouretski, V.V.; Ishii, M.; Johnson, G.C.; Palmer, M.D.; Willis, J.K. Robust warming of the global upper ocean. Nature 2010, 465, 334–337. [Google Scholar] [CrossRef]
- Levin, L.A.; Le, B.N. The deep ocean under climate change. Science 2015, 350, 766–768. [Google Scholar] [CrossRef]
- Lowe, J.A.; Gregory, J.M.; Flather, R.A. Changes in the occurrence of storm surges around the United Kingdom under a future climate scenario using a dynamic storm surge model driven by the Hadley Centre climate models. Clim. Dynam. 2001, 18, 179–188. [Google Scholar] [CrossRef]
- Mel, R.; Sterl, A.; Lionello, P. High resolution climate projection of storm surge at the Venetian coast. Nat. Hazard. Earth Sys. 2013, 13, 1135–1142. [Google Scholar] [CrossRef]
- Woth, K.; Weisse, R.; Von, S.H. Climate change and North Sea storm surge extremes: An ensemble study of storm surge extremes expected in a changed climate projected by four different regional climate models. Ocean. Dynam. 2006, 56, 3–15. [Google Scholar] [CrossRef]
- Mel, R.; Lionello, P. Storm surge ensemble prediction for the city of Venice. Weather. Forecast. 2014, 29, 1044–1057. [Google Scholar] [CrossRef]
- Li, J.; Sun, L.; Yang, Y.; Yan, H.; Liu, S. Upper Ocean Responses to Binary Typhoons in the Nearshore and Offshore Areas of Northern South China Sea: A Comparison Study. J. Coast. Res. 2020, 99, 115–125. [Google Scholar] [CrossRef]
- Li, J.; Sun, L.; Yang, Y.; Cheng, H. Accurate Evaluation of Sea Surface Temperature Cooling Induced by Typhoons Based on Satellite Remote Sensing Observations. Water 2020, 12, 1413. [Google Scholar] [CrossRef]
- Liu, S.; Li, J.; Sun, L.; Wang, G.; Tan, D.; Huang, P.; Yan, H.; Gao, S.; Liu, C.; Gao, Z.; et al. Basin-wide responses of the South China Sea environment to Super Typhoon Mangkhut (2018). Sci. Total Environ. 2020, 731. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Wu, R.; Li, T. Atmosphere–warm ocean interaction and its impacts on Asian–Australian monsoon variation. J. Clim. 2003, 16, 1195–1211. [Google Scholar] [CrossRef]
- Clemens, S.; Prell, W.; Murray, D.; Shimmield, G.; Weedon, G. Forcing mechanisms of the Indian Ocean monsoon. Nature 1991, 353, 720–725. [Google Scholar] [CrossRef]
- Turner, A.G.; Annamalai, H. Climate change and the South Asian summer monsoon. Nat. Clim. Change. 2012, 2, 587–595. [Google Scholar] [CrossRef]
- Zhisheng, A.; Guoxiong, W.; Jianping, L.; Youbin, S.; Yimin, L.; Weijian, Z.; Hai, C. Global monsoon dynamics and climate change. Annu. Rev. Earth Planet. Sci. 2015, 43, 29–77. [Google Scholar] [CrossRef]
- Loeb, N.G.; Lyman, J.M.; Johnson, G.C.; Allan, R.P.; Doelling, D.R.; Wong, T.; Stephens, G.L. Observed changes in top-of-the-atmosphere radiation and upper-ocean heating consistent within uncertainty. Nat. Geosci. 2012, 5, 110–113. [Google Scholar] [CrossRef]
- Fischer, M. Multivariate projection of ocean surface data onto subsurface sections. Geophys. Res. Lett. 2000, 27, 755–757. [Google Scholar] [CrossRef]
- Khedouri, E.; Szczechowski, C.; Cheney, R. Potential Oceanographic Applications of Satellite Altimetry for Inferring Subsurface Thermal Structure. In Proceedings, Oceans ’83: Technical Papers; IEEE: Piscataway, NJ, USA, 1983; pp. 274–280. [Google Scholar]
- Chu, P.C.; Fan, C.; Liu, W.T. Determination of Vertical Thermal Structure from Sea Surface Temperature. J. Atmos. Ocean. Tech. 2000, 17, 971–979. [Google Scholar] [CrossRef]
- Fox, D.N. The modular ocean data assimilation system. Oceanography 2002, 15, 22–28. [Google Scholar] [CrossRef]
- Guinehut, S.; Le Traon, P.Y.; Larnicol, G.; Philipps, S. Combining Argo and remote-sensing data to estimate the ocean three-dimensional temperature fields—A first approach based on simulated observations. J. Marine Syst. 2004, 46, 85–98. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Guinehut, S.; Pascual, A.; Drillet, Y.; Ruiz, S.; Mulet, S. Towards high resolution mapping of 3-D mesoscale dynamics from observations: Preliminary comparison of retrieval techniques and models within MESCLA project. Ocean. Sci. 2012, 8, 885–901. [Google Scholar] [CrossRef]
- Carnes, M.R.; Mitchell, J.L.; Witt, P.W. Synthetic temperature profiles derived from Geosat altimetry: Comparison with air-dropped expendable bathythermograph profiles. J. Geophys. Res. Oceans 1990, 95, 17979–17992. [Google Scholar] [CrossRef]
- Carnes, M.R.; Teague, W.J.; Mitchell, J.L. Inference of subsurface thermohaline structure from fields measurable by satellite. J. Atmos. Ocean. Tech. 1994, 11, 551–566. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Santoleri, R. Reconstructing synthetic profiles from surface data. J. Atmos. Ocean. Tech. 2004, 21, 693–703. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Santoleri, R. Methods for the reconstruction of vertical profiles from surface data: Multivariate analyses, residual GEM, and variable temporal signals in the NPO. J. Atmos. Ocean. Tech. 2005, 22, 1762–1781. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Cavalieri, O.; Rio, M.H.; Santoleri, R. Subsurface geostrophic velocities inference from altimeter data: Application to the Sicily Channel (Mediterranean Sea). J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Wang, H.; Wang, G.; Chen, D.; Zhang, R. Reconstruction of three-dimensional Pacific temperature with Argo and satellite observations. Atmos.-Ocean 2012, 50, 116–128. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Guinehut, S.; Verbrugge, N.; Cotroneo, Y.; Zambianchi, E.; Iudicone, D. Southern Ocean mixed-layer seasonal and interannual variations from combined satellite and in situ data. J. Geophys. Res. Oceans 2017, 122, 10042–10060. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Mulet, S.; Iudicone, D. Three-dimensional ageostrophic motion and water mass subduction in the Southern Ocean. J. Geophys. Res. Oceans 2018, 123, 1533–1562. [Google Scholar] [CrossRef]
- LaCasce, J.H.; Wang, J. Estimating subsurface velocities from surface fields with idealized stratification. J. Phys. Oceanogr. 2015, 45, 2424–2435. [Google Scholar] [CrossRef]
- Capet, X.; Roullet, G.; Klein, P.; Maze, G. Intensification of upper-ocean submesoscale turbulence through Charney baroclinic instability. J. Phys. Oceanogr. 2016, 46, 3365–3384. [Google Scholar] [CrossRef]
- Lapeyre, G. Surface quasi-geostrophy. Fluids 2017, 2, 7. [Google Scholar] [CrossRef]
- Klein, P.; Lapeyre, G.; Siegelman, L.; Qiu, B.; Fu, L.L.; Torres, H.; Su, Z.; Menemenlis, D.; Le Gentil, S. Ocean-scale interactions from space. Earth Space Sci. 2019, 6, 795–817. [Google Scholar] [CrossRef]
- Lapeyre, G.; Klein, P. Dynamics of the Upper Oceanic Layers in Terms of Surface Quasigeostrophy Theory. J. Phys. Oceanogr. 2006, 36, 165–176. [Google Scholar] [CrossRef]
- González, H.C.; Isern, F.J. Global Ocean current reconstruction from altimetric and microwave SST measurements. J. Geophys. Res. Oceans 2014, 119, 3378–3391. [Google Scholar] [CrossRef]
- Isern, F.J.; Chapron, B.; Lapeyre, G.; Klein, P. Potential use of microwave sea surface temperatures for the estimation of ocean currents. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Isern, F.J.; Guillaume, L.; Klein, P.; Chapron, B.; Hecht, M.W. Three-dimensional reconstruction of oceanic mesoscale currents from surface information. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Klein, P.; Lapeyre, G. The oceanic vertical pump induced by mesoscale and submesoscale turbulence. Annu. Rev. Mar. Sci. 2009, 1, 351–375. [Google Scholar] [CrossRef] [PubMed]
- Klein, P.; Hua, B.L.; Lapeyre, G.; Capet, X.; Gentil, S.L.; Sasaki, H. Upper ocean turbulence from high-resolution 3D simulations. J. Phys. Oceanogr. 2008, 38, 1748–1763. [Google Scholar] [CrossRef]
- Klein, P.; Isern-Fontanet, J.; Lapeyre, G.; Roullet, G.; Danioux, E.; Chapron, B. Diagnosis of vertical velocities in the upper ocean from high resolution sea surface height. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Lapeyre, G. What vertical mode does the altimeter reflect? On the decomposition in baroclinic modes and on a surfacetrapped mode. J. Phys. Oceanogr. 2009, 39, 2857–2874. [Google Scholar] [CrossRef]
- Ponte, A.L.; Klein, P.; Capet, X.; Le Traon, P.Y.; Chapron, B.; Lherminier, P. Diagnosing surface mixed layer dynamics from high-resolution satellite observations: Numerical insights. J. Phys. Oceanogr. 2013, 43, 1345–1355. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Klein, P.; Ubelmann, C.; Fu, L.L.; Sasaki, H. Reconstructability of three-dimensional upper-ocean circulation from SWOT sea surface height measurements. J. Phys. Oceanogr. 2016, 46, 947–963. [Google Scholar] [CrossRef]
- Wang, J.; Flierl, G.R.; LaCasce, J.H.; McClean, J.L.; Mahadevan, A. Reconstructing the ocean’s interior from surface data. J. Phys. Oceanogr. 2013, 43, 1611–1626. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Liu, L. Reconstruction of three-dimensional ocean structure from sea surface data: An application of isQG method in the Southwest Indian Ocean. J. Geophys. Res. Oceans 2020, 125, 1–18. [Google Scholar] [CrossRef]
- Liu, L.; Peng, S.; Wang, J.; Huang, R. Retrieving density and velocity fields of the ocean’s interior from surface data. J. Geophys. Res. Oceans 2014, 119, 8512–8529. [Google Scholar] [CrossRef]
- Liu, L.; Peng, S.; Huang, R. Reconstruction of ocean’s interior from observed sea surface information. J. Geophys. Res. Oceans 2017, 122, 1042–1056. [Google Scholar] [CrossRef]
- Yan, H.; Wang, H.; Zhang, R.; Chen, J.; Bao, S.; Wang, G. A dynamical-statistical approach to retrieve the ocean interior structure from surface data: SQG-mEOF-R. J. Geophys. Res. Oceans 2020, 125, 1–15. [Google Scholar] [CrossRef]
- Wu, X.; Yan, X.H.; Jo, Y.H.; Liu, W.T. Estimation of subsurface temperature anomaly in the North Atlantic using a self-organizing map neural network. J. Atmos. Ocean. Tech. 2012, 29, 1675–1688. [Google Scholar] [CrossRef]
- Bao, S.; Zhang, R.; Wang, H.; Yan, H.; Yu, Y.; Chen, J. Salinity profile estimation in the Pacific Ocean from satellite surface salinity observations. J. Atmos. Ocean. Tech. 2019, 36, 53–68. [Google Scholar] [CrossRef]
- Su, H.; Wu, X.; Yan, X.H.; Kidwell, A. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurements: A support vector machine approach. Remote Sens. Environ. 2015, 160, 63–71. [Google Scholar] [CrossRef]
- Su, H.; Li, W.; Yan, X.H. Retrieving temperature anomaly in the global subsurface and deeper ocean from satellite observations. J. Geophys. Res. Oceans 2018, 123, 399–410. [Google Scholar] [CrossRef]
- Su, H.; Huang, L.; Li, W.; Yang, X.; Yan, X.H. Retrieving Ocean Subsurface Temperature Using a Satellite-Based Geographically Weighted Regression Model. J. Geophys. Res. Oceans 2018, 123, 5180–5193. [Google Scholar] [CrossRef]
- Lu, W.; Su, H.; Yang, X.; Yan, X.H. Subsurface temperature estimation from remote sensing data using a clustering-neural network method. Remote Sens. Environ. 2019, 229, 213–222. [Google Scholar] [CrossRef]
- Ballabrera-Poy, J.; Mourre, B.; Garcia-Ladona, E.; Turiel, A.; Font, J. Linear and non-linear T–S models for the eastern North Atlantic from Argo data: Role of surface salinity observations. Deep Sea Res. Part I 2009, 56, 1605–1614. [Google Scholar] [CrossRef]
- Meijers, A.J.S.; Bindoff, N.L.; Rintoul, S.R. Estimating the four-dimensional structure of the Southern Ocean using satellite altimetry. J. Atmos. Ocean. Tech. 2011, 28, 548–568. [Google Scholar] [CrossRef]
- Zhang, K.; Geng, X.; Yan, X.H. Prediction of 3-D ocean temperature by multilayer convolutional LSTM. IEEE Geosci. Remote S. 2020, 17, 1303–1307. [Google Scholar] [CrossRef]
- Goh, A.T. Back-propagation neural networks for modeling complex systems. Artif. Intel. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Paola, J.D.; Schowengerdt, R.A. A detailed comparison of backpropagation neural network and maximum-likelihood classifiers for urban land use classification. IEEE Trans. Geosci. Remote Sens. 1995, 33, 981–996. [Google Scholar] [CrossRef]
- Paola, J.D.; Schowengerdt, R.A. A review and analysis of backpropagation neural networks for classification of remotely-sensed multi-spectral imagery. Int. J. Remote Sens. 1995, 16, 3033–3058. [Google Scholar] [CrossRef]
- Barnett, T.P.; Pierce, D.W.; Saravanan, R.; Schneider, N.; Dommenget, D.; Latif, M. Origins of the midlatitude Pacific decadal variability. Geophys. Res. Lett. 1999, 26, 1453–1456. [Google Scholar] [CrossRef]
- Di Lorenzo, E.; Schneider, N.; Cobb, K.M.; Franks, P.J.S.; Chhak, K.; Miller, A.J.; McWilliams, J.C.; Bograd, S.J.; Arango, H.; Curchitser, E.; et al. North Pacific Gyre Oscillation links ocean climate and ecosystem change. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Pierce, D.W.; Barnett, T.P.; Latif, M. Connections between the Pacific Ocean tropics and midlatitudes on decadal timescales. J. Clim. 2000, 13, 1173–1194. [Google Scholar] [CrossRef]
- Collins, M.; An, S.I.; Cai, W.; Ganachaud, A.; Guilyardi, E.; Jin, F.F.; Jochum, M.; Lengaigne, M.; Power, S.; Timmermann, A.; et al. The impact of global warming on the tropical Pacific Ocean and El Niño. Nat. Geosci. 2010, 3, 391–397. [Google Scholar] [CrossRef]
- Brierley, A.S.; Kingsford, M.J. Impacts of climate change on marine organisms and ecosystems. Curr. Biol. 2009, 19, R602–R614. [Google Scholar] [CrossRef]
- Shepherd, T.G. Atmospheric circulation as a source of uncertainty in climate change projections. Nat. Geosci. 2014, 7, 703–708. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Droghei, R.; Santoleri, R. Multi-dimensional interpolation of SMOS sea surface salinity with surface temperature and in situ salinity data. Remote Sens. Environ. 2016, 180, 392–402. [Google Scholar] [CrossRef]
- Miller, S.W.; Emery, W.J. An automated neural network and cloud classifier for use over land and ocean surfaces. J. Appl. Meteorol. 1997, 36, 1346–1362. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Cambridge, UK, 1995; pp. 77–112. [Google Scholar]
- Funahashi, K.I. On the approximate realization of continuous mappings by neural networks. Neural Netw. 1989, 2, 183–192. [Google Scholar] [CrossRef]
- Karsoliya, S. Approximating number of hidden layer neurons in multiple hidden layer BPNN architecture. Inter. J. Eng. Trends. Tech. 2012, 3, 714–717. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Modell. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Optimal division of data for neural network models in water resources applications. Water. Resour. Res. 2002, 38, 1–11. [Google Scholar] [CrossRef]
- Li, Q.Y.; Sun, L.; Lin, S.F. GEM: A dynamic tracking model for mesoscale eddies in the ocean. Ocean Sci. 2016, 12, 1249–1267. [Google Scholar] [CrossRef]
- Willis, J.K.; Roemmich, D.; Cornuelle, B. Combining altimetric height with broadscale profile data to estimate steric height, heat storage, subsurface temperature, and sea-surface temperature variability. J. Geophys. Res. Oceans 2003, 108. [Google Scholar] [CrossRef]
- Akbari, E.; Alavipanah, S.K.; Jeihouni, M.; Hajeb, M.; Haase, D.; Alavipanah, S. A review of ocean/sea subsurface water temperature studies from remote sensing and non-remote sensing methods. Water 2017, 9, 936. [Google Scholar] [CrossRef]
- Knoben, W.J.; Freer, J.E.; Woods, R.A. Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Sys. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. On the choice of calibration metrics for “high-flow” estimation using hydrologic models. Hydrol. Earth Sys. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: Towards a non-parametric variant of the Kling-Gupta efficiency. Hydrol. Sci. J. 2018, 63, 1941–1953. [Google Scholar] [CrossRef]
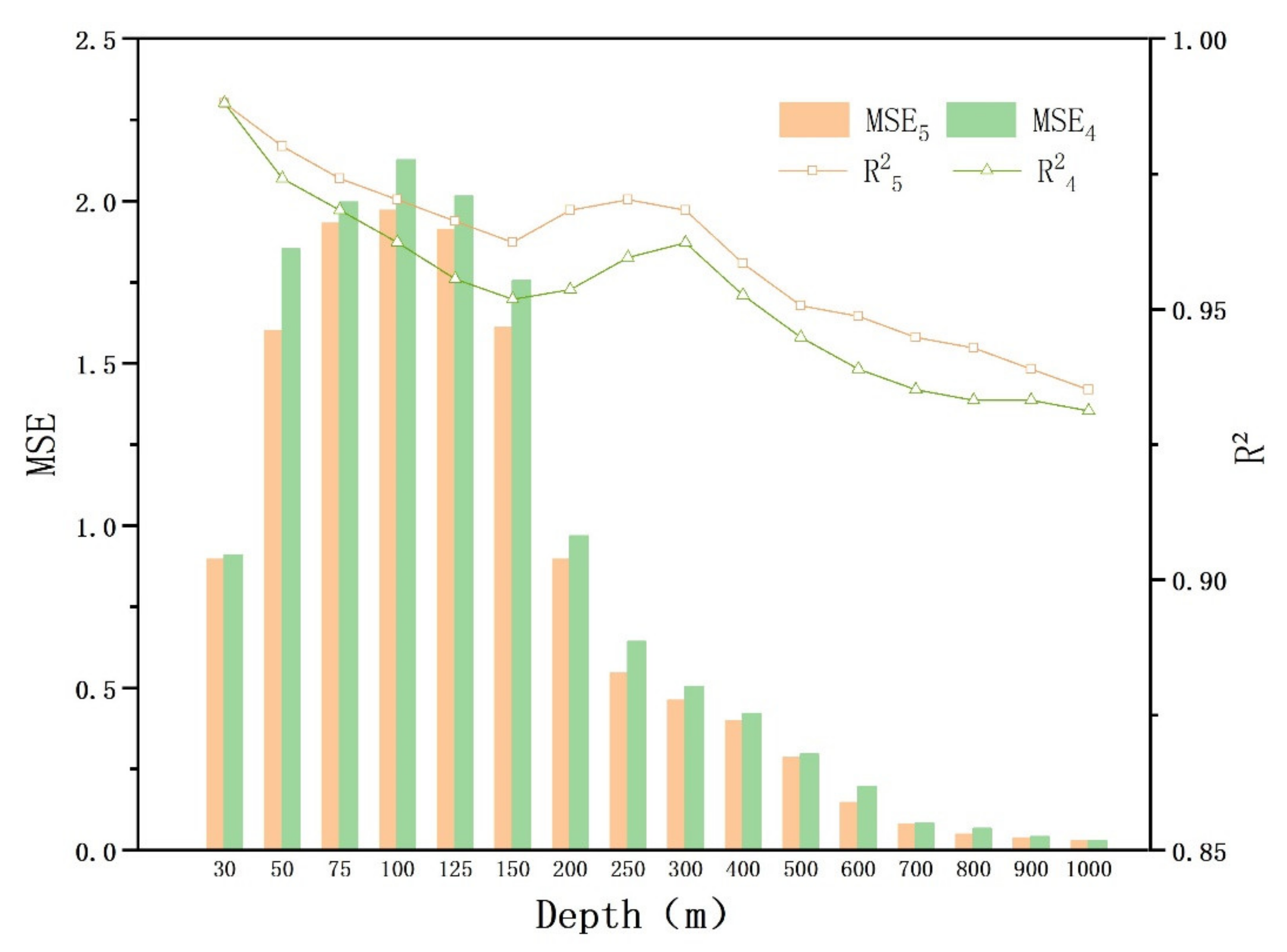
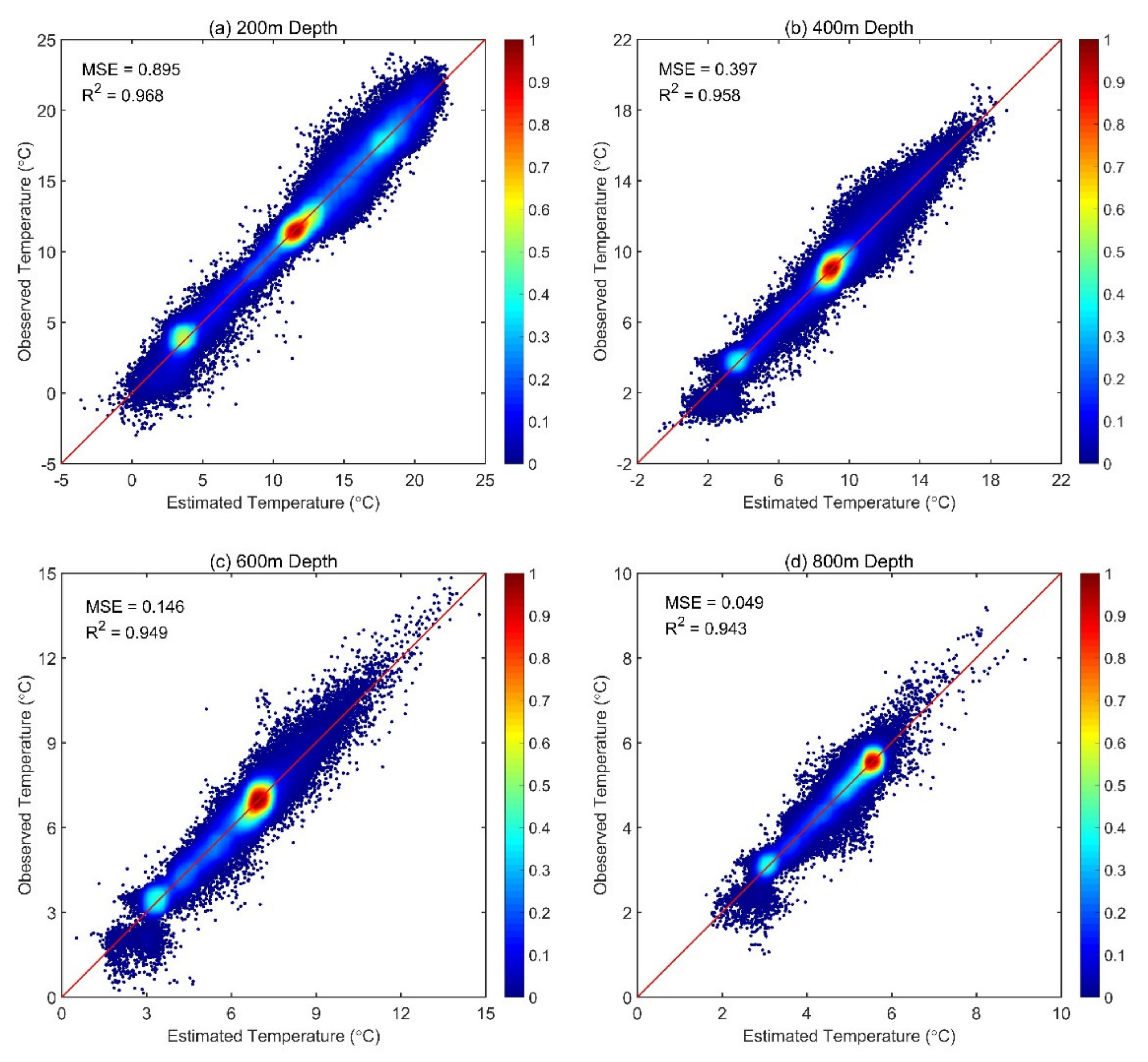
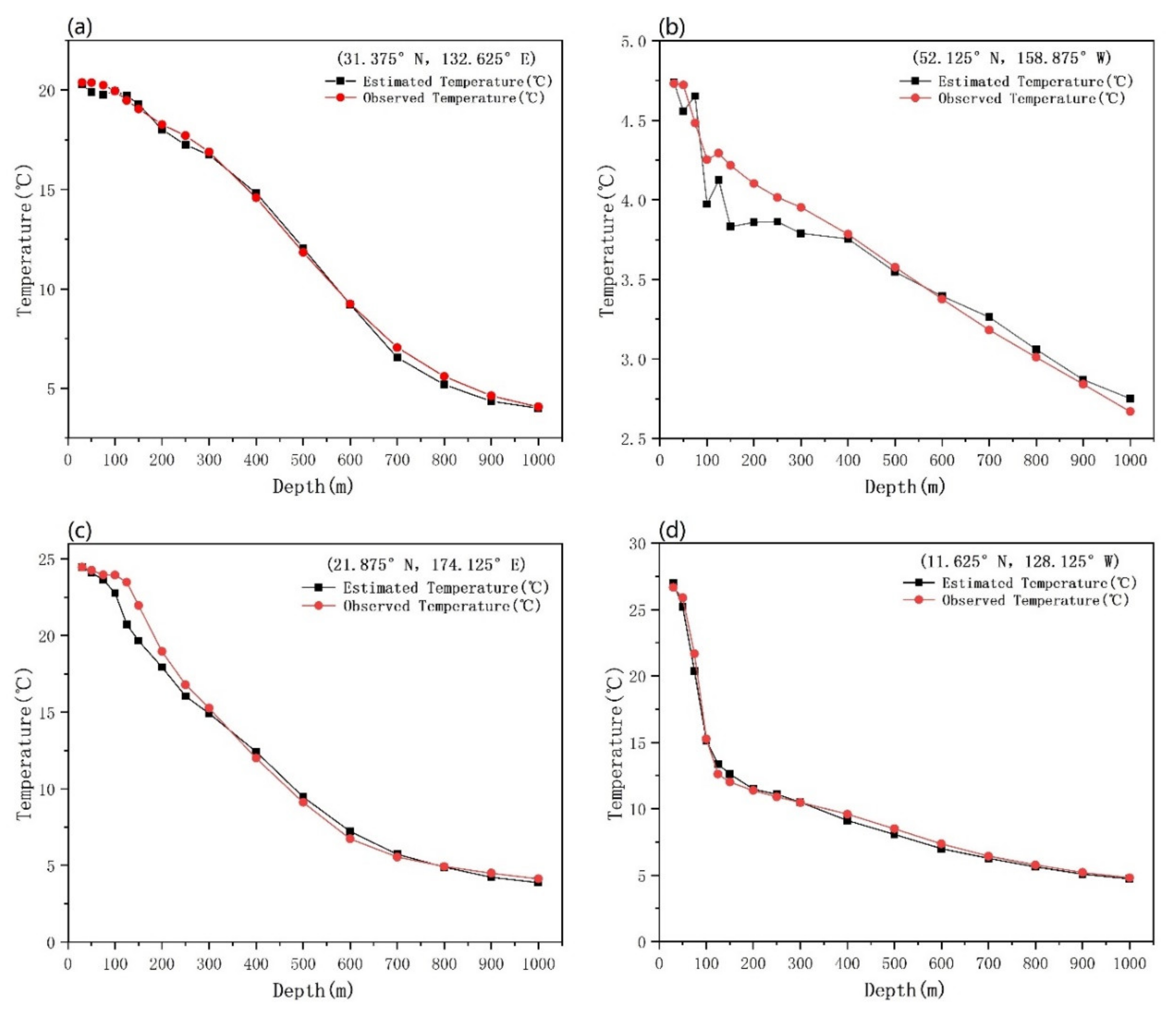
| Depth (m) | MSE (SSH, SST, SSS, SSW, SSV)/(SSH, SST, SSS, SSW)/Difference | R² (SSH, SST, SSS, SSW, SSV)/(SSH, SST, SSS, SSW)/Difference |
|---|---|---|
| 30 | 0.895/0.908/−0.013 | 0.988/0.988/0 |
| 50 | 1.605/1.852/−0.247 | 0.980/0.974/0.006 |
| 75 | 1.931/1.996/−0.065 | 0.974/0.968/0.006 |
| 100 | 1.970/2.125/−0.155 | 0.970/0.962/0.008 |
| 125 | 1.911/2.014/−0.103 | 0.966/0.955/0.011 |
| 150 | 1.612/1.754/−0.142 | 0.962/0.943/0.019 |
| 200 | 0.895/0.967/−0.072 | 0.968/0.951/0.017 |
| 250 | 0.545/0.642/−0.097 | 0.970/0.955/0.015 |
| 300 | 0.462/0.504/−0.042 | 0.968/0.966/0.002 |
| 400 | 0.397/0.421/−0.024 | 0.958/0.953/0.005 |
| 500 | 0.284/0.296/−0.012 | 0.951/0.945/0.006 |
| 600 | 0.146/0.196/−0.050 | 0.949/0.939/0.010 |
| 700 | 0.079/0.082/−0.003 | 0.945/0.935/0.010 |
| 800 | 0.049/0.067/−0.018 | 0.943/0.933/0.010 |
| 900 | 0.037/0.041/−0.004 | 0.939/0.933/0.006 |
| 1000 | 0.028/0.029/−0.001 | 0.935/0.931/0.004 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Sun, L.; Li, J. Neural Network Approach to Retrieving Ocean Subsurface Temperatures from Surface Parameters Observed by Satellites. Water 2021, 13, 388. https://doi.org/10.3390/w13030388
Cheng H, Sun L, Li J. Neural Network Approach to Retrieving Ocean Subsurface Temperatures from Surface Parameters Observed by Satellites. Water. 2021; 13(3):388. https://doi.org/10.3390/w13030388
Chicago/Turabian StyleCheng, Hao, Liang Sun, and Jiagen Li. 2021. "Neural Network Approach to Retrieving Ocean Subsurface Temperatures from Surface Parameters Observed by Satellites" Water 13, no. 3: 388. https://doi.org/10.3390/w13030388
APA StyleCheng, H., Sun, L., & Li, J. (2021). Neural Network Approach to Retrieving Ocean Subsurface Temperatures from Surface Parameters Observed by Satellites. Water, 13(3), 388. https://doi.org/10.3390/w13030388






