Abstract
During flooding, the suspended sediment transport usually experiences a wide-range of dilute to hyper-concentrated suspended sediment transport depending on the local flow and ground conditions. This paper assesses the distribution of sediment for a variety of hyper-concentrated and dilute flows. Due to the differences between hyper-concentrated and dilute flows, a linear-power coupled model is proposed to integrate these considerations. A parameterised method combining the sediment size, Rouse number, mean concentration, and flow depth parameters has been used for modelling the sediment profile. The accuracy of the proposed model has been verified against the reported laboratory measurements and comparison with other published analytical methods. The proposed method has been shown to effectively compute the concentration profile for a wide range of suspended sediment conditions from hyper-concentrated to dilute flows. Detailed comparisons reveal that the proposed model calculates the dilute profile with good correspondence to the measured data and other modelling results from literature. For the hyper-concentrated profile, a clear division of lower (bed-load) to upper layer (suspended-load) transport can be observed in the measured data. Using the proposed model, the transitional point from this lower to upper layer transport can be calculated precisely.
1. Introduction
Sediment transport is a common phenomenon during flooding. When sufficient lift force on sediment particles exists to overcome the frictional grips in between them, flow turbulence especially in the upward direction will generate sediment suspension [1,2]. Unlike the bed load, this suspended load is still not well-understood especially for those sediments with highly soluble behaviour in flow [3].
Two-phase flow is usually subjected to complex mixture between the solid and fluid phases. It is complex to mathematically model, in particular when one considers the natural flow in compound or irregular channels such as those studied by Pu [4] and Pu et al. [5]. Some models [6,7,8] resolve these complexities by neglecting turbulence and forces acting on the sediment particle surfaces, such as the effects of turbulent diffusion in laminar uniform flow or particle–particle collisions within dilute flows. However, applying these assumptions significantly hinders the modelling accuracy. As a result, recent studies have attempted to incorporate the resultant lift and drag forces acting on the particle phase [9,10,11], and this has resulted in diverse formulations for predicting the suspended sediment profile within the flow.
The general consensus when modelling the sediment-laden flow is to assume a representative two-dimensional plane due to the complexity of full 3D modelling [12]. The sediment concentration is normally considered to change with height from the bed [13]; and various flow parameters can be incorporated into mathematical models to determine the full concentration profile. These parameters commonly include: particle fall velocity, particle diameter, Rouse number and mean concentration [14,15]. Within the field of sediment profiling a range of mathematical concepts has been adopted to predict the concentration profile. Goree et al. [16] used continuum theory and incorporated the effect of drift flux due to flow turbulence implemented using large-eddy simulation. However, it was found that the computed results were less accurate in the near-wall region (also agree with [17,18]). Rouse [6] proposed diffusion theory to form one of the simplest mathematical approaches. Despite the apparent simplicity, this diffusion theory-based calculation gave reasonable and efficient prediction of the suspended solid behaviour and has subsequently been utilised as the basis for many further studies.
Another commonly used mathematical concept is that of kinetic theory. This theory is widely regarded as one of the most precise approaches to model sediment concentration distribution as it includes the response of both the solid and liquid phases as well as the interactions between them [11]. Other theories have also been produced and shown to give reasonable results, such as the combination between kinetic and diffusion theories proposed by Ni et al. [19].
In this paper, we are motivated to seek a representative model to analytically calculate the suspended sediment transport profile, since currently there is a lack of such modelling in literature to inclusively represent the diluted, transitional, and dense suspended sediment transport. In the view of this research gap, in this study, the reported models are analysed and prominent flow parameters are assessed. A method of parameterisation is introduced using an analytical regression analysis technique. Consequently, separate parameterised expressions have been proposed for a wide range of flow conditions (i.e., from dilute to hyper-concentrated flow), before being adopted into a coupled power-linear concentration model. Various tests have also been conducted to validate the proposed model with published experimental data to assess the model’s accuracy.
2. Models Review
Diffusion theory has played an important role in mathematical modelling of the suspended solid transport and has been used as the basis of the models by van Rijn [20], Wang and Ni [15], McLean [21], and Zhong et al. [22]. Rouse [6] derived his model from Fick’s Law, which defines diffusion theory, and states that diffusion from an area of high concentration to an area of low concentration should be balanced by the product of the settling velocity and concentration as described in Equation (1) [23]:
where is sediment diffusivity (m2/s), is concentration (dimensionless), is settling velocity (m/s), and represents the vertical space across a flow depth (m). Within Fick’s formula, assumptions about sediment diffusivity must be made, for which Rouse proposed that the upward diffusion was a result of the vertical flux due to turbulence and assumed that the suspended particles was only associated with fluid turbulence diffusivity [7]. This agrees with the law of wall such that the sediment diffusivity is defined by the shear velocity . Therefore, can be defined by (Equation (2)):
where is von Karman constant (dimensionless), is the shear velocity (m/s) and is the characteristic height (dimensionless) defined as the vertical distance, , from the boundary normalised by the flow depth (Equation (3)):
Hence is limited by .
Inserting Equation (2) into Equation (1) gives Equation (4) as follow:
Integrating Equation (4) between the boundaries and a reference characteristic height gives the Rouse formula (Equation (5))
where is the concentration at the reference height (dimensionless). is described as the point where suspended load transport begins to take place and suggested to be by Hsu et al. [7]. Under the assumption made by Rouse, the concentration distribution profile becomes more uniform with decreasing Rouse number which can be achieved by using sediment with low settling velocity or by increasing shear velocity, where the Rouse number can be described by Equation (6):
A modified model from Rouse has been presented by Kundu and Ghoshal [14] in which they recognised that the sediment concentration distribution can follow more than one profiles, as depicted in Figure 1. The most common profile (Type I) shows a monotonic decrease in concentration with height, and it happens when the flow concentration is dilute. The Type II profile shows an increase in concentration with height to a peak value above the bed, thereafter the concentration decreasing with height (it happens when flow is experiencing transitional concentration between dilute and dense condition). This Type II profile gives rise to a transitional point splitting the distribution into an upper flow region (above maximum concentration) and a lower flow region (below the maximum concentration in the near-bed region). The Type III profile occurs when the flow is subjected to hyper-concentration of sediment and exhibits a steady increase from the bed followed by a decrease in concentration towards the outer region of the flow.
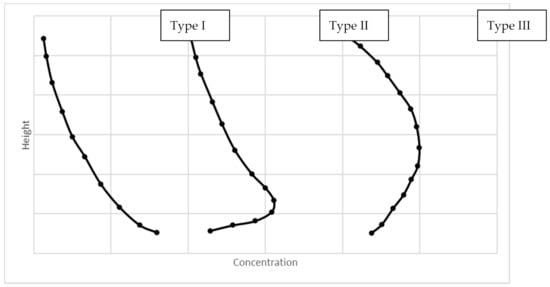
Figure 1.
Type I, II and III Concentration Profiles.
In terms of modelling, Type I allows the most simplistic solution as it can be fitted using the common Rouse approach. However, the heavy sediment-laden flows usually present Type II or III profile. In common with the Rouse model, the dependent variable for the model presented by Kundu and Ghoshal [14] is , where its functions can be defined as (Equations (7) and (8))
and,
in which and are empirical coefficients to be determined from experimental data.
Using the asymptotic matching technique by Almedeij [24], the concentration profile for both adjacent sections can be expressed in the Equation (9):
within which represents the lower suspension flow region and represents the upper suspension region. Using this technique, Kundu and Ghoshal [14] produced the empirical coefficients by calibration with previously published experimental data.
Several experimental studies (i.e., Einstein and Qian [25], Bouvard and Petkovic [26], Wang and Ni [15]) have also shown that the sediment profile follows a power law solution within the dilute-concentrated flow regime. This can be described by Equations (7) and (8) through the following simplification in Equation (10):
where it is formed when the parameter in Equations (7) and (8) is set as zero to produce a power law solution. In this formulation, Equation (10) reverts to a similar form as the Rouse formula shown in Equation (5).
However, within extreme flow conditions such as hyper-concentrated flow where the sediment profile has been proven to deviate from the power law distribution. Experimental results yield a linear profile due to an increase in particle–particle interactions. Equation (7) to (8) should thus take a form of the following in Equation (11):
with exponent equals to unity.
Limitations of this Rouse-type formulation have been evidenced by the measurements of Sumer et al. [27], Greimann and Holly [9], Jha and Bombardelli [10], Kironoto and Yulistiyanto [28], and Goeree et al. [16]. Owing to its derivation from diffusion theory, the Rouse formula provides a single-phase approach focusing on the sediment particles. As a result, the Rouse formula is limited to the representations of flows exhibiting Type I concentration profiles (Figure 1). Due to the boundary assumptions of the Rouse formula, the resultant concentration profile must always revert to zero at the fluid surface and infinity at the bed [29]. Huang et al. [8] further stated that the Rouse formula can lose its accuracy near-bed particularly when dealing with high boundary roughness. One of the attempts to improve the Rouse model is to incorporate an additional factor into the Rouse number producing a damping effect, where is the coefficient of proportionality for the diffusion coefficient for sediment transfer [29].
Greimann and Holly [9] derived a formula using a two-phase approach to the Rouse model. Within their study it is highlighted that, due to Rouse’s lack of consideration of particle–particle interactions, the Rouse formula is only valid when c < 0.1. As the Rouse formula is derived from Fick’s law, it is only applicable to flow when the bulk Stokes number (which is a parameter commonly used to define characteristic of suspended particles in a fluid flow) is very small such that the fluid and solid phases are transported almost in equilibrium. Therefore, it can be concluded that while the Rouse formula gives reasonable calculation to sediment profiling, it is limited by the absence of mechanical forces such as particle–particle interactions and particle inertia, and by its lack of effective sediment parameterisation, i.e., related to sediment size. In comparison, the models proposed by Wang and Ni [15], Ni et al. [19], and Zhong et al. [22] utilised either exponential or power laws to precisely represent suspended sediment profiles across the whole flow depth and with a variety of concentration levels. They adapted kinetic concepts for considering the particle concentration, thus can model two-phase interactions. Additionally, they used empirical fit to determine the profile characteristic, and identified various flow and sediment parameters that can be potentially used to define the concentration profile.
The aim of this study is to investigate the relationship between various flow and sediment parameters to form an improved representation to Equations (7)–(9). This will form a parameterised expression of final suspended particle characteristic model and allow an effective prediction of its concentration profile. The flow parameters to be investigated are Rouse number , size parameter , and mean concentration . Additionally, this kind of formulation using the parameterised expressions to improve the suspended sediment transport modelling has so far not been explored in other studies, hence this investigation is crucially needed to study the performance of such modelling.
3. Proposed Modelling
Many studies have investigated the relevant parameters for considering a concentration profile, including the Rouse number (defined in Equation (6)), particle size, mean concentration, and flow depth [6,27,30,31]. By referring to Equation (9), the variables are related to the coefficients of power-linear law as follows in Equation (12):
where, is the dimensionless size parameter (), in which is the sediment particle diameter and is the flow depth. In this investigation, we collected data from various reported experimental studies (as detailed in Table 1) to inspect the distribution of each power-linear law coefficient toward the physical parameters of Rouse number, particle size, and mean concentration, and to deduce a modified Rouse model for validation tests. It can be observed from Table 1 that the utilised data sources are in a wide range. In particular, the range in the utilised literature are ranging from 0.00013 to 0.147, which giving a thorough test of concentrations from dilute to hyper-concentrated flow conditions.

Table 1.
Data sources for parameterised modelling.
3.1. Rouse Number
Two of the main parameters affecting drag on a sediment particle are the settling and shear velocities. A dimensionless form of these parameters together with von Karman constant is the Rouse number as defined in Equation (6). By studying each parameter in Equation (9) against , we can produce Figure 2, Figure 3, Figure 4 and Figure 5 below.
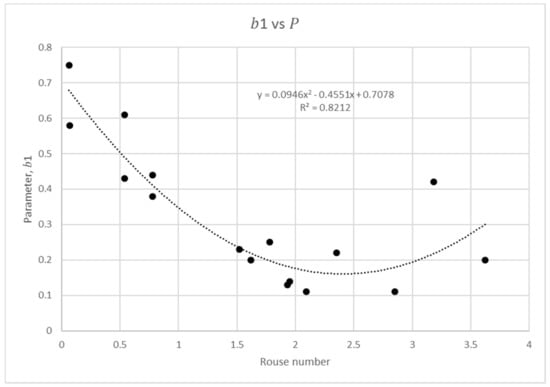
Figure 2.
Rouse number regression analysis for coefficient .
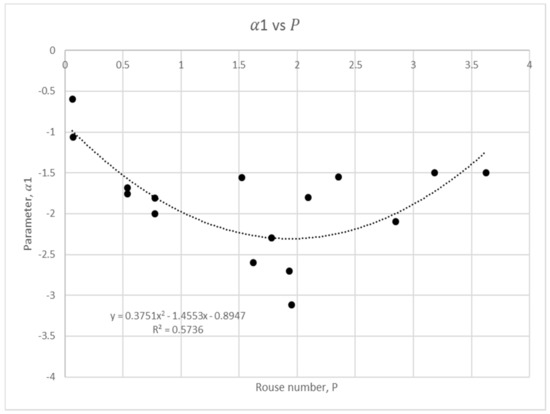
Figure 3.
Rouse number regression analysis for coefficient .
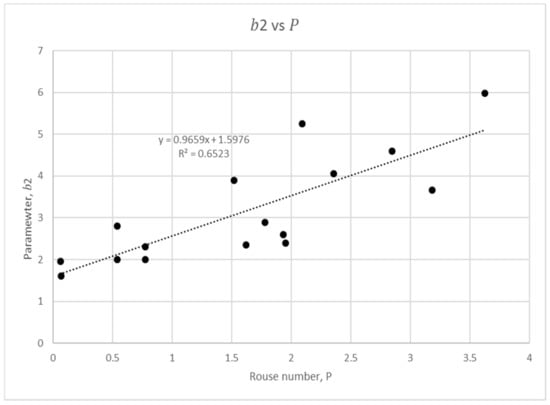
Figure 4.
Rouse number regression analysis for coefficient .
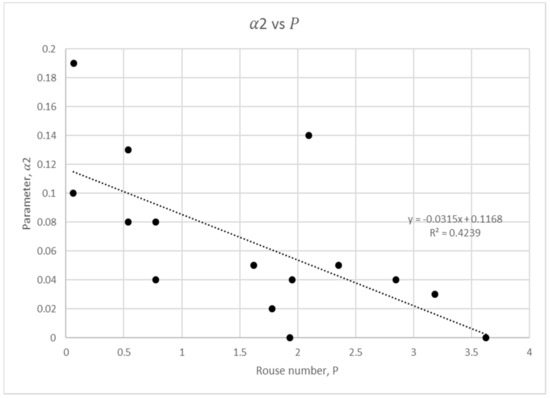
Figure 5.
Rouse number regression analysis for coefficient .
Figure 2, Figure 3, Figure 4 and Figure 5 show that there is a quadratic relationship for the parameters and , and a linear relationship for and against . The regression analysis shows all coefficients have , except for . This finding shows provides reasonable fit to be represented by power-law and its coefficients in wide range of measured data. As analysed by Kundu and Ghoshal [11], the Rouse number function does not provide a good representation to the hyper-concentrated profile, and hence the hyper-concentrated flow data have been omitted in Figure 2, Figure 3, Figure 4 and Figure 5.
3.2. Size Parameter
Particle size is another factor that significantly affects sediment drag and lift. The surface area of a particle, determined by the diameter for a spherical particle, can affect the effectiveness of interactive contacts act on the particle. Additionally, particle diameter also influences its settling velocity [34]. In Figure 6, Figure 7, Figure 8 and Figure 9, the dimensionless is plotted against the proposed model’s power-law coefficients. In the original Rouse approach [6] or modified Rouse model (as used in Kundu and Ghoshal [14]), the effect of particle size has not been considered, even though it is a crucial factor in determining the suspended sediment behaviour.
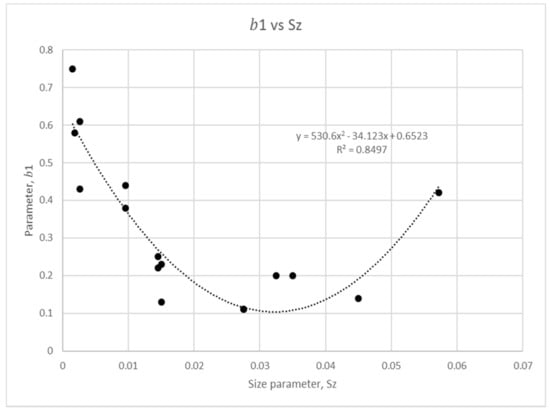
Figure 6.
Size parameter regression analysis for coefficient .
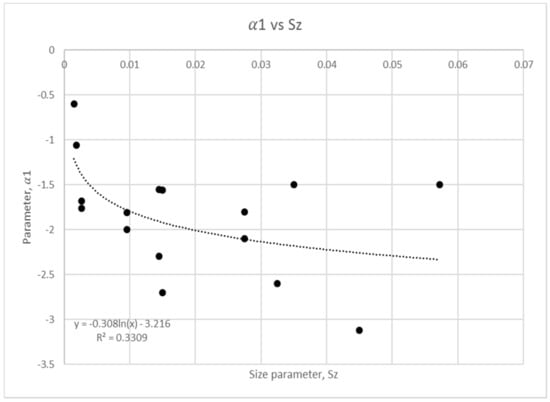
Figure 7.
Size parameter regression analysis for coefficient .
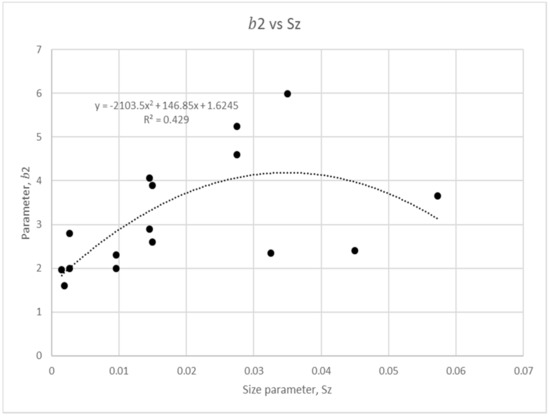
Figure 8.
Size parameter regression analysis for coefficient .
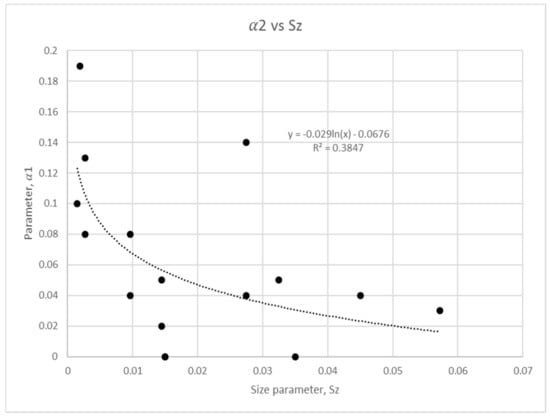
Figure 9.
Size parameter regression analysis for coefficient .
In Figure 6, Figure 7, Figure 8 and Figure 9, it can be observed that a quadratic relationship describes the variation of and with while a logarithmic relationship for and against is observed. All the figures show regression lower than 0.5 with the exception of . This low regression shows that and are harder to be represented by , which in turns exposes the difficulty of modelling using . Its analysis further suggests that the particle size factor is harder to be fixed. In the analytical modelling studies of Wang and Ni [15] and Ni et al. [19], the particle diameter has been fitted by using a coefficient in the concentration equation extracted from the measured data. The described tests have shown that it is hard to capture the characteristic of concentration profiles when different sediment diameters have been tested. This further affirms the difficulty of finding a representative function for the particle size parameter investigated here.
3.3. Mean Concentration
Michalik [35] and Cellino and Graf [32] investigated the measured sediment concentration profiles for hyper-concentrated flows. Their results showed that for such flows, the sediment profile follows a more linear distribution as opposed to the common power law observed in other dilute flow studies. Another empirical observation by Machalik [35] was that the mean concentration has key dominant impact on the characteristic of concentration distribution compared to Rouse number or particle size. Hence this study will formulate the analytical approach by mean concentration for use in the linear law modelling. Regression analysis was also used to identify the fit between the linear law coefficients and mean concentration, as presented in Figure 10, Figure 11, Figure 12 and Figure 13.
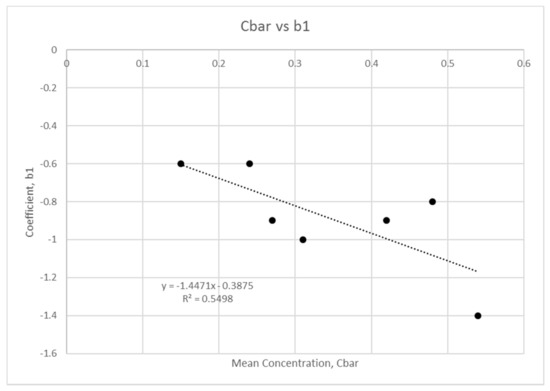
Figure 10.
Mean concentration regression analysis for coefficient .
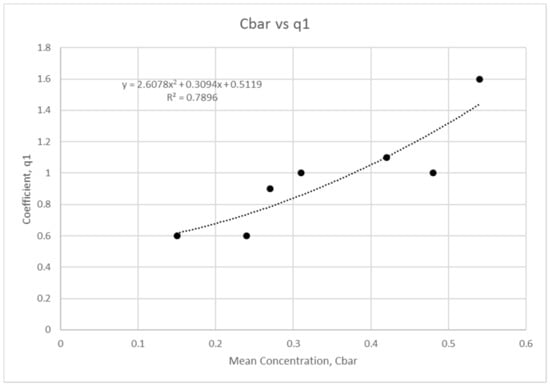
Figure 11.
Mean concentration regression analysis for coefficient .
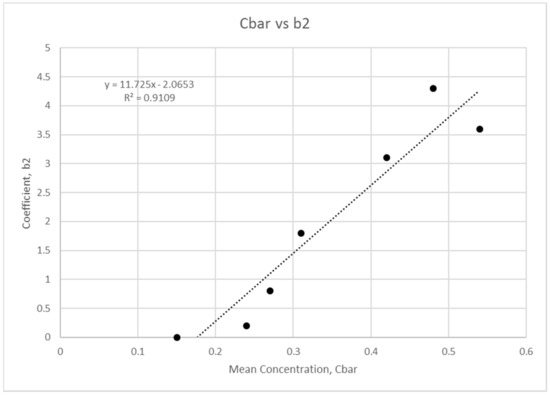
Figure 12.
Mean concentration regression analysis for coefficient .
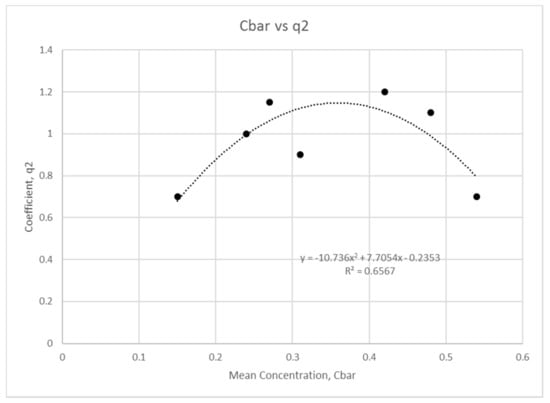
Figure 13.
Mean concentration regression analysis for coefficient .
The results show that a linear fit describes the variation for the coefficients and with mean concentration; while a quadratic relationship describes the variation of the coefficients and with . The fits show an regression higher than 0.5 without exception. This finding evidences a clear correlation between and the hyper-concentrated profile.
3.4. Hyper-To-Dilute Boundary
The findings from the above sections are adapted into the model of Equation (9) to form a parameterised expression for the sediment concentration distribution across the flow depth. The proposed sediment concentration calculative model is governed by a coupled approach. A power law is utilised to represent the dilute sediment concentration (when 0 < < 0.1), whereas a linear law is used for the dense hyper-concentration (when ≥ 0.1). This hyper-to-dilute boundary has been set by benchmarking the investigation of Greimann and Holly [9] on dilute flow definition and Rouse model limit. Our proposed coefficients found from the above sections can be represented as:
For the dilute regime, where 0 < < 0.1 (Equations (13)–(17)):
For the hyper-concentrated regime where ≥ 0.1 (Equations (18)–(22)):
4. Model Validations
The model presented within this paper is validated against the experimental data of Wang and Ni [31], Wang and Qian [36], and Michalik [35]. It has also been compared with the previously proposed models by Wang and Ni [31], Ni et al. [19], and Zhong et al. [22]. Wang and Ni [31] presented a theoretical distribution model derived from the kinetic theory. Their model is limited to dilute flow and therefore predicts Type I and limited Type II profiles only. In their assumption, the particle interaction has been neglected, and as a result, they attributed the classification of distribution profile solely to the fluid-induced lift forces. It is also noteworthy within their study that when particle size is small the distribution tends to follow the Type I profile.
The model proposed by Ni et al. [19] used a fusion of kinetic and continuum theories, where kinetic theory using the Boltzmann equation being applied to the solid-phase and continuum theory to the fluid-phase. Within their derivation, the empirically weighted forces have been used to act upon sediment to represent two-phase interactions. The model has been proposed to be applicable to both dilute and dense flows. The model proposed by Zhong et al. [22] is more complex when compared to the other two above-mentioned models. It is based on a tertiary approach where the model can be simplified under various empirically-driven assumptions. Within their research, the experimental testing covers Type I, II, and III profiles; though due to its complexity, their Type III profile required a dynamic value of the empirical damping function to fit for different flow conditions.
4.1. Wang and Ni
The measured data of Wang and Ni [31] assessed dilute flow within pipes. The concentrations tested were extremely dilute ranging from 0.00042 ≤ ≤ 0.0033, where these tested conditions are presented in Table 2. This validation exercise will provide a good test to the proposed model capability to capture extremely dilute flow. The sediments tested were grains and coarse sands with particle diameter ranging from 0.58 mm ≤ ≤ 2.29 mm. The results are presented in Figure 14A–J. The proposed model shows a reasonable correspondence to the experimental data. The measurements of Wang and Ni [31] show that for dilute flow the sediment concentration tends to follow the Type I or II concentration profile with the maximum concentration occurring in the near-bed region.

Table 2.
Data by Wang and Ni [31].
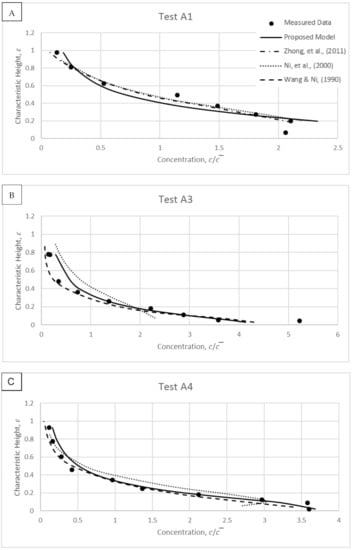
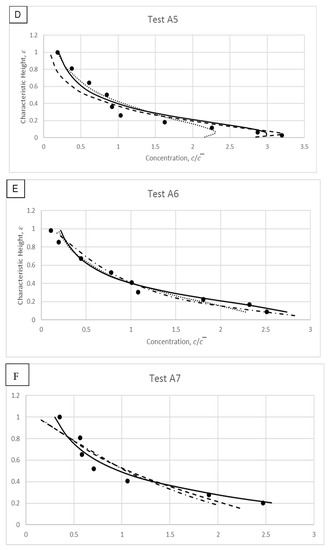
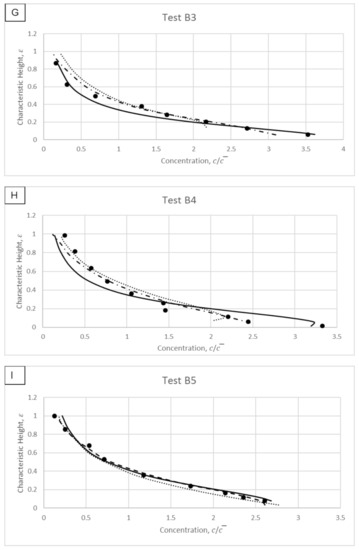
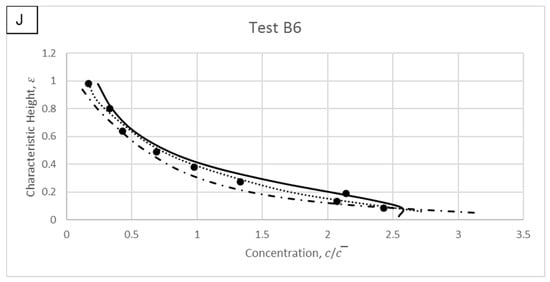
Figure 14.
Modelled results and comparisons against experimental data of Wang and Ni [31].
Observation of Figure 14A–J shows that overall there is a better fit by the proposed and other models away from the near-bed region. This is coherent with the suggestions from literature (i.e., Kundu and Ghoshal [11]; Greimann and Holly [9]) stating that the possibility of particle–particle interactions increases at near-bed to produce more challenging conditions for the mathematical modelling.
The experimental data in Figure 14F utilised the largest particles among all the measured data of Wang and Ni [31]. Therefore, larger interaction forces can be expected between the solid–fluid phases due to the larger surface area of each sediment particle. One can observe that the proposed model shows a concentration distribution for Figure 14F which is consistent with the measurements. Compared with the model of Zhong et al. [22], which does not take into account the particle size, the proposed model shows promising computation of big particle measured data.
4.2. Wang and Qian
Wang and Qian [36] studied the effect of dilute to dense concentrations in open channel flow using an experimental recirculating-tilting flume. Their experiments tested a wide range of sediment diameters 0.15 mm ≤ d ≤ 0.96 mm and concentrations 0.0102 ≤ ≤ 0.0906 (as shown in Table 3). Their tests are compared against the proposed and other models, with the results presented in Figure 15A–D. Overall, the models show lower accuracy to reproduced measured data throughout the flow depth with increasing mean concentration. The proposed model shows a reasonable fit to the experimental data in the upper flow region. Within this region, the main forces acting on the sediment particles are the lift and drag due to the fluid induced forces and particle inertia. This supports the hypothesis that the proposed model can compute the solid–fluid interactions for particles with reasonable accuracy owing to its inclusion of Rouse and size parameters.

Table 3.
Data by Wang and Qian [36].
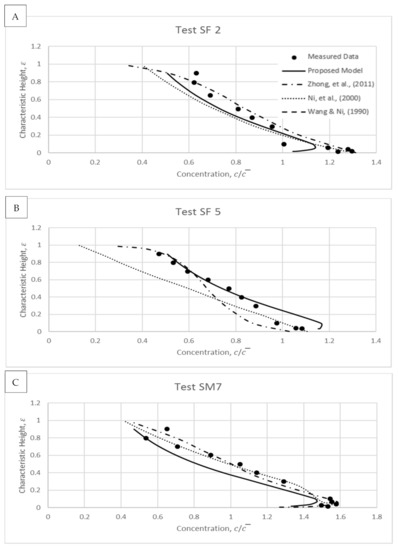
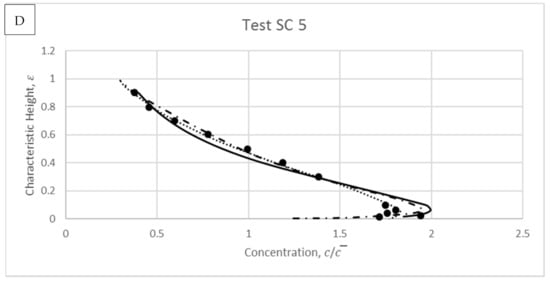
Figure 15.
Modelled results and comparisons against experimental data of Wang and Qian [36].
An overview of all the results displayed in Figure 15A–D demonstrates that the accuracy of different models reduces at the lower suspension region, including the proposed model. Within Type II profiles, the local maximum in concentration is observed closer to the bed compared to Type III profiles. Near to the wall boundary, the sediment distribution is governed by the bed-load behaviour as opposed to the suspended load. The plastic particles were used within the flows tested here, and they generate less significant movement than the normal and natural sediment under the acting of particle–particle interactive forces [36]. Due to this, the proposed model that deals with the forces by coupling expressions of Rouse and size parameters unable to simulate the near-bed concentrations reasonably, as compared to the models presented in Ni et al. [19] and Zhong et al. [22] which used imported empirical functions from the respective experiments into their modelling. In addition, the boundary conditions for flow with transitional concentration (from dilute to dense concentrations) are hard to be fixed, and hence this difficulty may cause discrepancy in the proposed modelling (especially presented by results at Figure 15A,B).
4.3. Michalik
The experimental data of Michalik [35] quantified the sediment profile of hyper-concentrated flows. The sediment material used was sand with a mean diameter of 0.45 mm and with concentration ranging between 0.15 ≤ ≤ 0.54 (all test conditions are shown in Table 4). In order to model Michalik’s tests, this study uses the linear law within the proposed model. The test results are shown in Figure 16A–F, where the modelled results are compared to measurements. Ni et al. [19] and Zhong et al. [22] models are also incorporated into these figures to compare with the measurements and proposed model.

Table 4.
Data by Michalik [35].
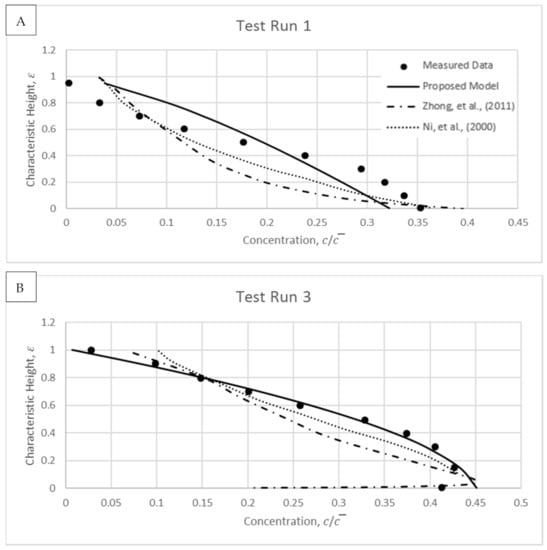
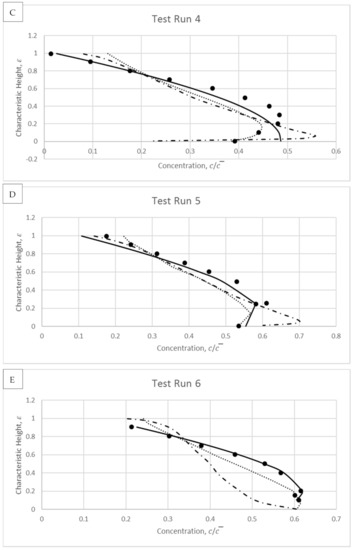
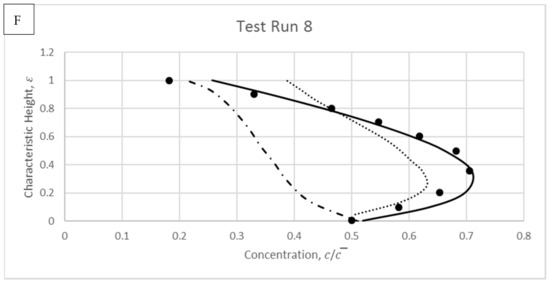
Figure 16.
Showing modelled results and comparisons for experimental data of Michalik [35].
From the tested hyper-concentrated flows, the sediment concentration distribution illustrates a Type III profile. Within hyper-concentrated flow, the maximum in concentration is difficult to model accurately since there exists no distinct boundary where the sediment changes from bed to suspended load but rather the bed load can diffuse into the suspended state through a transitional region. As a result, the suspended load has sometimes been estimated as part of the bed load, which increases the discrepency in suspended solid modelling. To accurately define the transition region and consequently the location of this maximum turning point, a good estimation of and is required [27]. In this study, the proposed model uses for the mathematical modelling, since it seems acceptable to conclude that is proportional to [37] given that they are both invariant for a given experiment.
The proposed calculated results show reasonable agreement to the experimental data, in which it exhibits better fit to the measurements compared to the rest of models by Ni et al. [19] and Zhong et al. [22] in Figure 16A–F. The figures demonstrate a Type III profiles that fit into the hyper-concentrated distribution. Studies of hyper-concentrated flow show that the sediment concentration distribution becomes more homogenous when increased as proven in Michalik [35]. Hence power law distributions might not be reasonable to model hyper-concentrated flow. Instead a linear model is adopted here and is evidenced to produce better accuracy. Even though the power-exponential models of Ni et al. [19] and Zhong et al. [22] are suitable to represent densely-concentrated flow, their accuracy are not encouraging compare to the measurements in majority of relatively hyper-concentrated tests (i.e., at Figure 16D–F).
Additionally, one can observe that an increase in the mean concentration shifts the height of maximum concentration upwards through the characteristic height due to the increase of potential bed-load layer. As the mean concentration is increased, the near-bed region becomes more saturated. The tests in Figure 16 show that when > 0.31 the settling velocity has limited influence and the dominating interaction forces must arise from particle–particle reactions. In these hyper-concentrated tests of > 0.31, the proposed model represents the concentration distribution well. In particular, the proposed model accurately predicts the height at which the maximum concentration occurs for most cases.
5. Conclusions
A parameterised power-linear coupled model has been introduced for inclusively computing the dilute- to hyper-concentrated distribution across the characteristic height within flow. The parameters used for the formulation of this model were size parameter, Rouse number, and mean concentration. As proven, the model is able to accurately compute the suspended sediment profile for a range of flow conditions including various Rouse numbers. The proposed model shows a reasonable accuracy for low and very high concentration tests across the Type I to III profiles. This can be seen from the comparisons with experimental data of Wang and Ni [31] on very dilute flows, Wang and Qian [36] on mixed dilute to dense flows, and Michalik [35] on hyper-concentrated flows. From the tests, the coupling approach of power to linear modelling has been proven to reasonably represent flow with a wide range of concentrations and sediment sizes.
This type of suspended modelling holds key importance to the accurate prediction of various natural flows, such as river, coastal, or flood flow. In flooded condition, the sediment mixture impacts the flow behaviour that can cause modelling failure in reproducing the real-world flood flow. With this analytical modelling study, the flood induced suspended sediment transport with wide range of dilute to dense concentration can be modelled adequately; and hence to provide the vital capability to flood flow modelling. Additionally, to further this work, different analytical modelling besides Rouse-based model can also be investigated.
Author Contributions
J.H.P.: writing—original draft preparation, writing—review and editing, funding acquisition, project administration, data curation, supervision; J.T.W.: writing—original draft preparation, writing—review and editing, data curation; M.A.K.: writing—review and editing, data curation; M.P.: writing—review and editing, data curation; H.P.: writing—review and editing, data curation; A.S.: writing—review and editing, data curation; P.R.H.: writing—review and editing, data curation; T.G.: writing—review and editing, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on reasonable request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pu, J.H.; Hussain, K.; Shao, S.-D.; Huang, Y.-F. Shallow sediment transport flow computation using time-varying sediment adaptation length. Int. J. Sediment Res. 2014, 29, 171–183. [Google Scholar] [CrossRef][Green Version]
- Pu, J.H.; Wei, J.; Huang, Y. Velocity Distribution and 3D Turbulence Characteristic Analysis for Flow over Water-Worked Rough Bed. Water 2017, 9, 668. [Google Scholar] [CrossRef]
- Pu, J.H.; Huang, Y.; Shao, S.; Hussain, K. Three-Gorges Dam Fine Sediment Pollutant Transport: Turbulence SPH Model Simulation of Multi-Fluid Flows. J. Appl. Fluid Mech. 2016, 9, 1–10. [Google Scholar] [CrossRef]
- Pu, J.H. Turbulent rectangular compound open channel flow study using multi-zonal approach. Environ. Fluid Mech. 2018, 19, 785–800. [Google Scholar] [CrossRef]
- Pu, J.H.; Pandey, M.; Hanmaiahgari, P.R. Analytical modelling of sidewall turbulence effect on streamwise velocity profile using 2D approach: A comparison of rectangular and trapezoidal open channel flows. HydroResearch 2020, 32, 17–25. [Google Scholar] [CrossRef]
- Rouse, H. Modern Conceptions of the Mechanics of Fluid Turbulence. J. Pap. Trans. Am. Soc. Civ. Eng. 1937, 102, 463–505. [Google Scholar]
- Hsu, T.-J.; Jenkins, J.T.; Liu, P.L. On two-phase sediment transport: Dilute flow. J. Geophys. Res. Space Phys. 2003, 108, 3057. [Google Scholar] [CrossRef]
- Huang, S.-H.; Sun, Z.-L.; Xu, D.; Xia, S.-S. Vertical distribution of sediment concentration. J. Zhejiang Univ. A 2008, 9, 1560–1566. [Google Scholar] [CrossRef]
- Greimann, B.; Holly, F.M., Jr. Two-Phase Flow Analysis of Concentration Profiles. J. Hydraul. Eng. 2001, 127, 753–762. [Google Scholar] [CrossRef]
- Jha, S.K.; Bombardelli, F.A. Two-phase modeling of turbulence in dilute sediment-laden, open-channel flows. Environ. Fluid Mech. 2009, 9, 237–266. [Google Scholar] [CrossRef]
- Kundu, S.; Ghoshal, K. A mathematical model for type II profile of concentration distribution in turbulent flows. Environ. Fluid Mech. 2016, 17, 449–472. [Google Scholar] [CrossRef]
- Pu, J.H.; Lim, S.Y. Efficient numerical computation and experimental study of temporally long equilibrium scour development around abutment. Environ. Fluid Mech. 2013, 14, 69–86. [Google Scholar] [CrossRef]
- Liang, C.-F.; Abbasi, S.; Pourshahbaz, H.; Taghvaei, P.; Tfwala, S. Investigation of Flow, Erosion, and Sedimentation Pattern around Varied Groynes under Different Hydraulic and Geometric Conditions: A Numerical Study. Water 2019, 11, 235. [Google Scholar] [CrossRef]
- Kundu, S.; Ghoshal, K. Explicit formulation for suspended concentration distribution with near-bed particle deficiency. Powder Technol. 2014, 253, 429–437. [Google Scholar] [CrossRef]
- Wang, G.; Ni, J. The kinetic theory for dilute solid/liquid two-phase flow. Int. J. Multiph. Flow 1991, 17, 273–281. [Google Scholar] [CrossRef]
- Goeree, J.C.; Keetels, G.H.; Munts, E.A.; Bugdayci, H.H.; Van Rhee, C. Concentration and velocity profiles of sediment-water mixtures using the drift flux model. Can. J. Chem. Eng. 2016, 94, 1048–1058. [Google Scholar] [CrossRef]
- Pourshahbaz, H.; Abbasi, S.; Taghvaei, P. Numerical scour modeling around parallel spur dikes in FLOW-3D. J. Drink. Water Eng. Sci. 2017, 1–16. [Google Scholar] [CrossRef]
- Pourshahbaz, H.; Abbasi, S.; Pandey, M.; Pu, J.H.; Taghvaei, P.; Tofangdar, N. Morphology and hydrodynamics numerical simulation around groynes. ISH J. Hydraul. Eng. 2020, 1–9. [Google Scholar] [CrossRef]
- Ni, J.R.; Wang, G.Q.; Borthwick, A.G.L. Kinetic Theory for Particles in Dilute and Dense Solid-Liquid Flows. J. Hydraul. Eng. 2000, 126, 893–903. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment Transport, Part II: Suspended Load Transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- McLean, S.R. On the calculation of suspended load for noncohesive sediments. J. Geophys. Res. Space Phys. 1992, 97, 5759. [Google Scholar] [CrossRef]
- Zhong, D.; Wang, G.; Sun, Q. Transport Equation for Suspended Sediment Based on Two-Fluid Model of Solid/Liquid Two-Phase Flows. J. Hydraul. Eng. 2011, 137, 530–542. [Google Scholar] [CrossRef]
- Fick, A. On liquid diffusion. J. Membr. Sci. 1995, 100, 33–38. [Google Scholar] [CrossRef]
- Almedeij, J. Asymptotic matching with a case study from hydraulic engineering. Proc. Recent Adv. Water Resour. Hydraul. Hydrol. Camb. 2009, 71–76. [Google Scholar] [CrossRef]
- Einstein, H.A.; Qian, N. Effects of Heavy Sediment Concentration Near the Bed on the Velocity and Sediment Distribution; Omaha: U.S. Army Engineer Division, Missouri River: Omaha, NE, USA, 1955. [Google Scholar]
- Bouvard, M.; Petković, S. Vertical dispersion of spherical, heavy particles in turbulent open channel flow. J. Hydraul. Res. 1985, 23, 5–20. [Google Scholar] [CrossRef]
- Sumer, B.; Kozakiewicz, A.; Fredsoe, J.; Deigaard, R. Velocity and Concentration Profiles in Sheet-Flow Layer of Movable Bed. J. Hydraul. Eng. 1996, 122, 549–558. [Google Scholar] [CrossRef]
- Kironoto, B.A.; Yulistiyanto, B. The validity of Rouse equation for predicting suspended sediment concentration profiles in transverse direction of uniform open channel flow. In Proceedings of the International Conference on Sustainable Development Water Waste Water Treatment, Yogyakarta, Indonesia, 14–15 December 2009. [Google Scholar]
- Kumbhakar, M.; Ghoshal, K.; Singh, V.P. Derivation of Rouse equation for sediment concentration using Shannon entropy. Phys. A Stat. Mech. Its Appl. 2017, 465, 494–499. [Google Scholar] [CrossRef]
- Coleman, N.L. Effects of Suspended Sediment on the Open-Channel Velocity Distribution. Water Resour. Res. 1986, 22, 1377–1384. [Google Scholar] [CrossRef]
- Wang, G.; Ni, J. Kinetic Theory for Particle Concentration Distribution in Two-Phase Flow. J. Eng. Mech. 1990, 116, 2738–2748. [Google Scholar] [CrossRef]
- Cellino, M.; Graf, W.H. Sediment-Laden Flow in Open-Channels under Noncapacity and Capacity Conditions. J. Hydraul. Eng. 1999, 125, 455–462. [Google Scholar] [CrossRef]
- Muste, M.; Yu, K.; Fujita, I.; Ettema, R. Two-phase versus mixed-flow perspective on suspended sediment transport in turbulent channel flows. Water Resour. Res. 2005, 41, 41. [Google Scholar] [CrossRef]
- Cheng, N.-S. Comparison of formulas for drag coefficient and settling velocity of spherical particles. Powder Technol. 2009, 189, 395–398. [Google Scholar] [CrossRef]
- Michalik, M.A. Density patterns of the inhomogeneous liquids in the industrial pipe-lines measured by means of radiometric scanning. La Houille Blanche 1973, 53–57. [Google Scholar] [CrossRef]
- Wang, X.; Qian, N. Turbulence Characteristics of Sediment-Laden Flow. J. Hydraul. Eng. 1989, 115, 781–800. [Google Scholar] [CrossRef]
- Ali, S.Z.; Dey, S. Mechanics of advection of suspended particles in turbulent flow. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160749. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).