A Framework to Assess the Reliability of a Multipurpose Reservoir under Uncertainty in Land Use
Abstract
1. Introduction
2. Materials and Methods
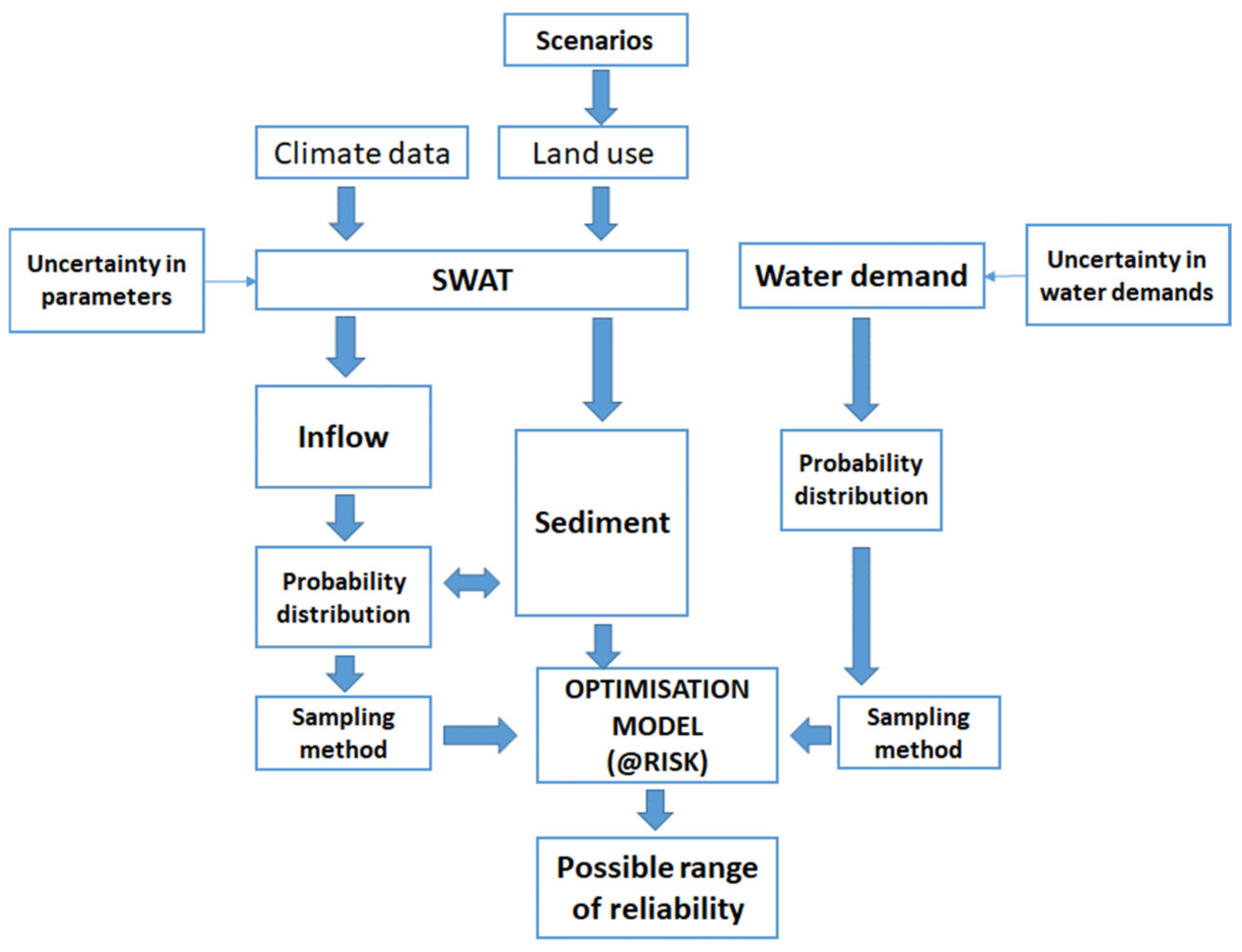
2.1. The Framework
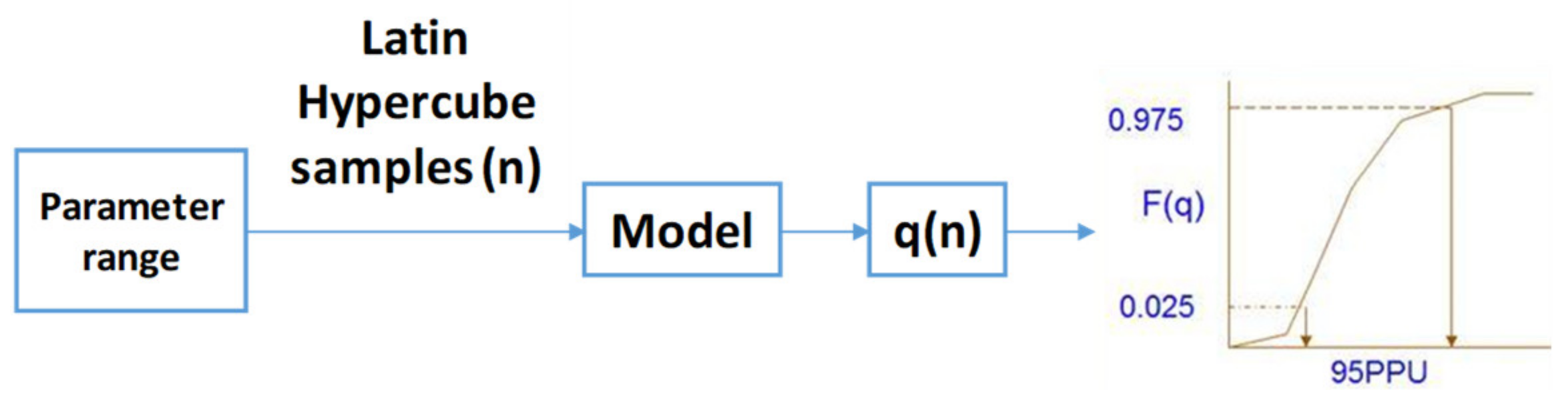
2.1.1. SWAT Modelling and Uncertainties
2.1.2. Optimisation Tool
- -
- Step 1: Determine the following key factors for the optimisation tool: (i) Objective function (Equation (1)), (ii) Decision variables (water releases), and (iii) Constraints (Equations (2)–(7)). Step 2: Set up a deterministic optimisation model using monthly deterministic input data.
- -
- Step 3: Replace monthly deterministic input data including monthly inflows, sediment values, and water demands by monthly probability distributions to include uncertainties.
- -
- Step 4: Generate a number of random possible combinations (n = 180 was chosen for this study because it balances computational cost vs. accuracy in obtaining a reliable solution) of water inflow, sediment inflow and water demand for the optimisation model using the Latin Hypercube sampling method in @RISK. Run the genetic optimisation algorithm in @RISK for each possible combination and evaluate the possible range of reservoir reliabilities.
- Penalty function when reservoir storage is greater than active storage (P1)
- Penalty function when water release is lower than minimum allowable release (P2)
2.1.3. Model Performance Indicators
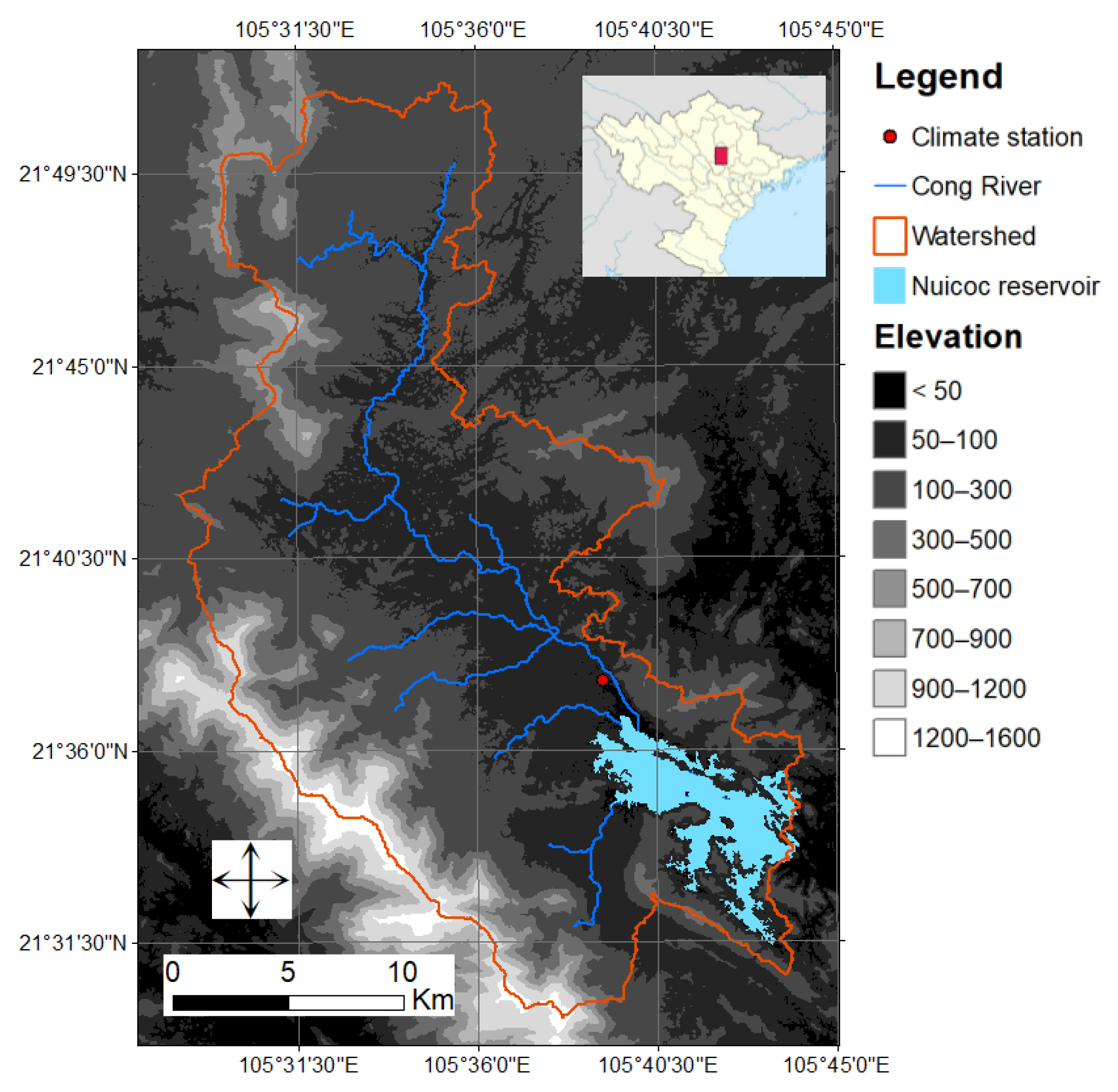
2.2. Nuicoc Watershed Case Study
2.2.1. Watershed and Reservoir
2.2.2. Data Sources and Pre-Processing for the Case Study
2.2.3. Case Study Calibration and Validation
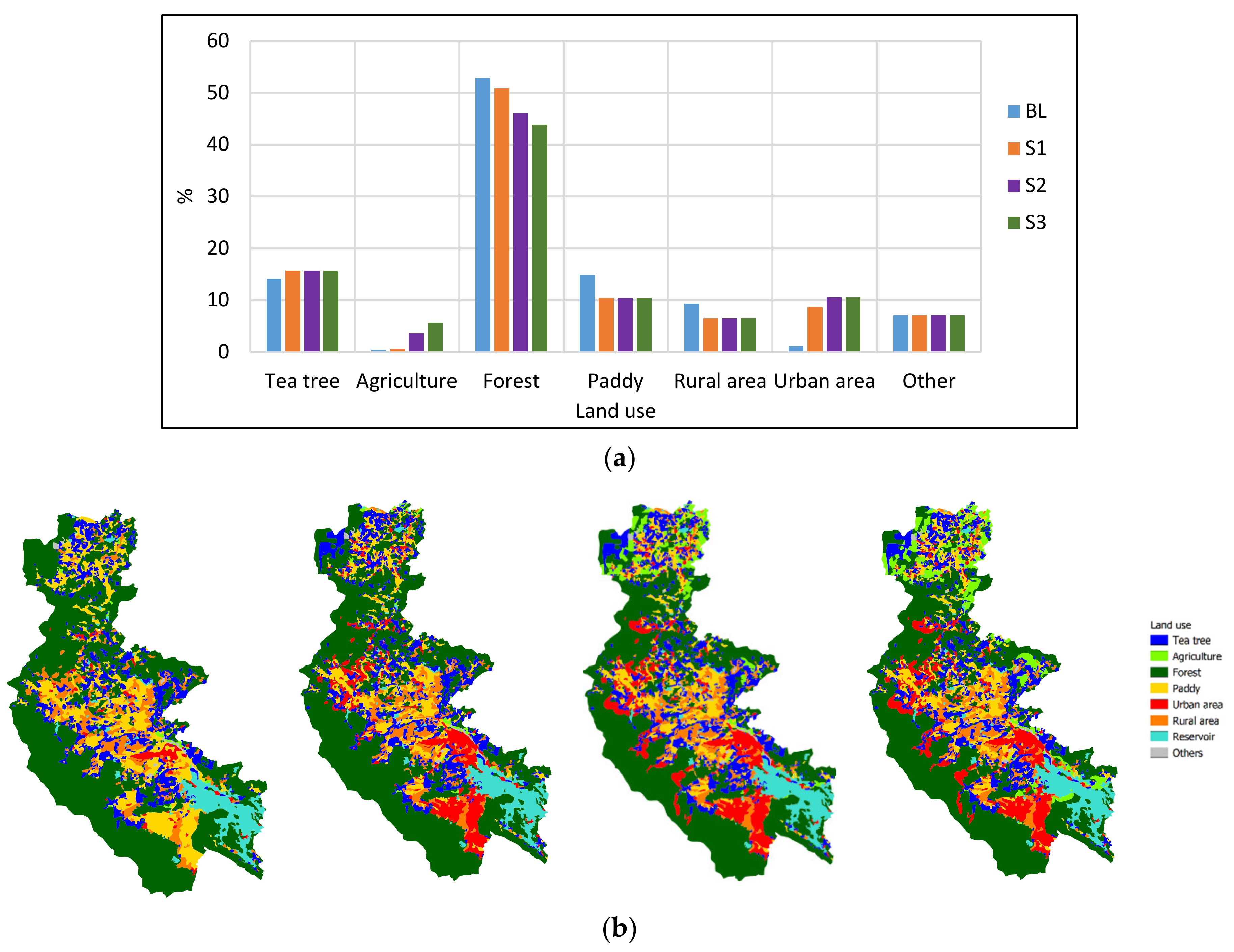
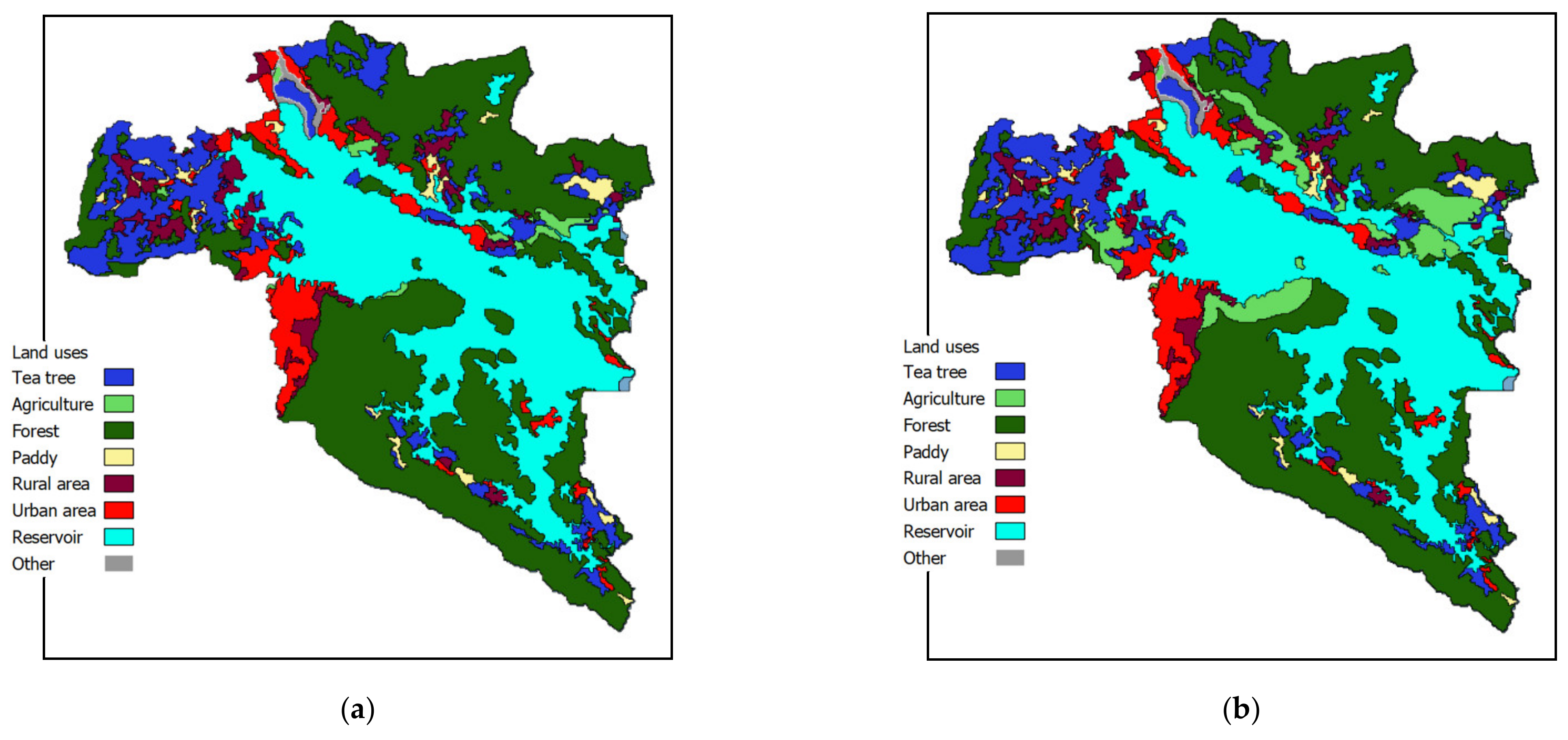
2.2.4. Land-Use Change Scenarios
- -
- The baseline map (BL) using the land-use map in 2014.
- -
- Scenario 1 (S1) shows a slight decrease in forest area, by 5%. The paddy and rural area decline considerably due to increase in the urban area, while the urban area will increase up to 8%.
- -
- Scenario 2 (S2) will witness a significant reduction in the forest area, by 8% while the urban and agricultural area will rise to over 10% and 4% respectively.
- -
- Scenario 3 (S3) is an extreme scenario with the highest urban and agricultural area and the lowest forest area.
2.2.5. Accounting for Uncertainties in Inflows and Water Demands
- Uncertainty in future potential land-use scenariosThe main drivers for land-use changes are urbanisation and conversion from forest to agricultural area. The study considers three possible scenarios (S1, S2, and S3) in the watershed.
- Uncertainty of water inflows to the reservoir due to uncertainty in parametersMonthly inflows generated by SUFI2 in SWAT-CUP within 95PPU vary based on their frequency distributions. To simplify the quantification of inflow uncertainties, we assumed that monthly inflows to the reservoir are independent and uniformly distributed within an area bounded by the lower values and upper values of 95PPU. The combination of the random monthly inflows over the simulation period creates a unique inflow time series that was fed to the optimisation tool.
- Uncertainty of demandsAs this study only considers the impact of land-use changes on reservoir reliability, the climate data and water demands were kept constant. The uncertainty in monthly water demands during the operational timeframe is considered. Based on the summary of the historical data (Figure 5), the monthly demands from urban use, agriculture and downstream flow requirements during the operational period are assumed to follow uniform (max, min) and triangular distributions (max, median, min), respectively. The combination of the random monthly water demand generates a water demand time series for the optimisation tool.
- Uncertainty in sediment inflowsParameter uncertainty will in turn result in uncertainty in streamflow, which is described by the 95% prediction uncertainty (95PPU) in SWAT-CUP. This also leads to uncertainty in sediment inflows, which is also expressed as 95PPU. To quantify the uncertainty of water inflow in simulations, a uniform distribution was applied for each month to generate monthly water inflows randomly. However, this approach cannot be used for sediment inflows as it depends on water inflows. It is therefore assumed that the relation between water inflows and sediment inflows is linear. The study also assumes that, at the beginning of simulation, sediment will be distributed equally on the bottom of the reservoir within the active storage since the reservoir dead storage has been full after 40 years of operation, from 1982; and that, the inclusion of sediment will not affect the reservoir surface.
3. Results
3.1. SWAT Model Calibration and Validation for Water Inflows and Evapotranspiration
3.2. SWAT Model Output
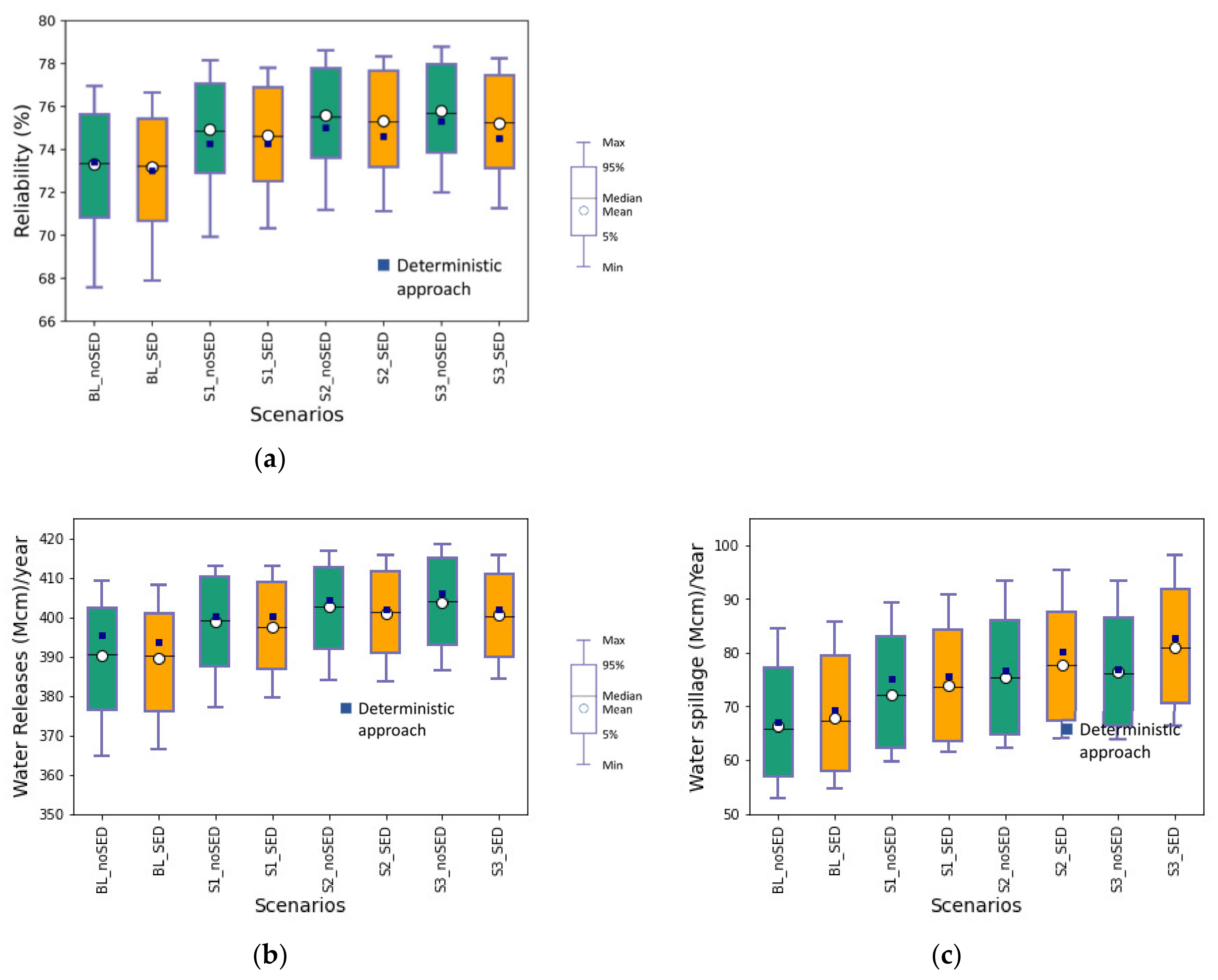
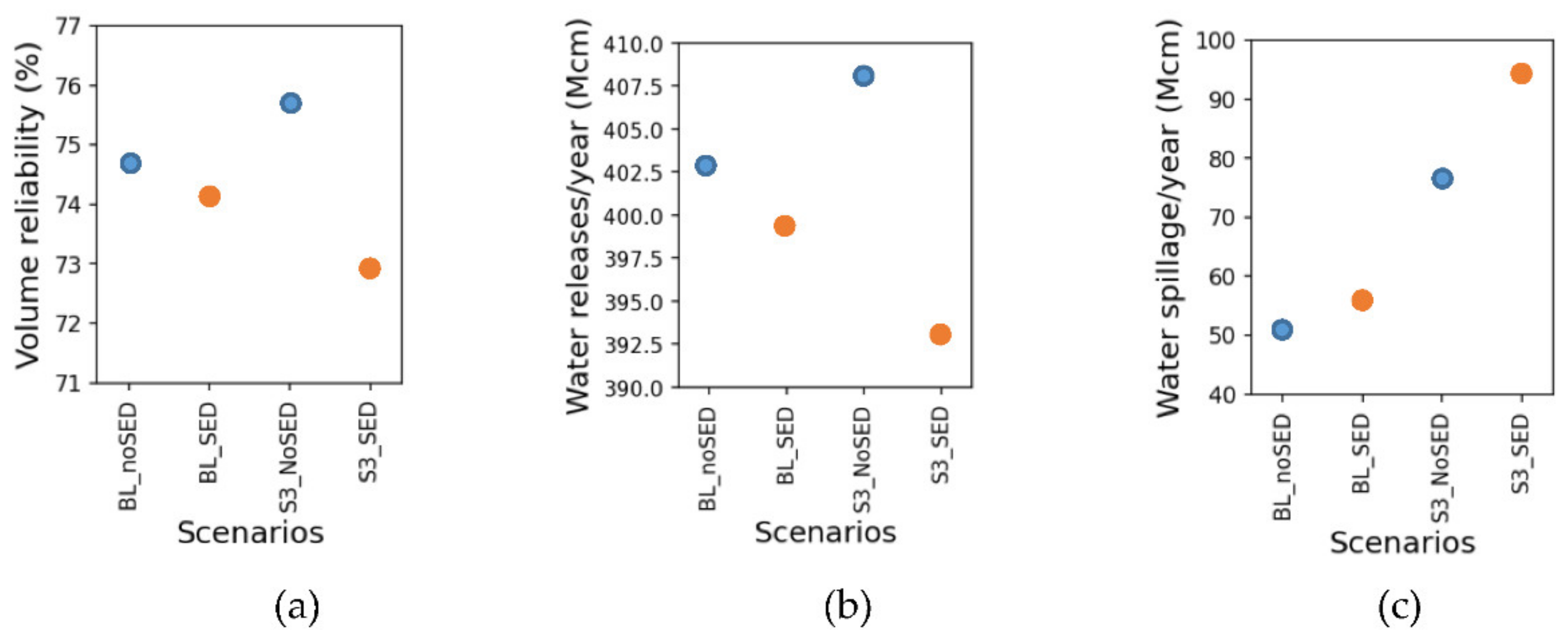
3.3. The Impact of Land-Use Changes on Performance Indicators of the Reservoir
4. Discussion
4.1. The Modelling Framework
4.2. Impact of the Change in Urban Areas and Conversion from Forest to Agricultural Areas on Performance Indicators
4.3. Impact of Spatial Distribution of Land-Uses
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ziaei, M.; Shui, L.T.; Goodarzi, E. Optimization and simulation modelling for operation of the Zayandeh Rud Reservoir. Water Int. 2012, 37, 305–318. [Google Scholar] [CrossRef]
- Pokhrel, B.K. Impact of land use change on flow and sediment yields in the Khokana Outlet of the Bagmati River, Kathmandu, Nepal. Hydrology 2018, 5, 22. [Google Scholar] [CrossRef]
- Shrestha, B.; Cochrane, T.A.; Caruso, B.S.; Arias, M.E. Land use change uncertainty impacts on streamflow and sediment projections in areas undergoing rapid development: A case study in the Mekong Basin. Land Degrad. Dev. 2018, 29, 835–848. [Google Scholar] [CrossRef]
- Goodarzi, E.; Ziaei, M.; Shokri, N. Reservoir operation management by optimization and stochastic simulation. J. Water Supply Res. Technol. 2013, 62, 138–154. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, H.; Chen, H.; Peng, D.; Liu, P.; Pang, B. A reservoir flood forecasting and control system for China. Hydrol. Sci. J. 2004, 49, 972. [Google Scholar] [CrossRef]
- Bieger, K.; Hörmann, G.; Fohrer, N. The impact of land use change in the Xiangxi Catchment (China) on water balance and sediment transport. Reg. Environ. Chang. 2015, 15, 485–498. [Google Scholar] [CrossRef]
- Abera, F.F.; Asfaw, D.H.; Engida, A.N.; Melesse, A.M. Optimal operation of hydropower reservoirs under climate change: The case of Tekeze reservoir, Eastern Nile. Water 2018, 10, 273. [Google Scholar] [CrossRef]
- Saddique, N.; Mahmood, T.; Bernhofer, C. Quantifying the impacts of land use/land cover change on the water balance in the afforested River Basin, Pakistan. Environ. Earth Sci. 2020, 79, 1–13. [Google Scholar] [CrossRef]
- Yalew, S.; Pilz, T.; Schweitzer, C.; Liersch, S.; Van Der Kwast, J.; Van Griensven, A.; Mul, M.L.; Dickens, C.; van der Zaag, P. Coupling land-use change and hydrologic models for quantification of catchment ecosystem services. Environ. Model. Softw. 2018, 109, 315–328. [Google Scholar] [CrossRef]
- Dwarakish, G.; Ganasri, B. Impact of land use change on hydrological systems: A review of current modeling approaches. Cogent Geosci. 2015, 1, 1115691. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, X.; Wang, H.; Yang, M. Simulated runoff and sediment yield responses to land-use change using the SWAT model in northeast China. Water 2019, 11, 915. [Google Scholar] [CrossRef]
- Choto, M.; Fetene, A. Impacts of land use/land cover change on stream flow and sediment yield of Gojeb watershed, Omo-Gibe basin, Ethiopia. Remote Sens. Appl. Soc. Environ. 2019, 14, 84–99. [Google Scholar] [CrossRef]
- Ehteram, M.; Singh, V.P.; Karami, H.; Hosseini, K.; Dianatikhah, M.; Hossain, M.; Ming Fai, C.; El-Shafie, A. Irrigation Management Based on Reservoir Operation with an Improved Weed Algorithm. Water 2018, 10, 1267. [Google Scholar] [CrossRef]
- Sheibani, H.; Alizadeh, H.; Shourian, M. Optimum design and operation of a reservoir and irrigation network considering uncertainty of hydrologic, agronomic and economic factors. Water Resour. Manag. 2019, 33, 863–879. [Google Scholar] [CrossRef]
- Anand, J.; Gosain, A.K.; Khosa, R. Optimisation of multipurpose reservoir operation by coupling Soil and Water Assessment Tool (SWAT) and genetic algorithm for optimal operating policy (Case Study: Ganga River Basin). Sustainability 2018, 10, 1660. [Google Scholar] [CrossRef]
- Ahmed, J.A.; Sarma, A.K. Genetic Algorithm for Optimal Operating Policy of a Multipurpose Reservoir. Water Resour. Manag. 2005, 19, 145–161. [Google Scholar] [CrossRef]
- Jothiprakash, V.; Shanthi, G. Single Reservoir Operating Policies Using Genetic Algorithm. Water Resour. Manag. 2006, 20, 917–929. [Google Scholar] [CrossRef]
- Nicklow, J.; Reed, P.; Savic, D.; Dessalegne, T.; Harrell, L.; Chan-Hilton, A.; Karamouz, M.; Minsker, B.; Ostfeld, A.; Singh, A.; et al. State of the Art for Genetic Algorithms and Beyond in Water Resources Planning and Management. J. Water Resour. Plan. Manag. 2010, 136, 412–432. [Google Scholar] [CrossRef]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Maier, H.R.; Guillaume, J.H.A.; van Delden, H.; Riddell, G.A.; Haasnoot, M.; Kwakkel, J.H. An uncertain future, deep uncertainty, scenarios, robustness and adaptation: How do they fit together? Environ. Model. Softw. 2016, 81, 154–164. [Google Scholar] [CrossRef]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; pp. 1–25. [Google Scholar] [CrossRef]
- Tukimat, N.N.A.; Harun, S. Optimization of Water Supply Reservoir in the Framework of Climate Variation. Int. J. Softw. Eng. Its Appl. 2014, 8, 361–378. [Google Scholar]
- Vucetic, D.; Simonovic, S.P. Water Resources Decision Making under Uncertainty; 0771429010; Department of Civil and Environmental Engineering, The University of Western Ontario: London, ON, Canada, 2011; p. 148. [Google Scholar]
- Singh, A.; Minsker, B.S. Uncertainty-based multiobjective optimization of groundwater remediation design. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Al-Harthy, M.H. Number of Development Wells: A Decision under Uncertainty. Eng. Econ. 2010, 55, 328–349. [Google Scholar] [CrossRef]
- Loucks, D.P.; van Beek, E. Water Resources Planning and Management: An Overview. In Water Resource Systems Planning and Management: An Introduction to Methods, Models, and Applications; Springer: Cham, Switzerland, 2017; pp. 1–624. [Google Scholar] [CrossRef]
- Palisade. Guide to Using@ RISK: Risk Analysis and Simulation Add-in for Microsoft Excel, 7th ed.; Version 7; Palisade: Ithaca, NY, USA, 2016. [Google Scholar]
- Ashraf, S.; Abbaspour, K.C.; Faramarzi, M.; Srinivasan, R.; Arnold, J.G. Modeling crop water productivity using a coupled SWAT–MODSIM model. Water 2017, 9, 157. [Google Scholar] [CrossRef]
- Goodarzi, E. Introduction to Risk and Uncertainty in Hydrosystem Engineering; Springer: Dordrecht, The Netherlands, 2013; Volume 22. [Google Scholar]
- Neitsch, S.L.; Williams, J.R.; Arnold, J.G.; Kiniry, J.R. Soil and Water Assessment Tool Theoretical Documentation—Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Arnold, J.; Allen, P.; Muttiah, R.; Bernhardt, G. Automated base flow separation and recession analysis techniques. Groundwater 1995, 33, 1010–1018. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT Calibration Uncertainty Program (SWAT-CUP)—A User Manual; Eawag: Zurich, Switzerland, 2013. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- ASABE. Guidelines for Calibrating, Validating, and Evaluating Hydrologic and Water Quality (H/WQ) Models; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2017. [Google Scholar]
- SWAT Group. 2020. Available online: https://groups.google.com/forum/#!forum/swat-cup (accessed on 15 May 2020).
- Holland, J.H. Adaptation in natural and artificial systems. In An Introductory Analysis with Application to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Bozorg-Haddad, O.; Mani, M.; Aboutalebi, M.; Loáiciga, H.A. Choosing an Optimization Method for Water Resources Problems Based on the Features of Their Solution Spaces. J. Irrig. Drain. Eng. 2018, 144, 04017061. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Optimization, Search and Machine Learning; Reading; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Jain, S.; Bhunya, P. Reliability, resilience and vulnerability of a multipurpose storage reservoir/Confiance, résilience et vulnérabilité d’un barrage multi-objectifs. Hydrol. Sci. J. 2008, 53, 434–447. [Google Scholar] [CrossRef]
- Earthdata Search. Greenbelt, MD: Earth Science Data and Information System (ESDIS) Project, Earth Science Projects Division (ESPD), Flight Projects Directorate, Goddard Space Flight Center (GSFC) National Aeronautics and Space Administration (NASA). Available online: https://search.earthdata.nasa.gov/ (accessed on 15 January 2019).
- FAO/UNESCO. Soil Map of the World. Available online: http://www.fao.org/soils-portal/data-hub/soil-maps-and-databases/faounesco-soil-map-of-the-world/en/ (accessed on 15 March 2018).
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Handbook of Plants. Available online: http://camnangcaytrong.com/ (accessed on 15 February 2019).
- Ngo, L. Assessment of Nui Coc Reservoir’s Deposition, Proposing Solutions to Protect and Sustainable Use. J. Water Resour. Environ. Eng. 2010, 31, 46–51. [Google Scholar]
- Brune, G.M. Trap efficiency of reservoirs. Eos Trans. Am. Geophys. Union 1953, 34, 407–418. [Google Scholar] [CrossRef]
- Winchell, M.; Srinivasan, R.; Di Luzio, M.; Arnold, J. ArcSWAT interface for SWAT2012—User’s Guide; Blackland Research Center, AgriLife Research: College Station, TX, USA, 2013. [Google Scholar]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Eastman, J.R. IDRISI Taiga Guide to GIS and Image Processing; Clark Labs Clark University: Worcester, MA, USA, 2009. [Google Scholar]
- Daac, O. MODIS and VIIRS Land Products Global Subsetting and Visualization Tool—Subset Obtained for MOD16A2 Product at 21.6N, 105.6W, Time Period: 1 January 2004 to 31 December 2013, and Subset Size: 100.25 × 100.25 km. Available online: https://lpdaac.usgs.gov/products/mod16a2v006/ (accessed on 15 February 2018).
- Thomopoulos, N.T. Essentials of Monte Carlo Simulation: Statistical Methods for Building Simulation Models; Springer: New York, NY, USA, 2012. [Google Scholar]
- Munthali, K.G.; Irvine, B.J.; Murayama, Y. Reservoir sedimentation and flood control: Using a geographical information system to estimate sediment yield of the Songwe river watershed in Malawi. Sustainability 2011, 3, 254–269. [Google Scholar] [CrossRef]
- Mescher, A. Reservoir Sedimentation and Water Supply Reliability; ASPEN 2 October 2020; ASPEN Environmental Group: Agoura Hills, CA, USA, 2020. [Google Scholar]
- Le Ngo, L.; Madsen, H.; Rosbjerg, D. Simulation and optimisation modelling approach for operation of the Hoa Binh reservoir, Vietnam. J. Hydrol. 2007, 336, 269–281. [Google Scholar] [CrossRef]
- Ausseil, A.; Dymond, J. Estimating the spatial distribution of sediment concentration in the Manawatu River, New Zealand, under different land-use scenarios. IAHS Publ. 2008, 325, 502. [Google Scholar]
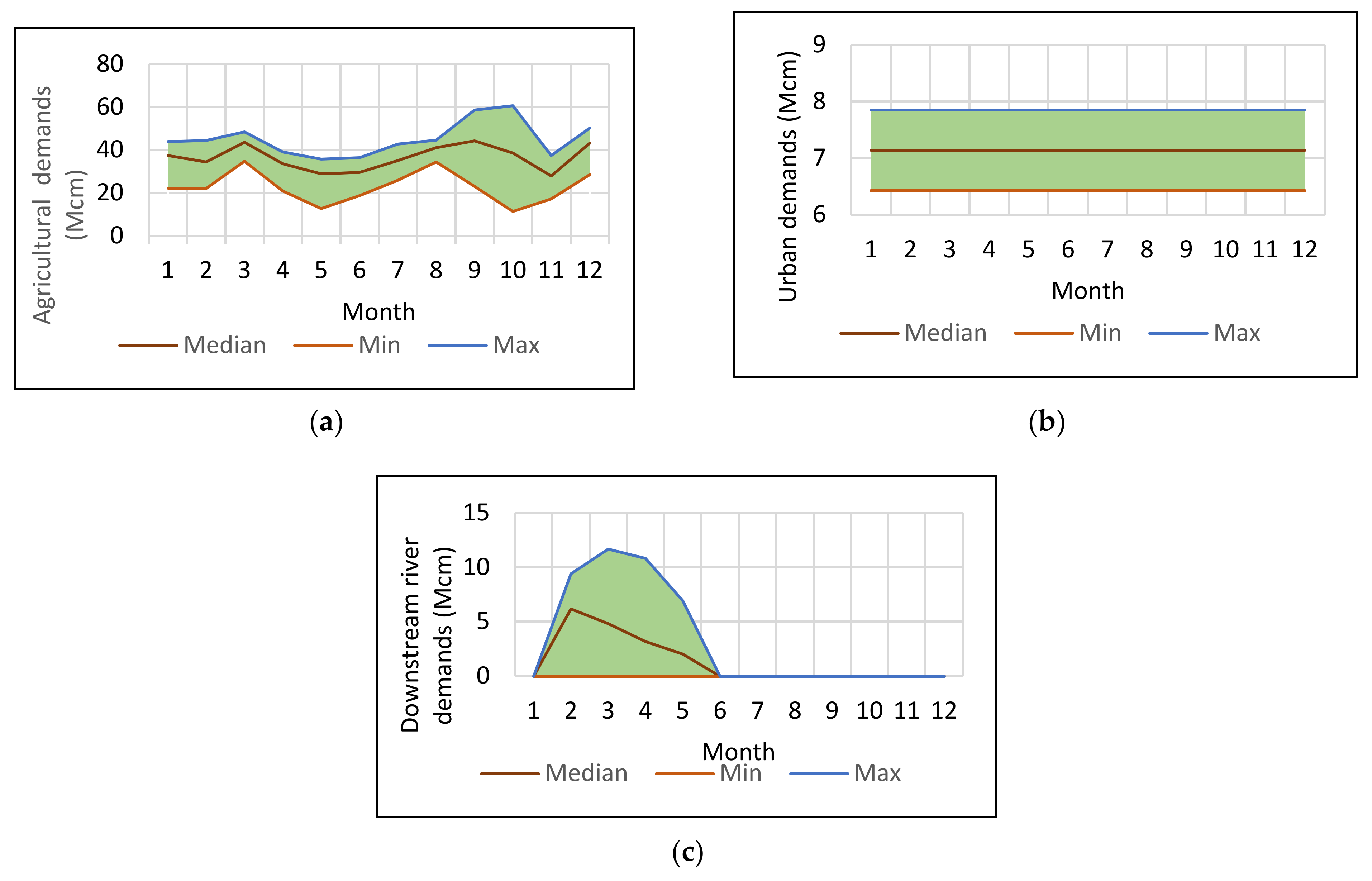
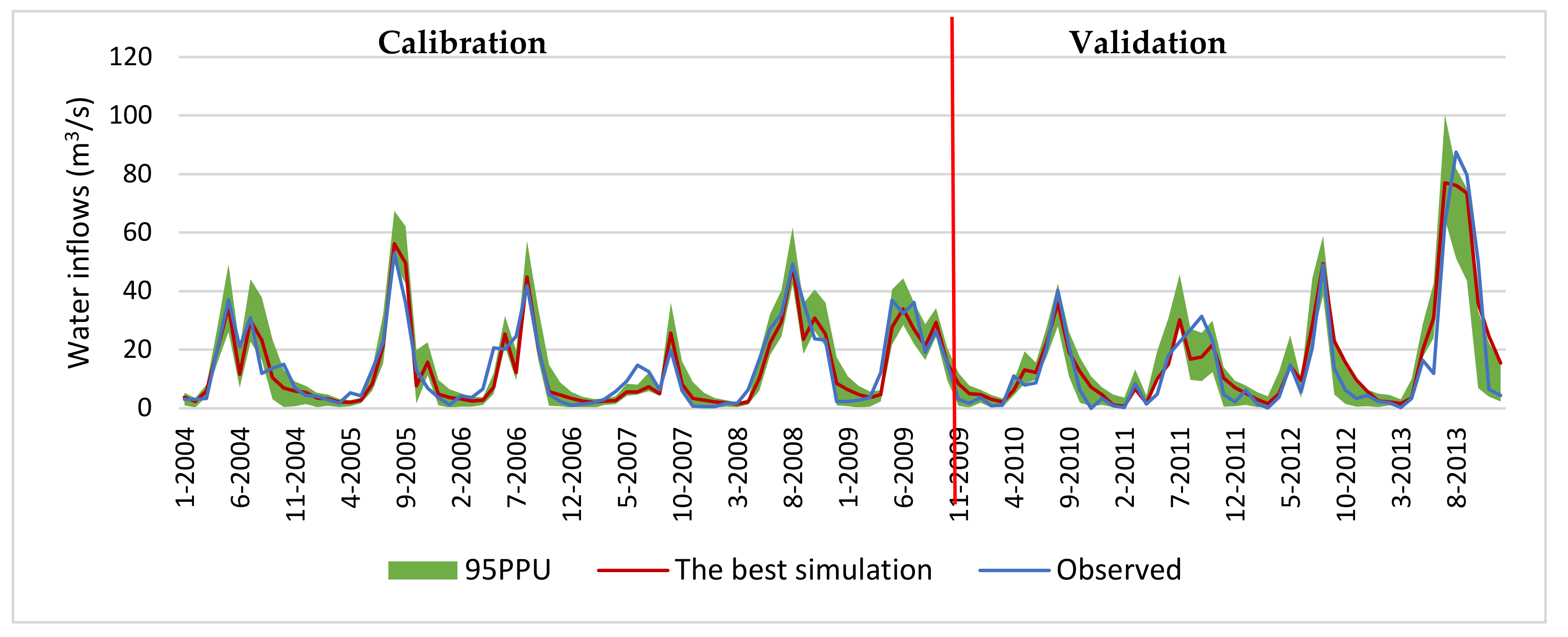
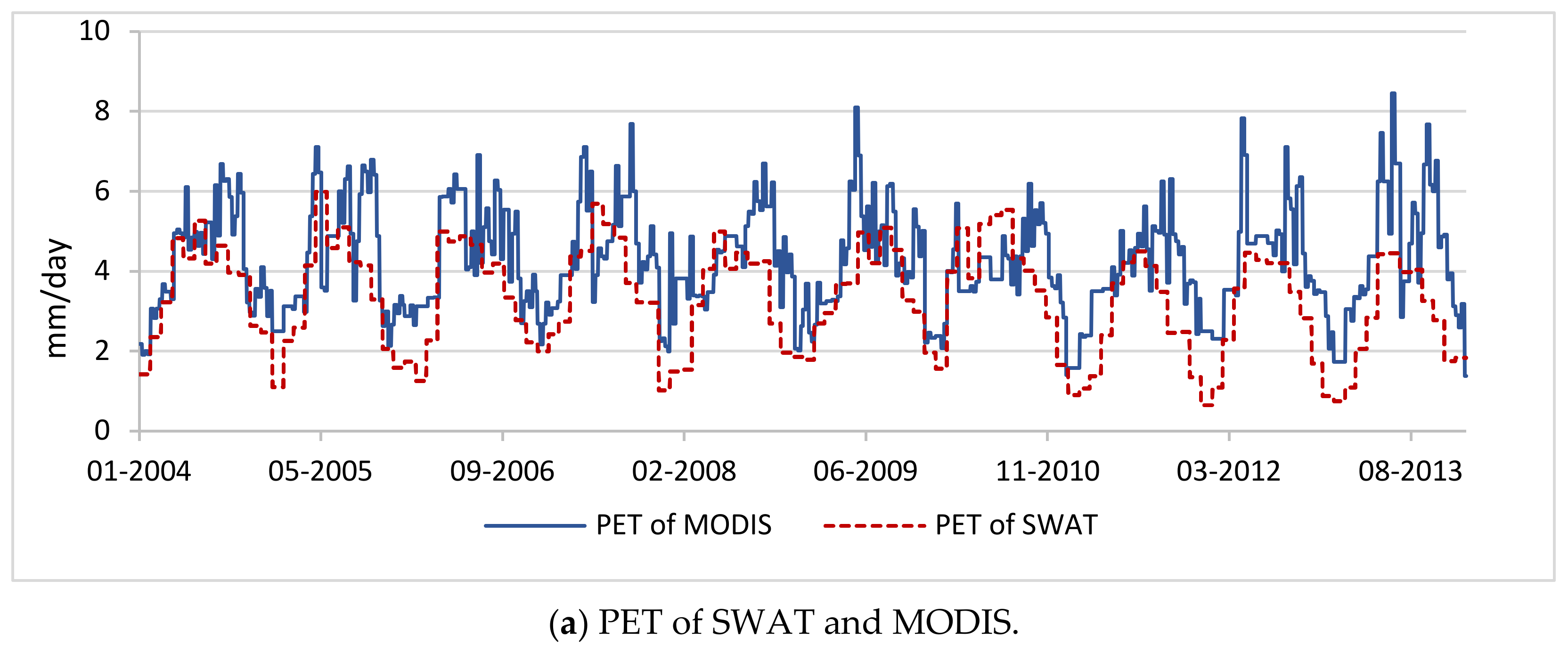
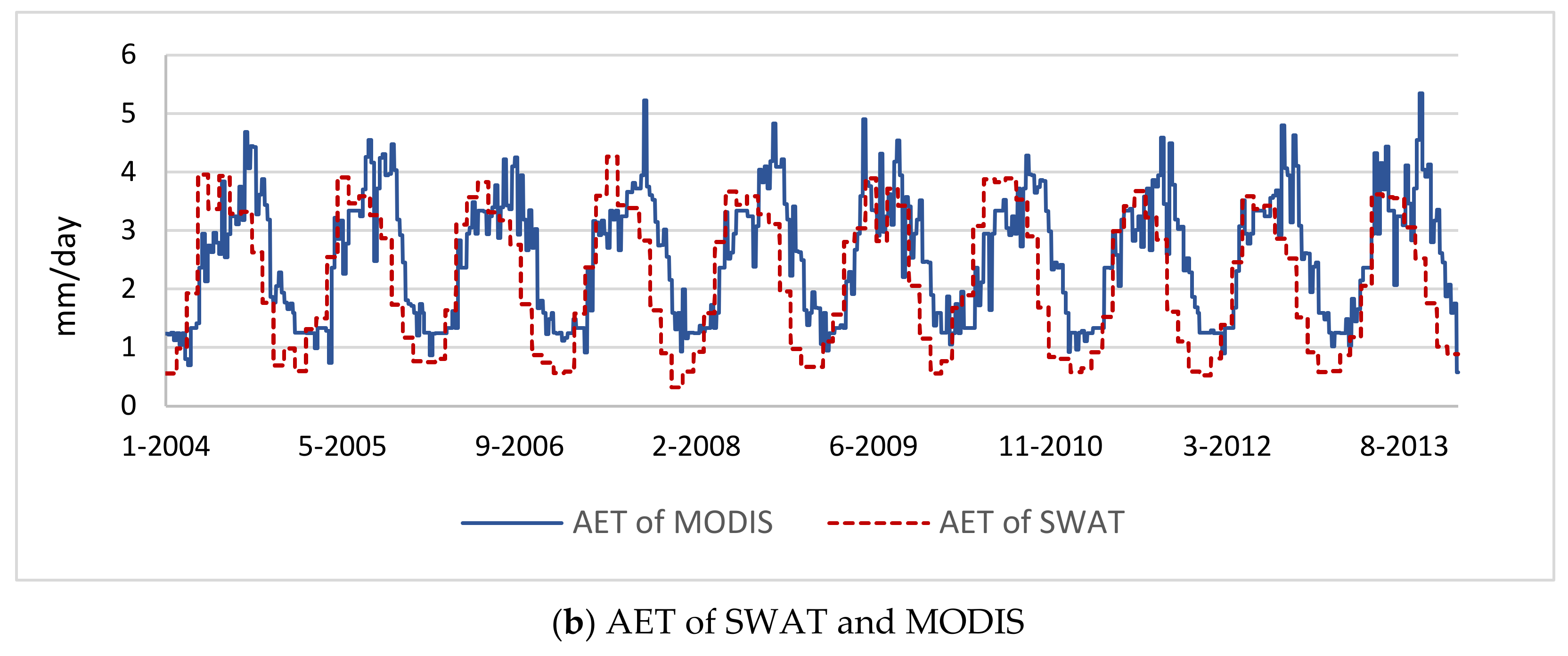


| Data | Duration | Source | Collection Month |
|---|---|---|---|
| Digital Elevation Model (DEM) (30 m × 30 m) | The Shuttle Radar Topography Mission database [43] | ||
| Land-use | 2004, 2014 | Thainguyen Department of Resources and Environment, 2018 | 2/2018 |
| Soil map and properties | FAO [44] | ||
| Rainfall | 2002–2013 | Vietbac Centre for Hydrology and Meteorology, 2018 | 2/2018 |
| Calculated inflow | 2004–2013 | Thainguyen Irrigation Management Company, 2018 | 2/2018 |
| Other climate data | 1979–2013 | Climate Forecast System Reanalysis [45] | |
| Growth phases of crops | Handbook of plantings [46] |
| Modelling Period | Land-Use Map | Evaluation Statistics for Model Uncertainty | The Best Simulation | |||
|---|---|---|---|---|---|---|
| P-Factor | R-Factor | NS | PBIAS | R2 | ||
| Calibration (2004–2010) | 2004 | 0.79 | 0.75 | 0.85 | 2.37% | 0.86 |
| Validation (2011–2013) | 2014 | 0.75 | 0.59 | 0.88 | −4.96% | 0.88 |
| Scenarios | Water Inflows (m3/s) | Sediment Inflows (Mcm/10 Year) | Water Inflows in Wet Seasons (m3/s) | Water Inflows in Dry Seasons (m3/s) |
|---|---|---|---|---|
| BL | 15.49 | 5.16 | 25.998 | 4.973 |
| S1 | 15.88 | 5.02 | 26.799 | 4.966 |
| S2 | 16.07 | 5.83 | 27.196 | 4.949 |
| S3 | 16.12 | 11.54 | 27.304 | 4.928 |
| n-Value | Range of Reliability (%) | Median Reliability (%) | Mean Reliability (%) | Computational Cost (Hours) |
|---|---|---|---|---|
| 50 | 73.7–78.6 | 75.7 | 75.7 | 14 |
| 100 | 72.9–78.6 | 75.6 | 75.8 | 28 |
| 180 | 72.0–78.8 | 75.7 | 75.8 | 51 |
| 300 | 72.1–78.9 | 75.7 | 75.8 | 85 |
| 500 | 72.1–79.4 | 75.8 | 75.7 | 141 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, A.; Cochrane, T.A.; Pahlow, M. A Framework to Assess the Reliability of a Multipurpose Reservoir under Uncertainty in Land Use. Water 2021, 13, 287. https://doi.org/10.3390/w13030287
Nguyen A, Cochrane TA, Pahlow M. A Framework to Assess the Reliability of a Multipurpose Reservoir under Uncertainty in Land Use. Water. 2021; 13(3):287. https://doi.org/10.3390/w13030287
Chicago/Turabian StyleNguyen, Anh, Thomas A. Cochrane, and Markus Pahlow. 2021. "A Framework to Assess the Reliability of a Multipurpose Reservoir under Uncertainty in Land Use" Water 13, no. 3: 287. https://doi.org/10.3390/w13030287
APA StyleNguyen, A., Cochrane, T. A., & Pahlow, M. (2021). A Framework to Assess the Reliability of a Multipurpose Reservoir under Uncertainty in Land Use. Water, 13(3), 287. https://doi.org/10.3390/w13030287







