Development of a Deep Learning Emulator for a Distributed Groundwater–Surface Water Model: ParFlow-ML
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Integrated Hydrologic Model, ParFlow
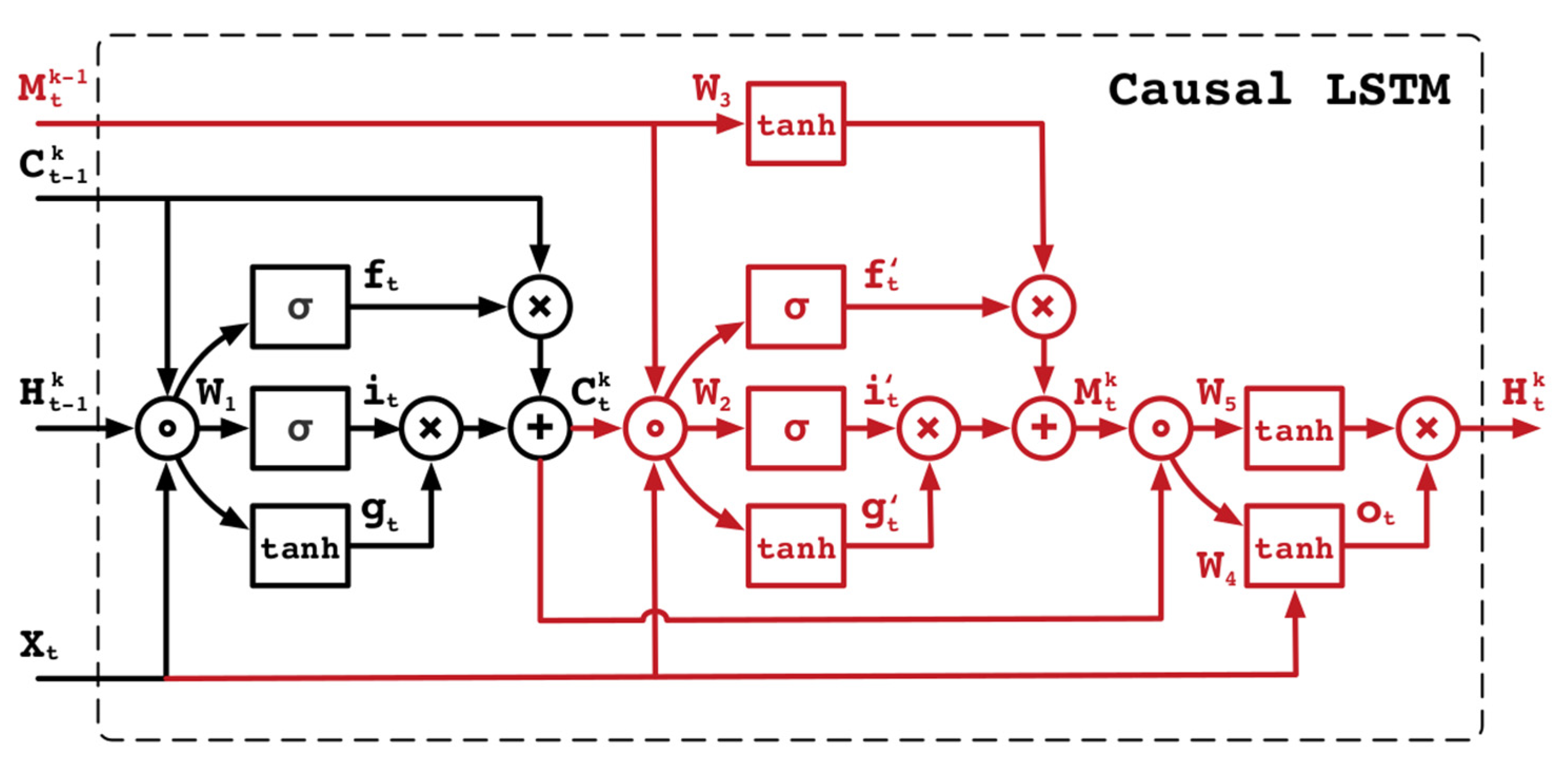
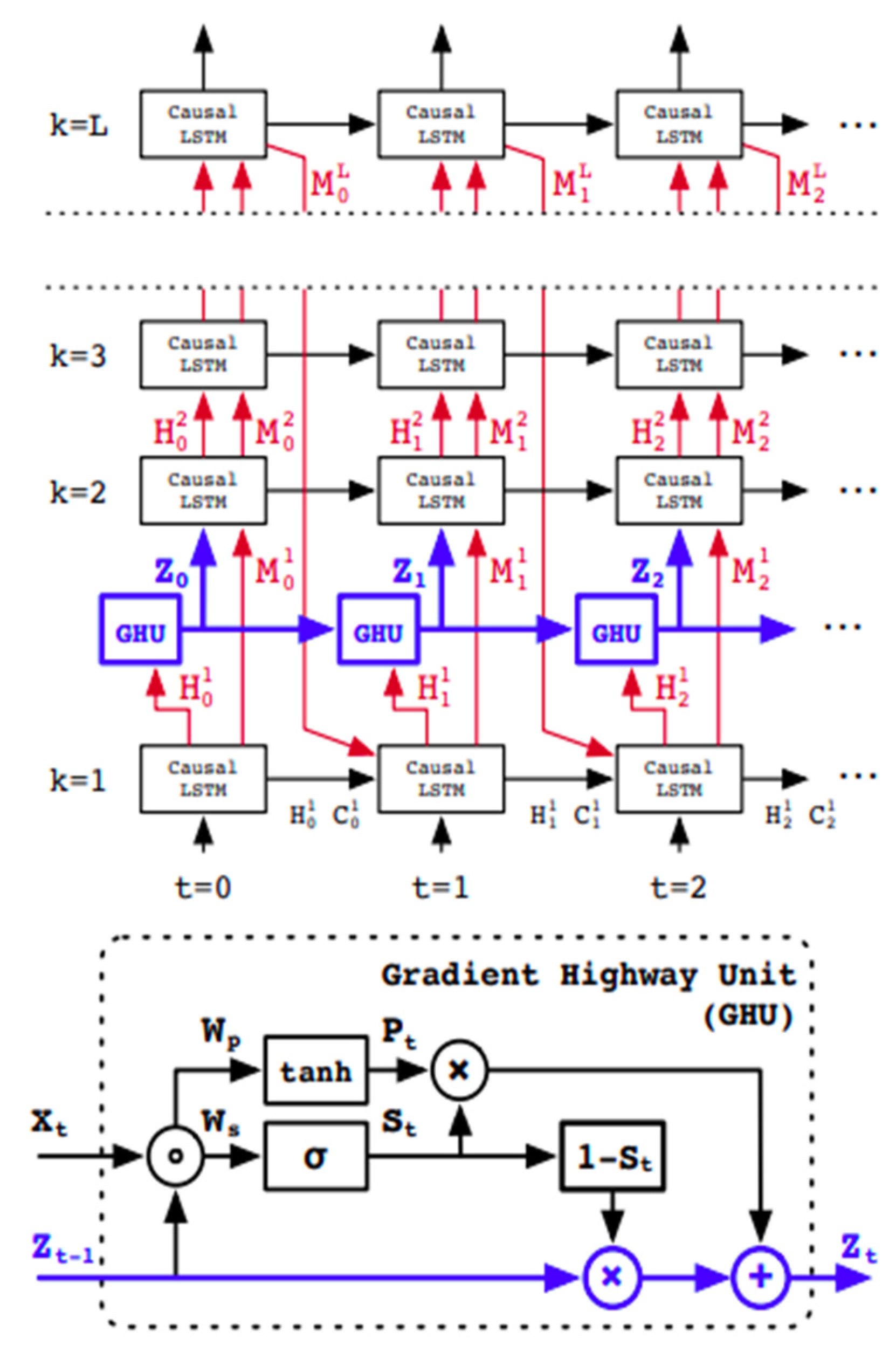
2.2. The Emulator Version of ParFlow, ParFlow-ML
2.3. Experiment Design
2.3.1. Study Areas
2.3.2. The Emulator Setup
2.3.3. Model Setup
2.3.4. Rainfall–Runoff Scenarios
2.4. Training Process
2.5. Performance Metrics
3. Results
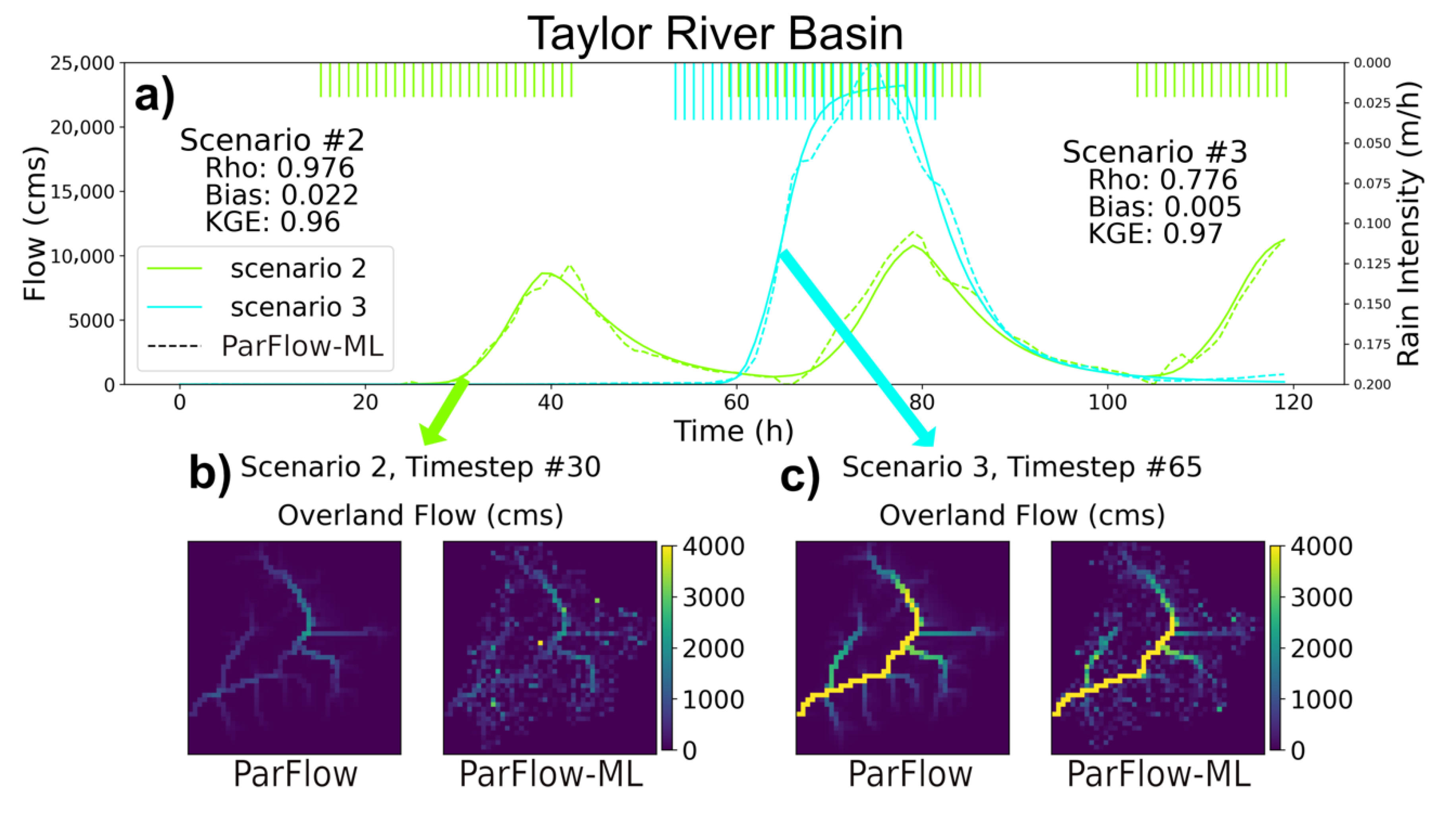
3.1. Streamflow Evaluation
3.2. Water Table Depth (WTD) Evaluation
3.3. Total Water Storage Evaluation
3.4. Execution Time
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wood, E.F.; Roundy, J.K.; Troy, T.J.; van Beek, L.P.H.; Bierkens, M.F.P.; Blyth, E.; de Roo, A.; Döll, P.; Ek, M.; Famiglietti, J.; et al. Hyperresolution global land surface modeling: Meeting a grand challenge for monitoring Earth’s terrestrial water. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Bierkens, M.F.P.; Bell, V.A.; Burek, P.; Chaney, N.; Condon, L.E.; David, C.H.; de Roo, A.; Döll, P.; Drost, N.; Famiglietti, J.S.; et al. Hyper-resolution global hydrological modelling: What is next?: “Everywhere and locally relevant”. Hydrol. Process. 2015, 29, 310–320. [Google Scholar] [CrossRef]
- Burstedde, C.; Fonseca, J.A.; Kollet, S. Enhancing speed and scalability of the ParFlow simulation code. Comput. Geosci. 2018, 22, 347–361. [Google Scholar] [CrossRef] [Green Version]
- Kollet, S.J.; Maxwell, R.M.; Woodward, C.S.; Smith, S.; Vanderborght, J.; Vereecken, H.; Simmer, C. Proof of concept of regional scale hydrologic simulations at hydrologic resolution utilizing massively parallel computer resources. Water Resour. Res. 2010, 46, 4201. [Google Scholar] [CrossRef]
- Hokkanen, J.; Kollet, S.; Kraus, J.; Herten, A.; Hrywniak, M.; Pleiter, D. Leveraging HPC accelerator architectures with modern techniques—Hydrologic modeling on GPUs with ParFlow. Comput. Geosci. 2021, 25, 1579–1590. [Google Scholar] [CrossRef]
- Le, P.V.V.; Kumar, P.; Valocchi, A.J.; Dang, H.V. GPU-based high-performance computing for integrated surface-sub-surface flow modeling. Environ. Model. Softw. 2015, 73, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Gentine, P.; Pritchard, M.; Rasp, S.; Reinaudi, G.; Yacalis, G. Could Machine Learning Break the Convection Parameterization Deadlock? Geophys. Res. Lett. 2018, 45, 5742–5751. [Google Scholar] [CrossRef]
- Rasp, S.; Pritchard, M.S.; Gentine, P. Deep learning to represent subgrid processes in climate models. Proc. Natl. Acad. Sci. USA 2018, 115, 9684–9689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zanna, L.; Brankart, J.M.; Huber, M.; Leroux, S.; Penduff, T.; Williams, P.D. Uncertainty and scale interactions in ocean ensembles: From seasonal forecasts to multidecadal climate predictions. Q. J. R. Meteorol. Soc. 2019, 145, 160–175. [Google Scholar] [CrossRef] [Green Version]
- Hsu, K.-L.; Gupta, H.V.; Sorooshian, S. Artificial Neural Network Modeling of the Rainfall-Runoff Process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gupta, H.V.; Gao, X.; Sorooshian, S.; Imam, B. Self-organizing linear output map (SOLO): An artificial neural network suitable for hydrologic modeling and analysis. Water Resour. Res. 2002, 38, 38-1–38-17. [Google Scholar] [CrossRef] [Green Version]
- Tao, Y.; Gao, X.; Hsu, K.; Sorooshian, S.; Ihler, A. A deep neural network modeling framework to reduce bias in satellite precipitation products. J. Hydrometeorol. 2016, 17, 931–945. [Google Scholar] [CrossRef]
- Tao, Y.; Gao, X.; Ihler, A.; Sorooshian, S.; Hsu, K. Precipitation identification with bispectral satellite information using deep learning approaches. J. Hydrometeorol. 2017, 18, 1271–1283. [Google Scholar] [CrossRef]
- Wang, C.; Tang, G.; Gentine, P. PrecipGAN: Merging Microwave and Infrared Data for Satellite Precipitation Estimation Using Generative Adversarial Network. Geophys. Res. Lett. 2021, 48, e2020GL092032. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C. Full-flow-regime storage-streamflow correlation patterns provide insights into hydrologic functioning over the continental US. Water Resour. Res. 2017, 53, 8064–8083. [Google Scholar] [CrossRef]
- Feng, D.; Fang, K.; Shen, C. Enhancing Streamflow Forecast and Extracting Insights Using Long-Short Term Memory Networks With Data Integration at Continental Scales. Water Resour. Res. 2020, 56, e2019WR026793. [Google Scholar] [CrossRef]
- Ha, S.; Liu, D.; Mu, L. Prediction of Yangtze River streamflow based on deep learning neural network with El Niño–Southern Oscillation. Sci. Rep. 2021, 11, 11738. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward Improved Predictions in Ungauged Basins: Exploiting the Power of Machine Learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef] [Green Version]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) neural network for flood forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef] [Green Version]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Afzaal, H.; Farooque, A.A.; Abbas, F.; Acharya, B.; Esau, T. Groundwater estimation from major physical hydrology components using artificial neural networks and deep learning. Water 2020, 12, 5. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Gao, L.; Crosbie, R.S.; Zhang, N.; Fu, G.; Doble, R. Groundwater recharge prediction using linear regression, multi-layer perception network, and deep learning. Water 2019, 11, 1879. [Google Scholar] [CrossRef] [Green Version]
- Lähivaara, T.; Malehmir, A.; Pasanen, A.; Kärkkäinen, L.; Huttunen, J.M.J.; Hesthaven, J.S. Estimation of groundwater storage from seismic data using deep learning. Geophys. Prospect. 2019, 67, 2115–2126. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Montzka, C.; Bayat, B.; Kollet, S. Using Long Short-Term Memory networks to connect water table depth anomalies to precipitation anomalies over Europe. Hydrol. Earth Syst. Sci. 2021, 25, 3555–3575. [Google Scholar] [CrossRef]
- Malakar, P.; Mukherjee, A.; Bhanja, S.N.; Ray, R.K.; Sarkar, S.; Zahid, A. Machine-learning-based regional-scale groundwater level prediction using GRACE. Hydrogeol. J. 2021, 29, 1027–1042. [Google Scholar] [CrossRef]
- Su, Y.; Sen, N.C.F.; Li, W.C.; Lee, I.H.; Lin, C.P. Applying deep learning algorithms to enhance simulations of large-scale groundwater flow in IoTs. Appl. Soft Comput. J. 2020, 92, 106298. [Google Scholar] [CrossRef]
- Pan, B.; Hsu, K.; AghaKouchak, A.; Sorooshian, S. Improving Precipitation Estimation Using Convolutional Neural Network. Water Resour. Res. 2019, 55, 2301–2321. [Google Scholar] [CrossRef] [Green Version]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A.R. DeepSD: Generating high resolution climate change projections through single image super-resolution. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1663–1672. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 28th International Conference on Neural Information Processing Systems, NIPS’15, Montreal, QC, Canada, 7–12 December 2015; Volume 1, pp. 802–810. [Google Scholar]
- Miao, Q.; Pan, B.; Wang, H.; Hsu, K.; Sorooshian, S. Improving monsoon precipitation prediction using combined convolutional and long short term memory neural network. Water 2019, 11, 977. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Yu, P.S. PredRNN++: Towards a Resolution of the Deep-in-Time Dilemma in Spatiotemporal Predictive Learning. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholm, Sweden, 15 July 2018; Volume 11, pp. 8122–8131. [Google Scholar]
- Wang, Y.; Wu, H.; Zhang, J.; Gao, Z.; Wang, J.; Yu, P.S.; Long, M. PredRNN: A Recurrent Neural Network for Spatiotemporal Predictive Learning. arXiv 2021, arXiv:2103.09504. [Google Scholar]
- Kuffour, B.N.O.; Engdahl, N.B.; Woodward, C.S.; Condon, L.E.; Kollet, S.; Maxwell, R.M. Simulating Coupled Surface-Subsurface Flows with ParFlow v3.5.0: Capabilities, Applications, and Ongoing Development of an Open-Source, Massively Parallel, Integrated Hydrologic Model. Geosci. Model Dev. 2020, 13, 1373–1397. [Google Scholar] [CrossRef] [Green Version]
- Ashby, S.F.; Falgout, R.D. A Parallel Multigrid Preconditioned Conjugate Gradient Algorithm for Groundwater Flow Simulations. Nucl. Sci. Eng. 1996, 124, 145–159. [Google Scholar] [CrossRef]
- Jones, J.E.; Woodward, C.S. Newton-Krylov-Multigrid Solvers for Large-Scale, Highly Heterogeneous, Variably Saturated Flow Problems. Adv. Water Resour. 2001, 24, 763–774. [Google Scholar] [CrossRef] [Green Version]
- Kollet, S.J.; Maxwell, R.M. Integrated Surface-Groundwater Flow Modeling: A Free-Surface Overland Flow Boundary Condition in a Parallel Groundwater Flow Model. Adv. Water Resour. 2006, 29, 945–958. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, R.M. A Terrain-Following Grid Transform and Preconditioner for Parallel, Large-Scale, Integrated Hydrologic Modeling. Adv. Water Resour. 2013, 53, 109–117. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Condon, L.E.; Kollet, S.J. A High-Resolution Simulation of Groundwater and Surface Water over Most of the Continental US with the Integrated Hydrologic Model ParFlow V3. Geosci. Model Dev. 2015, 8, 923–937. [Google Scholar] [CrossRef] [Green Version]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training Very Deep Networks. In NIPS’15, Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Neural Information Processing Systems Foundation: Montreal, QC, Canada, 2015; Volume 2, pp. 2377–2385. [Google Scholar]
- Condon, L.E.; Maxwell, R.M. Modified Priority Flood and Global Slope Enforcement Algorithm for Topographic Processing in Physically Based Hydrologic Modeling Applications. Comput. Geosci. 2019, 126, 73–83. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J. Database-Related Accuracy and Uncertainty of Pedotransfer Functions. Soil Sci. 1998, 163, 765–779. [Google Scholar] [CrossRef]
- Gleeson, T.; Smith, L.; Moosdorf, N.; Hartmann, J.; Dürr, H.H.; Manning, A.H.; van Beek, L.P.H.; Jellinek, A.M. Mapping Permeability over the Surface of the Earth. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, R.M.; Condon, L.E. Connections between Groundwater Flow and Transpiration Partitioning. Science 2016, 353, 377–380. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff Conditions in the Upper Danube Basin under an Ensemble of Climate Change Scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Mehran, A. Extended Contingency Table: Performance Metrics for Satellite Observations and Climate Model Simulations. Water Resour. Res. 2013, 49, 7144–7149. [Google Scholar] [CrossRef] [Green Version]
- Beucler, T.; Pritchard, M.; Rasp, S.; Ott, J.; Baldi, P.; Gentine, P. Enforcing Analytic Constraints in Neural Networks Emulating Physical Systems. Phys. Rev. Lett. 2021, 126, 098302. [Google Scholar] [CrossRef] [PubMed]

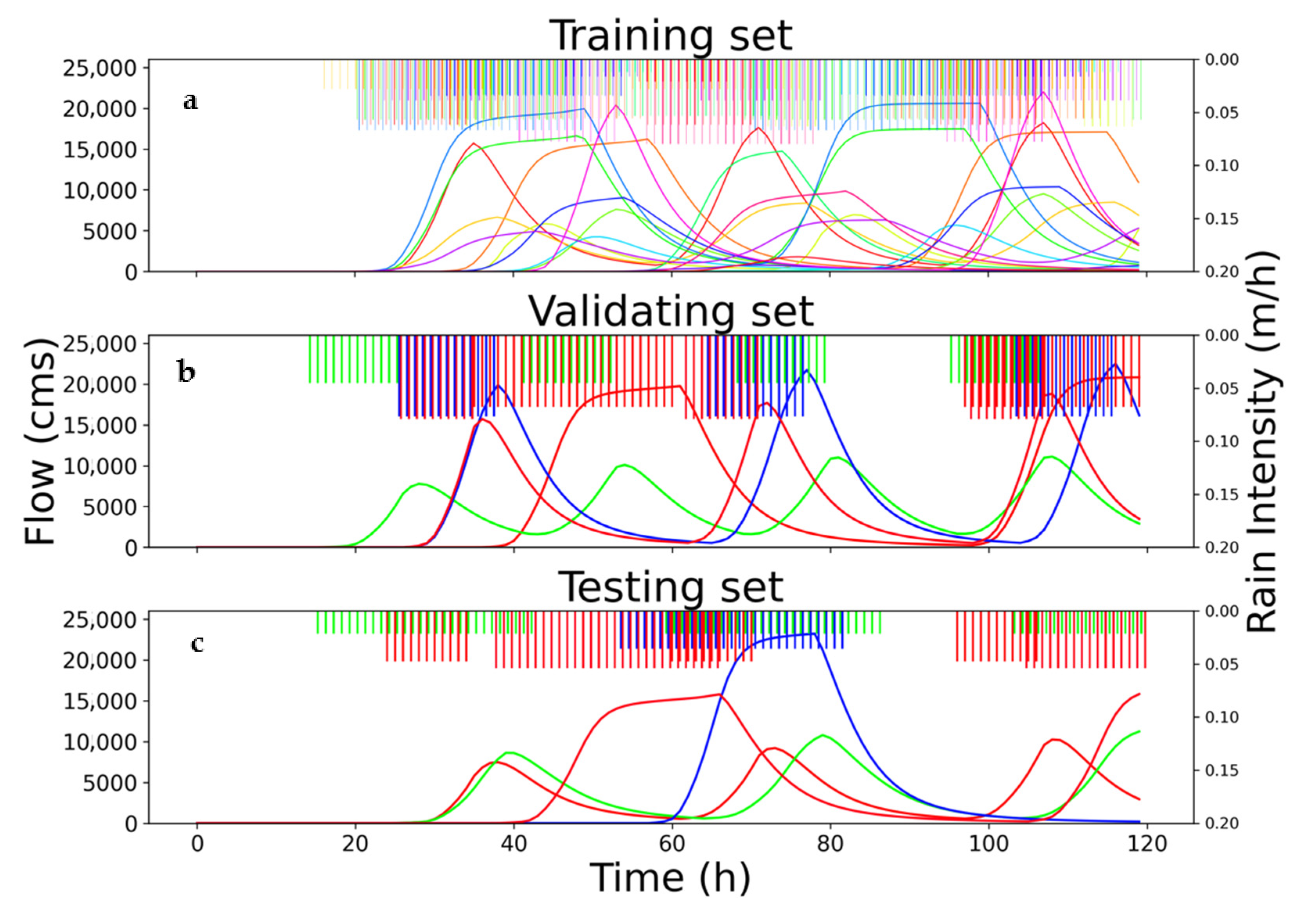

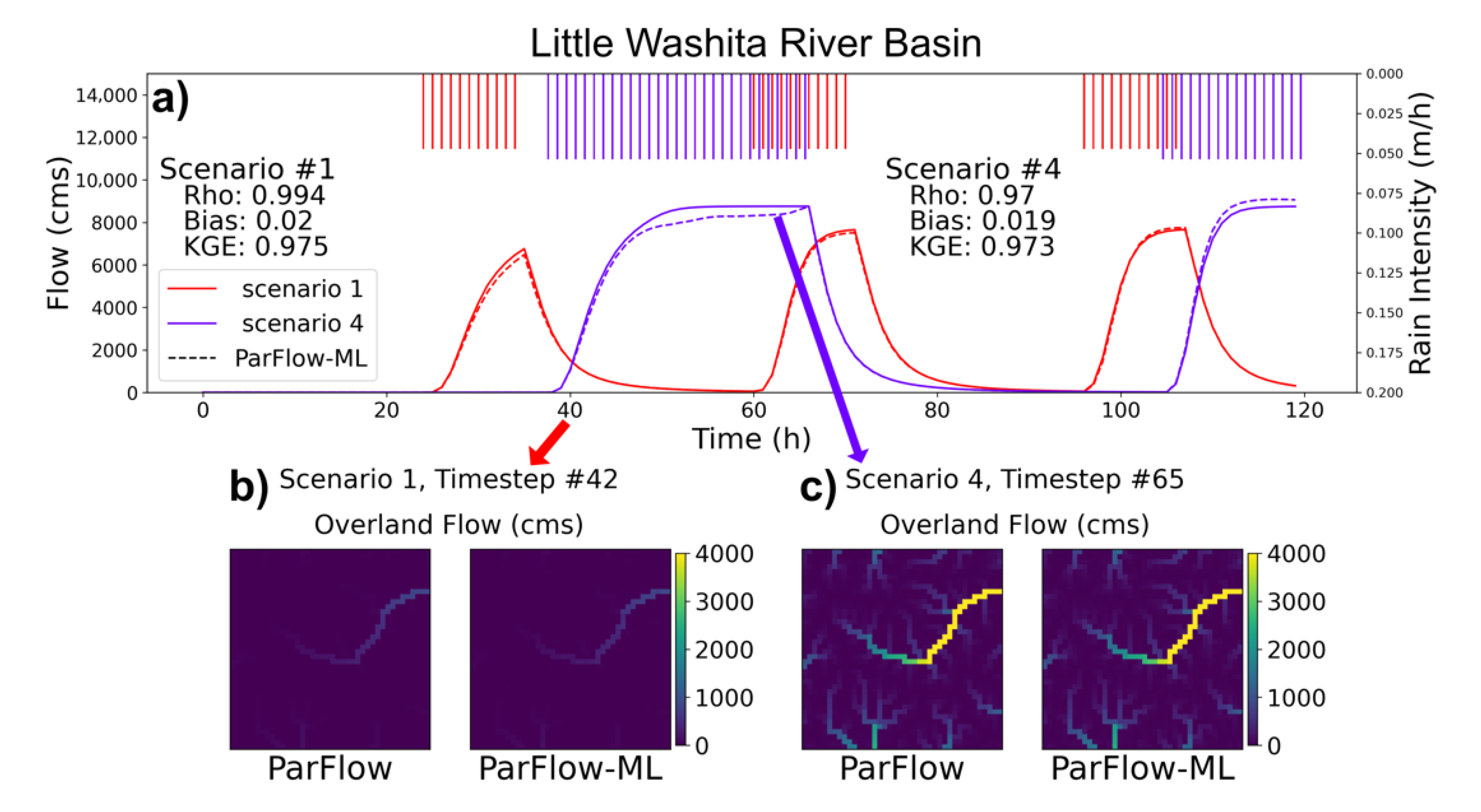

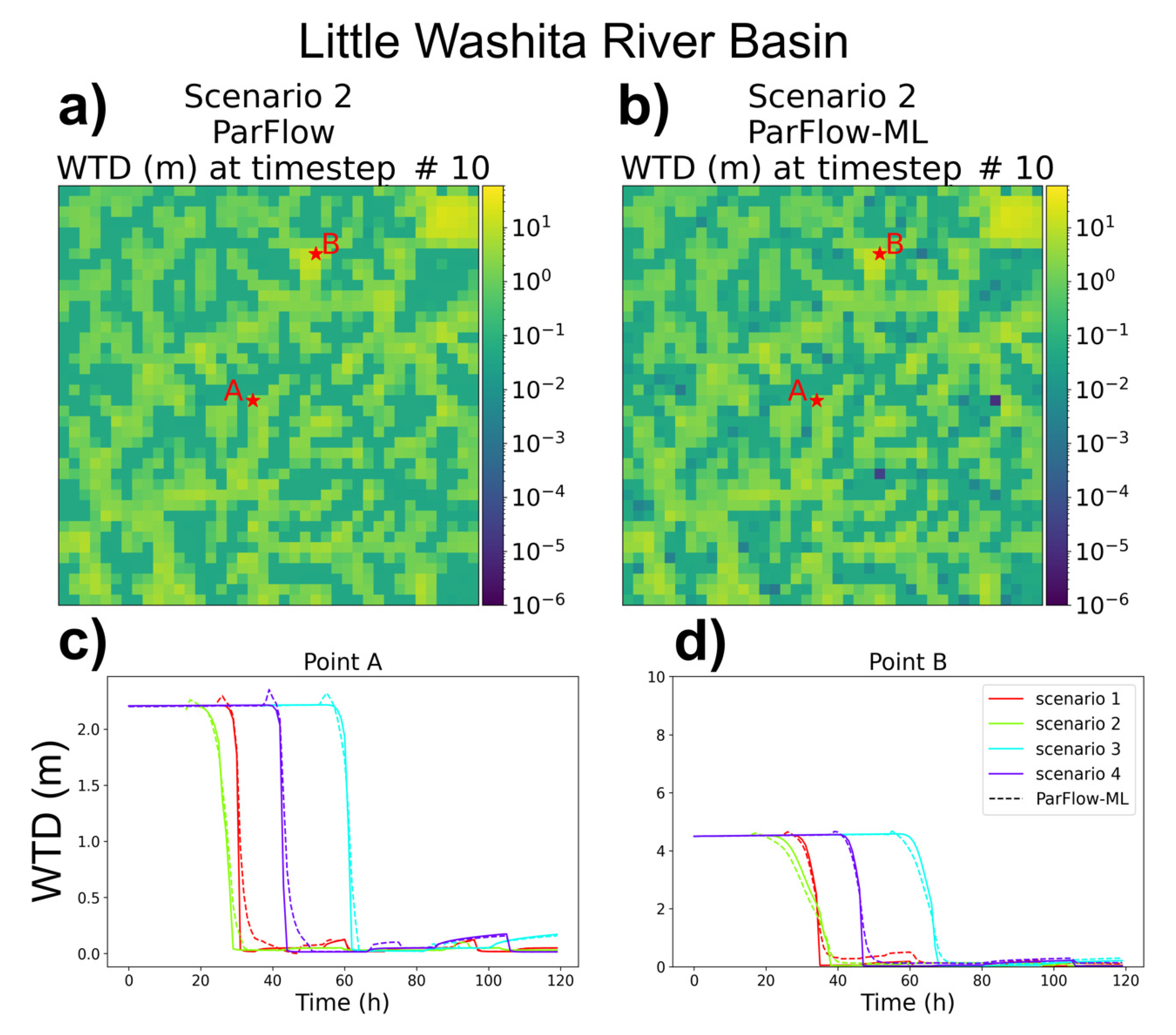

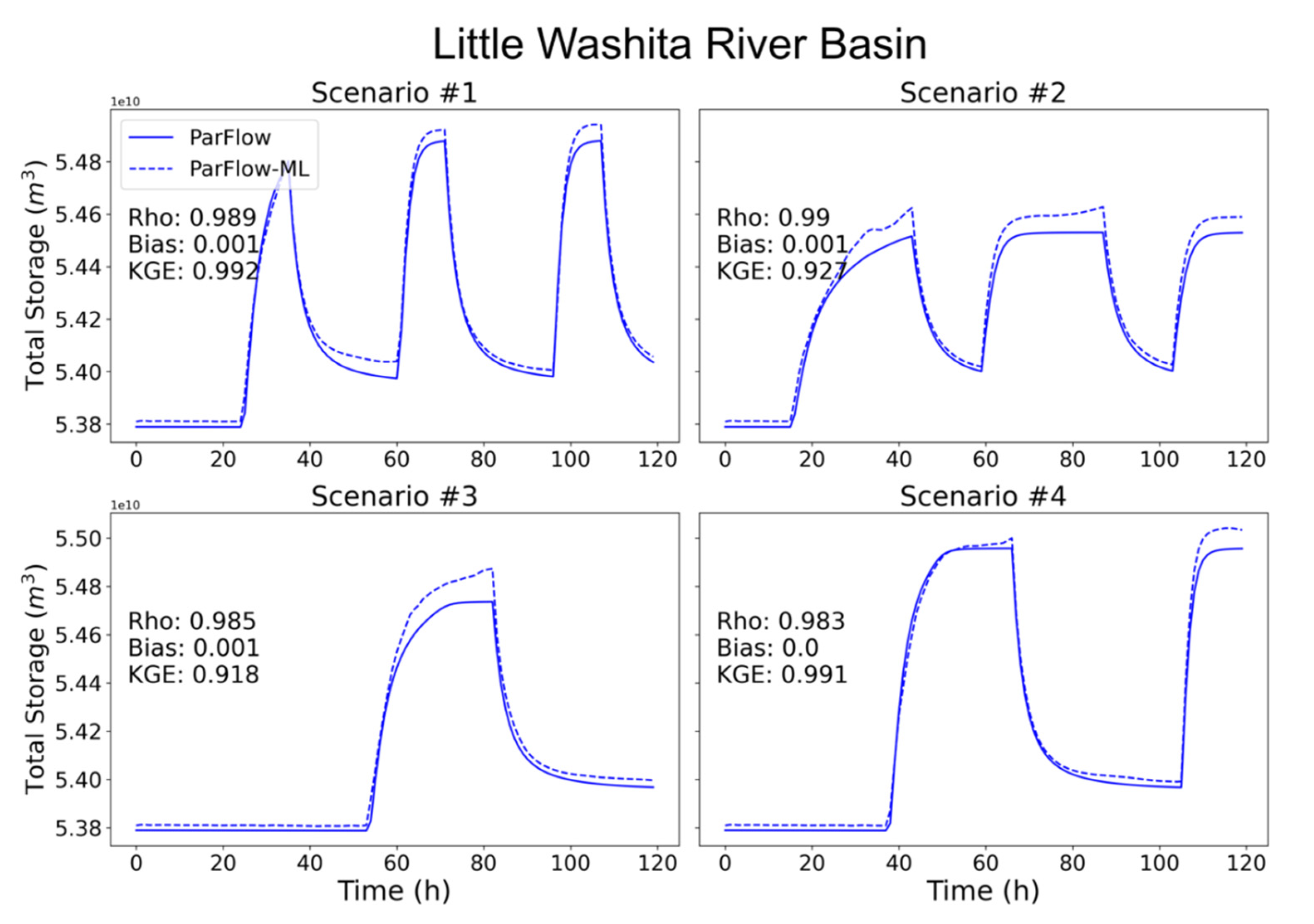

| Scenarios | Rain Intensity (m/h) | Rain Length (h) | Recession Length (h) |
|---|---|---|---|
| 1 | 0.0619 | 14 | 22 |
| 2 | 0.0557 | 28 | 30 |
| 3 | 0.0283 | 22 | 17 |
| 4 | 0.0631 | 7 | 33 |
| 5 | 0.0334 | 18 | 36 |
| 6 | 0.0569 | 28 | 21 |
| 7 | 0.0532 | 21 | 54 |
| 8 | 0.0119 | 7 | 52 |
| 9 | 0.0331 | 12 | 35 |
| 10 | 0.0668 | 29 | 21 |
| 11 | 0.0344 | 25 | 30 |
| 12 | 0.0161 | 10 | 47 |
| 13 | 0.0389 | 16 | 24 |
| 14 | 0.0775 | 13 | 41 |
| 15 | 0.0797 | 22 | 57 |
| 16 | 0.0213 | 12 | 56 |
| 17 | 0.0677 | 26 | 36 |
| 18 | 0.0451 | 12 | 15 |
| 19 | 0.0765 | 13 | 26 |
| 20 | 0.0792 | 10 | 26 |
| 21 | 0.0474 | 11 | 25 |
| 22 | 0.0215 | 28 | 16 |
| 23 | 0.0357 | 29 | 54 |
| 24 | 0.0539 | 29 | 38 |
| Testing Scenarios | KGE | Relative Bias | Spearman’s Rho | |||
|---|---|---|---|---|---|---|
| Taylor | LW | Taylor | LW | Taylor | LW | |
| 21 | 0.747 | 0.975 | 0.177 | 0.020 | 0.947 | 0.994 |
| 22 | 0.960 | 0.882 | 0.022 | 0.082 | 0.976 | 0.992 |
| 23 | 0.970 | 0.854 | 0.005 | 0.103 | 0.776 | 0.872 |
| 24 | 0.787 | 0.973 | 0.135 | 0.019 | 0.937 | 0.970 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, H.; Leonarduzzi, E.; De la Fuente, L.; Hull, R.B.; Bansal, V.; Chennault, C.; Gentine, P.; Melchior, P.; Condon, L.E.; Maxwell, R.M. Development of a Deep Learning Emulator for a Distributed Groundwater–Surface Water Model: ParFlow-ML. Water 2021, 13, 3393. https://doi.org/10.3390/w13233393
Tran H, Leonarduzzi E, De la Fuente L, Hull RB, Bansal V, Chennault C, Gentine P, Melchior P, Condon LE, Maxwell RM. Development of a Deep Learning Emulator for a Distributed Groundwater–Surface Water Model: ParFlow-ML. Water. 2021; 13(23):3393. https://doi.org/10.3390/w13233393
Chicago/Turabian StyleTran, Hoang, Elena Leonarduzzi, Luis De la Fuente, Robert Bruce Hull, Vineet Bansal, Calla Chennault, Pierre Gentine, Peter Melchior, Laura E. Condon, and Reed M. Maxwell. 2021. "Development of a Deep Learning Emulator for a Distributed Groundwater–Surface Water Model: ParFlow-ML" Water 13, no. 23: 3393. https://doi.org/10.3390/w13233393
APA StyleTran, H., Leonarduzzi, E., De la Fuente, L., Hull, R. B., Bansal, V., Chennault, C., Gentine, P., Melchior, P., Condon, L. E., & Maxwell, R. M. (2021). Development of a Deep Learning Emulator for a Distributed Groundwater–Surface Water Model: ParFlow-ML. Water, 13(23), 3393. https://doi.org/10.3390/w13233393







