Improving Drought Modeling Using Hybrid Random Vector Functional Link Methods
Abstract
:1. Introduction
2. Materials and Methods
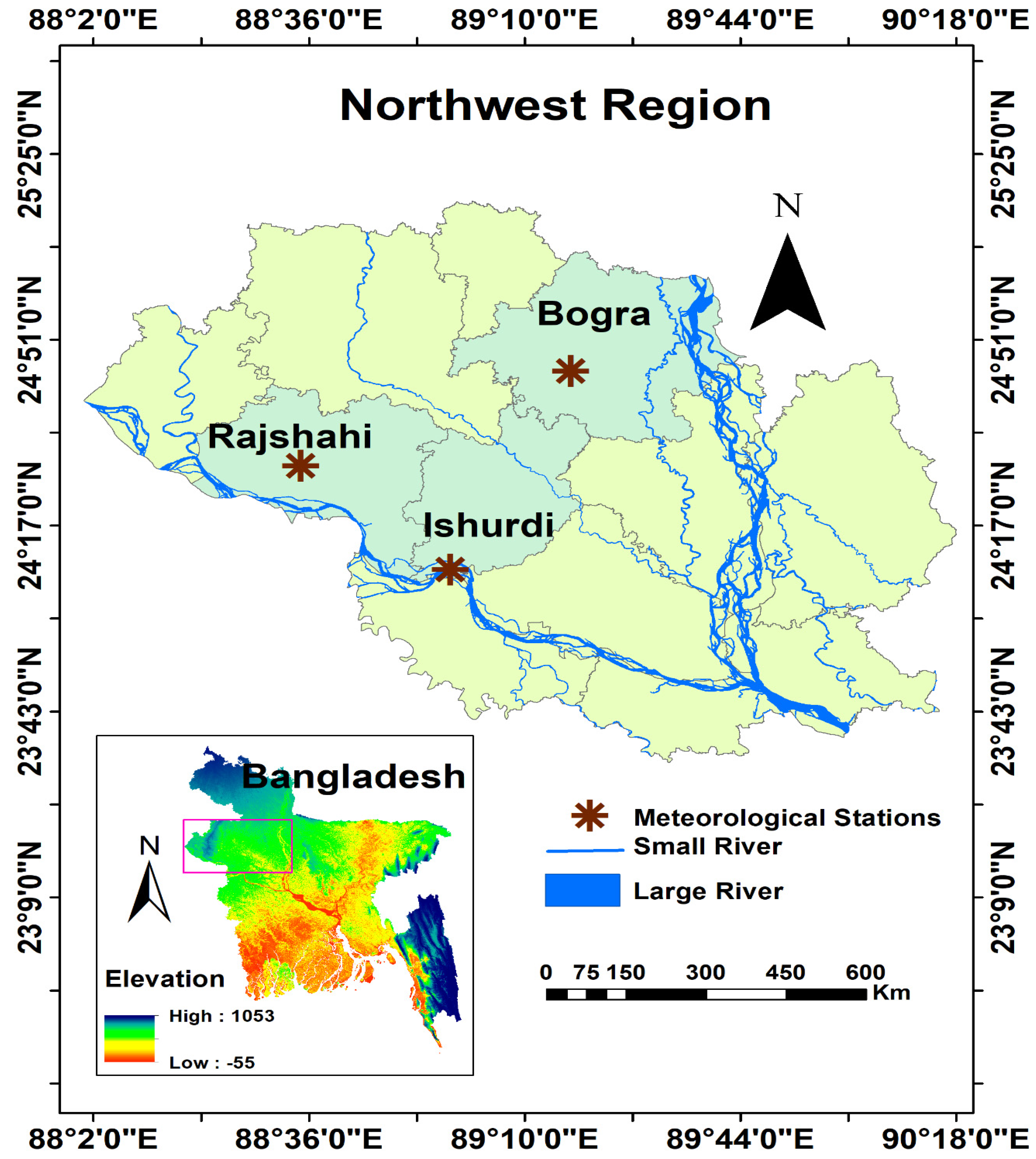
2.1. Case Study
2.2. Standard Precipitation Index (SPI)
2.3. Random Vector Functional Link Networks (RVFL)
2.4. Particle Swarm Optimization (PSO)
2.5. Genetic Algorithm (GA)
2.6. Grey Wolves Optimization (GWO)
2.7. Social Spider Optimization (SSO)
2.8. Salp SWARM Algorithm (SSA)
2.9. Hunger Games Search (HGS)
2.10. Model Performance Evaluation Matrices
3. Application and Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, J.; Fang, J.; Xu, W.; Shi, P. Analysis of dry/wet conditions using the standardized precipitation index and its potential usefulness for drought/flood monitoring in Hunan Province, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 377–387. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; Volume 30.
- Nicault, A.; Alleaume, S.; Brewer, S.; Carrer, M.; Nola, P.; Guiot, J. Mediterranean drought fluctuation during the last 500 years based on tree-ring data. Clim. Dyn. 2008, 31, 227–245. [Google Scholar] [CrossRef]
- Hanjra, M.A.; Qureshi, M.E. Global water crisis and future food security in an era of climate change. Food Policy 2010, 35, 365–377. [Google Scholar] [CrossRef]
- Mancosu, N.; Snyder, R.L.; Kyriakakis, G.; Spano, D. Water Scarcity and Future Challenges for Food Production. Water 2015, 7, 975–992. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A.; Nakhjiri, N.; Farahmand, A. Global integrated drought monitoring and prediction system. Sci. Data 2014, 1, 140001. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Brasil Neto, R.M.; da Silva, R.M.; dos Santos, D.C. Innovative approach for geospatial drought severity classification: A case study of Paraíba state, Brazil. Stoch. Environ. Res. Risk Assess. 2019, 33, 545–562. [Google Scholar] [CrossRef] [Green Version]
- Spinoni, J.; Vogt, J.V.; Naumann, G.; Barbosa, P.; Dosio, A. Will drought events become more frequent and severe in Europe? Int. J. Climatol. 2017, 38, 1718–1736. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal Drought Prediction: Advances, Challenges, and Future Prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef] [Green Version]
- Svoboda, M.; LeComte, D.; Hayes, M.; Heim, R.; Gleason, K.; Angel, J.; Rippey, B.; Tinker, R.; Palecki, M.; Stooksbury, D.; et al. The drought monitor. Bull. Am. Meteorol. Soc. 2002, 83, 1181–1190. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Ackerly, D.D.; Dawson, T.E.; Manzoni, S.; Skelton, R.P.; Vico, G.; Thompson, S.E. The ecohydrological context of drought and classification of plant responses. Ecol. Lett. 2018, 21, 1723–1736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreira, E.E.; Coelho, C.A.; Paulo, A.A.; Pereira, L.S.; Mexia, J.T. SPI-based drought category prediction using loglinear models. J. Hydrol. 2008, 354, 116–130. [Google Scholar] [CrossRef] [Green Version]
- AghaKouchak, A. A multivariate approach for persistence-based drought prediction: Application to the 2010–2011 East Africa drought. J. Hydrol. 2015, 526, 127–135. [Google Scholar] [CrossRef]
- Kumar, M.N.; Murthy, C.S.; Sai, M.V.R.S.; Roy, P.S. On the use of Standardized Precipitation Index (SPI) for drought intensity assessment. Meteorol. Appl. 2009, 16, 381–389. [Google Scholar] [CrossRef] [Green Version]
- Livada, I.; Assimakopoulos, V.D. Spatial and temporal analysis of drought in greece using the Standardized Precipitation Index (SPI). Theor. Appl. Clim. 2006, 89, 143–153. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, A.; Pires, C. Seasonal drought predictability in Portugal using statistical–dynamical techniques. Phys. Chem. Earth Parts A/B/C 2015, 94, 155–166. [Google Scholar] [CrossRef]
- Hosseini-Moghari, S.M.; Araghinejad, S. Monthly and seasonal drought forecasting using statistical neural networks. Environ. Earth Sci. 2015, 74, 397–412. [Google Scholar] [CrossRef]
- AghaKouchak, A. A baseline probabilistic drought forecasting framework using standardized soil moisture index: Application to the 2012 United States drought. Hydrol. Earth Syst. Sci. 2014, 18, 2485–2492. [Google Scholar] [CrossRef] [Green Version]
- Poornima, S.; Pushpalatha, M. Drought prediction based on SPI and SPEI with varying time-scales using LSTM recurrent neural network. Soft Comput. 2019, 23, 8399–8412. [Google Scholar] [CrossRef]
- Mohamadi, S.; Sammen, S.S.; Panahi, F.; Ehteram, M.; Kisi, O.; Mosavi, A.; Ahmed, A.N.; El-Shafie, A.; Al-Ansari, N. Zoning map for drought prediction using integrated machine learning models with a nomadic people optimization algorithm. Nat. Hazards 2020, 104, 537–579. [Google Scholar] [CrossRef]
- Başakın, E.E.; Ekmekcioğlu, Ö.; Özger, M. Drought prediction using hybrid soft-computing methods for semi-arid region. Model. Earth Syst. Environ. 2021, 7, 2363–2371. [Google Scholar] [CrossRef]
- Deo, R.C.; Kisi, O.; Singh, V.P. Drought forecasting in eastern Australia using multivariate adaptive regression spline, least square support vector machine and M5Tree model. Atmos. Res. 2017, 184, 149–175. [Google Scholar] [CrossRef] [Green Version]
- Tosunoglu, F.; Kisi, O. Trend analysis of maximum hydrologic drought variables using Mann–Kendall and Şen’s innovative trend method. River Res. Appl. 2017, 33, 597–610. [Google Scholar] [CrossRef]
- Kisi, O.; Gorgij, A.D.; Zounemat-Kermani, M.; Mahdavi-Meymand, A.; Kim, S. Drought forecasting using novel heuristic methods in a semi-arid environment. J. Hydrol. 2019, 578, 124053. [Google Scholar] [CrossRef]
- Tao, H.; Al-Sulttani, A.O.; Ameen, A.M.S.; Ali, Z.H.; Al-Ansari, N.; Salih, S.Q.; Mostafa, R.R. Training and Testing Data Division Influence on Hybrid Machine Learning Model Process: Application of River Flow Forecasting. Complexity 2020, 2020, 8844367. [Google Scholar] [CrossRef]
- Alizamir, M.; Kisi, O.; Adnan, R.M.; Kuriqi, A. Modelling reference evapotranspiration by combining neuro-fuzzy and evolutionary strategies. Acta Geophys. 2020, 68, 1113–1126. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Adnan, R.M. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Karimi, S.; Adnan, R.M. Three Different Adaptive Neuro Fuzzy Computing Techniques for Forecasting Long-Period Daily Streamflows. In Big Data in Engineering Applications; Springer: Singapore, 2018; pp. 303–321. [Google Scholar]
- Adnan, R.; Parmar, K.; Heddam, S.; Shahid, S.; Kisi, O. Suspended Sediment Modeling Using a Heuristic Regression Method Hybridized with Kmeans Clustering. Sustainability 2021, 13, 4648. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A. Meteorological drought prediction using heuristic approaches based on effective drought index: A case study in Uttarakhand. Arab. J. Geosci. 2020, 13, 1–17. [Google Scholar] [CrossRef]
- Banadkooki, F.B.; Singh, V.P.; Ehteram, M. Multi-timescale drought prediction using new hybrid artificial neural network models. Nat. Hazards 2021, 106, 2461–2478. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Kisi, O.; Yaseen, Z.M.; Shahid, S.; Zounemat-Kermani, M. Improving streamflow prediction using a new hybrid ELM model combined with hybrid particle swarm optimization and grey wolf optimization. Knowl. Based Syst. 2021, 230, 107379. [Google Scholar] [CrossRef]
- Abraham, A.; Jain, R. Soft Computing Models for Network Intrusion Detection Systems. In Classification and Clustering for Knowledge Discovery; Halgamuge, S.K., Wang, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 191–207. [Google Scholar]
- Fahim, S.R.; Hasanien, H.M.; Turky, R.A.; Alkuhayli, A.; Al-Shamma’A, A.A.; Noman, A.M.; Tostado-Véliz, M.; Jurado, F. Parameter Identification of Proton Exchange Membrane Fuel Cell Based on Hunger Games Search Algorithm. Energies 2021, 14, 5022. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, H.; Heidari, A.A.; Gandomi, A.H. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021, 177, 114864. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.-N. A Novel Hunger Games Search Optimization-Based Artificial Neural Network for Predicting Ground Vibration Intensity Induced by Mine Blasting. Nat. Resour. Res. 2021, 30, 3865–3880. [Google Scholar] [CrossRef]
- AbuShanab, W.S.; Abd Elaziz, M.; Ghandourah, E.I.; Moustafa, E.B.; Elsheikh, A.H. A new fine-tuned random vector functional link model using Hunger games search optimizer for modeling friction stir welding process of polymeric materials. J. Mater. Res. Technol. 2021, 14, 1482–1493. [Google Scholar] [CrossRef]
- Zinat, M.R.M.; Salam, R.; Badhan, M.A.; Islam, A.R.M.T. Appraising drought hazard during Boro rice growing period in western Bangladesh. Int. J. Biometeorol. 2020, 64, 1687–1697. [Google Scholar] [CrossRef]
- Jerin, J.N.; Islam, H.M.T.; Islam, A.R.M.T.; Shahid, S.; Hu, Z.; Badhan, M.A.; Chu, R.; Elbeltagi, A. Spatiotemporal trends in reference evapotranspiration and its driving factors in Bangladesh. Theor. Appl. Clim. 2021, 144, 793–808. [Google Scholar] [CrossRef]
- Islam, A.R.M.T.; Shen, S.; Hu, Z.; Rahman, M.A. Drought Hazard Evaluation in Boro Paddy Cultivated Areas of Western Bangladesh at Current and Future Climate Change Conditions. Adv. Meteorol. 2017, 2017, 3514381. [Google Scholar] [CrossRef]
- Uddin, J.; Hu, J.; Islam, A.R.M.T.; Eibek, K.U.; Nasrin, Z.M. A comprehensive statistical assessment of drought indices to monitor drought status in Bangladesh. Arab. J. Geosci. 2020, 13, 323. [Google Scholar] [CrossRef]
- Islam, A.; Karim, M.; Mondol, M. Appraising trends and forecasting of hydroclimatic variables in the north and northeast regions of Bangladesh. Theor. Appl. Climatol. 2020, 143, 33–50. [Google Scholar] [CrossRef]
- Szalai, S.; Szinell, C. Comparison of Two Drought Indices for Drought Monitoring in Hungary—A Case Study. Drought Drought Mitig. Eur. 2000, 161–166. [Google Scholar] [CrossRef]
- Hayes, M.; Svoboda, M.D.; Wilhite, D.A.; Vayarkho, O.V. Monitoring the 1996 drought using the standardized precipitation index. Bull. Am. Meteorol. Soc. 1999, 80, 429–438. [Google Scholar] [CrossRef] [Green Version]
- Edwards, D.; McKee, T. Characteristics of 20th Century Drought in the United States at Multiple Time Scales. Available online: http://hdl.handle.net/10217/170176 (accessed on 20 November 2021).
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Boston, MA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; Volume 17, pp. 179–183. [Google Scholar]
- Adnan, R.M.; Liang, Z.; El-Shafie, A.; Zounemat-Kermani, M.; Kisi, O. Prediction of Suspended Sediment Load Using Data-Driven Models. Water 2019, 11, 2060. [Google Scholar] [CrossRef] [Green Version]
- Pao, Y.-H.; Park, G.-H.; Sobajic, D.J. Learning and generalization characteristics of the random vector functional-link net. Neurocomputing 1994, 6, 163–180. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks IV, Perth, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 1942–1948. [Google Scholar]
- Menad, N.A.; Noureddine, Z.; Sarapardeh, A.H.; Shamshirband, S. Modeling temperature-based oil-water relative permeability by integrating advanced intelligent models with grey wolf optimization: Application to thermal enhanced oil recovery processes. Fuel 2019, 242, 649–663. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems; Univ. Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Gupta, I.; Gupta, A.; Khanna, P. Genetic algorithm for optimization of water distribution systems. Environ. Model. Softw. 1999, 14, 437–446. [Google Scholar] [CrossRef]
- Benhachmi, M.K.; Ouazar, D.; Naji, A.; Cheng, A.H.D.; Harrouni, K.E. Optimal Management in Saltwater-Intruded Coastal Aquifers by Simple Genetic Algorithm. First International Conference on Saltwater Intrusion and Coastal Aquifers—Monitoring, Modeling, and Management. Essaouira Moroc. 2001, 1, 23–25. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Cuevas, E.; Cienfuegos, M.; Zaldívar, D.; Pérez-Cisneros, M. A swarm optimization algorithm inspired in the behavior of the social-spider. Expert Syst. Appl. 2013, 40, 6374–6384. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Yuan, X.; Kisi, O.; Akhlaq, M.; Li, B. Comparison of LSSVR, M5RT, NF-GP, and NF-SC Models for Predictions of HourlyWind Speed and Wind Power Based on Cross-Validation. Energies 2019, 12, 329. [Google Scholar] [CrossRef] [Green Version]
- Clutton-Brock, T. Cooperation between non-kin in animal societies. Nat. Cell Biol. 2009, 462, 51–57. [Google Scholar] [CrossRef]
- Friedman, M.; Ulrich, P.; Mattes, R. A Figurative Measure of Subjective Hunger Sensations. Appetite 1999, 32, 395–404. [Google Scholar] [CrossRef] [PubMed]
- Kisi, O.; Heddam, S.; Yaseen, Z.M. The implementation of univariable scheme-based air temperature for solar radiation prediction: New development of dynamic evolving neural-fuzzy inference system model. Appl. Energy 2019, 241, 184–195. [Google Scholar] [CrossRef]
- Yaseen, Z.; Mohtar, W.H.M.W.; Ameen, A.M.S.; Ebtehaj, I.; Razali, S.F.M.; Bonakdari, H.; Salih, S.Q.; Al-Ansari, N.; Shahid, S. Implementation of univariate paradigm for streamflow simulation using hybrid data-driven model: Case study in tropical region. IEEE Access 2019, 2019, 74471–74481. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.-H.; Mernik, M. Exploration and Exploitation in Evolutionary Algorithms: A Survey. ACM Comput. Surv. 2013, 45, 1–33. [Google Scholar] [CrossRef]
- Kisi, O. Streamflow Forecasting and Estimation Using Least Square Support Vector Regression and Adaptive Neuro-Fuzzy Embedded Fuzzy c-means Clustering. Water Resour. Manag. 2015, 29, 5109–5127. [Google Scholar] [CrossRef]
- Muhammad Adnan, R.; Yuan, X.; Kisi, O.; Yuan, Y.; Tayyab, M.; Lei, X. Application of soft computing models in streamflow forecasting. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd.: London, UK, 2019; Volume 172, pp. 123–134. [Google Scholar]
- Belayneh, A.; Adamowski, J. Drought forecasting using new machine learning methods. J Water Land Dev. 2013, 18, 3–12. [Google Scholar] [CrossRef]
- Jalalkamali, A.; Moradi, M.; Moradi, N. Application of several artificial intelligence models and ARIMAX model for forecasting drought using the Standardized Precipitation Index. Int. J. Environ. Sci. Technol. 2015, 12, 1201–1210. [Google Scholar] [CrossRef] [Green Version]
- Hosseini-Moghari, S.M.; Araghinejad, S.; Azarnivand, A. Drought forecasting using data-driven methods and an evolutionary algorithm. Model. Earth Syst. Environ. 2017, 3, 1675–1689. [Google Scholar] [CrossRef]


| RFVL | Activation function | radial basis |
| Hidden neurons | 200 | |
| PSO | ) | 2 |
| ) | 2 | |
| inertia weight | 0.2–0.9 | |
| GA | Crossover percentage | 0.9 |
| Mutation percentage | 0.5 | |
| Mutation rate | 0.1 | |
| GWO | decreased from 2 to 0 | |
| HGS | 0.03 | |
| 1000 | ||
| SSO | 0.7 | |
| SSA | 0 | |
| All algorithms | Population | 40 |
| Number of iterations | 100 | |
| Number of runs for each algorithm | 20 |
| Drought Indices | Input Comb. | Models | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |||
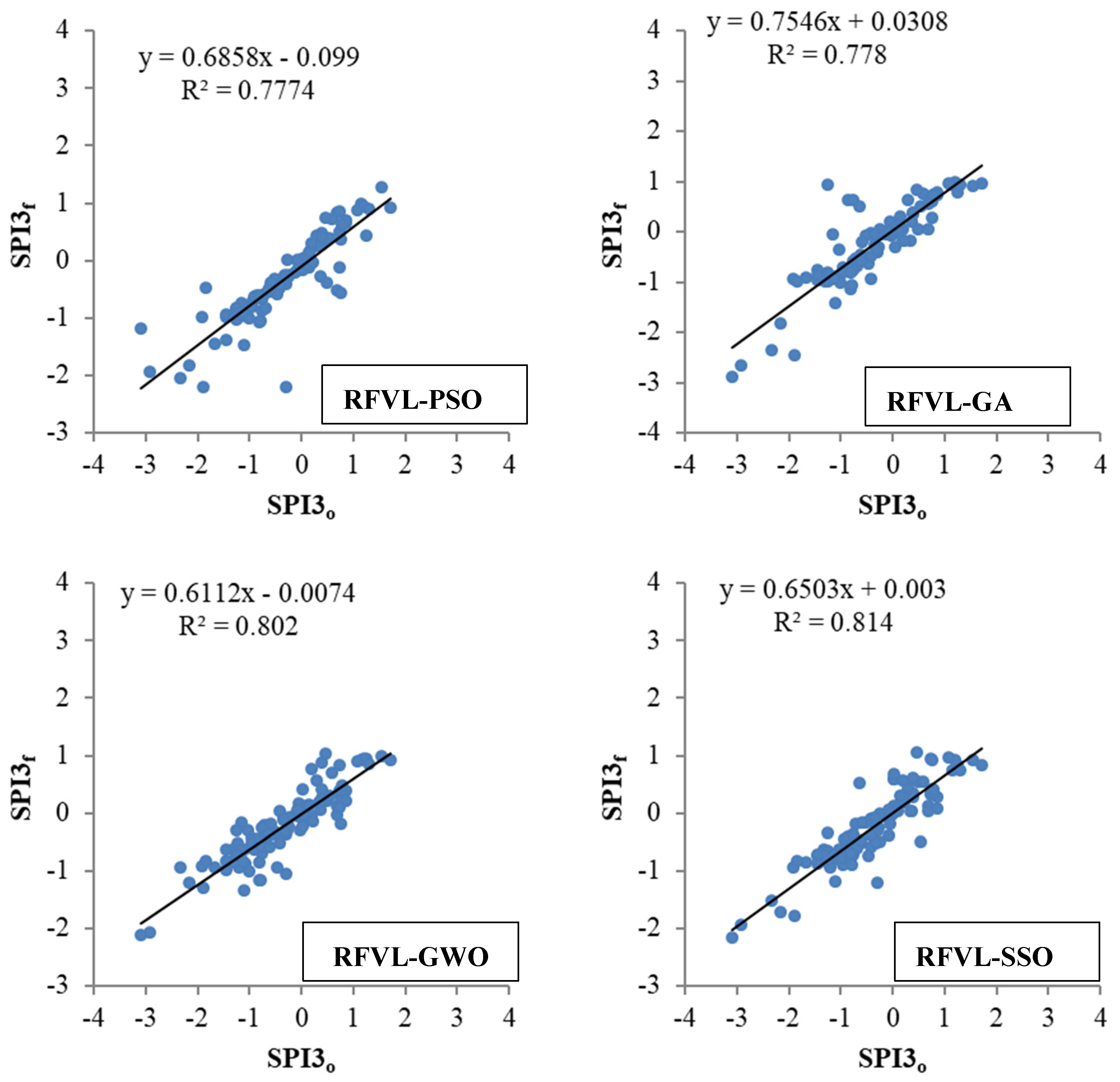
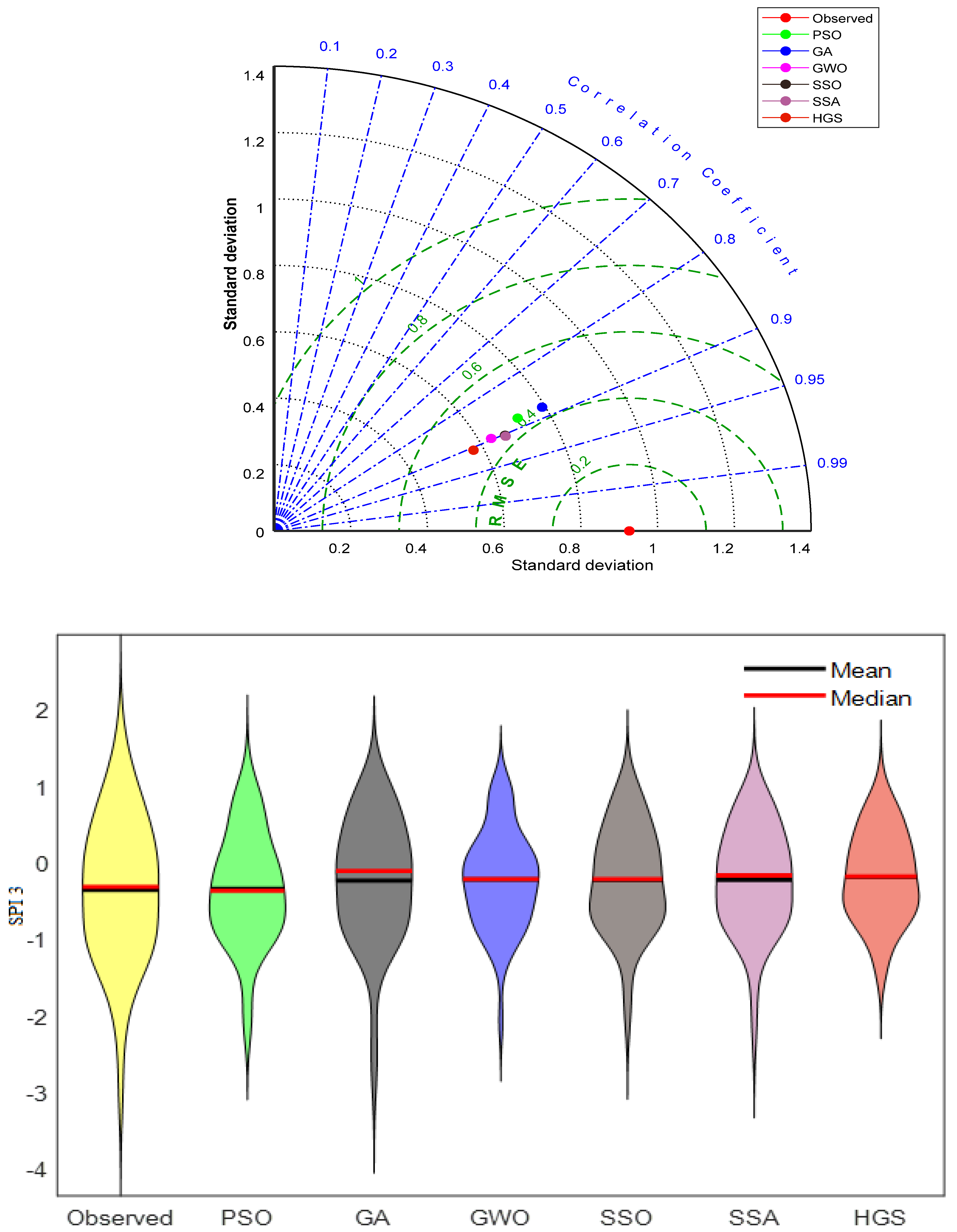
| SPI3 | SPI3t-1 | RFVL | 0.506 | 0.392 | 0.803 | 0.803 | 0.570 | 0.409 | 0.705 | 0.647 |
| PSO | 0.495 | 0.381 | 0.814 | 0.814 | 0.547 | 0.374 | 0.740 | 0.688 | ||
| GA | 0.493 | 0.380 | 0.817 | 0.817 | 0.537 | 0.363 | 0.748 | 0.706 | ||
| GWO | 0.482 | 0.377 | 0.837 | 0.837 | 0.535 | 0.357 | 0.757 | 0.710 | ||
| SSO | 0.472 | 0.368 | 0.865 | 0.865 | 0.523 | 0.351 | 0.765 | 0.730 | ||
| SSA | 0.470 | 0.366 | 0.870 | 0.870 | 0.523 | 0.344 | 0.767 | 0.731 | ||
| HGS | 0.454 | 0.351 | 0.883 | 0.883 | 0.511 | 0.340 | 0.769 | 0.734 | ||
| SPI3t-1,SPI3t-2 | RFVL | 0.492 | 0.378 | 0.820 | 0.820 | 0.543 | 0.368 | 0.736 | 0.696 | |
| PSO | 0.479 | 0.374 | 0.842 | 0.842 | 0.541 | 0.363 | 0.746 | 0.700 | ||
| GA | 0.474 | 0.372 | 0.851 | 0.851 | 0.525 | 0.349 | 0.760 | 0.727 | ||
| GWO | 0.465 | 0.359 | 0.865 | 0.865 | 0.522 | 0.346 | 0.764 | 0.733 | ||
| SSO | 0.463 | 0.360 | 0.868 | 0.868 | 0.516 | 0.339 | 0.773 | 0.743 | ||
| SSA | 0.444 | 0.344 | 0.898 | 0.898 | 0.507 | 0.331 | 0.781 | 0.748 | ||
| HGS | 0.440 | 0.335 | 0.905 | 0.905 | 0.502 | 0.328 | 0.784 | 0.759 | ||
| SPI6 | SPI6t-1,SP6t-2 | RFVL | 0.375 | 0.268 | 0.843 | 0.843 | 0.489 | 0.260 | 0.751 | 0.705 |
| PSO | 0.365 | 0.253 | 0.858 | 0.858 | 0.446 | 0.229 | 0.788 | 0.740 | ||
| GA | 0.364 | 0.258 | 0.858 | 0.858 | 0.440 | 0.218 | 0.791 | 0.749 | ||
| GWO | 0.353 | 0.249 | 0.875 | 0.875 | 0.404 | 0.223 | 0.832 | 0.755 | ||
| SSO | 0.329 | 0.229 | 0.858 | 0.858 | 0.389 | 0.212 | 0.824 | 0.778 | ||
| SSA | 0.304 | 0.218 | 0.891 | 0.891 | 0.378 | 0.190 | 0.823 | 0.794 | ||
| HGS | 0.304 | 0.218 | 0.891 | 0.891 | 0.372 | 0.190 | 0.831 | 0.802 | ||
| SPI6t-1,SPI6t-2,SPI6t-3,SPI6t-4 | RFVL | 0.370 | 0.252 | 0.850 | 0.850 | 0.465 | 0.219 | 0.774 | 0.709 | |
| PSO | 0.340 | 0.245 | 0.859 | 0.859 | 0.417 | 0.205 | 0.792 | 0.746 | ||
| GA | 0.339 | 0.241 | 0.864 | 0.864 | 0.406 | 0.196 | 0.798 | 0.780 | ||
| GWO | 0.332 | 0.238 | 0.871 | 0.871 | 0.377 | 0.192 | 0.810 | 0.785 | ||
| SSO | 0.320 | 0.231 | 0.880 | 0.880 | 0.384 | 0.188 | 0.812 | 0.786 | ||
| SSA | 0.299 | 0.214 | 0.898 | 0.898 | 0.355 | 0.175 | 0.840 | 0.798 | ||
| HGS | 0.284 | 0.195 | 0.921 | 0.921 | 0.342 | 0.159 | 0.848 | 0.803 | ||
| Drought Indices | Input Comb. | Models | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |||
| SPI9 | SPI9t-1,SPI9t-2, SPI9t-3, | RFVL | 0.395 | 0.242 | 0.796 | 0.796 | 0.430 | 0.291 | 0.788 | 0.760 |
| PSO | 0.390 | 0.242 | 0.801 | 0.801 | 0.400 | 0.288 | 0.815 | 0.801 | ||
| GA | 0.389 | 0.241 | 0.803 | 0.803 | 0.397 | 0.277 | 0.825 | 0.806 | ||
| GWO | 0.379 | 0.239 | 0.816 | 0.815 | 0.386 | 0.267 | 0.830 | 0.810 | ||
| SSO | 0.346 | 0.218 | 0.853 | 0.853 | 0.379 | 0.265 | 0.833 | 0.812 | ||
| SSA | 0.313 | 0.190 | 0.878 | 0.878 | 0.374 | 0.262 | 0.835 | 0.816 | ||
| HGS | 0.307 | 0.189 | 0.884 | 0.884 | 0.372 | 0.260 | 0.838 | 0.823 | ||
| SPI9t-1,SPI9t-2,SPI9t-3,SPI9t-4,SPI9t-5 | RFVL | 0.416 | 0.273 | 0.770 | 0.769 | 0.490 | 0.315 | 0.733 | 0.709 | |
| PSO | 0.396 | 0.244 | 0.794 | 0.794 | 0.427 | 0.293 | 0.793 | 0.765 | ||
| GA | 0.395 | 0.241 | 0.795 | 0.795 | 0.420 | 0.288 | 0.806 | 0.778 | ||
| GWO | 0.366 | 0.226 | 0.828 | 0.828 | 0.408 | 0.275 | 0.820 | 0.790 | ||
| SSO | 0.355 | 0.220 | 0.842 | 0.842 | 0.401 | 0.270 | 0.827 | 0.804 | ||
| SSA | 0.349 | 0.218 | 0.849 | 0.849 | 0.397 | 0.267 | 0.831 | 0.806 | ||
| HGS | 0.340 | 0.210 | 0.860 | 0.860 | 0.395 | 0.264 | 0.834 | 0.810 | ||
| SPI12 | SPI12t-1,SPI12t-2, SPI12t-3, | RFVL | 0.300 | 0.165 | 0.897 | 0.897 | 0.346 | 0.208 | 0.793 | 0.778 |
| PSO | 0.298 | 0.162 | 0.900 | 0.900 | 0.337 | 0.213 | 0.804 | 0.789 | ||
| GA | 0.295 | 0.163 | 0.902 | 0.902 | 0.327 | 0.203 | 0.814 | 0.801 | ||
| GWO | 0.284 | 0.158 | 0.914 | 0.913 | 0.302 | 0.181 | 0.837 | 0.820 | ||
| SSO | 0.247 | 0.140 | 0.947 | 0.947 | 0.287 | 0.163 | 0.874 | 0.851 | ||
| SSA | 0.240 | 0.134 | 0.953 | 0.953 | 0.271 | 0.156 | 0.883 | 0.864 | ||
| HGS | 0.225 | 0.118 | 0.966 | 0.966 | 0.260 | 0.151 | 0.888 | 0.875 | ||
| SPI12t-1,SPI12t-2,SPI12t-3,SPI12t-4,SPI12t-5 | RFVL | 0.312 | 0.174 | 0.885 | 0.885 | 0.409 | 0.276 | 0.722 | 0.708 | |
| PSO | 0.309 | 0.164 | 0.895 | 0.895 | 0.355 | 0.233 | 0.790 | 0.766 | ||
| GA | 0.301 | 0.161 | 0.896 | 0.896 | 0.353 | 0.224 | 0.798 | 0.769 | ||
| GWO | 0.293 | 0.157 | 0.907 | 0.907 | 0.329 | 0.194 | 0.826 | 0.816 | ||
| SSO | 0.284 | 0.152 | 0.913 | 0.913 | 0.291 | 0.169 | 0.869 | 0.845 | ||
| SSA | 0.272 | 0.145 | 0.925 | 0.925 | 0.287 | 0.159 | 0.875 | 0.856 | ||
| HGS | 0.249 | 0.137 | 0.946 | 0.946 | 0.269 | 0.157 | 0.884 | 0.867 | ||
| Station | Input Comb. | Models | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |||
| Station 1 | OPT SPI3+MN | RFVL | 0.493 | 0.343 | 0.788 | 0.788 | 0.519 | 0.361 | 0.764 | 0.678 |
| PSO | 0.476 | 0.328 | 0.816 | 0.816 | 0.500 | 0.343 | 0.812 | 0.718 | ||
| GA | 0.475 | 0.323 | 0.818 | 0.817 | 0.498 | 0.344 | 0.791 | 0.723 | ||
| GWO | 0.473 | 0.318 | 0.821 | 0.821 | 0.496 | 0.343 | 0.796 | 0.727 | ||
| SSO | 0.450 | 0.310 | 0.856 | 0.856 | 0.491 | 0.341 | 0.801 | 0.731 | ||
| SSA | 0.439 | 0.303 | 0.873 | 0.873 | 0.487 | 0.338 | 0.810 | 0.746 | ||
| HGS | 0.430 | 0.290 | 0.892 | 0.892 | 0.482 | 0.327 | 0.821 | 0.756 | ||
| Station 2 | OPT SPI3+MN | RFVL | 0.467 | 0.321 | 0.782 | 0.782 | 0.541 | 0.367 | 0.768 | 0.730 |
| PSO | 0.456 | 0.310 | 0.798 | 0.798 | 0.537 | 0.365 | 0.777 | 0.733 | ||
| GA | 0.445 | 0.304 | 0.818 | 0.818 | 0.535 | 0.362 | 0.778 | 0.735 | ||
| GWO | 0.442 | 0.301 | 0.823 | 0.823 | 0.526 | 0.356 | 0.802 | 0.762 | ||
| SSO | 0.435 | 0.286 | 0.838 | 0.838 | 0.512 | 0.345 | 0.814 | 0.784 | ||
| SSA | 0.431 | 0.283 | 0.845 | 0.845 | 0.509 | 0.343 | 0.817 | 0.784 | ||
| HGS | 0.402 | 0.261 | 0.890 | 0.890 | 0.505 | 0.341 | 0.819 | 0.787 | ||
| Station 3 | OPT SPI3+MN | RFVL | 0.489 | 0.376 | 0.823 | 0.823 | 0.541 | 0.365 | 0.739 | 0.700 |
| PSO | 0.476 | 0.371 | 0.845 | 0.845 | 0.538 | 0.360 | 0.749 | 0.702 | ||
| GA | 0.471 | 0.370 | 0.854 | 0.854 | 0.522 | 0.346 | 0.763 | 0.730 | ||
| GWO | 0.463 | 0.357 | 0.869 | 0.869 | 0.517 | 0.343 | 0.767 | 0.735 | ||
| SSO | 0.460 | 0.355 | 0.872 | 0.872 | 0.513 | 0.336 | 0.777 | 0.746 | ||
| SSA | 0.440 | 0.340 | 0.902 | 0.902 | 0.504 | 0.328 | 0.782 | 0.750 | ||
| HGS | 0.434 | 0.332 | 0.908 | 0.908 | 0.500 | 0.325 | 0.787 | 0.765 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adnan, R.M.; Mostafa, R.R.; Islam, A.R.M.T.; Gorgij, A.D.; Kuriqi, A.; Kisi, O. Improving Drought Modeling Using Hybrid Random Vector Functional Link Methods. Water 2021, 13, 3379. https://doi.org/10.3390/w13233379
Adnan RM, Mostafa RR, Islam ARMT, Gorgij AD, Kuriqi A, Kisi O. Improving Drought Modeling Using Hybrid Random Vector Functional Link Methods. Water. 2021; 13(23):3379. https://doi.org/10.3390/w13233379
Chicago/Turabian StyleAdnan, Rana Muhammad, Reham R. Mostafa, Abu Reza Md. Towfiqul Islam, Alireza Docheshmeh Gorgij, Alban Kuriqi, and Ozgur Kisi. 2021. "Improving Drought Modeling Using Hybrid Random Vector Functional Link Methods" Water 13, no. 23: 3379. https://doi.org/10.3390/w13233379
APA StyleAdnan, R. M., Mostafa, R. R., Islam, A. R. M. T., Gorgij, A. D., Kuriqi, A., & Kisi, O. (2021). Improving Drought Modeling Using Hybrid Random Vector Functional Link Methods. Water, 13(23), 3379. https://doi.org/10.3390/w13233379











