Abstract
The objective of this study was to test pre-treatment hydrologic calibration relationships between paired headwater watersheds (WS77 (treatment) and WS80 (control)) and explain the difference in flow, compared to earlier published data, using daily rainfall, runoff, and a water table measured during 2011–2019 in the Santee Experimental Forest in coastal South Carolina, USA. Mean monthly runoff difference between WS80 and WS77 of −6.80 mm for 2011–2019, excluding October 2015 with an extreme flow event, did not differ significantly from −8.57 mm (p = 0.27) for the 1969–1978 period or from −3.89 mm for 2004–2011, the post-Hurricane Hugo (1989) recovery period. Both the mean annual runoff coefficient and monthly runoff were non-significantly higher for WS77 than for WS80. The insignificant higher runoff by chance was attributed to WS77’s three times smaller surface storage and higher hypsometrical integral than those of WS80, but not to rainfall. The 2011–2019 geometric mean regression-based monthly runoff calibration relationship, excluding the October 2015 runoff, did not differ from the relationship for the post-Hugo recovery period, indicating complete recovery of the forest stand by 2011. The 2011–2019 pre-treatment regression relationship, which was not affected by periodic prescribed burning on WS77, was significant and predictable, providing a basis for quantifying longleaf pine restoration effects on runoff later in the future. However, the relationship will have to be used cautiously when extrapolating for extremely large flow events that exceed its flow bounds.
1. Introduction
Restoration of longleaf pine (LLP) (Pinus palustris) ecosystems is a public land management objective throughout the southeastern United States, and it is a principal goal in the Forest Plan for the Francis Marion National Forest in South Carolina, USA. While there have been numerous plot or stand-scale studies of LLP ecology, silviculture, and ecosystem services [1], there are uncertainties regarding the watershed-scale runoff effects of reestablishing longleaf pine communities due to the spatial heterogeneity of soil conditions, microtopography, slope, and understory vegetation, all of which affect soil water storage. In contrast to loblolly pine (Pinus taeda L.) (LP) stands managed for timber production, LLP stands managed for the open canopy with frequent prescribed fire have a much lower stocking, a longer period of open canopy, a sparse mid-story, and an understory generally dominated by grasses and sedges, potentially influencing soil moisture and evapotranspiration (ET) [2]. As a result of these differences in stand structure and composition, it may be expected that LLP stands will exhibit less leaf area, less interception loss and transpiration, more infiltration of rainfall recharging groundwater, and increasing runoff than stands managed for timber production, especially LP stands where fire is excluded.
Runoff generation in coastal watersheds with shallow water table (WT) (<2–3 m deep) soils with variable permeability and infiltration rates is dominated by saturation excess flow [3,4,5,6]. The runoff process is complicated by interactions of forest management and extreme events [7,8,9,10,11]. The near-surface or shallow WT, a surrogate of soil water storage regulated by ET [12,13,14], drives most streamflow (as shallow surface runoff and drainage) in these shallow coastal systems [15]. Furthermore, microtopography influencing both surface and subsurface storage [16,17,18,19,20], (dis)connectivity [21], and drainage network pathways [7,22] have been shown to be important factors affecting runoff and its timing. Thus, a careful examination of such spatial catchment characteristics, including the above-canopy and below-canopy leaf areas that regulate soil moisture and ET, is fundamental for an accurate interpretation of water yield [23].
A paired watershed approach, in which two neighboring watersheds (one reference or control and one treatment) are monitored concurrently during calibration (pre-treatment) and post-treatment periods [24,25,26], has been used extensively to assess the effects of water management and silvicultural practices on hydrologic variables (water yield, peak flow rate, ET, and the water table) and ecosystem services [27,28,29,30]. The control watershed accounts for year-to-year or seasonal climate variations and management practices and remains the same during the treatment period [31]. The basis for the paired watershed approach is that there is a significant and quantifiable relationship between the two watersheds that provides a basis for comparing whether a treatment alters that relationship. This approach has been used primarily on first-order headwater watersheds [28,32], although its applicability for predicting effects of flood events on larger systems has been challenged [33].
The aim of this study was to affirm a current pre-treatment (baseline) flow relationship, between a pair of headwater watersheds reported earlier [34,35] and discussed below, that is significant and predictable. The planned treatment will test the hypothesis that watershed-scale restoration to mature LLP stands will increase water yield, primarily due to reduced ET from the forest.
2. Baseline Paired Hydrology Relationship
The approach for this study has been to use the first-order paired watersheds (WS77 for treatment and WS80 for control) on the Santee Experimental Forest (SEF), located within the Francis Marion National Forest (Figure 1). This study has a long record that supported the comparative analyses, including a statistically significant relationship between monthly flows established between control and treatment watersheds [34], to evaluate effects of partial prescribed burning on streamflow for 1976–1980 [35,36]. However, the authors [35,36] found no significant difference in streamflow between the watersheds after partial prescribed burning. Monitoring of the paired watersheds, which was discontinued in early 1982, was restarted in 1990, soon after Hurricane Hugo (1989) significantly (>80%) damaged the forest canopy in the region [37]. Richter [36] found that the average annual streamflows from WS77 and WS80 were 28% and 20%, respectively, of precipitation. Richter also analyzed four possible explanations for this difference in water yield: (a) differences in deep seepage losses, (b) difference in vegetation, which influences ET and interception, (c) watershed boundaries, and (d) calibration errors in weir rating tables.
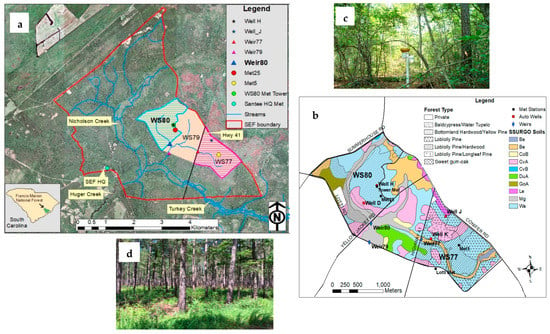
Figure 1.
(a) Location map of the paired watersheds (WS77—treatment and WS80—control) and (b) their experimental layouts with existing monitoring stations, SSURGO soil types, and forest land cover types of both watersheds, and the forest stands of (c) WS80 and (d) WS77 within the Santee Experimental Forest (SEF) at Francis Marion National Forest, SC.
Richter [36] suggested negligible deep seepage losses for these poorly drained soils and found no evidence of weir leakage on either watershed. Based upon seasonal flows and vegetation composition analysis, the author also argued that differences in water yield cannot be explained by vegetational differences. His analysis also ruled out watershed boundary effects in these low-gradient systems, in which the watershed drainage areas are bounded by the elevated roads built with well compacted soils, minimizing any possible lateral seepage, except for the northeast corner of WS80, which is a watershed divide. However, Richter [36] suggested that because of the consistency in annual ET (rainfall–runoff) and predictability of runoff measured on WS77, differences were attributed possibly to WS80 runoff estimates, particularly for high flows. Nonetheless, the author also suggested a need for calibration of both stream gauges. In a long-term paired watershed study on grasslands in Uruguay, Chescheir et al. [38] also found similar inherent differences between the paired watersheds for the pre-treatment period, with higher runoff from the treatment than from the control, which was attributed to a higher baseflow from the treatment watershed, likely due to lower ET from its shallow soils or groundwater inflow from outside the watershed.
Interestingly, the paired pre-Hugo flow relationship (WS77 > WS80), reported by Richter [36] for 1969–1978, reversed (WS80 > WS77) four years after Hurricane Hugo’s 1989 arrival for 10 years (1994–2003) before the relationship recovered to the pre-Hugo direction (WS77 > WS80) by 2004, as did the forest stands [24] (Figure S1). Jayakaran et al. [24], who analyzed pre- and post-Hugo monthly data over 2011, suggested that lowered vegetative water use likely increased outflows in both watersheds because trees were lost to the hurricane. However, WS77 recovered to its pre-hurricane runoff level by 1993, having an abundance of pine seedlings and saplings there compared to WS80, which recovered its flow pattern in 2003. Jayakaran et al. [24] noted that it seems likely that high rainfall in 2003 would have saturated soils in both watersheds, and 2004’s drought-like conditions would have substantially drawn down the water table. The heavy rainfall and subsequent dry conditions in the following year might have somewhat confounded the exact timing and mechanisms responsible for the return of flow relationships to those pre-Hugo. Therefore, the authors cautioned that whether the 2003 wet and 2004 dry years accelerated the recovery to the pre-Hugo (WS77 > WS80) direction is an area for further study. Although the relationship was restored, the difference (WS77 > WS80) in the average magnitude in 2004 through to 2011 was 2–3 times smaller than before Hugo (Figure S1). Since these authors did not find any significant difference in the monthly rainfall totals between the two watersheds for any of the three periods, they attributed the relative periodical magnitude differences in paired streamflow to relative changes in ET dynamics between the watersheds.
Therefore, the objective of this study was to re-evaluate and re-establish the paired calibration relationship of watersheds, recovered since the 1989 hurricane, using climatic data for 2011–2019, which includes very large rainfall and dry events [39] (Table 1). This period was chosen because the stands reported by Jayakaran et al. [24] as being recovered by 2004, as stated above, were hypothesized to be fully recovered by 2011 (Figure S1) or 22 years after the hurricane. This hypothesis is consistent with studies reporting a recovery period of 7 to 25 years for the annual water yield in three forested watersheds in the northeastern US [8], as many as 20 years in the US and > 14 years in Japan [40], and 10 to 15 years for recovery of the water table and drainage outflow in managed pine forest watersheds in coastal North Carolina [26,41].

Table 1.
Measured annual flow, with the average annual and standard deviation (StdDev), for paired watersheds WS77 and WS80 and the difference in flow between them for 2011–2019, pre-Hurricane Hugo (1969–1978), and post-Hugo (2004–2011), reported by Jayakaran et al. [24] (See also Figure S1).
In addition, the choice of the 2011–2019 period as a pre-treatment baseline reference was supported by its closer agreement of the computed average annual flow difference of 82.1 mm between the treatment and control watersheds, than the 46.7 mm for 2004–2011, with the pre-Hugo average difference of 102.8 mm (Table 1). Furthermore, the StdDev of the flow difference for the baseline was closer to the pre-Hugo period than that of the post-Hugo, indicating their similar intra-annual variability. A similar approach was reported by Oda et al. [40] for testing disturbance effects using a paired watershed approach.
Regarding choosing a stable and sufficient record length for a baseline calibration period, Ssegane et al. [42] found statistically significant pre-treatment calibration relationships using only 762 days and 608 days, respectively, for two treatment watersheds from 2009 to 2012 that included some disturbances. Similarly, Bren and Lane [32] found a rapid increase in the quality of calibration relationship as the record length increased up to 3 years, but no increase was found beyond that, for all temporal scales of flow. The authors suggested that 5 years were adequate for most purposes, consistent with Clausen and Spooner [31], and the main advantage of longer periods was lower mean errors.
It was hypothesized, therefore, that the nine-year (2011–2019) record period, covering years with very low (2012) and very high (2015) runoff (Table 1), should be adequate for obtaining a stable pre-treatment (baseline) calibration relationship that is significant and quantifiable for future applications in treatment evaluations. This model would be applied using the measured flow from the control watershed to estimate expected flows for the WS77 treatment, assuming no disturbance, starting in 2020 when the harvesting and thinning treatments began for longleaf restoration. Next, the expected flow from the treatment watershed would be compared with actual measured flow. Deviations of the treated watershed’s measured flow from expected values were considered to represent treatment effects if the deviations fell outside specified confidence intervals (95%) placed around the calibration regression line. In addition, the treatment regressions would also be evaluated against the pre-treatment baseline.
Various potential reasons, including rainfall and storm events, and understory prescribed burning implemented in 2013, 2016, and 2018 on the WS77, as shown by Richter et al. [35] and discussed above, were evaluated for the inherent differences in paired watershed flows. This study is novel in that no other studies, to the authors’ knowledge, have reassessed the paired watershed calibration relationship after the reported recovery of forests following a major natural disturbance that altered the pre-disturbance flow regime between the watersheds.
Objective 1: Evaluate the annual rainfall, runoff coefficient, and ET (as the difference between rainfall and flow) in the paired watersheds for the pre-treatment baseline period and compare them with the 2004–2011 post-recovery period.
Hypothesis 1.
There will be no significant difference in the pre-treatment mean annual runoff coefficient (ROC) or in mean monthly rainfall between the paired watersheds, consistent with the post-recovery period, despite the effects of relatively very wet and dry years (defined, respectively, as 30% above and below the long-term average rainfall).
Objective 2: Evaluate the difference in pre-treatment monthly runoff between the paired watersheds compared to the post-recovery period and the possible reasons for difference, if any, building upon earlier studies [24,36].
Hypothesis 2.
The difference in the monthly runoff response between the paired watersheds will be similar (WS77 > WS80) to that in the post-recovery period.
Objective 3: Evaluate the pre-treatment monthly runoff calibration relationship between the watersheds compared to the post-recovery period.
Hypothesis 3.
The paired pre-treatment monthly runoff calibration relationship will not be different from the relationship for the post-recovery period and will be significant and quantifiable, with predictive capability.
Hypothesis 4.
The periodic prescribed burning treatments in the pre-treatment period will not affect the change in paired runoff relationship between the watersheds.
3. Materials and Methods
3.1. Site Description
The paired watersheds (WS77 and WS80) drain into Fox Gulley Creek and further down to Turkey Creek, a tributary of Huger Creek. These are parts of the headwaters of Huger Creek, a fourth-order stream and a major tributary of the East Branch of Cooper River, which drains into Charleston Harbor (Figure 1a). Basic characteristics of the watersheds are given in Table 2. The original WS80 watershed area was 206 ha when it was installed in 1968 [35], but on 6 November 2001, a culvert was installed to drain its northeastern portion, thus reducing its area by 46 ha to 160 ha (Table 2). The vegetation in WS80 is a mixed hardwood-pine stand, regenerated since Hugo (Figure 1b,c). The vegetation in WS77 is dominated by loblolly pine (Figure 1b,d), planted for silvicultural research in the late 1970s. Soils in the watersheds are poorly to moderately well-drained sandy clay loam overlaying clay, typified by the Wahee and Craven soil series in the uplands and the Megget and Betheera soils in the riparian zones (Figure 1b). The control watershed is 48% wetlands compared to only 11% in WS77, as estimated from recent National Wetland Inventory data (Table 1). The mean surface depressional storage reported by Amoah et al. [17] for the WS80 watershed was nine times higher than for the WS77 (Table 1). The climate is warm-humid temperate, with an average daily temperature of 17.8 °C and annual rainfall of about 1370 mm [43]. Chronological activities of both watersheds are given in Table S1, and more details are described elsewhere [15,17,43].

Table 2.
General characteristics of the paired watersheds.
3.2. Hydro-Meteorologic Monitoring
Beginning in 2003, digital records of precipitation were collected using automatic tipping bucket gauges backed up by a manual gauge at the Met5 station in WS77 and at the Met25 station in WS80. Data from nearby gauges (Figure 1a,b) were also used to fill gaps [44,45]. Digital measurements of stage, also beginning in 2003, were recorded every 10 min by the Teledyne ISCO flowmeters installed upstream of both the WS77 and WS80 watershed weir outlet gauging stations (Figure 1a,b). These digital stage data were used with established rating curves for compound V-notch weirs for estimating streamflow rates [39,44,45]. Details of stream gauges, stage measurements, and estimates of flow rates and the quality control are given in [44,45]. The flow data have been recently verified and are of a high quality for the rating range they were developed for. Daily average weather parameters obtained from weather sensors installed on a 27-m tall tower (above the forest canopy) in WS80 in 2010 (Figure 1a,b) were used to estimate daily Penman–Monteith (P-M) [46] based potential evapotranspiration (PET) for the forest conditions following Amatya et al. [47] (Table 3). A 3 m weather station installed on open grass at the nearby SEF Headquarters (SHQ) (Figure 1a) [48] provided data to fill in some missing values for a few short periods [45].

Table 3.
Measured annual rainfall, flow, ET (rainfall–flow), and ROC (runoff coefficient = flow/rainfall) and estimated PET for the WS77 and WS80 watersheds for 2011–2019.
The WT in upland well H and riparian well D in WS80 and upland well J in WS77 have been measured hourly since 2004 using pressure transducers with a datalogger (Figure 1a,b). Well K near the riparian area in WS77 was installed in 2018 (Figure 1b). All wells were approximately 2.8 to 3 m deep. Plots of the daily water table depths of well J and well H for 2011–2019 are presented in Figure S2. Measurements of the leaf area index (LAI) were conducted every 2 or 3 weeks in 2019–2020 (n = 9) at three locations proposed for LLP treatment in WS77 (Figure 1b). The average LAI measured during 2008–2009 (n = 40) and reported by Dai et al. [43] for WS80 were used, assuming the LAI of the fully recovered stands on this control watershed remained unchanged. A comparison of WS77 LAI with WS80 LAI is shown in Figure S3. Details of all hydro-meteorologic measurements, including data quality control, can be found elsewhere [15,17,43,44,49].
3.3. Data and Statistical Analyses
Measured daily rainfall, streamflow or runoff (watershed area-based depth), and PET, estimated from the daily weather data for the 2011–2019 period, were used to obtain monthly and annual totals and to compute the annual rainfall normalized runoff coefficient (ROC). The number of daily rain events > 25 mm in each year was also logged. Flow data were lost for both watersheds for Hurricane Joaquin (3–4 October 2015), while only WS77 lost some data for Hurricane Matthew (8 October 2016), because the measured stage exceeded the rating curve range of each watershed. The exceptionally high flow of October 4, 2015 was assumed to be an outlier, as discussed in the Results section below, so that month was excluded from both watersheds in the comparative monthly analysis. Data for WS77 for October 8, 2016 were constructed by assuming the maximum rating curve flow value for less than 9 h of the day when the measured stage exceeded the rating curve limit. Integration of all 10-min interval flow rates, including the peak rates for this day, yielded 242.2 mm of flow as a response to 204 mm rain on that day, preceded by 90.4 mm rain the day before with only 1.7 mm flow, indicating that most of the two-day rain contributed to this single day large event. This daily value of 242.2 mm, which was lower than the 187.6 mm observed for WS80, was used in the analyses. Daily flow data were used to derive the daily flow duration curves to identify differences in flow magnitudes, frequencies, and duration of daily runoff between the watersheds. Daily WT depths were obtained by integrating hourly data.
Monthly rainfall, as well as annual runoff and ROC, for both watersheds were statistically analyzed to test Hypothesis 1. Measured monthly runoff data were used to (a) compare the mean monthly difference in flow between the paired watersheds against the post-recovery period to test Hypothesis 2 and (b) develop a baseline calibration regression of the monthly flow between the paired watersheds to test Hypothesis 3. Finally, a MOSUM (moving sums of recursive residuals) approach was used to detect changes in the paired flow regime, if any, and also in the paired calibration relationship, due to the prescribed burning, to test Hypothesis 4.
The Shapiro–Wilk normality test [50] showed a non-normal distribution (p < 0.001) of monthly runoff. Therefore, the nonparametric Wilcoxon signed-rank test was used to assess the significance of differences in mean monthly runoff between the two watersheds measured for 108 months or nine (2011–2019) years. An ordinary least squares regression (OLS) was used to develop a calibration equation between the control and treatment watersheds and its significance test [51]. However, since the Durbin–Watson (DW) test [50] showed a positive autocorrelation of the monthly runoff of both watersheds (DW_WS77 = 0.054, p < 0.0001; DW_WS80 = 0.029, p < 0.0001), regression relationships using an OLS versus geometric mean (GM) regression were compared. Based on Ssegane et al. [42], the ts and lmodel2 R statistical packages [52] were used to examine if the OLS was significantly different from the GM. The ts function is used to create time-series objects. These are vectors or matrices with a class of “ts” (and additional attributes), which represent data which have been sampled at equispaced points in time. In the matrix case, each column of the matrix data is assumed to contain a single (univariate) time series. Similarly, the lmodel2 function computes model II simple linear regression using the following methods: ordinary least squares (OLS), major axis (MA), standard major axis (SMA), and reduced major axis (RMA) of the GM. The model accepts only one response and one explanatory variable. Model II regression should be used when the two variables in the regression equation are random, i.e., not controlled by the researcher. GM regression is a resampling technique that accounts for autocorrelation in the time series by resampling the original data in pre-determined blocks 1000 times to estimate regression coefficients. GM, also known as the reduced major axis (RMA) regression, is suited for paired watershed analysis, because it assumes errors are associated with both dependent (treatment watershed) and independent (control watershed) variables [53]. The coefficient of determination (R2), Nash–Sutcliffe efficiency (NSE), and root mean squared error (RMSE) were used to evaluate the strength and significance of the regression. For R2 (0 ≤ R2 ≤ 1.0) and for NSE (−∞ ≤ NSE ≤ 1.0), a value of 1.0 indicates an optimal model. All statistical significance tests for similarity with no difference were conducted for the α = 0.05 level.
An OLS-based MOSUM (moving sums of recursive residuals) approach using monthly flow data was conducted to detect the change in flow behavior, if any, between the watersheds due to prescribed burning of the WS77 watershed and potential effects on the monthly flow regression relationship. The null hypothesis (Hypothesis 4) tested by the MOSUM is that regression coefficients of a linear model are constant over time; the alternative hypothesis is that the coefficients change over time due to external factors [24,42].
A morphometric analysis, among other factors, was also used for explaining possible reasons for inherent differences in streamflow between the paired watersheds, with a higher, but insignificant, flow from the treatment than from the control watershed since the historic study [36]. A morphologic analysis was conducted by deriving the hypsometric curves and indices [54,55] to examine the effects of land morphologic characteristics on runoff generation for the paired watersheds. A system for automated geoscientific analysis (SAGA)-GIS [56] and LiDAR-based DEM were used to generate the hypsometric curves of WS77 and WS80. The hypsometric integral (HI), skewness (skew), and kurtosis of the hypsometric curves were computed using general formulations by Harlin [57] and Pérez-Peña, Azañón, and Azor [58].
4. Results
4.1. Annual Rainfall, Runoff, Runoff Coefficient (ROC), and ET
The first year (2011) of the pre-treatment (baseline) period was relatively dry, with rainfall below 32% of the long-term average (1370 mm) [43], and 2015 was relatively wet, with 58% above average rainfall. The nine-year average baseline period rainfall in WS77 was about 9% above the long-term average (Table 3). The nine-year baseline and the eight-year post-recovery periods yielded the highest and the lowest mean annual flow, respectively, for both watersheds (WS77 > WS80) (Table 1). An unusually high outflow in 2015 due to an extreme October event [59] might have caused the largest average flow in the baseline period. However, the mean annual ROC values, although almost consistently higher in WS77 (mean of 0.24) than in WS80 (0.19) (Table 3), were not statistically different (p = 0.17) between the pair and not different (p > 0.80) from those reported for the pre-Hugo period (1969–1978) (WS77 ROC = 0.25; WS80 ROC = 0.18) [36,41] and the 2004–2011 post-Hugo period (p > 0.20) (WS77 ROC = 0.18; WS80 ROC = 0.14). These results indicate consistency of the rainfall normalized flow (ROCs) between the paired watersheds in each of the three periods, supporting Hypothesis 1.
The annual ET, calculated as a difference between the annual rainfall and runoff, assuming no change in storage, varied from 903 mm in the relatively dry year of 2011 to as high as 1272 mm in the relatively wet year of 2018, with an average of 1167 mm for the control watershed (WS80) (Table 3). The annual ET was consistently lower in WS77, although not significantly so (p = 0.07), with a mean of only 1105 mm, primarily because it had a higher runoff than WS80. The mean annual ET for WS80 was very close to the estimated P-M PET, with no significant difference (p = 0.46), while the ET for WS77 was significantly lower (p = 0.046) than the PET, potentially indicating WS77’s soil water limitations (Table 3). However, the annual ET increased insignificantly with rainfall, yielding a higher R2 (0.71) for WS77 than for WS80 (R2 = 0.42), indicating, again, WS77 as being more soil water limited than WS80.
4.2. Monthly Rainfall and Runoff between the Watersheds
A plot of the monthly rainfall averaged from each month of the 2009–2011 period is shown in Figure 2a for the paired watersheds with their standard deviations. Data show similar rainfall between the watersheds but higher values with larger variabilities in June-October, influenced by tropical storms/hurricanes, than in winter for both. For example, October 2015 yielded a very large rainfall of 667 mm for WS80 and 686 mm for WS77 due to an extreme two-day rainfall of nearly 500 mm on 3–4 October caused by Hurricane Joaquin [59], followed by the second large rainfall event of 296 mm for WS80 and 294 mm for WS77 in October of 2016 as a result of Hurricane Matthew (October 8). These data highly influenced the variability of rainfall in October (Figure 2a). However, the paired watershed monthly rainfall for this study period showed similar means (124.7 ± 93.4 mm for WS77 and 122.9 ± 90.8 mm for WS80) with no significant difference (p = 0.89), consistent with the earlier post-Hugo period reported by Jayakaran et al. [24]. However, the mean monthly rainfall for that period was insignificantly lower, by chance, than the baseline period. This was likely due to more than six times the average number of daily rain events > 25 mm during the 2011–2019 baseline period (not shown), compared to the earlier long-term (1946–2008) period reported by Dai et al. [43]. Moreover, the 2011–2019 period had eight rainfall events exceeding 100 mm in 24 h, induced by hurricanes and tropical depressions.
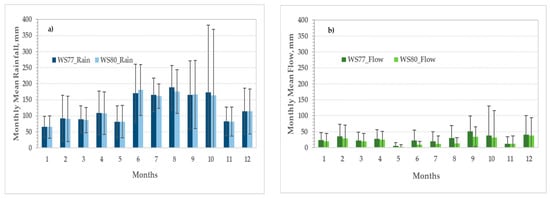
Figure 2.
Distribution of (a) mean monthly rainfall and (b) mean monthly streamflow (runoff) of WS77 and WS80 for 2011–2019. Black vertical bars represent standard deviations.
The distribution of the monthly mean runoff (without October 2015) for the 2011–2019 baseline period depicted the lowest flow during May for both watersheds and the highest in September for WS77 (Figure 2b). The monthly mean runoff was consistently but not significantly (p = 0.22) higher for WS77 than WS80, with WS77 averaging 26.7 mm (0–210 mm) and WS80 averaging 20.4 mm (0–234 mm) without the October 2015 extreme event month (Figure S4a). Similarly, there was no difference in variance in the monthly flow between WS77 and WS80 (p = 0.21).
The effects of extreme rainfall on the water table influencing runoff for both watersheds during the October 2015 and 2016 hurricanes (Figure 2a,b) were similar due to fully saturated antecedent soil conditions (Figure S2). Monthly runoff responses to hurricanes in the following years, i.e., Irma (11–12 September 2017, with rainfall of 130 mm), Florence (14–15 September 2018, with rainfall of 110 mm), and Dorian (4–5 September 2019, with rainfall of 190 mm), were smaller than the two previous ones. The study period also experienced relatively drier months with more no-flow months for the control watershed than for WS77 (Figure 2b), with slightly more variability in monthly summer rainfall between the pair.
Data in Figure 3 for the monthly difference in runoff between the watersheds for 2011–2019 showed WS77 yielding somewhat higher flows (negative difference) than WS80, except for a few periods, consistent with the pre-Hugo (1969–1978) pattern [36] (Figure S1). The mean monthly runoff difference of −6.80 mm (±1.49 mm as standard error [SE]) between WS80 and WS77 for 2011–2019 (Figure 3) (without October 2015)) was 64% higher, although not significantly different (p = 0.54), than the −3.89 mm (±1.09 mm [SE]) obtained by Jayakaran et al. [24] for the 2004–2011 period, when the forest stands recovered. The difference for the 2011–2019 period was slightly, but not statistically (p = 0.27), lower than the pre-Hugo (1969–1978) mean of −8.57 mm (±1.65 mm [SE]) obtained by Richter [36], although the difference between the baseline and each of the pre- and post-Hugo periods was in the same direction. Thus, this result supports Hypothesis 2, confirming the validity of the 2011–2019 period data for pre-treatment calibration.
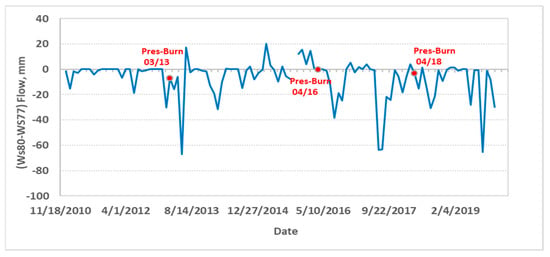
Figure 3.
Difference in measured monthly flow (runoff) between the watersheds WS80 (control) and WS77 (treatment) for 2011–2019. The October 2015 data with an extreme event were omitted. Pres-Burn is prescribed burning.
4.3. Ordinary Least Squares Regression versus Geometric Mean Regression for Paired Monthly Runoff
The plot in Figure 4a compares the relationships of monthly runoff using ordinary least squares (OLS) and geometric mean (GM) regressions between the control watershed (WS80) and the treatment watershed (WS77) without October 2015 because of its extreme flow event. Results showed that the regression slope for the GM (WS77 = 1.15 × WS80 + 3.70; R2 = 0.87) lay just at the border of the 95% confidence bounds (0.99–1.15) of the slope of the OLS regression (WS77 = 1.07 × WS80 + 5.39; R2 = 0.87) (Figure 4a), and so it was barely statistically different (p = 0.01). Therefore, subsequent analysis focused only on the GM regression, which was also just within the bounds of the OLS slope for the recent post-Hugo regeneration (2004–2011) period (Figure 4b).
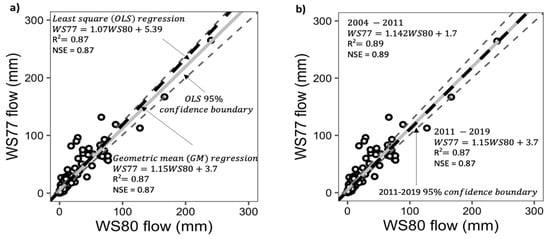
Figure 4.
Comparison of regression lines for relationships between the monthly flow (runoff) for WS77 and WS80 using (a) OLS (solid line), with its 95% confidence intervals, and GM (dashed line) for 2011–2019, both without October 2015, and (b) GM (solid line) for the 2011–2019 period and GM for the 2004–2011 post-Hugo period, which was within the 95% confidence boundaries for the 2011–2019 GM mean.
4.4. Calibration Regression of Paired Monthly Flows
The plot in Figure 4a shows the regression relationships of measured monthly runoff between the control (WS80) and treatment (WS77) watersheds for the pre-treatment calibration period of 2011–2019, without October 2015 because of its extreme rainfall event. The GM regression in Figure 4a yielded a significant monthly runoff relationship (WS77 = 1.15 × WS80 + 3.70; R2 = 0.87) between the paired watersheds. Both the slope of 1.15 and an intercept of 3.7 mm were significant (p < 0.0001). This significance indicates that both the flow rate as well as the shift from the zero intercept could be attributed to the average difference in monthly flow, with WS77 insignificantly higher than WS80, as discussed above (Figure 3). The variability of flow around the 95% confidence limits of the regression line showed somewhat higher discharges for WS77 than for WS80 for most of the months for a flow of less than 100 mm. However, the regression with slope = 1.15 and intercept = 3.7 for the 2011–2019 pre-treatment period differed significantly from the 1969–1978 period with a slope = 1.43 and intercept of −0.68 [36] but not from the 2004–2011 post-Hugo period with 1.14 slope and 1.70 intercept [24] (Figure 4b). Thus, it both validates and invalidates Hypothesis 3. However, the relationship has to be cautiously interpreted as it includes one large event with flow >200 mm on October 8, 2016 (Hurricane Matthew), when a few hours of the unusable data during the peak flow of WS77 were estimated as explained above in Section 3.3, and thus it may have some uncertainties [60]. This event was included in this pre-treatment regression analysis because WS80 had good data, and frequencies of such large events are expected to increase in coming years [11]. For example, 17 out of 17 flow events >30 mm per day−1 occurred mostly because of hurricanes and tropical depressions within the 5 years since 2015 in this study (Figure 5).
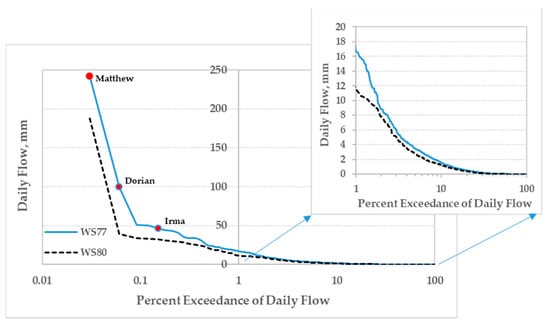
Figure 5.
Daily flow duration curves for WS77 and WS80 for 2011–2019, without the three days (3–5 October) of an extreme event in 2015. Shown is an enlarged plot for a flow of less than 20 mm per day−1.
4.5. Daily Flow (Runoff) Duration Curves
The watersheds’ daily flow frequency duration curves for 2011–2020 are compared in Figure 5. Daily runoff was consistently lower from WS80 than from WS77, as in 1969–1978 [36]. The magnitude of daily runoff of 20 mm was exceeded 0.74% of the time for WS77 and 0.49% of the time for WS80 (Figure 5).
For 10% of the time, daily runoff exceeded 1.53 mm for WS77 and 1.23 mm for WS80. Similarly, WS77 had zero runoff 41.2% of the time, compared to 46.6% of the time for WS80 (Figure 5), which was somewhat similar to the 1969–1978 period, when WS77 had zero runoff 35.6% of the time and WS80 43.8% of the time (not shown). Furthermore, the difference in the percentage of zero runoff days between the watersheds was found to be smaller (5.5%) for the current period than the 8.2% for 1969–1978, although the two periods covered different numbers of days. Excluding the three days of the extreme event in October 2015, runoff exceeded nearly 100 mm day−1 for two hurricanes (Irma and Dorian, in September 2017 and September 2019, respectively), with a steeper slope for both, which indicates a flooding regime consistent with Amatya et al. [7]. Two other storm event days exceeded a 50 mm runoff, in August 2016 and July 2017, indicating an increasing pattern of large flow events during 2015–2019 for these low-gradient watersheds (Figure 5).
5. Discussion
The paired watersheds, besides being adjacent, are similar in many characteristics, including the area, topography, drainage, dominant soil types (Table 2), and mean Leaf Area Index (LAI) of the existing forest stands (Figure S3). Despite these similarities, the treatment watershed (WS77) yielded non-significantly, by chance, a higher monthly runoff than WS80 (Figure 3), except for a few periods with saturated soils (WT near the surface) in July 2013, March 2015, November–December 2015, and October 2016 (Figure S2), when WS80 runoff exceeded that of WS77 (Figure 3). The events in those periods resulted in large peak discharges of WS80, consistent with Harder et al. [15], who found exponentially increasing runoff as the WT in well H neared the surface or got ponded (Figure S2). The insignificantly higher monthly runoff (WS77 > WS80) (Figure 3), consistent with earlier studies [24,36], was also supported by the daily flow duration curves for 2011–2019 (Figure 5). Richter [36], in his study prior to Hugo (1989), ruled out the possible causes of groundwater seepage, drainage area, and vegetation effects for this difference in flow. However, he speculated some possible shortfalls in WS80 flow measurements for that period, particularly during high flow periods with a daily flow > 5 mm. Since that historic study, however, several recent studies, including this one, have verified the flow measurements for WS80, as well as the drainage area and seepage [4,15,17,24,41,59,61]. Therefore, the flow measurements were consistent, except for the October 2015 hurricane [44], when flow rates exceeded the limits of the established rating curves for both watersheds and were estimated using theoretical equations for the WS80 outlet structure [59]. October 2015 was assumed to be an outlier and not used in the monthly analysis of this study.
Below, a few other potential factors were examined that may help explain the reasons why WS77 yielded slightly, but non-significantly, higher runoff than WS80. The mean annual rainfall, as a primary driver of runoff, was not significantly different (p = 0.90) between the watersheds, but both had more rainfall than the long-term average of 1370 mm reported by Dai et al. [43] for 1946–2008, meaning the study period was wetter. Total rainfall for each month was not significantly (α = 0.05) different between the two watersheds, although WS77 experienced somewhat more (Table 3). This finding was consistent with Jayakaran et al. [24], who suggested that given the similarity of rainfall across the two watersheds, relative changes in streamflow are good indicators of relative changes in ET dynamics, as shown in Table 3. Data in Table 3 also show that WS77 is slightly more energy limited (ET/PET) than WS80, which is slightly more moisture limited (ET/Rain) than WS77 [7]. These observations are also supported by the annual rainfall–runoff relationships between the paired watersheds (Figure S4b), which yielded similar slopes, indicating similar rates of runoff response to rainfall. However, WS80 had a larger intercept, indicating more storage, potentially due to its greater ET than that of WS77 (Table 3). For example, although the annual ET through the baseline period was relatively constant, with a coefficient of variation (COV) <0.1 for both watersheds, WS80 yielded a somewhat higher mean value (1167 mm) than WS77 (1105 mm). These results, including the ROCs, are consistent with Boulet et al. [62], who also found such a hydrological difference between two paired Mediterranean headwater catchments with dissimilar land covers (Pinis pinaster and Eucalyptus globulus). In addition, the watersheds in this study differed in three important land use and management aspects, which were not addressed in earlier studies and are discussed below.
First, historic land use differed between WS80 and WS77. The lower reaches of WS80 were used for rice cultivation. As a result, the watershed has historical water management structures which WS77 does not have. LiDAR data analysis also revealed some depressions caused by legacy dikes on downstream riparian areas of WS80 [63]. More evidence comes from Amoah et al. [17], who found a nine-times higher mean overall surface depressional storage capacity (DSC) in WS80 than WS77, as well as more than four-times more wetland area in WS80 (Table 2). Thus, it is very likely that the high WS80 DSC values may have contributed to a higher water table during winter with lower ET demands and an increased ET with a lower water table during the summer growing season (Figure S2). Another likely cause of WS80’s reduced streamflow is modulated peaks caused by the storage, as evidenced by WS80’s flatter slope in the range of an approximately 10–40 mm daily flow (Figure 5), consistent with historical records [36]. The smaller flow rates of WS80 were further evidenced by the daily flow and 10-min hydrographs for two events of 8 June and 5 September in 2019, as an example (Figure 6a,b), in which the flow rates of WS77 with a much lower DSC were 3–4 times higher than that of WS80, consistent with some other years as well (not shown). These observations are consistent with other studies [18,19,64,65,66,67] that reported a water table position and microtopography influence storage, and they are critical factors that affect streamflow patterns, stormflow peaks, and volume on shallow coastal forests. For example, Rains et al. [66] noted that the cumulative effect of depressions (WS80 in our study) can play an important role in landscape-scale hydrology by regulating the frequency, magnitude, timing, duration, and rate of flows to downgradient waters along overland and groundwater flow paths. Similarly, Acreman and Holden’s conclusions [64] on five characteristics (landscape location and configuration, topography, soil characteristics, soil moisture status, and drainage management) largely determined the influence on floods, consistent with our runoff observations for these two watersheds.
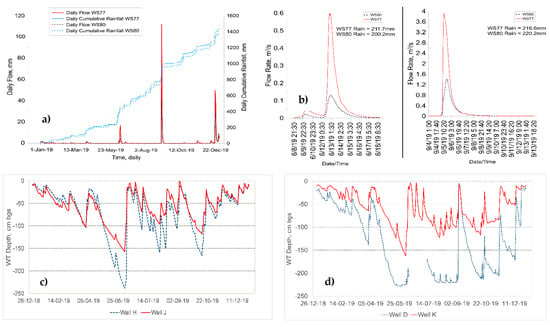
Figure 6.
Measured (a) daily flow and daily cumulative rainfall and (b) hydrographs of June 8 and September 5 storm events for both WS77 and WS80, (c) daily water table depths of upland well H (WS80) and well J (WS77), and (d) daily water table depths for riparian well D (WS80) and well K (WS77) for 2019.
Secondly, a contemporary difference between the two watersheds is that WS80 has not received any forest management activities since it was established in 1968, while WS77 has been actively managed for loblolly pine silvicultural research using prescribed fire in a 2–3-year cycle (Figure S5a) for the past 20 years. There is a potential for flow to increase soon after fire [68,69]. For example, reduced understory vegetation (Figure S5b), LAI, and ET caused by prescribed burning in March 2013, April 2016, and April 2018 (Figure 3) might have contributed to some temporary increased runoff in June 2013, August 2016, and August 2018. Accordingly, a detailed analysis using a MOSUM test in Figure 7 shows that the months immediately after prescribed burning captured a slight change in the relationship of paired flow, as shown by the upward or downward movement of the MOSUM curve, but not significantly impacting the linear regression coefficients (curve within the two red horizontal lines). Change was detected in June 2017, more than a year after prescribed burning. In addition, earlier studies [34,35] showed that prescribed fire had minimal or non-significant effects on soil properties, water quality, and water yield compared to the untreated reference for these watersheds. Furthermore, no heavy equipment, which may compact the soil, potentially reducing the conductivity, was used in this treatment. In addition, a rapid establishment of ground cover after the fire stabilizes the soil.
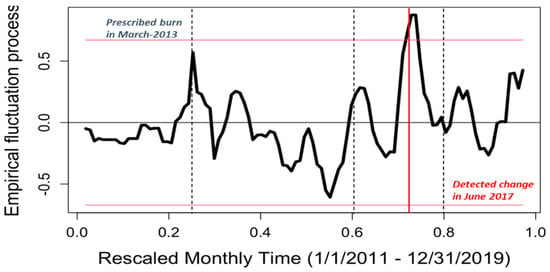
Figure 7.
Ordinary least squares moving sums of recursive residuals (OLS-MOSUM) for monthly linear regression between WS77 (treatment) and WS80 (control) flow data. A shift of the MOSUM outside the 95% confidence intervals (horizontal red lines) is indicative of a structural break in the linear relationship. The vertical solid red line is the estimated structural break point. The three dotted vertical lines represent the months of the prescribed burning.
The fact that the mean monthly difference (WS80–WS77) in runoff (−6.8 mm) for the 2011–2019 period was found to be not different from the 1969–1978 (−8.6 mm) and 2004–2011 (−3.9 mm) periods further indicated the initiation of forest regeneration by 2004, with complete recovery by 2011 [24], as shown in Figure S1.
Third, active management of WS77 results in a stand that is predominately loblolly pine, in contrast to WS80, which is mixed hardwood-pine. Despite this difference in stand composition, the mean LAI of 2.31 m2 m−2 (1.23 m2 m−2–3.36 m2 m−2), measured on the control watershed with pine-mixed-hardwood forest [43], was not significantly different (p = 0.34) from the mean of 2.54 m2 m−2 (1.62 m2 m−2–2.92 m2 m−2) measured in 2019–2020 in WS77 with pine stands (Figure S3). Although the WS77 mean LAI was slightly higher than that of WS80, the growing season LAI, with a potential to influence ET, was higher (as high as 4–6 m2 m−2) in some plots during the growing season for WS80. Therefore, the lower WS80 runoff during growing season was partially attributed to a higher ET of the mixed hardwood-pine forest. For example, in the daily flow comparison for 2019 in Figure 6a, despite a lower WS77 total rainfall (235 mm) from Hurricane Dorian (September 5) than WS80′s 242 mm, the WS77 daily flow was larger by 80 mm than WS80’s. The larger flow of WS77 was likely due to its shallower WT, with less storage than that of WS80 in late August/early September (Figure 6c,d), resulting in an early initiation of flows. Accordingly, for WS80, a deeper WT and larger storage possibly caused larger ET loss than for WS77, with no flows for 54 days until this September 5 event, in contrast with only 2 days without flows for WS77. This pattern, with deeper WT depths and larger growing season deficits of WS80 than of WS77, was also evident in the summers of 2011 to 2014, as well as briefly in 2016, 2017, and 2019 when WT fell below 100 cm (Figure S2), potentially contributing to higher ET and lower flows.
In addition, land morphology, defined by the hypsometric curve, also might have played a role in the runoff difference between the watersheds. The shape of the hypsometric curve is represented by a hypsometric integral, HI [70,71], with a value of 0.5 representing a threshold between the concave (HI < 0.5) and convex (HI ≥ 0.5) hypsometric forms. Vivoni et al. [71] found, keeping all other watershed variables constant (e.g., land use, land cover, rainfall), that modeled watersheds with a higher HI yielded higher runoff than those with a lower HI. Concave hypsometric curves for WS77 and WS80 (Figure 8a,b) clearly indicated that WS77 may be expected to yield more runoff than WS80 because of its higher HI of 0.405, compared to 0.285 for WS80 until 2001. The recomputed HI value of 0.313 after the drainage area of WS80 changed from 206 ha to 160 ha in 2001 was still < 0.405 (WS77). These results suggest that the shape of the basin hypsometry could be another reason for the difference in runoff between the two watersheds.
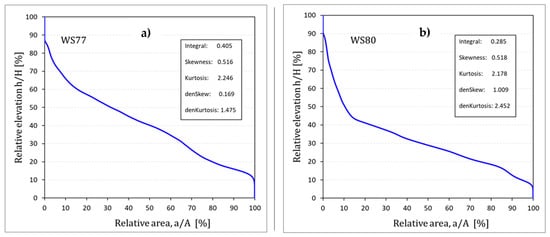
Figure 8.
Hypsometric curves for watersheds (a) WS77 and (b) WS80. A hypsometric integral less than 0.5 and positive density skewness are characteristics of landforms dominated by surface runoff rather than subsurface drainage [71].
The pre-treatment monthly paired flow relationship without the October 2015 extreme runoff did not differ significantly from the 2004–2011 relationship (Figure 4b) reported by Jayakaran et al. [24]. The estimated monthly runoff of 609 mm was dominated by a one-day (4 October 2015) estimated extreme runoff of 311 mm on WS80. The peak flow rate for this hurricane event, estimated as 17.4 m3 s−1 (10.9 m3 s−1 km−2), was assumed to have exceeded the 500-year flood [59,72], and therefore, this month, as an outlier, was omitted from the monthly analysis. However, the daily flow frequency duration analysis in this study also included the October 2015 month, except for the 3–5 October extreme flow days, and other large flow events caused by other hurricanes (Figure 5). These data may explain how the 2011–2019 calibration relationship might have been influenced by an increased number of high precipitation events. However, the fact that the 2004–2011 regression for the period with a reportedly recovered forest [24], but not the pre-Hugo 1969–1978, was like that of 2011–2019 may indicate the similar runoff response to rainfall during the two recent periods, dissimilar from 1969–1978. This similarity is potentially supported by the observations of Dai et al. [43], who reported more annual average storms > 50 mm in the 1982 to 2008 period than in 1946–2008, with even more storms by 2019 (not shown). We suggest, therefore, that the 2011–2019 relationship, which included some hurricane/tropical storm events, with no difference in either the mean monthly flow or regression relationship of the recent 2004–2011 period, is more justified than the pre-Hugo 1969–78 for its application in treatment effects evaluation of WS77 water yield later.
Our computed p-value, R2, NSE, and RMSE statistics characterizing statistical significance and predictive quantifiable regression were also consistent with similar statistics (R2 = 0.97, NSE = 0.97) for the paired daily flow relationships for 1988–1989 and higher than R2 = 0.48 and NSE = 0.34 for the 2007–2008 calibration period reported by Ssegane [26] in their North Carolina pine forest study. Those values were also similar to R2 = 0.83 and NSE = 0.82 and R2 = 0.91 and NSE = 0.91 for two separate paired watersheds for the 2009–2012 calibration periods reported for studies in coastal North Carolina by Ssegane et al. [42].
Thus, the strong and significant 2011–2019 geometric regression-based pre-treatment baseline monthly runoff calibration relationship with given confidence limits (Figure 4b) could be used to compare the actual measured WS77 flow response with its expected flow response compared to WS80, within the bounds of data used in the calibration regression for quantifying the magnitude and significance of effects of longleaf pine restoration treatments in the near future. Nevertheless, it should still be cautiously interpreted and applied if frequencies of extreme events, like the October 2015 hurricane excluded from this study, continue to increase, as predicted by regional studies across the southeastern region [73]. This study also emphasizes a need to analyze long-term datasets, when available, to better understand the role of hydrological dynamics and their evolution and adaptation, including the paired watershed calibration for assessing treatment effects, in the context of a changing climate [74].
6. Conclusions
This study evaluated the seasonal rainfall and runoff response pattern and the flow calibration relationship using nine years (2011–2019) of hydro-meteorologic data for two long-term paired watersheds (155 ha, WS77 (treatment) and 160 ha, WS80 (control)) designated for a longleaf pine (LLP) restoration project at Santee Experimental Forest on the Atlantic Coastal Plain. The geometric mean regression-based monthly runoff relationship, proposed as a pre-treatment baseline, was compared to relationships reported earlier using 1969–1978 for pre-hurricane Hugo and 2004–2011 as post-Hugo recovery periods by Jayakaran et al. [24]. Other paired hydrologic metrics with a potential to influence the runoff were also used. Results revealed that the historical pattern in the runoff difference of WS77 > WS80 was maintained in the current baseline assessment. Furthermore, the difference in the mean monthly runoff between the two watersheds did not vary significantly (α = 0.05) from the pre-Hugo and post-Hugo periods, indicating a complete runoff recovery, as shown earlier by Jayakaran et al. [24]. The insignificantly higher, by chance, mean seasonal flow for WS77 than for WS80 was attributed to a lower surface storage (mean depressional storage capacity; Table 2) and higher hypsometric integral (a land morphological characteristic; Figure 8) for WS77 than for WS80, with a larger surface storage as well as subsurface storage indicated by a deeper average water table than that of WS77. In addition, the baseline monthly runoff calibration relationship, with multiple large flow events covering 2011–2019, except for an extreme of October 2015, did not differ from the 2004–2011 period but differed from 1969–1978, indicating a complete forest recovery and, possibly, a similarity in the climatic pattern of two recent periods. The baseline calibration relationship, found to be unaffected by periodic prescribed burning, was also significant (α = 0.05), predictable, and consistent, thereby providing a basis for quantifying post-treatment effects of the full LLP restoration on water yield later in the future. However, the relationship will have to be used cautiously when extrapolating for extremely large flow events, exceeding flow limits of the relationship as well as possibly exceeding the rating curve limits of the current gauging stations, otherwise equipped with well-defined compound weir control structures and dual sensors, including a backup for precise measurements of stage elevations.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/w13213121/s1, Figure S1: 12-month moving average of difference in monthly flow between WS80 and WS77 for 2011–2019 climatic conditions compared to those in 1969–1978 and 2004–2011 using whole long-term data with a large gap from 1982 to 1989, Figure S2: Measured daily water table depths on WS77 (Well J) and WS80 (Well H) watersheds for the years 2011 to 2019, Figure S3: LiCOR-2000 measured watershed averaged LAI for WS77 (top) and WS80 (bottom) for the 2019–2020 and 2008–2011 periods, respectively, Figure S4: (a) Box plot with median and interquartile range of monthly flow (MonFlow) measured on WS77 and WS80 watersheds in 2011–2019 without October 2015 as an outlier, and (b) Annual rainfall versus annual runoff between paired watersheds for 2011–2019, showing larger storage on WS80 than on WS77, Figure S5: Pictures of (a) operational prescribed burning and (b) post-burn land cover on WS77 treatment watershed, Table S1: Chronology of activities that took place on the WS77 and WS80 watersheds.
Author Contributions
Conceptualization, D.M.A. and C.C.T.; methodology, D.M.A. and S.H.; software, S.H. and M.D.H.; validation of formats, M.D.H.; formal analysis, D.M.A. and S.H.; investigation, D.M.A.; resources, D.M.A. and C.C.T.; writing—D.M.A.; writing—review and editing, D.M.A., S.H., C.C.T. and M.D.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data used in this paper can be accessed at https://doi.org/10.2737/RDS-2019-0033 for WS77 and https://doi.org/10.2737/RDS-2021-0043 for WS80.
Acknowledgments
The authors would like to acknowledge Andy Harrison and Julie Arnold of the Hydrologic Technician and Forestry Technician, respectively, at the US Forest Service Santee Experimental Forest for providing hydro-meteorologic data and Figure 1, respectively. The authors also thank the reviewers Ge Sun, USDA Forest Service, and Jami Nettles, Research Hydrologist at Weyerhaeuser, for their constructive comments and suggestions; Stephanie Siegel at Leading Solutions LLC for help with editing; and Priyanka Rao at Washington State University for help with providing plots and statistics from R-software. The opinions presented in this article are those of the authors and should not be construed to represent any official USDA or U.S. Government determination or policy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Samuelson, L.J.; Stokes, T.A.; Johnsen, K.H. Ecophysiological comparison of 50-year-old longleaf pine, slash pine and loblolly pine. For. Ecol. Manag. 2012, 274, 108–115. [Google Scholar] [CrossRef]
- Brantley, S.T.; Vose, J.M.; Wear, D.N.; Band, L. Potential of longleaf pine restoration to mitigate water scarcity and sustain carbon sequestration: Planning for an uncertain future. In Proceedings of the Ecological Restoration and Management of Longleaf Pine Forests; CRC Press: Boca Raton, FL, USA, 2018; pp. 291–310. [Google Scholar]
- Eshleman, K.N.; Pollard, J.S.; O’Brien, A.K. Interactions between groundwater and surface water in a Virginia coastal plain watershed. 1. Hydrological flowpaths. Hydrol. Process. 1994, 8, 389–410. [Google Scholar] [CrossRef]
- Griffin, M.P.; Callahan, T.J.; Vulava, V.M.; Williams, T.M. Storm-event flow pathways in lower coastal plain forested watersheds of the southeastern United States. Water Resour. Res. 2014, 50, 8265–8280. [Google Scholar] [CrossRef]
- Slattery, M.C.; Gares, P.A.; Phillips, J.D. Multiple modes of storm runoff generation in a North Carolina coastal plain watershed. Hydrol. Process. 2006, 20, 2953–2969. [Google Scholar] [CrossRef]
- Williams, T.M. Evidence of runoff production mechanisms in low gradient coastal forested watersheds. In Proceedings of the 2007 Minneapolis, St. Joseph, MI, USA, 17–20 June 2007; Paper # 072228. American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2007; Volume 5, pp. 1–13. [Google Scholar]
- Amatya, D.M.; Williams, T.M.; Nettles, J.E.; Skaggs, R.W.; Trettin, C.C. Comparison of hydrology of two Atlantic coastal plain forests. Trans. ASABE 2019, 62, 1509–1529. [Google Scholar] [CrossRef]
- Hornbeck, J.W.; Adams, M.B.; Corbett, E.S.; Verry, E.S.; Lynch, J.A. Long-Term Impacts of Forest Treatments on Water Yield: A Summary for Northeastern USA; Scientific Research Publishing: Wuhan, China, 1993; Volume 150, pp. 323–344. [Google Scholar] [CrossRef]
- Kelly, C.N.; McGuire, K.J.; Miniat, C.F.; Vose, J.M. Streamflow response to increasing precipitation extremes altered by forest management. Geophys. Res. Lett. 2016, 43, 3727–3736. [Google Scholar] [CrossRef]
- Shelby, J.D.; Chescheir, G.M.; Skaggs, R.W.; Amatya, D.M. Hydrologic and Water-Quality Response of Forested and Agricultural Lands During The 1999 Extreme Weather Conditions in Eastern North Carolina. Am. Soc. Agric. Eng. 2006, 48, 2179–2188. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Acharya, S.; Jawitz, J.W.; Mylavarapu, R.S. Analytical expressions for drainable and fillable porosity of phreatic aquifers under vertical fluxes from evapotranspiration and recharge. Water Resour. Res. 2012, 48, 11526. [Google Scholar] [CrossRef]
- Amatya, D.M.; Skaggs, R.W.; Gregory, J.D. Effects of controlled drainage on the hydrology of drained pine plantations in the North Carolina coastal plain. J. Hydrol. 1996, 181, 211–232. [Google Scholar] [CrossRef]
- Loheide, S.P.; Butler, J.J.; Gorelick, S.M. Estimation of groundwater consumption by phreatophytes using diurnal water table fluctuations: A saturated-unsaturated flow assessment. Water Resour. Res. 2005, 41, 1–14. [Google Scholar] [CrossRef]
- Harder, S.V.; Amatya, D.M.; Callahan, T.J.; Trettin, C.C.; Hakkila, J. Hydrology and Water Budget for a Forested Atlantic Coastal Plain Watershed, South Carolina. J. Am. Water Resour. Assoc. 2007, 43, 563–575. [Google Scholar] [CrossRef]
- Evaristo, J.; McDonnell, J.J. Global analysis of streamflow response to forest management. Nature 2019, 570, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Amoah, J.K.O.; Amatya, D.M.; Nnaji, S. Quantifying watershed surface depression storage: Determination and application in a hydrologic model. Hydrol. Process. 2013, 27, 2401–2413. [Google Scholar] [CrossRef]
- Hu, L.; Bao, W.; Shi, P.; Wang, J.; Lu, M. Simulation of overland flow considering the influence of topographic depressions. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Walega, A.; Amatya, D.M.; Caldwell, P.; Marion, D.; Panda, S. Assessment of storm direct runoff and peak flow rates using improved SCS-CN models for selected forested watersheds in the Southeastern United States. J. Hydrol. Reg. Stud. 2020, 27, 100645. [Google Scholar] [CrossRef]
- Wu, K.; Johnston, C.A. Hydrologic comparison between a forested and a wetland/lake dominated watershed using SWAT. Hydrol. Process. 2008, 22, 1431–1442. [Google Scholar] [CrossRef]
- Ares, M.G.; Varni, M.; Chagas, C. Runoff response of a small agricultural basin in the argentine Pampas considering connectivity aspects. Hydrol. Process. 2020, 34, 3102–3119. [Google Scholar] [CrossRef]
- Todd, A.K.; Buttle, J.M.; Taylor, C.H. Hydrologic dynamics and linkages in a wetland-dominated basin. J. Hydrol. 2006, 319, 15–35. [Google Scholar] [CrossRef]
- Trettin, C.C.; Amatya, D.M.; Gaskins, A.H.; Miniat, C.F.; Chow, A.; Callahan, T. Watershed response to longleaf pine restoration–application of paired watersheds on the Santee Experimental Forest. In Proceedings of the 6th Interagency Conference on Research in Watershed, Shepherdstown, WV, USA, 23–26 July 2018; Volume 2018, pp. 194–201. [Google Scholar]
- Jayakaran, A.D.; Williams, T.M.; Ssegane, H.; Amatya, D.M.; Song, B.; Trettin, C.C. Hurricane impacts on a pair of coastal forested watersheds: Implications of selective hurricane damage to forest structure and streamflow dynamics. Hydrol. Earth Syst. Sci. 2014, 18, 1151–1164. [Google Scholar] [CrossRef]
- Loftis, J.C.; MacDonald, L.H.; Streett, S.; Iyer, H.K.; Bunte, K. Detecting cumulative watershed effects: The statistical power of pairing. J. Hydrol. 2001, 251, 49–64. [Google Scholar] [CrossRef]
- Ssegane, H.; Amatya, D.M.; Chescheir, G.M.; Skaggs, W.R.; Tollner, E.W.; Nettles, J.E. Consistency of Hydrologic Relationships of a Paired Watershed Approach. Am. J. Clim. Chang. 2013, 2, 147–164. [Google Scholar] [CrossRef][Green Version]
- Amatya, D.M.; Gregory, J.D.; Skaggs, R.W. Effects of Controlled Drainage on Storm Event Hydrology in A Loblolly Pine Plantation. J. Am. Water Resour. Assoc. 2000, 36, 175–190. [Google Scholar] [CrossRef]
- Bosch, J.M.; Hewlett, J.D. A review of catchment experiments to determine the effect of vegetation changes on water yield and evapotranspiration. J. Hydrol. 1982, 55, 3–23. [Google Scholar] [CrossRef]
- Brown, A.E.; Zhang, L.; McMahon, T.A.; Western, A.W.; Vertessy, R.A. A review of paired catchment studies for determining changes in water yield resulting from alterations in vegetation. J. Hydrol. 2005, 310, 28–61. [Google Scholar] [CrossRef]
- Tomer, M.D.; Schilling, K.E. A simple approach to distinguish land-use and climate-change effects on watershed hydrology. J. Hydrol. 2009, 376, 24–33. [Google Scholar] [CrossRef]
- Clausen, J.; Spooner, J. Paired Watershed Study Design; Technical Report R841-F-93-009; United States Environmental Protection Agency, Office of Water: Washington, DC, USA, 1993.
- Bren, L.J.; Lane, P.N.J. Optimal development of calibration equations for paired catchment projects. J. Hydrol. 2014, 519, 720–731. [Google Scholar] [CrossRef]
- Alila, Y.; Kuraś, P.K.; Schnorbus, M.; Hudson, R. Forests and floods: A new paradigm sheds light on age-old controversies. Water Resour. Res. 2009, 45, 8416. [Google Scholar] [CrossRef]
- Binstock, D.A. Effects of a Prescribed Winter Burn on Anion Nutrient Budgets in the Santee Experimental Forest Watershed Ecosystem. Ph.D. Thesis, Duke University, Durham, NC, USA, 1978. [Google Scholar]
- Richter, D.D.; Ralston, C.W.; Harms, W.R. Prescribed fire: Effects on water quality and forest nutrient cycling. Science 1982, 215, 661–663. [Google Scholar] [CrossRef]
- Richter, D. Effects of Water Quality and Nutrient Cycling in Forested Watersheds of the Santee Experimental Forest in South Carolina. Ph.D. Thesis, Duke University, Durham, NC, USA, 1980. [Google Scholar]
- Hook, D.D.; Buford, M.A.; Williams, T.M. Impact of Hurricane Hugo on the South Carolina Coastal Plain. J. Coast. Res. 1991, 291–300. [Google Scholar] [CrossRef]
- Chescheir, G.M.; Skaggs, R.W.; Amatya, D.M. Quantifying the Hydrologic Impacts of Afforestation in Uruguay: A Paired Watershed Study. In Proceedings of the XIII World Forestry Congress, Buenos Aires, Argentina, 18–23 October 2009. [Google Scholar]
- Amatya, D.M.; Trettin, C.C. Long-Term Ecohydrologic Monitoring: A Case Study from the Santee Experimental Forest, South Carolina. J. South Carolina Water Resour. 2020, 6, 46–55. [Google Scholar] [CrossRef]
- Oda, T.; Green, M.B.; Urakawa, R.; Scanlon, T.M.; Sebestyen, S.D.; McGuire, K.J.; Katsuyama, M.; Fukuzawa, K.; Adams, M.B.; Ohte, N. Stream Runoff and Nitrate Recovery Times After Forest Disturbance in the USA and Japan. Water Resour. Res. 2018, 54, 6042–6054. [Google Scholar] [CrossRef]
- Amatya, D.M.; Miwa, M.; Harrison, C.A.; Trettin, C.C.; Sun, G. Hydrology and Water Quality of Two First Order Forested Watersheds in Coastal South Carolina; 2006, Paper # 062182; American Society of Agricultural and Biological Engineers: Portland, OR, USA, 2006. [Google Scholar]
- Ssegane, H.; Amatya, D.M.; Muwamba, A.; Chescheir, G.M.; Appelboom, T.; Tollner, E.W.; Nettles, J.E.; Youssef, M.A.; Birgand, F.; Skaggs, R.W. Calibration of paired watersheds: Utility of moving sums in presence of externalities. Hydrol. Process. 2017, 31, 3458–3471. [Google Scholar] [CrossRef]
- Dai, Z.; Trettin, C.C.; Amatya, D.M. Effects of Climate Variability on Forest Hydrology and Carbon Sequestration on the Santee Experimental Forest in Coastal South Carolina; General Technical Report 172; United States Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2013.
- Amatya, D.M.; Trettin, C.C. Santee Experimental Forest, Watershed 77: Streamflow, Water Chemistry, Water Table, and Weather Data; Forest Service Research Data Archive: Fort Collins, CO, USA, 2019; Updated 9 June 2020. [CrossRef]
- Amatya, D.M.; Trettin, C.C. Santee Experimental Forest, Watershed 80: Streamflow, Water Chemistry, Water Table, and Weather Data; Forest Service Research Data Archive: Fort Collins, CO, USA, 2021. [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [CrossRef]
- Amatya, D.M.; Harrison, C.A. Grass and Forest Potential Evapotranspiration Comparison Using Five Methods in the Atlantic Coastal Plain. J. Hydrol. Eng. 2016, 21, 05016007. [Google Scholar] [CrossRef]
- Amatya, D.M.; Trettin, C.C. Santee Experimental Forest, Headquarters: Climate Data; Forest Service Research Data Archive: Fort Collins, CO, USA, 2020. [CrossRef]
- Amatya, D.M.; Trettin, C.C. Development of watershed hydrologic studies at Santee Experimental Forest, South Carolina. In Advancing the Fundamental Sciences, Proceedings of the Forest Service National Earth Sciences Conference, San Diego, CA, 18–22 October 2004; Furniss, M.J., Clifton, C.F., Ronnenberg, K.L., Eds.; Pacific Northwest Research Station: Portland, OR, USA, 2007; pp. 180–190. [Google Scholar]
- SAS Base SAS 9.1.3 Procedures Guide; SAS Institute, Inc.: Cary, NC, USA, 2006.
- Warton, D.I.; Wright, I.J.; Falster, D.S.; Westoby, M. Bivariate line-fitting methods for allometry. Biol. Rev. 2006, 81, 259. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Friedman, J.; Bohonak, A.J.; Levine, R.A. When are two pieces better than one: Fitting and testing OLS and RMA regressions. Environmetrics 2013, 24, 306–316. [Google Scholar] [CrossRef]
- Krug, J.A.; Wrather, W.E.; Langbein, W.B. Topographic characteristics of drainage basins. Water Supply Pap. 1947, 125–157. [Google Scholar] [CrossRef]
- Strahler, A.N. Hypsometric (Area-Altitude) Analysis of Erosional Topography. GSA Bull. 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- Olaya, V.; Conrad, O. Chapter 12 Geomorphometry in SAGA. Dev. Soil Sci. 2009, 33, 298–308. [Google Scholar]
- Harlin, J.M. Statistical moments of the hypsometric curve and its density function. J. Int. Assoc. Math. Geol. 1978, 10, 59–72. [Google Scholar] [CrossRef]
- Pérez-Peña, J.V.; Azañón, J.M.; Azor, A. CalHypso: An ArcGIS extension to calculate hypsometric curves and their statistical moments. Applications to drainage basin analysis in SE Spain. Comput. Geosci. 2009, 35, 1214–1223. [Google Scholar] [CrossRef]
- Amatya, D.M.; Harrison, C.A.; Trettin, C.C. Hydro-meteorologic Assessment of October 2015 Extreme Precipitation Event on Santee Experimental Forest Watersheds, South Carolina. J. South Carol. Water Resour. 2016, 3, 12. [Google Scholar]
- Saleh, F.; Ramaswamy, V.; Georgas, N.; Blumberg, A.F.; Pullen, J. A retrospective streamflow ensemble forecast for an extreme hydrologic event: A case study of Hurricane Irene and on the Hudson River basin. Hydrol. Earth Syst. Sci. 2016, 20, 2649–2667. [Google Scholar] [CrossRef]
- Callahan, T.J.; Vulava, V.M.; Passarello, M.C.; Garrett, C.G. Estimating groundwater recharge in lowland watersheds. Hydrol. Proc. 2012, 26, 2845–2855. [Google Scholar] [CrossRef]
- Boulet, A.-K.; Rial-Rivas, M.E.; Ferreira, C.; Coelho, C.O.A.; Kalantari, Z.; Keizer, J.J.; Ferreira, A.J.D. Hydrological Processes in Eucalypt and Pine Forested Headwater Catchments within Mediterranean Region. Water 2021, 13, 1418. [Google Scholar] [CrossRef]
- Amatya, D.; Trettin, C.; Panda, S.; Ssegane, H. Application of LiDAR Data for Hydrologic Assessments of Low-Gradient Coastal Watershed Drainage Characteristics. J. Geogr. Inf. Syst. 2013, 05, 175–191. [Google Scholar] [CrossRef]
- Acreman, M.; Holden, J. How wetlands affect floods. Wetlands 2013, 33, 773–786. [Google Scholar] [CrossRef]
- Amatya, D.M.; Chescheir, G.M.; Skaggs, R.W. Hydrologic effects of the location and size of a natural wetland in an agricultural landscape. In Proceedings of the AWRA/ASAE International Conference on “Versatility of Wetlands in the Agricultural Landscape”; American Society of Agricultural Engineers: Tampa, FL, USA, 1995; pp. 477–488. [Google Scholar]
- Rains, M.C.; Leibowitz, S.G.; Cohen, M.J.; Creed, I.F.; Golden, H.E.; Jawitz, J.W.; Kalla, P.; Lane, C.R.; Lang, M.W.; Mclaughlin, D.L. Geographically isolated wetlands are part of the hydrological landscape. Hydrol. Process. 2016, 30, 153–160. [Google Scholar] [CrossRef]
- Vogel, R.M.; Fennessey, N.M. Flow Duration Curves II: A Review of Applications in Water Resources Planning. J. Am. Water Resour. Assoc. 1995, 31, 1029–1039. [Google Scholar] [CrossRef]
- Ebel, B.A.; Moody, J.A.; Martin, D.A. Hydrologic conditions controlling runoff generation immediately after wildfire. Water Resour. Res. 2012, 48, 3529. [Google Scholar] [CrossRef]
- Robichaud, P.R. Fire effects on infiltration rates after prescribed fire in Northern Rocky Mountain forests, USA. J. Hydrol. 2000, 231, 220–229. [Google Scholar] [CrossRef]
- Luo, W. Quantifying groundwater-sapping landforms with a hypsometric technique. J. Geophys. Res. Planets 2000, 105, 1685–1694. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Di Benedetto, F.; Grimaldi, S.; Eltahir, E.A.B. Hypsometric control on surface and subsurface runoff. Water Resour. Res. 2008, 44, 12502. [Google Scholar] [CrossRef]
- Amatya, D.M.; Radecki-Pawlik, A.A. Flow Dynamics of Three Experimental Forested Watersheds in Coastal South Carolina (USA). ACTA Sci. Pol. Form. Circumiectus 2007, 6, 3–17. [Google Scholar]
- Ingram, K.T.; Dow, K.; Carter, L.; Anderson, J.A. Climate of the Southeast United States: Variability, Change, Impacts, and Vulnerability; Island Press-Center for Resource Economics: Washington, DC, USA, 2013; ISBN 9781610915090. [Google Scholar]
- Juez, C.; Pena-Angulo, D.; Khorchani, M.; Regues, D.; Nadal-Romero, E. 20-Years of hindsight into hydrological dynamics of a mountain forest catchment in the Central Spanish Pyrenees. Sci. Total Environ. 2021, 766. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).