An Analysis of Precipitation Extreme Events Based on the SPI and EDI Values in the Free State Province, South Africa
Abstract
1. Introduction
2. Materials and Methods
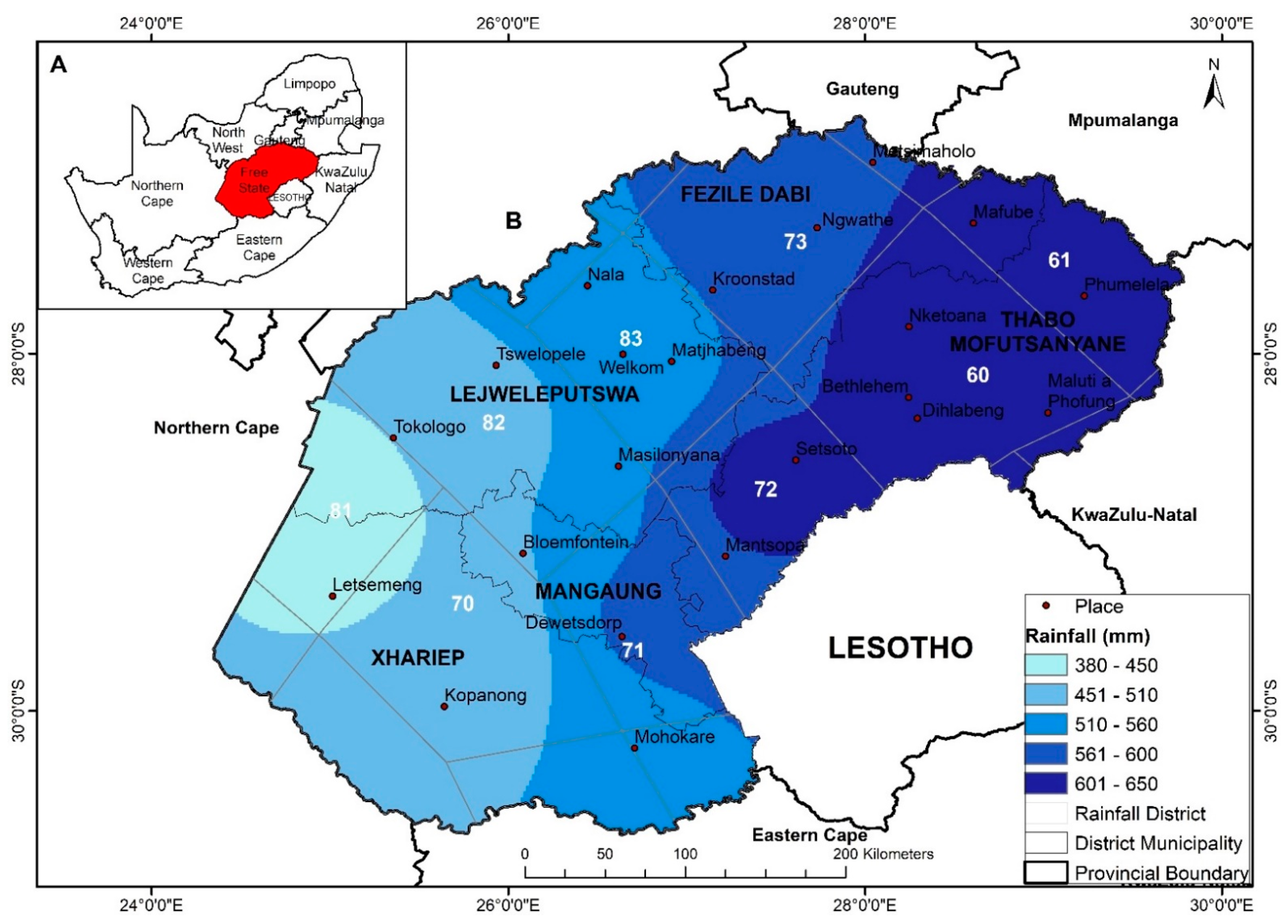
2.1. Study Area
2.2. Materials
2.3. Methods
2.3.1. Standardized Precipitation Index
2.3.2. Effective Drought Index
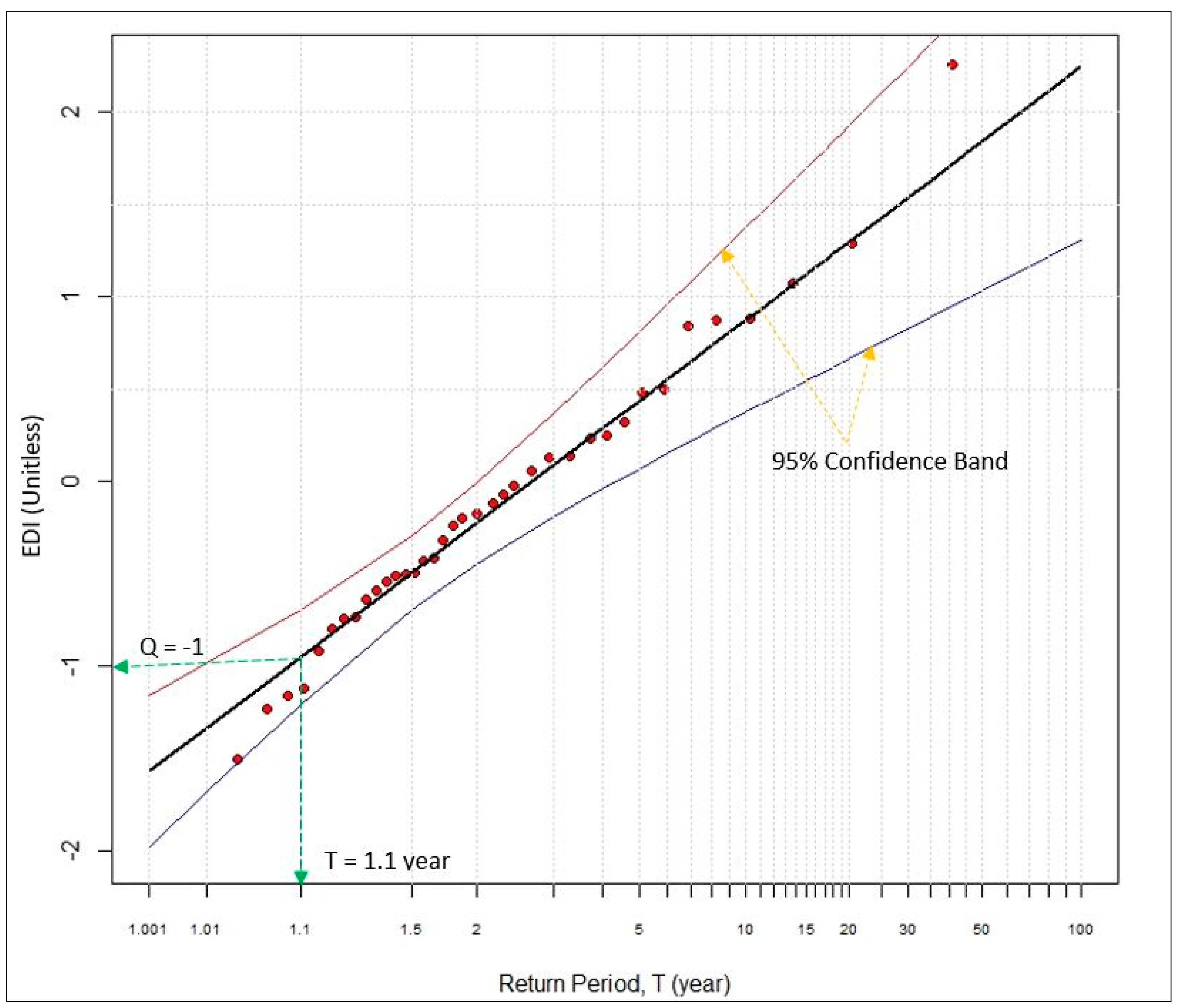
2.3.3. Extreme Value and Return Level Analyses
2.3.4. Extreme Frequency Analysis (EFA)
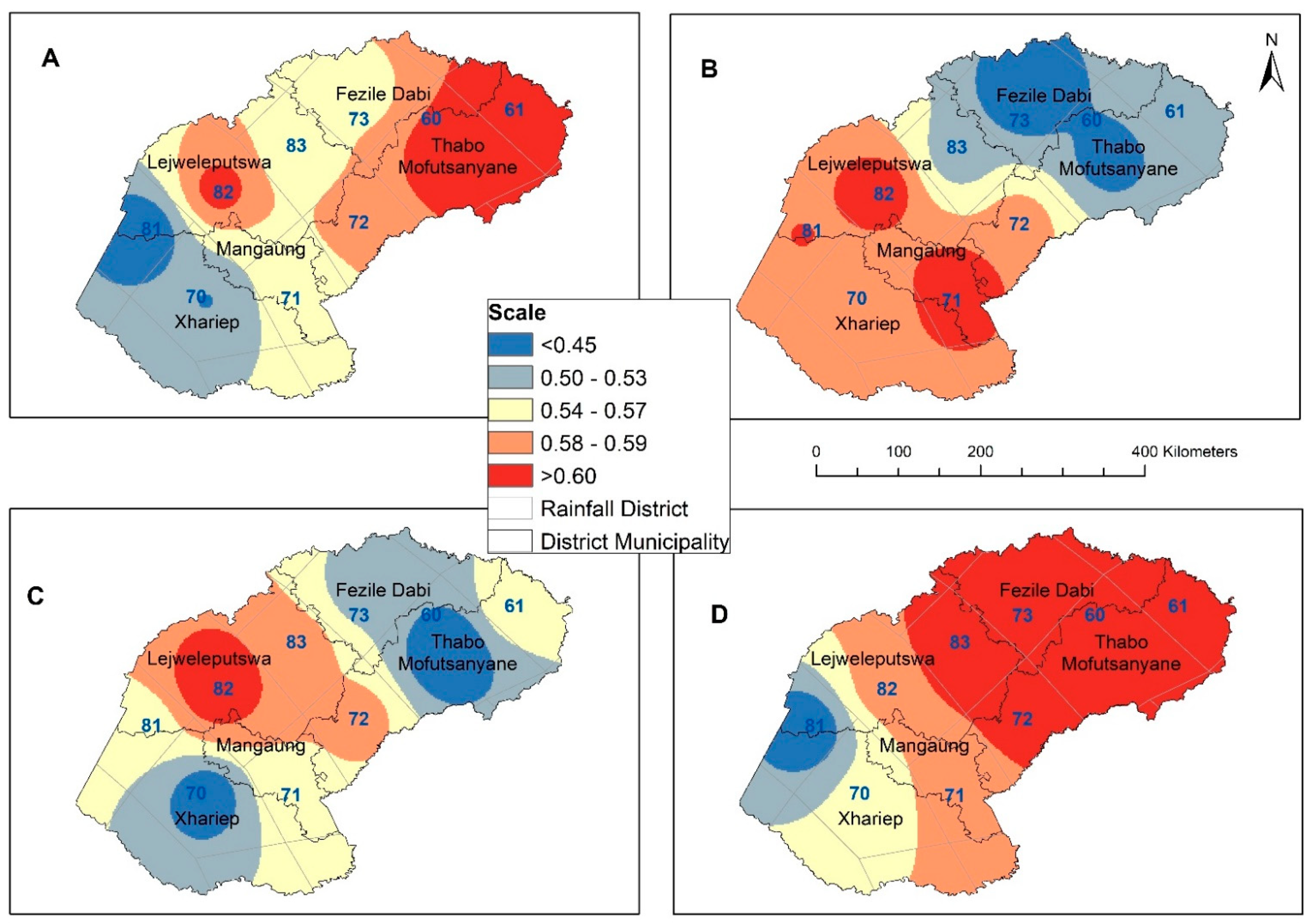
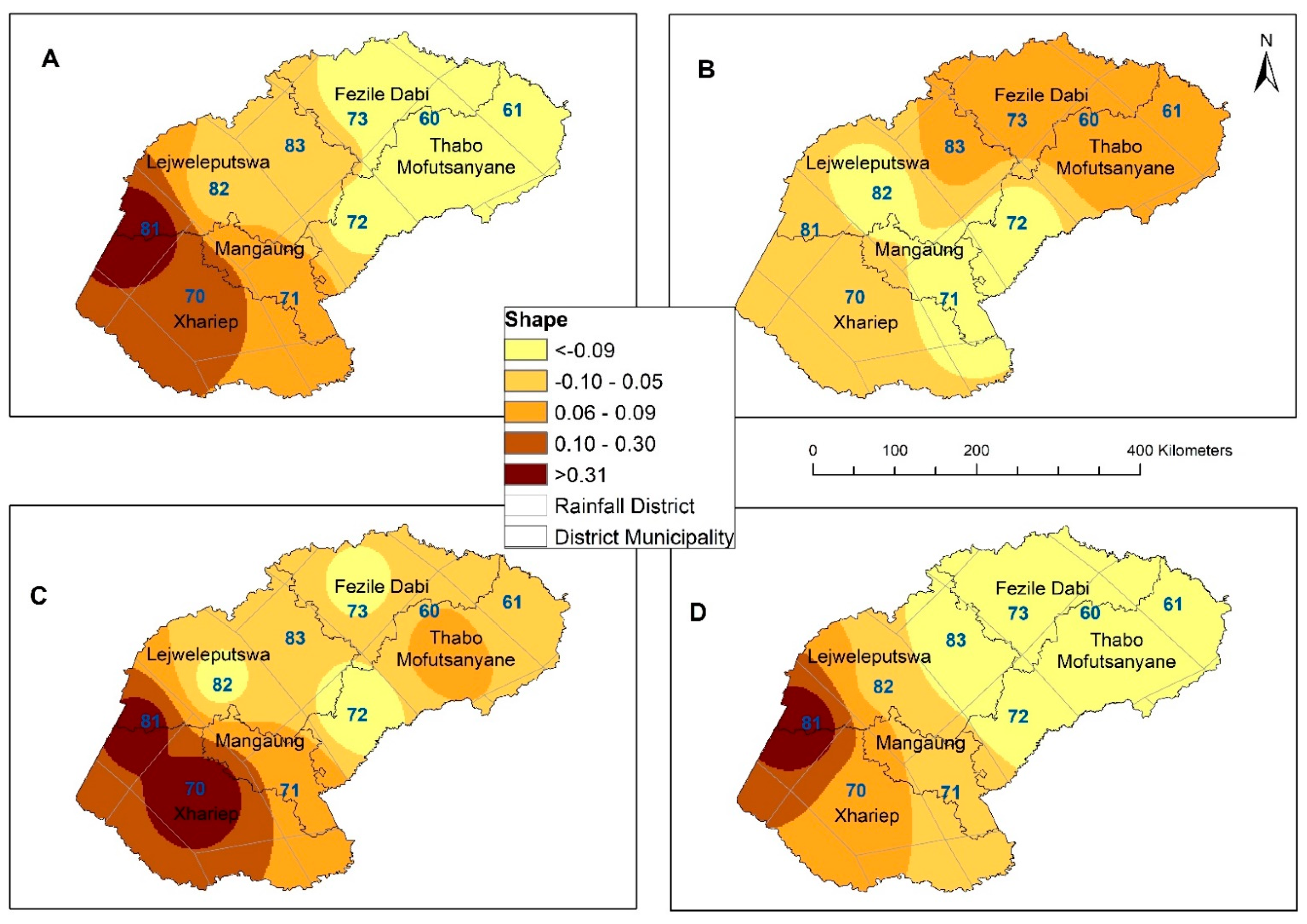
3. Results
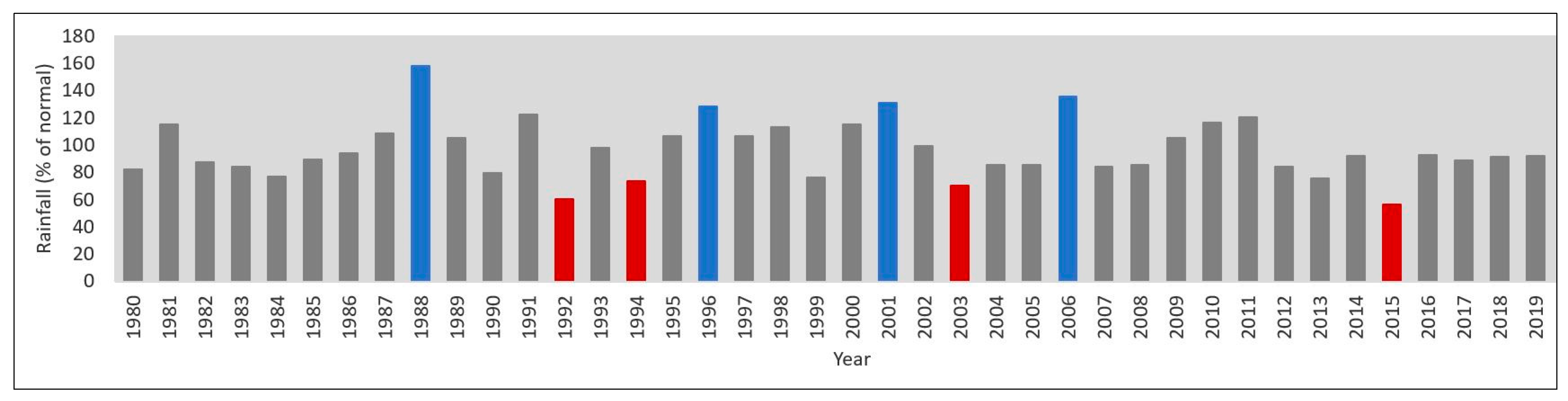
3.1. Historical Analysis
3.2. Trend Analysis
3.3. Extreme Value Analysis
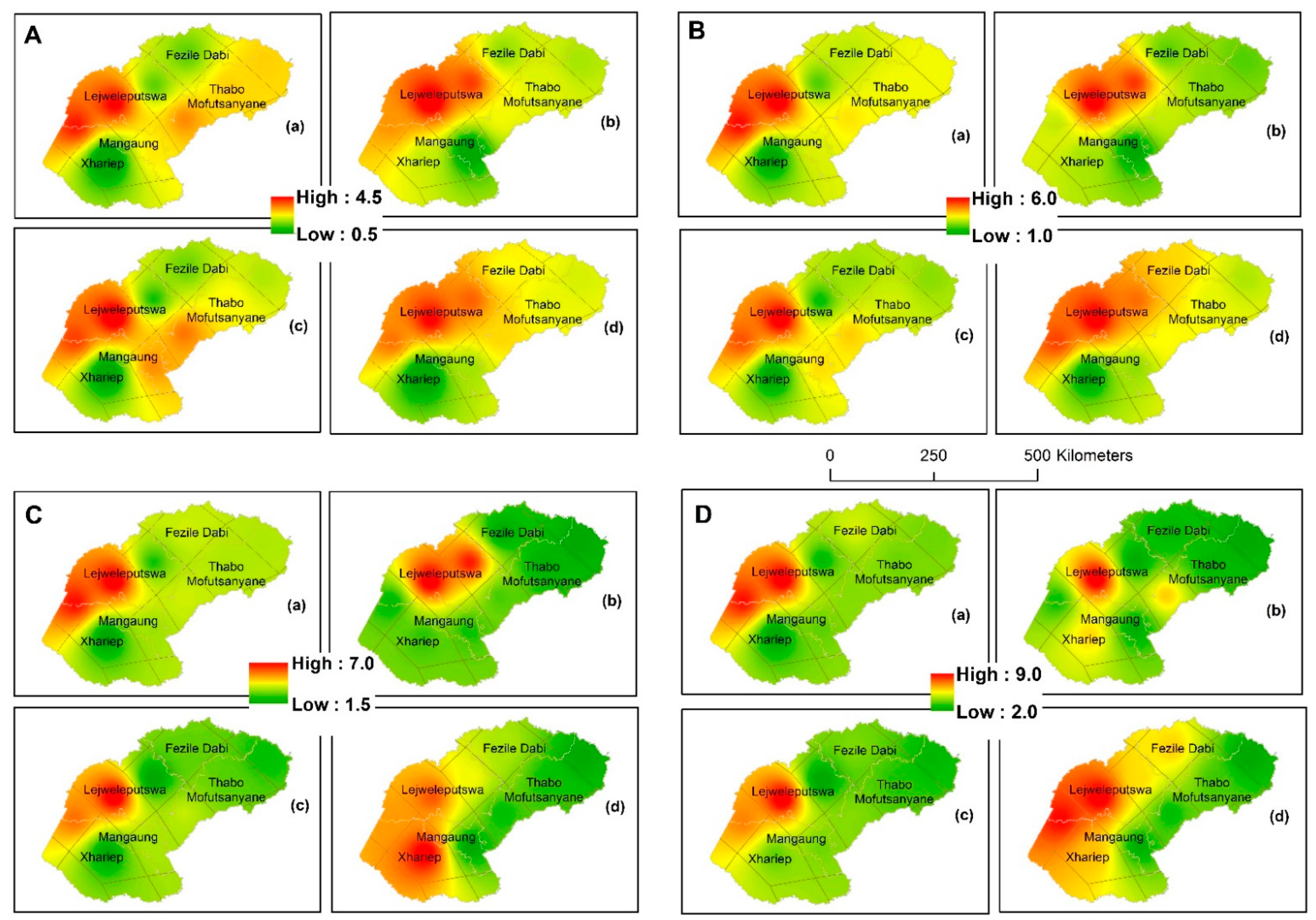
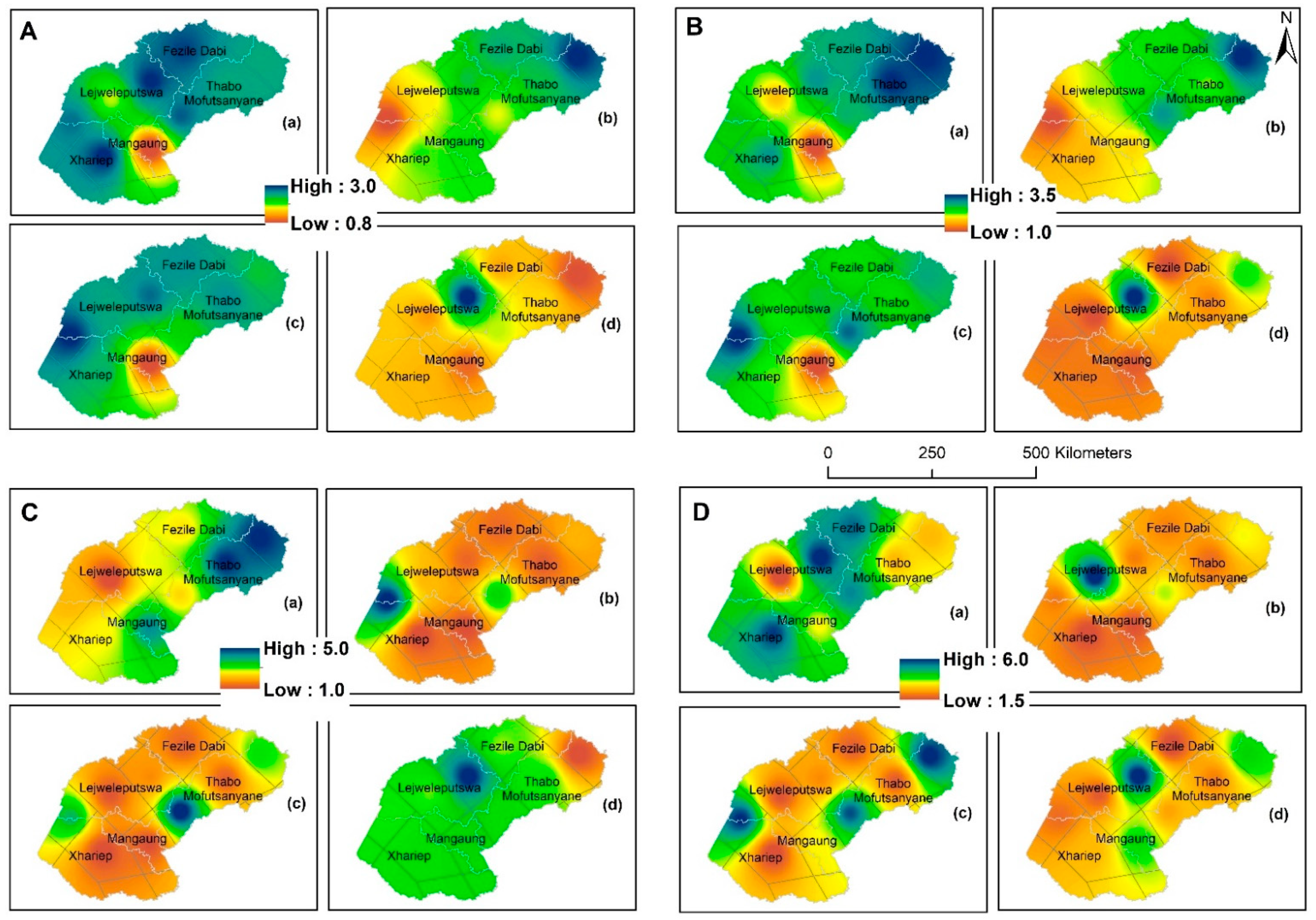
3.4. Return Level Analysis
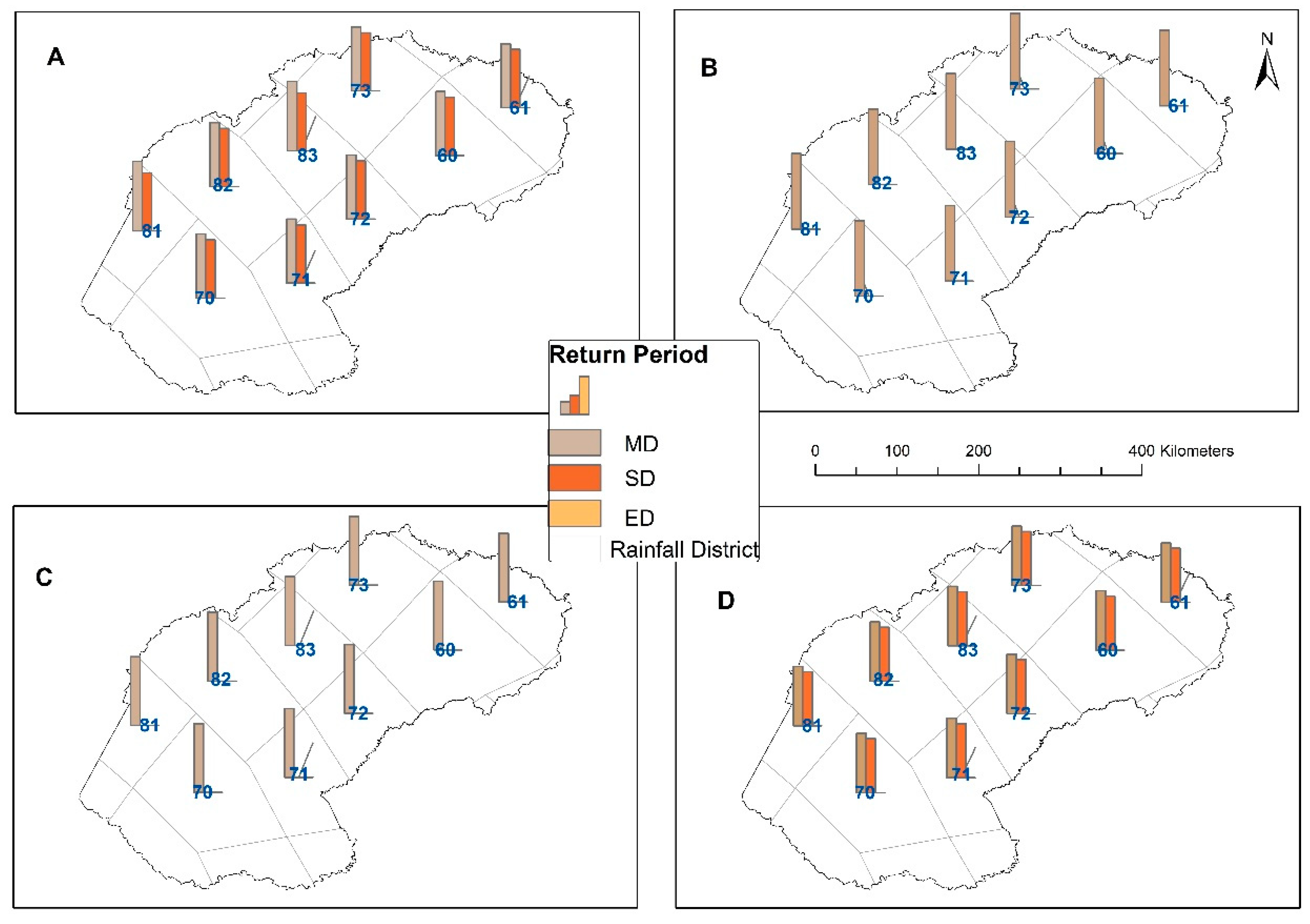
3.4.1. Return Level Analysis for Drought Conditions
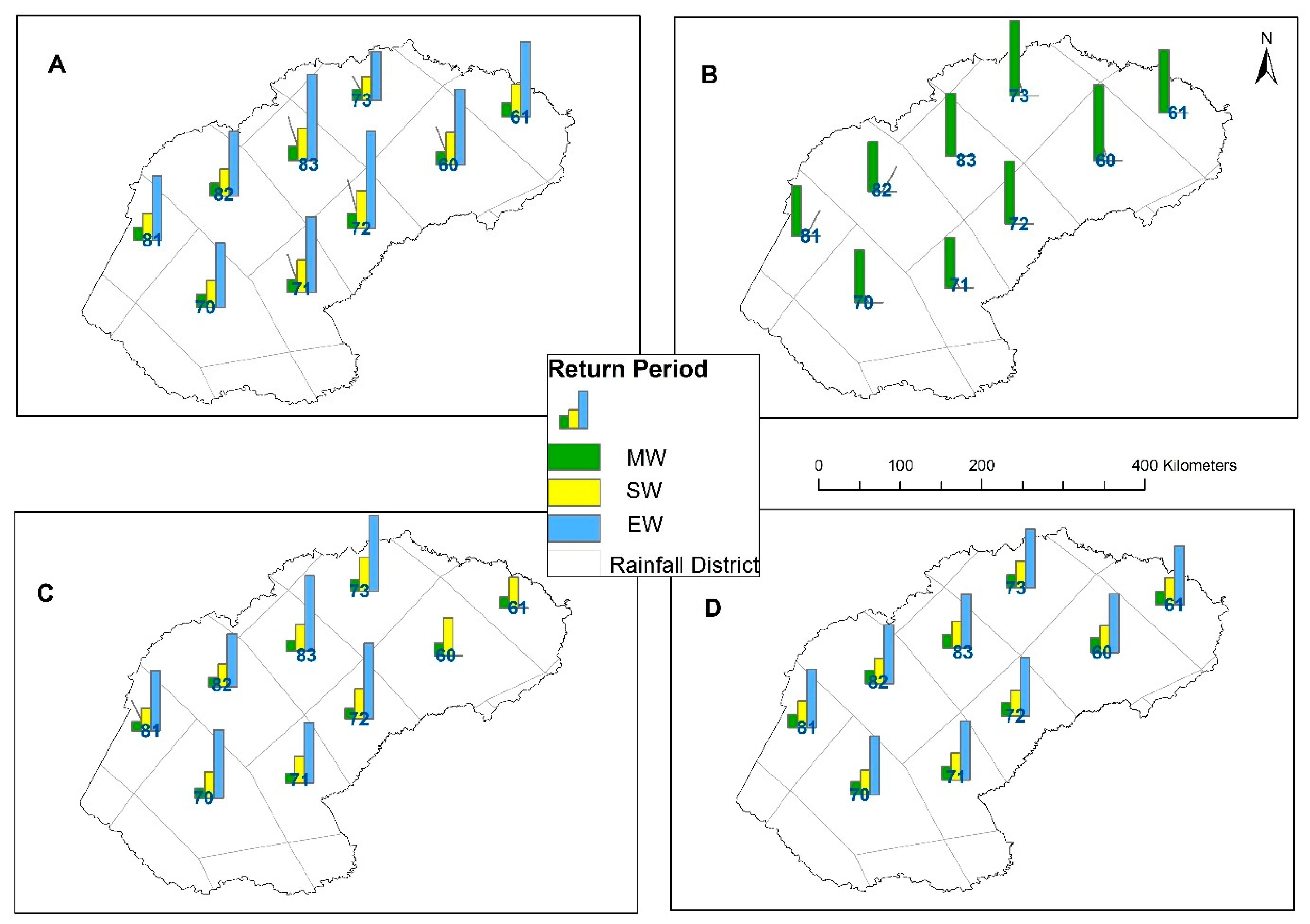
3.4.2. Return Level Analysis for Wet Conditions
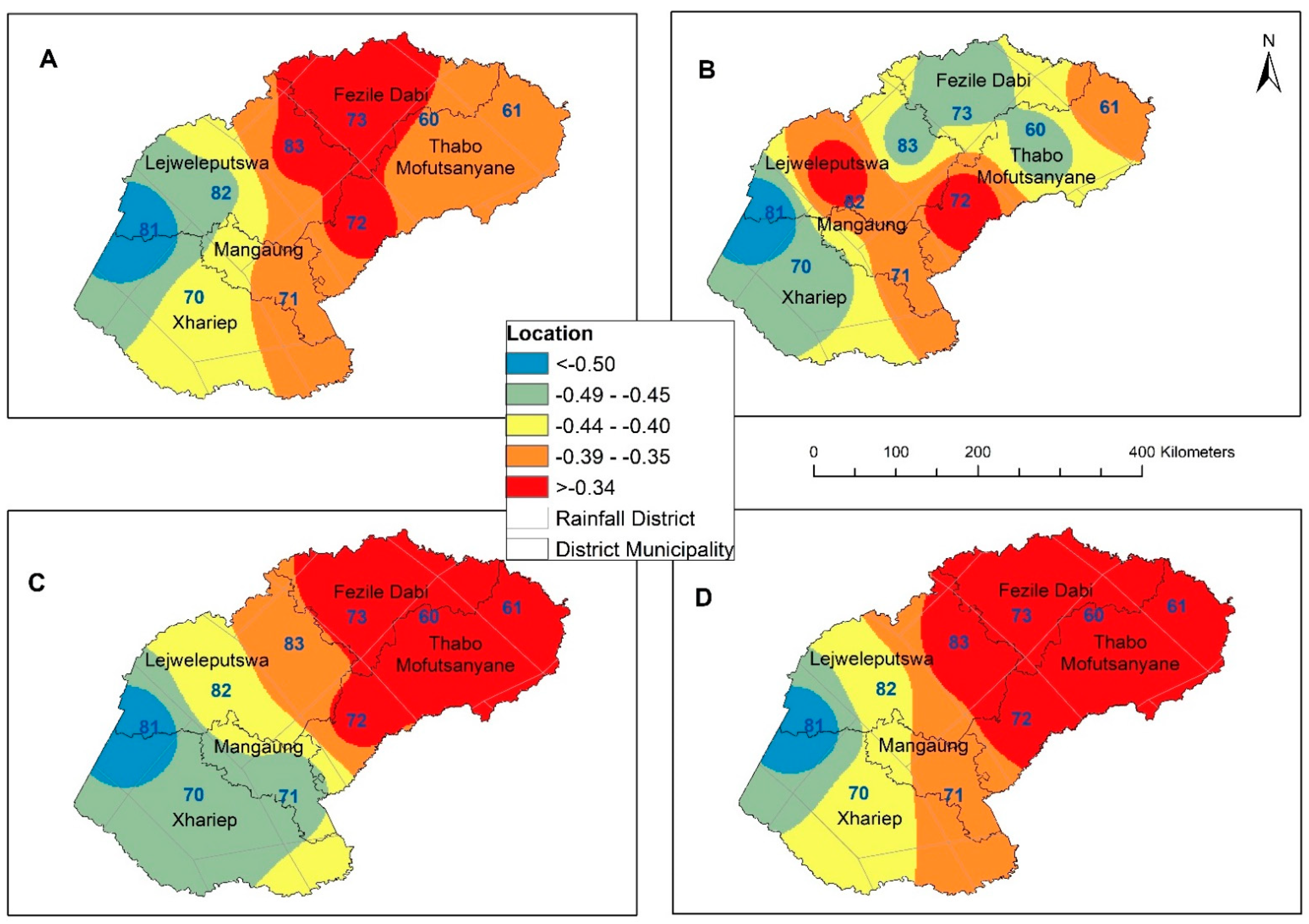
3.5. Dry Return Periods Based on Extreme Frequency Analysis (EFA) in the Free State Province
3.6. Wet Return Periods Based on Extreme Frequency Analysis (EFA) in the Free State Province
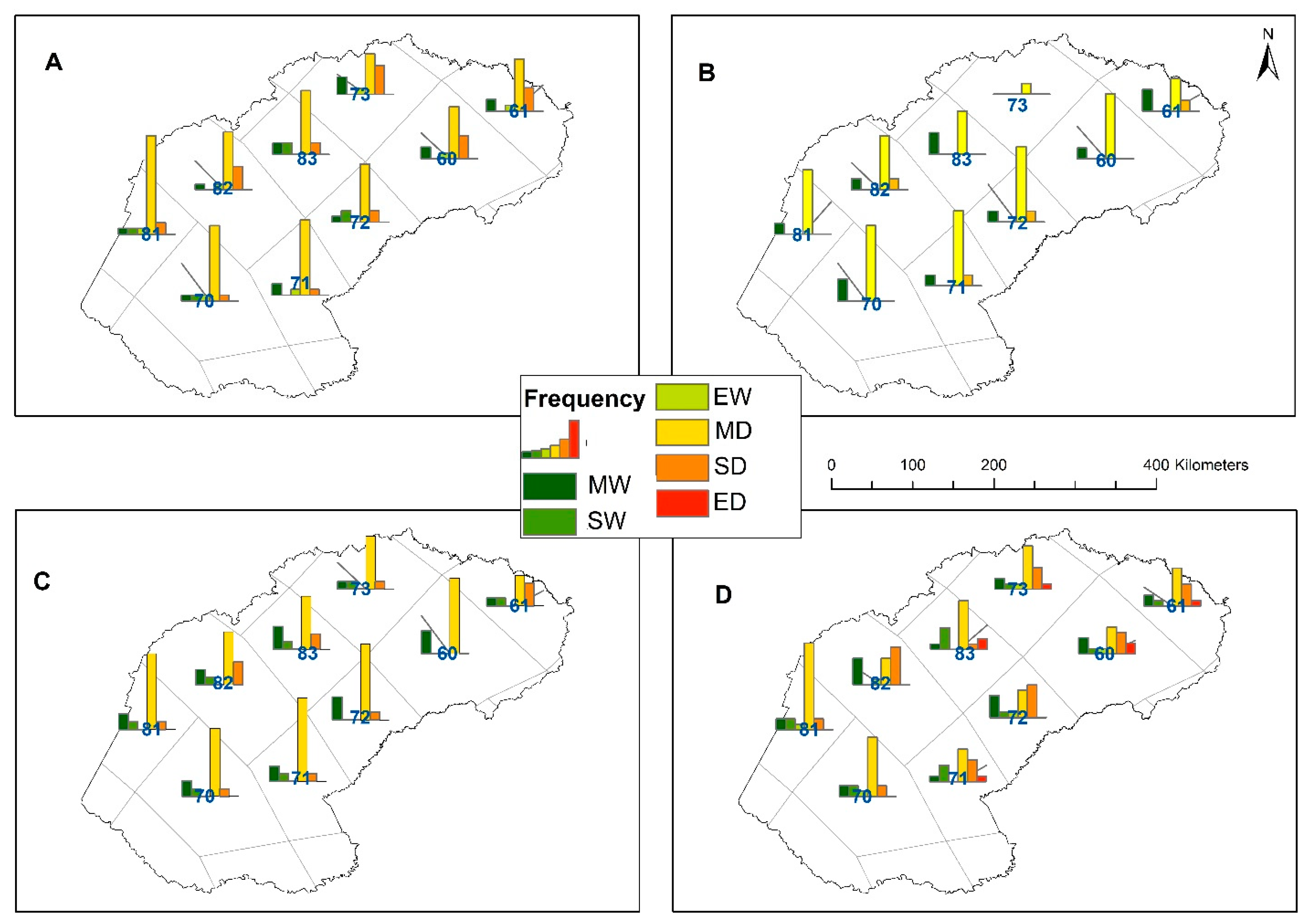
3.7. Frequency Distribution of Precipitation and the Drought Indices
4. Discussion and Conclusions
- (a)
- Whilst the return levels for the drought/wet duration and severity of EDI and SPI-3, -6 and -12 values generally showed increasing patterns across the corresponding return periods, the spatial contrasts were only noticeable in the return levels derived from the wet/drought duration and severity derived from SPI-3, -6, and -12 values (and not from the EDI values).
- (b)
- The EFA results point to a noticeable spatial contrast in the return periods derived from the EDI and SPI-3, -6, and -12 values for each of the extreme precipitation categories: moderately wet, severely wet, extremely wet to moderately, and severely dry.
- (c)
- Over the four decades, the Free State Province has generally experienced a suite of extreme precipitation categories ranging from moderately wet, severely wet, extremely wet to moderately dry, severely dry, and extremely dry conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dalu, M.T.; Shackleton, C.M.; Dalu, T. Influence of land cover, proximity to streams and household topographical location on flooding impact in informal settlements in the Eastern Cape, South Africa. Int. J. Disaster Risk Reduct. 2018, 28, 481–490. [Google Scholar] [CrossRef]
- Simane, B.; Beyene, H.; Deressa, W.; Kumie, A.; Berhane, K.; Samet, J. Review of climate change and health in Ethiopia: Status and gap analysis. Ethiop J. Health Dev. 2016, 30, 28–41. [Google Scholar] [PubMed]
- Ligtvoet, W.; Van Minnen, J.; Franken, R. The Effect of Climate Change in the Netherlands: 2012; PBL Netherlands Environmental Assessment Agency: The Hague, The Netherlands, 2013. [Google Scholar]
- Gornall, J.; Betts, R.; Burke, E.; Clark, R.; Camp, J.; Willett, K.; Wiltshire, A. Implications of climate change for agricultural productivity in the early twenty-first century. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 2973–2989. [Google Scholar] [CrossRef] [PubMed]
- Bates, B.C.; Kundzewicz, Z.W.; Wu, S.; Palutikof, J.P. (Eds.) Climate Change and Water; Technical Paper of the Intergovernmental Panel on Climate Change; IPCC Secretariat: Geneva, Switzerland, 2008; p. 210. [Google Scholar]
- Douglas, I.; Alam, K.; Maghenda, M.; Mcdonnell, Y.; Mclean, L.; Campbell, J. Unjust waters: Climate change, flooding and the urban poor in Africa. Environ. Urban. 2008, 20, 187–205. [Google Scholar] [CrossRef]
- Turral, H.; Burke, J.; Faures, J.M. Climate Change, Water and Food Security; FAO: Rome, Italy, 2008. [Google Scholar]
- Nchito, W.S. Flood risk in unplanned settlements in Lusaka. Environ. Urban. 2007, 19, 539–551. [Google Scholar] [CrossRef]
- Kjeldsen, T.; Smithers, J.; Schulze, R. Regional flood frequency analysis in the KwaZulu-Natal province, South Africa, using the index-flood method. J. Hydrol. 2002, 255, 194–211. [Google Scholar] [CrossRef]
- Tebaldi, C.; Hayhoe, K.; Arblaster, J.M.; Meehl, G.A. Going to the Extremes—An Intercomparison of Model-Simulated His-torical and Future Changes in Extreme Events. Clim. Chang. 2006, 79, 185–211. [Google Scholar] [CrossRef]
- Abiodun, B.J.; Makhanya, N.; Petja, B.; Abatan, A.A.; Oguntunde, P.G. Future projection of droughts over major river basins in Southern Africa at specific global warming levels. Theor. Appl. Clim. 2018, 137, 1785–1799. [Google Scholar] [CrossRef]
- Trenberth, K. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Marengo, J.A.; Torres, R.R.; Alves, L.M. Drought in Northeast Brazil—Past, Present, and Future. Theor. Appl. Climatol. 2016, 129, 1189–1200. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Cunha, A.P.; Tomasella, J.; Ribeiro-Neto, G.G.; Brown, M.; Garcia, S.R.; Brito, S.B.; Carvalho, M.A. Changes in the spatial-temporal patterns of droughts in the Brazilian Northeast. Atmos. Sci. Lett. 2018, 19, e855. [Google Scholar] [CrossRef]
- Cunha, A.P.; Zeri, M.; Leal, K.D.; Costa, L.; Cuartas, L.A.; Marengo, J.A.; Tomasella, J.; Vieira, R.M.; Barbosa, A.A.; Cunningham, C.; et al. Extreme Drought Events over Brazil from 2011 to 2019. Atmosphere 2019, 10, 642. [Google Scholar] [CrossRef]
- Tyson, P.D.; Whyte, R.A. The Weather and Climate of South Africa; Oxford University Press: Cape Town, Southern Africa, 2000; pp. 212–213. ISBN 0195718062. [Google Scholar]
- Botai, C.; Botai, J.O.; Adeola, A. Spatial distribution of temporal precipitation contrasts in South Africa. South Afr. J. Sci. 2018, 114, 70–78. [Google Scholar] [CrossRef]
- Adisa, O.M.; Botai, J.O.; Adeola, A.M.; Botai, C.M.; Hassen, A.; Darkey, D.; Tesfamariam, E.; Adisa, A.T.; Adisa, A.F. Analysis of drought conditions over major maize producing provinces of South Africa. J. Agric. Meteorol. 2019, 75, 173–182. [Google Scholar] [CrossRef]
- Woli, P.; Jones, J.E.; Ingram, K.; Paz, J. Forecasting Drought Using the Agricultural Reference Index for Drought (ARID): A Case Study. Weather Forecast. 2013, 28, 427–443. [Google Scholar] [CrossRef]
- Bhalme, H.N.; Mooley, D.A. Large-Scale droughts/floods and monsoon circulation. Mon. Weather Rev. 1980, 108, 1197–1211. [Google Scholar] [CrossRef]
- Palmer, W.C. Keeping Track of Crop Moisture Conditions, Nationwide: The New Crop Moisture Index. Weatherwise 1968, 21, 156–161. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Weiss, A.; Hu, Q. An evaluation of the Standardized Precipitation Index, the China-Z Index and the Statistical Z-Score. Int. J. Clim. 2001, 21, 745–758. [Google Scholar] [CrossRef]
- Byun, H.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional Drought Assessment Based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2006, 21, 821–833. [Google Scholar] [CrossRef]
- Hollinger, S.E.; Isard, S.A.; Welford, M.R. A new soil moisture drought index for predicting crop yields. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 187–190. [Google Scholar]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; Lopez-Moreno, I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Shafer, B.A.; Dezman, L.E. Development of a surface water supply index (SWSI) to assess the severity of drought conditions in snowpack runoff areas. In Proceedings of the 50th Annual Western Snow Conference, Colorado State University, Fort Collins, CO, USA, 19–23 April 1982; pp. 164–175. (In Preprints). [Google Scholar]
- Dalezios, N.; Blanta, A.; Spyropoulos, N.; Tarquis, A. Risk identification of agricultural drought for sustainable agroecosys-tems. Nat. Hazards Earth Syst. Sci. 2014, 14, 2435–2448. [Google Scholar] [CrossRef]
- WMO (World Meteorological Organization). Drought and Agriculture; Technical Note No. 138, Report of the CAgM Workin Group on Assessment of Drough; WMO: Geneva, Switzerland, 1975; p. 127. [Google Scholar]
- Jain, V.K.; Pandey, R.P.; Jain, M.; Byun, H.-R. Comparison of drought indices for appraisal of drought characteristics in the Ken River Basin. Weather. Clim. Extremes 2015, 8, 1–11. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Moghaddasi, M. Comparison of seven meteorological indexes for drought monitoring in Iran. Int. J. Climatol. 2006, 26, 971–985. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Okpara, J.N.; Tarhule, A. Evaluation of drought indices in the Niger Basin, West Africa. J. Geogr. Earth Sci. 2015, 3, 1–32. [Google Scholar]
- Adisa, O.M.; Masinde, M.; Botai, J.O. Assessment of the Dissimilarities of EDI and SPI Measures for Drought Determination in South Africa. Water 2021, 13, 82. [Google Scholar] [CrossRef]
- Reis, D.; Stedinger, J.R. Bayesian MCMC flood frequency analysis with historical information. J. Hydrol. 2005, 313, 97–116. [Google Scholar] [CrossRef]
- Bobee, B.; Rasmussen, P.F. Recent Advances in Flood Frequency Analysis. U.S. National Report 1991–1994. In Proceedings of the Twenty-First General Assembly International Union of Geodesy and Geophysics Boulder, Boulder, CO, USA, 2–14 July 1995; pp. 1111–1116. [Google Scholar]
- Van Campenhout, J.; Houbrechts, G.; Peeters, A.; Petit, F. Return Period of Characteristic Discharges from the Comparison between Partial Duration and Annual Series, Application to the Walloon Rivers (Belgium). Water 2020, 12, 792. [Google Scholar] [CrossRef]
- Kanae, S.; Oki, T.; Kashida, A. Changes in Hourly Heavy Precipitation at Tokyo from 1890 to 1999. J. Meteorol. Soc. JPN. 2004, 82, 241–247. [Google Scholar] [CrossRef]
- IPCC. Working Group I Contribution to the IPCC Fifth Assessment Report, Climate Change 2013: The Physical Science Basis; IPCC: Geneva, Switzerland, 2013. [Google Scholar]
- IPCC. Climate change 2007: Impacts, Adaptations, and Vulnerability. Contribution of Working Group Fourth Assessment Report of the IPCC.; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Nicholson, S.E.; Nash, D.J.; Chase, B.M.; Grab, S.W.; Shanahan, T.M.; Verschuren, D.; Asrat, A.; Lézine, A.M.; Umer, M. Tem-perature variability over Africa during the last 2000 years. Holocene 2013, 23, 1085–1094. [Google Scholar] [CrossRef]
- Stern, D.I.; Gething, P.; Kabaria, C.; Temperley, W.H.; Noor, A.M.; Okiro, E.; Shanks, G.D.; Snow, R.; Hay, S. Temperature and Malaria Trends in Highland East Africa. PLoS ONE 2011, 6, e24524. [Google Scholar] [CrossRef][Green Version]
- Giuliani, M.; Li, Y.; Castelletti, A.; Gandolfi, C. A coupled human-natural systems analysis of irrigated agriculture under changing climate. Water Resour. Res. 2016, 52, 6928–6947. [Google Scholar] [CrossRef]
- Zhang, X.; Harvey, K.D.; Hogg, W.D.; Yuzyk, T.R. Trends in Canadian streamflow. Water Resour. Res. 2001, 37, 987–998. [Google Scholar] [CrossRef]
- Brabets, T.P.; Walvoord, M.A. Trends in streamflow in the Yukon River Basin from 1944 to 2005 and the influence of the Pacific Decadal Oscillation. J. Hydrol. 2009, 371, 108–119. [Google Scholar] [CrossRef]
- Love, D.; Uhlenbrook, S.; Twomlow, S.; van der Zaag, P. Changing hydroclimatic and discharge patterns in the northern Limpopo Basin, Zimbabwe. SA J. Radiol. 2010, 36, 1–14. [Google Scholar]
- Kruger, A.; Nxumalo, M. Historical rainfall trends in South Africa: 1921–2015. Water SA 2017, 43, 285. [Google Scholar] [CrossRef]
- Muchuru, S.; Botai, C.M.; Botai, J.O.; Adeola, A.M. The hydrometeorology of the Kariba Catchment Area based on the Prob-ability distributions. Earth Interact. 2015, 19, 1–18. [Google Scholar] [CrossRef]
- Arreyndip, N.A.; Joseph, E. Generalized extreme value distribution models for the assessment of seasonal wind energy po-tential of Debuncha, Cameroon. J. Renew. Energy 2016, 2016, 9357812. [Google Scholar]
- Botai, C.M.; Botai, J.O.; Adeola, A.M.; deWit, J.P.; Ncongwane, K.P.; Zwane, N.N. Drought risk assessment in the Eastern Cape Province of South Africa. Copulas Lens. Water 2020, 12, 1938. [Google Scholar]
- Botai, C.M.; Botai, J.O.; Dlamini, L.; Zwane, N.; Phaduli, E. Characteristics of Droughts in South Africa: A Case Study of Free State and Northwest Provinces. Water 2016, 8, 439. [Google Scholar] [CrossRef]
- Botai, C.M.; Botai, J.O.; De Wit, J.P.; Ncongwane, K.P.; Adeola, A.M. Drought Characteristics over the Western Cape Province, South Africa. Water 2017, 9, 876. [Google Scholar] [CrossRef]
- Rouault, M.; Richard, Y. Intensity and spatial extent of droughts in southern Africa. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Free State Province (FSP). Free State Province Provincial Growth and Development Strategy (PGDS) 2005–2014; Free State Provincial Government: Bloemfontein, South Africa, 2005; p. 18.
- Hamed, K.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar] [CrossRef]
- Kumar, S.; Merwade, V.; Kam, J.; Thurner, K. Streamflow trends in Indiana: Effects of long term persistence, precipitation and subsurface drains. J. Hydrol. 2009, 374, 171–183. [Google Scholar] [CrossRef]
- Klemow, M.K.; Bartlow, A.; Crawford, J.; Kocher, N.; Shah, J.; Ritsick, M. Herbal Medicine Biomolecular and Clinical Aspects, 2nd ed.; Benzie, I.F.F., Wachtel-Galor, S., Eds.; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9781439807132. [Google Scholar]
- Brunet-Moret, Y. Rank statistics. Mr. Cah. Orstom. Série Hydrol. 1973, 10, 133–151. [Google Scholar]
- Kruger, A.C. Observed trends in daily precipitation indices in South Africa: 1910–2004. Int. J. Clim. 2006, 26, 2275–2285. [Google Scholar] [CrossRef]
- Moeletsi, M.; Walker, S. Rainy season characteristics of the Free State Province of South Africa with reference to rain-fed maize production. Water SA 2012, 38, 775–782. [Google Scholar] [CrossRef]
- Thomas, A.C.; Pershing, A.J.; Friedland, K.D.; Nye, J.; Mills, K.E.; Alexander, M.A.; Record, N.R.; Weatherbee, R.; Henderson, M.E. Seasonal trends and phenology shifts in sea surface temperature on the North American northeastern continental shelf. Elem. Sci. Anthr. 2017, 5, 48. [Google Scholar] [CrossRef]
- Moeletsi, M.; Moopisa, S.G.; Walker, S.; Tsubo, M. Development of an agroclimatological risk tool for dryland maize production in the Free State Province of South Africa. Comput. Electron. Agric. 2013, 95, 108–121. [Google Scholar] [CrossRef]
- Department of Agriculture, Forestry and Fisheries. Abstract of Agricultural Statistics; National Department of Agri-culture, Forestry and Fisheries: Pretoria, South Africa, 2019; p. 8. Available online: www.daff.gov.za (accessed on 5 October 2021).
- Free State Economy Green Strategy. 2014. Available online: https://www.environment.gov.za/sites/default/files/docs/greeneconomystrategy_freestate.pdf (accessed on 21 September 2021).

| Category | Range of Drought Index Values | |
|---|---|---|
| SPI | EDI | |
| Extremely dry | −2.0 | −2.0 |
| Severely dry | From −1.5 to −1.99 | From −1.5 to −1.99 |
| Moderately dry | From −1.0 to −1.49 | From 1.0 to −1.49 |
| Normal | From −0.99 to 0.99 | From −0.99 to 0.99 |
| Moderately wet | From 1.0 to 1.49 | From 1.0 to 1.49 |
| Severely wet | From 1.5 to 1.99 | From 1.5 to 1.99 |
| Extremely wet | 2.0 | 2.0 |
| Effective Drought Index | |||||
| DISTRICT | 2 Year Period | 5 Year Period | 10 Year Period | 20 Year Period | 50 Year Period |
| 60 | 4.08 | 4.72 | 4.87 | 4.94 | 4.98 |
| 61 | 4.08 | 4.72 | 4.87 | 4.94 | 4.98 |
| 70 | 2 | 2 | 2 | 2 | 2 |
| 71 | 3 | 3 | 3 | 3 | 3 |
| 72 | 3.40 | 4.78 | 5.69 | 6.56 | 7.69 |
| 73 | 2 | 2 | 2 | 2 | 2 |
| 81 | 2 | 2 | 2 | 2 | 2 |
| 82 | 3 | 3 | 3 | 3 | 3 |
| 83 | 5.64 | 6.59 | 6.82 | 6.92 | 6.97 |
| Standardized Precipitation Index (3) | |||||
| 60 | 2 | 2 | 2.01 | 2.12 | 5.53 |
| 61 | 2 | 2 | 2 | 2 | 2 |
| 70 | 3.58 | 3.90 | 3.96 | 3.98 | 4 |
| 71 | 3.26 | 4.50 | 5.44 | 6.44 | 7.90 |
| 72 | 2 | 2 | 2 | 2 | 2.23 |
| 73 | 2.80 | 3.40 | 3.72 | 3.98 | 4.27 |
| 81 | 4.01 | 4.69 | 4.85 | 4.93 | 4.97 |
| 82 | 3 | 3 | 3 | 3 | 3 |
| 83 | 3 | 3 | 3 | 3 | 3 |
| Standardized Precipitation Index (6) | |||||
| 60 | 2 | 2 | 2 | 2 | 2 |
| 61 | 2 | 2 | 2 | 2 | 2.23 |
| 70 | 5.17 | 5.85 | 5.95 | 5.98 | 6 |
| 71 | 3 | 3 | 3 | 3 | 3 |
| 72 | 2 | 2 | 2 | 2 | 2 |
| 73 | 2 | 2 | 2 | 2 | 2 |
| 81 | 3.86 | 5.78 | 7.26 | 8.86 | 11.23 |
| 82 | 3.89 | 5.66 | 7.89 | 11.45 | 19.73 |
| 83 | 3.89 | 5.66 | 7.89 | 11.45 | 19.73 |
| Standardized Precipitation Index (12) | |||||
| 60 | 2 | 2 | 2 | 2 | 2 |
| 61 | 3.02 | 3.55 | 3.80 | 3.99 | 4.17 |
| 70 | 2 | 2 | 2 | 2 | 2 |
| 71 | 3.44 | 4.82 | 5.78 | 6.44 | 7.90 |
| 72 | 2.89 | 3.91 | 4.70 | 5.56 | 6.82 |
| 73 | 2 | 2 | 2 | 2 | 2 |
| 81 | 2 | 2 | 2 | 2 | 2 |
| 82 | 3.56 | 6.03 | 8.61 | 12.17 | 19.11 |
| 83 | 4.82 | 5.67 | 5.86 | 5.94 | 5.98 |
| Effective Drought Index | |||||
| DISTRICT | 2-Year | 5-Year | 10-Year | 20-Year | 50-Year |
| 60 | 2.66 | 2.89 | 2.95 | 2.98 | 2.99 |
| 61 | 2.66 | 2.89 | 2.95 | 2.98 | 2.99 |
| 70 | 2 | 2 | 2 | 2 | 2 |
| 71 | 2.66 | 2.89 | 2.95 | 2.98 | 2.99 |
| 72 | 2.98 | 3.99 | 4.75 | 5.55 | 6.72 |
| 73 | 2.99 | 3 | 3 | 3 | 3 |
| 81 | 2 | 2 | 2 | 2 | 2 |
| 82 | 2.55 | 2.85 | 2.93 | 2.97 | 2.99 |
| 83 | 3.02 | 3.55 | 3.80 | 3.99 | 4.17 |
| Standardized Precipitation Index (3) | |||||
| 60 | 2 | 2 | 2 | 2 | 2 |
| 61 | 3.65 | 3.95 | 3.99 | 4 | 4 |
| 70 | 2 | 2 | 2.07 | 4.42 | 5.25 |
| 71 | 3.02 | 3.55 | 3.80 | 3.99 | 4.17 |
| 72 | 2 | 2 | 2 | 2 | 2 |
| 73 | 3.07 | 3.63 | 3.87 | 4.02 | 4.16 |
| 81 | 3.02 | 3.55 | 3.80 | 3.99 | 4.17 |
| 82 | 2.80 | 3.40 | 3.72 | 3.98 | 4.27 |
| 83 | 3.54 | 3.93 | 3.98 | 3.99 | 4 |
| Standardized Precipitation Index (6) | |||||
| 60 | 3.02 | 3.55 | 3.80 | 3.99 | 4.17 |
| 61 | 2.66 | 2.89 | 2.95 | 2.98 | 2.99 |
| 70 | 2 | 2 | 2 | 2 | 2 |
| 71 | 3.43 | 3.82 | 3.91 | 3.96 | 3.98 |
| 72 | 2 | 2 | 2 | 2 | 2 |
| 73 | 2.98 | 3.99 | 4.75 | 5.55 | 6.72 |
| 81 | 2 | 2 | 2 | 2 | 2 |
| 82 | 3.02 | 3.55 | 3.80 | 3.99 | 4.17 |
| 83 | 3.02 | 3.55 | 3.80 | 3.99 | 4.17 |
| Standardized Precipitation Index (12) | |||||
| 60 | 2.80 | 3.40 | 3.72 | 3.98 | 4.27 |
| 61 | 2 | 2 | 2 | 2 | 2 |
| 70 | 2 | 2 | 2 | 2 | 2 |
| 71 | 2.66 | 2.89 | 2.95 | 2.98 | 2.99 |
| 72 | 4.11 | 4.72 | 4.87 | 4.94 | 4.98 |
| 73 | 2.80 | 3.40 | 3.72 | 3.98 | 4.27 |
| 81 | 2 | 2 | 2 | 2 | 2 |
| 82 | 2 | 2 | 2.07 | 4.42 | 5.15 |
| 83 | 3.34 | 5.17 | 6.88 | 9.03 | 12.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeola, O.M.; Masinde, M.; Botai, J.O.; Adeola, A.M.; Botai, C.M. An Analysis of Precipitation Extreme Events Based on the SPI and EDI Values in the Free State Province, South Africa. Water 2021, 13, 3058. https://doi.org/10.3390/w13213058
Adeola OM, Masinde M, Botai JO, Adeola AM, Botai CM. An Analysis of Precipitation Extreme Events Based on the SPI and EDI Values in the Free State Province, South Africa. Water. 2021; 13(21):3058. https://doi.org/10.3390/w13213058
Chicago/Turabian StyleAdeola, Omolola M., Muthoni Masinde, Joel O. Botai, Abiodun M. Adeola, and Christina M. Botai. 2021. "An Analysis of Precipitation Extreme Events Based on the SPI and EDI Values in the Free State Province, South Africa" Water 13, no. 21: 3058. https://doi.org/10.3390/w13213058
APA StyleAdeola, O. M., Masinde, M., Botai, J. O., Adeola, A. M., & Botai, C. M. (2021). An Analysis of Precipitation Extreme Events Based on the SPI and EDI Values in the Free State Province, South Africa. Water, 13(21), 3058. https://doi.org/10.3390/w13213058







