Application of a Single Porous Basket as a Pier Scour Countermeasure
Abstract
:1. Introduction
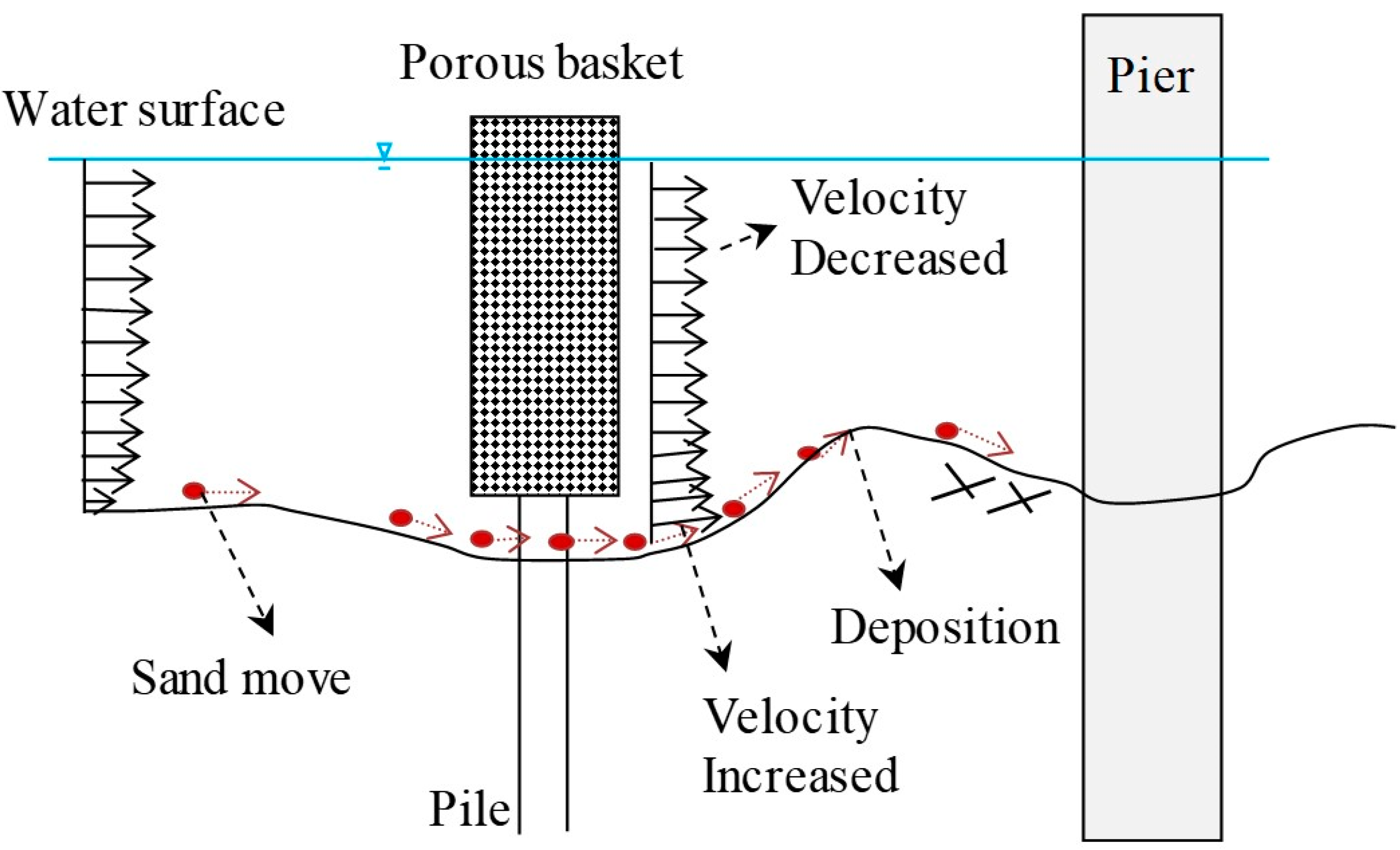
2. Similitude of Approach Flow around Single Porous Basket
- Flow condition factors: water depth H, flow velocity V, fluid density , kinematic viscosity of water , and gravity acceleration g;
- Bed sediment factors: particle shape factor Kd, standard deviation in geometric size distribution g, sand density , and median distribution size d50;
- Pier geometry factors: pier shape factor Kp, pier diameter b, and flow approaching angle to the pier axis ;
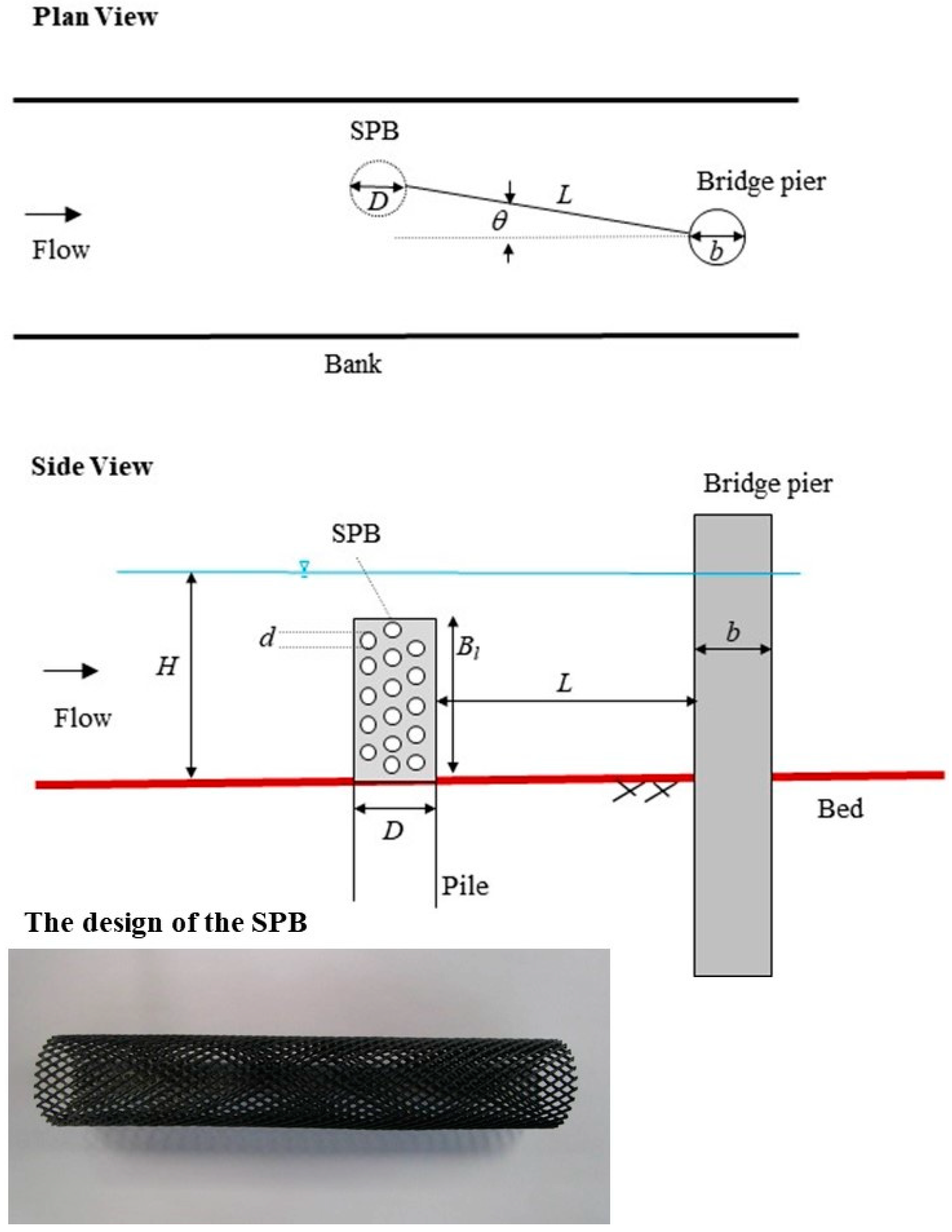
- SPB setup factors: basket diameter , basket shape factor Kl, basket length Bl, distance from the protected pier L, hole size d, attack angle of approach flow , and porosity e.
3. Procedure of the Experimental Work
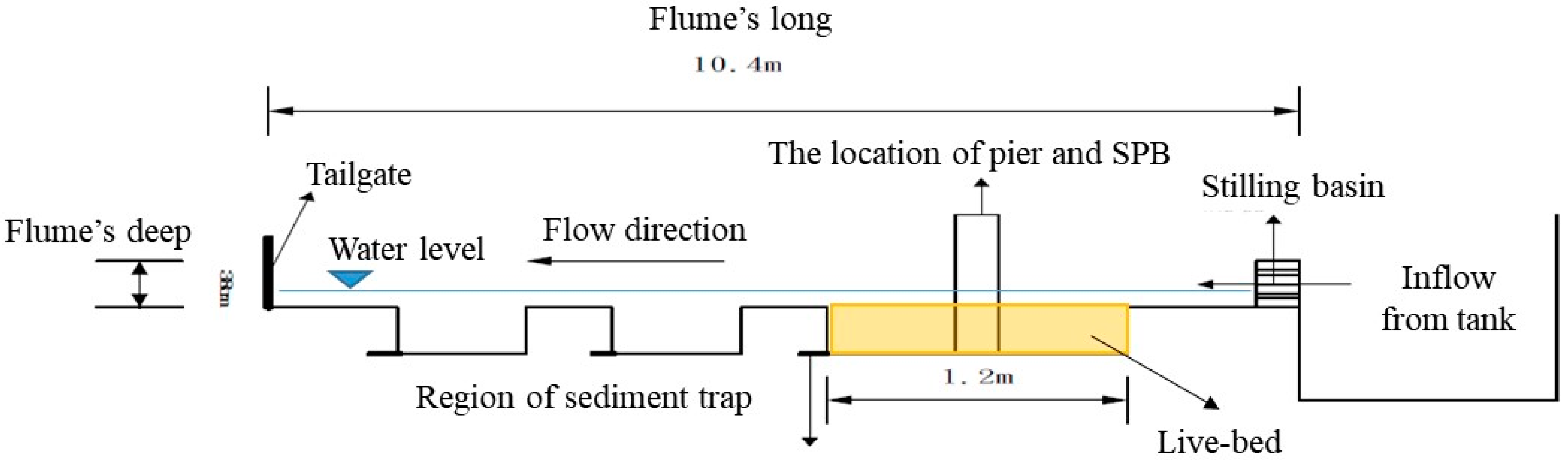
3.1. Experimental Set-Up
3.2. Experimental Procedure
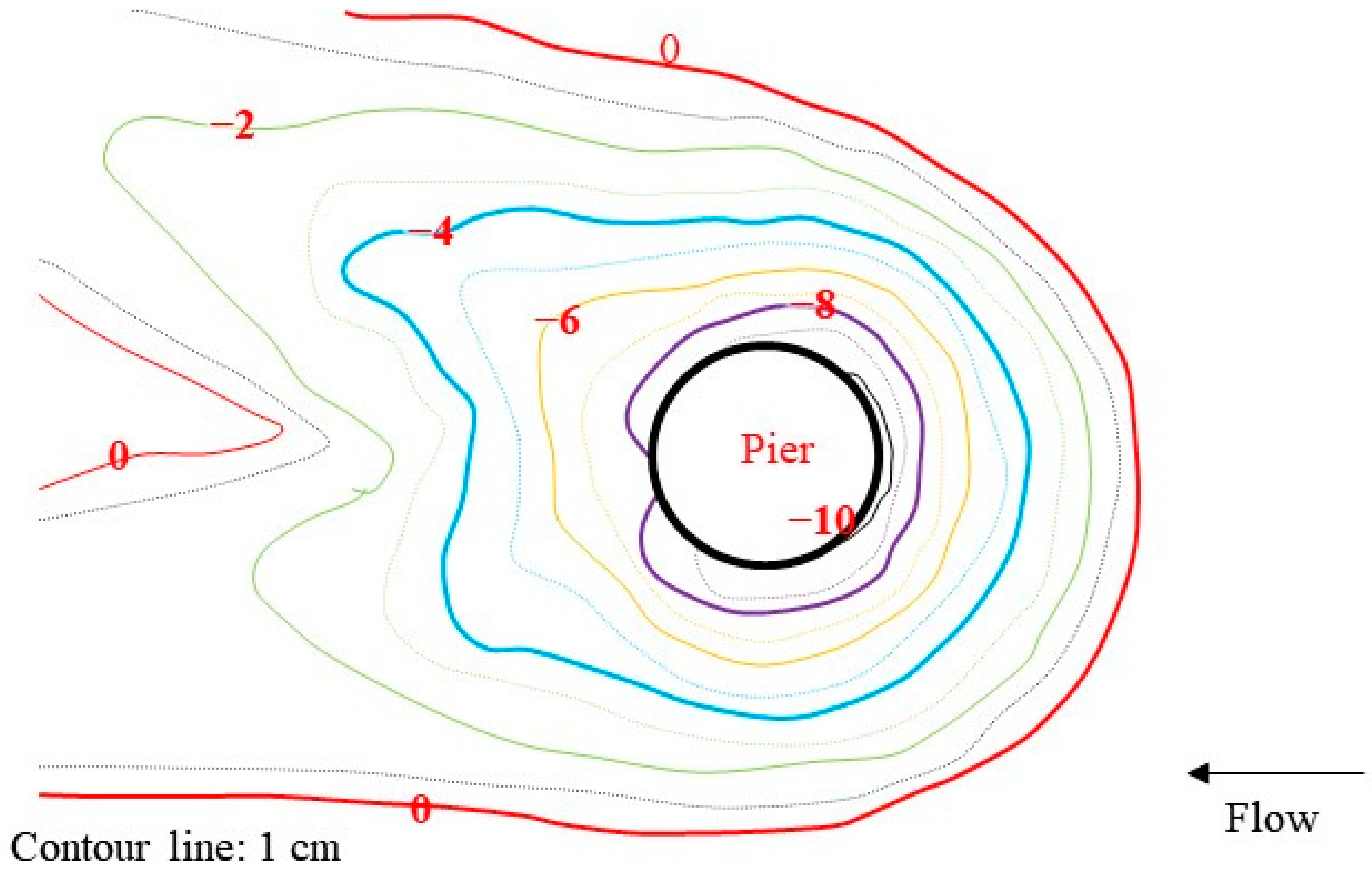
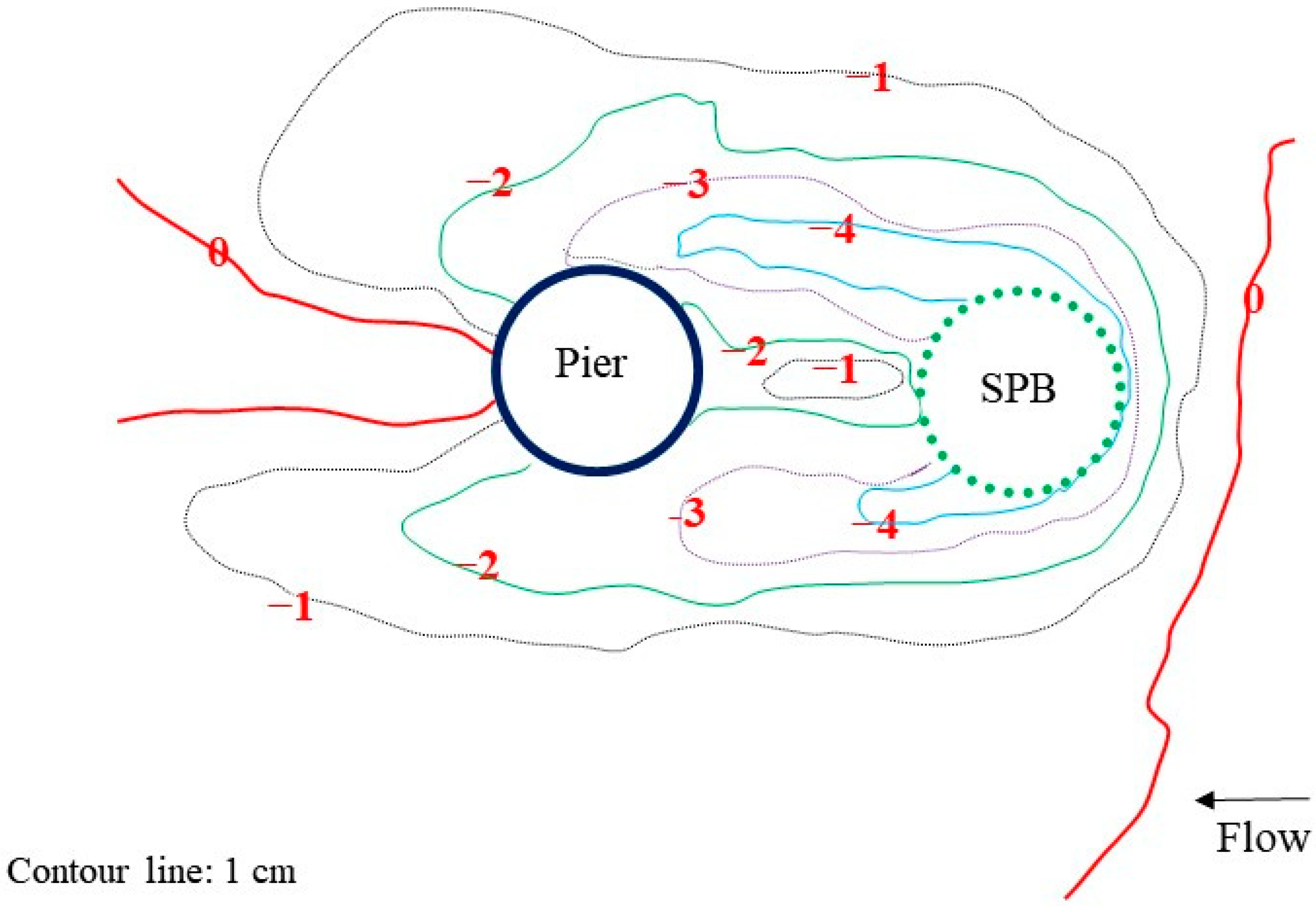
4. Result and Discussions
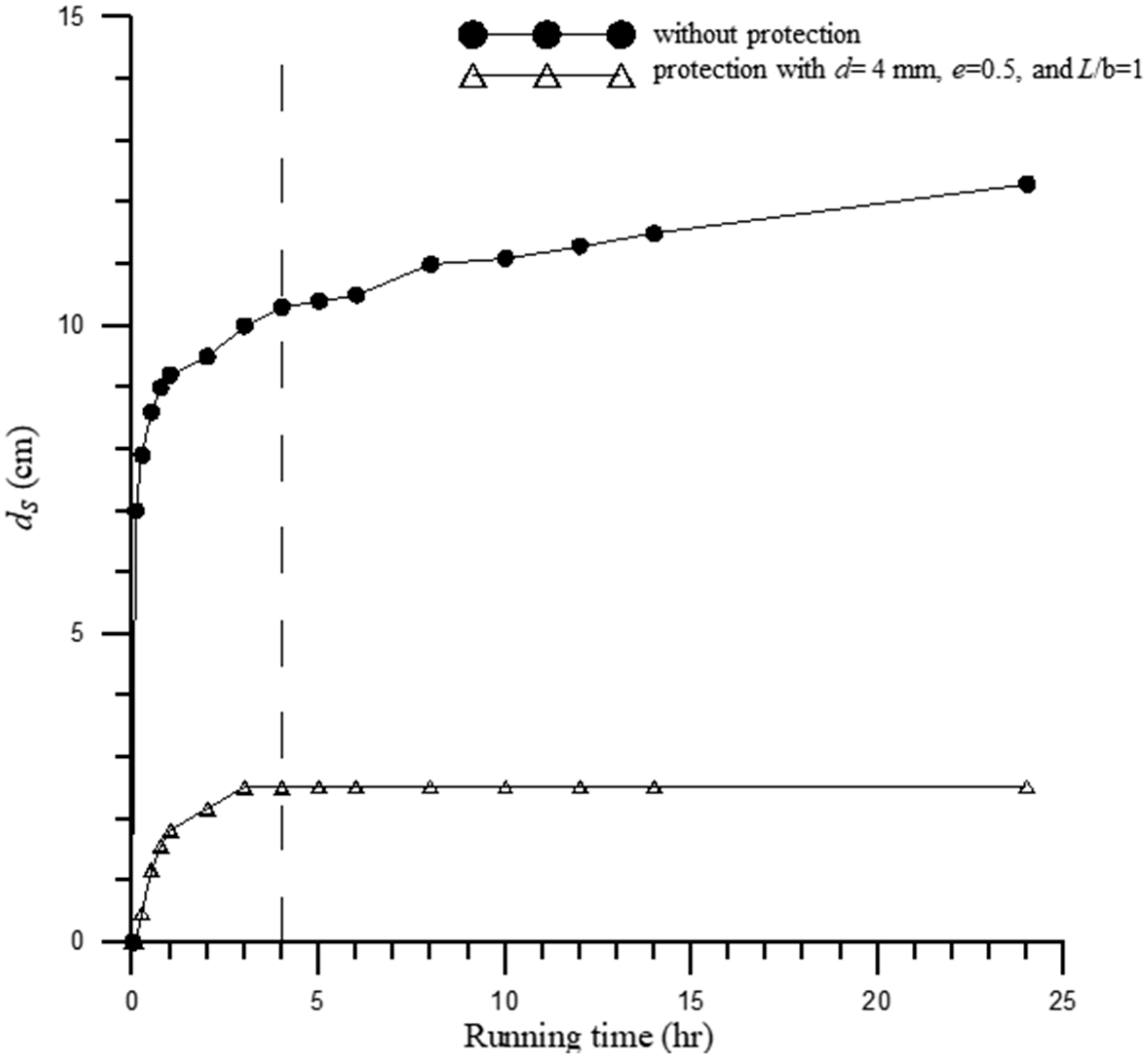
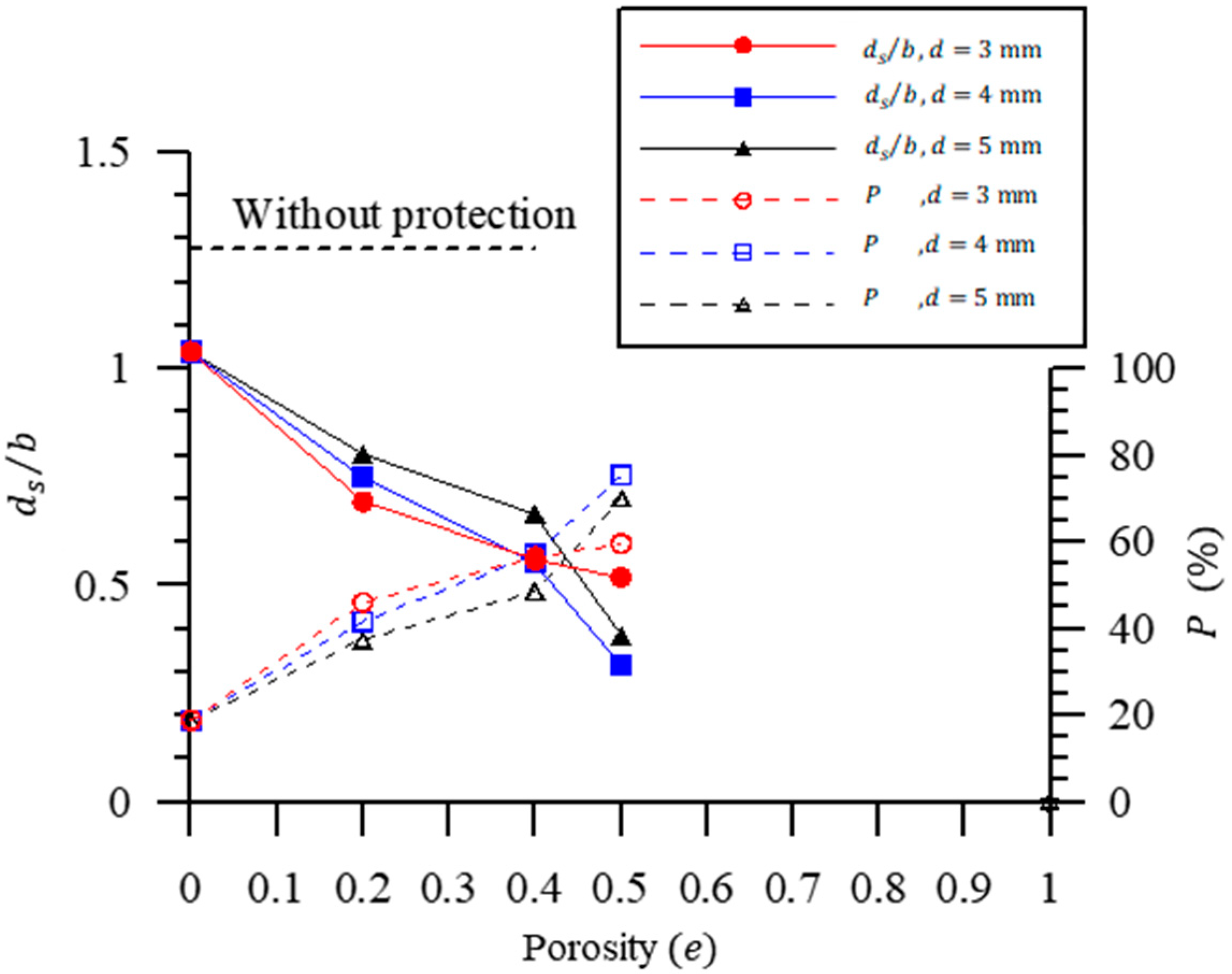
4.1. The Influence of Porosity of SPB on Pier Scour Reduction
4.2. The Influence of Hole Size of SPB on Pier Scour Reduction
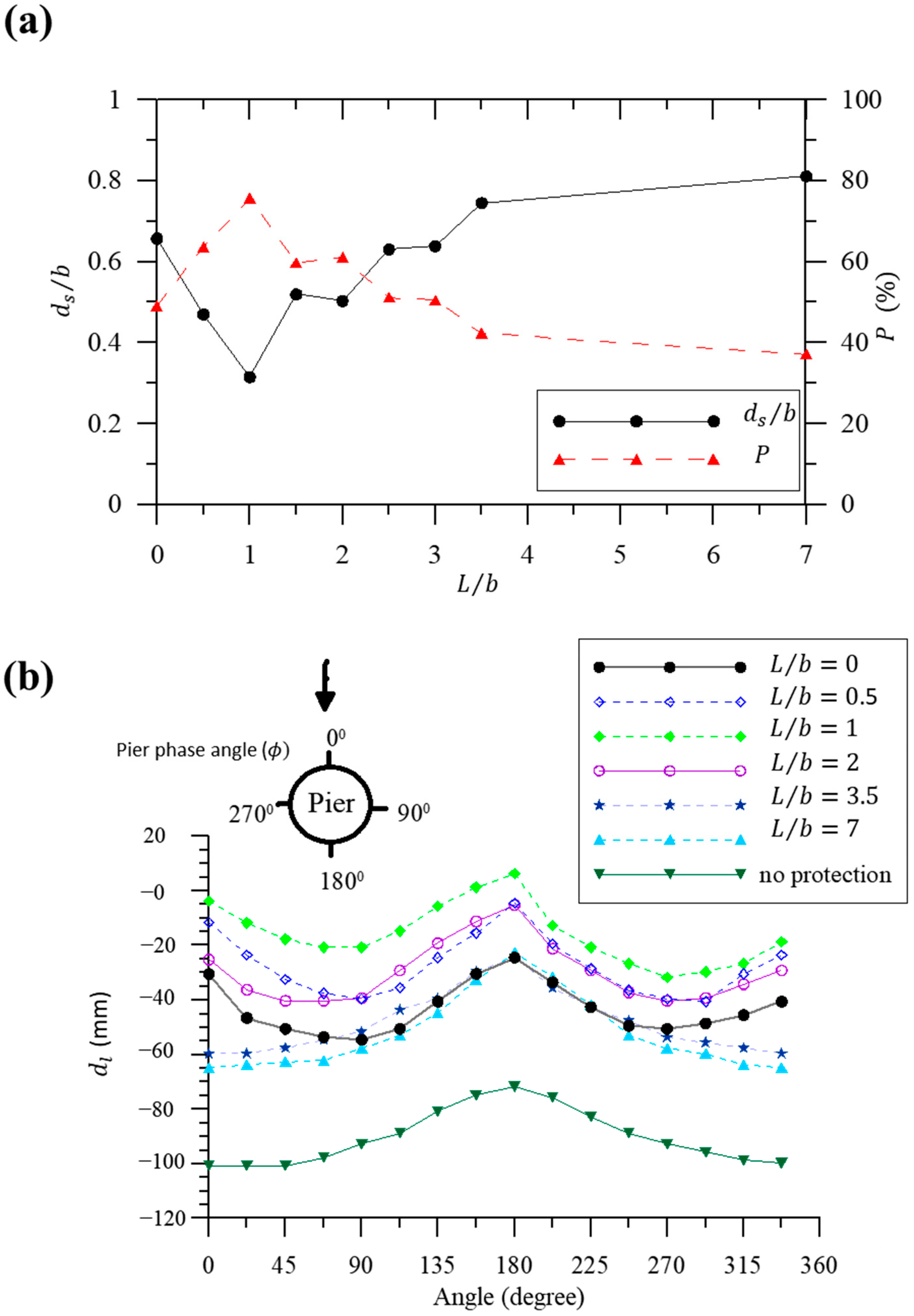
4.3. The Influence of Distance between Basket and Bridge Pier on Pier Scour Reduction
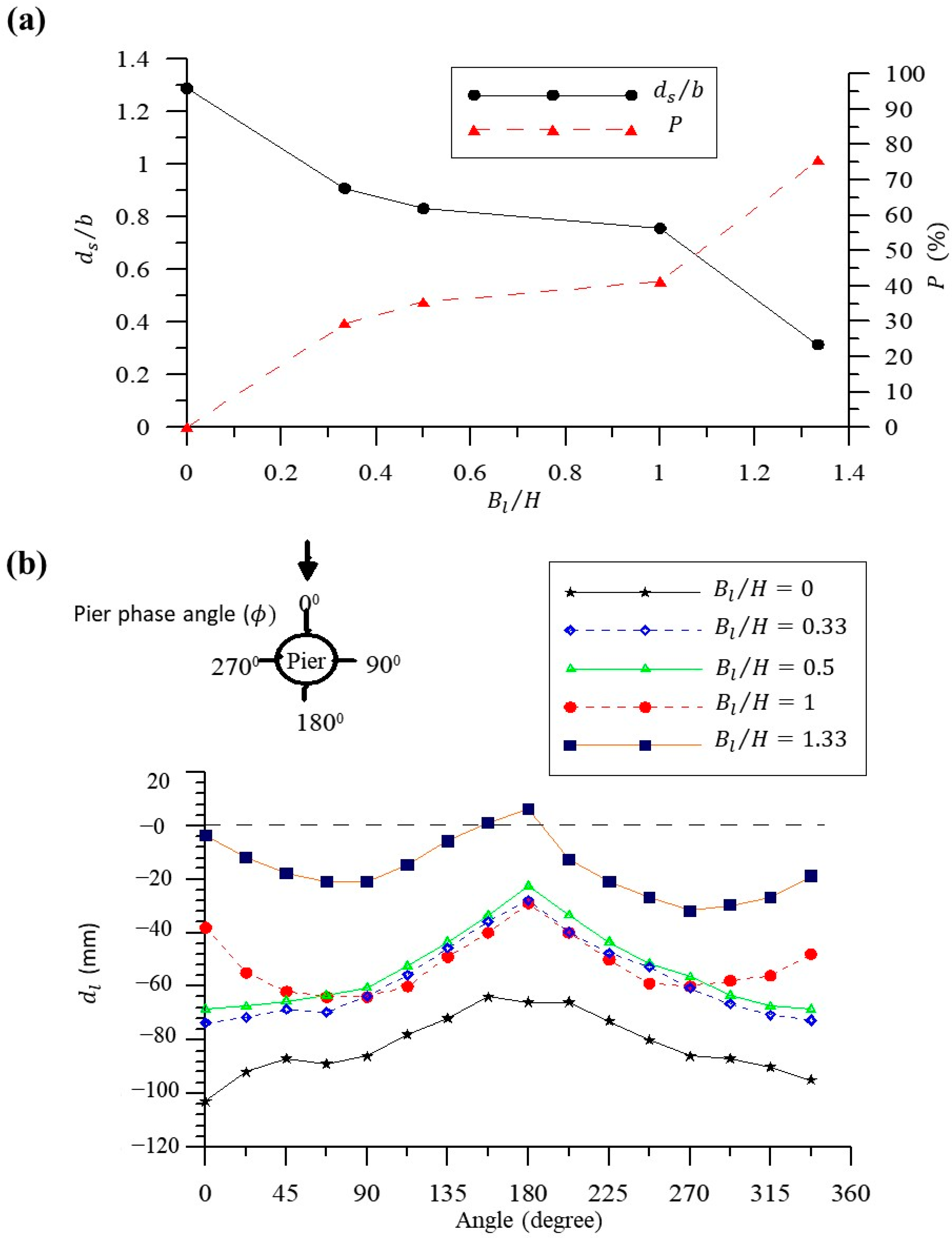
4.4. The Influence of Height of SPB on Pier Scour Reduction
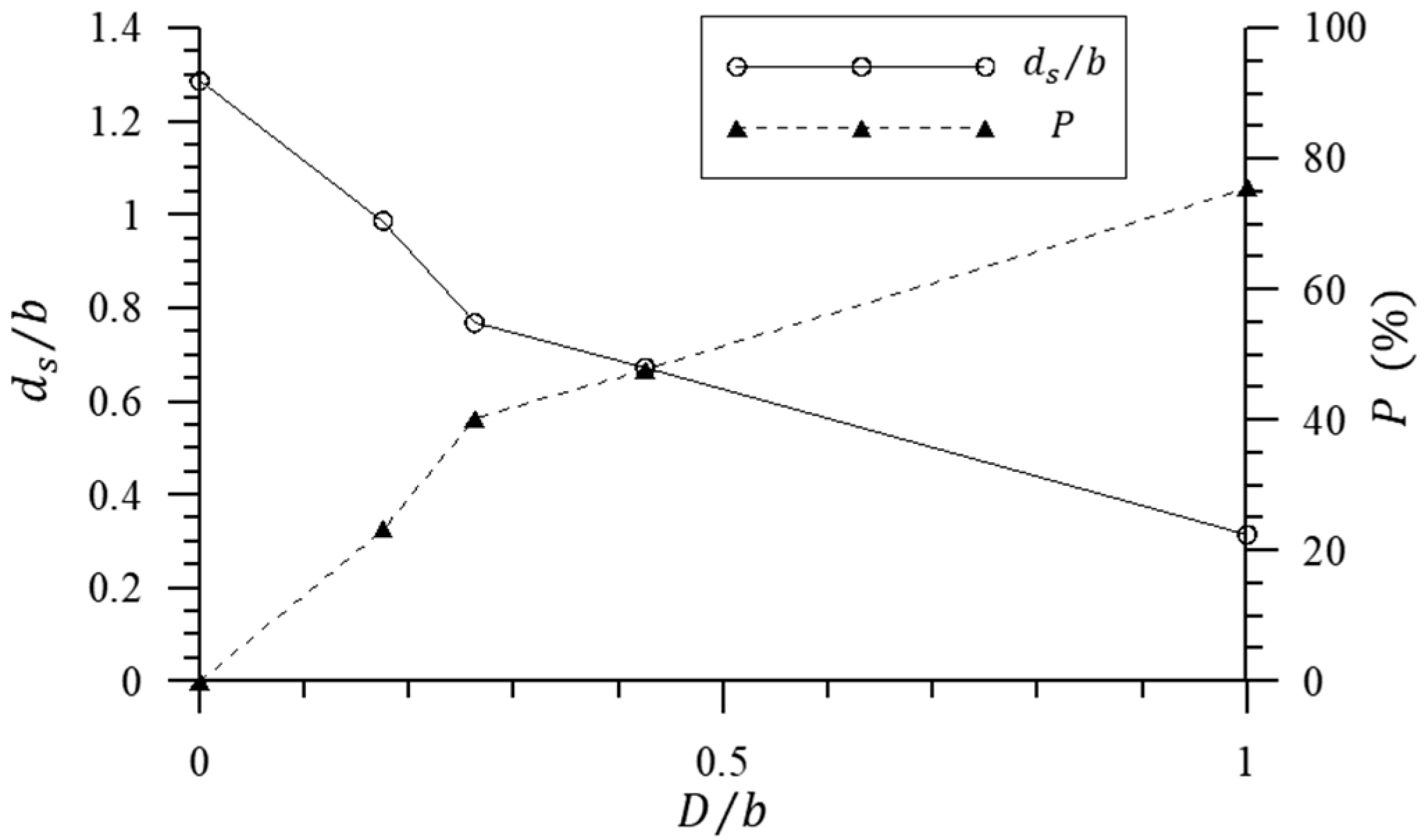
4.5. The Influence of Diameter of SPB on Pier Scour Reduction
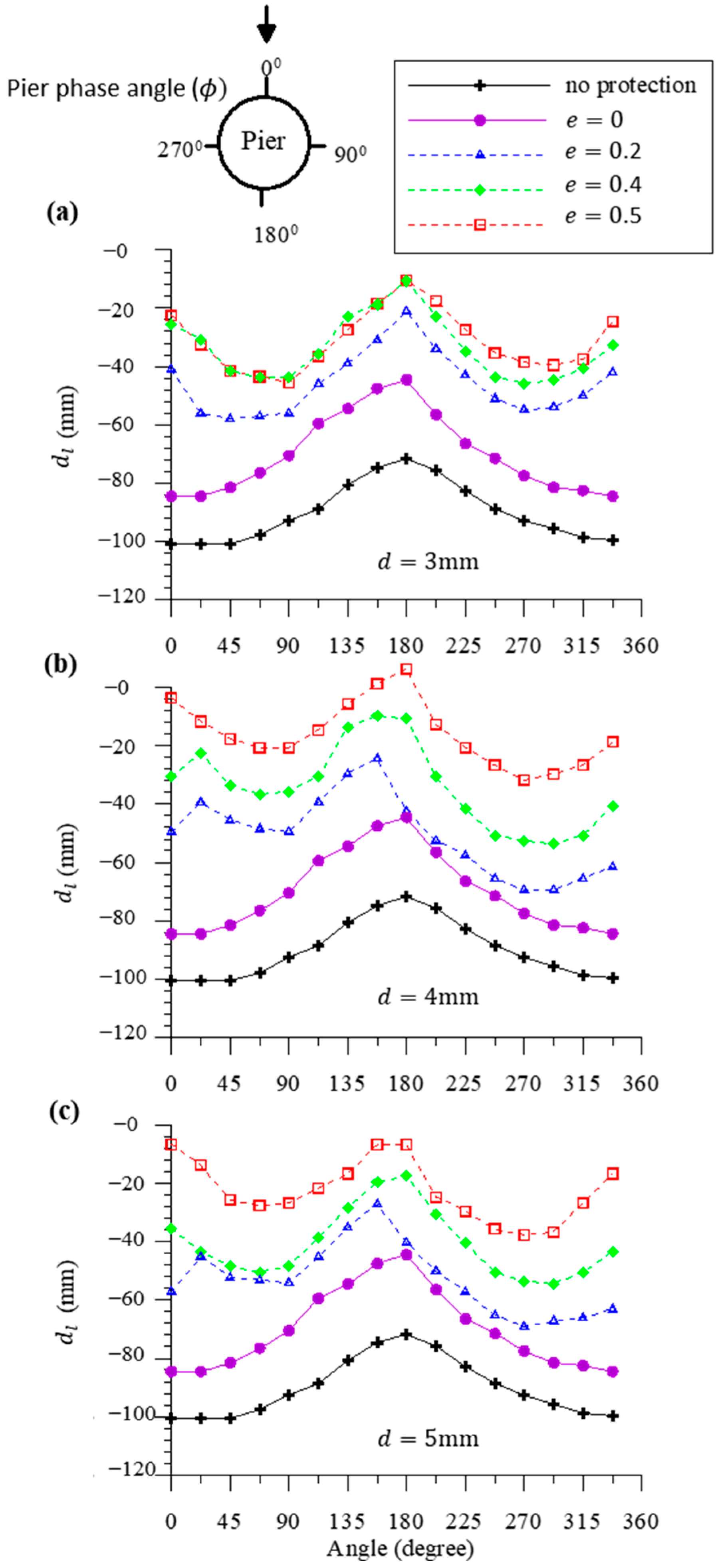
4.6. The Influence of Attack Angle () on Pier Scour Reduction
4.7. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notation
| A | total surface area of the basket; |
| A0 | the total hole area of the basket; |
| Bd | depth of basket under water; |
| Bl | length of basket; |
| b | diameter of pier; |
| D | diameter of SPB; |
| d | hole size; |
| d50 | median size of the sediment; |
| dl | the level of bed around the pier; |
| ds | the max. scour depth of the pier with SPB protection; |
| dsn | the max. scour depth of the pier without any protection; |
| e | porosity; |
| g | specific gravity of sand; |
| H | average depth of flow; |
| Kd | particle shape factor; |
| Kl | basket shape factor; |
| L | distance between panel and pier; |
| P | the percentages in maximum scour depth reduction ratio at pier; |
| V | average velocity; |
| Vc | mean velocity at threshold of motion of bed material; |
| skew angle between the approach flow and basket axis; | |
| phase angle at pier; | |
| fluid density; | |
| kinematic viscosity of water; | |
| specific gravity of sand; | |
| g | geometric standard deviation. |
References
- Kao, S.J.; Lee, T.Y.; Milliman, J.D. Calculating highly fluctuated suspended sediment fluxes from mountainous rivers in Taiwan. Terr. Atmos. Ocean. Sci. 2005, 16, 653. Available online: https://scholarworks.wm.edu/vimsarticles/102/ (accessed on 29 October 2021). [CrossRef] [Green Version]
- Khan, K.A.; Muzzammil, M.; Alam, J. Bridge Pier Scour: A review of mechanism, causes and geotechnical aspects. Proc. Adv. Geotech. Eng. 2016, 8–9. Available online: https://www.reserachgate.net/publication/312499136_Bridge_Pier_Scour_A_review_of_mechanism_causes_and_geotechnical_aspects (accessed on 29 October 2021).
- Melville, B.W.; Hadfield, A.C. Use of sacrificial piles as pier scour countermeasures. J. Hydraul. Eng. 1999, 125, 1221–1224. [Google Scholar] [CrossRef]
- Chiew, Y.M. Scour protection at bridge piers. J. Hydraul. Eng. 1992, 118, 1260–1269. [Google Scholar] [CrossRef]
- Tafarojnoruz, A.; Gaudio, R.; Dey, S. Flow-altering countermeasures against scour at bridge piers: A review. J. Hydraul. Res. 2010, 48, 441–452. [Google Scholar] [CrossRef]
- Lauchlan, C.S. Countermeasures for Pier Scour. Ph.D. Thesis, The University of Auckland, Auckland, New Zealand, 1999. Available online: https://trid.trb.org/view/855383 (accessed on 29 October 2021).
- Huang, C.K.; Tang, C.J.; Kuo, T.Y. Use of Surface Guide Panels as Pier Scour Countermeasures. Int. J. Sediment Res. 2005, 20, 117–128. [Google Scholar]
- Khaple, S.; Hanmaiahgari, P.R.; Gaudio, R.; Dey, S. Splitter plate as a flow-altering pier scour countermeasure. Acta Geophys. 2017, 65, 957–975. [Google Scholar] [CrossRef]
- Gaudio, R.; Tafarojnoruz, A.; Calomino, F. Combined flow-altering countermeasures against bridge pier scour. J. Hydraul. Res. 2012, 50, 35–43. [Google Scholar] [CrossRef]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publication: Littleton, CO, USA, 2000. [Google Scholar]
- Ettema, R.; Mostafa, E.A.; Melville, B.W.; Yassin, A.A. Local scour at skewed piers. J. Hydraul. Eng. 1998, 124, 756–759. [Google Scholar] [CrossRef]
- Bozkus, Z.; Yildiz, O. Effects of inclination of bridge piers on scouring depth. J. Hydraul. Eng. 2004, 130, 827–832. [Google Scholar] [CrossRef]
- Ettema, R. Scour at Bridge Piers; Auckland University: Auckland, New Zealand, 1980; Available online: https://trid.trb.org/view/171850 (accessed on 29 October 2021).
- Chiew, Y.M. Local Scour at Bridge Piers; Auckland University: Auckland, New Zealand, 1984; Available online: http://trid.trb.org/view/277693 (accessed on 29 October 2020).
- Baker, R.E. Local Scour at Bridge Piers in Non Uniform Sediment; Auckland University: Auckland, New Zealand, 1986; Available online: https://trid.trb.org/view/1196837 (accessed on 29 October 2020).
- Chee, R.K.W. Live-Bed Scour at Bridge Piers; Auckland University: Auckland, New Zealand, 1982; Available online: http://trid.trb.org/view/271201 (accessed on 29 October 2020).
- Raudkivi, A.J. Functional trends of scour at bridge piers. J. Hydraul. Eng. 1986, 112, 1–13. [Google Scholar] [CrossRef]
- Melville, B.W. The physics of local scour at bridge piers. In Proceedings of the 4th International Conference on Scour and Erosion (ICSE-4), Tokyo, Japan, 5–7 November 2008; pp. 28–40. Available online: https://hdl.handle.net/20.500.11970/100095 (accessed on 29 October 2021).
- Raudkivi, A.J.; Ettema, R. Effect of sediment gradation on clear water scour. J. Hydraul. Div. 1977, 103, 1209–1213. [Google Scholar] [CrossRef]
- Melville, B.W.; Sutherland, A.J. Design method for local scour at bridge piers. J. Hydraul. Eng. 1988, 114, 1210–1226. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.M. Time scale for local scour at bridge piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Further results to time-dependent local scour at bridge elements. J. Hydraul. Eng. 2005, 131, 97–105. [Google Scholar] [CrossRef]

| V (m/s) | H (cm) | d50 (mm) | b (cm) | Fr | V/Vc | H/b | ||
|---|---|---|---|---|---|---|---|---|
| 0.2146 | 6 | 0.515 | 1.064 | 8 | 0.280 | 0.7 | 2.6 | 0.75 |
| Case | d mm | e | D mm | L mm | Bl mm | degree | ds mm | ds/b | P % |
|---|---|---|---|---|---|---|---|---|---|
| PP | Without protection | 103.0 | 1.29 | 18.93 | |||||
| OR | 0 | 0 | 80 | 80 | 80 | 0 | 83.5 | 1.04 | 18.93 |
| A1 | 3 | 0.2 | 80 | 80 | 80 | 0 | 55.5 | 0.69 | 46.12 |
| A2 | 3 | 0.4 | 80 | 80 | 80 | 0 | 44.7 | 0.56 | 56.60 |
| A3 | 3 | 0.5 | 80 | 80 | 80 | 0 | 41.5 | 0.52 | 59.71 |
| A4 | 4 | 0.2 | 80 | 80 | 80 | 0 | 60.0 | 0.75 | 41.75 |
| A5 | 4 | 0.4 | 80 | 80 | 80 | 0 | 44.2 | 0.55 | 57.09 |
| A6 * | 4 | 0.5 | 80 | 80 | 80 | 0 | 25.2 | 0.32 | 75.53 |
| A7 | 5 | 0.2 | 80 | 80 | 80 | 0 | 64.3 | 0.80 | 37.57 |
| A8 | 5 | 0.4 | 80 | 80 | 80 | 0 | 53.0 | 0.66 | 48.54 |
| A9 | 5 | 0.5 | 80 | 80 | 80 | 0 | 30.7 | 0.38 | 70.19 |
| B1 | 4 | 0.5 | 80 | 0 | 80 | 0 | 52.5 | 0.66 | 49.03 |
| B2 | 4 | 0.5 | 80 | 40 | 80 | 0 | 37.5 | 0.47 | 63.59 |
| B3 * | 4 | 0.5 | 80 | 80 | 80 | 0 | 25.2 | 0.32 | 75.53 |
| B4 | 4 | 0.5 | 80 | 120 | 80 | 0 | 41.5 | 0.52 | 59.71 |
| B5 | 4 | 0.5 | 80 | 160 | 80 | 0 | 40.2 | 0.50 | 60.97 |
| B6 | 4 | 0.5 | 80 | 200 | 80 | 0 | 50.4 | 0.63 | 51.07 |
| B7 | 4 | 0.5 | 80 | 240 | 80 | 0 | 51.0 | 0.64 | 50.49 |
| B8 | 4 | 0.5 | 80 | 280 | 80 | 0 | 59.5 | 0.74 | 42.23 |
| B9 | 4 | 0.5 | 80 | 560 | 80 | 0 | 64.8 | 0.81 | 37.09 |
| C1 | 4 | 0.5 | 80 | 80 | 0 | 0 | 103.0 | 1.29 | 0.00 |
| C2 | 4 | 0.5 | 80 | 80 | 20 | 0 | 72.7 | 0.91 | 29.42 |
| C3 | 4 | 0.5 | 80 | 80 | 30 | 0 | 66.5 | 0.83 | 35.44 |
| C4 | 4 | 0.5 | 80 | 80 | 60 | 0 | 60.5 | 0.76 | 41.26 |
| C5 * | 4 | 0.5 | 80 | 80 | 80 | 0 | 25.2 | 0.32 | 75.53 |
| D1 | 3 | 0.5 | 14 | 80 | 80 | 0 | 79.0 | 0.99 | 23.30 |
| D2 | 3 | 0.5 | 21 | 80 | 80 | 0 | 61.2 | 0.77 | 40.58 |
| D3 | 3 | 0.5 | 34 | 80 | 80 | 0 | 53.8 | 0.67 | 47.77 |
| D4 * | 4 | 0.5 | 80 | 80 | 80 | 0 | 25.2 | 0.32 | 75.53 |
| E1 * | 4 | 0.5 | 80 | 80 | 80 | 0 | 25.2 | 0.32 | 75.53 |
| E2 | 4 | 0.5 | 80 | 80 | 80 | 30 | 89.8 | 1.12 | 12.82 |
| E3 | 4 | 0.5 | 80 | 80 | 80 | 45 | 114.5 | 1.43 | −11.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, W.-L.; Lu, C.-W.; Huang, C.-K. Application of a Single Porous Basket as a Pier Scour Countermeasure. Water 2021, 13, 3052. https://doi.org/10.3390/w13213052
Lee W-L, Lu C-W, Huang C-K. Application of a Single Porous Basket as a Pier Scour Countermeasure. Water. 2021; 13(21):3052. https://doi.org/10.3390/w13213052
Chicago/Turabian StyleLee, Wei-Lin, Chih-Wei Lu, and Chin-Kun Huang. 2021. "Application of a Single Porous Basket as a Pier Scour Countermeasure" Water 13, no. 21: 3052. https://doi.org/10.3390/w13213052
APA StyleLee, W.-L., Lu, C.-W., & Huang, C.-K. (2021). Application of a Single Porous Basket as a Pier Scour Countermeasure. Water, 13(21), 3052. https://doi.org/10.3390/w13213052







