Modelling and Incorporating the Variable Demand Patterns to the Calibration of Water Distribution System Hydraulic Model
Abstract
1. Introduction
2. Materials and Methods
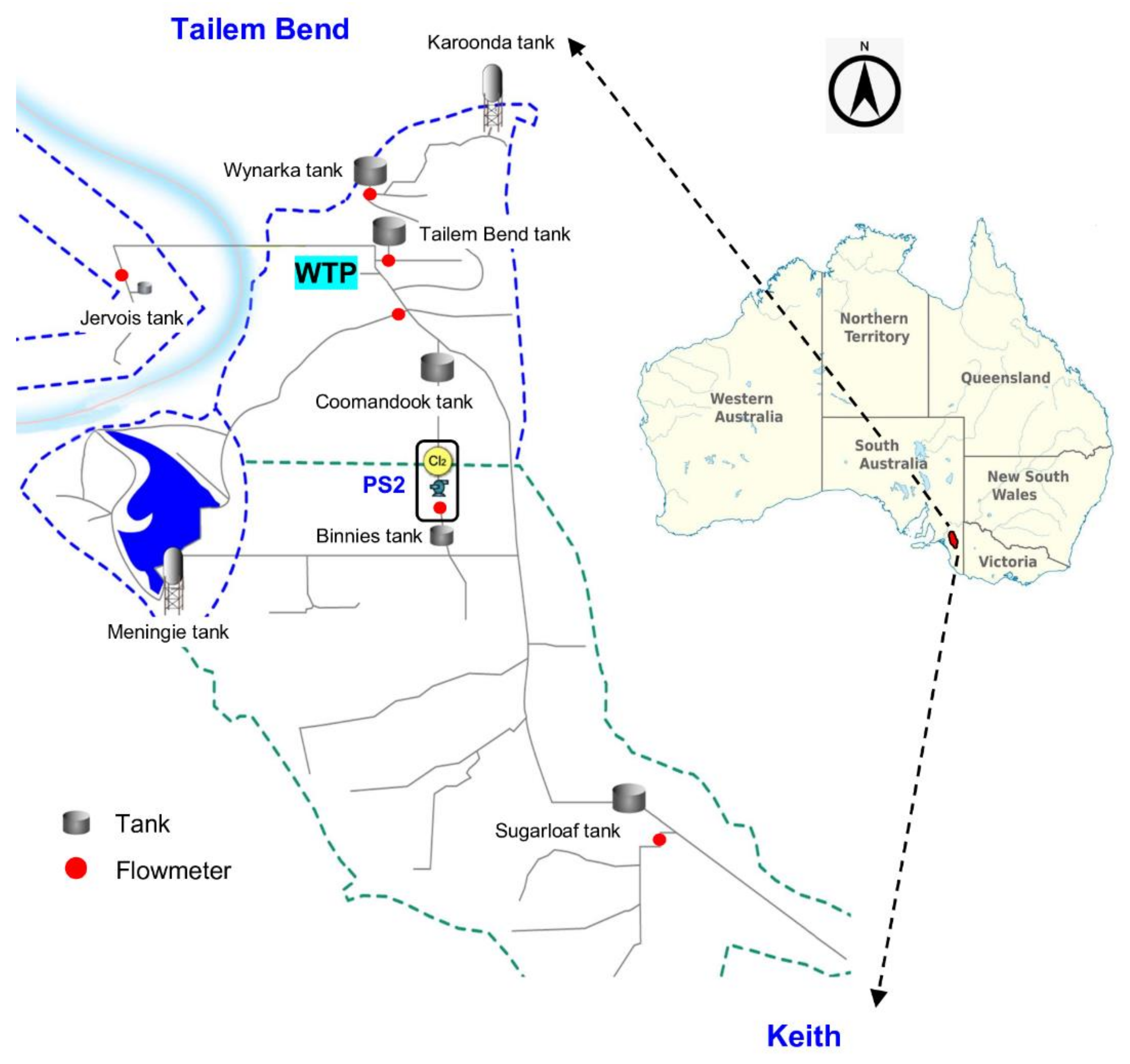
2.1. Study Area
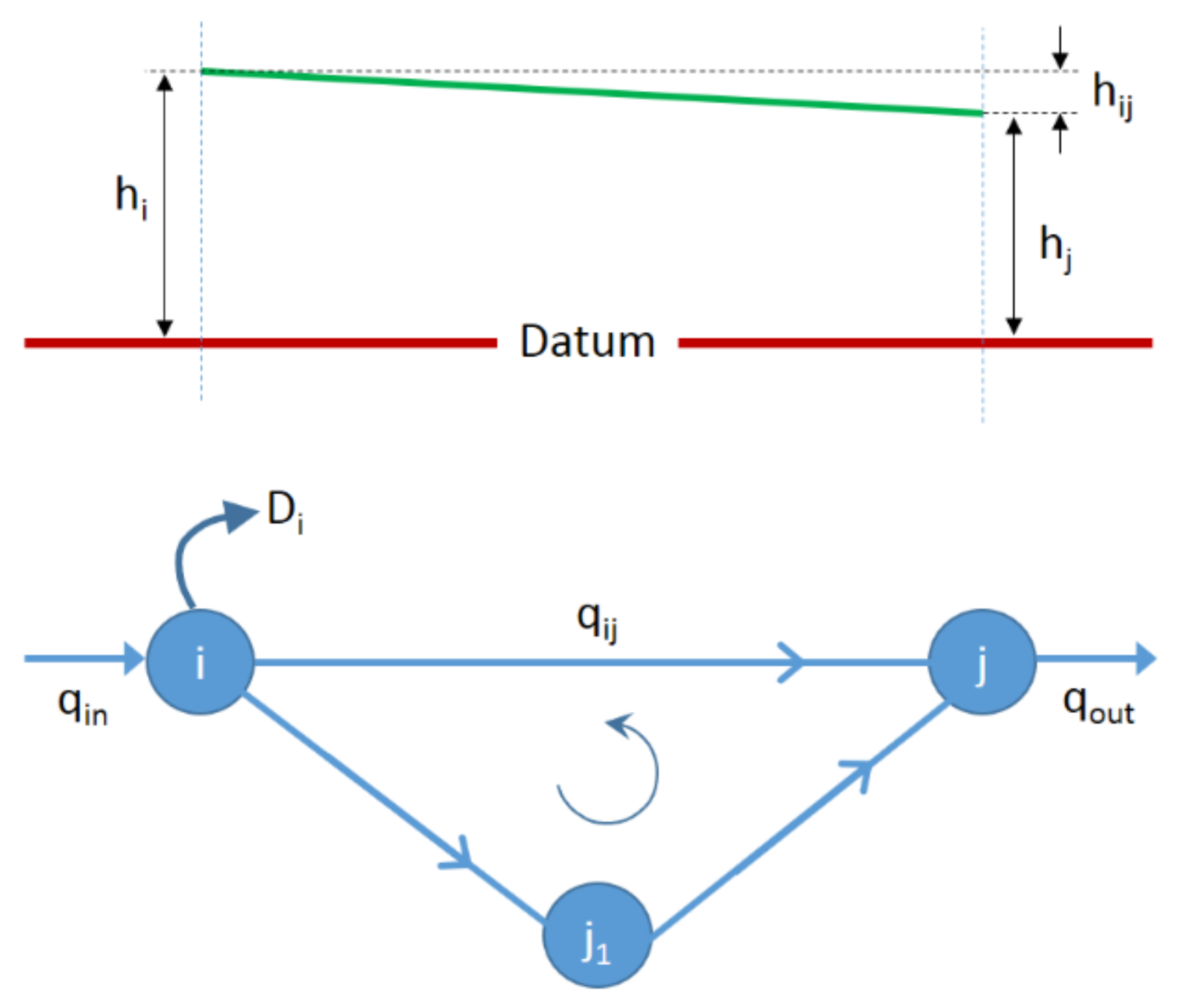
2.2. Hydraulic Modelling Tool
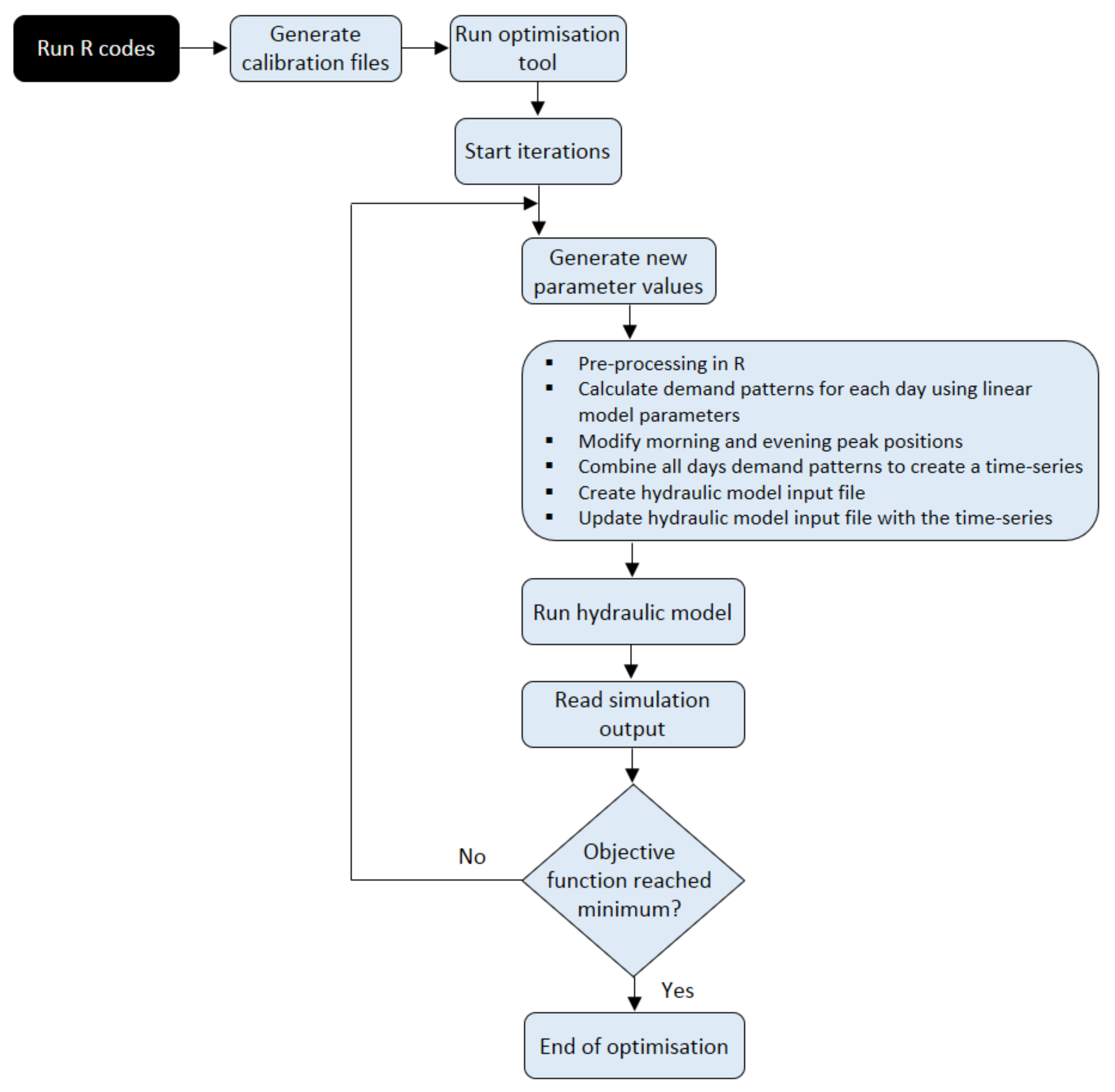
2.3. Optimisation Tool
2.4. Optimisation Algorithm
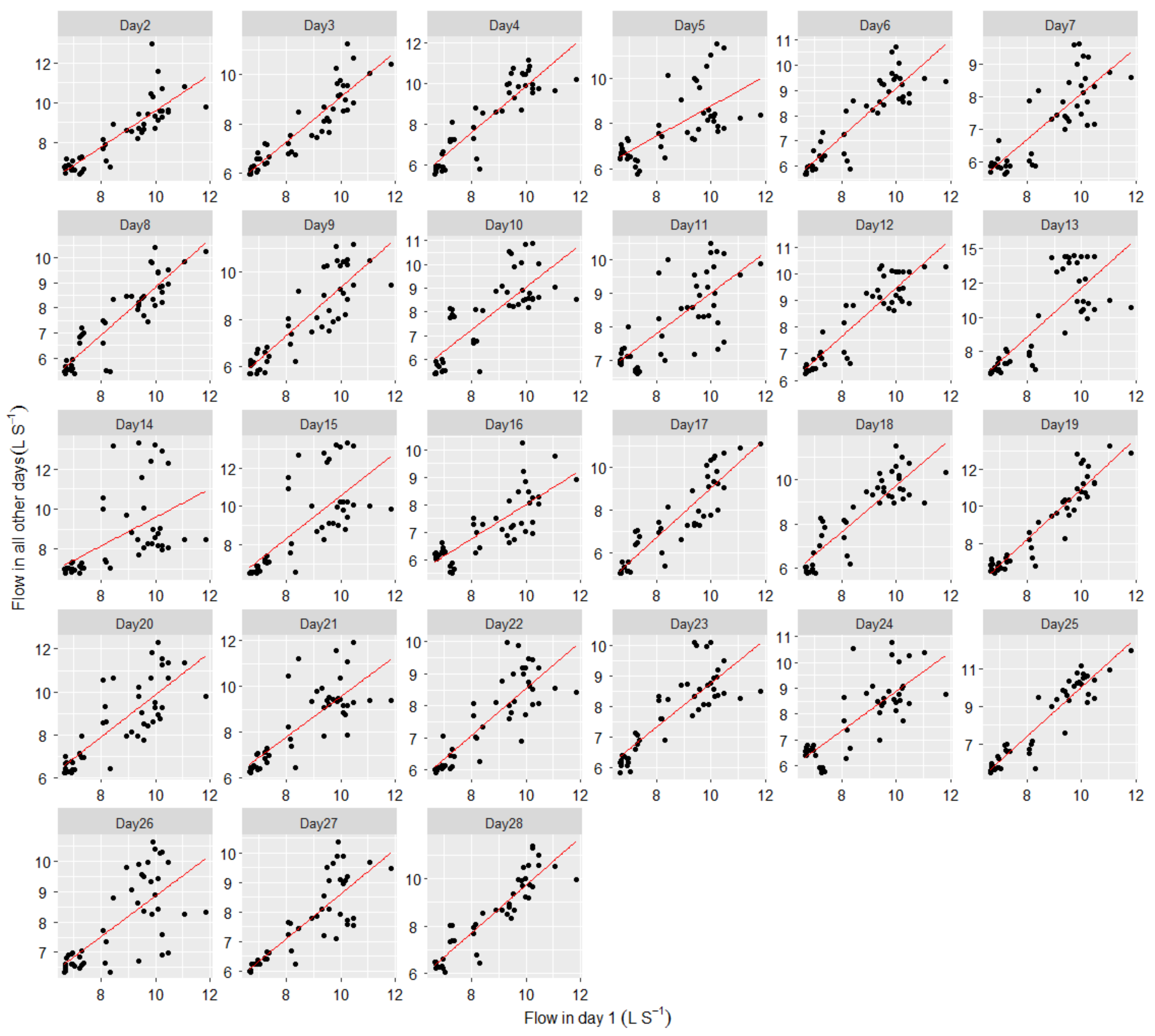
2.5. Hydraulic and Calibration Setup
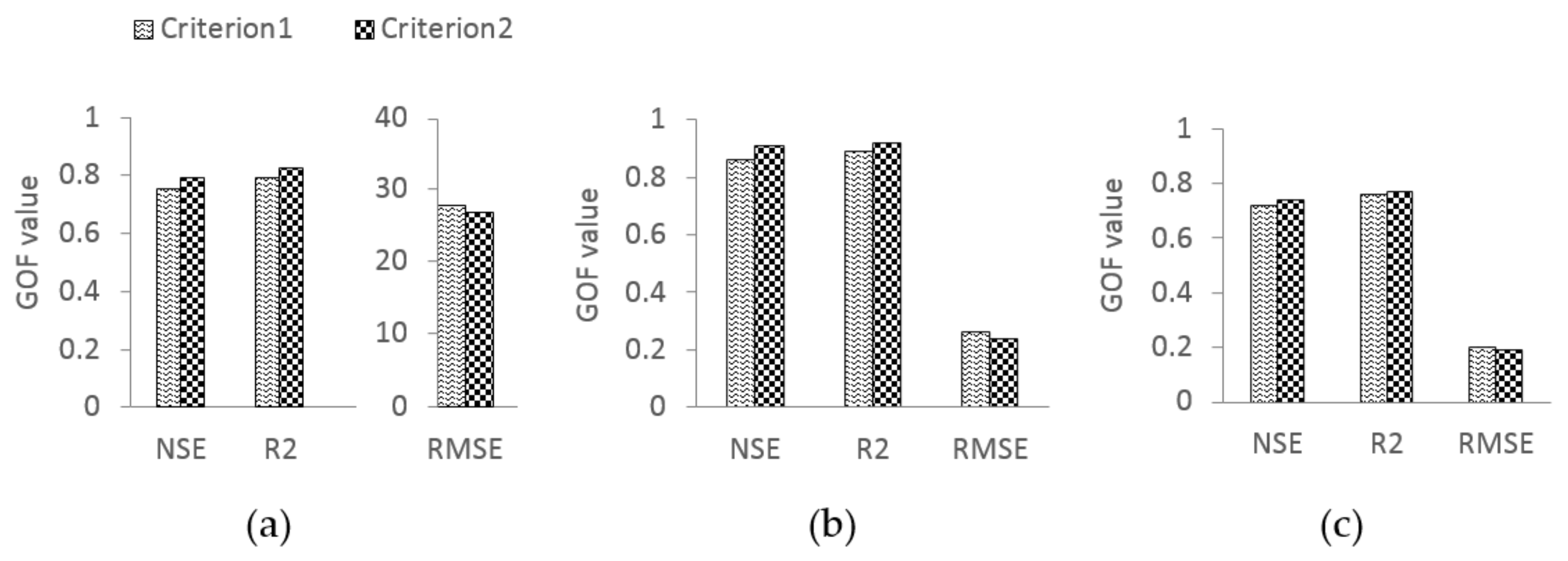
2.6. Goodness-of-Fit (GOF)
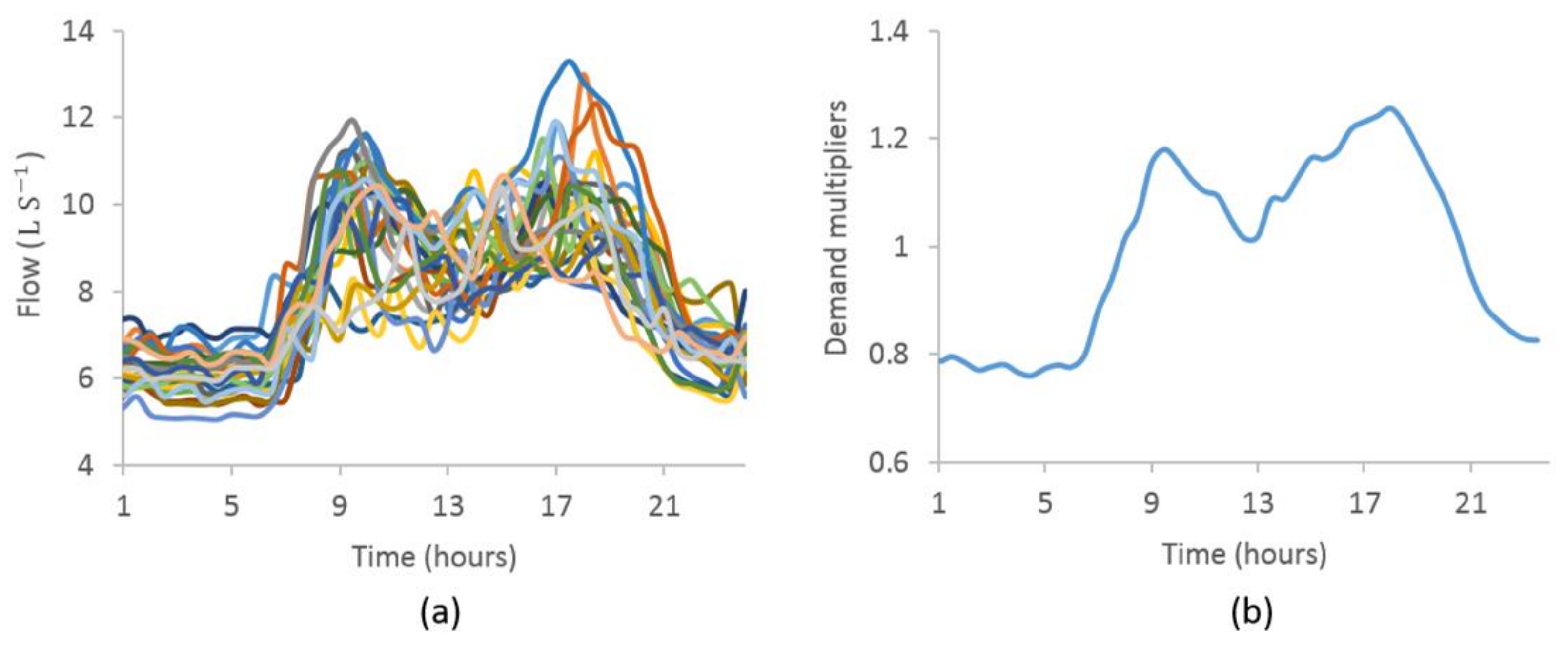
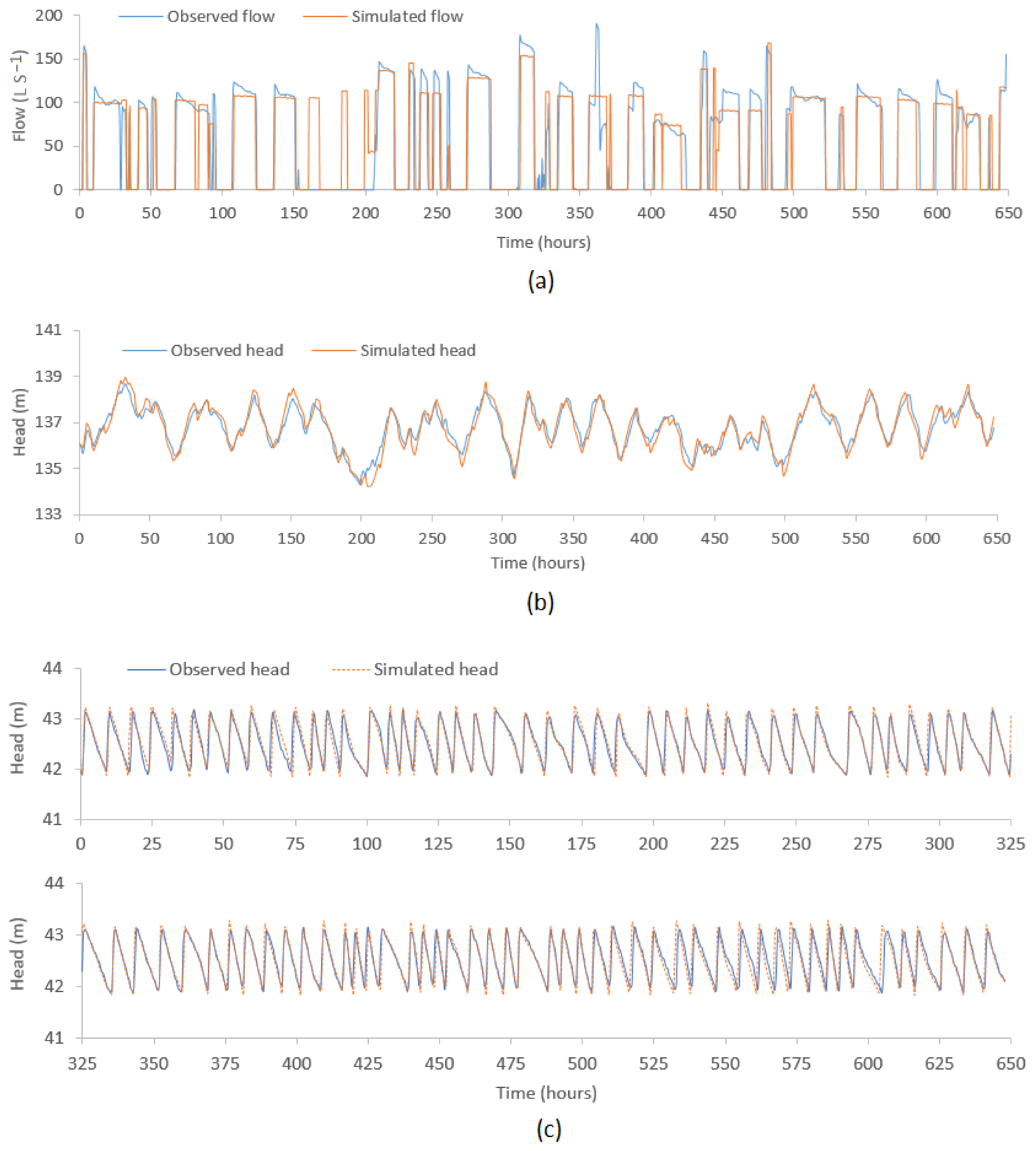
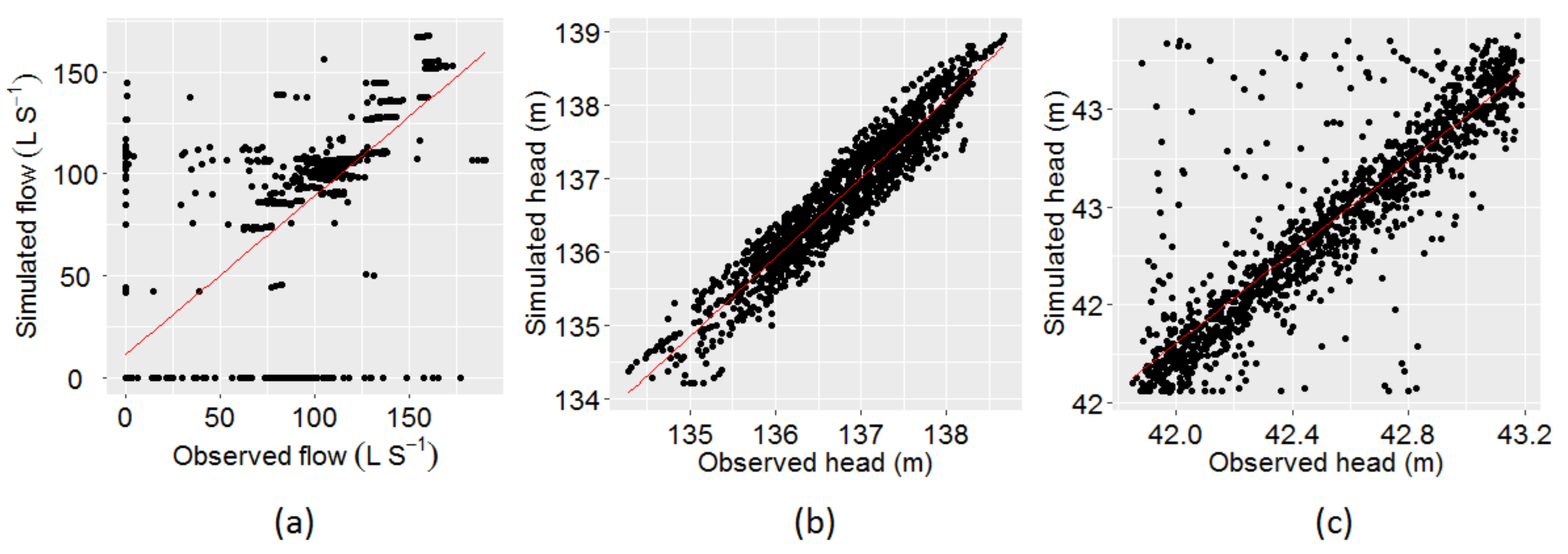
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peters, A.; Liang, B.; Tian, H.; Li, Z.; Doolan, C.; Vitanage, D.; Norris, H.; Simpson, K.; Wang, Y.; Chen, F. Data-driven water quality prediction in chloraminated systems. Water e-J. 2020, 5, 1–19. [Google Scholar] [CrossRef]
- Kara, S.; Karadirek, I.E.; Muhammetoglu, A.; Muhammetoglu, H. Hydraulic Modeling of a Water Distribution Network in a Tourism Area with Highly Varying Characteristics. Procedia Eng. 2016, 162, 521–529. [Google Scholar] [CrossRef]
- Ormsbee, L.E.; Lingireddy, S. Calibrating hydraulic network models. J. AWWA 1997, 89, 42–50. [Google Scholar] [CrossRef]
- Shen, H.; McBean, E. Hydraulic calibration for a small water distribution network. In Water Distribution Systems Analysis 2010; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 1545–1557. [Google Scholar]
- Alves, Z.; Muranho, J.; Albuquerque, T.; Ferreira, A. Water Distribution Network’s Modeling and Calibration. A Case Study based on Scarce Inventory Data. Procedia Eng. 2014, 70, 31–40. [Google Scholar] [CrossRef]
- Liong, S.-Y.; Atiquzzaman, M. Optimal design of water distribution network using shuffled complex evolution. J. Inst. Eng. 2004, 44, 93–107. [Google Scholar]
- Moosavian, N.; Jaefarzadeh, M.R. Hydraulic analysis of water distribution network using shuffled complex evolution. J. Fluids 2014, 2014, 979706. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef]
- Hansen, N.; Kern, S. Evaluating the CMA Evolution Strategy on Multimodal Test Functions. In Parallel Problem Solving from Nature—PPSN VIII; Springer: Berlin/Heidelberg, Germany, 2004; pp. 282–291. [Google Scholar]
- Doherty, J. PEST: Model Independent Parameter Estimation—User Manual, 5th ed.; Watermark Numerical Computing: Brisbane, Australia, 2005. [Google Scholar]
- Khedr, A.; Tolson, B.; Ziemann, S. Water distribution system calibration: Manual versus optimization-based approach. Procedia Eng. 2015, 119, 725–733. [Google Scholar] [CrossRef]
- Zanfei, A.; Menapace, A.; Santopietro, S.; Righetti, M. Calibration Procedure for Water Distribution Systems: Comparison among Hydraulic Models. Water 2020, 12, 1421. [Google Scholar] [CrossRef]
- Do, N.C.; Simpson, A.R.; Deuerlein, J.W.; Piller, O. Calibration of Water Demand Multipliers in Water Distribution Systems Using Genetic Algorithms. J. Water Resour. Plan. Manag. 2016, 142, 04016044. [Google Scholar] [CrossRef]
- Do, N.C.; Simpson, A.R.; Deuerlein, J.W.; Piller, O. Particle Filter-Based Model for Online Estimation of Demand Multipliers in Water Distribution Systems under Uncertainty. J. Water Resour. Plan. Manag. 2017, 143, 04017065. [Google Scholar] [CrossRef]
- Letting, L.K.; Hamam, Y.; Abu-Mahfouz, A.M. Estimation of Water Demand in Water Distribution Systems Using Particle Swarm Optimization. Water 2017, 9, 593. [Google Scholar] [CrossRef]
- Elhay, S.; Simpson, A.R. Dealing with Zero Flows in Solving the Nonlinear Equations for Water Distribution Systems. J. Hydraul. Eng. 2011, 137, 1216–1224. [Google Scholar] [CrossRef][Green Version]
- Farley, M. Leakage Management and Control: A Best Practice Training Manual; World Health Organization: Geneva, Switzerland, 2001. [Google Scholar]
- Ávila, C.A.M.; Sánchez-Romero, F.-J.; López-Jiménez, P.A.; Pérez-Sánchez, M. Leakage Management and Pipe System Efficiency: Its Influence in the Improvement of the Efficiency Indexes. Water 2021, 13, 1909. [Google Scholar] [CrossRef]
- García-Ávila, F.; Avilés-Añazco, A.; Ordoñez-Jara, J.; Guanuchi-Quezada, C.; Flores del Pino, L.; Ramos-Fernández, L. Pressure management for leakage reduction using pressure reducing valves. Case study in an Andean city. Alex. Eng. J. 2019, 58, 1313–1326. [Google Scholar] [CrossRef]
- Puust, R.; Kapelan, Z.; Savic, D.A.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Zyl, J.E.v.; Clayton, C.R.I. The effect of pressure on leakage in water distribution systems. Water Manag. 2007, 160, 109–114. [Google Scholar] [CrossRef]
- García, I.F.; Novara, D.; Mc Nabola, A. A Model for Selecting the Most Cost-Effective Pressure Control Device for More Sustainable Water Supply Networks. Water 2019, 11, 1297. [Google Scholar] [CrossRef]
- Karimov, A.; Molden, D.; Khamzina, T.; Platonov, A.; Ivanov, Y. A water accounting procedure to determine the water savings potential of the Fergana Valley. Agric. Water Manag. 2012, 108, 61–72. [Google Scholar] [CrossRef]
- Mercedes Garcia, A.V.; López-Jiménez, P.A.; Sánchez-Romero, F.-J.; Pérez-Sánchez, M. Objectives, Keys and Results in the Water Networks to Reach the Sustainable Development Goals. Water 2021, 13, 1268. [Google Scholar] [CrossRef]
- Dandy, G.; Roberts, A.; Hewitson, C.; Chrystie, P. Sustainability Objectives for the Optimization of Water Distribution Networks. In Water Distribution Systems Analysis Symposium 2006; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 1–11. [Google Scholar]
- Kang, D.; Lansey, K. Demand and Roughness Estimation in Water Distribution Systems. J. Water Resour. Plan. Manag. 2011, 137, 20–30. [Google Scholar] [CrossRef]
- Hossain, S.; Chow, C.W.K.; Hewa, G.A.; Cook, D.; Harris, M. Spectrophotometric Online Detection of Drinking Water Disinfectant: A Machine Learning Approach. Sensors 2020, 20, 6671. [Google Scholar] [CrossRef]
- Muranho, J.; Ferreira, A.; Sousa, J.; Gomes, A.; Marques, A.S. Convergence issues in the EPANET solver. Procedia Eng. 2015, 119, 700–709. [Google Scholar] [CrossRef][Green Version]
- Rossman, L.A.; Woo, H.; Tryby, M.; Shang, F.; Janke, R.; Haxton, T. EPANET 2.2 User Manual; U.S. Environmental Protection Agency: Washington, DC, USA, 2020. [Google Scholar]
- Todini, E.; Pilati, S. A gradient method for the solution of looped pipe networks. In Computer Applications in Water Supply: Volume 1—System Analysis and Simulation; Coulbeck, B., Orr, C.H., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1988; pp. 1–20. [Google Scholar]
- Doherty, J.; Skahill, B.E. An advanced regularization methodology for use in watershed model calibration. J. Hydrol. 2006, 327, 564–577. [Google Scholar] [CrossRef]
- Hossain, S.; Hewa, G.A.; Wella-Hewage, S. A Comparison of Continuous and Event-Based Rainfall–Runoff (RR) Modelling Using EPA-SWMM. Water 2019, 11, 611. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2019. [Google Scholar]
- Nishida, K.; Akimoto, Y. PSA-CMA-ES: CMA-ES with population size adaptation. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 865–872. [Google Scholar]
- Auger, A.; Hansen, N. A restart CMA evolution strategy with increasing population size. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 1762, pp. 1769–1776. [Google Scholar]
- Kuczera, G. Efficient subspace probabilistic parameter optimization for catchment models. Water Resour. Res. 1997, 33, 177–185. [Google Scholar] [CrossRef]
- Lepot, M.; Aubin, J.-B.; Clemens, F.H.L.R. Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water 2017, 9, 796. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; van Liew, M.W.; Bingner, R.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Optimization Strategy for Improving the Energy Efficiency of Irrigation Systems by Micro Hydropower: Practical Application. Water 2017, 9, 799. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Calibrating a flow model in an irrigation network: Case study in Alicante, Spain. Span. J. Agric. Res. 2017, 15, 1202. [Google Scholar] [CrossRef]
- Georgescu, A.-M.; Georgescu, S.-C.; Cosoiu, C.I.; Hasegan, L.; Anton, A.; Bucur, D.M. EPANET Simulation of Control Methods for Centrifugal Pumps Operating under Variable System Demand. Procedia Eng. 2015, 119, 1012–1019. [Google Scholar] [CrossRef]
| Parameter Group | No. of Parameters | Group Range |
|---|---|---|
| Pipe roughness | 9 | 87–165 |
| Pump settings/rotor speed | 42 | 0.80–1.33 |
| Time-based controls for pump operation | 83 | 2–644 |
| Morning and evening peak shifting | 56 | ±3 |
| Linear model slope parameter | 28 | 0.70–1.40 |
| Linear model Intercept parameter | 28 | 0.00–0.30 |
| Optimisation Algorithm | Algorithm Type | Number of Model Runs | Elapsed Time | % Reduction of Objective Function |
|---|---|---|---|---|
| CMAES | Global search | 14,338 | 16 h using 28 processors | 29 |
| SCE | Global search | 90,000 | 9 days and 16 h using 5 processors | 22 |
| GLMA | Local search | 3196 | 1 day and 15 h using single processer | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, S.; Hewa, G.A.; Chow, C.W.K.; Cook, D. Modelling and Incorporating the Variable Demand Patterns to the Calibration of Water Distribution System Hydraulic Model. Water 2021, 13, 2890. https://doi.org/10.3390/w13202890
Hossain S, Hewa GA, Chow CWK, Cook D. Modelling and Incorporating the Variable Demand Patterns to the Calibration of Water Distribution System Hydraulic Model. Water. 2021; 13(20):2890. https://doi.org/10.3390/w13202890
Chicago/Turabian StyleHossain, Sharif, Guna A. Hewa, Christopher W. K. Chow, and David Cook. 2021. "Modelling and Incorporating the Variable Demand Patterns to the Calibration of Water Distribution System Hydraulic Model" Water 13, no. 20: 2890. https://doi.org/10.3390/w13202890
APA StyleHossain, S., Hewa, G. A., Chow, C. W. K., & Cook, D. (2021). Modelling and Incorporating the Variable Demand Patterns to the Calibration of Water Distribution System Hydraulic Model. Water, 13(20), 2890. https://doi.org/10.3390/w13202890






