Methodology for Pumping Station Design Based on Analytic Hierarchy Process (AHP)
Abstract
:1. Introduction
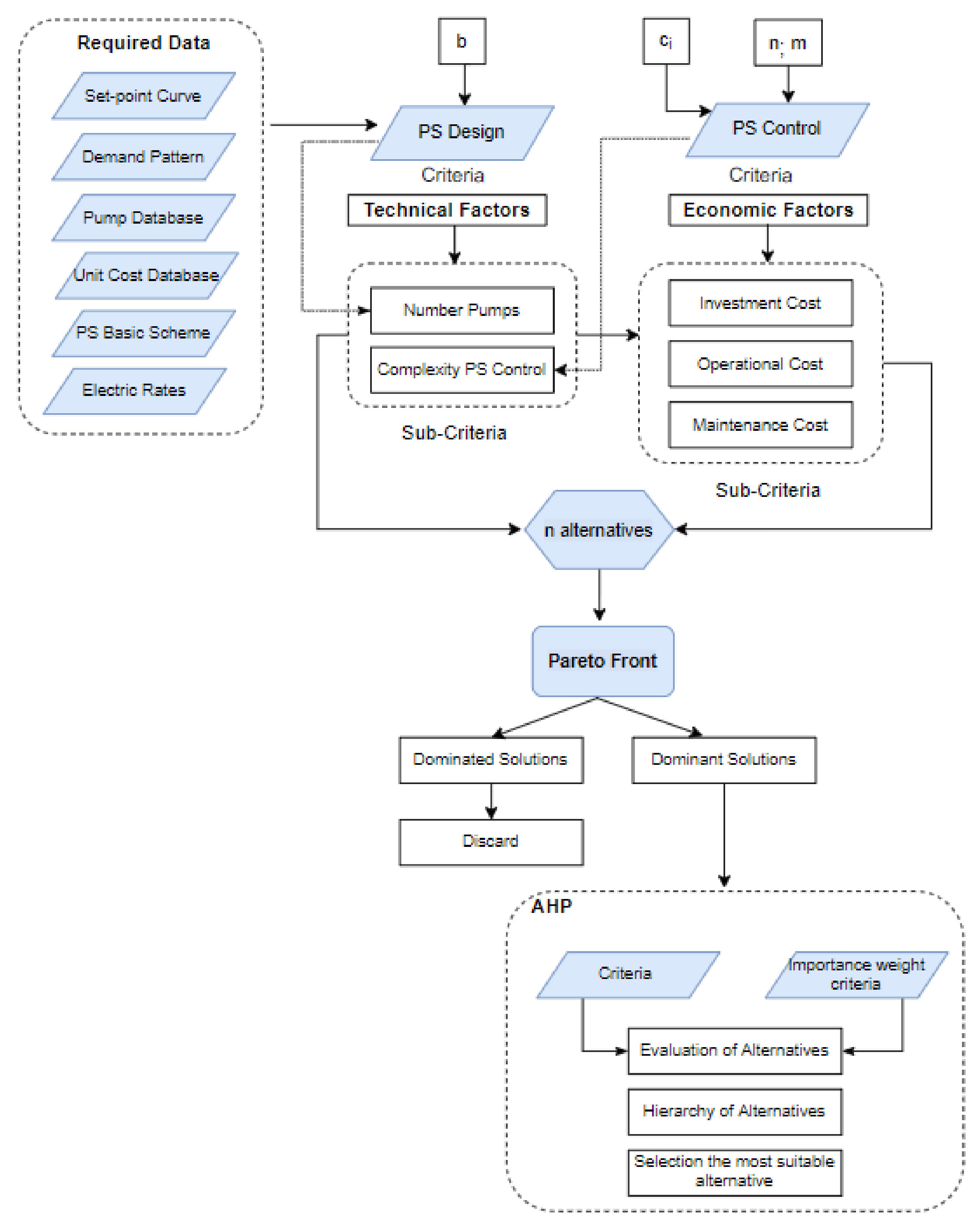
2. Materials and Methods
2.1. Problem Statement
2.2. Required Data for Pumping Station Design
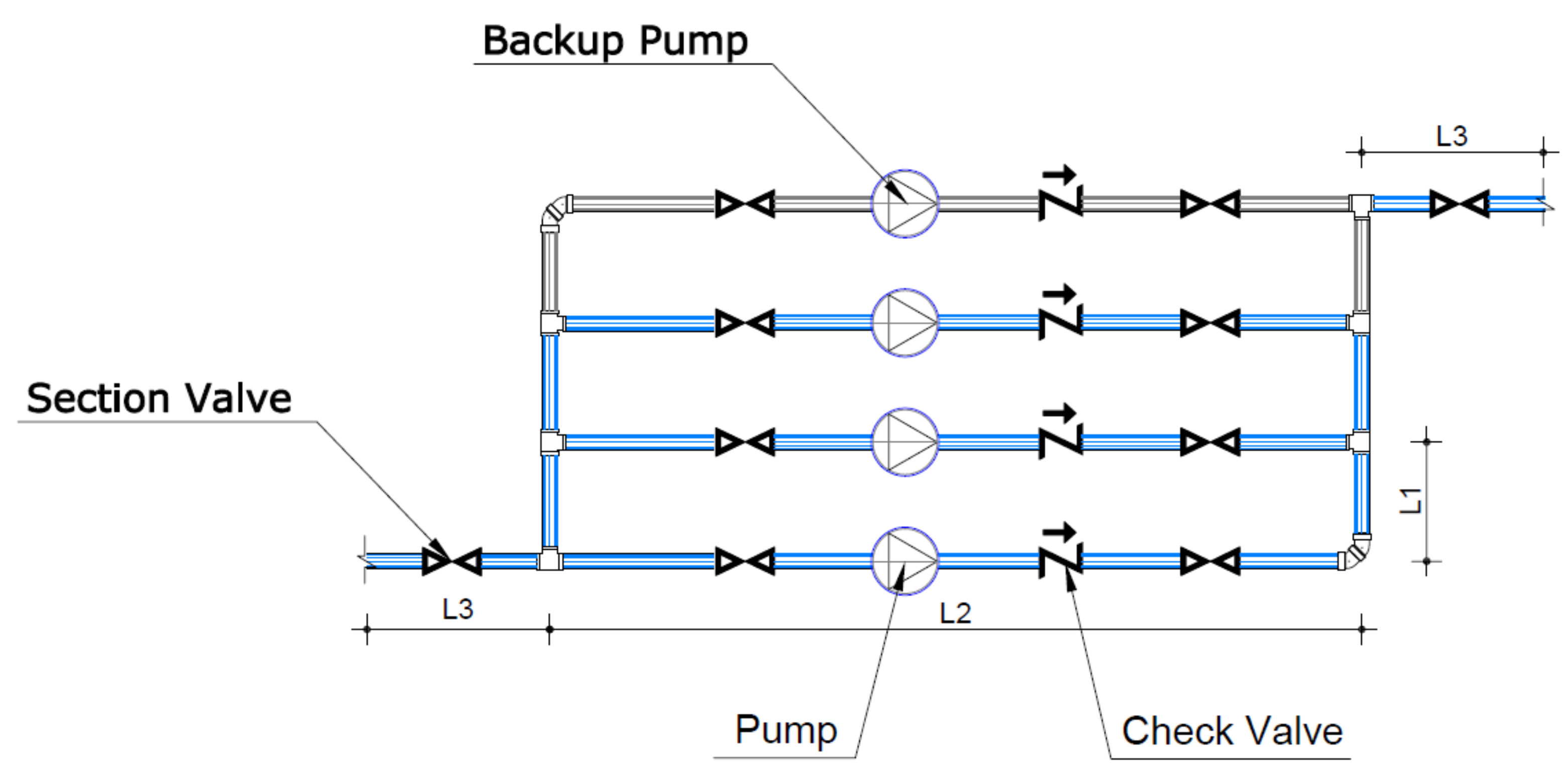
- Iglesias-Rey et al. [34] proposed a basic scheme of a PS (Figure 1). This scheme includes a backup pump to guarantee the reliability of the PS. The scheme is defined by three characteristic lengths (L1, L2 and L3). These lengths are considered proportional to the nominal diameter of the pipelines (DNi) through a factor fni, as shown in Equation (1). It was also assumed that the diameter DNi was calculated from the maximum required flow (Qmax) and a maximum design velocity of 2 m/s.
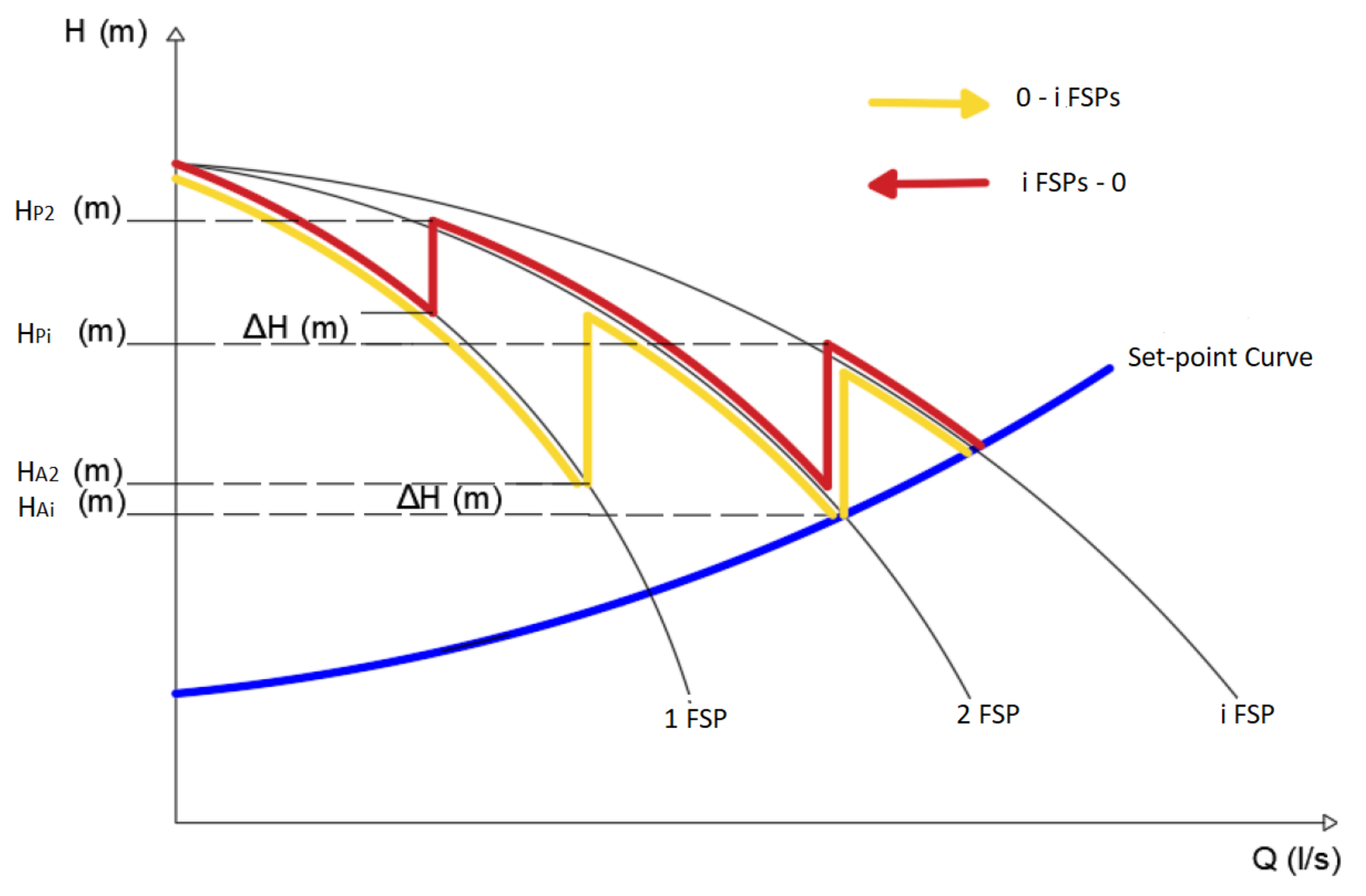
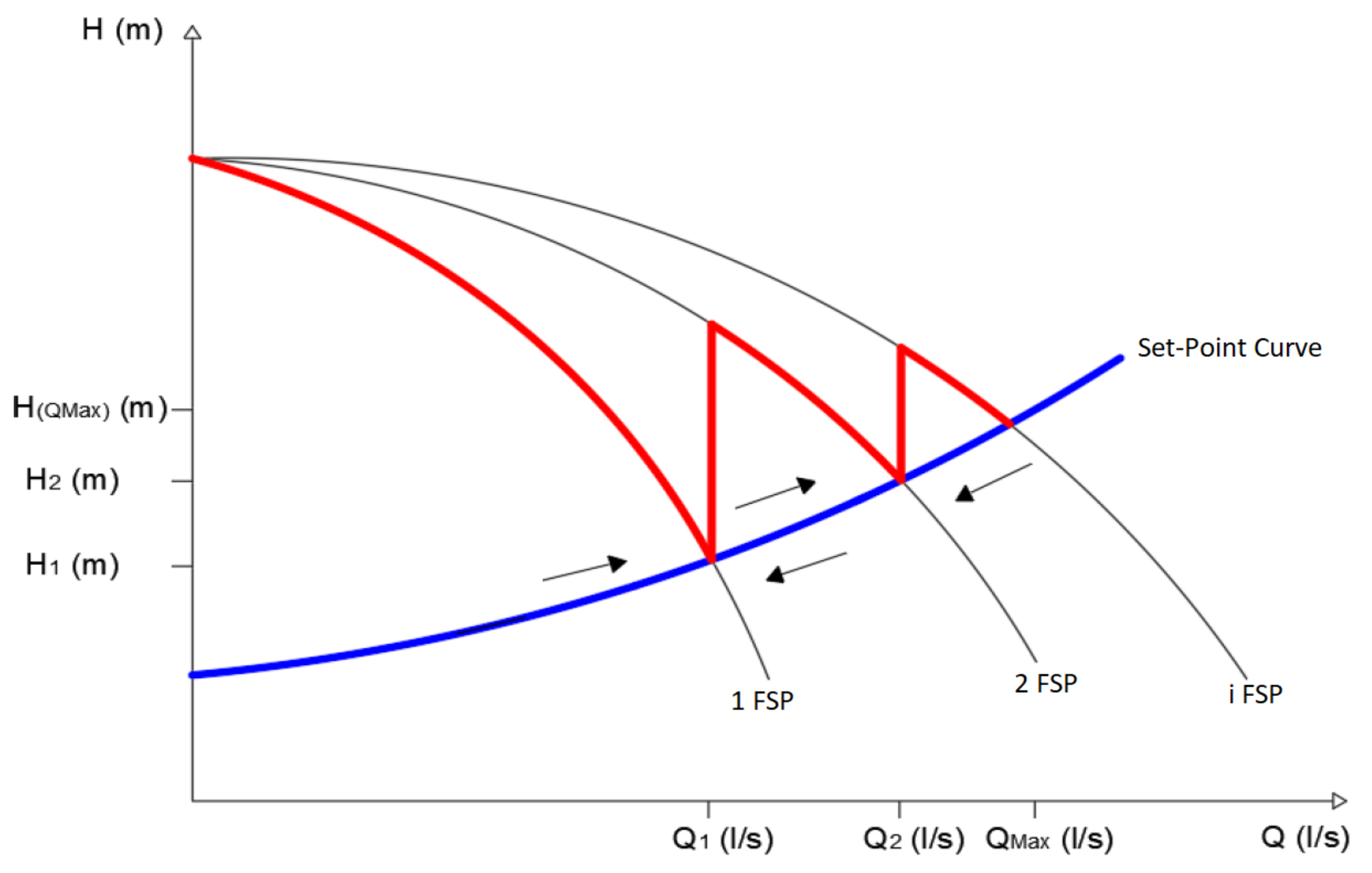
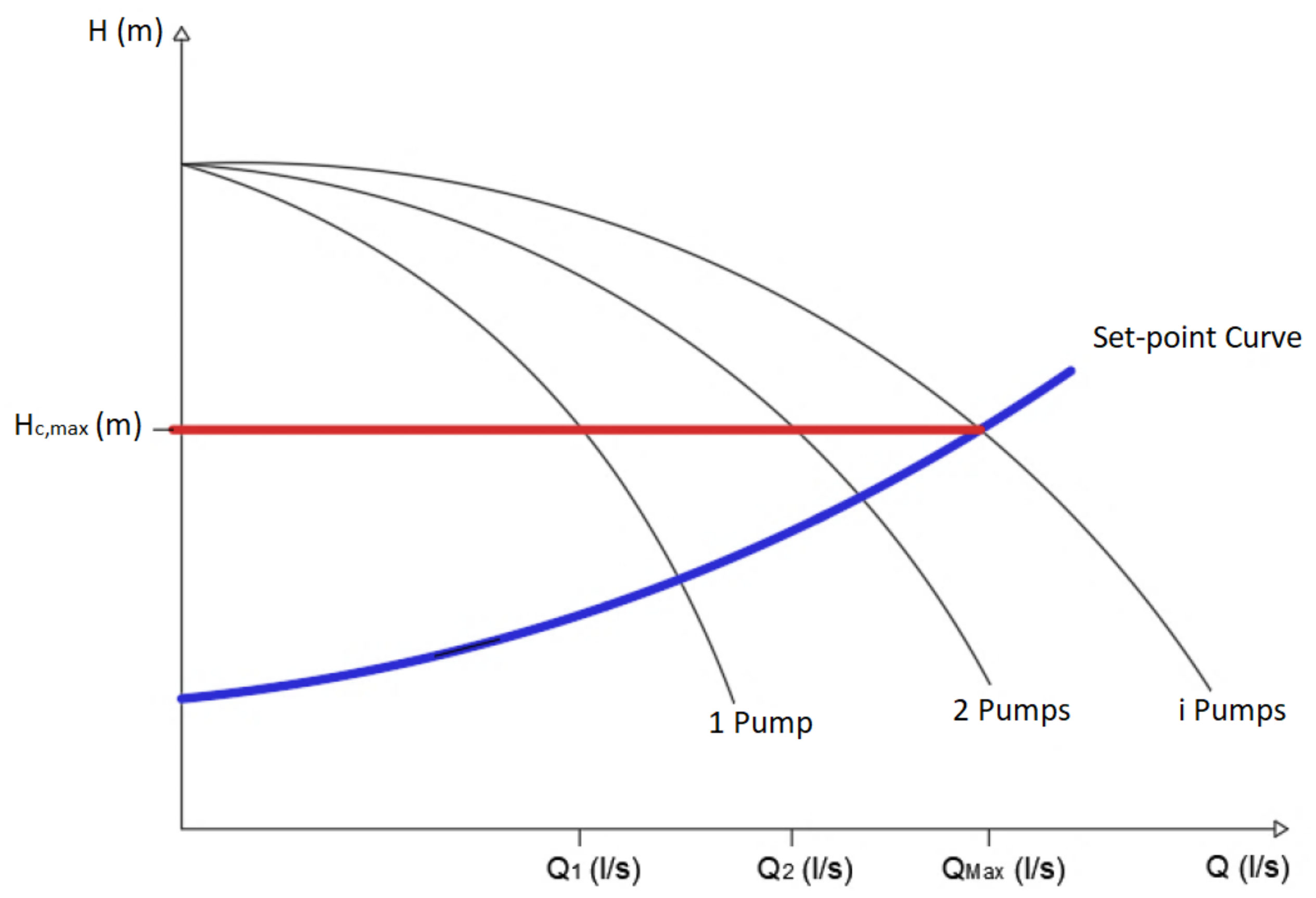
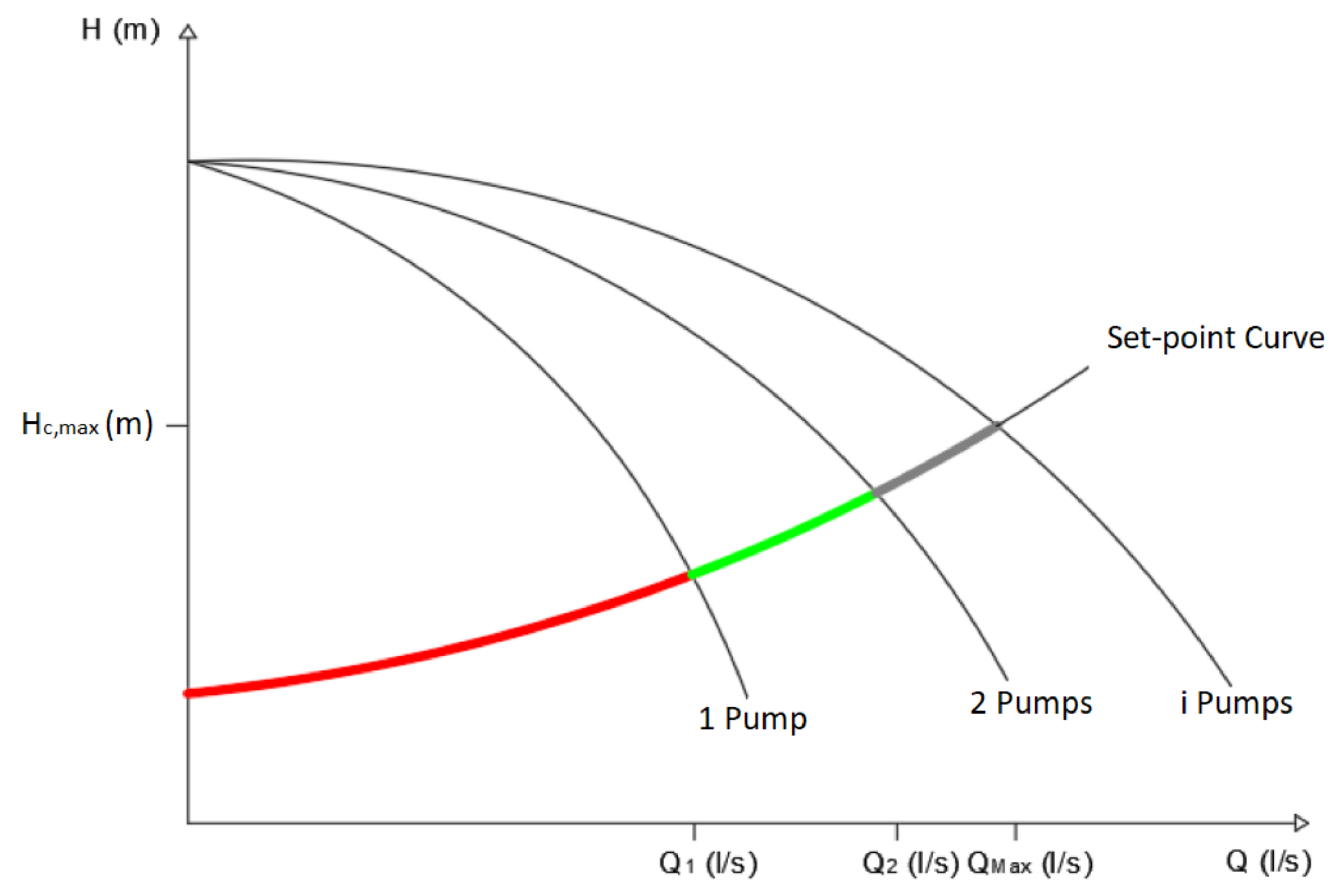
- The setpoint curve represents the total dynamic head required (Hc) for each required demand flow (Q) of the network to satisfy consumption nodes. This curve is defined as the total dynamic head needed by the pump station to supply the demand flow and maintaining the minimum pressure required at the critical consumption node of the network [12]. Usually, the setpoint curve can be written as in Equation (2):
- 3.
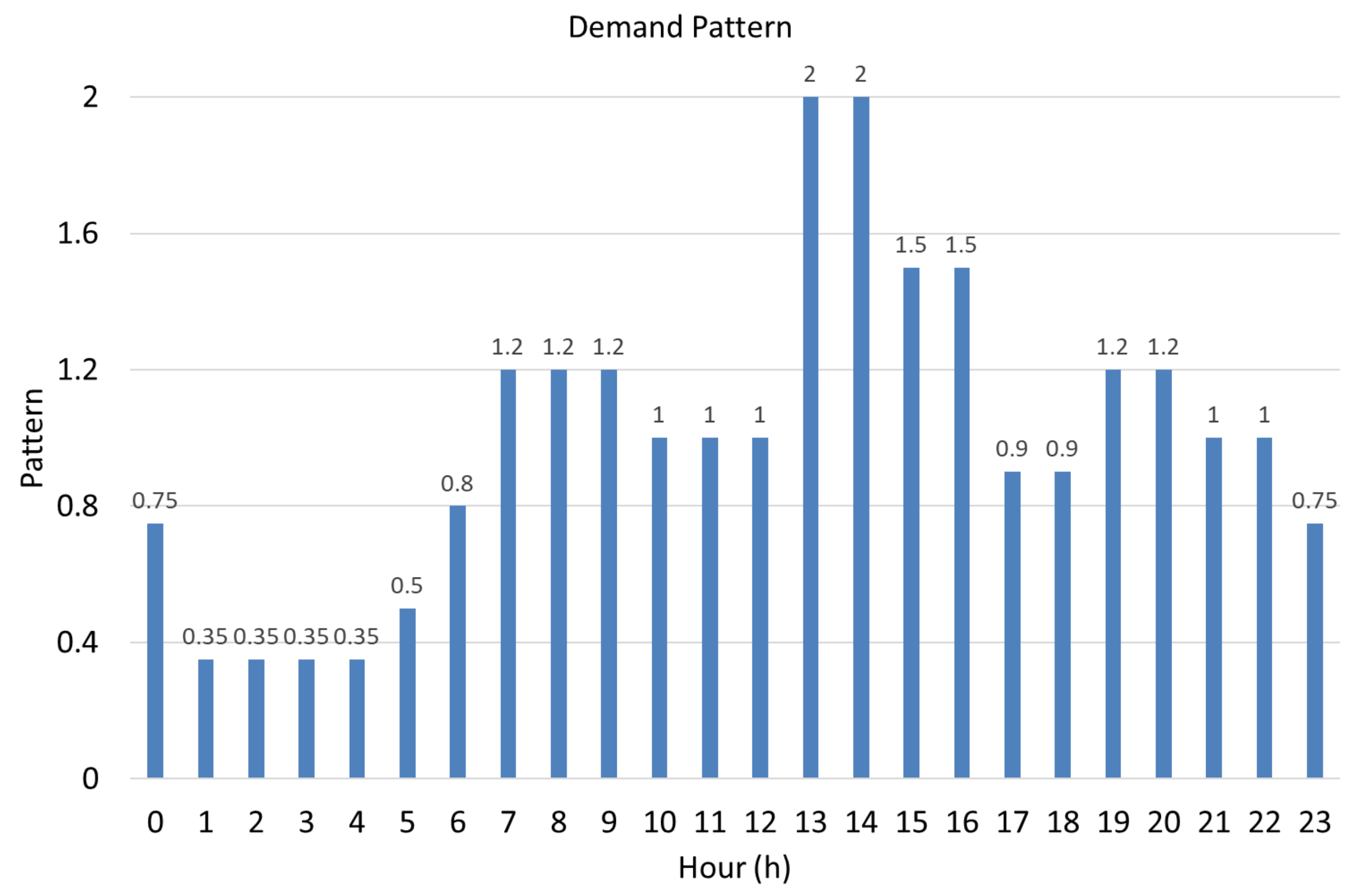
- Demand patterns correspond to the variation of consumed flow in a period (day hour, weekday, year season).
- 4.
- To select a pump, it is accepted that there is a list of available commercial pumps. Each pump model is defined by the best efficient point (BEP), that is, nominal rotational speed (N0), nominal flow (Q0), nominal head (H0), nominal efficiency (η0) and the parameters used to describe the curves of the pump (H-Q and η-Q). Relationships among these variables are used as follows:
- 5.
- Electric tariffs are managed by companies that provide energy service to the users. These tariffs could be different in a period of a day, year, season or could not have any kind of variation. This work contemplates three different electric tariff hours: peak hours, off-peak hours and plain hours, and two seasons: summer and winter.
- 6.
- In addition, every element of a PS, such as pumps, pipes, valves, control elements and other accessories has a database with its commercial costs including the installation costs.
- 7.
- Seven different modes of control systems have been used in this work based on two aspects. The PS may content FSP, VSP or a combination of both. Besides, measurements devices may supply readings for pressure only (pressure control, PC) or pressure and flow (flow control, FC) [32]. Table 1 described the required equipment of every control system. For a detailed description of these control systems, the reader can find t. The operational modes of these seven configurations of control system are detailed in Appendix A of this document.
2.3. Definition of the Techno-Economical Criteria Used
2.4. Methodology of Analytic Hierarchy Process (AHP)
3. Case Studies
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| Ai,j | Assessment of the alternative for each criterion |
| Criteria comparison matrix | |
| H1; A; B; E; F | Coefficients that characterized the pumping curve |
| E | Consumed Energy of the pumping station |
| c | Coefficient that characterized the set-point curve |
| CI | Consistency Index |
| Cci | Complexity priority of every regulation mode |
| CR | Consistency ratio |
| Q | Demand flow |
| CDi,j | Deviation of the importance weight of every criterion for each group of experts concerning the overall priority |
| Dj | Deviation of the priority of every group of experts respect to the overall priority |
| PAi | Distributive priority of the overall normalized assessment of each alternative |
| η; η0 | The efficiency of the pump; Nominal efficiency of the pumps |
| R | Energy losses in the network |
| Final vector of criteria comparison matrix with their importance weight | |
| Li | Length of the pipelines |
| Ci | Priority or importance weight of every criterion |
| CPi | Priority considering the consistency of every criterion |
| λmax | Maximum quotient between and |
| Hmax | Maximum total dynamic head |
| Qman | Maximum demand flow |
| Ai(max),j; Ai(max),j | Maximum and minimum assessment values of the alternatives in each criterion |
| PAi,max | Maximum distributive priority of the overall normalized assessment of each alternative |
| Qm | Mean demand flow |
| Qmin | Minimum demand flow |
| fni | Multiplication factor for the length of the pipelines |
| H0 | Nominal head of the pump |
| DNi | Nominal diameter of the pipelines |
| Q0 | Nominal flow of the pump |
| Nai,j | Normalized values of the pairwise comparison |
| NAi,j | Normalized assessment of the alternatives for each criterion |
| nc | Number of criteria |
| ne | Number of groups of experts |
| b | Number of pumps |
| n | Number of FSPs |
| m | Number of VSPs |
| ONAi | Overall normalized assessment of the alternative |
| ORi | Overall rating of the alternative |
| ai,j | Quantitative values of the pairwise comparison of the criteria |
| RI | Random consistency index |
| Rci | Rating of complexity priority of every regulation mode |
| N; N0 | Rotational speed; Nominal rotational speed |
| ΔH | Static head of the system |
| CPi,GM | The geometric mean of the priority considering the consistency of every criterion |
| CP0,i | The general priority considering the consistency of every criterion |
| PT | Total consumed power of a pump |
| H | Total dynamic head |
Abbreviations
| AHP | Analytic hierarchy process |
| FC | Flow control |
| FSP | Fixed speed pump |
| MEI | Minimum Efficiency Index |
| PC | Pressure control |
| PS | Pumping station |
| VSP | Variable speed pump |
| VFD | Variable frequency drive |
Appendix A
Control System
| Element | C(X) (EUR) | X | C1 | C2 | C3 |
|---|---|---|---|---|---|
| Pipe | ND (mm) | 10.13 | 0.20 | 0.0005 | |
| Elbow connector | ND (mm) | 29.17 | 0.01 | - | |
| Tee connector | ND (mm) | 42.60 | 0.01 | - | |
| Section Valve | ND (mm) | 63.63 | 0.79 | 0.01 | |
| Check Valve | ND (mm) | 35.63 | −0.14 | 0.01 | |
| Flow meter | Din (mm) | 885.70 | −9.22 | 0.06 | |
| Variable Frequency Drive | P (KW) | 168.19 | 116.08 | −0.60 |
References
- Conti, J.; Holtberg, P.; Diefenderfer, J.; LaRose, A.; Turnure, J.T.; Westfall, L. International Energy Outlook 2016 with Projections to 2040. In International Energy Outlook 2016 with Projections; USDOE Energy Information Administration (EIA): Washington, DC, USA, 2016; Volume 0484. [Google Scholar]
- Tolvanen, H.J. Life cycle energy cost savings and pump selection. World Pumps 2007, 2007, 34–37. [Google Scholar] [CrossRef]
- Bunn, S. Pump Scheduling Optimization in Four US Cities: Case Studies. In Proceedings of the Eighth Annual Water Distribution Systems Analysis Symposium (WDSA), Cincinnati, OH, USA, 27–30 August 2006; pp. 1–12. [Google Scholar] [CrossRef]
- Cohen, D.; Shamir, U.; Sinai, G. Sensitivity analysis of optimal operation of irrigation supply systems with water quality considerations. Irrig. Drain. Syst. 2004, 18, 227–253. [Google Scholar] [CrossRef]
- McCormick, G.; Powell, R. Optimal Pump Scheduling in Water Supply Systems with Maximum Demand Charges. J. Water Resour. Plan. Manag. 2003, 129, 372–379. [Google Scholar] [CrossRef]
- Cimorelli, L.; D’Aniello, A.; Cozzolino, L. Boosting Genetic Algorithm Performance in Pump Scheduling Problems with a Novel Decision-Variable Representation. J. Water Resour. Plan. Manag. 2020, 146, 04020023. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Tabesh, M.; Ataeekia, B. Ant-colony optimization of pumping schedule to minimize the energy cost using variable-speed pumps in water distribution networks. Urban Water J. 2013, 11, 335–347. [Google Scholar] [CrossRef]
- Abdallah, M.; Kapelan, Z. Iterative Extended Lexicographic Goal Programming Method for Fast and Optimal Pump Scheduling in Water Distribution Networks. J. Water Resour. Plan. Manag. 2017, 143, 04017066. [Google Scholar] [CrossRef]
- Abdallah, M.; Kapelan, Z. Fast Pump Scheduling Method for Optimum Energy Cost and Water Quality in Water Distribution Networks with Fixed and Variable Speed Pumps. J. Water Resour. Plan. Manag. 2019, 145, 04019055. [Google Scholar] [CrossRef] [Green Version]
- Luna, T.; Ribau, J.; Figueiredo, D.; Alves, R. Improving energy efficiency in water supply systems with pump scheduling optimization. J. Clean. Prod. 2019, 213, 342–356. [Google Scholar] [CrossRef]
- Carpitella, S.; Brentan, B.; Montalvo, I.; Izquierdo, J.; Certa, A. Multi-criteria analysis applied to multi-objective optimal pump scheduling in water systems. Water Supply 2019, 19, 2338–2346. [Google Scholar] [CrossRef] [Green Version]
- León-Celi, C.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Mora-Melia, D. A Methodology for the Optimization of Flow Rate Injection to Looped Water Distribution Networks through Multiple Pumping Stations. Water 2016, 8, 575. [Google Scholar] [CrossRef] [Green Version]
- León-Celi, C.F.; Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Savic, D. Operation of Multiple Pumped-Water Sources with No Storage. J. Water Resour. Plan. Manag. 2018, 144, 04018050. [Google Scholar] [CrossRef]
- Briceño-león, C.X.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Mora-Melia, D. Use of Fixed and Variable Speed Pumps in Water Distribution Networks with Different Control Strategies. Water 2021, 479, 23. [Google Scholar]
- Mahar, P.S.; Singh, R.P. Optimal Design of Pumping Mains Considering Pump Characteristics. J. Pipeline Syst. Eng. Pr. 2014, 5, 04013010. [Google Scholar] [CrossRef]
- Bhave, P.R.; Gupta, R. Optimal design of water distribution networks for fuzzy demands. Civ. Eng. Environ. Syst. 2004, 21, 229–245. [Google Scholar] [CrossRef]
- Nault, J.; Papa, F. Lifecycle Assessment of a Water Distribution System Pump. J. Water Resour. Plan. Manag. 2015, 141, 1–9. [Google Scholar] [CrossRef]
- Walski, T.; Creaco, E. Selection of Pumping Configuration for Closed Water Distribution Systems. J. Water Resour. Plan. Manag. 2016, 142, 04016009. [Google Scholar] [CrossRef]
- Walski, T.M. Planning-Level Capital Cost Estimates for Pumping. J. Water Resour. Plan. Manag. 2012, 138, 307–310. [Google Scholar] [CrossRef]
- Diao, K.; Sitzenfrei, R.; Rauch, W. The Impacts of Spatially Variable Demand Patterns on Water Distribution System Design and Operation. Water 2019, 11, 567. [Google Scholar] [CrossRef] [Green Version]
- Martin-Candilejo, A.; Santillán, D.; Iglesias, A.; Garrote, L. Optimization of the Design of Water Distribution Systems for Variable Pumping Flow Rates. Water 2020, 12, 359. [Google Scholar] [CrossRef] [Green Version]
- Greco, S.; Figueira, J.; Ehrgott, M. Multiple Criteria Decision Analysis, 2nd ed.; Springer: New York, NY, USA, 2016. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hil: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83. [Google Scholar] [CrossRef] [Green Version]
- Ariff, H.; Salit, M.S.; Ismail, N.; Nukman, Y. Use of Analytical Hierarchy Process (AHP) for Selecting The Best Design Concept. J. Teknol. 2012, 49, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.; Qureshi, M.R.; Mallick, J.; Hasan, M.A.; Hussain, M. Decision Support Model for Design of High-Performance Concrete Mixtures Using Two-Phase AHP-TOPSIS Approach. Adv. Civ. Eng. 2019, 2019, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Al-barqawi, H.; Zayed, T. Infrastructure Management: Integrated AHP/ANN Model to Evaluate Municipal Water Mains’ Performance. Infrastruct. Syst. 2008, 14, 305–318. [Google Scholar] [CrossRef]
- Aşchilean, I.; Badea, G.; Giurca, I.; Naghiu, G.S.; Iloaie, F.G. Choosing the Optimal Technology to Rehabilitate the Pipes in Water Distribution Systems Using the AHP Method. Energy Procedia 2017, 112, 19–26. [Google Scholar] [CrossRef]
- Karleuša, B.; Hajdinger, A.; Tadić, L. The Application of Multi-Criteria Analysis Methods for the Determination of Priorities in the Implementation of Irrigation Plans. Water 2019, 11, 501. [Google Scholar] [CrossRef] [Green Version]
- Saaty, T.L. Perspectives on the Theory and Practice of Decision Making with the Analytic Hierarchy Process. Sci. Iran 1994, 9, 215–229. [Google Scholar] [CrossRef]
- Ward, M.; Poleacovschi, C.; Perez, M. Using AHP and Spatial Analysis to Determine Water Surface Storage Suitability in Cambodia. Water 2021, 13, 367. [Google Scholar] [CrossRef]
- Khamudkhanov, M.; Abdullabekov, I.; Khamudkhanova, B.; Dusmatov, K.; Fayzullayev, K. Controls of the modes of operation of the pumping station with the application of frequency-controlled electric drive Controls of the modes of operation of the pumping station with the application of frequency-controlled electric drive. IOP Conf. Ser. Mater. Sci. Eng. 2020, 862, 062048. [Google Scholar] [CrossRef]
- Saaty, T.L. Rank from comparisons and from ratings in the analytic hierarchy/network processes. Eur. J. Oper. Res. 2006, 168, 557–570. [Google Scholar] [CrossRef]
- Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Arango-Gil, F.; Lozano-Cortés, V. Methodology for the selection of pumping stations considering its mode of operation. In Proceedings of the 10th International Perspectives on Water Resources and the Environmental (IPWE), Cartagena, Colombia, 5–7 December 2018; Volume 13. [Google Scholar]
- Jensen Engineered Systems. Pump Station Design Guidelines, 2nd ed.; Jensen EngineeredSystems.com: Sparks, NV, USA, 2012; p. 34. [Google Scholar]
- Jayanthi, M.; Ravishankar, T. Techno economic evaluation of windmill for water pumping in coastal areas for aquaculture. Indian J. Fish 2005, 52, 413–419. [Google Scholar]
- Murugaperumal, K.; Vimal, P.A.D. Feasibility design and techno-economic analysis of hybrid renewable energy system for rural electrification. Sol. Energy 2019, 188, 1068–1083. [Google Scholar] [CrossRef]
- Vilotijević, V.; Karadžić, U.; Vujadinović, R.; Kovijanić, V.; Božić, I. An Improved Techno-Economic Approach to Determination of More Precise Installed Parameter for Small Hydropower Plants. Water 2021, 13, 2419. [Google Scholar] [CrossRef]
- Naval, N.; Yusta, J.M. Optimal short-term water-energy dispatch for pumping stations with grid-connected photovoltaic self-generation. J. Clean. Prod. 2021, 316, 128386. [Google Scholar] [CrossRef]
- Liu, X.; Li, N.; Mu, H.; Li, M.; Liu, X. Techno-energy-economic assessment of a high capacity offshore wind-pumped-storage hybrid power system for regional power system. J. Energy Storage 2021, 41, 102892. [Google Scholar] [CrossRef]
- Department of the Army Corps of Engineers United States. Structural and Architectural Design of Pumping Stations (Engineer Manual); Department of the Army Corps of Engineers United States: Washington, DC, USA, 1989.
- Leiby, V.M.; Burke, M.E. Energy Efficiency Best Practices for North American Drinking Water Utilities; Water Research Foundation: Albany, NY, USA, 2011. [Google Scholar]
- Celi, C.F.L. Optimization of Both Energy Use and Pumping Costs in Water Distribution Networks with Several Water Sources Using the Setpoint Curve. Ph.D. Thesis, Universitat Politécnica de Valencia, Valencia, Spain, 2018. [Google Scholar]

| Control System | Frequency Inverter | Pressure Switches | Pressure Transducer | Flowmeter | PLC | No. Regulation Equipment | |
|---|---|---|---|---|---|---|---|
| 1.0 | Without regulation | 0 | |||||
| 2.1 | PC with FSPs | X | 1 | ||||
| 2.2 | FC with FSPs | X | X | 2 | |||
| 3.1 | PC with VSPs | X | X | X | 3 | ||
| 3.2 | FC with VSPs | X | X | X | X | 4 | |
| 4.1 | PC with FSPs and VSPs | X | X | X | 3 | ||
| 4.2 | FC with FSPs and VSPs | X | X | X | X | 4 | |
| Regulation Mode (i) | 1.0 | 2.1 | 2.2 | 3.1 | 3.2 | 4.1 | 4.2 | Complexity Assessment (Cci) | Rating (Ri) |
|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 1 | 3 | 5 | 7 | 9 | 7 | 9 | 0.43 | 1.00 |
| 2.1 | 1/3 | 1 | 3 | 5 | 7 | 5 | 7 | 0.24 | 0.57 |
| 2.2 | 1/5 | 1/3 | 1 | 3 | 5 | 3 | 5 | 0.14 | 0.32 |
| 3.1 | 1/7 | 1/5 | 1/3 | 1 | 3 | 1 | 3 | 0.07 | 0.15 |
| 3.2 | 1/9 | 1/7 | 1/5 | 1/3 | 1 | 1/3 | 1 | 0.03 | 0.07 |
| 4.1 | 1/7 | 1/5 | 1/3 | 1 | 3 | 1 | 3 | 0.07 | 0.15 |
| 4.2 | 1/9 | 1/7 | 1/5 | 1/3 | 1 | 1/3 | 1 | 0.03 | 0.07 |
| Time Zones | |||||
|---|---|---|---|---|---|
| Summer Season | Winter Season | ||||
| Type of Hours | Electric Tariff | From | To | From | To |
| Off-peak hours | 0.069 | 0 | 8 | 0 | 8 |
| Peak hours | 0.095 | 11 | 15 | 18 | 21 |
| Plain hours | 0.088 | 9 | 10 | 8 | 18 |
| 16 | 23 | 21 | 23 | ||
| TF-PS1 | TF-PS2 | CAT-PS2 | CAT-PS3 | |
|---|---|---|---|---|
| Qm (l/s) | 35.00 | 24.44 | 18.00 | 37.00 |
| Qmin (l/s) | 12.30 | 8.60 | 6.30 | 13.00 |
| Qmax (l/s) | 70.00 | 48.88 | 36.00 | 74.00 |
| Data | TF-PS1 | TF-PS2 | CAT-PS2 | CAT-PS3 |
|---|---|---|---|---|
| ΔH | 25.00 | 28.00 | 25.00 | 22.00 |
| R | 0.0020 | 0.0059 | 0.0106 | 0.0015 |
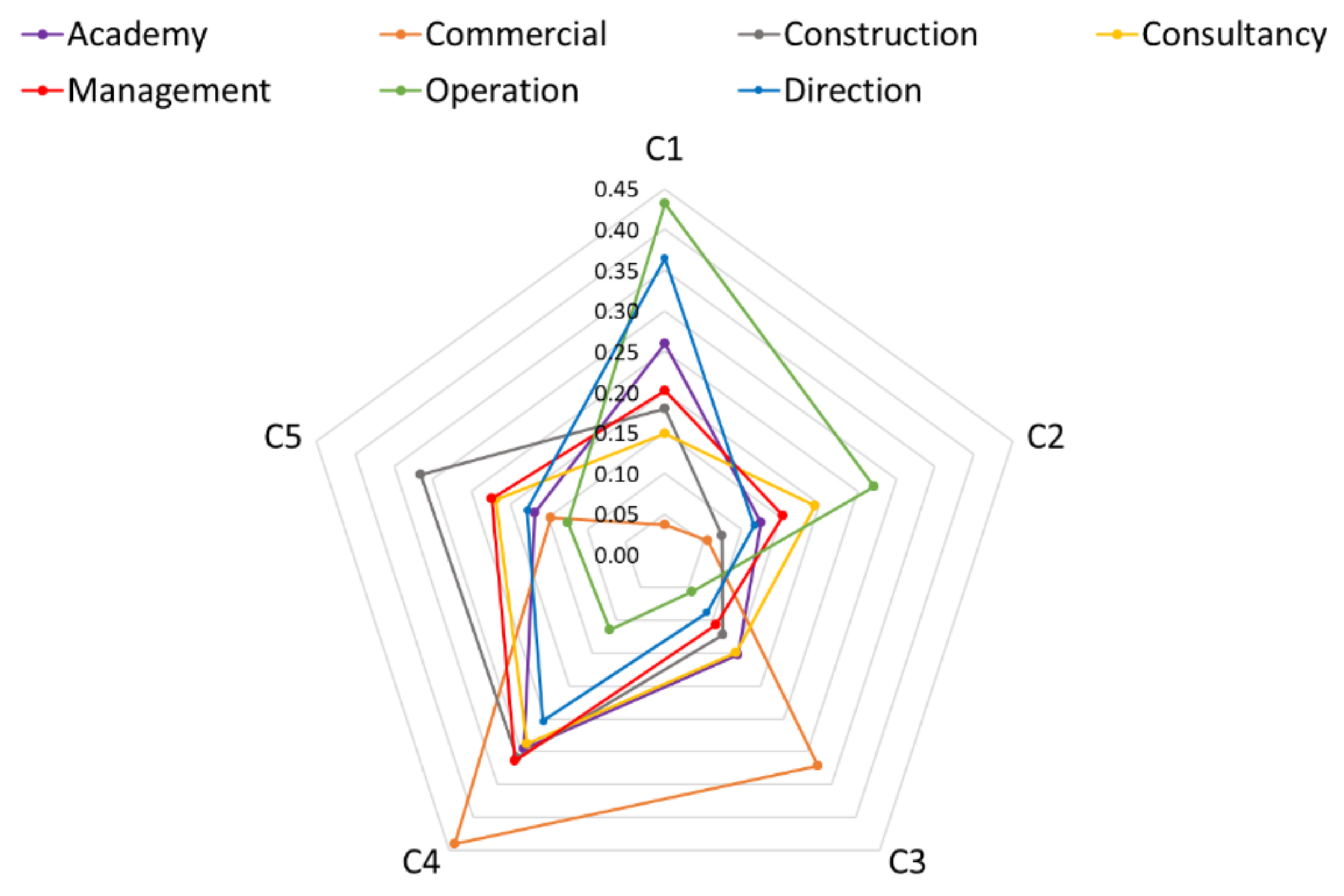
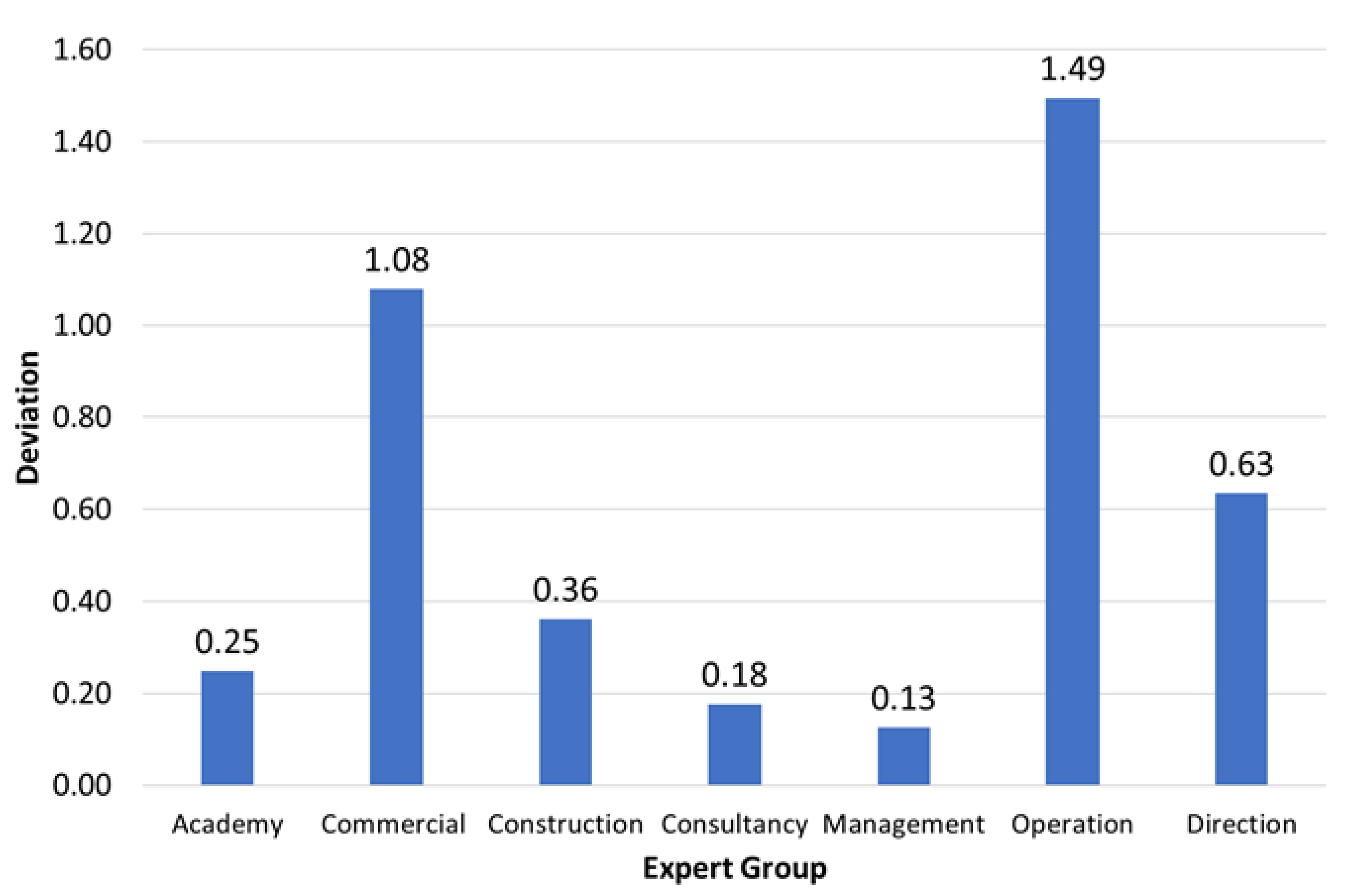
| Overall | Academic | Commercial | Constructor | Consultancy | Management | Operation | Direction | ||
|---|---|---|---|---|---|---|---|---|---|
| TF | Technical Factor | 0.33 | 0.38 | 0.09 | 0.25 | 0.34 | 0.36 | 0.70 | 0.48 |
| EF | Economic Factor | 0.67 | 0.62 | 0.91 | 0.75 | 0.66 | 0.64 | 0.30 | 0.52 |
| C1 | Number of pumps | 0.20 | 0.26 | 0.04 | 0.18 | 0.15 | 0.20 | 0.43 | 0.36 |
| C2 | Control system complexity | 0.13 | 0.13 | 0.06 | 0.07 | 0.19 | 0.15 | 0.27 | 0.12 |
| C3 | Investment Cost | 0.14 | 0.15 | 0.32 | 0.12 | 0.15 | 0.11 | 0.06 | 0.09 |
| C4 | Operational Cost | 0.31 | 0.29 | 0.44 | 0.31 | 0.29 | 0.31 | 0.11 | 0.25 |
| C5 | Maintenance Cost | 0.21 | 0.17 | 0.15 | 0.32 | 0.22 | 0.22 | 0.12 | 0.18 |
| Viable Solutions | Pareto Front | ||||
|---|---|---|---|---|---|
| No. Models | No. Solutions | No. Models | No. Final Solutions | Reduction Rate Solutions | |
| TF-PS1 | 43 | 471 | 12 | 49 | 89.60% |
| TF-PS2 | 39 | 359 | 14 | 40 | 88.86% |
| CAT-PS2 | 45 | 357 | 15 | 30 | 91.60% |
| CAT-PS3 | 45 | 490 | 7 | 31 | 93.67% |
| Priory Weight of Factors | Technical Factors (0.33) | Economic Factors (0.67) | ||||||
|---|---|---|---|---|---|---|---|---|
| Priority Weight of Criteria | C1 (0.20) | C2 (0.13) | C3 (0.14) | C4 (0.31) | C5 (0.21) | |||
| Hierarchy | ID Model | No. Pumps bi | ni FSP | mi VSP | Complexity | Investment Cost (EUR) | Operational Cost (EUR/Year) | Maintenance Cost (EUR/Year) |
| 1 | B30 | 3 | 3 | 0 | 2.1 | EUR 77,091.61 | EUR 18,094.16 | EUR 1040.11 |
| 2 | B65 | 3 | 3 | 0 | 1.0 | EUR 100,767.32 | EUR 21,387.13 | EUR 1136.44 |
| 3 | B61 | 3 | 3 | 0 | 2.1 | EUR 109,645.45 | EUR 15,351.70 | EUR 1148.58 |
| 8 | B33 | 2 | 0 | 2 | 3.2 | EUR 76,896.63 | EUR 16,099.10 | EUR 1018.72 |
| 12 | B31 | 3 | 2 | 1 | 4.1 | EUR 81,049.03 | EUR 14,910.76 | EUR 1107.24 |
| 15 | B59 | 4 | 4 | 0 | 1.0 | EUR 120,430.57 | EUR 18,320.99 | EUR 1420.55 |
| 22 | B66 | 3 | 0 | 3 | 3.2 | EUR 126,266.96 | EUR 10,723.13 | EUR 1318.83 |
| 24 | B28 | 4 | 4 | 0 | 2.2 | EUR 98,748.70 | EUR 13,046.24 | EUR 1407.69 |
| 37 | B58 | 5 | 5 | 0 | 2.2 | EUR 145,699.82 | EUR 11,328.55 | EUR 1787.40 |
| 38 | B27 | 6 | 6 | 0 | 2.2 | EUR 134,865.79 | EUR 11,963.36 | EUR 1960.90 |
| 39 | B57 | 8 | 8 | 0 | 2.2 | EUR 205,690.01 | EUR 11,123.06 | EUR 2617.86 |
| 40 | B49 | 10 | 10 | 0 | 2.2 | EUR 243,678.07 | EUR 9936.37 | EUR 3178.36 |
| Priory Weight of Factors | Technical Factors (0.33) | Economic Factors (0.67) | |||||
|---|---|---|---|---|---|---|---|
| Priority Weight of Criteria | C1 (0.20) | C2 (0.13) | C3 (0.14) | C4 (0.31) | C5 (0.21) | ||
| Hierarchy | ID Model | Rating N. Pumps | Rating Complexity | Rating Investment Cost | Rating Operational Cost | Rating Maintenance Cost | Final Rating |
| 1 | B30 | 0.88 | 0.57 | 0.95 | 0.71 | 0.93 | 1.00 |
| 2 | B65 | 0.88 | 1.00 | 0.83 | 0.60 | 0.89 | 1.00 |
| 3 | B61 | 0.88 | 0.57 | 0.79 | 0.80 | 0.89 | 1.00 |
| 8 | B33 | 1.00 | 0.07 | 0.95 | 0.78 | 0.94 | 0.98 |
| 12 | B31 | 0.88 | 0.15 | 0.93 | 0.82 | 0.90 | 0.96 |
| 15 | B59 | 0.75 | 1.00 | 0.74 | 0.70 | 0.78 | 0.96 |
| 22 | B66 | 0.88 | 0.07 | 0.71 | 0.95 | 0.82 | 0.94 |
| 24 | B28 | 0.75 | 0.32 | 0.84 | 0.88 | 0.79 | 0.94 |
| 37 | B58 | 0.63 | 0.32 | 0.61 | 0.93 | 0.64 | 0.85 |
| 38 | B27 | 0.50 | 0.32 | 0.66 | 0.91 | 0.57 | 0.80 |
| 39 | B57 | 0.25 | 0.32 | 0.31 | 0.94 | 0.31 | 0.62 |
| 40 | B49 | 0.00 | 0.32 | 0.12 | 0.98 | 0.10 | 0.48 |
| Priory Weight of Factors | Technical Factors (0.33) | Economic Factors (0.67) | ||||||
|---|---|---|---|---|---|---|---|---|
| Priority Weight of Criteria | C1 (0.20) | C2 (0.13) | C3 (0.14) | C4 (0.31) | C5 (0.21) | |||
| Hierarchy | ID Model | No. Pumps bi | ni FSP | mi VSP | Complexity | Investment Cost (EUR) | Operational Cost (EUR/Year) | Maintenance Cost (EUR/Year) |
| 1 | B32 | 2 | 0 | 2 | 3.2 | EUR 40,033.75 | EUR 11,033.00 | EUR 890.95 |
| 4 | B29 | 3 | 3 | 0 | 2.1 | EUR 36,392.86 | EUR 14,103.42 | EUR 1022.96 |
| 9 | B60 | 3 | 3 | 0 | 2.1 | EUR 60,626.74 | EUR 11,562.38 | EUR 1131.43 |
| 10 | B30 | 3 | 0 | 3 | 3.2 | EUR 45,312.38 | EUR 9220.70 | EUR 1193.21 |
| 11 | B31 | 3 | 0 | 3 | 3.2 | EUR 47,703.25 | EUR 9194.79 | EUR 1193.21 |
| 23 | B63 | 3 | 2 | 1 | 4.1 | EUR 77,860.25 | EUR 10,228.48 | EUR 1198.55 |
| 24 | B61 | 3 | 0 | 3 | 3.1 | EUR 85,229.43 | EUR 9529.86 | EUR 1243.41 |
| 26 | B52 | 4 | 4 | 0 | 1.0 | EUR 66,574.52 | EUR 16,032.72 | EUR 1388.39 |
| 28 | B59 | 4 | 4 | 0 | 2.2 | EUR 68,867.09 | EUR 9965.95 | EUR 1483.99 |
| 32 | B62 | 4 | 2 | 2 | 4.1 | EUR 84,374.22 | EUR 9472.57 | EUR 1490.08 |
| 36 | B51 | 5 | 5 | 0 | 1.0 | EUR 76,708.45 | EUR 15,975.26 | EUR 1655.77 |
| 37 | B58 | 5 | 5 | 0 | 2.2 | EUR 79,132.91 | EUR 9269.51 | EUR 1751.38 |
| 39 | B28 | 6 | 6 | 0 | 2.2 | EUR 60,527.23 | EUR 11,276.87 | EUR 1918.87 |
| 40 | B50 | 7 | 7 | 0 | 2.2 | EUR 87,848.31 | EUR 9047.27 | EUR 2303.30 |
| Priory Weight of Factors | Technical Factors (0.33) | Economic Factors (0.67) | |||||
|---|---|---|---|---|---|---|---|
| Priority Weight of Criteria | C1 (0.20) | C2 (0.13) | C3 (0.14) | C4 (0.31) | C5 (0.21) | ||
| Hierarchy | ID Model | Rating N. Pumps | Rating Complexity | Rating Investment Cost | Rating Operational Cost | Rating Maintenance Cost | Final Rating |
| 1 | B32 | 1.00 | 0.07 | 0.88 | 0.83 | 0.90 | 1.00 |
| 4 | B29 | 0.80 | 0.57 | 0.94 | 0.68 | 0.81 | 0.99 |
| 9 | B60 | 0.80 | 0.57 | 0.55 | 0.80 | 0.75 | 0.97 |
| 10 | B30 | 0.80 | 0.07 | 0.80 | 0.92 | 0.71 | 0.97 |
| 11 | B31 | 0.80 | 0.07 | 0.76 | 0.92 | 0.71 | 0.97 |
| 23 | B63 | 0.80 | 0.15 | 0.27 | 0.87 | 0.70 | 0.94 |
| 24 | B61 | 0.80 | 0.15 | 0.15 | 0.90 | 0.67 | 0.94 |
| 26 | B52 | 0.60 | 1.00 | 0.45 | 0.58 | 0.58 | 0.92 |
| 28 | B59 | 0.60 | 0.32 | 0.41 | 0.88 | 0.52 | 0.91 |
| 32 | B62 | 0.60 | 0.15 | 0.16 | 0.91 | 0.52 | 0.91 |
| 36 | B51 | 0.40 | 1.00 | 0.28 | 0.58 | 0.41 | 0.85 |
| 37 | B58 | 0.40 | 0.32 | 0.25 | 0.92 | 0.35 | 0.85 |
| 39 | B28 | 0.20 | 0.32 | 0.55 | 0.82 | 0.24 | 0.62 |
| 40 | B50 | 0.00 | 0.32 | 0.10 | 0.93 | 0.00 | 0.48 |
| Priory Weight of Factors | Technical Factors (0.33) | Economic Factors (0.67) | ||||||
|---|---|---|---|---|---|---|---|---|
| Priority Weight of Criteria | C1 (0.20) | C2 (0.13) | C3 (0.14) | C4 (0.31) | C5 (0.21) | |||
| Hierarchy | ID Model | No. Pumps bi | ni FSP | mi VSP | Complexity | Investment Cost (EUR) | Operational Cost (EUR/Year) | Maintenance Cost (EUR/Year) |
| 1 | B29 | 2 | 2 | 0 | 2.1 | EUR 26,857.50 | EUR 8709.77 | EUR 737.07 |
| 2 | B33 | 1 | 0 | 1 | 3.2 | EUR 36,172.84 | EUR 7584.03 | EUR 601.57 |
| 3 | B60 | 2 | 2 | 0 | 2.1 | EUR 45,032.91 | EUR 7529.47 | EUR 845.53 |
| 8 | B30 | 2 | 0 | 2 | 3.2 | EUR 33,929.54 | EUR 6267.96 | EUR 890.95 |
| 11 | B31 | 2 | 0 | 2 | 3.1 | EUR 34,140.13 | EUR 7678.38 | EUR 832.69 |
| 14 | B61 | 2 | 0 | 2 | 3.1 | EUR 62,754.16 | EUR 6476.45 | EUR 941.16 |
| 15 | B28 | 3 | 3 | 0 | 2.2 | EUR 35,755.30 | EUR 8198.96 | EUR 1097.85 |
| 16 | B58 | 3 | 3 | 0 | 1.0 | EUR 52,068.90 | EUR 10,959.26 | EUR 1110.71 |
| 21 | B59 | 3 | 0 | 3 | 3.2 | EUR 66,803.39 | EUR 5229.30 | EUR 1293.10 |
| 22 | B62 | 3 | 0 | 3 | 3.1 | EUR 73,330.86 | EUR 6405.97 | EUR 1234.83 |
| 23 | B15 | 5 | 5 | 0 | 2.2 | EUR 43,682.33 | EUR 8035.18 | EUR 1642.91 |
| 24 | B50 | 5 | 5 | 0 | 2.2 | EUR 66,086.69 | EUR 6721.67 | EUR 1751.38 |
| 25 | B41 | 5 | 5 | 0 | 2.2 | EUR 64,990.43 | EUR 7054.42 | EUR 1751.38 |
| 26 | B40 | 6 | 6 | 0 | 2.2 | EUR 68,421.27 | EUR 6627.74 | EUR 2027.34 |
| 27 | B38 | 8 | 8 | 0 | 2.2 | EUR 80,856.08 | EUR 5918.28 | EUR 2455.36 |
| Priory Weight of Factors | Technical Factors (0.33) | Economic Factors (0.67) | |||||
|---|---|---|---|---|---|---|---|
| Priority Weight of Criteria | C1 (0.20) | C2 (0.13) | C3 (0.14) | C4 (0.31) | C5 (0.21) | ||
| Hierarchy | ID Model | Rating N. Pumps | Rating Complexity | Rating Investment Cost | Rating Operational Cost | Rating Maintenance Cost | Final Rating |
| 1 | B29 | 0.86 | 0.57 | 1.00 | 0.76 | 0.88 | 1.00 |
| 2 | B33 | 1.00 | 0.07 | 0.86 | 0.84 | 0.94 | 1.00 |
| 3 | B60 | 0.86 | 0.57 | 0.73 | 0.84 | 0.83 | 1.00 |
| 8 | B30 | 0.86 | 0.07 | 0.90 | 0.93 | 0.81 | 0.98 |
| 11 | B31 | 0.86 | 0.15 | 0.89 | 0.83 | 0.84 | 0.97 |
| 14 | B61 | 0.86 | 0.15 | 0.48 | 0.92 | 0.79 | 0.96 |
| 15 | B28 | 0.71 | 0.32 | 0.87 | 0.80 | 0.72 | 0.96 |
| 16 | B58 | 0.71 | 1.00 | 0.63 | 0.61 | 0.72 | 0.96 |
| 21 | B59 | 0.71 | 0.07 | 0.42 | 1.00 | 0.64 | 0.94 |
| 22 | B62 | 0.71 | 0.15 | 0.32 | 0.92 | 0.66 | 0.94 |
| 23 | B15 | 0.43 | 0.32 | 0.75 | 0.81 | 0.49 | 0.94 |
| 24 | B50 | 0.43 | 0.32 | 0.43 | 0.90 | 0.44 | 0.94 |
| 25 | B41 | 0.43 | 0.32 | 0.45 | 0.88 | 0.44 | 0.93 |
| 26 | B40 | 0.29 | 0.32 | 0.40 | 0.91 | 0.32 | 0.92 |
| 27 | B38 | 0.00 | 0.32 | 0.22 | 0.95 | 0.13 | 0.92 |
| Priory Weight of Factors | Technical Factors (0.33) | Economic Factors (0.67) | ||||||
|---|---|---|---|---|---|---|---|---|
| Priority Weight of Criteria | C1 (0.20) | C2 (0.13) | C3 (0.14) | C4 (0.31) | C5 (0.21) | |||
| Hierarchy | ID Model | No. Pumps bi | ni FSP | mi VSP | Complexity | Investment Cost (EUR) | Operational Cost (EUR/Year) | Maintenance Cost (EUR/Year) |
| 1 | B28 | 3 | 3 | 0 | 1.0 | EUR 76,003.47 | EUR 18,694.99 | EUR 1036.55 |
| 7 | B33 | 2 | 0 | 2 | 3.1 | EUR 78,954.39 | EUR 18,257.10 | EUR 973.32 |
| 10 | B27 | 4 | 4 | 0 | 1.0 | EUR 92,400.92 | EUR 18,663.93 | EUR 1312.08 |
| 12 | B61 | 3 | 0 | 3 | 3.1 | EUR 125,959.65 | EUR 11,041.80 | EUR 1269.14 |
| 14 | B59 | 4 | 4 | 0 | 1.0 | EUR 120,430.57 | EUR 18,564.49 | EUR 1420.55 |
| 20 | B58 | 5 | 5 | 0 | 2.2 | EUR 145,699.82 | EUR 11,276.69 | EUR 1787.40 |
| 24 | B49 | 7 | 7 | 0 | 1.0 | EUR 173,427.47 | EUR 16,154.81 | EUR 2255.73 |
| Priory Weight of Factors | Technical Factors (0.33) | Economic Factors (0.67) | |||||
|---|---|---|---|---|---|---|---|
| Priority Weight of Criteria | C1 (0.20) | C2 (0.13) | C3 (0.14) | C4 (0.31) | C5 (0.21) | ||
| Hierarchy | ID Model | Rating N. Pumps | Rating Complexity | Rating Investment Cost | Rating Operational Cost | Rating Maintenance Cost | Final Rating |
| 1 | B28 | 0.80 | 1.00 | 0.97 | 0.68 | 0.90 | 1.00 |
| 7 | B33 | 1.00 | 0.15 | 0.94 | 0.69 | 0.94 | 0.98 |
| 10 | B27 | 0.60 | 1.00 | 0.83 | 0.68 | 0.73 | 0.97 |
| 12 | B61 | 0.80 | 0.15 | 0.56 | 0.92 | 0.76 | 0.96 |
| 14 | B59 | 0.60 | 1.00 | 0.60 | 0.68 | 0.67 | 0.96 |
| 20 | B58 | 0.40 | 0.32 | 0.39 | 0.91 | 0.45 | 0.94 |
| 24 | B49 | 0.00 | 1.00 | 0.17 | 0.76 | 0.16 | 0.94 |
| Hierarchy | ID Model | bi N° Pumps | ni FSP | mi VSP | Control Mode | Investment Cost (EUR/Year) | Operational Cost (EUR/Year) | Maintenance Cost (EUR/Year) | Total Cost (EUR/Year) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | B28 | 4 | 2 | 2 | 4.2 | EUR 7021.77 | EUR 10,259.15 | EUR 1472.04 | EUR 18,754.75 |
| Design Method | ID Model | bi | ni FSP | mi VSP | Control Mode | Investment Cost (EUR/Year) | Operational Cost (EUR/Year) | Maintenance Cost (EUR/Year) | Cycle Life Cost (EUR/Year) |
|---|---|---|---|---|---|---|---|---|---|
| Cycle Life Cost | B27 | 6 | 2 | 4 | 4.2 | EUR 8741.36 | EUR 10,707.82 | EUR 2025.25 | EUR 21,474.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Briceño-León, C.X.; Sanchez-Ferrer, D.S.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Mora-Melia, D. Methodology for Pumping Station Design Based on Analytic Hierarchy Process (AHP). Water 2021, 13, 2886. https://doi.org/10.3390/w13202886
Briceño-León CX, Sanchez-Ferrer DS, Iglesias-Rey PL, Martinez-Solano FJ, Mora-Melia D. Methodology for Pumping Station Design Based on Analytic Hierarchy Process (AHP). Water. 2021; 13(20):2886. https://doi.org/10.3390/w13202886
Chicago/Turabian StyleBriceño-León, Christian X., Diana S. Sanchez-Ferrer, Pedro L. Iglesias-Rey, F. Javier Martinez-Solano, and Daniel Mora-Melia. 2021. "Methodology for Pumping Station Design Based on Analytic Hierarchy Process (AHP)" Water 13, no. 20: 2886. https://doi.org/10.3390/w13202886
APA StyleBriceño-León, C. X., Sanchez-Ferrer, D. S., Iglesias-Rey, P. L., Martinez-Solano, F. J., & Mora-Melia, D. (2021). Methodology for Pumping Station Design Based on Analytic Hierarchy Process (AHP). Water, 13(20), 2886. https://doi.org/10.3390/w13202886








