Evaluating the Cost of Failure Risk: A Case Study of the Kang-Wei-Kou Stream Diversion Project
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
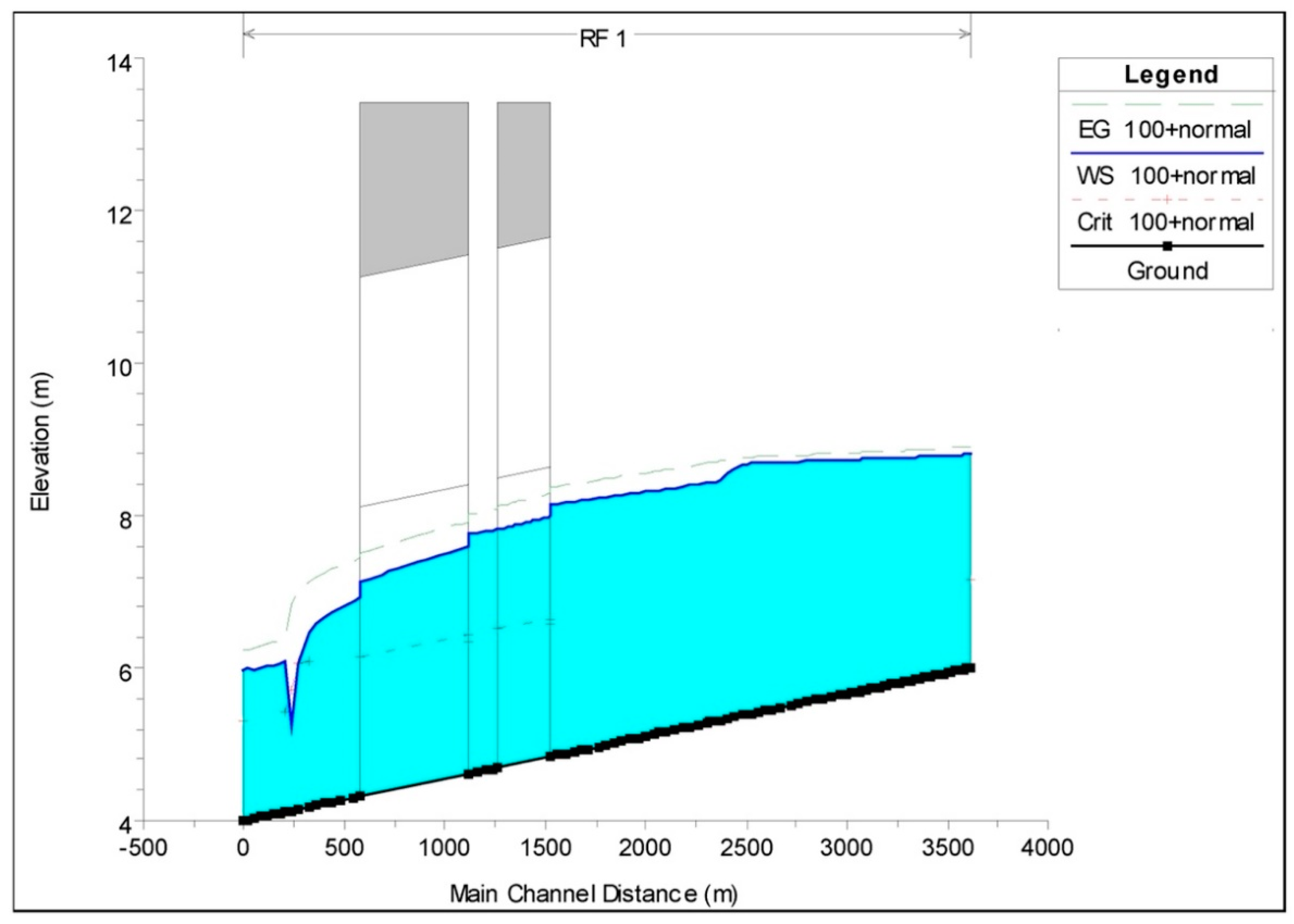
2.2. HEC-RAS Simulation
2.3. Hydrologic Conditions
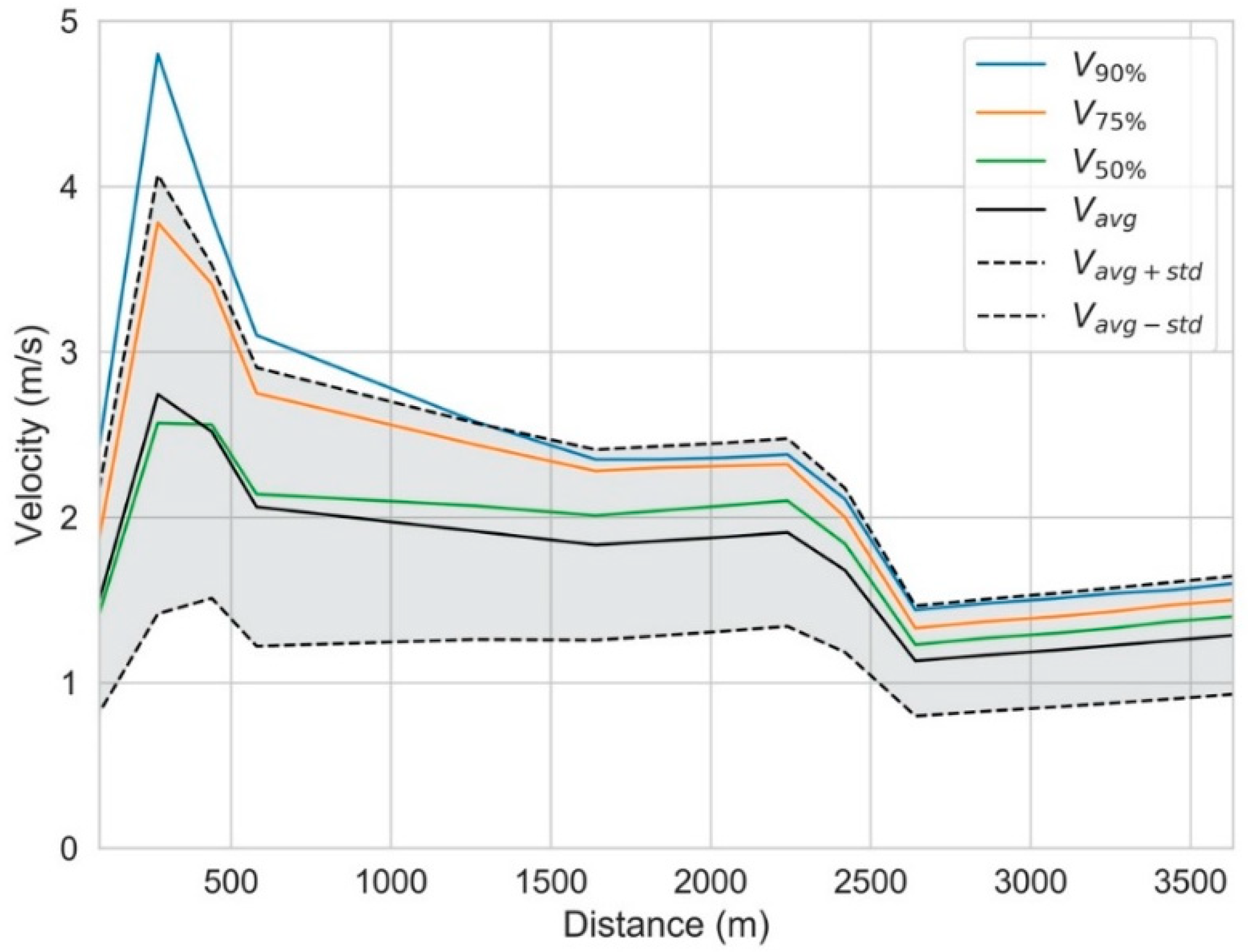
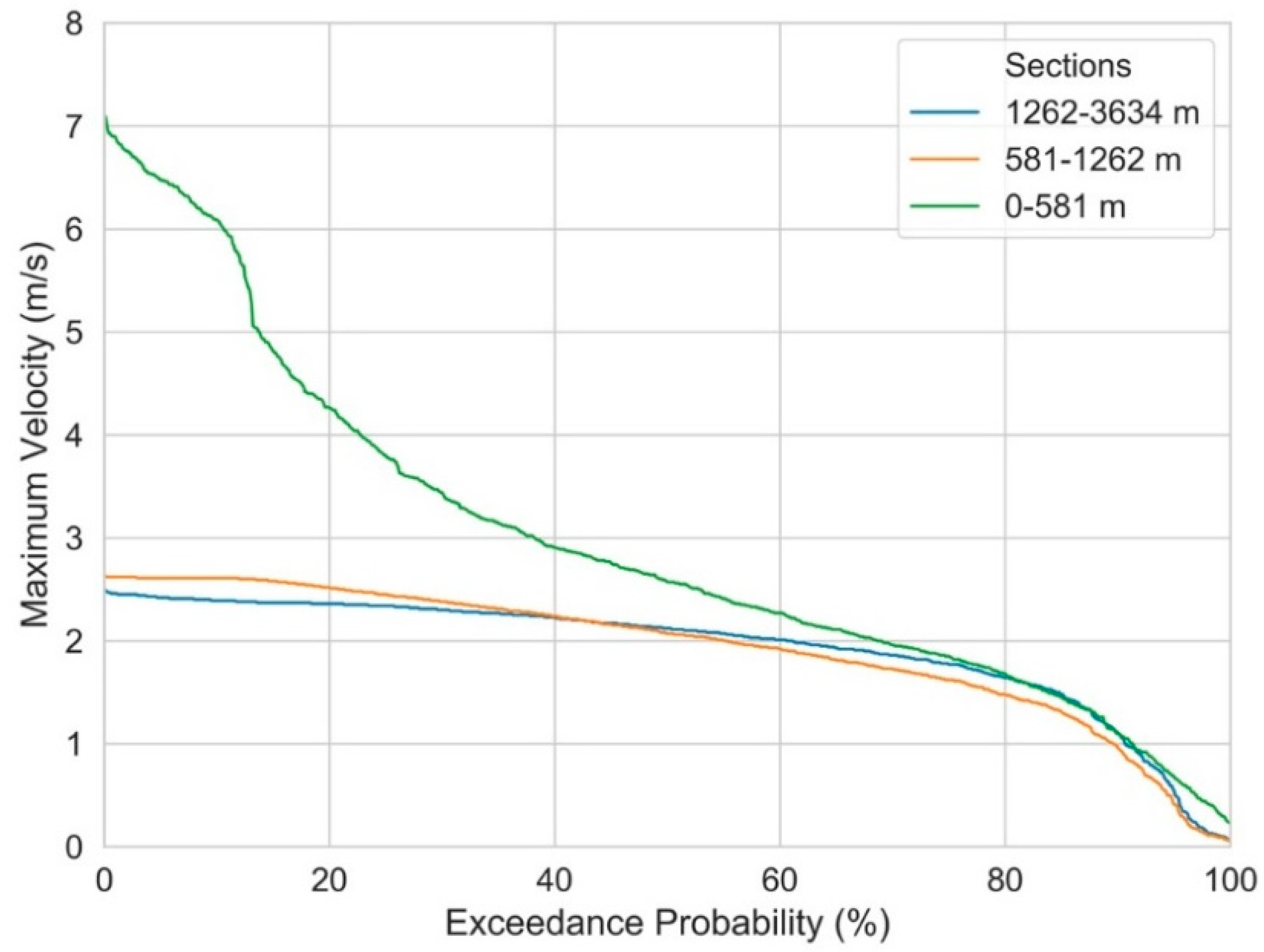
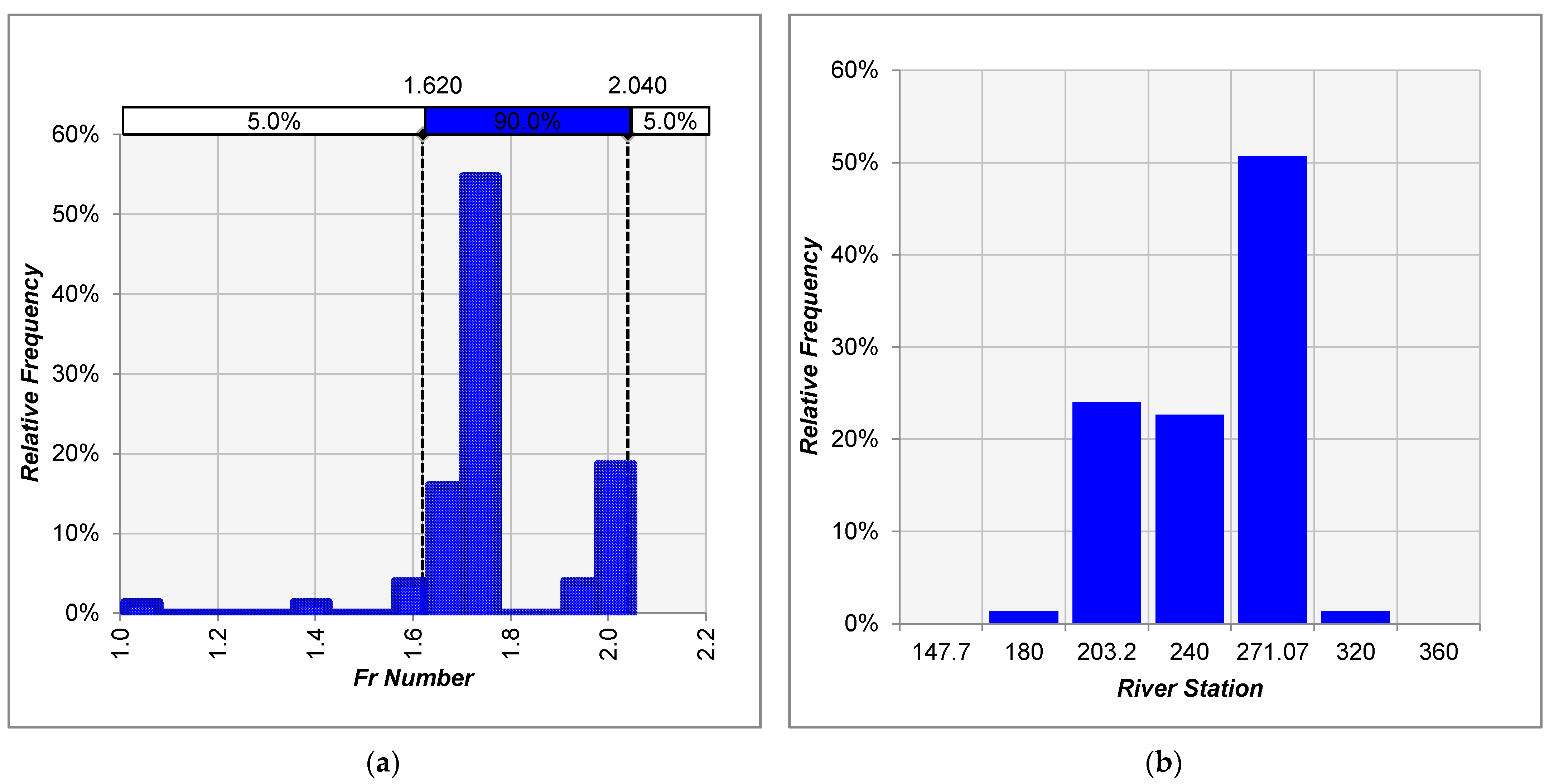
3. Results
4. Discussion
- Scenario A: concrete lined channel (alternative plan)
- Scenario B: concrete retaining wall for riverbanks only (original plan)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yiping, W.; Cong, C.; Gaofeng, H.; Qiuxia, Z. Landslide stability analysis based on random-fuzzy reliability: Taking Liangshuijing landslide as a case. Stoch. Environ. Res. Risk Assess. 2014, 28, 1723–1732. [Google Scholar] [CrossRef]
- Goda, K. Time-dependent probabilistic tsunami hazard analysis using stochastic rupture sources. Stoch. Environ. Res. Risk Assess. 2019, 33, 341–358. [Google Scholar] [CrossRef]
- Hall, J.; Solomatine, D. A framework for uncertainty analysis in flood risk management decisions. Int. J. River Basin Manag. 2008, 6, 85–98. [Google Scholar] [CrossRef]
- Mays, L.W. The role of risk analysis in water resources engineering. J. Contemp. Water Res. Educ. 2011, 103, 3. [Google Scholar]
- Yen, B.C.; Cheng, S.T.; Melching, C.S. First order reliability analysis. In Stochastic and Risk Analysis in Hydraulic Engineering; Water Resource Publications: Littleton, CO, USA, 1986; pp. 1–36. [Google Scholar]
- Lian, Y.; Yen, B.C. Comparison of risk calculation methods for a culvert. J. Hydraul. Eng. 2003, 129, 140–152. [Google Scholar] [CrossRef][Green Version]
- Mays, L.W.; Tung, Y.K. Hydrosystems Engineering and Management; Water Resource Publications: Littleton, CO, USA, 2002. [Google Scholar]
- Singh, V.P. (Ed.) Application of Frequency and Risk in Water Resources: Proceedings of the International Symposium on Flood Frequency and Risk Analyses, 14–17 May 1986, Louisiana State University, Baton Rouge, USA; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Bowles, D.S.; Anderson, L.R.; Glover, T.F.; Chauhan, S.S. Portfolio risk assessment: A tool for dam safety risk management. In Proceedings of the USCOLD 1998 Annual Lecture, Buffalo, NY, USA, 8–14 August 1998. [Google Scholar]
- Stedinger, J.R. Frequency analysis of extreme events. In Handbook of Hydrology; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Rajagopalan, B.; Salas, J.D.; Lall, U. Stochastic methods for modeling precipitation and streamflow. In Advances in Data-Based Approaches for Hydrologic Modeling and Forecasting; World Scientific: Singapore, 2010; pp. 17–52. [Google Scholar]
- Salas, J.D.; Obeysekera, J. Return period and risk for nonstationary hydrologic extreme events. In Proceedings of the World Environmental and Water Resources Congress 2013: Showcasing the Future, Cincinnati, OH, USA, 19–23 May 2013; pp. 1213–1223. [Google Scholar]
- Rasmussen, P.F.; Rosbjerg, D. Evaluation of risk concepts in partial duration series. Stoch. Hydrol. Hydraul. 1991, 5, 1–16. [Google Scholar] [CrossRef]
- Salas, J.D.; Burlando, P.; Heo, J.H.; Lee, D.J. The axis of risk and uncertainty in hydrologic design. Hydrol. Days 2003, 153–164. [Google Scholar]
- Arnaud, P.; Cantet, P.; Aubert, Y. Relevance of an at-site flood frequency analysis method for extreme events based on stochastic simulation of hourly rainfall. Hydrol. Sci. J. 2016, 61, 36–49. [Google Scholar] [CrossRef]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Elsevier: Amsterdam, The Netherlands, 1994; Volume 45. [Google Scholar]
- Marco, J.B.; Harboe, R.; Salas, J.D. (Eds.) Stochastic Hydrology and Its Use in Water Resources Systems Simulation and Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 237. [Google Scholar]
- MacNeill, I.B.; Umphrey, G. (Eds.) Advances in the Statistical Sciences: Stochastic Hydrology: Volume IV Festschrift in Honor of Professor VM Joshi’s 70th Birthday; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 37. [Google Scholar]
- You, G.J.Y.; Thum, B.H.; Lin, F.H. The examination of reproducibility in hydro-ecological characteristics by daily synthetic flow models. J. Hydrol. 2014, 511, 904–919. [Google Scholar] [CrossRef]
- Hall, J.W. Handling uncertainty in the hydroinformatic process. J. Hydroinformatics 2003, 5, 215–232. [Google Scholar] [CrossRef]
- National Research Council. Risk Analysis and Uncertainty in Flood Damage Reduction Studies; National Academies Press: Washington, DC, USA, 2000. [Google Scholar]
- Sayers, P.B.; Hall, J.W.; Meadowcroft, I.C. Towards risk-based flood hazard management in the UK. In Proceedings of the Institution of Civil Engineers-Civil Engineering; Thomas Telford Ltd.: London, UK, May, 2002; Volume 150, Issue 5, pp. 36–42. [Google Scholar]
- Vrijling, J.K. Development in probabilistic design of flood defenses in the Netherlands. In Reliability and Uncertainty Analyses in Hydraulic Design; Yen, B.C., Tung, Y.-K., Eds.; ASCE: New York, NY, USA, 1993; pp. 133–178. [Google Scholar]
- U.S. Army Corps of Engineers. Risk-based analysis for flood damage reduction studies. In Manual, EM 1110-2-1619; U.S. Army Corps of Engineers: Washington, DC, USA, 1996. [Google Scholar]
- Goldman, D. Estimating expected annual damage for levee retrofits. J. Water Resour. Plan. Manag. 1997, 123, 89–94. [Google Scholar] [CrossRef]
- Tang, W.H.; Yen, B.C. Hydrologic and hydraulic design under uncertainties. Proc. Int. Symp. Uncertainties Hydrol. Water Resour. Syst. 1973, 2, 868–882. [Google Scholar]
- Yen, B.C.; Tung, Y.K. (Eds.) Reliability and Uncertainty Analyses in Hydraulic Design; ASCE: New York, NY, USA, 1993. [Google Scholar]
- Melching, C.S. Reliability Estimation. In Computer Models of Watershed Hydrology; Water Resources Publications: Highlands Ranch, CO, USA, 1995. [Google Scholar]
- Ayyub, B.M.; McCuen, R.H. Probability, Statistics, and Reliability for Engineers and Scientists; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Tung, Y.K.; Mays, L.W. Optimal risk-based design of water resource engineering projects. NASA STI/Recon Tech. Rep. N 1980, 81, 20316. [Google Scholar]
- Tung, Y.K.; Mays, L.W. Risk models for flood levee design. Water Resour. Res. 1981, 17, 833–841. [Google Scholar] [CrossRef]
- Lee, H.L.; Mays, L.W. Improved risk and reliability model for hydraulic structures. Water Resour. Res. 1983, 19, 1415–1422. [Google Scholar] [CrossRef]
- Lee, H.L.; Mays, L.W. Hydraulic uncertainties in flood levee capacity. J. Hydraul. Eng. 1986, 112, 928–934. [Google Scholar] [CrossRef]
- Anselmo, V.; Galeati, G.; Palmieri, S.; Rossi, U.; Todini, E. Flood risk assessment using an integrated hydrological and hydraulic modelling approach: A case study. J. Hydrol. 1996, 175, 533–554. [Google Scholar] [CrossRef]
- Apel, H.; Thieken, A.H.; Merz, B.; Blöschl, G. A probabilistic modelling system for assessing flood risks. Nat. Hazards 2006, 38, 79–100. [Google Scholar] [CrossRef]
- Thompson, K.D.; Stedinger, J.R.; Heath, D.C. Evaluation and presentation of dam failure and flood risks. J. Water Resour. Plan. Manag. 1997, 123, 216–227. [Google Scholar] [CrossRef]
- Kuo, J.T.; Yen, B.C.; Hsu, Y.C.; Lin, H.F. Risk analysis for dam overtopping—Feitsui reservoir as a case study. J. Hydraul. Eng. 2007, 133, 955–963. [Google Scholar] [CrossRef]
- Lee, B.S.; You, G.J.Y. An assessment of long-term overtopping risk and optimal termination time of dam under climate change. J. Environ. Manag. 2013, 121, 57–71. [Google Scholar] [CrossRef]
- Bellos, V.; Tsakiris, V.K.; Kopsiaftis, G.; Tsakiris, G. Propagating Dam Breach Parametric Uncertainty in a River Reach Using the HEC-RAS Software. Hydrology 2020, 7, 72. [Google Scholar] [CrossRef]
- Merz, B.; Kreibich, H.; Thieken, A.; Schmidtke, R. Estimation uncertainty of direct monetary flood damage to buildings. Nat. Hazards Earth Syst. Sci. 2004, 4, 153–163. [Google Scholar] [CrossRef]
- Tsai, C.W.; Yeh, J.J.; Huang, C.H. Development of probabilistic inundation mapping for dam failure induced floods. Stoch. Environ. Res. Risk Assess. 2019, 33, 91–110. [Google Scholar] [CrossRef]
- Aven, T.; Pörn, K. Expressing and interpreting the results of quantitative risk analyses. Review and discussion. Reliab. Eng. Syst. Saf. 1998, 61, 3–10. [Google Scholar] [CrossRef]
- Apel, H.; Merz, B.; Thieken, A.H. Quantification of uncertainties in flood risk assessments. Int. J. River Basin Manag. 2008, 6, 149–162. [Google Scholar] [CrossRef]
- Morgan, M.G.; Henrion, M.; Small, M. Uncertainty: A Guide to Dealing with Uncertainty in Quantitative Risk and Policy Analysis; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Johnson, P.A. Uncertainty of hydraulic parameters. J. Hydraul. Eng. 1996, 122, 112–114. [Google Scholar] [CrossRef]
- Gates, T.K.; Al-Zahrani, M.A. Spatiotemporal stochastic open-channel flow. I: Model and its parameter data. J. Hydraul. Eng. 1996, 122, 641–651. [Google Scholar] [CrossRef]
- Johnson, P.A.; Dock, D.A. Probabilistic bridge scour estimates. J. Hydraul. Eng. 1998, 124, 750–754. [Google Scholar] [CrossRef]
- U.S. Department of Defense. Military Standard: Procedures for Performing a Failure Mode Effects and Criticality Analysis; Department of Defense: Washington, DC, USA, 1980. [Google Scholar]
- Bluvband, Z.; Zilberberg, E. Knowledge base approach to integrated FMEA. In Proceedings of the Annual Quality Congress Proceedings-American Society for Quality Control, Philadelpha, PA, USA, 4–6 May 1998; pp. 535–545. [Google Scholar]
- Krasich, M. Use of fault tree analysis for evaluation of system-reliability improvements in design phase. In Proceedings of the Annual Reliability and Maintainability Symposium. 2000 Proceedings. International Symposium on Product Quality and Integrity (Cat. No. 00CH37055), Los Angeles, CA, USA, 24–27 January 2000; pp. 1–7. [Google Scholar]
- U.S. Army Corps of Engineers. USACE Process for the National Flood Insurance Program (NFIP) Levee System Evaluation; EC 1110-2-6067; U.S. Army Corps of Engineers: Washington, DC, USA, 2010.
- Wahalathantri, B.L.; Lokuge, W.; Karunasena, W.; Setunge, S. Vulnerability of floodways under extreme flood events. Nat. Hazards Rev. 2015, 17, 04015012. [Google Scholar] [CrossRef]
- Wang, Y.H.; Hsu, Y.C.; You, G.J.Y.; Yen, C.L.; Wang, C.M. Flood Inundation Assessment Considering Hydrologic Conditions and Functionalities of Hydraulic Facilities. Water 2018, 10, 1879. [Google Scholar] [CrossRef]
- Yen, B.C. Safety factor in hydrologic and hydraulic engineering design. Proceedings 1978, 1. [Google Scholar]
- Johnson, P.A.; Clopper, P.E.; Zevenbergen, L.W.; Lagasse, P.F. Quantifying uncertainty and reliability in bridge scour estimations. J. Hydraul. Eng. 2015, 141, 04015013. [Google Scholar] [CrossRef]
- Pizarro, A.; Manfreda, S.; Tubaldi, E. The science behind scour at bridge foundations: A review. Water 2020, 12, 374. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. HEC-RAS River Analysis System Hydraulic Reference Manual. Version 5.0; U.S. Army Corps of Engineers: Washington, DC, USA, 2016.
- Water Resources Agency, Taiwan. Regulation Project of Flood-prone Areas (Formulation Report of Tainan County Governmental Gang-Wei-Gou Drainage System); Water Resources Agency: Taichung, Taiwan, 2009. [Google Scholar]
- Water Resources Planning Institute, Taiwan. Regional Drainage and Environmental Planning Reference Manual; Water Resources Planning Institute: Taichung, Taiwan, 2006. [Google Scholar]
- FEMA. Hydraulics: One-dimensional analysis. In Guidance for Flood Risk Analysis and Mapping; FEMA: Washington, DC, USA, 2016. [Google Scholar]
- Viero, D.P.; Defina, A. Extended theory of hydraulic hysteresis in open-channel flow. J. Hydraul. Eng. 2017, 143, 06017014. [Google Scholar] [CrossRef]
- Mel, R.A.; Viero, D.P.; Carniello, L.; D’Alpaos, L. Multipurpose use of artificial channel networks for flood risk reduction: The case of the waterway Padova–Venice (Italy). Water 2020, 12, 1609. [Google Scholar] [CrossRef]
- Mel, R.A.; Viero, D.P.; Carniello, L.; D’Alpaos, L. Optimal floodgate operation for river flood management: The case study of Padova (Italy). J. Hydrol. Reg. Stud. 2020, 30, 100702. [Google Scholar] [CrossRef]
- Wang, Y.H.; Chu, C.C.; You, G.J.Y.; Gupta, H.V.; Chiu, P.H. Evaluating Uncertainty in Fluvial Geomorphic Response to Dam Removal. J. Hydrol. Eng. 2020, 25, 04020022. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]



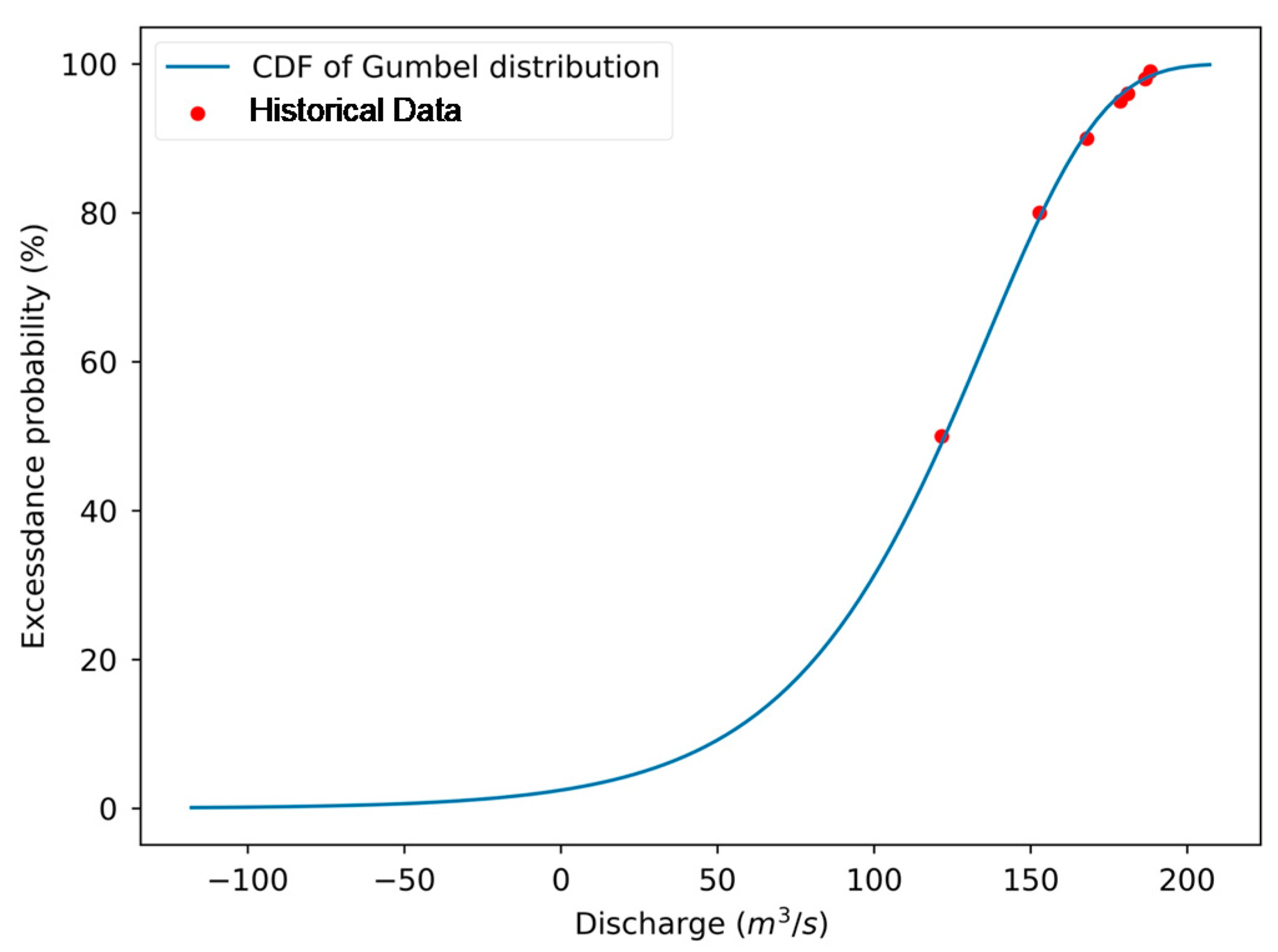
| Return period (year) | 2 | 5 | 10 | 20 | 25 | 50 | 100 |
| Discharge (m3/s) | 121.65 | 152.89 | 168.00 | 178.65 | 181.00 | 186.58 | 188.24 |
| Water surface elevation (m) | 7.90 | 8.80 | 9.46 | 9.55 | 9.65 | 9.91 | 10.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, C.-Y.; Wang, Y.-H.; You, G.J.-Y.; Chen, P.-C.; Lo, E. Evaluating the Cost of Failure Risk: A Case Study of the Kang-Wei-Kou Stream Diversion Project. Water 2021, 13, 2881. https://doi.org/10.3390/w13202881
Liang C-Y, Wang Y-H, You GJ-Y, Chen P-C, Lo E. Evaluating the Cost of Failure Risk: A Case Study of the Kang-Wei-Kou Stream Diversion Project. Water. 2021; 13(20):2881. https://doi.org/10.3390/w13202881
Chicago/Turabian StyleLiang, Chung-Yuan, Yuan-Heng Wang, Gene Jiing-Yun You, Po-Chun Chen, and Emilie Lo. 2021. "Evaluating the Cost of Failure Risk: A Case Study of the Kang-Wei-Kou Stream Diversion Project" Water 13, no. 20: 2881. https://doi.org/10.3390/w13202881
APA StyleLiang, C.-Y., Wang, Y.-H., You, G. J.-Y., Chen, P.-C., & Lo, E. (2021). Evaluating the Cost of Failure Risk: A Case Study of the Kang-Wei-Kou Stream Diversion Project. Water, 13(20), 2881. https://doi.org/10.3390/w13202881







