1. Introduction
Meyer–Peter, Favre and Einstein [
1] published a formula in 1934 related to the transport of uniform sediment on a plane bed, while Meyer–Peter and Müller [
2,
3] published in 1948 and 1949 the definitive formula related to the transport of sediment mixtures with different values of specific gravity. The main characteristic of the Meyer–Peter and Müller (MPM) formula is the distinction of bed roughness due to individual particles from that bed roughness due to bed forms or the distinction of bed resistance due to skin friction from bed resistance due to bed forms. The historical development of the MPM formula is described in detail in Hager and Boes [
4]. In this formula, the unit submerged sediment discharge is calculated, and the roughness effect of the channel bottom and walls is taken into account. Wong and Parker [
5], by using the same databases of Meyer–Peter and Müller, have suggested two substantially revised forms of the MPM (1948) formula, in which no correction for bed forms is made. According to Wong and Parker [
5], the form drag correction of the MPM formula is unnecessary in the context of the plane bed transport data. The amended bed load transport relations of Wong and Parker are valid for lower-regime plane bed equilibrium transport of uniform sediment.
In the formula applied in our study, the unit sediment discharge is calculated, while the channel bottom roughness is distinguished into roughness due to individual particles and roughness due to bed forms.
Herbertson [
6] has examined the bed load formula of Meyer–Peter and Müller (1948) as well as other conventional bed load formulas using similitude theory as a common basis of comparison. Especially for wide channels with invariable grain size and ratio of sediment density to water density, Herbertson [
6] suggests that the MPM formula is still incomplete in that the depth effect is not included. The final conclusion of Herbertson regarding the MPM formula is cited as: “…the Meyer–Peter and Müller (1948) formula applies only to material rolling or sliding along the bed load and not to material in suspension, however temporarily. The latter condition would limit the formula to the lower regime of transport and presumably the formula will not take account of material transported by saltation”.
Gomez and Church [
7] have tested twelve bed load sediment transport formulas for gravel bed channels, among which is the MPM (1948) formula, using four sets of river data and three sets of flume data. On the basis of the tests performed, which were conducted in each case as if no sediment transport information were available for the river, none of the selected formulas and no other formula is capable of generally predicting bed load transport in gravel bed rivers.
Reid et al. [
8] assessed the performance of several popular bed load formulas in the Negev Desert, Israel, and found that the Meyer–Peter and Müller [
2] and Parker [
9] equations performed best, but their analysis considered only one gravel bed river (Barry et al. [
10]).
Martin [
11] took advantage of ten years of sediment transport and morphologic surveys on the Vedder River, British Columbia, to test the performance of the Meyer–Peter and Müller [
2] equation and two variants of the Bagnold equation [
12]. The author concluded that the formulas generally under-predicted gravel transport rates [
10].
The MPM formula [
2] was also tested in comparison with the formulas of Parker [
13], Schoklitsch [
14] and Recking [
15], by means of a field data set of 6319 bed load samples from sand and gravel bed rivers in the USA. The Meyer–Peter and Müller as well as the Parker equations were chosen because they permit a surface-based calculation with limited knowledge of sediment characteristics, and they are widely used [
15]. The discrepancy ratio (average percentage of predicted bed load discharge not exceeding a factor of two in relation to the observed bed load discharge) obtained the value of 3% for the MPM formula, which is the lowest value in comparison to the corresponding values of the other three formulas.
López et al. [
16] have tested the predictive power of ten bed load formulas against bed load rates for a large, regulated gravel bed river (Ebro River, NE Iberian Peninsula). The bed load MPM formula [
2,
3] was included in the ten bed load formulas tested. The discrepancy ratio, as it was defined above, was one of the formula’s performance criteria applied. Especially for the MPM formula, the discrepancy ratio obtained the value 3% for the case of using surface bed material.
Overall, the predictive power of the MPM formula was relatively low. The MPM formula [
2] belongs to that category of bed load formulas which are based on the assumption of a critical situation characterizing the incipient motion of grains on the bed. According to Meyer–Peter and Müller, the dimensionless critical shear stress amounts to 0.047. The same critical size for rough, turbulent flow, according to Shields [
17], amounts to about 0.06. Gessler [
18] reported a value of about 0.046 for a 50% probability of grain movement in a rough, turbulent flow. Miller et al. [
19] arrived at a similar value of about 0.045 for rough, turbulent flow without consideration of the probability of movement.
Yang [
20] suggested a dimensionless unit stream power equation for the computation and prediction of total sediment concentration without using any criterion for incipient motion. This equation was compared with a similar dimensionless unit stream power equation proposed by Yang [
21], with the inclusion of criteria for incipient motion. In accordance with the comparison results, both equations are equally accurate in predicting the total sediment concentration in the sand size range. It should be noted that the new equation of Yang [
20] is valid for sediment concentration greater than 20 ppm by weight. Both of Yang’s equations were calibrated especially for Nestos River (northeastern Greece) on the basis of available measurements for bed load and suspended load. Regarding the comparison between predicted and measured values of total load transport rate, the values of the statistical criteria used for both equations were very satisfactory, as reported by Avgeris et al. [
22].
Several studies have shown that omitting the incipient motion criterion may lead to better results, compared to the existing formulas. For example, Barry et al. [
10], on the basis of 2104 bed load transport observations in 24 gravel bed rivers in Idaho (USA), concluded that formulas containing a transport threshold typically exhibit poor performance. Kitsikoudis et al. [
23] have employed data-driven techniques, namely artificial neural networks, adaptive-network-based fuzzy inference system and symbolic regression based on genetic programming, for the prediction of bed load transport rates in gravel-bed steep mountainous streams and rivers in Idaho (USA). The derived models generated results superior to those of some of the widely used bed load formulas, without the need to set a threshold for the initiation of motion, and consequently avoid predicting erroneous zero transport rates.
Some previous studies of the authors on the calibration of MPM formula are reported below:
Papalaskaris et al. [
24] have attempted to calibrate the MPM formula both manually and on the basis of the least squares method, in terms of roughness coefficient, for two streams in northeastern Greece: Kosynthos River and Kimmeria Torrent. Papalaskaris et al. [
25] have also manually calibrated the MPM formula, in terms of roughness coefficient, for Nestos River (northeastern Greece). In a following study, Sidiropoulos et al. [
26] have calibrated the same formula for Nestos River by means of a nonlinear optimization of two suitable parameters, while utilizing the average value of the roughness coefficient found by the manual calibration. In all three studies, the comparison between calculations and measurements of bed load transport rate was made on the basis of the following statistical criteria: root mean square error, relative error, efficiency coefficient, linear correlation coefficient, determination coefficient and discrepancy ratio. The values of the above statistical criteria for the case of manual calibration were more satisfactory, compared to the case of nonlinear optimization. However, the manual calibration was carried out on partial measurement sets, while the nonlinear optimization was carried out on the whole measurement set.
In view of the fact that the predictive power of the MPM formula did not reach particularly high levels, the present paper proposes an Enhanced MPM (EMPM) formula, demonstrating that, under suitable calibration, it shows a much better fitness to field data. Moreover, the performance of the enhanced formula is compared to machine learning methods, showing the competitiveness of the semi-empirical formula versus purely data-driven approaches.
One of the adjustment parameters of the formula is the critical shear stress, the value of which has been discussed and re-adjusted by various researchers, as already cited. In line with these investigations and under the data of this study, a zero value of this parameter gave the optimal calibration results.
Calibration of the EMPM formula was also performed on smoothed data, with the prospect of mitigating possible noise of the field measurements. A nearest neighbor smoothing is introduced and applied both in regard to the MPM formula calibration and to typical machine learning methods. In the case of the smoothed data, the performance of the EMPM formula turns out to be superior.
The introduction of machine learning methods into the field of sediment transport modeling brought about new standards in the error metrics of predicted versus measured data, sometimes tending to overshadow physically based and semi-empirical equations. This paper aims at turning attention back to such equations by introducing generalized forms and by establishing competitive and, in the case of smoothing, even better performance versus machine learning methods.
2. Materials and Methods
2.1. Study Area and Data
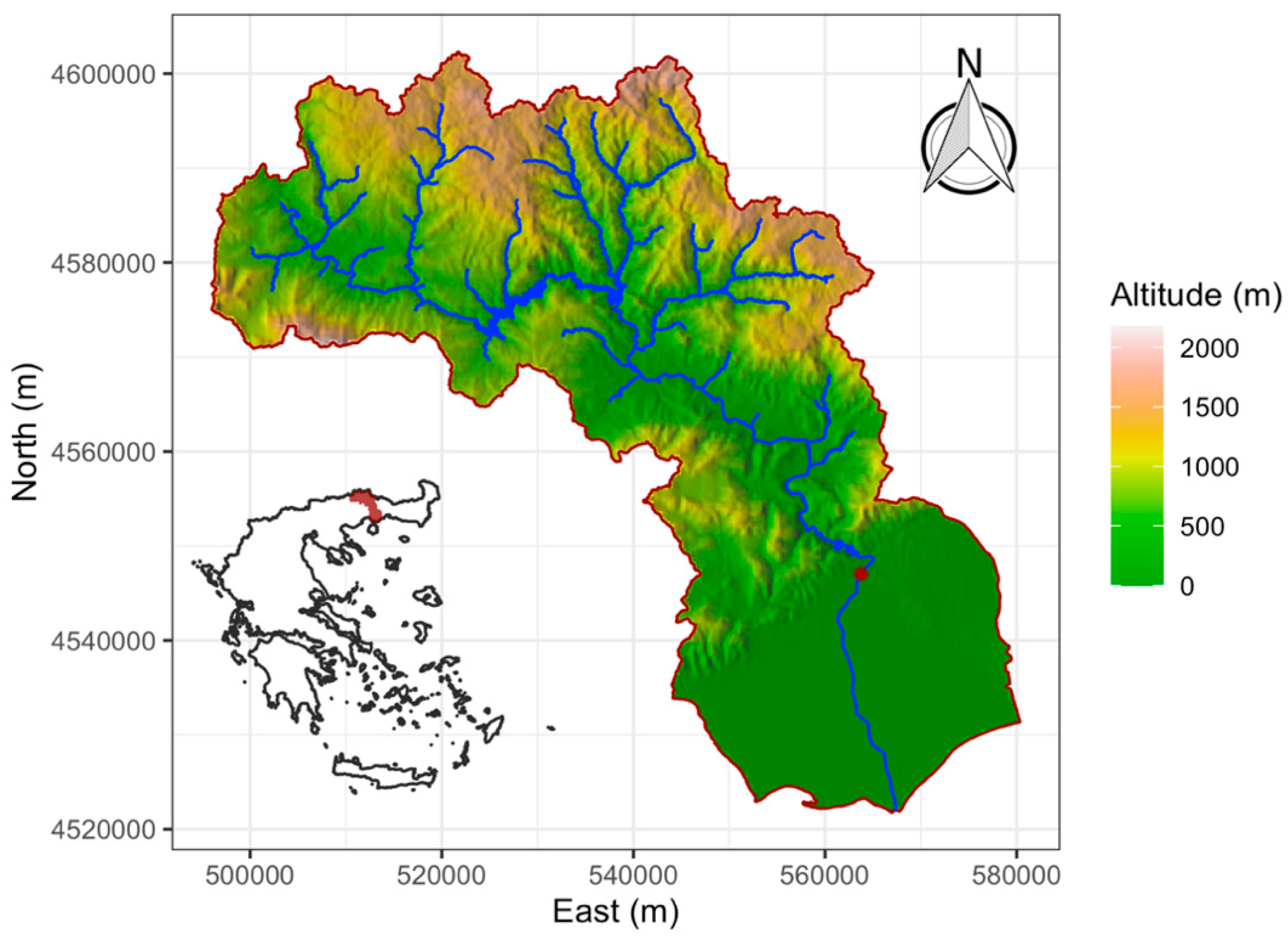
The Nestos River basin (
Figure 1, northeastern Greece) considered in this study drains an area of 838 km
2 and lies downstream of Platanovrysi Dam. The river basin outlet is located at Toxotes. The river basin terrain is covered by forest (48%), bush (20%), cultivated land (24%), urban area (2%) and no significant vegetation (6%). The altitude ranges between 80 m and 1600 m, whereas the length of Nestos River is 55 km. The mean slope of Nestos River in the basin is 0.35%. The stream flow rate and bed load transport rate measurements concerning Nestos River were conducted at a location between the outlet of Nestos River basin (Toxotes) and the river delta. The measurement procedures are described in [
25].
The first four statistical moments (mean, standard deviation, skewness and kurtosis) and other statistical properties were used to describe the bed load measured related values (
Table 1).
In concrete terms, mGm (kg/(s m)) is the measured bed load transport rate per unit width, Q (m3/s) is the measured stream discharge, b (m) is the measured width of the assumed rectangular cross section, h (m) is the measured flow depth, um (m/s) is the measured mean flow velocity, d50 (m) is the median grain diameter of bed load, determined by the granulometric curves, and d90 (m) is a characteristic grain size diameter (in case of taking a stream bed load sample, concerning the sample weight, 90% is composed of grains with size less than or equal to d90).
2.2. Meyer–Peter and Müller (MPM) Bed Load Transport Formula
In the MPM formula, referred to in the introduction, the unit submerged sediment discharge is calculated and the roughness effect of the channel bottom and walls is taken into account.
In the formula, as applied in our study, the unit sediment discharge is calculated while the channel bottom roughness is distinguished into roughness due to individual particles and roughness due to bed forms:
where:
The symbols of Equations (1) and (2) are explained below:
mGc: computed bed load transport rate per unit width (kg/(s·m))
g: gravity acceleration (m/s2)
ρF: sediment density (kg/m3)
ρw: water density (kg/m3)
τo: actual shear stress (N/m2)
τo,cr: critical shear stress (N/m2), characterizing the incipient motion of bed grains
Ir: energy line slope due to individual grains
Rs: hydraulic radius of the specific part of the cross section under consideration which affects the bed load transport (m).
dm: mean diameter of bed load grains (m)
kst: Strickler coefficient, the value of which depends on the roughness due to individual grains, as well as to stream bed forms (m1/3/s).
kr: coefficient, with value depending on the roughness due to individual grain (m1/3/s)
I: energy line slope due to individual grains and stream bed forms
d
90: characteristic grain size diameter (m). It was defined for
Table 1.
The basic limitations for the MPM formula are the following:
Slope of energy line (I) from 0.04% to 2%
Sediment particle size (d50) from 0.4 mm to 20 mm
Flow depth (h) from 0.01 m to 1.20 m
Specific stream discharge (Q/b) from 0.002 m2/s to 2 m2/s
Relative sediment density (ρF/ρw) from 0.25 to 3.2
Particle size > 1 mm, to avoid the effects of apparent cohesion
Flow depth > 0.05 m, to assure Froude similitude.
At this point, it should be noted that the mean values of the measured energy line slope (longitudinal bed slope in the case of uniform flow), sediment particle size, flow depth, specific stream discharge and relative sediment density are included in the ranges given above.
According to the Einstein–Barbarossa method (e.g., [
27])
where A (m
2) is the stream cross section, assuming a rectangular section, approximately, and where R (m) is the hydraulic radius and U (m) is the wetted perimeter. The indices s and w stand for bed and walls, respectively. The hydraulic radius R
w is given by the familiar Manning formula:
where u
m (m/s) is the mean flow velocity through the cross-sectional area A and k
w (m
1/3/s), a coefficient depending on the roughness of the walls. It is assumed that k
w = k
st. Additionally, I is set equal to the longitudinal stream bed slope on the basis of the assumption of uniform flow.
Then R
s, by combining Equations (3) and (4), turns out as
Equation (1) can be converted to a non-dimensional form (see
Appendix A):
where
where ν is the kinematic viscosity of water. The size m
Gc becomes dimensionless by means of Equation (7). The derivation of Equation (9) is given in
Appendix A.
Due to the sandy composition of the bed load in the river locations, the mean grain diameter d
m can be approximated by the median grain diameter d
50. Therefore, Equation (6) acquires the simpler non-dimensional form:
The above non-dimensional scheme is in accordance with the dimensional analysis of Parker and Anderson [
28], as utilized in a related paper by Kitsikoudis et al. [
23]. Indeed, the non-dimensional groups appearing in Equation (10) are consistent with the dimensionless variables envisaged in the Parker and Anderson analysis. An analogous non-dimensional form has been presented by Wong and Parker [
5], attributed originally to N. Chien in a 1954 publication of the US Army Corps of Engineers.
From the non-dimensional form (10), it turns out that, in a way compatible with the dimensional analysis of [
28], the following non-dimensional variables determine bed load transport: Re
p50 (Equation (8)), an explicit particle Reynolds number, Re* (Equation (9)), a shear Reynolds number, ρ′ (appearing in the third one of Equations (2)), the submerged specific gravity of the sediment.
2.3. Calibration of an Enhanced Meyer–Peter and Müller (EMPM) Formula
The available data comprise measured values for the physical parameters A, u
m, U
w, U
s and d
50, as well as measured values of bed transport rates m
Gm, denoted respectively as A
i, u
mi, U
wi, U
si, d
50,i and m
Gmi, for i = 1, 2,…, N, where N is the number of data points. These subscripted quantities are substituted into the corresponding Equations (7)–(10), giving the non-dimensional bed load transport rate of Equation (10) in terms of measured quantities:
In Equation (11), k
st emerges as an adjustment parameter. Therefore, the following expression can be used for the calibration of the MPM formula:
where
and m
Gmi, i = 1,…,N, denote measured values of bed load transport rate. Calibration with respect to one parameter only, namely k
st, has already been tried (Sidiropoulos et al., 2018). In this paper, Equation (12) is further extended, so as to include more adjustment parameters:
Equation (14) will be referred to as the Enhanced Meyer–Peter and Müller (EMPM) formula.
Equation (14) can be written as follows in a generalized form:
where
dM = (k
st, α, β, γ) is the vector of parameters,
is the vector of measured quantities that were suitably grouped in Equation (10), and
In analogy to Equations (11) and (12), the difference between computed and measured quantities is defined as
where
is given by Equation (13) and f
M by Equation (17).
The objective function of the calibration problem is
where N is the number of measurement points.
The minimization of the objective function FM of Equation (19) was executed by a genetic algorithm followed by a Nelder–Mead local search.
2.4. Application of Machine Learning Schemes
A common pitfall in the use of machine learning algorithms is the expectation of performance regardless of the nature and limitations of the problem and of the presence of noisy data. In the context of bed load estimation, especially for data that are coming from natural streams, errors are expected to be higher, as testified by the sediment transport literature, in which errors are predominantly reported as ratios and not as differences of compared quantities.
In a preliminary stage of analysis, various machine and statistical learning methods have been evaluated, such as neural networks (various architectures and regularization techniques), support vector regression, decision trees, linear models, K-NN regression, Gaussian Processes Regression (GPR) and Random Forests (RF). Most methods gave similar results with the exception of neural networks, which had a tendency to overfit or, in other words, they fitted too closely on the data, memorizing the noise and, as a result, were unable to adequately generalize on new data.
In the sequel, RF and GPR algorithms are presented so as to have a broader representation of machine learning methods. RF had the best performance and the results obtained regarding their generalization ability in this problem and dataset justify their use, as reported later in
Section 3.
2.4.1. Random Forests
Random Forests (RF) is a data-driven algorithm in the area of supervised learning which tries to fit a model using a set of paired input variables and their associated output responses, and can be used in classification and regression problems. In summary, RF consists of a number of decision trees [
29]. For each tree, a random set is created from the dataset via bootstrapping [
29], and in each node of the tree a random set of n input variables from the p variables of the dataset is considered to pick the best split [
29]. The prediction of the output response in regression problems is the mean value of the estimations of these random decision trees. RF is one of the most popular methods applied in machine learning because of: (a) its robustness to outliers and overfitting, (b) its ability to perform feature selection and (c) the fact that its default hyperparameters (i.e., the set of parameters that have to be selected a priori in order to train a RF), as implemented in software, give satisfactory results [
30].
The measured data quantities defined above, under the vector pi, serve as input variables in the RF learning scheme, while will be the corresponding target for the output. The general form of Equations (18) and (19) can be used again for the formation of the objective function, as follows:
Let
in analogy to Equation (15), where
dR is the vector of the RF parameters (i.e., the set of decision trees that operate as an ensemble) that will be determined through training.
Then the deviation of measured from computed values is
and the objective value of the problem will be
2.4.2. Gaussian Processes Regression
A completely different alternative is Gaussian Processes Regression (GPR), which can be briefly described as follows: In the area of machine learning, Williams and Rasmussen [
31] developed a regression algorithm based on Gaussian processes, which is a non-parametric, Bayesian approach that has the ability to work well with small datasets. In the framework of that algorithm, the prediction for an input test point
x is derived by means of a Gaussian stochastic process with an assumed mean equal to 0 and with a variance σ
2 calculated in terms of covariances involving
x and the training data. A suitable covariance function is selected and parametrized, and finally, the hyperparameters involved are determined through optimization.
In this case, the formal scheme of Equations (20)–(22) is retained, with dR replaced by dG for GPR. The vector dG represents the internal parameters of the respective machine learning process, which will be optimally determined according to the above outline.
2.5. Training and Testing Procedures
Three methods are presented here for modeling bed load sediment transport. The first one is the calibration of the EMPM formula, while the second and the third consist in the application of RF and GPR machine learning methods respectively. In all three cases, a resampling method needs to be executed in order to estimate the generalization error of the methods or, specifically, the measure of accuracy of the methods to predict outcome values from data that are not known a priori. For that reason, bootstrapping [
29] is applied, a procedure that was repeated 100 times.
Every bootstrap sample dataset consists of 116 points generated through random sampling with replacement of the original 116 data points. Consequently, some observations may appear more than once and some not at all. The latter are used to estimate the generalization error (out-of-the-bag error) and the former lead to the training error of the methods.
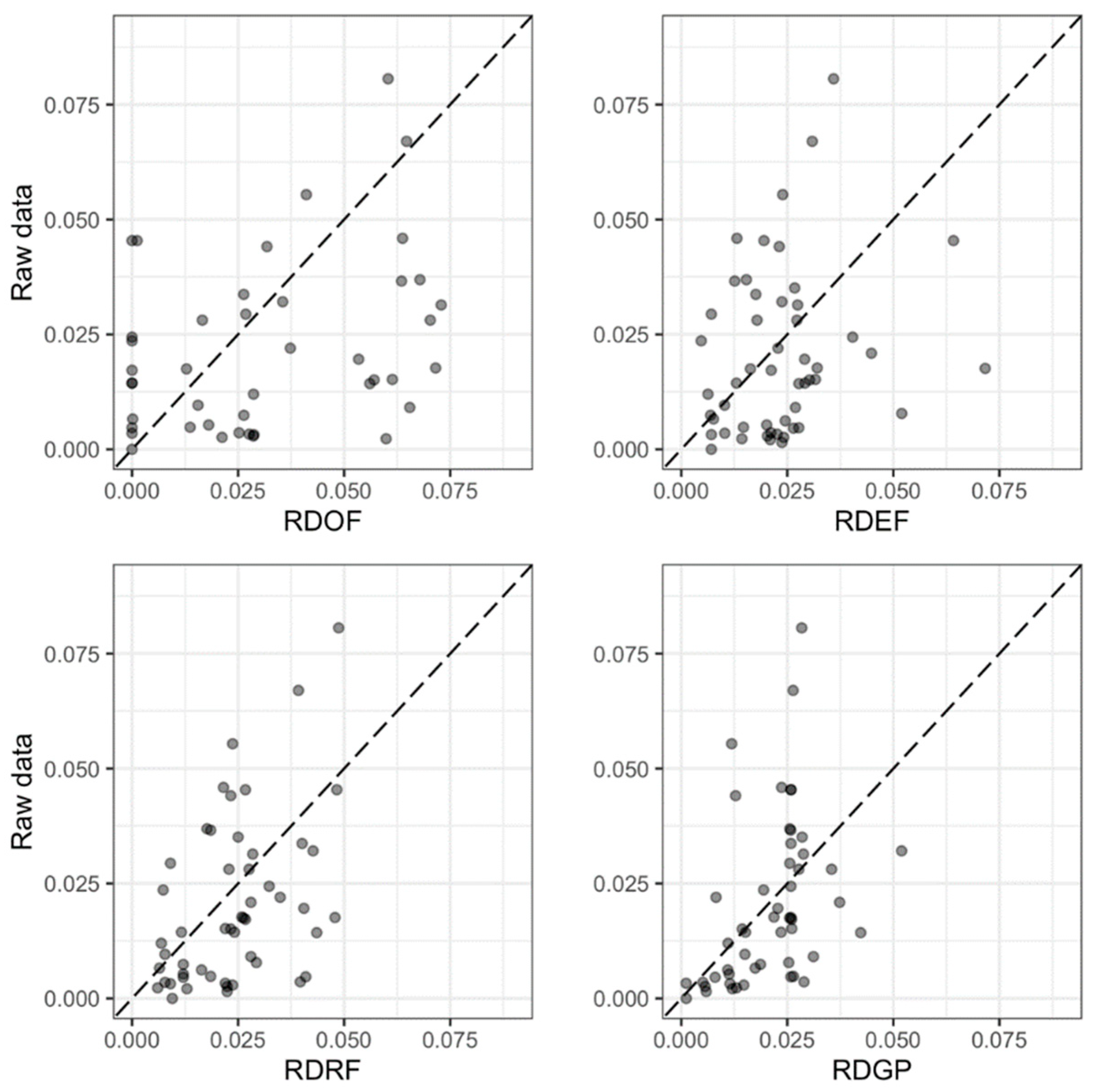
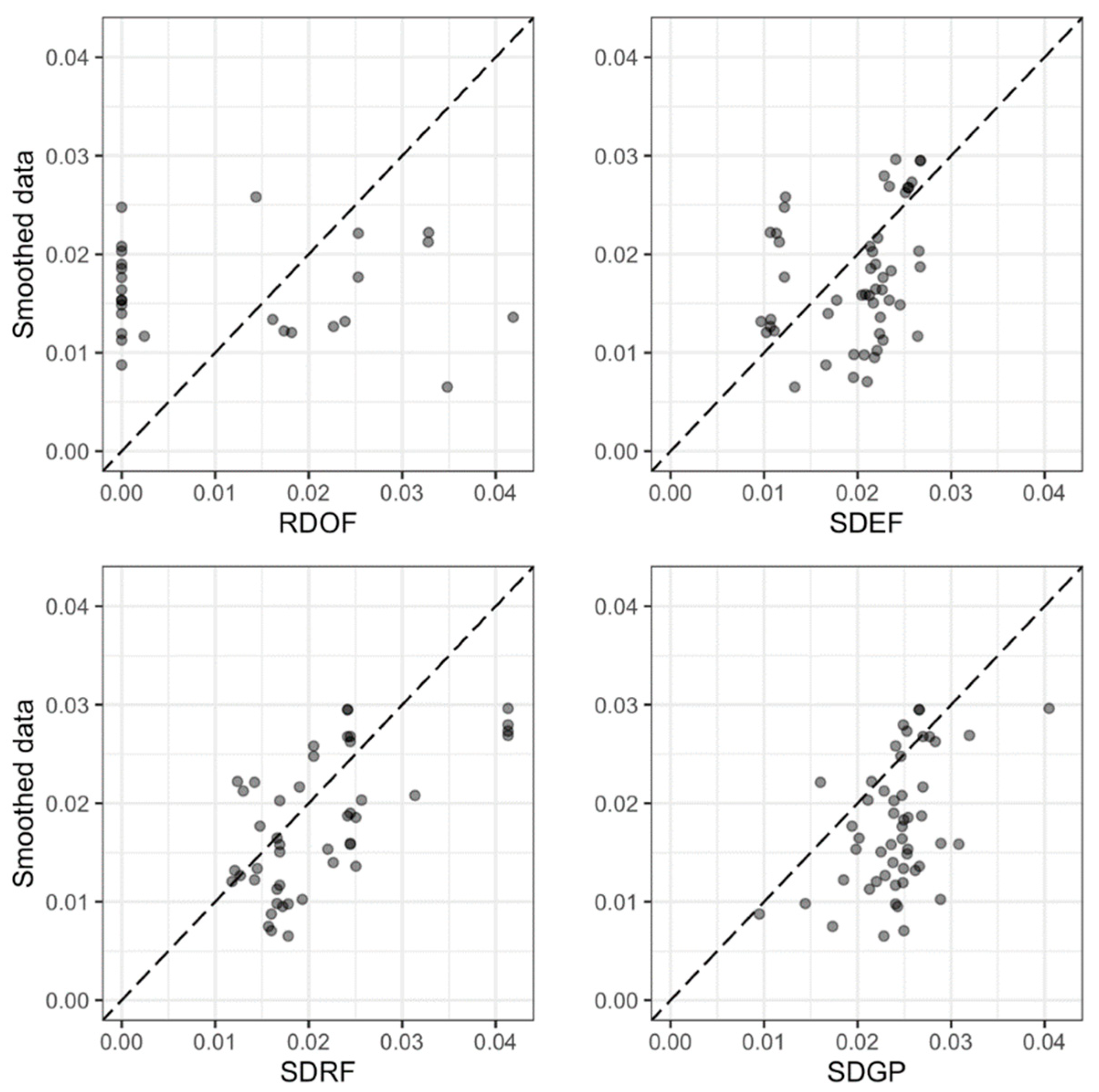
The simulation will be carried out for the original raw data, first by calibration of the EMPM formula and then by training the RF and GPR machine learning methods. Thereafter, the original data will be subjected to smoothing and the simulation will be repeated for the smoothed data by the same three methods.
2.6. Nearest Neighbor Smoothing
A smoothing process based on nearest neighbors is introduced as follows:
For each vector pi of input measured quantities (Equation (16)), the distances are computed to all other vectors pj, j = 1, 2,…, N, where N is the number of available measurement points. The k nearest neighbors to pi are then picked out and the average of these is taken, as well as the average of the corresponding bed load transport measurements. These averages will replace the original data. The process is formalized as follows:
Let
be the distances between
pi and all
pj’s, including
pi itself.
Let
be the set of the distances of p
i from all other parameter vectors, as computed according to Equation (22).
Let
be the k smallest members of the set D
i of Equation (23) and let
be the corresponding k vectors and associated bed load measurements expressed in non-dimensional form as above (Equation (13)).
Then the following averaging is performed:
The pair ) will replace the pair ) in Equations (18) and (19) for the formation of objective function FM, and in Equations (21) and (22) for the formation of objective function FR.
It needs to be noted here that the nearest neighbor technique is used for smoothing only and not for prediction, as known from the literature (e.g., [
29]). Prediction is performed by the nonlinear regression that follows the smoothing.
4. Conclusions
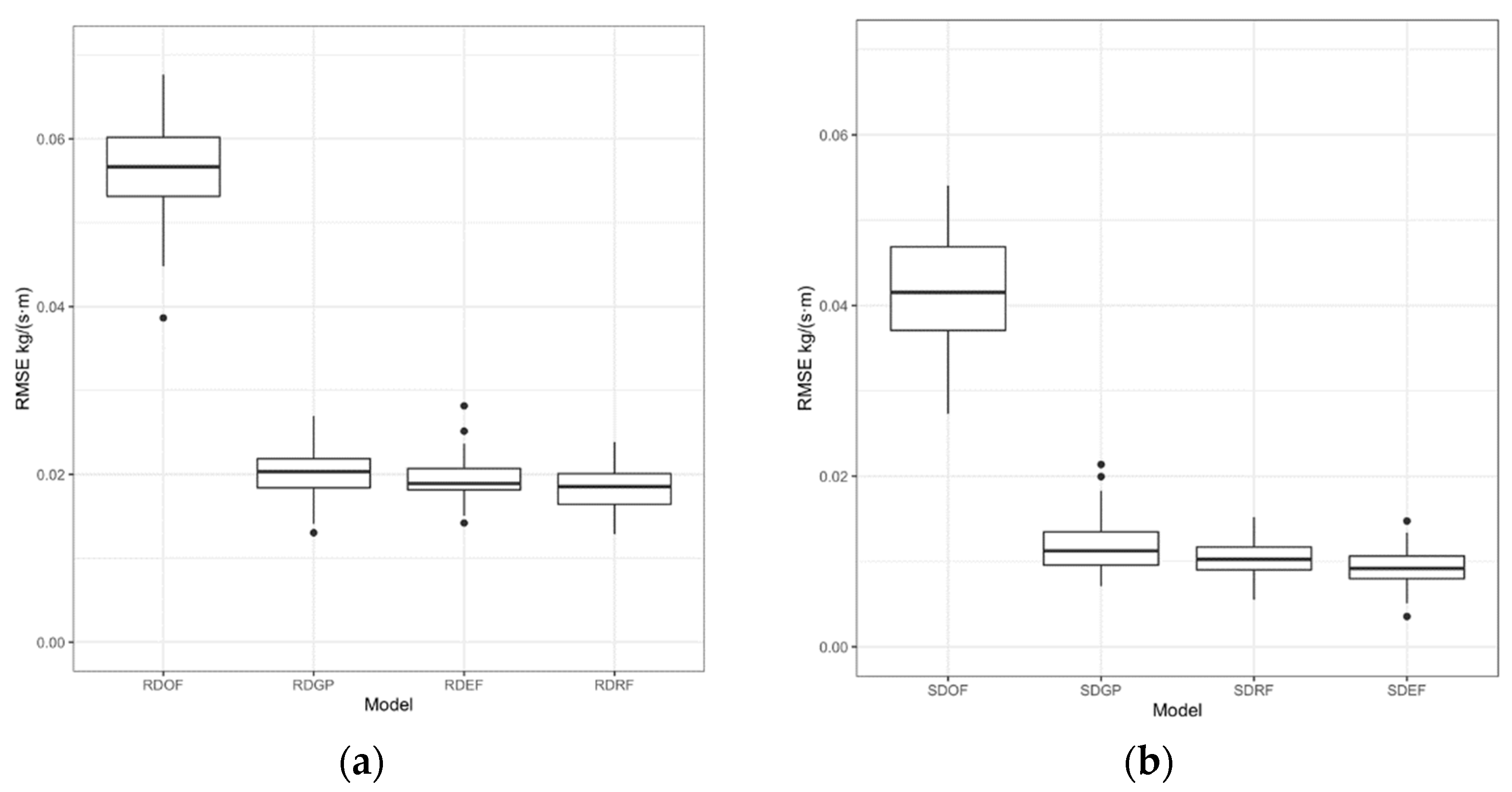
The advent of machine learning methods has also contributed to progress in the area of sediment transport modeling. Purely data-driven methods that appeared in the literature were found to outperform well-known physically based and semi-empirical equations. In an effort to enhance the performance of such equations, the Meyer–Peter and Müller bed load transport formula is extended in the present paper by the addition of suitable adjustment parameters, for the purpose of reinforcing its predictive abilities.
The resulting Enhanced Meyer–Peter and Müller formula presented a definitely improved performance in comparison to the original formula, one which is also competitive to purely data-driven techniques and even superior in the case of smoothed data. As a characteristic data-driven technique, the Random Forests learning scheme was chosen, due to its advantages in terms of robustness against outliers and overfitting, considering the noise contained in the field data of this study. A completely different machine learning method, Gaussian Processes Regression, was also tried and gave similar results, but was found to overfit on the training data.
For the purpose of countering noise effects, data smoothing is important and needs to be further considered for problems involving sediment transport field data, such as the present one. A nearest neighbor data smoothing process is presented and combined with nonlinear regression, a scheme different from the well-known nearest neighbor regression of the literature. Under smoothing, the enhanced MPM formula shows better performance, even compared to the machine learning methods.
The methods presented in this paper call for further applications in other natural streams with values of the variables beyond the range of boundary values given in the present article, as well as in modeling with laboratory data. Additionally, further research would be useful in the direction of hybrids involving both machine learning and sediment transport formulas.