Optimal Operation Model of Drainage Works for Minimizing Waterlogging Loss in Paddy Fields
Abstract
:1. Introduction
2. Model Development
2.1. Assumptions
- Ignore the duration it takes to open and close a specific drainage work, and all drainage works are scheduled once only for one waterlogging event.
- All drainage works only have two states—fully open and fully closed—the sluice is opened with opening height above the water surface or the pumping station is in operation at the rated flow, respectively. For the pump station with gate, the pump was launched only when the gate was closed. A pump station with multiple pumps is considered as one work.
- The flow rate and power consumption of a specific pump station are assumed to be constant and are calculated according to the rated value.
2.2. Objective Functions and Calculation Formula
2.2.1. Waterlogging Loss Estimation
2.2.2. Waterlogging Process Simulation
2.3. Constraint Conditions
3. Model Solving by Using Genetic Algorithm
Genetic Algorithm
4. Result and Discussion
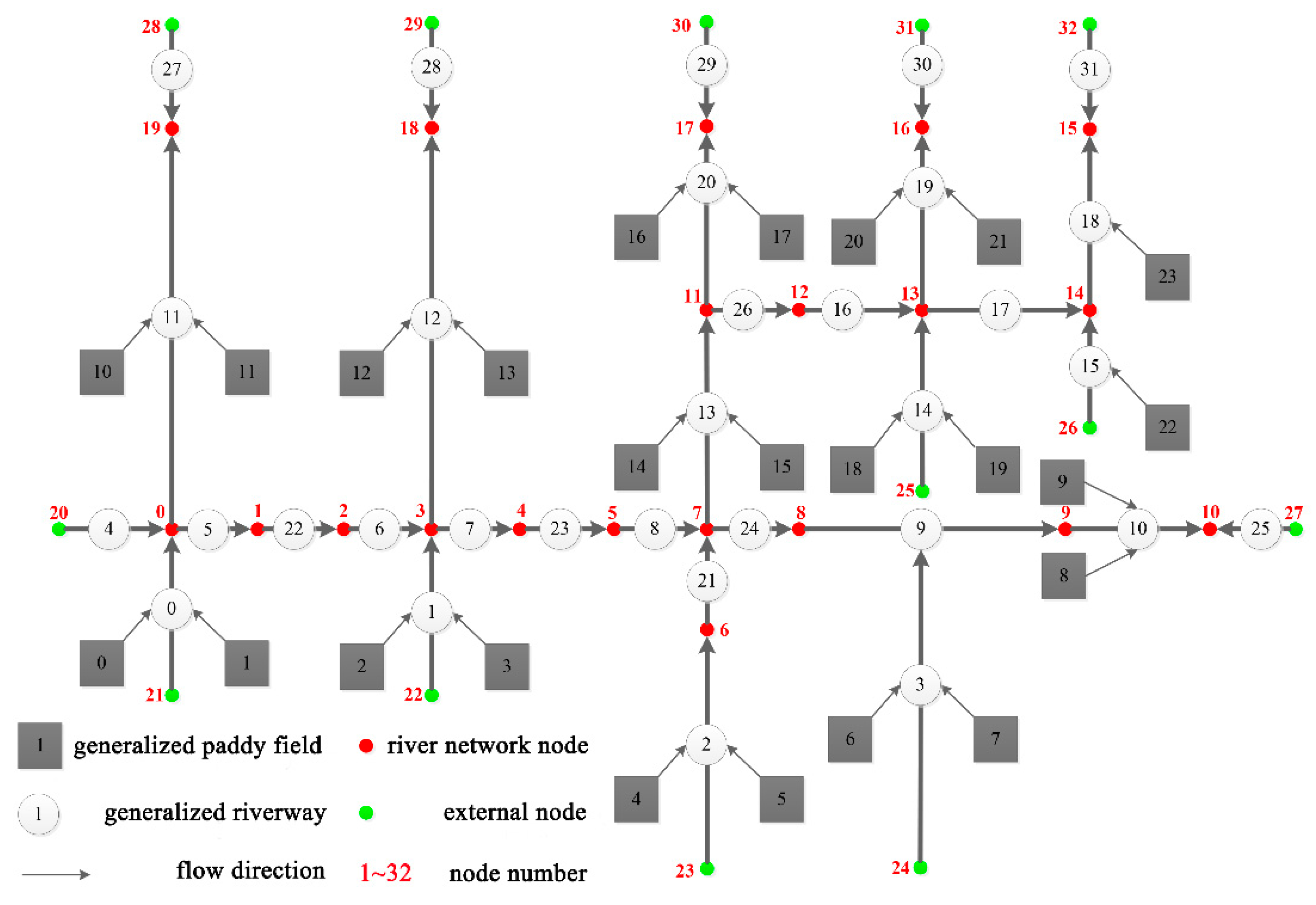
4.1. Study Area
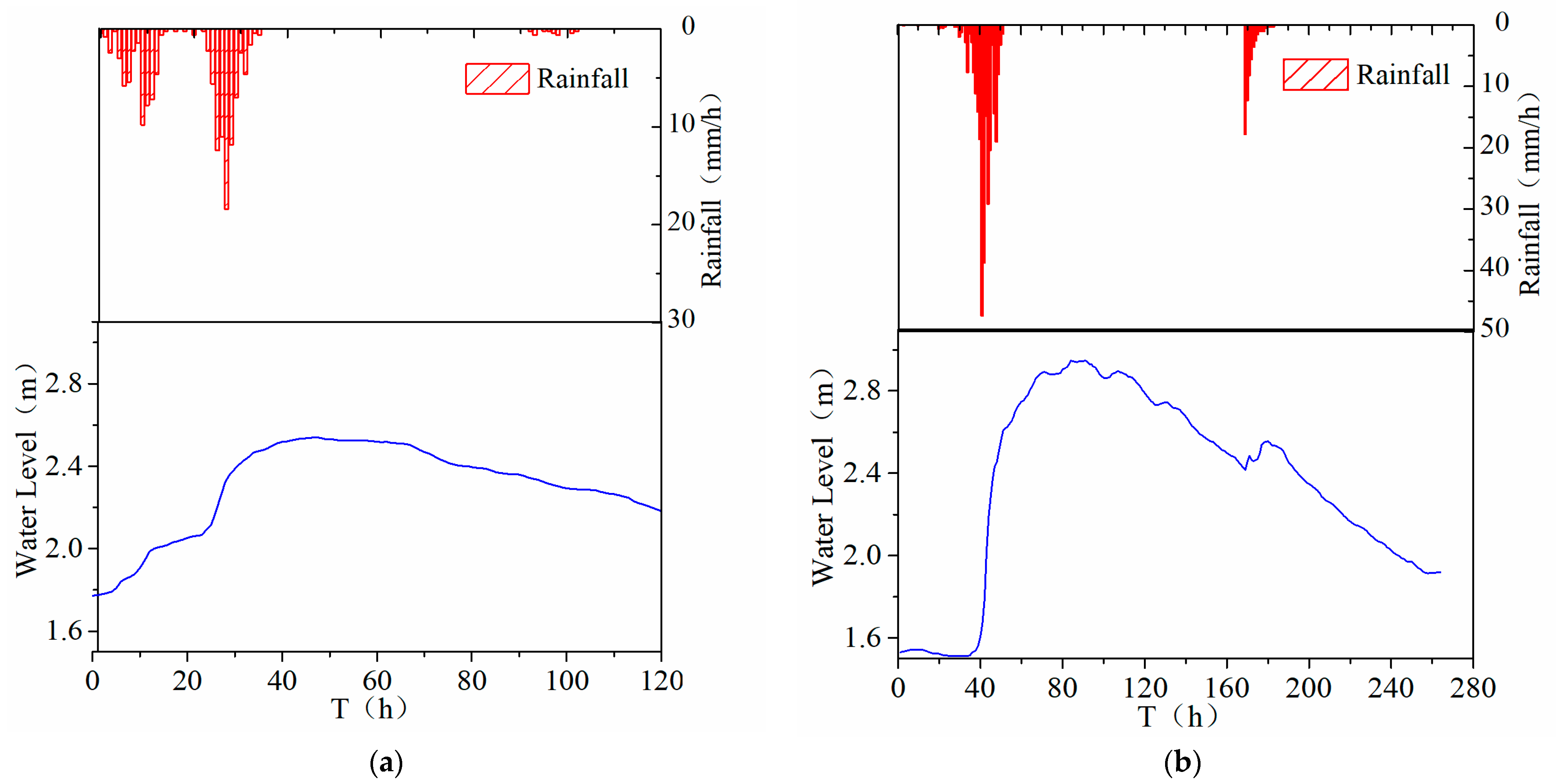
4.2. Calibration and Vertification
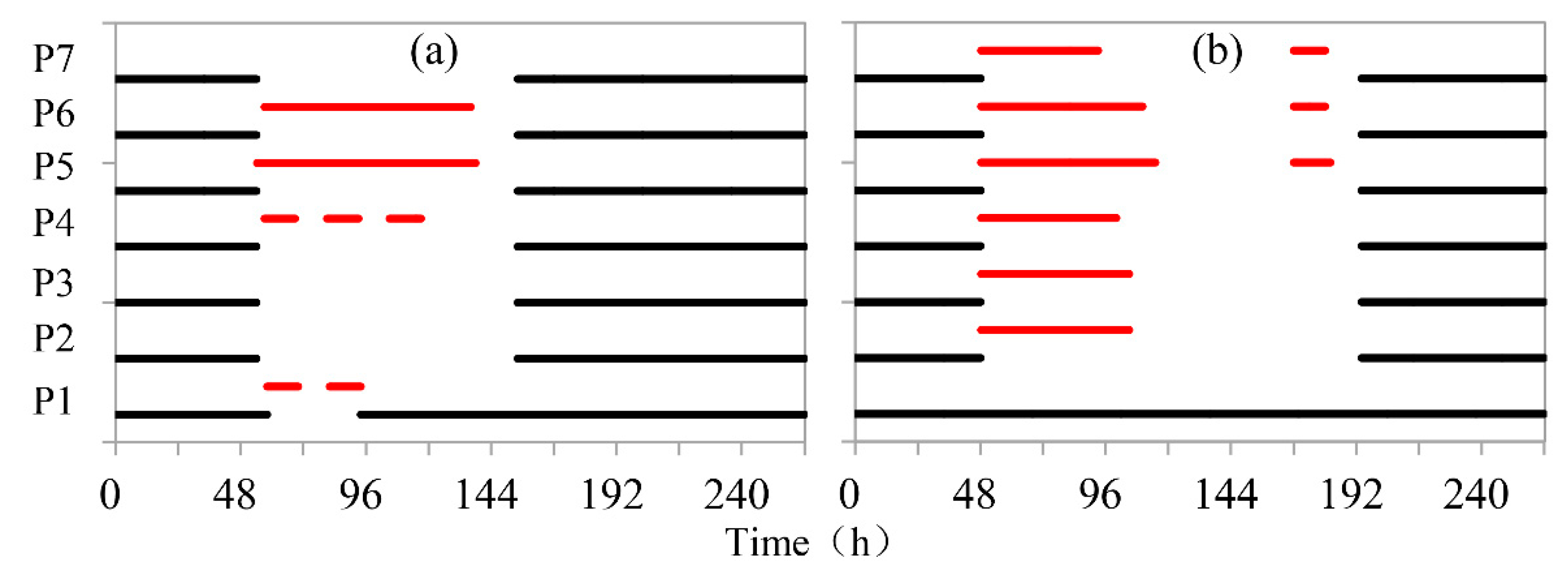
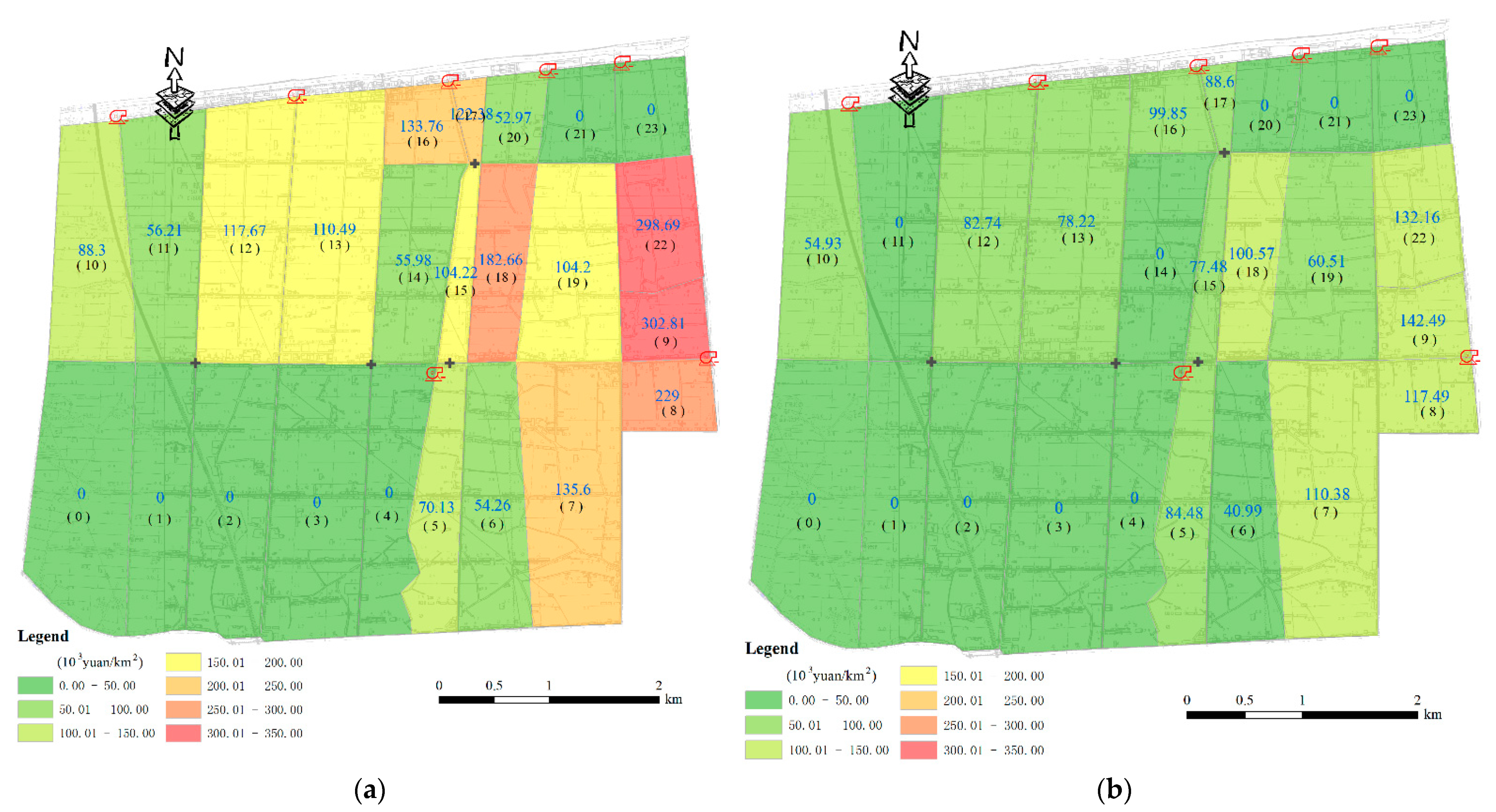
4.3. Model Application
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huo, Z.; Fan, Y.; Yang, J.; Shang, Y. Review on agricultural flood disaster in China. J. Appl. Meteor. Sci. 2017, 28, 641–653. [Google Scholar] [CrossRef]
- Arif, C.; Setiawan, B.I.; Saptomo, S.K.; Matsuda, H.; Tamura, K.; Inoue, Y.; Hikmah, Z.M.; Nugroho, N.; Agustiani, N.; Suwarno, W.B. Performances of Sheet-Pipe Typed Subsurface Drainage on Land and Water Productivity of Paddy Fields in Indonesia. Water 2021, 13, 48. [Google Scholar] [CrossRef]
- Keesstra, S.; Nunes, J.P.; Saco, P.; Parsons, T.; Poeppl, R.; Masselink, R.; Cerda, A. The way forward: Can connectivity be useful to design better measuring and modelling schemes for water and sediment dynamics? Sci. Total Environ. 2018, 644, 1557–1572. [Google Scholar] [CrossRef] [PubMed]
- Singh, A. Soil salinization and waterlogging: A threat to environment and agricultural sustainability. Ecol. Indic. 2015, 57, 128–130. [Google Scholar] [CrossRef]
- Liu, A.; Zhu, J.; Jin, T. Advance of the research on crop suffering from waterlogged stress. In Proceedings of the 2013 Third International Conference on Intelligent System Design and Engineering Applications, Hong Kong, China, 16–18 January 2013; pp. 227–230. [Google Scholar]
- Ministry of Water Resources of the People’s Republic of China. 2019 Bulletin on Flood and Drought Disaster Prevention in China; 9 April 2021; Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2021.
- Liang, Y.L.; Wang, Y.L.; Zhao, Y.J.; Lu, Y.; Liu, X.Y. Analysis and Projection of Flood Hazards over China. Water 2019, 11, 1022. [Google Scholar] [CrossRef] [Green Version]
- Saraphirom, P.; Wirojanagud, W.; Srisuk, K. Impact of climate change on waterlogging and salinity distributions in Huai Khamrian subwatershed, NE Thailand. Environ. Earth Sci. 2013, 70, 887–900. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J.; Chen, X. Future changes of drought and flood events in China under a global warming scenario. Atmos. Ocean. Sci. Lett. 2013, 6, 8–13. [Google Scholar] [CrossRef]
- Yousefi, S.; Pourghasemi, H.R.; Rahmati, O.; Keesstra, S.; Emami, S.N.; Hooke, J. Geomorphological change detection of an urban meander loop caused by an extreme flood using remote sensing and bathymetry measurements (a case study of Karoon River, Iran). J. Hydrol. 2021, 597, 10. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Jolly, I.; Sophocleous, M.; Zhang, L. Global impacts of conversions from natural to agricultural ecosystems on water resources: Quantity versus quality. Water Resour. Res. 2007, 43, 18. [Google Scholar] [CrossRef] [Green Version]
- Lagacherie, P.; Rabotin, M.; Colin, F.; Moussa, R.; Voltz, M. Geo-MHYDAS: A landscape discretization tool for distributed hydrological modeling of cultivated areas. Comput. Geosci. 2010, 36, 1021–1032. [Google Scholar] [CrossRef]
- Maharjan, G.R.; Park, Y.S.; Kim, N.W.; Shin, D.S.; Choi, J.W.; Hyun, G.W.; Jeon, J.-H.; Ok, Y.S.; Lim, K.J. Evaluation of SWAT sub-daily runoff estimation at small agricultural watershed in Korea. Front. Env. Sci. Eng. 2013, 7, 109–119. [Google Scholar] [CrossRef]
- Xiao, J.; Luo, Q.; Luo, W. Calculation of Drainage Flow Rate of Urban Drainage Channels Based on Hydraulic Model. China Water Wastewater 2016, 32, 140–146. [Google Scholar]
- Oconnell, P.E.; Todini, E. Modelling of rainfall, flow and mass transport in hydrological systems: An overview. J. Hydrol. 1996, 175, 3–16. [Google Scholar] [CrossRef]
- Zhou, W.; Dong, B.; Liu, J. Study on the water and nitrogen balance in paddy fields with irrigation and drainage dual-purpose channel mode using the tank model. Paddy Water Environ. 2020, 18, 121–138. [Google Scholar] [CrossRef]
- Chen, R.S.; Pi, L.C. Diffusive tank model application in rainfall-runoff analysis of upland fields in Taiwan. Agric. Water Manage. 2004, 70, 39–50. [Google Scholar] [CrossRef]
- Nguyen Manh, H.; Le Van, C.; Hiramatsu, K.; Harada, M.; Dao Ngoc, T. Flood inundation analysis using a distributed tank model for a flat, low-lying agricultural area undergoing urbanization in Hanoi, Vietnam. Irrig. Drain. 2013, 62, 52–62. [Google Scholar] [CrossRef]
- Xu, J.J.; Bai, D. Multi-Objective Optimal Operation of the Inter-Basin Water Transfer Project Considering the Unknown Shapes of Pareto Fronts. Water 2019, 11, 2644. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, R.; Loucks, D.P. Operating rules for multireservoir systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Chang, L.C.; Chang, F.J. Intelligent control for modelling of real-time reservoir operation. Hydrol. Process. 2001, 15, 1621–1634. [Google Scholar] [CrossRef]
- Akter, T.; Simonovic, S.P. Modelling uncertainties in short-term reservoir operation using fuzzy sets and a genetic algorithm. Hydrolog. Sci. J. 2004, 49, 1081–1097. [Google Scholar] [CrossRef]
- Wardlaw, R.; Sharif, M. Evaluation of genetic algorithms for optimal reservoir system operation. J. Water Res. Plan. Man. 1999, 125, 25–33. [Google Scholar] [CrossRef]
- Sharif, M.; Wardlaw, R. Multireservoir systems optimization using genetic algorithms: Case study. J. Comput. Civ. Eng. 2000, 14, 255–263. [Google Scholar] [CrossRef]
- Zeng, L.H.; Lesch, S.M.; Grieve, C.M. Rice growth and yield respond to changes in water depth and salinity stress. Agric. Water Manage. 2003, 59, 67–75. [Google Scholar] [CrossRef]
- Xiong, Y.; Xu, J.; Li, Y.; Li, J.; Sun, Y. Modeling waterlogging process of paddy field at flat irrigation district in South China. J. Drain. Irrig. Mach. Eng. 2018, 36, 725–731. [Google Scholar]
- Chen, R.S.; Pi, L.C. Application of diffusive tank model in drainage analysis of paddy fields. J. Am. Water Resour. Assoc. 2004, 40, 33–41. [Google Scholar] [CrossRef]
- Chen, R.S.; Pi, L.C.; Huang, Y.H. Analysis of rainfall-runoff relation in paddy fields by diffusive tank model. Hydrol. Process. 2003, 17, 2541–2553. [Google Scholar] [CrossRef]
- Sampson, J.R. Adaptation in natural and artificial systems (John H. Holland). SIAMR 1976, 18, 529–530. [Google Scholar] [CrossRef]
- Yan, B.; Yan, C.; Long, F.; Tan, X.C. Multi-objective optimization of electronic product goods location assignment in stereoscopic warehouse based on adaptive genetic algorithm. J. Intell. Manuf. 2018, 29, 1273–1285. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Xiong, Y.; Liu, Z.; Liu, F.; Yuan, N.; Fu, H. The Waterlogging Process Model in the Paddy Fields of Flat Irrigation Districts. Water 2021, 13, 2668. [Google Scholar] [CrossRef]
- Shaw, R.E.; Meyer, W.S.; McNeill, A.; Tyerman, S.D. Waterlogging in Australian agricultural landscapes: A review of plant responses and crop models. Crop Pasture Sci. 2013, 64, 549–562. [Google Scholar] [CrossRef]
- Wei, M.; She, L.; You, X.Y. Establishment of urban waterlogging pre-warning system based on coupling RBF-NARX neural networks. Water Sci. Technol. 2020, 82, 1921–1931. [Google Scholar] [CrossRef] [PubMed]
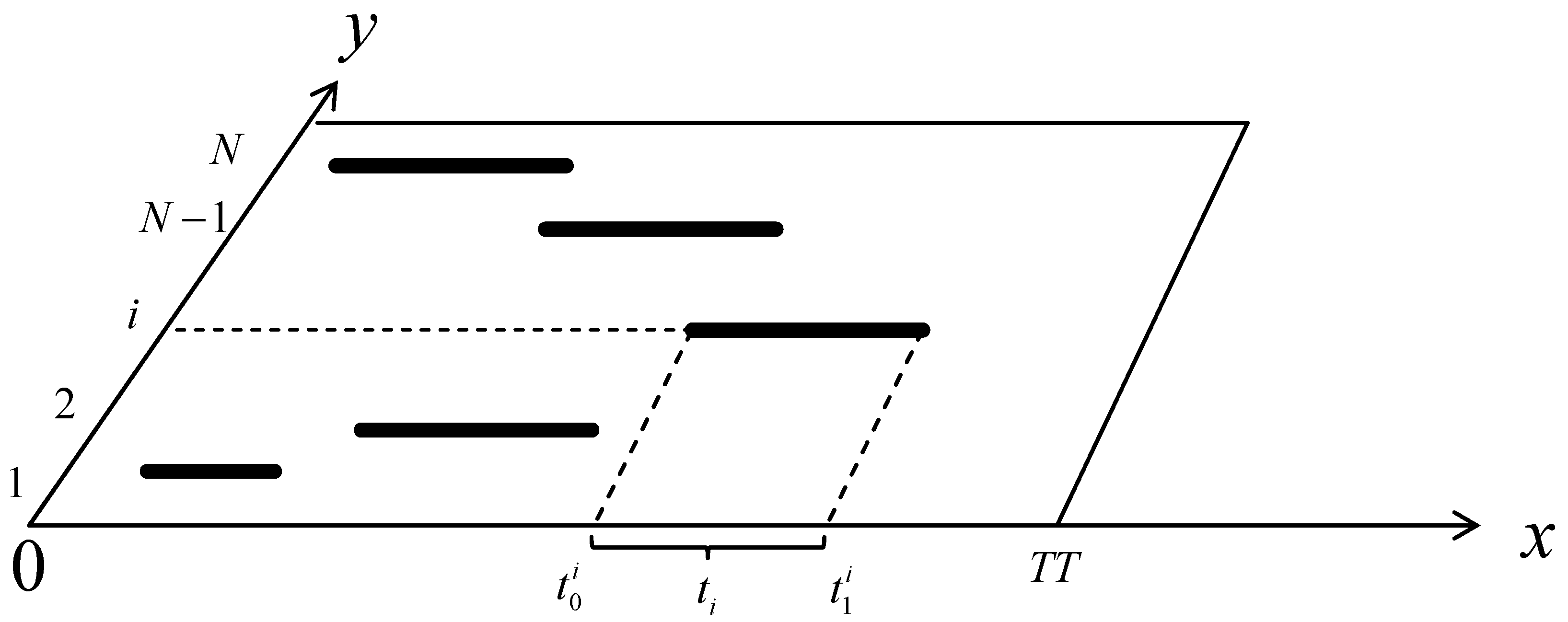
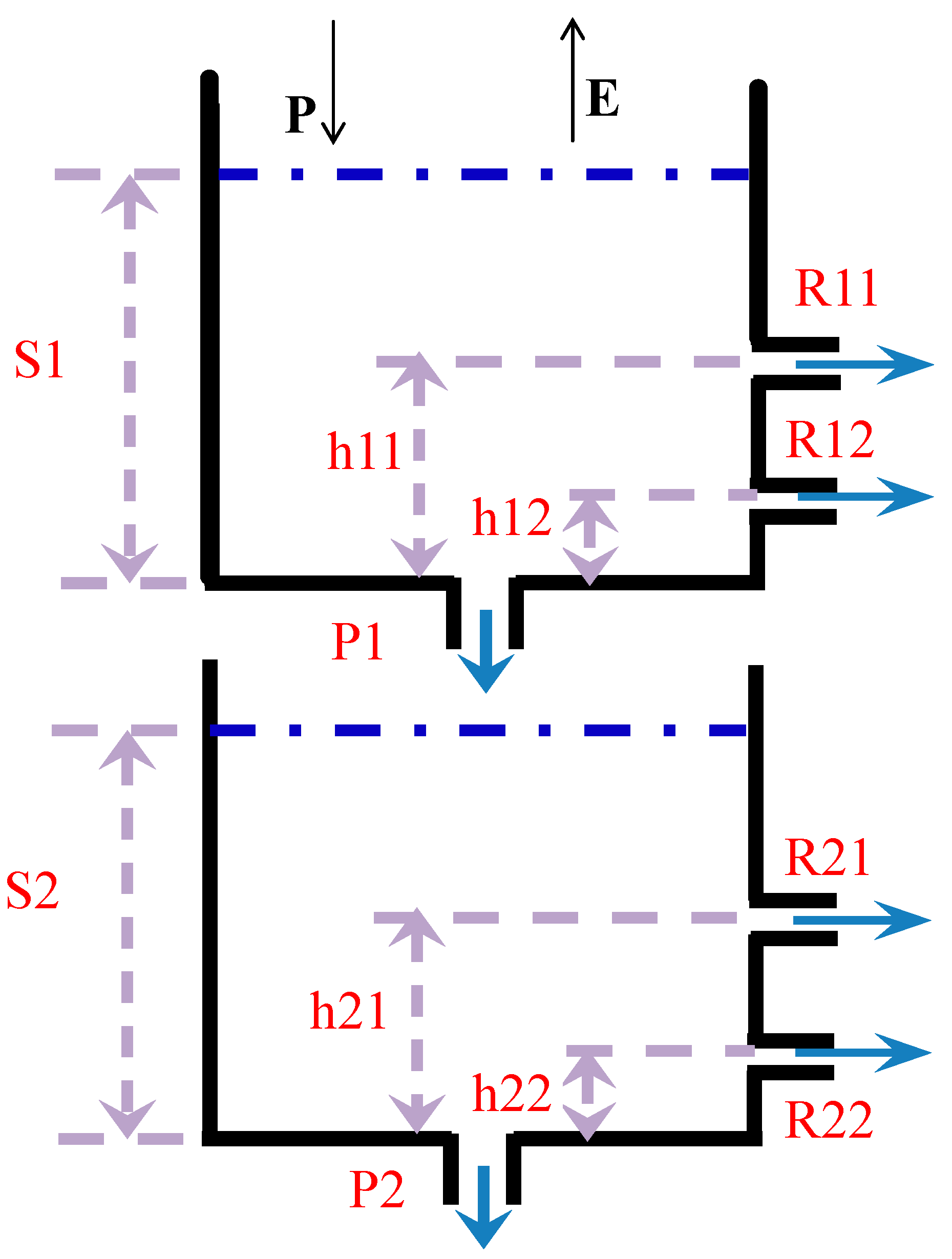
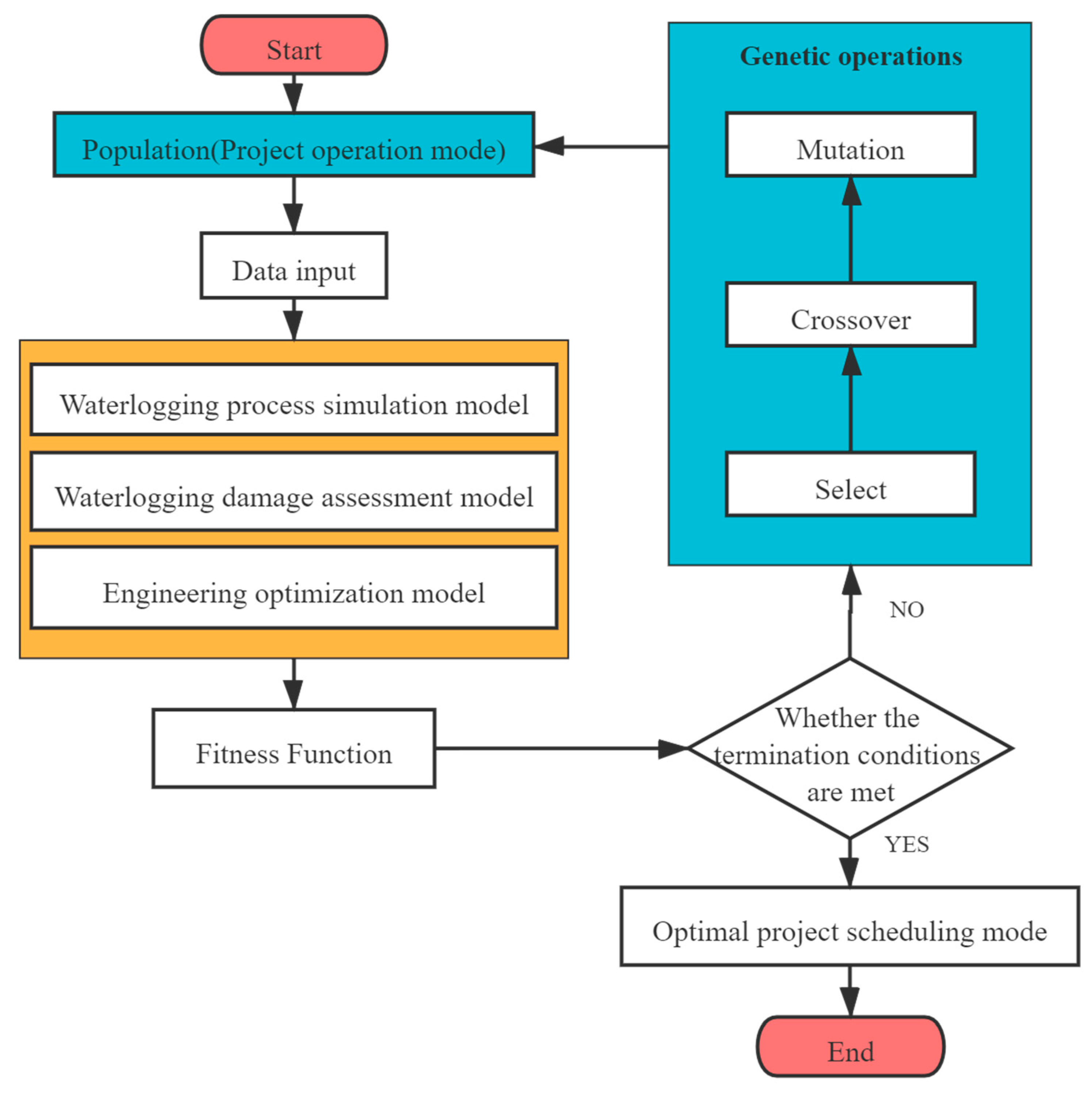
| Stage | Function |
|---|---|
| Tillering stage | |
| Booting stage | |
| Heading stage |
| Layer | Parameter/Unit | Optimal Value | Describe of Parameter | Outflow Formula |
|---|---|---|---|---|
| First | 0.047 | the height of upper hole—represents the water storage capacity of the rice field | , is calculated by the weir width of the broad-crested weir overflow formula. | |
| 0.0 | the height of lower hole—reflects the infiltration of the ridge of the paddy field | |||
| 0.000014 | weir width of broad-crested weir overflow formula | |||
| 0.008 | outflow coefficient of infiltration hole | |||
| Second | 0.41 | outflow coefficient of upper hole | ||
| 0.019 | outflow coefficient of lower hole | |||
| 0.50 | height of upper hole—equal to soil water storage depth corresponding to the soil saturation capacity | |||
| 0.40 | height of lower hole—equivalent to the soil water storage depth corresponding to field moisture capacity | |||
| 0.00076 | weir width of broad-crested weir overflow formula | |||
| 0.032 | outflow coefficient of infiltration hole |
| Factor | Time | ||||
|---|---|---|---|---|---|
| 1 h | 3 h | 6 h | 24 h | ||
| Parameter | EX 1 (mm) | 40.96 | 63.14 | 81.13 | 110.00 |
| Cv | 0.35 | 0.36 | 0.39 | 0.41 | |
| Cs/Cv | 2.66 | 2.33 | 2.77 | 2.93 | |
| Design rainfall | P1% (mm) | 83.25 | 127.44 | 172.06 | 250.46 |
| P2% (mm) | 76.96 | 119.31 | 162.65 | 228.41 | |
| P5% (mm) | 67.68 | 105.12 | 140.95 | 196.10 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Xiong, Y.; Xu, J.; Yang, S.; Jiang, Z.; Liu, F. Optimal Operation Model of Drainage Works for Minimizing Waterlogging Loss in Paddy Fields. Water 2021, 13, 2811. https://doi.org/10.3390/w13202811
Liu Z, Xiong Y, Xu J, Yang S, Jiang Z, Liu F. Optimal Operation Model of Drainage Works for Minimizing Waterlogging Loss in Paddy Fields. Water. 2021; 13(20):2811. https://doi.org/10.3390/w13202811
Chicago/Turabian StyleLiu, Zhenyang, Yujiang Xiong, Juzeng Xu, Shihong Yang, Zewei Jiang, and Fangping Liu. 2021. "Optimal Operation Model of Drainage Works for Minimizing Waterlogging Loss in Paddy Fields" Water 13, no. 20: 2811. https://doi.org/10.3390/w13202811
APA StyleLiu, Z., Xiong, Y., Xu, J., Yang, S., Jiang, Z., & Liu, F. (2021). Optimal Operation Model of Drainage Works for Minimizing Waterlogging Loss in Paddy Fields. Water, 13(20), 2811. https://doi.org/10.3390/w13202811









