Uncertain Analysis of Fuzzy Evaluation Model for Water Resources Carrying Capacity: A Case Study in Zanhuang County, North China Plain
Abstract
:1. Introduction
2. Materials and Methods
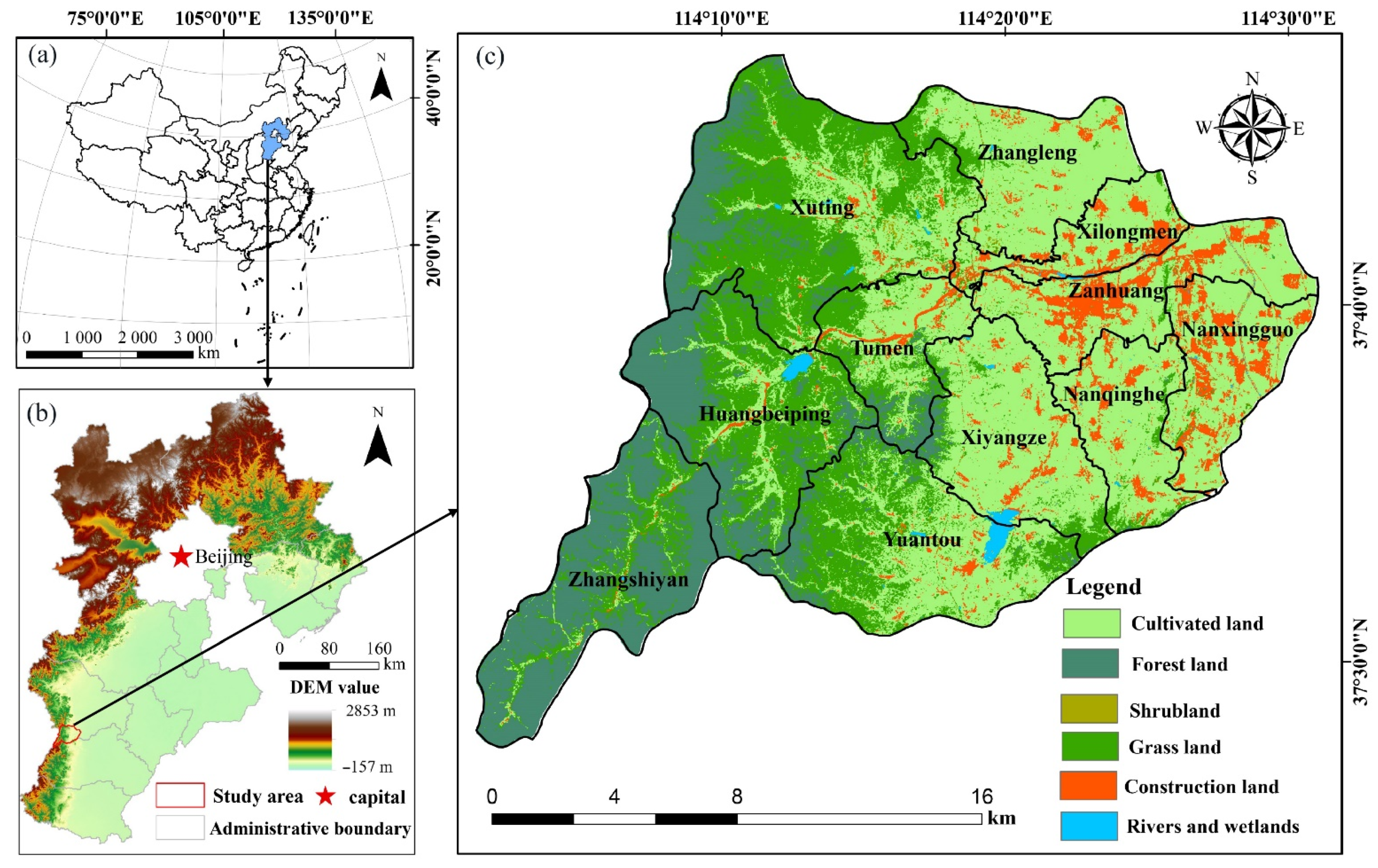
2.1. Study Area
2.2. Methods
2.2.1. Fuzzy Comprehensive Evaluation Model
2.2.2. Index Weight Calculation Methods
Analytic Hierarchy Process
- (1)
- Establish the hierarchical structure model;
- (2)
- Construct judgment matrix by comparing paired indexes;
- (3)
- Calculate the maximum eigenvalue and eigenvector of the judgment matrix, and carry out the consistency test;
- (4)
- Calculate the weight of each evaluation index.
Entropy Weight Method
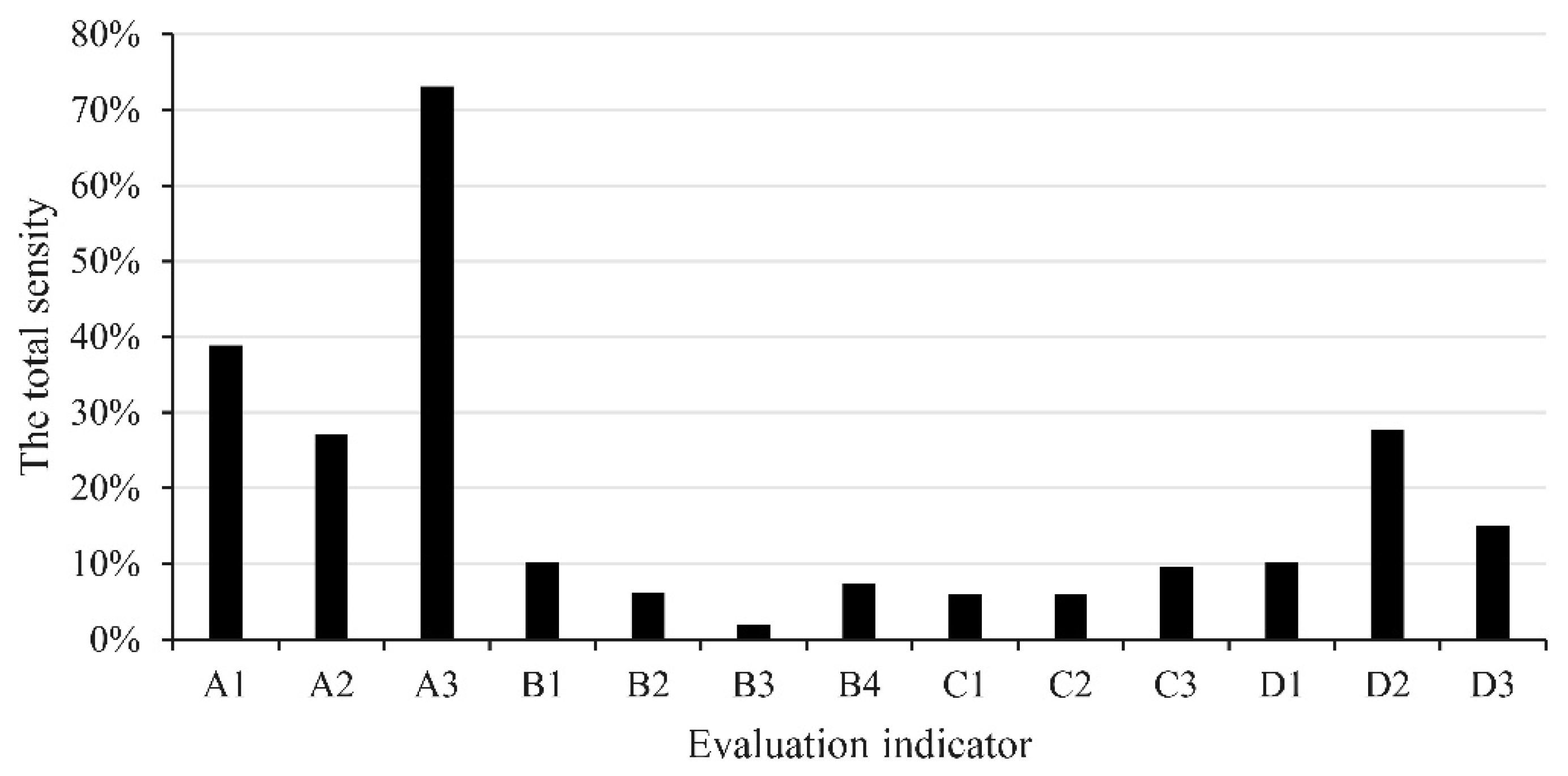
2.2.3. Calculation Method of Weight Sensitivity
3. Results and Discussion
3.1. Construction of the Evaluation Index System and Classification Standard
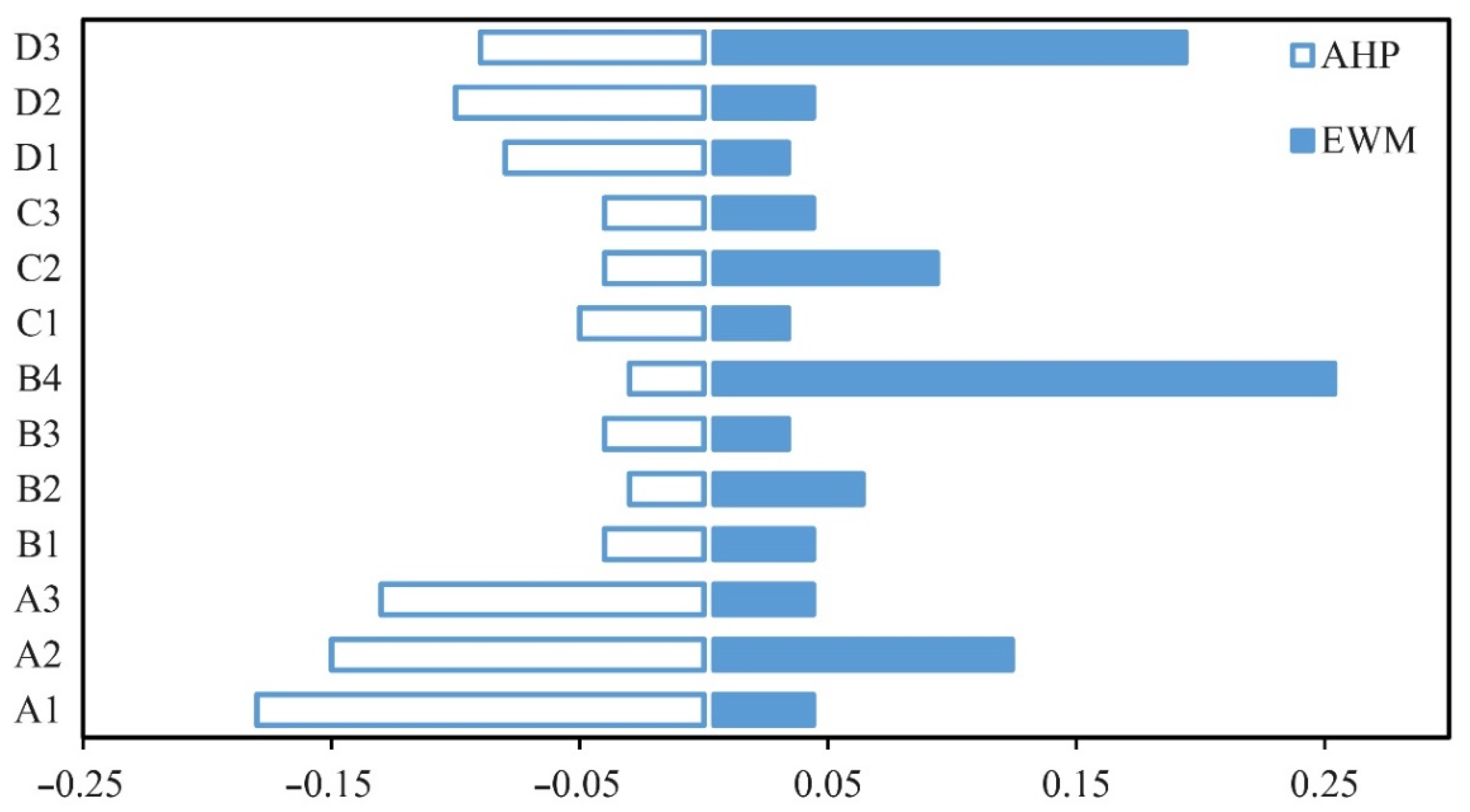
3.2. Comparison of Weight Results between the Analytic Hierarchy Process and the Entropy Weight Method
3.3. Comparative Study of Fuzzy Comprehensive Evaluation
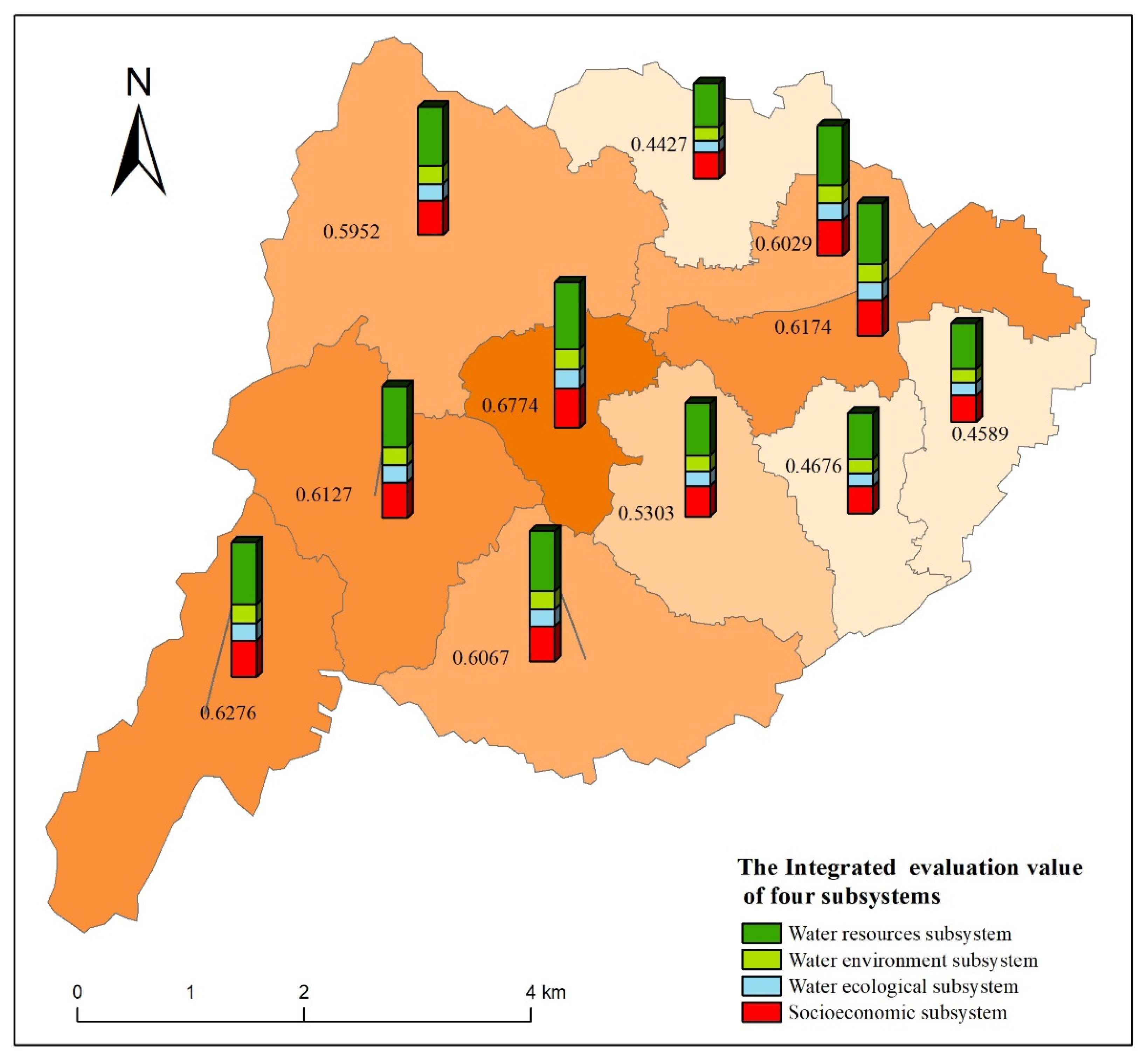
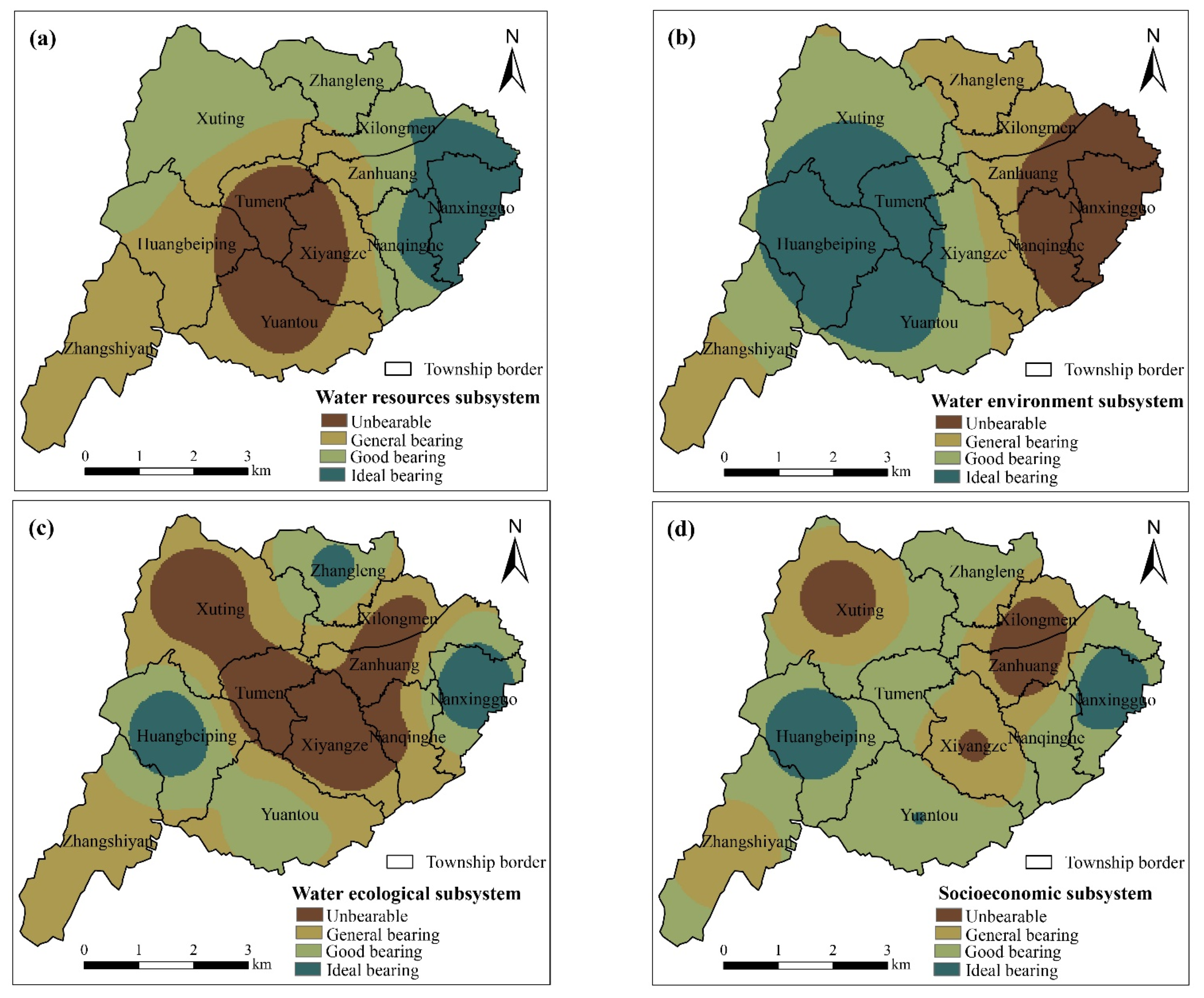
3.4. Analysis of Evaluation Results
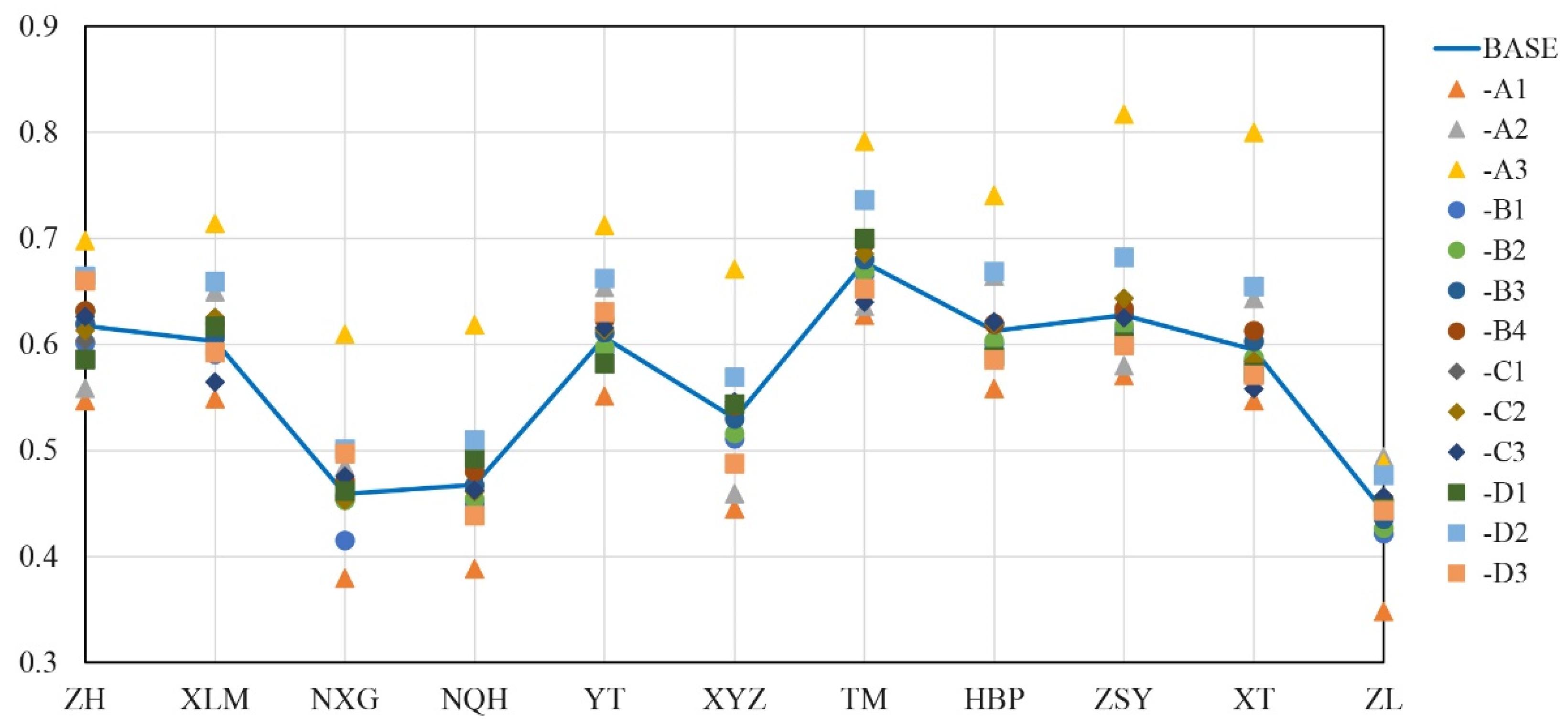
3.5. Sensitivity Analysis Results of Weight
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Song, J.; Cheng, D.; Xia, J.; Li, Q.; Ahamad, M.I. Comprehensive evaluation and scenario simulation for the water resources carrying capacity in Xi′an city, China. J. Environ. Manag. 2019, 230, 221–233. [Google Scholar] [CrossRef]
- Cai, Y.P.; Huang, G.H.; Tan, Q.; Liu, L. An integrated approach for climate-change impact analysis and adaptation planning under multi-level uncertainties. Part II. Case study. Renew. Sustain. Energy Rev. 2011, 15, 3051–3073. [Google Scholar] [CrossRef]
- Cai, Y.P.; Huang, G.H.; Wang, X.; Li, G.C.; Tan, Q. An inexact programming approach for supporting ecologically sustainable water supply with the consideration of uncertain water demand by ecosystems. Stoch. Environ. Res. Risk Assess. 2011, 25, 721–735. [Google Scholar] [CrossRef]
- Ren, C.; Guo, P.; Li, M.; Li, R. An innovative method for water resources carrying capacity research—Metabolic theory of regional water resources. J. Environ. Manag. 2016, 167, 139–146. [Google Scholar] [CrossRef]
- Peng, T.; Deng, H. Comprehensive evaluation on water resource carrying capacity based on DPESBR framework: A case study in Guiyang, southwest China. J. Clean. Prod. 2020, 268, 122235. [Google Scholar] [CrossRef]
- Chi, M.; Zhang, D.; Zhao, Q.; Yu, W.; Liang, S. Determining the scale of coal mining in an ecologically fragile mining area under the constraint of water resources carrying capacity. J. Environ. Manag. 2021, 279, 111621. [Google Scholar] [CrossRef]
- Yang, G.; Dong, Z.; Feng, S.; Li, B.; Sun, Y.; Chen, M. Early warning of water resource carrying status in Nanjing City based on coordinated development index. J. Clean. Prod. 2021, 284, 124696. [Google Scholar] [CrossRef]
- Wheida, E.; Verhoeven, R. An alternative solution of the water shortage problem in Libya. Water Resour. Manag. 2007, 21, 961–982. [Google Scholar] [CrossRef]
- Martin, R.; Savage, R.; Pyvis, R. Groundwater as a sustainable source of income and wealth creation. Environ. Earth Sci. 2013, 70, 1965–1969. [Google Scholar] [CrossRef]
- Ellis, T.; Hatton, T.; Nuberg, I. An ecological optimality approach for predicting deep drainage from tree belts of alley farms in water-limited environments. Agric. Water Manag. 2005, 75, 92–116. [Google Scholar] [CrossRef]
- Song, X.; Kong, F.; Zhan, C. Assessment of Water Resources Carrying Capacity in Tianjin City of China. Water Resour. Manag. 2011, 25, 857–873. [Google Scholar] [CrossRef]
- Peng, T.; Deng, H.; Lin, Y.; Jin, Z. Assessment on water resources carrying capacity in karst areas by using an innovative DPESBRM concept model and cloud model. Sci. Total Environ. 2021, 767, 144353. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Zhang, X.; Luo, G. Application of system dynamics in analyzing the carrying capacity of water resources in Yiwu City, China. Math. Comput. Simul. 2008, 79, 269–278. [Google Scholar] [CrossRef]
- Wang, G.; Xiao, C.; Qi, Z.; Meng, F.; Liang, X. Development tendency analysis for the water resource carrying capacity based on system dynamics model and the improved fuzzy comprehensive evaluation method in the Changchun city, China. Ecol. Indic. 2021, 122, 107232. [Google Scholar] [CrossRef]
- Gong, L.; Jin, C. Fuzzy Comprehensive Evaluation for Carrying Capacity of Regional Water Resources. Water Resour. Manag. 2009, 23, 2505–2513. [Google Scholar] [CrossRef]
- Li, N.; Kinzelbach, W.; Li, H.; Li, W.; Chen, F. Decomposition technique for contributions to groundwater heads from inside and outside of an arbitrary boundary: Application to Guantao County, North China Plain. Hydrol. Earth Syst. Sci. 2019, 23, 2823–2840. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Zhou, L.; Jin, J.; Ning, S.; Zhang, Z.; Bai, L. Regional water resource carrying capacity evaluation based on multi-dimensional precondition cloud and risk matrix coupling model. Sci. Total Environ. 2020, 710, 136324. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, P.; Chen, J.; Qian, H.; Qu, W.; Liu, R. Evaluation of groundwater quality using an integrated approach of set pair analysis and variable fuzzy improved model with binary semantic analysis: A case study in Jiaokou Irrigation District, east of Guanzhong Basin, China. Sci. Total Environ. 2021, 767, 145247. [Google Scholar] [CrossRef]
- Wu, L.; Su, X.; Ma, X.; Kang, Y.; Jiang, Y. Integrated modeling framework for evaluating and predicting the water resources carrying capacity in a continental river basin of Northwest China. J. Clean. Prod. 2018, 204, 366–379. [Google Scholar] [CrossRef]
- Yang, J.; Lei, K.; Khu, S.; Meng, W. Assessment of Water Resources Carrying Capacity for Sustainable Development Based on a System Dynamics Model: A Case Study of Tieling City, China. Water Resour. Manag. 2015, 29, 885–899. [Google Scholar] [CrossRef]
- Wang, C.; Hou, Y.; Xue, Y. Water resources carrying capacity of wetlands in Beijing: Analysis of policy optimization for urban wetland water resources management. J. Clean. Prod. 2017, 161, 1180–1191. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J.; Zhou, H.; Deng, C.; Fang, C. Analysis of sustainable utilization of water resources based on the improved water resources ecological footprint model: A case study of Hubei Province, China. J. Environ. Manag. 2020, 262, 110331. [Google Scholar] [CrossRef]
- Mou, S.; Yan, J.; Sha, J.; Deng, S.; Gao, Z.; Ke, W.; Li, S. A Comprehensive Evaluation Model of Regional Water Resource Carrying Capacity: Model Development and a Case Study in Baoding, China. Water 2020, 12, 2637. [Google Scholar] [CrossRef]
- Yu, F.; Fang, G.; Shen, R. Study on comprehensive early warning of drinking water sources for the Gucheng Lake in China. Environ. Earth Sci. 2014, 72, 3401–3408. [Google Scholar] [CrossRef]
- Deng, L.; Yin, J.; Tian, J.; Li, Q.; Guo, S. Comprehensive Evaluation of Water Resources Carrying Capacity in the Han River Basin. Water 2021, 13, 249. [Google Scholar] [CrossRef]
- Koop, S.H.A.; van Leeuwen, C.J. Assessment of the Sustainability of Water Resources Management: A Critical Review of the City Blueprint Approach. Water Resour. Manag. 2015, 29, 5649–5670. [Google Scholar] [CrossRef] [Green Version]
- Bjørn, A.; Hauschild, M.Z. Introducing carrying capacity-based normalisation in LCA: Framework and development of references at midpoint level. Int. J. Life Cycle Assess. 2015, 20, 1005–1018. [Google Scholar] [CrossRef] [Green Version]
- Matos, C.; Teixeira, C.A.; Duarte, A.A.L.S.; Bentes, I. Domestic water uses: Characterization of daily cycles in the north re-gion of Portugal. Sci. Total Environ. 2013, 458–460, 444–450. [Google Scholar] [CrossRef]
- Ahmed, M.; Sauck, W.; Sultan, M.; Yan, E.; Soliman, F.; Rashed, M. Geophysical Constraints on the Hydrogeologic and Structural Settings of the Gulf of Suez Rift-Related Basins: Case Study from the El Qaa Plain, Sinai, Egypt. Surv. Geophys. 2014, 35, 415–430. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Engel, B. Water environment carrying capacity in Bosten Lake basin. J. Clean. Prod. 2018, 199, 574–583. [Google Scholar] [CrossRef]
- Ren, B.; Zhang, Q.; Ren, J.; Ye, S.; Yan, F. A Novel Hybrid Approach for Water Resources Carrying Capacity Assessment by Integrating Fuzzy Comprehensive Evaluation and Analytical Hierarchy Process Methods with the Cloud Model. Water 2020, 12, 3241. [Google Scholar] [CrossRef]
- Han, L.; Song, Y.; Duan, L.; Yuan, P. Risk assessment methodology for Shenyang Chemical Industrial Park based on fuzzy comprehensive evaluation. Environ. Earth Sci. 2015, 73, 5185–5192. [Google Scholar] [CrossRef]
- El Baba, M.; Kayastha, P.; Huysmans, M.; De Smedt, F. Evaluation of the Groundwater Quality Using the Water Quality Index and Geostatistical Analysis in the Dier al-Balah Governorate, Gaza Strip, Palestine. Water 2020, 12, 262. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhang, C.; Shi, W.; Fu, Y. Quantitative evaluation and optimized utilization of water resources-water environment carrying capacity based on nature-based solutions. J. Hydrol. 2019, 568, 96–107. [Google Scholar] [CrossRef]
- Liao, H.; Yang, X.; Xu, F.; Xu, H.; Zhou, J. A fuzzy comprehensive method for the risk assessment of a landslide-dammed lake. Environ. Earth Sci. 2018, 77, 750. [Google Scholar] [CrossRef]
- Liao, X.; Ren, Y.; Shen, L.; Shu, T.; He, H.; Wang, J. A “carrier-load” perspective method for investigating regional water resource carrying capacity. J. Clean. Prod. 2020, 269, 122043. [Google Scholar] [CrossRef]
- Wu, J.; Li, J.; Teng, Y.; Chen, H.; Wang, Y. A partition computing-based positive matrix factorization (PC-PMF) approach for the source apportionment of agricultural soil heavy metal contents and associated health risks. J. Hazard. Mater. 2020, 388, 121766. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Wang, Y. Comprehensive evaluation and influencing factors of urban agglomeration water resources carrying capacity. J. Clean. Prod. 2021, 288, 125097. [Google Scholar] [CrossRef]
- Gao, F.; Wang, H.; Liu, C. Long-term assessment of groundwater resources carrying capacity using GRACE data and Budyko model. J. Hydrol. 2020, 588, 125042. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Su, X.; Qi, L.; Liu, M. Evaluation of the comprehensive carrying capacity of interprovincial water resources in China and the spatial effect. J. Hydrol. 2019, 575, 794–809. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Wang, J. Urban Water Conservation Evaluation Based on Multi-grade Uncertain Comprehensive Evaluation Method. Water Resour. Manag. 2018, 32, 417–431. [Google Scholar] [CrossRef]
- Shijiazhuang Water Bureau, 2017. Shijiazhuang Water Bureau, the Shijiazhuang Water Resources Bulletin; China Statistics Press: Beijing, China, 2017. [Google Scholar]
- Statistics Bureau of Zanhuang County, Hebei Province. Statistics Bureau of Zanhuang County, Hebei Province, Statistical Yearbook of Zanhuang; China Statistics Press: Beijing, China, 2017. [Google Scholar]
- Varis, O.; Vakkilainen, P. China’s 8 challenges to water resources management in the first quarter of the 21st Century. Ge-omorphology 2001, 41, 93–104. [Google Scholar] [CrossRef]
- Ren, L.; Gao, J.; Song, S.; Li, Z.; Ni, J. Evaluation of Water Resources Carrying Capacity in Guiyang City. Water 2021, 13, 2155. [Google Scholar] [CrossRef]
- Kiziltan, M. Water-energy nexus of Turkey’s municipalities: Evidence from spatial panel data analysis. Energy 2021, 226, 120347. [Google Scholar] [CrossRef]
- Chi, M.; Zhang, D.; Fan, G.; Zhang, W.; Liu, H. Prediction of water resource carrying capacity by the analytic hierarchy process-fuzzy discrimination method in a mining area. Ecol. Indic. 2019, 96, 647–655. [Google Scholar] [CrossRef]
- Teng, Y.; Zuo, R.; Xiong, Y.; Wu, J.; Zhai, Y.; Su, J. Risk assessment framework for nitrate contamination in groundwater for regional management. Sci. Total Environ. 2019, 697, 134102. [Google Scholar] [CrossRef] [PubMed]
- Dadmand, F.; Naji-Azimi, Z.; Motahari Farimani, N.; Davary, K. Sustainable allocation of water resources in water-scarcity conditions using robust fuzzy stochastic programming. J. Clean. Prod. 2020, 276, 123812. [Google Scholar] [CrossRef]
| Target Layer | Criterion Layer | Index Layer | Index Type | Code | Unit | Classification Standard | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V5 | ||||||
| Comprehensive water resources carrying capacity evaluation index system | Water Resources Subsystem (A) | Water resources development and utilization rate | Negative | A1 | % | <15 | 15–20 | 20–35 | 35–60 | >60 |
| Water consumption per unit of GDP | Negative | A2 | m3/104 yuan | <50 | 50–75 | 75–80 | 80–100 | >100 | ||
| Water area index | Positive | A3 | % | >5 | 4–5 | 3–4 | 2–3 | <2 | ||
| Water Environment Subsystem (B) | Water environmental quality index | Positive | B1 | % | >90 | 80–90 | 70–80 | 60–70 | <60 | |
| Industrial wastewater discharge index | Negative | B2 | % | <10 | 10–20 | 20–40 | 40–50 | >50 | ||
| Fertilizer intensity index | Negative | B3 | kg/hm2 | <100 | 100–150 | 150–200 | 200–250 | >250 | ||
| Urban sewage discharge index | Negative | B4 | % | <10 | 10–20 | 20–40 | 40–50 | >50 | ||
| Water Ecological Subsystem (C) | The vegetation coverage rate of coastal zone | Negative | C1 | % | <20 | 20–30 | 30–40 | 40–60 | >60 | |
| Ecological base flow guarantee rate | Positive | C2 | % | >60 | 40–60 | 30–40 | 20–30 | <20 | ||
| River network density index | Positive | C3 | 1/km | >0.8 | 0.6–0.8 | 0.4–0.6 | 0.2–0.4 | <0.2 | ||
| Socioeconomic Sub-system (D) | Population density | Negative | D1 | 1/km2 | <300 | 300–500 | 500–700 | 700–900 | >900 | |
| Per capital GDP | Positive | D2 | 104 yuan | >7.5 | 6–7.5 | 4.5–6 | 3–4.5 | <3 | ||
| Domestic water quota | Positive | D3 | liter/day | >130 | 110–130 | 90–110 | 70–90 | <70 | ||
| Indicator | Definition | Criterion |
|---|---|---|
| Water Resources Subsystem | ||
| Water resources development and utilization rate | Regional water consumption/regional water resources | The Shijiazhuang Water Resources Bulletin |
| Water consumption per unit of GDP | Regional water consumption/total regional GDP | The Shijiazhuang Water Resources Bulletin and Statistical Yearbook of Zanhuang |
| Water area index | Area of water area/ the total area | Statistical Yearbook of Zanhuang and Google Satellite Map |
| Water Environment Subsystem | ||
| Water environmental quality index | The rate of water quality discharge up to standard | Environmental monitoring Reports |
| Industrial wastewater discharge index | Regional industrial water discharge/total wastewater discharge | The Shijiazhuang Water Resources Bulletin and Environmental monitoring Reports |
| Fertilizer intensity index | Total amount of fertilizer applied (discounted)/cultivated area of evaluation area | Statistical Yearbook of Zanhuang |
| Urban sewage discharge index | Regional urban sewage discharge/total wastewater discharge | The Shijiazhuang Water Resources Bulletin and Environmental monitoring Reports |
| Water Ecological Subsystem | ||
| The vegetation coverage rate of coastal zone | Length of plant cover/length of shoreline | Statistical Yearbook of Zanhuang and Google Satellite Map |
| Ecological base flow guarantee rate | Average monthly actual flow/minimum ecological flow | Rain station monitoring reports |
| River network density index | River length/watershed area | Statistical Yearbook of Zanhuang and Google Satellite Map |
| Socioeconomic Subsystem | ||
| Population density | Regional population/regional administrative area | Statistical Yearbook of Zanhuang |
| Per capital GDP | Regional GDP/regional population | Statistical Yearbook of Zanhuang |
| Domestic water quota | Domestic water consumption/ (regional population· days) | The Shijiazhuang Water Resources Bulletin and Statistical Yearbook of Zanhuang |
| Sites | V1 | V2 | V3 | V4 | V5 | Comprehensive Evaluation Value θ | Theta Ranked from High to Low |
|---|---|---|---|---|---|---|---|
| Zanhuang | 0.2500 | 0.0026 | 0.0879 | 0.1395 | 0.5000 | 0.6174 | 3 |
| Xilongmen | 0.1700 | 0.1813 | 0.2056 | 0.2107 | 0.3124 | 0.6029 | 6 |
| Nanxingguo | 0.3900 | 0.1811 | 0.1833 | 0.0956 | 0.2300 | 0.4589 | 10 |
| Nanqinghe | 0.3277 | 0.1838 | 0.1015 | 0.0971 | 0.2900 | 0.4676 | 9 |
| Yuantou | 0.1300 | 0.2708 | 0.2182 | 0.1519 | 0.3300 | 0.6067 | 5 |
| Xiyangze | 0.3550 | 0.1186 | 0.0364 | 0.0000 | 0.4900 | 0.5303 | 8 |
| Tumen | 0.1800 | 0.0950 | 0.1528 | 0.1622 | 0.4900 | 0.6774 | 1 |
| Huangbeiping | 0.1000 | 0.1932 | 0.2202 | 0.0166 | 0.4700 | 0.6127 | 4 |
| Zhangshiyan | 0.2433 | 0.0636 | 0.0766 | 0.0470 | 0.5700 | 0.6276 | 2 |
| Xuting | 0.2600 | 0.1641 | 0.1559 | 0.0400 | 0.4600 | 0.5952 | 7 |
| Zhangleng | 0.3750 | 0.1232 | 0.1654 | 0.0865 | 0.2500 | 0.4427 | 11 |
| Scheme 1. | V1 | V2 | V3 | V4 | V5 | Comprehensive Evaluation Value θ | Theta Ranked from High to Low |
|---|---|---|---|---|---|---|---|
| Zanhuang | 0.5434 | 0.0021 | 0.0733 | 0.1049 | 0.2582 | 0.3974 | 9 |
| Xilongmen | 0.5594 | 0.1436 | 0.1492 | 0.1476 | 0.0729 | 0.3426 | 10 |
| Nanxingguo | 0.3701 | 0.1275 | 0.0973 | 0.1821 | 0.2229 | 0.4520 | 7 |
| Nanqinghe | 0.2906 | 0.3073 | 0.2385 | 0.0682 | 0.1653 | 0.4370 | 8 |
| Yuantou | 0.4672 | 0.0549 | 0.0271 | 0.0000 | 0.4507 | 0.4824 | 6 |
| Xiyangze | 0.3245 | 0.0717 | 0.1416 | 0.0839 | 0.4507 | 0.5891 | 2 |
| Tumen | 0.0370 | 0.2726 | 0.2963 | 0.0055 | 0.3885 | 0.5872 | 3 |
| Huangbeiping | 0.1093 | 0.1729 | 0.2006 | 0.0409 | 0.4771 | 0.6211 | 1 |
| Zhangshiyan | 0.3339 | 0.1360 | 0.1247 | 0.0362 | 0.4415 | 0.5593 | 4 |
| Xuting | 0.5464 | 0.1255 | 0.1535 | 0.0358 | 0.1389 | 0.3190 | 11 |
| Zhangleng | 0.3775 | 0.1435 | 0.1193 | 0.2333 | 0.1989 | 0.4827 | 5 |
| Weighting Methods | Evaluation Level | Mean Value | Standard Deviation | V1 | V2 | V3 | V4 | V5 | θ |
| AHP | V1 | 0.2528 | 0.1003 | 1 | |||||
| V2 | 0.1434 | 0.0729 | −0.251 | 1 | |||||
| V3 | 0.1458 | 0.0620 | −0.512 | −0.679 * | 1 | ||||
| V4 | 0.0952 | 0.0661 | −0.303 | 0.073 | 0.391 | 1 | |||
| V5 | 0.3993 | 0.1182 | −0.368 | −0.575 | −0.488 | −0.361 | 1 | ||
| θ | 0.5672 | 0.0791 | −0.815 ** | 0.679 * | 0.871 ** | 0.235 | 0.737 ** | 1 | |
| EWM | V1 | 0.3599 | 0.1715 | 1 | |||||
| V2 | 0.1416 | 0.0883 | −0.638 * | 1 | |||||
| V3 | 0.1474 | 0.0756 | −0.717 * | 0.871 ** | 1 | ||||
| V4 | 0.0853 | 0.0750 | 0.316 | −0.148 | −0.266 | 1 | |||
| V5 | 0.2969 | 0.1477 | −0.561 | −0.159 | −0.031 | −0.560 | 1 | ||
| θ | 0.4791 | 0.1019 | −0.833 ** | 0.192 | 0.299 | −0.299 | 0.869 ** | 1 |
| Evaluation Results | 0–0.25 | 0.25–0.50 | 0.50–0.75 | 0.75–1.00 |
|---|---|---|---|---|
| Bearing level | Unbearable | General bearing | Good bearing | Ideal bearing |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Y.; Wu, J.; Zhang, D.; Jia, R.; Yang, H. Uncertain Analysis of Fuzzy Evaluation Model for Water Resources Carrying Capacity: A Case Study in Zanhuang County, North China Plain. Water 2021, 13, 2804. https://doi.org/10.3390/w13202804
Ge Y, Wu J, Zhang D, Jia R, Yang H. Uncertain Analysis of Fuzzy Evaluation Model for Water Resources Carrying Capacity: A Case Study in Zanhuang County, North China Plain. Water. 2021; 13(20):2804. https://doi.org/10.3390/w13202804
Chicago/Turabian StyleGe, Yinxin, Jin Wu, Dasheng Zhang, Ruitao Jia, and Haotian Yang. 2021. "Uncertain Analysis of Fuzzy Evaluation Model for Water Resources Carrying Capacity: A Case Study in Zanhuang County, North China Plain" Water 13, no. 20: 2804. https://doi.org/10.3390/w13202804
APA StyleGe, Y., Wu, J., Zhang, D., Jia, R., & Yang, H. (2021). Uncertain Analysis of Fuzzy Evaluation Model for Water Resources Carrying Capacity: A Case Study in Zanhuang County, North China Plain. Water, 13(20), 2804. https://doi.org/10.3390/w13202804







