SWMM-UrbanEVA: A Model for the Evapotranspiration of Urban Vegetation
Abstract
1. Introduction
2. Materials and Methods
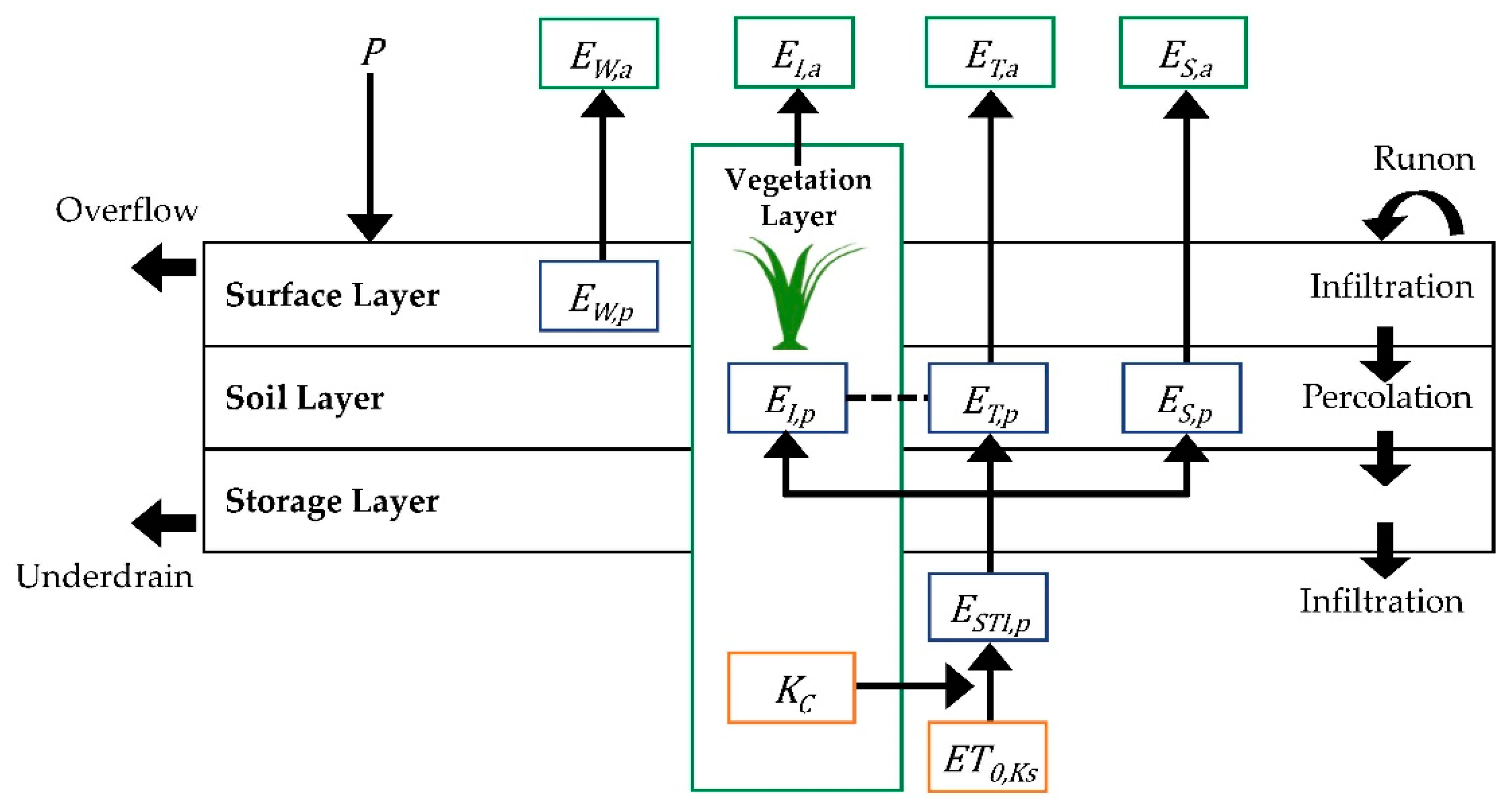
2.1. Model Description
2.1.1. Model Development
2.1.2. Submodule 1: Shading
2.1.3. Submodule 2: Evapotranspiration
2.1.4. Software Implementation
2.2. Study Area and Data
2.3. Model Sensitivity Analysis, Calibration, and Validation
2.3.1. Set Up and Goodness-of-Fit Criteria
2.3.2. Submodule 1: Shading
2.3.3. Submodule 2: Evapotranspiration
2.3.4. Blue Green Infrastructure
3. Results
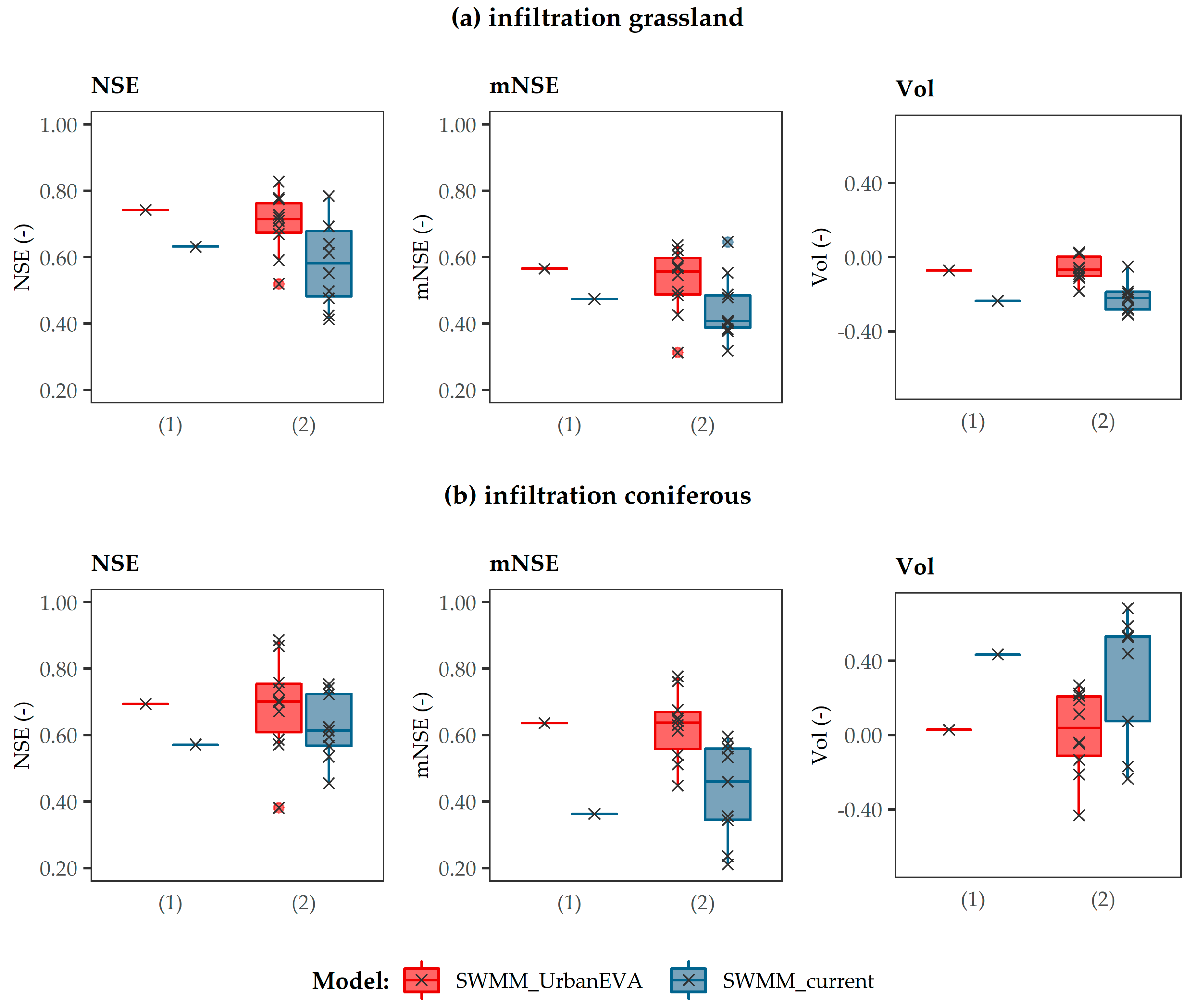
3.1. Submodule 1: Shading
3.2. Submodule 2: Evapotranspiration
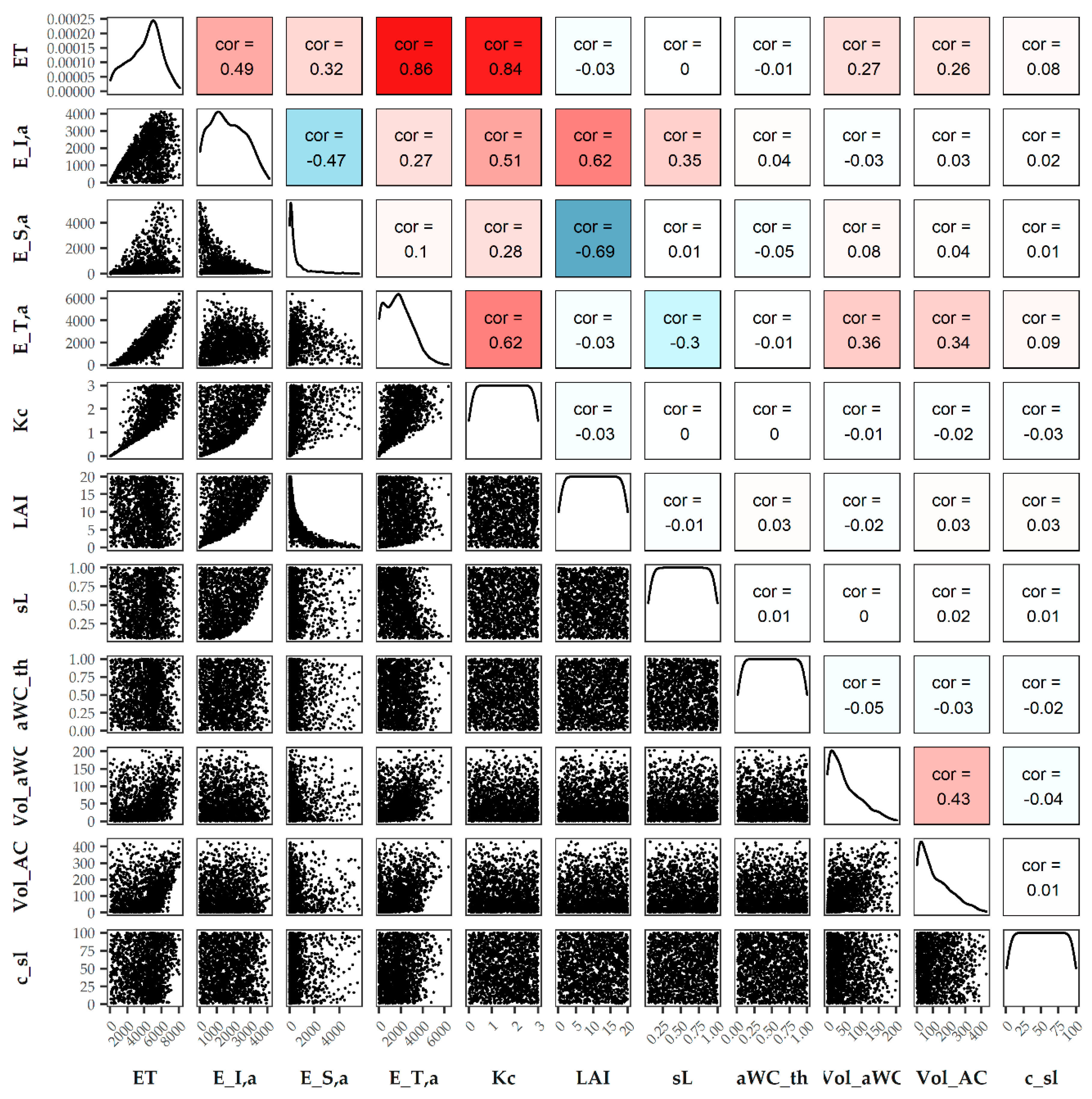
3.2.1. Sensitivity Analysis
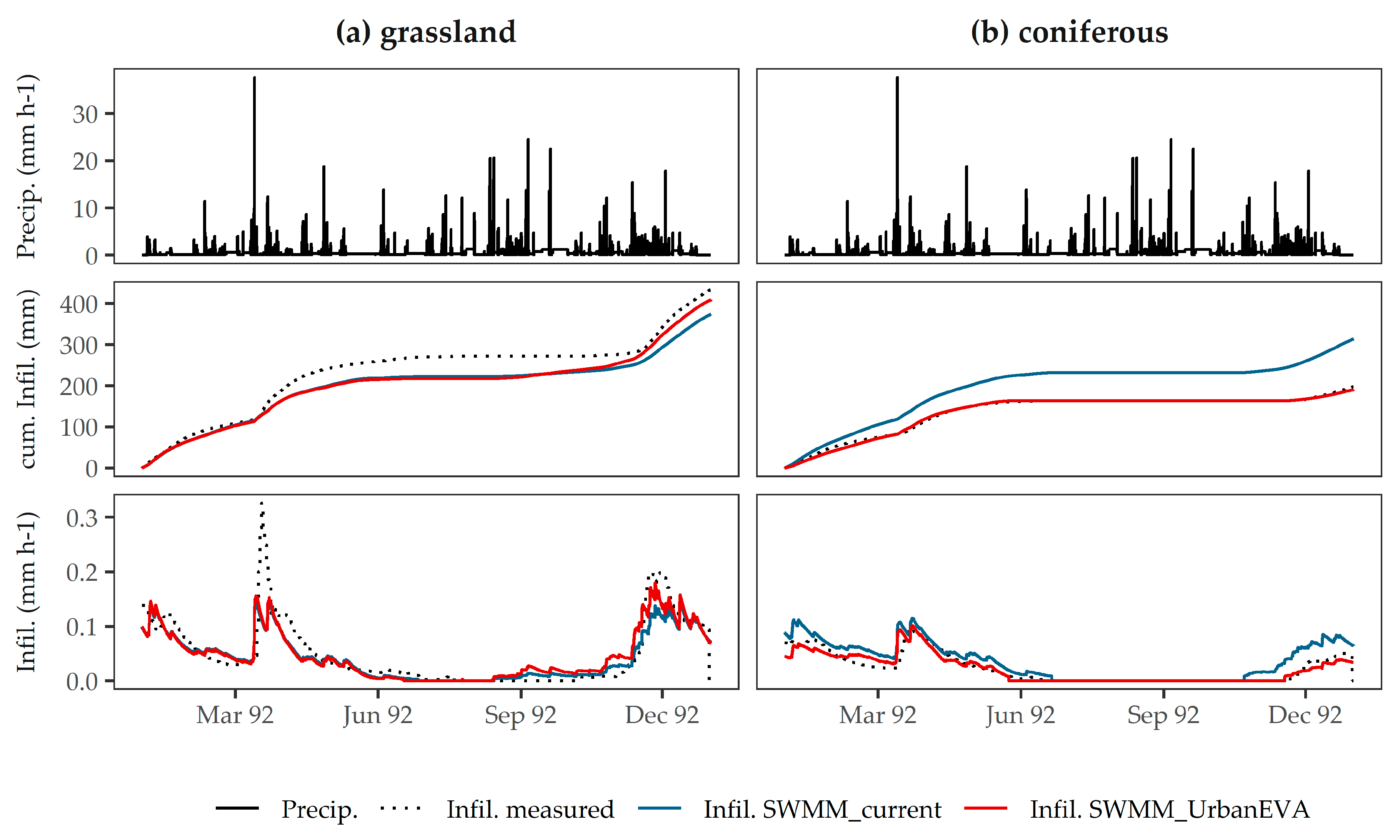
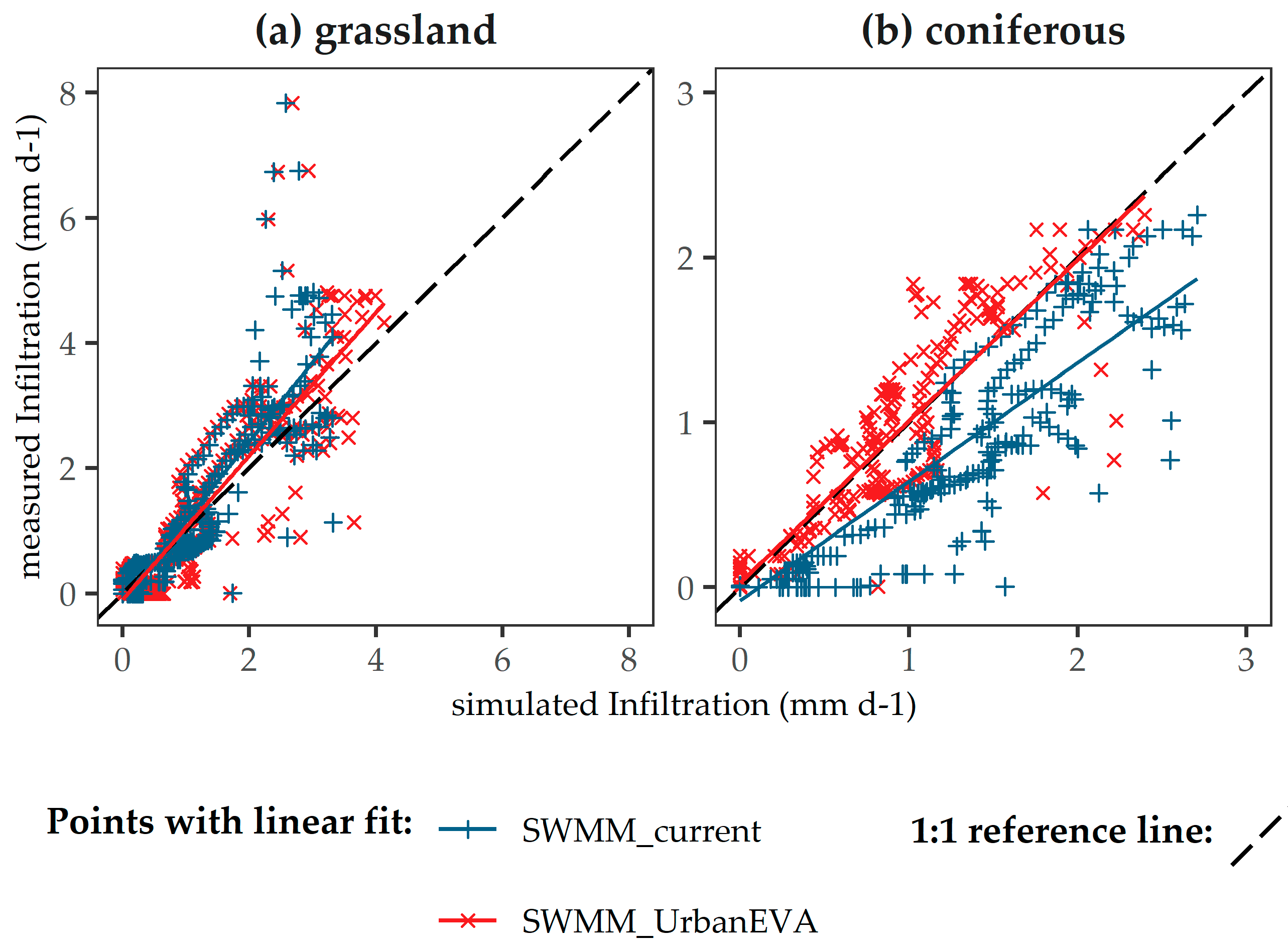
3.2.2. Model Calibration and Validation
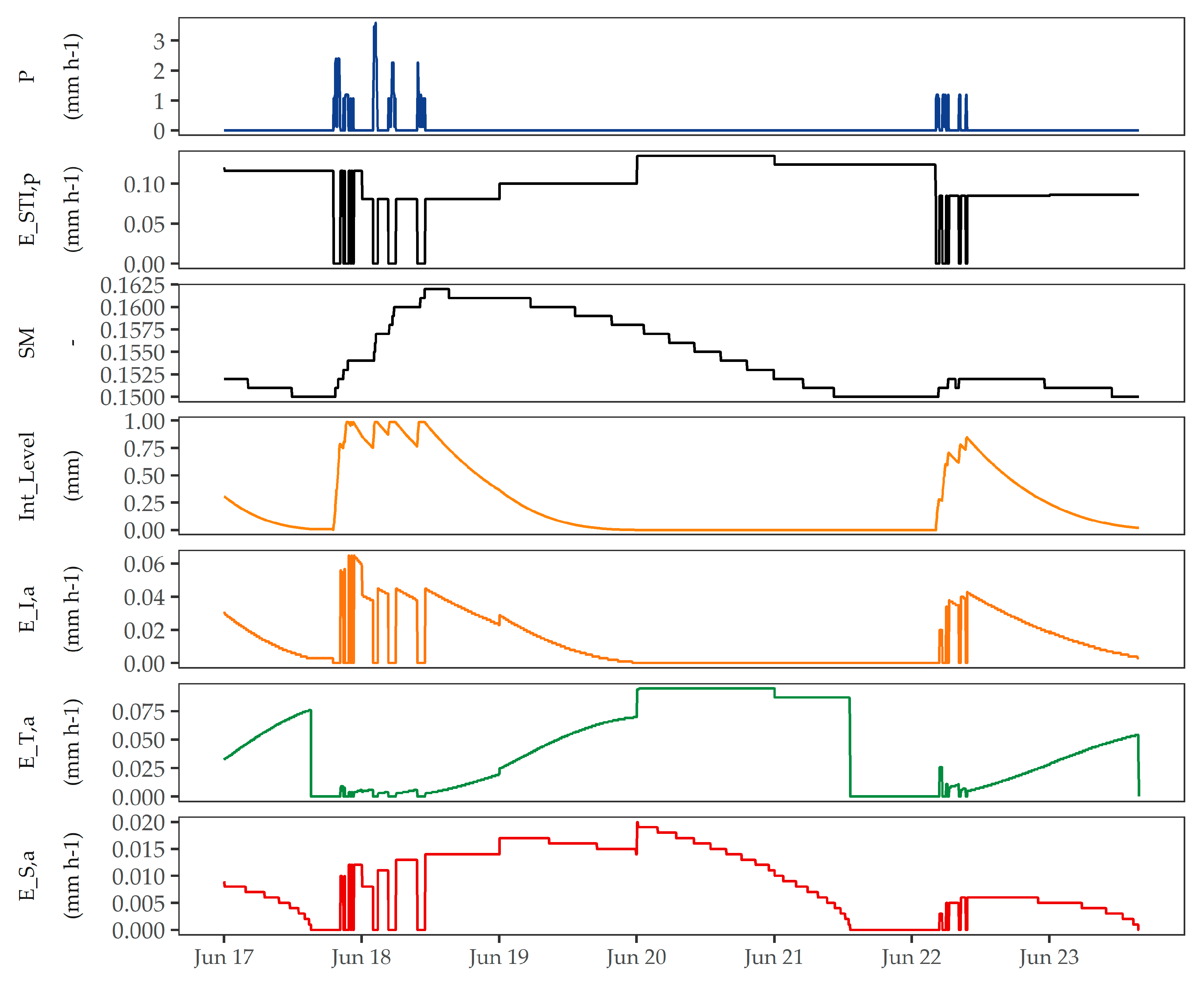
3.2.3. Analysis of the Modeled Process Dynamics
3.3. Blue Green Infrastructure
4. Discussion
- SWMM-UrbanEVA models ET with good performance. By introducing process-oriented ET-modeling, long-term water balances can be improved significantly in contrast to current SWMM. Being fully integrated into SWMM, the model enables good applicability for urban planning purposes.
- SM1 allows the integration of local variability of shading effects on both, pervious and impervious catchments which has not been possible before within urban rainfall runoff models. It only addresses one aspect of urban energy balance. The submodule’s performance depends on the quality of -values.
- SM2 is well applicable for vegetation in general. When modeling BGI and urban heat infected vegetation, SWMM-UrbanEVA still implies distinct improvements, but shows needs for further research.
- For model parameterization the shading factor and the crop factor must be considered as most influential variables. Further sensitive model inputs are the soil characteristics. The controls ET flux interactions.
- A proper model calibration is essential for good model performance. The calibration’s set up should be chosen carefully according to later model use (e.g., period, goodness-of-fit, timestep).
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, Management and Modelling of Urban Hydrology and Its Consequences for Receiving Waters: A State of the Art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Landsberg, H.E. The Urban Climate; International Geophysics Series; Academic Press: Maryland, MD, USA, 1981; Volume 28, ISBN 0-08-092419-0. [Google Scholar]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, MA, USA, 2017; ISBN 0-521-84950-0. [Google Scholar]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.-L.; et al. SUDS, LID, BMPs, WSUD and More—The Evolution and Application of Terminology Surrounding Urban Drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Palla, A.; Gnecco, I.; La Barbera, P. Assessing the Hydrologic Performance of a Green Roof Retrofitting Scenario for a Small Urban Catchment. Water 2018, 10, 1052. [Google Scholar] [CrossRef]
- Vijayaraghavan, K.; Joshi, U.M.; Balasubramanian, R. A Field Study to Evaluate Runoff Quality from Green Roofs. Water Res. 2012, 46, 1337–1345. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, D.Q.; Su, J.; Dong, J.W.; Tan, S.K. Assessing Hydrological Effects and Performance of Low Impact Development Practices Based on Future Scenarios Modeling. J. Clean. Prod. 2018, 179, 12–23. [Google Scholar] [CrossRef]
- Rahman, M.A.; Hartmann, C.; Moser-Reischl, A.; Freifrau von Strachwitz, M.; Peath, H.; Pretzsch, H.; Pauleit, S.; Rötzer, T. Tree Cooling Effects and Human Thermal Comfort under Contrasting Species and Sites. Agric. For. Meteorol. 2020, 287. [Google Scholar] [CrossRef]
- Zinzi, M.; Agnoli, S. Cool and Green Roofs. An Energy and Comfort Comparison between Passive Cooling and Mitigation Urban Heat Island Techniques for Residential Buildings in the Mediterranean Region. Energy Build. 2012, 55, 66–76. [Google Scholar] [CrossRef]
- Zölch, T.; Maderspacher, J.; Wamsler, C.; Pauleit, S. Using Green Infrastructure for Urban Climate-Proofing: An Evaluation of Heat Mitigation Measures at the Micro-Scale. Urban For. Urban Green. 2016, 20, 305–316. [Google Scholar] [CrossRef]
- Langergraber, G.; Pucher, B.; Simperler, L.; Kisser, J.; Katsou, E.; Buehler, D.; Mateo, M.C.G.; Atanasova, N. Implementing Nature-Based Solutions for Creating a Resourceful Circular City. Blue Green Syst. 2020, 173–185. [Google Scholar] [CrossRef]
- Panno, A.; Carrus, G.; Lafortezza, R.; Mariani, L.; Sanesi, G. Nature-Based Solutions to Promote Human Resilience and Wellbeing in Cities during Increasingly Hot Summers. Environ. Res. 2017, 159, 249–256. [Google Scholar] [CrossRef]
- Raymond, C.M.; Frantzeskaki, N.; Kabisch, N.; Berry, P.; Breil, M.; Nita, M.R.; Geneletti, D.; Calfapietra, C. A Framework for Assessing and Implementing the Co-Benefits of Nature-Based Solutions in Urban Areas. Environ. Sci. Policy 2017, 77, 15–24. [Google Scholar] [CrossRef]
- Palla, A.; Gnecco, I.; La Barbera, P. The Impact of Domestic Rainwater Harvesting Systems in Storm Water Runoff Mitigation at the Urban Block Scale. J. Environ. Manag. 2017, 191, 297–305. [Google Scholar] [CrossRef]
- Sims, A.W.; Robinson, C.E.; Smart, C.C.; Voogt, J.A.; Hay, G.J.; Lundholm, J.T.; Powers, B.; O’Carroll, D.M. Retention Performance of Green Roofs in Three Different Climate Regions. J. Hydrol. 2016, 542, 115–124. [Google Scholar] [CrossRef]
- Mitchell, V.G.; Cleugh, H.A.; Grimmond, C.S.B.; Xu, J. Linking Urban Water Balance and Energy Balance Models to Analyse Urban Design Options. Hydrol. Process. 2008, 22, 2891–2900. [Google Scholar] [CrossRef]
- Feng, Y.; Burian, S.J.; Pardyjak, E.R. Observation and Estimation of Evapotranspiration from an Irrigated Green Roof in a Rain-Scarce Environment. Water 2018, 10, 262. [Google Scholar] [CrossRef]
- Feng, Y.; Burian, S. Improving Evapotranspiration Mechanisms in the U.S. Environmental Protection Agency’s Storm Water Management Model. J. Hydrol. Eng. 2016, 21, 06016007. [Google Scholar] [CrossRef]
- Johannessen, B.G.; Hamouz, V.; Gragne, A.S.; Muthanna, T.M. The Transferability of SWMM Model Parameters between Green Roofs with Similar Build-Up. J. Hydrol. 2019, 569, 816–828. [Google Scholar] [CrossRef]
- Krebs, G.; Kuoppamäki, K.; Kokkonen, T.; Koivusalo, H. Simulation of Green Roof Test Bed Runoff: Simulation of Green Roof Test Bed Runoff. Hydrol. Process. 2016, 30, 250–262. [Google Scholar] [CrossRef]
- Poë, S.; Stovin, V.; Berretta, C. Parameters Influencing the Regeneration of a Green Roof’s Retention Capacity via Evapotranspiration. J. Hydrol. 2015, 523, 356–367. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R.; Steyn, D.G. Urban Water Balance: 1. A Model for Daily Totals. Water Resour. Res. 1986, 22, 1397–1403. [Google Scholar] [CrossRef]
- Henrichs, M.; Langner, J.; Uhl, M. Development of a Simplified Urban Water Balance Model (WABILA). Water Sci. Technol. 2016, 73, 1785–1795. [Google Scholar] [CrossRef]
- Kroes, J.G.; van Dam, J.C.; Groenendijk, P.; Hendriks, R.F.A.; Jacobs, C.M.J. SWAP Version 3.2—Theory Description and User Manual; Alterra Wageningen, Ed.; Alterra Report; Alterra Wageningen: Wageningen, The Netherlands, 2008. [Google Scholar]
- Schulla, J. Model Description WaSiM (Water Balance Simulation Model); Hydrology Software Consulting: Zürich, Switzerland, 2017. [Google Scholar]
- Rossman, L. Storm Water Management Model User’s Manual Version 5.1; EPA U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2015.
- Cipolla, S.S.; Maglionico, M.; Stojkov, I. A Long-Term Hydrological Modelling of an Extensive Green Roof by Means of SWMM. Ecol. Eng. 2016, 95, 876–887. [Google Scholar] [CrossRef]
- Peng, Z.; Stovin, V. Independent Validation of the SWMM Green Roof Module. J. Hydrol. Eng. 2017, 22, 04017037. [Google Scholar] [CrossRef]
- Stovin, V.; Poe, S.; Berretta, C. A Modelling Study of Long Term Green Roof Retention Performance. J. Environ. Manag. 2013, 131, 206–215. [Google Scholar] [CrossRef]
- Weiler, M.; Schütz, T.; Schaffitel, A.; Koelbing, M.; Steibrich, A.; Brendt, T. Der Naturnahe Wasserhaushalt Als Leitbild in Der Siedlungswasserbewirtschaftung; Freiburg Hydro Notes; Professur für Hydrologie, Fakultät für Umwelt und Natürliche Ressourcen, Universität Freiburg: Freiburg, Germany, 2019. [Google Scholar]
- Hörnschemeyer, B. Modellierung Der Verdunstung Urbaner Vegetation—Weiterentwicklung Des LID-Bausteins Im US EPA Storm Water Management Model, 1st ed.; Forschungsreihe der FH Münster; Springer Spektrum: Münster, Germany, 2019; ISBN 978-3-658-26283-9. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper; FAO: Rome, Italy, 1998; Volume 56. [Google Scholar]
- Koelbing, M.; Schuetz, T.; Weiler, M. Spatial Impacts of Urban Structures on Micrometeorological Variables. In EGU General Assembly; Geophysical Research Abstracts: Vienna, Austria, 2016; Volume 18, p. 14996. [Google Scholar]
- Rossman, L.; Huber, W.C. Storm Water Management Model Reference Manual Volume III—Water Quality; EPA U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2016.
- Watson, D.J. Comparative Physiological Studies on the Growth of Field Crops: I. Variation in Net Assimilation Rate and Leaf Area between Species and Varieties, and within and between Years. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Breuer, L.; Eckhardt, K.; Frede, H.-G. Plant Parameter Values for Models in Temperate Climates. Ecol. Model. 2003, 169, 237–293. [Google Scholar] [CrossRef]
- Kattge, J.; Bönisch, G.; Díaz, S.; Lavorel, S.; Prentice, I.C.; Leadley, P.; Tautenhahn, S.; Werner, G.D.; Aakala, T.; Abedi, M. TRY Plant Trait Database–Enhanced Coverage and Open Access. Glob. Chang. Biol. 2019, 2019, 1–70. [Google Scholar] [CrossRef] [PubMed]
- Löpmeier, F.-J. Agrarmeteorologisches Modell zur Berechnung der aktuellen Verdunstung (AMBAV), 1983; Volume 39.
- Ludwig, K.; Bremicker, M. The Water Balance Model LARSIM—Design, Content and Applications; Freiburger Schriften zur Hydrologie: Freiburg, Germany, 2006; Volume 22, ISBN 0945-1609. [Google Scholar]
- Bremicker, M. Aufbau eines Wasserhaushaltsmodells für das Weser-und das Ostsee-Einzugsgebiet als Baustein eines Atmosphären-Hydrologie-Modells. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, 1998. [Google Scholar]
- Bremicker, M. Das Wasserhaushaltsmodell LARSIMModellgrundlagen Und Anwendungsbeispiele; Freiburger Schriften für Hydrologie: Freiburg, Germany, 2000; Volume 11, ISBN 0945-1609. [Google Scholar]
- Grant, D.R. Comparison of Evaporation from Barley with Penman Estimates. Agric. Meteorol. 1975, 15, 49–60. [Google Scholar] [CrossRef]
- Dunin, F.X.; O’Loughlin, E.M.; Reyenga, W. Interception Loss from Eucalypt Forest: Lysimeter Determination of Hourly Rates for Long Term Evaluation. Hydrol. Process. 1988, 2, 315–329. [Google Scholar] [CrossRef]
- Hatton, T.; Walker, J.; Dawes, W.; Dunin, F. Simulations of Hydroecological Responses to Elevated CO2 at the Catchment Scale. Aust. J. Bot. 1992, 40, 679–696. [Google Scholar] [CrossRef]
- Running, S.W.; Coughlan, J.C. A General Model of Forest Ecosystem Processes for Regional Applications I. Hydrologic Balance, Canopy Gas Exchange and Primary Production Processes. Ecol. Model. 1988, 42, 125–154. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media—Version 4.17; Department of Environmental Sciences, Ed.; University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Vertessy, R.A.; Hatton, T.J.; Benyon, R.G.; Dawes, W.R. Long Term Growth and Water Balance for a Mountain Ash (Eucalyptus Regnans) Forest Catchment Subject to Clear Felling and Regeneration. Tree Physiol. 1996, 16, 221–232. [Google Scholar] [CrossRef]
- Wang, J.; Endreny, T.A.; Nowak, D.J. Mechanistic Simulation of Tree Effects in an Urban Water Balance Model. JAWRA J. Am. Water Resour. Assoc. 2008, 44, 75–85. [Google Scholar] [CrossRef]
- Braden, H. Ein Energiehaushalts-Und Verdunstungsmodell Für Wasser Und Stoffhaushaltsuntersuchungen Landwirtschaftlich Genutzer Einzugsgebiete. Mitt. Dtsch. Bodenkd. Ges. 1985, 42, 294–299. [Google Scholar]
- Monteith, J.L. Evaporation and Environment. Symposia Soc. Exper. Biol. 1965, 19, 205–234. [Google Scholar]
- Allen, R.G.; Elliott, R.L.; Howell, T.A.; Itenfisu, D.; Jensen, M.E.; Snyder, R.L. The ASCE Standardized Reference Evapotranspiration Equation; ASCE-EWRI Task Committee Report; Task Committee on Standardization of Reference Evapotranspiration: Idaho, ID, USA, 2005; ISBN 978-0-7844-0805-6. [Google Scholar]
- Beven, K. A Sensitivity Analysis of the Penman-Monteith Actual Evapotranspiration Estimates. J. Hydrol. 1979, 44, 169–190. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. A Measurement Based Sensitivity Analysis of the Penman-Monteith Actual Evapotranspiration Model for Crops of Different Height and in Contrasting Water Status. Theor. Appl. Climatol. 1998, 60, 141–149. [Google Scholar] [CrossRef]
- Körner, C.; Scheel, J.A.; Bauer, H. Maximum Leaf Diffusive Conductance in Vascular Plants (Review). Photosynthetica 1979, 13, 45–82. [Google Scholar]
- Jarvis, P.G.; James, G.B.; Landsberg, J.J. Coniferous forest. In Vegetation and the Atmosphere, Volume 2 Case Studies; Monteith, J.L., Ed.; Academic Press: London, UK, 1976; pp. 171–240. ISBN 978-0-12-505102-6. [Google Scholar]
- Jones, H.G. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology, 3rd ed.; Cambridge University Press: Cambridge, CA, USA, 2014; ISBN 978-0-521-27959-8. [Google Scholar]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: New York, NY, USA, 1987; ISBN 978-0-415-04319-9. [Google Scholar]
- Guerra, E.; Ventura, F.; Snyder, R.L. Crop Coefficients: A Literature Review. J. Irrig. Drain. Eng. 2016, 142, 06015006. [Google Scholar] [CrossRef]
- Deardorff, J.W. Efficient Prediction of Ground Surface Temperature and Moisture, with Inclusion of a Layer of Vegetation. J. Geophys. Res. 1978, 83, 1889–1903. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Henderson-Sellers, A.; Kennedy, P.J. Biosphere-Atmosphere Transfer Scheme (BATS) Version Le as Coupled to the NCAR Community Climate Model; NCAR Technical Note; National Centre for Atmospheric Research: Boulder, CO, USA, 1993. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Nijssen, B.; Strorck, P. The distributed hydrology soil vegetation model. In Mathematical Models of Small Watershed Hydrology and Applications; Water Resources Publications LLC.: Chelsea, MI, USA, 2002; pp. 7–42. [Google Scholar]
- Zhao, L.; Xia, J.; Xu, C.; Wang, Z.; Sobkowiak, L.; Long, C. Evapotranspiration Estimation Methods in Hydrological Models. J. Geogr. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]
- Disse, M. Modellierung der Verdunstung und der Grundwasserneubildung in ebenen Einzugsgebieten; Institut für Hydrologie und Wasserwirtschaft Karlsruhe: Karlsruhe, Germany, 1995. [Google Scholar]
- Minhas, B.S.; Parikh, K.S.; Srinivasan, T.N. Toward the Structure of a Production Function for Wheat Yields with Dated Inputs of Irrigation Water. Water Resour. Res. 1974, 10, 383–393. [Google Scholar] [CrossRef]
- WWU Münster Climate Station Department of Climatology. Available online: https://www.uni-muenster.de/Klima/wetter/wetter.php (accessed on 8 June 2020).
- Scherer, I.; Henrichs, M.; Uhl, M.; Schuetz, T.; Weiler, M.; Hackenbrock, K.; Florenz, K.; Freytag, T. Planungsinstrumente und Bewirtschaftungskonzepte für den Wasserhaushalt in Siedlungen. KW-Korresp. Wasserwirtsch. 2017, 221–228. [Google Scholar] [CrossRef]
- Harsch, N.; Brandenburg, M.; Klemm, O. Large-Scale Lysimeter Site St. Arnold, Germany: Analysis of 40 Years of Precipitation, Leachate and Evapotranspiration. Hydrol. Earth Syst. Sci. 2009, 13, 305–317. [Google Scholar] [CrossRef]
- Henrichs, M.; Steinbrich, A.; Leistert, H.; Scherer, I.; Schuetz, T.; Uhl, M.; Weiler, M. Model Based Estimation of a Natural Water Balance as Reference for Planning in Urban Areas. In New Trends in Urban Drainage Modelling; Mannina, G., Ed.; Springer International Publishing: Palermo, Italy, 2019; pp. 953–957. [Google Scholar]
- Henrichs, M.; Leutnant, D.; Schleifenbaum, R.; Uhl, M. KALIMOD—Programm-Dokumentation; Institut für Wasser Ressourcen Umwelt-Fachhochschule Münster: Münster, Germany, 2014. [Google Scholar]
- Henrichs, M. Einfluss von Unsicherheiten auf die Kalibrierung Urbanhydrologischer Modelle (“Influence of Uncertainties on the Calibration of Urban Hydrological Models”). Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2015. (In German). [Google Scholar]
- Ballinas-González, H.A.; Alcocer-Yamanaka, V.H.; Canto-Rios, J.J.; Simuta-Champo, R. Sensitivity Analysis of the Rainfall–Runoff Modeling Parameters in Data-Scarce Urban Catchment. Hydrology 2020, 7, 73. [Google Scholar] [CrossRef]
- Xu, Z.; Xiong, L.; Li, H.; Xu, J.; Cai, X.; Chen, K.; Wu, J. Runoff Simulation of Two Typical Urban Green Land Types with the Stormwater Management Model (SWMM): Sensitivity Analysis and Calibration of Runoff Parameters. Environ. Monit. Assess. 2019, 191, 343. [Google Scholar] [CrossRef]
- Kachholz, F.; Tränckner, J. Long-Term Modelling of an Agricultural and Urban River Catchment with SWMM Upgraded by the Evapotranspiration Model UrbanEVA. Water 2020, 12, 3089. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin Hypercube Sampling and the Propagation of Uncertainty in Analyses of Complex Systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity Analysis of Environmental Models: A Systematic Review with Practical Workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Cohen, I., Huang, Y., Chen, J., Benesty, J., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2009; pp. 1–4. ISBN 978-3-642-00296-0. [Google Scholar]
- Uhl, M.; Henrichs, M.; Leutnant, D.; Vosswinkel, N. Kalibrierverfahren Für Hydrologische Prozessmodelle; Münster, F.H., Ed.; Labor für Wasserbau und Wasserwirtschaft: Münster, Germany, 2008. [Google Scholar]
- Duan, Q. Global Optimization for Watershed Model Calibration. In Calibration of Watershed Models, Water Science and Application 6; Duan, Q., Gupta, H.V., Sorooshian, S., Rousseau, A.R., Turcotte, R., Eds.; American Geophysical Union: Washington, DC, USA, 2003; pp. 89–104. ISBN 0-87590-355-X. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the Use of “Goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Klein, M. Langjähriger Wasserhaushalt von Gras- Und Waldbeständen-Entwicklung, Kalibrierung Und Anwendung Des Modells LYFE Am Groß-Lysimeter St. Arnold. Ph.D. Thesis, Universität Osnabrück, Osnabrück, Germany, 2000. [Google Scholar]
- Peck, A.; Mayer, H. Einfluß von Bestandesparametern auf die Verdunstung von Wäldern. Forstwiss. Cent. 1996, 115, 1–9. [Google Scholar] [CrossRef]
- Schaap, M.G.; Bouten, W.; Verstraten, J.M. Forest Floor Water Content Dynamics in a Douglas fir Stand. J. Hydrol. 1997, 201, 367–383. [Google Scholar] [CrossRef]
- Tiktak, A.; Bouten, W. Soil Water Dynamics and Long-Term Water Balances of a Douglas fir Stand in the Netherlands. J. Hydrol. 1994, 156, 265–283. [Google Scholar] [CrossRef]
- Schneider, K.-J.; Albert, A. Bautabellen Für Ingenieure: Mit Berechnungshinweisen Und Beispielen, 24th ed.; Reguvis: Köln, Germany, 2020; ISBN 978-3-8462-1140-3. [Google Scholar]
- Blume, H.-P.; Stahr, K.; Leinweber, P. Bodenkundliches Praktikum: Eine Einführung in pedologisches Arbeiten für Ökologen, insbesondere Land- und Forstwirte, und für Geowissenschaftler, 3rd ed.; Spektrum, Akad. Verl: Heidelberg, Germany, 2011; ISBN 978-3-8274-1553-0. [Google Scholar]
- Burszta-Adamiak, E.; Mrowiec, M. Modelling of Green Roofs’ Hydrologic Performance Using EPA’s SWMM. Water Sci. Technol. 2013, 68, 36. [Google Scholar] [CrossRef]
- Dupont, S.; Mestayer, P.G. Parameterization of the Urban Energy Budget with the Submesoscale Soil Model. J. Appl. Meteorol. Climatol. 2006, 45, 1744–1765. [Google Scholar] [CrossRef]


| Parameter | Unit | St. Arnold | Geo | Leo | Lincoln |
|---|---|---|---|---|---|
| (1966–2008) | (2017–2018) | (2017–2018) | (2017–2018) | ||
| Precipitation | mm·a−1 | 793 | 596 | 691 | 647 |
| ET0 | mm·a−1 | 460 | 648 | 490 | 524 |
| Parameter | STEP 1: Shading (SM1) | STEP 2: ET Vegetation (SM2) | STEP 3 BGI (SM1 + SM2) | |
|---|---|---|---|---|
| Sensitivity | Calibration | |||
| Location | Münster (“Leo” and “Lincoln”) | St. Arnold | Münster (“Leo” and “FHZ”) | |
| Reference station | “Geo” | St. Arnold (no shading) | “Geo” | |
| Measurement | ET0,loc “Leo” and “Lincoln” | infiltration grassland/coniferous | exfiltration green roofs “Leo” and “FHZ” | |
| Timestep | 5 min | daily | 5 min | |
| Methods | - | LHS | SCEUA | SCEUA |
| Period | 2017 | 1989/1999 | 1989/1999, 1989, …, 1999 | 2017-01/2017-03; 2017-04/2017-06; 2017-02-21/2017-02-27; 2017-03-07/2017-03-17 |
| Varied input parameters | KS,spring, KS,summer, KS,winter, (see Table 4) | all LID + SWMM-UrbanEVA variables, (see Table 5) | KC, SoDepth, Por, WP, c_sl (see Table 7) | KC, Por, WP, c_sl, FCoef, FEx (see Table 7) |
| Evaluated result parameters | “Leo” and “Lincoln” | ET, EI,a, ET,a, ES,a | infiltration grass./ conif. | exfiltration green roofs “Leo” and “FHZ” |
| Goodness-of-fit | NSE, mNSE, Vol | |||
| Goodness-of-Fit Criterion | Formula | Equation No. |
|---|---|---|
| Nash-Sutcliffe model efficiency | (43) | |
| Modified Nash-Sutcliffe model efficiency | (44) | |
| Volume Error | (45) |
| Parameter | Unit | Leo | Lincoln | |||||
|---|---|---|---|---|---|---|---|---|
| Spring | Summer | Winter | Spring | Summer | Winter | |||
| (i) | - | −0.15 | −0.12 | −0.25 | −0.13 | −0.07 | −0.12 | |
| (ii) | - | 0.75 | 0.78 | 0.66 | 0.78 | 0.84 | 0.79 | |
| Parameter | Unit | Min | Max | Reference | ||
|---|---|---|---|---|---|---|
| vegetation | crop factor | Kc | - | 1 | 3 | [32] |
| leaf area index | LAI | - | 1 | 16 | [36] | |
| leaf storage coefficient | SL | - | 0 | 1 | - | |
| aWCthreshold | aWC-th | - | 0 | 1 | - | |
| surface | surface storage | SuStor | mm | 1 | 10 | site specific |
| surface roughness | SuManN | s·m−1/3 | 0.001 | 0.8 | [87] | |
| surface slope | SuSlope | % | 0 | 6 | site specific | |
| soil | soil depth | SoDepth | mm | 1 | 2000 | site specific |
| porosity | Por | - | 0.22 | 0.65 | [88] | |
| field capacity | FC | - | 0.21 | 0.21 | [88] | |
| wilting point | WP | - | 0 | 0.20 | [88] | |
| conductivity | cond | mm·h−1 | 0.25 | 360 | [87] | |
| conductivity slope | c_sl | - | 1 | 100 | [34] | |
| suction head | SucH | mm | 49 | 320 | [34] | |
| storage | storage height | StHeight | mm | 1 | 5000 | site specific |
| void ratio | VoidR | - | 0 | 1 | [88] | |
| seepage rate | SR | mm·h−1 | 0.25 | 360 | [87] | |
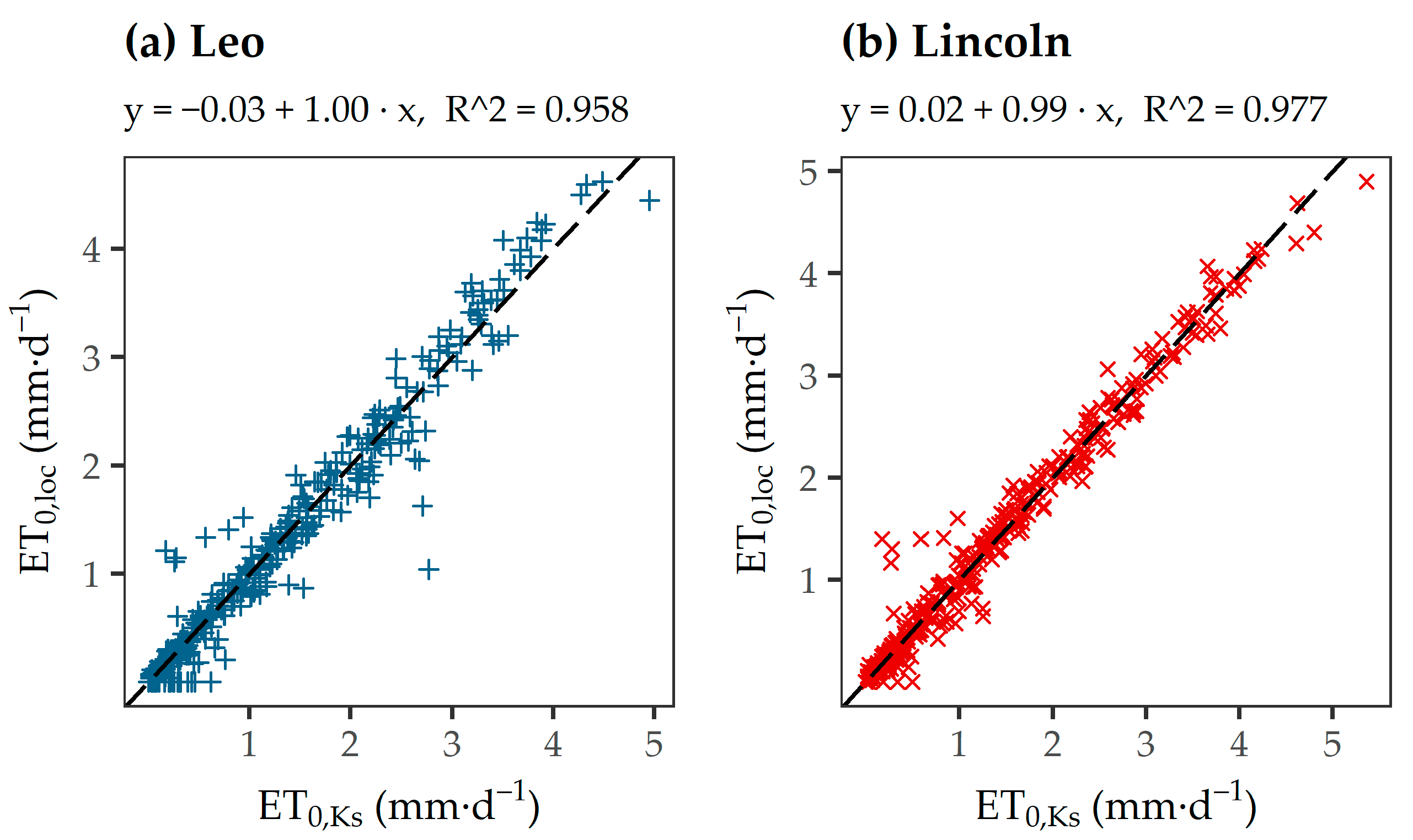
| Month in 2017 | Leo | Lincoln | ||||||
|---|---|---|---|---|---|---|---|---|
| ET0,loc | ET0,Ks | Diff. | ET0,loc | ET0,Ks | Diff. | |||
| (mm) | (mm) | (mm) | (%) | (mm) | (mm) | (mm) | (%) | |
| January | 2.9 | 7.4 | 4.5 | 153.2 | 5.5 | 8.4 | 3.0 | 54.4 |
| February | 13.0 | 13.1 | 0.1 | 0.6 | 12.5 | 14.2 | 1.7 | 13.5 |
| March | 37.8 | 32.9 | −4.9 | −13.0 | 38.7 | 34.2 | −4.5 | −11.6 |
| April | 49.4 | 47.3 | −2.2 | −4.4 | 52.3 | 49.5 | −2.7 | −5.3 |
| May | 77.5 | 75.4 | −2.1 | −2.7 | 81.2 | 80.3 | −0.9 | −1.1 |
| June | 82.3 | 82.6 | 0.3 | 0.3 | 88.8 | 89.1 | 0.4 | 0.4 |
| July | 80.0 | 77.3 | −2.8 | −3.4 | 84.3 | 82.7 | −1.6 | −1.9 |
| August | 58.7 | 61.9 | 3.3 | 5.6 | 64.7 | 65.2 | 0.5 | 0.8 |
| September | 34.2 | 35.6 | 1.4 | 4.1 | 37.9 | 37.0 | −0.8 | −2.2 |
| October | 17.2 | 21.8 | 4.6 | 26.5 | 20.7 | 23.4 | 2.7 | 13.1 |
| November | 6.3 | 7.2 | 0.9 | 14.5 | 7.1 | 8.1 | 1.0 | 14.5 |
| December | 4.7 | 4.3 | −0.5 | −9.5 | 5.8 | 5.1 | −0.7 | −12.1 |
| ∑ | 464 | 467 | 3 | 1 | 499 | 497 | −2 | −0.4 |
| Parameter | Unit | Full Scale Lysimeter St. Arnold | Green Roofs | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SWMM-UrbanEVA | SWMM-Current | |||||||||
| Grass | Conif. | Grass | Conif. | Leo | FHZ | |||||
| General | area | Area | M2 | 400 | 400 | 400 | 400 | 3 | 80 | |
| width | Width | m | 20 | 20 | 20 | 20 | 1 | 9 | ||
| initial saturation | InitSat | - | 0 | 0 | 0 | 0 | 0 | 0 | ||
| slope | Slope | % | 2 | 2 | 2 | 2 | 3 | 3 | ||
| SM1 | shading factor spring | KS,spring | - | 1 | 1 | - | - | 0.75 | 1 | |
| shading fact. summer | KS,summer | - | 1 | 1 | - | - | 0.78 | 1 | ||
| shading factor winter | KS,winter | - | 1 | 1 | - | - | 0.66 | 1 | ||
| SM2 | vegetation | crop factor | Kc | - | 1.04 | 1.56 | - | - | 1.80 | 1.14 |
| leaf area index | LAI | - | 2 | 11 | - | - | 3 | 3 | ||
| leaf storage coefficient | SL | % | 0.29 | 0.29 | - | - | 0.29 | 0.29 | ||
| aWCthreshold | aWC-th | % | 0.6 | 0.6 | - | - | 0.6 | 60 | ||
| gf scheme | gf | - | Table S1, no. 7 | |||||||
| surface | surface storage | SuStor | mm | 2 | 2 | 2 | 2 | 20 | 20 | |
| surface roughness | SuManN | s·m−1/3 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | ||
| surface slope | SuSlope | % | 1 | 1 | 1 | 1 | 3 | 3 | ||
| soil | soil depth | SoDepth | mm | 1596 | 1639 | 1616 | 2331 | 150 | 60 | |
| porosity | Por | - | 0.48 | 0.57 | 0.46 | 0.50 | 0.29 | 0.40 | ||
| volume air capacity | VolAC | mm | 431 | 590 | 404 | 676 | 14 | 10 | ||
| field capacity | FC | - | 0.21 | 0.21 | 0.21 | 0.21 | 0.20 | 0.23 | ||
| wilting point | WP | - | 0.18 | 0.10 | 0.19 | 0.11 | 0.10 | 0.07 | ||
| volume avail. water cap. | VolaWC | mm | 35 | 180 | 32 | 233 | 15 | 10 | ||
| conductivity | cond | mm·h−1 | 250 | 250 | 250 | 250 | 61 | 27 | ||
| conductivity slope | c_sl | - | 40.6 | 28.4 | 36.5 | 34.8 | 63.8 | 37.6 | ||
| suction head | SucH | mm | 58 | 58 | 58 | 58 | 58 | 58 | ||
| storage | storage height | StHeight | mm | 3000 | 3000 | 3000 | 3000 | 25 | 30 | |
| void ratio | VoidR | - | 0.27 | 0.27 | 0.27 | 0.27 | 0.75 | 0.30 | ||
| seepage rate | SR | mm·h−1 | 250 | 250 | 250 | 250 | 0 | 0 | ||
| drain | flow coefficient | FCoef | 1·h−1 | - | - | - | - | 53 | 43 | |
| flow exponent | FEx | - | - | - | - | - | 0.9 | 0.2 | ||
| offset | Off | mm | - | - | - | - | 0 | 0 | ||
| Parameter | Unit | Grassland | Coniferous | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | SD | VarC | Mean | SD | VarC | |||
| crop factor | Kc | - | 1.05 | 0.17 | 16% | 1.57 | 0.19 | 15% |
| soil depth | SoDepth | mm | 1463 | 146 | 10% | 1555 | 268 | 17% |
| porosity | Por | - | 0.50 | 0.02 | 4% | 0.55 | 0.04 | 8% |
| volume air capacity | VolAC | mm | 431 | 40 | 9% | 545 | 113 | 21% |
| wilting point | WP | - | 0.18 | 0.02 | 9% | 0.10 | 0.02 | 21% |
| volume available water capacity | VolaWC | mm | 29 | 20 | 67% | 167 | 39.5 | 24% |
| Parameter | Unit | SWMM-UrbanEVA | SWMM-Current | ||
|---|---|---|---|---|---|
| Grassland | Coniferous | Grassland | Coniferous | ||
| NSE | - | 0.74 | 0.87 | 0.73 | 0.47 |
| mNSE | - | 0.59 | 0.75 | 0.63 | 0.41 |
| Vol | - | −0.06 | −0.14 | −0.04 | 0.59 |
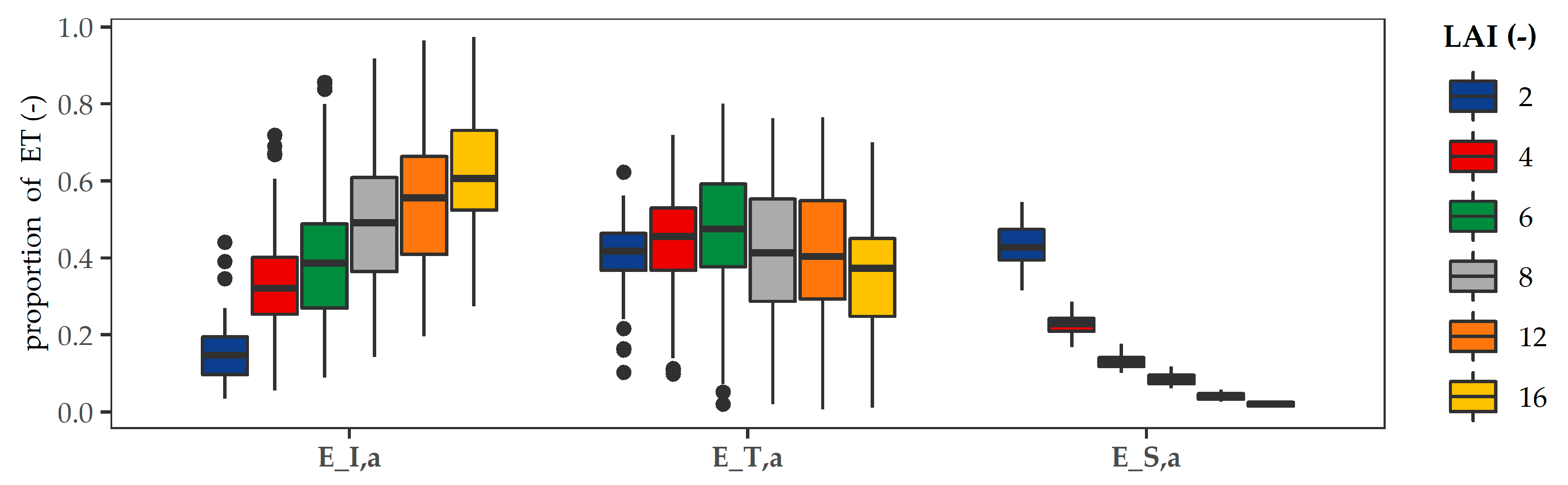
| Species | LAI | Literature | SWMM-UrbanEVA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EI,a/ET | ET,a/ET | ES,a/ET | EI,a/ET | ET,a/ET | ES,a/ET | ||||||||
| Frac. | Frac. | Frac. | Frac. | Abs. Dev. | Rel. Dev | Frac. | Abs. Dev. | Rel. Dev | Frac. | Abs. Dev. | Rel. Dev | ||
| (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | ||
| grassland | 2 | 0.25 1 | 0.50 1 | 0.25 1 | 0.15 | −0.10 | −0.60 | 0.42 | −0.08 | −0.19 | 0.43 | 0.18 | 0.72 |
| pine | 8 | 0.45 2. | 0.47 2 | 0.08 2 | 0.49 | 0.04 | 0.09 | 0.42 | −0.05 | −0.07 | 0.09 | 0.01 | 0.13 |
| spruce | 12 | 0.50 3 | 0.44 3 | 0.06 3 | 0.56 | 0.06 | 0.12 | 0.40 | −0.04 | −0.10 | 0.04 | −0.02 | -0.33 |
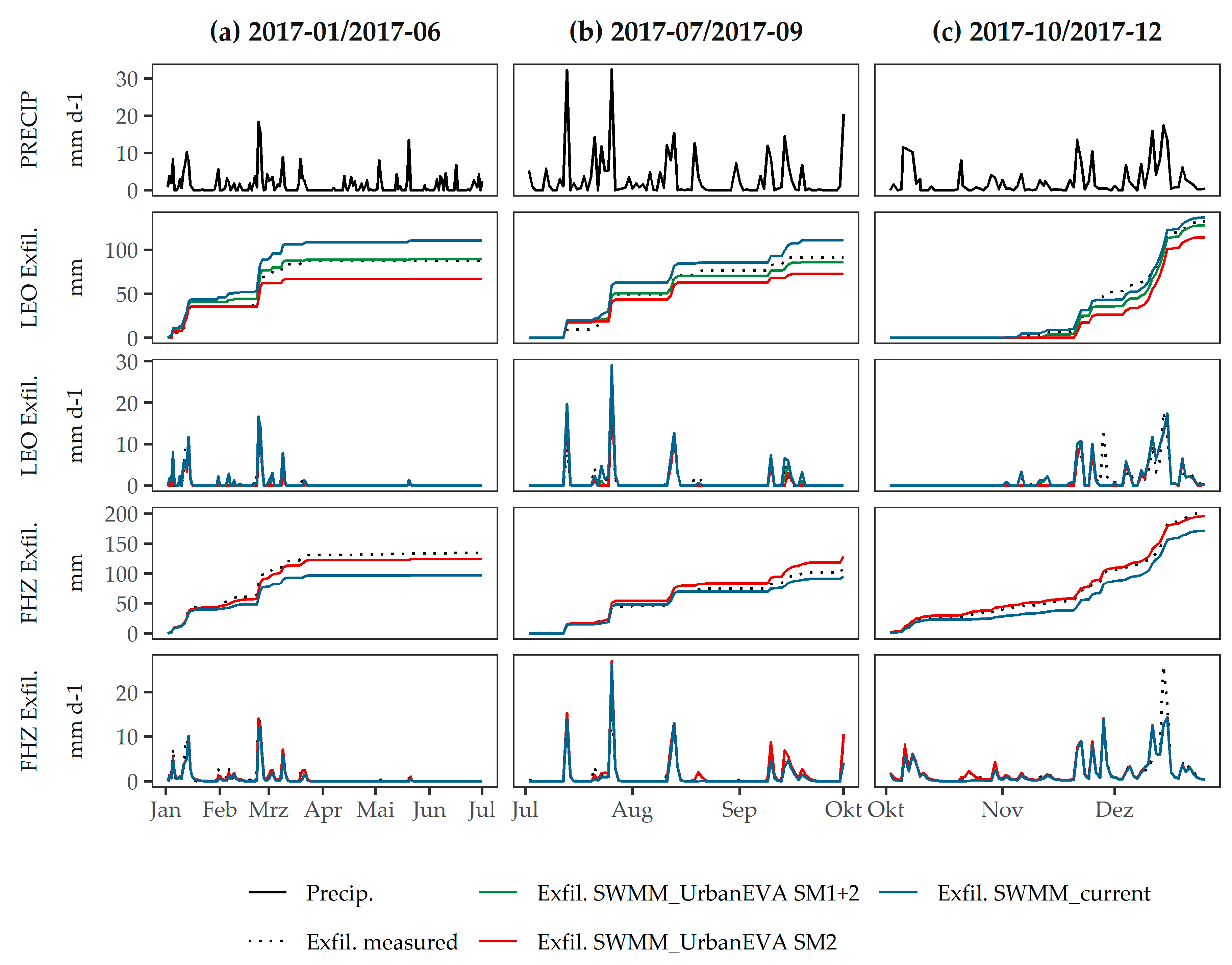
| Model | (a) Calibration (2017-01 and 2017-06) | (b) Validation 1 (2017-07 and 2017-09) | (c) Validation 2 (2017-10 and 2017-12) | 2017 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NSE | mNSE | Vol | NSE | mNSE | Vol | NSE | mNSE | Vol | NSE | mNSE | Vol | ||
| Leo | UE SM1+2 | 0.84 | 0.71 | 0.01 | 0.85 | 0.72 | −0.06 | 0.71 | 0.61 | −0.01 | 0.79 | 0.69 | −0.02 |
| UE SM2 | 0.82 | 0.69 | −0.24 | 0.82 | 0.70 | −0.21 | 0.72 | 0.62 | −0.11 | 0.78 | 0.68 | −0.17 | |
| current | 0.79 | 0.65 | 0.25 | 0.83 | 0.73 | 0.21 | 0.70 | 0.60 | 0.06 | 0.77 | 0.67 | 0.15 | |
| FHZ | UE SM1+2 | - | - | - | - | - | - | - | - | - | - | - | - |
| UE SM2 | 0.95 | 0.81 | −0.08 | 0.88 | 0.78 | 0.18 | 0.81 | 0.78 | −0.03 | 0.89 | 0.81 | 0.00 | |
| current | 0.90 | 0.74 | −0.28 | 0.89 | 0.79 | −0.13 | 0.80 | 0.74 | −0.15 | 0.87 | 0.78 | −0.18 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hörnschemeyer, B.; Henrichs, M.; Uhl, M. SWMM-UrbanEVA: A Model for the Evapotranspiration of Urban Vegetation. Water 2021, 13, 243. https://doi.org/10.3390/w13020243
Hörnschemeyer B, Henrichs M, Uhl M. SWMM-UrbanEVA: A Model for the Evapotranspiration of Urban Vegetation. Water. 2021; 13(2):243. https://doi.org/10.3390/w13020243
Chicago/Turabian StyleHörnschemeyer, Birgitta, Malte Henrichs, and Mathias Uhl. 2021. "SWMM-UrbanEVA: A Model for the Evapotranspiration of Urban Vegetation" Water 13, no. 2: 243. https://doi.org/10.3390/w13020243
APA StyleHörnschemeyer, B., Henrichs, M., & Uhl, M. (2021). SWMM-UrbanEVA: A Model for the Evapotranspiration of Urban Vegetation. Water, 13(2), 243. https://doi.org/10.3390/w13020243




