Flood Susceptibility Assessment Using Novel Ensemble of Hyperpipes and Support Vector Regression Algorithms
Abstract
1. Introduction
2. Materials and Methods
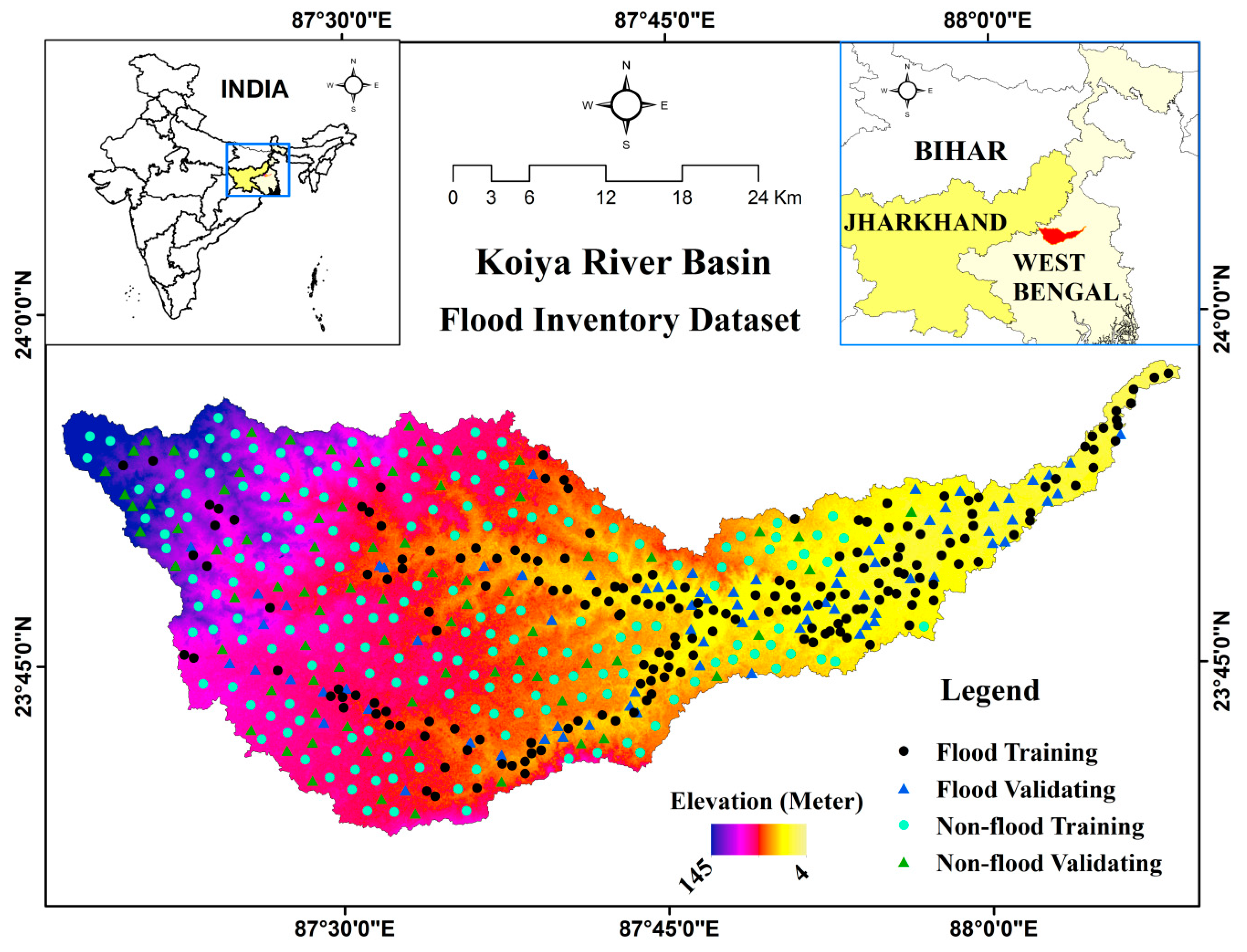
2.1. Study Area
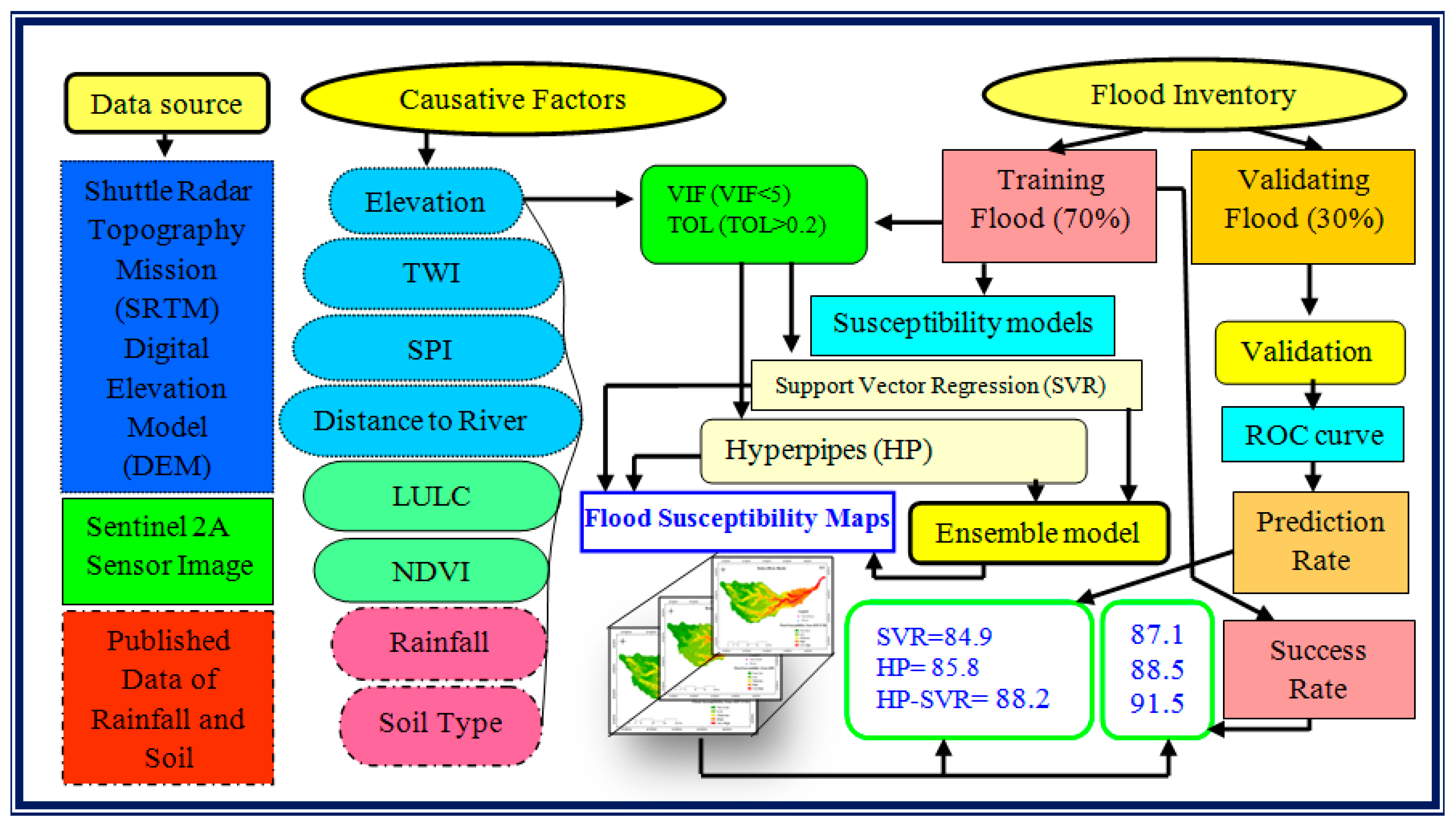
2.2. Methodology
- Preparation of flood inventory map and several flood susceptibility conditioning factors (FSCFs): a total of 264, in which 132 historical flood points were collected from the multi-hazard district disaster management plan of Birbhum for the two respective year of 2017 and 2018 (http://www.birbhum.gov.in/DMD/MH_DM_Plan_Birbhum) and verified through Google earth satellite images. Alongside this, an extensive field survey was carried out to check flood level marker posts during the flood time. Afterward, 132 non-flood points were randomly selected throughout the river basin area with the help of the ArcGIS platform. Additionally, a total of eight FSCFs were chosen, namely land use land cover (LULC), soil types, rainfall, normalized difference vegetation index (NDVI), distance to river, elevation, topographic wetness index (TWI), and stream power index (SPI) based on the local geo-environmental conditions for further progress of our research work.
- Multi-collinearity analysis was carried out among the selected factors by using tolerance (TOL) and variance inflation factor (VIF) techniques to reduce the bias.
- Relative importance of eight variables and their sub-classes was analyzed through the mean decrease accuracy (MDA) method of the random forest (RF) algorithm and step-wise weight assessment ratio analysis (SWARA).
- Flood susceptibility modeling and mapping was done through hyperpipes (HP), support vector regression (SVR) ML algorithms, and their novel ensemble of HP-SVR.
- The prediction performance of the aforementioned three models was validated through the statistical methods of sensitivity, specificity, accuracy, receiver operating characteristics-area under curve (ROC-AUC), and Kappa coefficient analysis.
2.3. Flood Inventory Map
2.4. Data Preparation
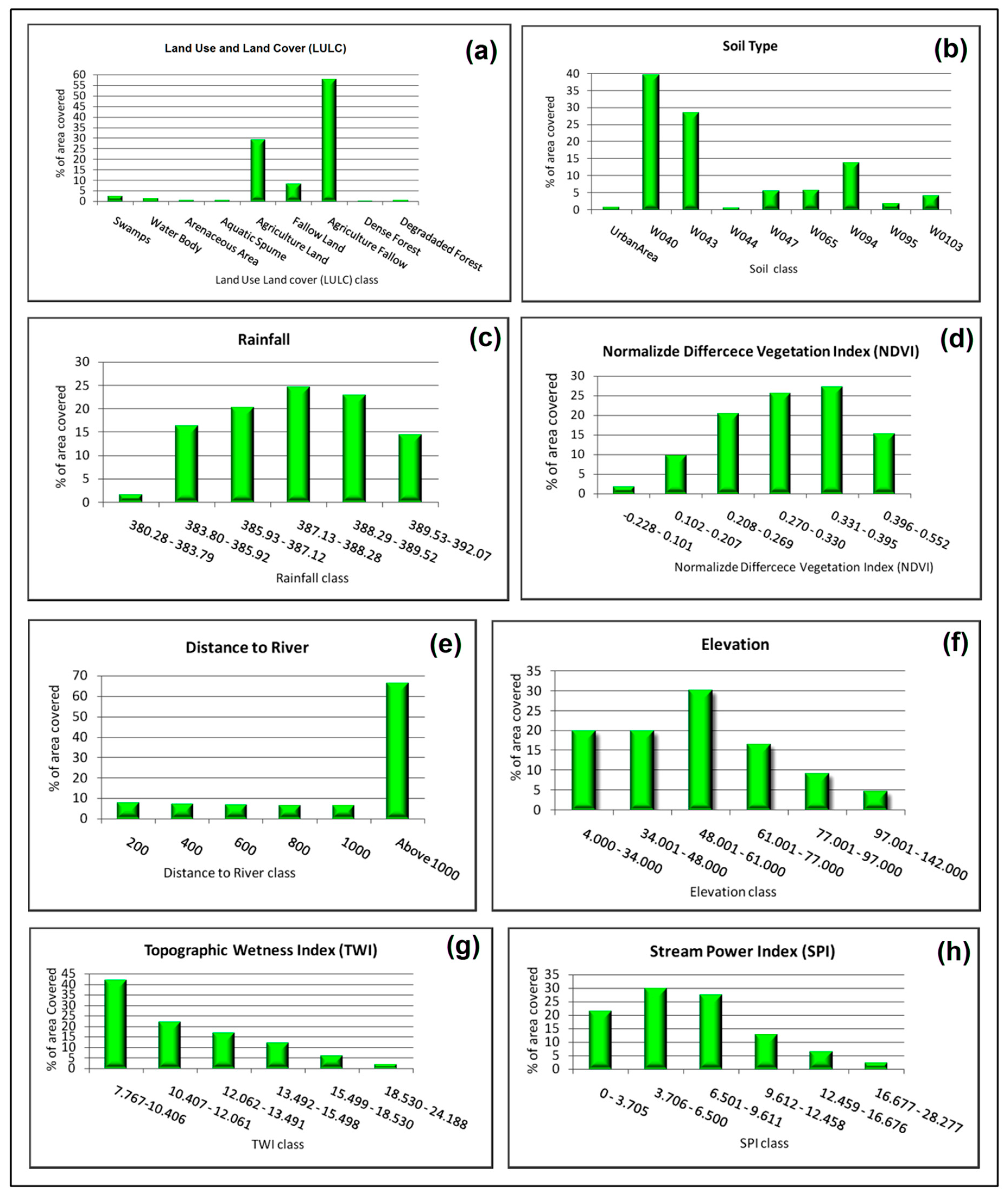
2.4.1. Land Use Land Cover (LULC)
2.4.2. Soil types
2.4.3. Rainfall
2.4.4. Normalized Difference Vegetation Index (NDVI)
2.4.5. Distance to River
2.4.6. Elevation
2.4.7. Topographic Wetness Index (TWI)
2.4.8. Stream Power Index (SPI)
2.5. Multicollinearity (MC) Test
2.6. Relative Importance of Factors and Respective Sub-Class Factors
2.6.1. Random Forest (RF)
2.6.2. Step-Wise Weight Assessment Ratio Analysis (SWARA)
2.7. Machine Learning Methods for Flood Susceptibility Modelling
2.7.1. Hyperpipes (HP)
- By using the training dataset, a single pipe was developed for each class and this pipe was matching with the respective class.
- All the data were analyzed instance by instance.
- If attribute value had not occurred yet, each instance value was attached to the respective pipe.
- Comparison of instance value and attribute value was done through class pipes.
- Finally, the instances were selected with the respective class pipe for optimal match.
2.7.2. Support Vector Regression (SVR)
2.7.3. Ensemble of HP-SVR
2.8. Accuracy Assessment
3. Results
3.1. Multi-Collinearity (MC) Analysis
3.2. Relative Importance of the Variables and Their Sub-Classes
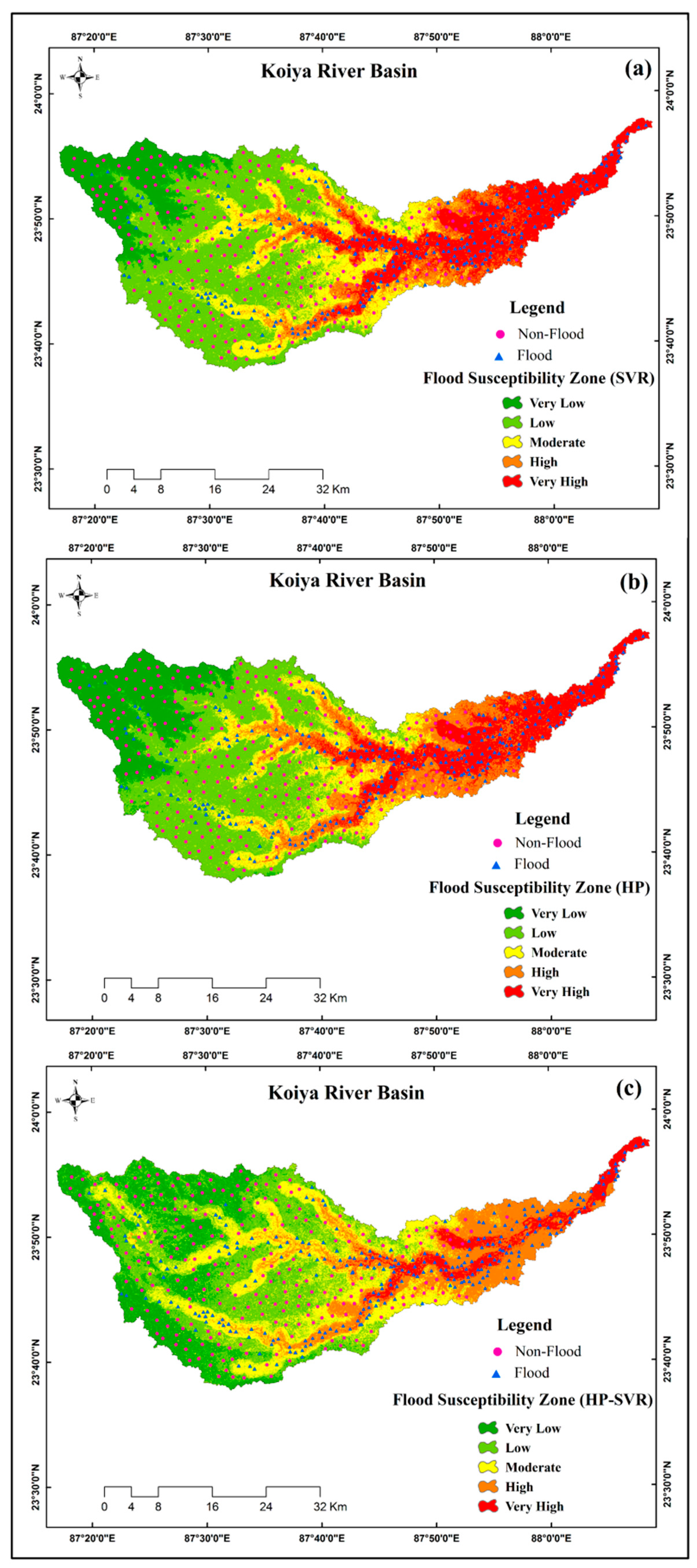
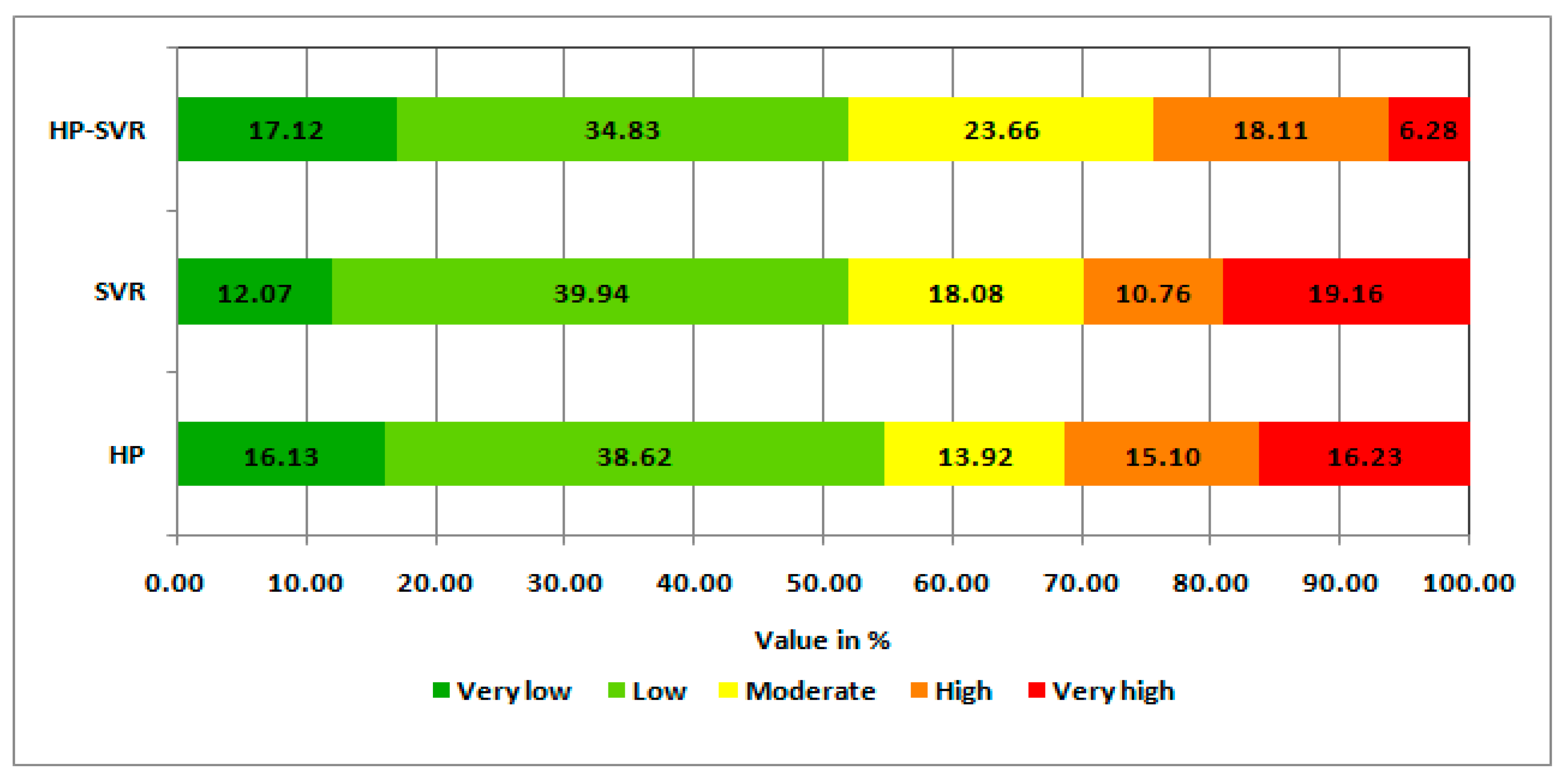
3.3. Spatial Assessment of Flood Susceptibility Mapping
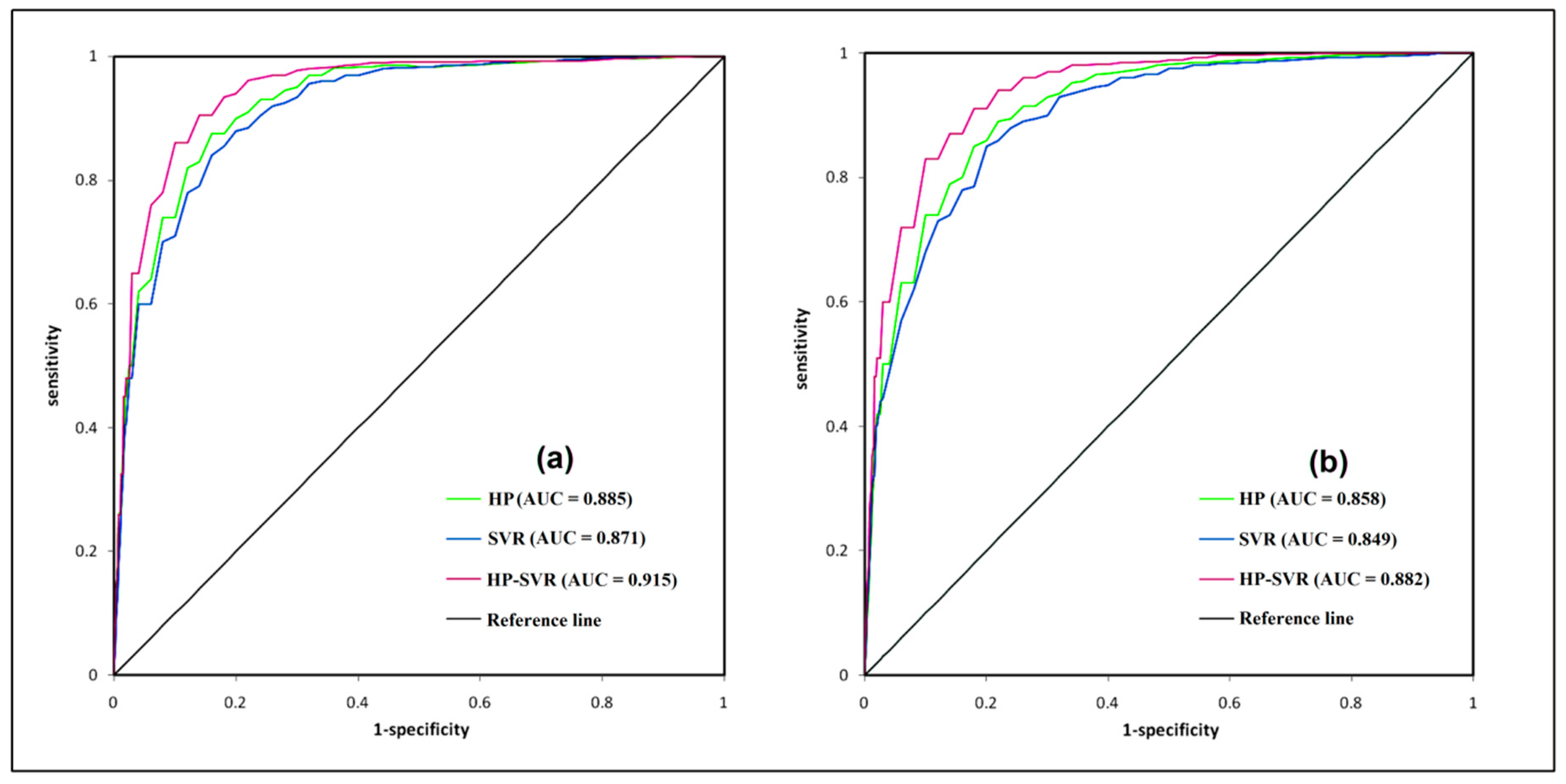
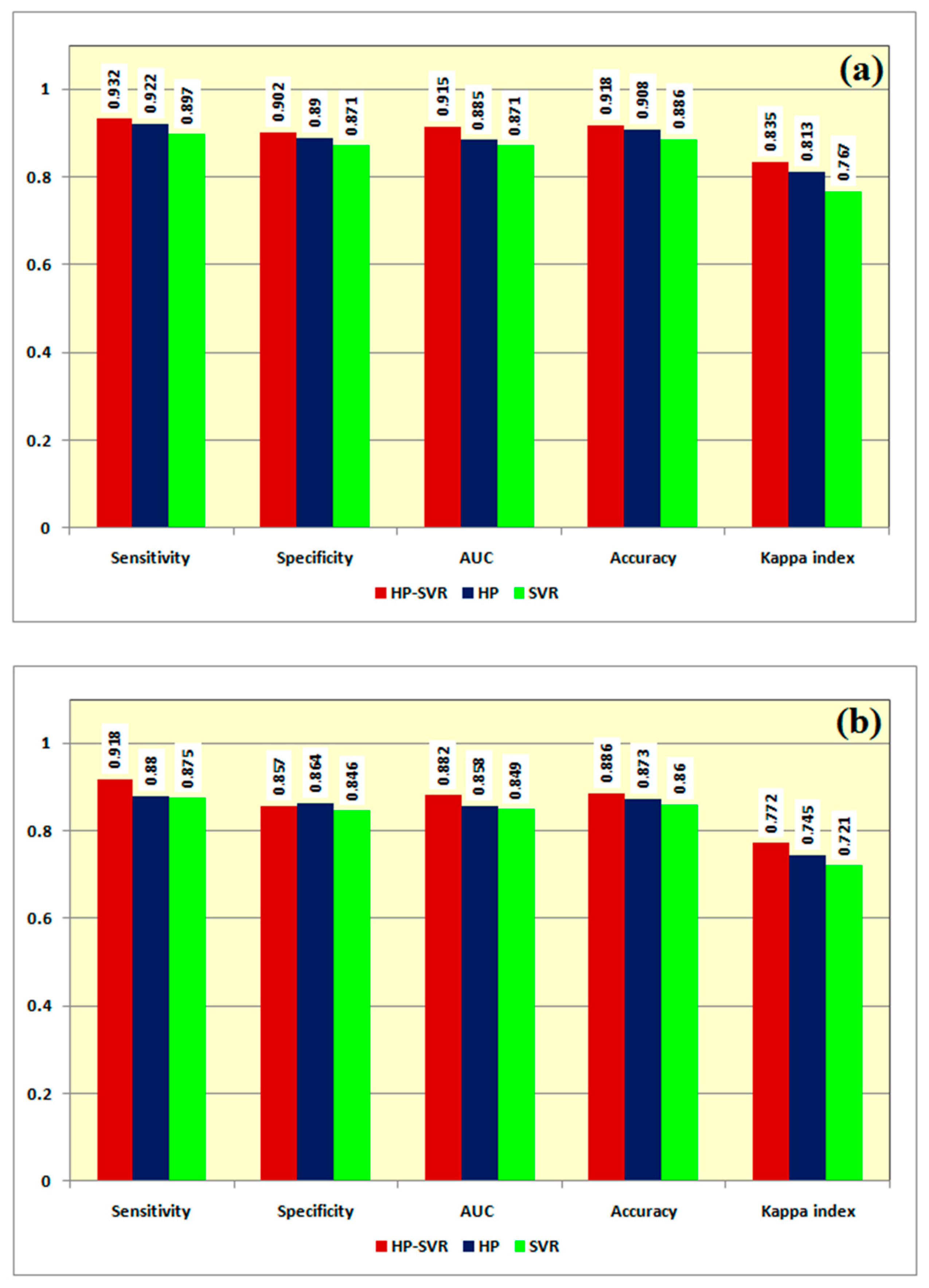
3.4. Evaluation of Validation Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mosavi, A.; Golshan, M.; Janizadeh, S.; Choubin, B.; Melesse, A.M.; Dineva, A.A. Ensemble Models of GLM, FDA, MARS, and RF for Flood and Erosion Susceptibility Mapping: A Priority Assessment of Sub-Basins. Geocarto Int. 2020, 1–20. [Google Scholar] [CrossRef]
- Arora, A.; Arabameri, A.; Pandey, M.; Siddiqui, M.A.; Shukla, U.K.; Bui, D.T.; Mishra, V.N.; Bhardwaj, A. Optimization of State-of-the-Art Fuzzy-Metaheuristic ANFIS-Based Machine Learning Models for Flood Susceptibility Prediction Mapping in the Middle Ganga Plain, India. Sci. Total. Environ. 2021, 750, 141565. [Google Scholar] [CrossRef] [PubMed]
- Keesstra, S.; Mol, G.; De Leeuw, J.; Okx, J.; Molenaar, C.; De Cleen, M.; Visser, S. Soil-Related Sustainable Development Goals: Four Concepts to Make Land Degradation Neutrality and Restoration Work. Land 2018, 7, 133. [Google Scholar] [CrossRef]
- Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Thai Pham, B.; Pradhan, B.; et al. Novel GIS Based Machine Learning Algorithms for Shallow Landslide Susceptibility Mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef] [PubMed]
- Kalantari, Z.; Ferreira, C.S.S.; Koutsouris, A.J.; Ahlmer, A.-K.; Cerdà, A.; Destouni, G. Assessing Flood Probability for Transportation Infrastructure Based on Catchment Characteristics, Sediment Connectivity and Remotely Sensed Soil Moisture. Sci. Total Environ. 2019, 661, 393–406. [Google Scholar] [CrossRef]
- Band, S.S.; Janizadeh, S.; Chandra Pal, S.; Saha, A.; Chakrabortty, R.; Melesse, A.M.; Mosavi, A. Flash Flood Susceptibility Modeling Using New Approaches of Hybrid and Ensemble Tree-Based Machine Learning Algorithms. Remote Sens. 2020, 12, 3568. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, H.; Chen, W.; Li, S.; Panahi, M.; Khosravi, K.; Shirzadi, A.; Shahabi, H.; Panahi, S.; Costache, R. Flood Susceptibility Mapping in Dingnan County (China) Using Adaptive Neuro-Fuzzy Inference System with Biogeography Based Optimization and Imperialistic Competitive Algorithm. J. Environ. Manag. 2019, 247, 712–729. [Google Scholar] [CrossRef]
- Ligtvoet, W.; Witte, F.; Goldschmidt, T.; Oijen, M.J.P.V.; Wanink, J.H.; Goudswaard, P.C. Species Extinction and Concomitant Ecological Changes in Lake Victoria. Neth. J. Zool. 1991, 42, 214–232. [Google Scholar] [CrossRef]
- Roy, P.; Chandra Pal, S.; Chakrabortty, R.; Chowdhuri, I.; Malik, S.; Das, B. Threats of Climate and Land Use Change on Future Flood Susceptibility. J. Clean. Prod. 2020, 272, 122757. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Mukherjee, K.; Blaschke, T.; Chen, W.; Ngo, P.T.T.; Band, S.S. Modeling Spatial Flood Using Novel Ensemble Artificial Intelligence Approaches in Northern Iran. Remote Sens. 2020, 12, 3423. [Google Scholar] [CrossRef]
- Rozalis, S.; Morin, E.; Yair, Y.; Price, C. Flash Flood Prediction Using an Uncalibrated Hydrological Model and Radar Rainfall Data in a Mediterranean Watershed under Changing Hydrological Conditions. J. Hydrol. 2010, 394, 245–255. [Google Scholar] [CrossRef]
- Mirza, M.M.Q. Climate Change, Flooding in South Asia and Implications. Reg. Environ. Chang. 2011, 11, 95–107. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Ghosh, P.K.; Jana, N.C.; Sinha, S. Probability of Flooding and Vulnerability Assessment in the Ajay River, Eastern India: Implications for Mitigation. Environ. Earth Sci. 2016, 75, 578. [Google Scholar] [CrossRef]
- Ganugula, G.; Venkata, B.; Sinha, R. GIS in Flood Hazard Mapping: A Case Study of Kosi River Basin, India. 2005. Available online: http://www.gisdevelopment.net/application/natural_hazards/floods/floods001pf.htm (accessed on 9 September 2020).
- Kale, V.S. Is Flooding in South Asia Getting Worse and More Frequent? Singap. J. Trop. Geogr. 2014, 35, 161–178. [Google Scholar] [CrossRef]
- Han, C.; Zhang, B.; Chen, H.; Wei, Z.; Liu, Y. Spatially distributed crop model based on remote sensing. Agric. Water Manag. 2019, 218, 165–173. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Tian, L.; Waller, L.; Asundi, A. Transport of intensity phase retrieval and computational imaging for partially coherent fields: The phase space perspective. Opt. Lasers Eng. 2015, 71, 20–32. [Google Scholar] [CrossRef]
- Yan, J.; Pu, W.; Zhou, S.; Liu, H.; Bao, Z. Collaborative Detection and Power Allocation Framework for Target Tracking in Multiple Radar System. Inf. Fusion 2019, 55, 173–183. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Gu, G.; Feng, S.; Feng, F.; Li, R.; Shen, G. High-speed three-dimensional shape measurement for dynamic scenes using bi-frequency tripolar pulse-width-modulation fringe projection. Opt. Lasers Eng. 2013, 51, 953–960. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Li, Z.; Zhu, Y.; Wang, J.; Yu, Z. Geographically weighted regression based methods for merging satellite and gauge precipitation. J. Hydrol. 2018, 558, 275–289. [Google Scholar] [CrossRef]
- Zhu, J.; Wu, P.; Chen, M.; Kim, M.J.; Wang, X.; Fang, T. Automatically Processing IFC Clipping Representation for BIM and GIS Integration at the Process Level. Appl. Sci. 2020, 10, 2009. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Wang, P.; Wu, Z.; Kim, M.J. Integration of BIM and GIS: Geometry from IFC to shapefile using open-source technology. Autom. Constr. 2019, 102, 105–119. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Chen, M.; Wu, P.; Kim, M.J. Integration of BIM and GIS: IFC geometry transformation to shapefile using enhanced open-source approach. Autom. Constr. 2019, 106, 102859. [Google Scholar] [CrossRef]
- Wu, T.; Cao, J.; Xiong, L.; Zhang, H. New Stabilization Results for Semi-Markov Chaotic Systems with Fuzzy Sampled-Data Control. Complexity 2019. [Google Scholar] [CrossRef]
- Wu, T.; Xiong, L.; Cheng, J.; Xie, X. New results on stabilization analysis for fuzzy semi-Markov jump chaotic systems with state quantized sampled-data controller. Inf. Sci. 2020, 521, 231–250. [Google Scholar] [CrossRef]
- Shi, K.; Wang, J.; Tang, Y.; Zhong, S. Reliable asynchronous sampled-data filtering of T–S fuzzy uncertain delayed neural networks with stochastic switched topologies. Fuzzy Sets Syst. 2020, 381, 1–25. [Google Scholar] [CrossRef]
- Chen, H.; Qiao, H.; Xu, L.; Feng, Q.; Cai, K. A Fuzzy Optimization Strategy for the Implementation of RBF LSSVR Model in Vis–NIR Analysis of Pomelo Maturity. IEEE Trans. Ind. Inform. 2019, 15, 5971–5979. [Google Scholar] [CrossRef]
- Shi, K.; Wang, J.; Zhong, S.; Tang, Y.; Cheng, J. Non-fragile memory filtering of TS fuzzy delayed neural networks based on switched fuzzy sampled-data control. Fuzzy Sets Syst. 2020, 394, 40–64. [Google Scholar] [CrossRef]
- Xu, M.; Li, T.; Wang, Z.; Deng, X.; Yang, R.; Guan, Z. Reducing complexity of HEVC: A deep learning approach. IEEE Trans. Image Process. 2018, 27, 5044–5059. [Google Scholar] [CrossRef]
- Lv, Z.; Qiao, L. Deep belief network and linear perceptron based cognitive computing for collaborative robots. Appl. Soft Comput. 2020, 92, 106300. [Google Scholar] [CrossRef]
- Lv, Z.; Xiu, W. Interaction of edge-cloud computing based on SDN and NFV for next generation IoT. IEEE Internet Things J. 2019, 7, 5706–5712. [Google Scholar] [CrossRef]
- Chen, H.; Chen, A.; Xu, L.; Xie, H.; Qiao, H.; Lin, Q.; Cai, K. A deep learning CNN architecture applied in smart near-infrared analysis of water pollution for agricultural irrigation resources. Agric. Water Manag. 2020, 240, 106303. [Google Scholar] [CrossRef]
- Qian, J.; Feng, S.; Tao, T.; Hu, Y.; Li, Y.; Chen, Q.; Zuo, C. Deep-learning-enabled geometric constraints and phase unwrapping for single-shot absolute 3D shape measurement. APL Photonics 2020, 5, 046105. [Google Scholar] [CrossRef]
- Qian, J.; Feng, S.; Li, Y.; Tao, T.; Han, J.; Chen, Q.; Zuo, C. Single-shot absolute 3D shape measurement with deep-learning-based color fringe projection profilometry. Opt. Lett. 2020, 45, 1842–1845. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Chan, F.T.S.; Ran, W. Decision making for the selection of cloud vendor: An improved approach under group decision-making with integrated weights and objective/subjective attributes. Expert Syst. Appl. 2016, 55, 37–47. [Google Scholar] [CrossRef]
- Wu, C.; Wu, P.; Wang, J.; Jiang, R.; Chen, M.; Wang, X. Critical review of data-driven decision-making in bridge operation and maintenance. Struct. Infrastruct. Eng. 2020, 1–24. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Cerdà, A.; Conoscenti, C.; Kalantari, Z. A Comparison of Statistical Methods and Multi-Criteria Decision Making to Map Flood Hazard Susceptibility in Northern Iran. Sci. Total Environ. 2019, 660, 443–458. [Google Scholar] [CrossRef]
- Lee, M.; Kang, J.; Jeon, S. Application of Frequency Ratio Model and Validation for Predictive Flooded Area Susceptibility Mapping Using GIS. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 895–898. [Google Scholar]
- Rahmati, O.; Zeinivand, H.; Besharat, M. Flood Hazard Zoning in Yasooj Region, Iran, Using GIS and Multi-Criteria Decision Analysis. Geomat. Nat. Hazards Risk 2016, 7, 1000–1017. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood Susceptibility Assessment Using GIS-Based Support Vector Machine Model with Different Kernel Types. CATENA 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Chen, W.; Roy, J.; Pradhan, B.; Bui, D.T. Flash Flood Susceptibility Modelling Using Functional Tree and Hybrid Ensemble Techniques. J. Hydrol. 2020, 587, 125007. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Chakrabortty, R. Flood Susceptibility Mapping by Ensemble Evidential Belief Function and Binomial Logistic Regression Model on River Basin of Eastern India. Adv. Space Res. 2020, 65, 1466–1489. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Q.; Chao, L.; Ye, J.; Li, Z.; Yu, Z.; Yang, T.; Ju, Q. Ground Observation-based Analysis of Soil Moisture Spatiotemporal Variability Across A Humid to Semi-Humid Transitional Zone in China. J. Hydrol. 2019, 574, 903–914. [Google Scholar] [CrossRef]
- Bellu, A.; Sanches Fernandes, L.F.; Cortes, R.M.V.; Pacheco, F.A.L. A Framework Model for the Dimensioning and Allocation of a Detention Basin System: The Case of a Flood-Prone Mountainous Watershed. J. Hydrol. 2016, 533, 567–580. [Google Scholar] [CrossRef]
- Samanta, R.K.; Bhunia, G.S.; Shit, P.K.; Pourghasemi, H.R. Flood Susceptibility Mapping Using Geospatial Frequency Ratio Technique: A Case Study of Subarnarekha River Basin, India. Model. Earth Syst. Environ. 2018, 4, 395–408. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Shabani, F.; Jebur, M.N.; Hong, H.; Chen, W.; Xie, X. GIS-Based Spatial Prediction of Flood Prone Areas Using Standalone Frequency Ratio, Logistic Regression, Weight of Evidence and Their Ensemble Techniques. Geomat. Nat. Hazards Risk 2017, 8, 1538–1561. [Google Scholar] [CrossRef]
- Zhang, K.; Ruben, G.B.; Li, X.; Li, Z.; Yu, Z.; Xia, J.; Dong, Z. A comprehensive assessment framework for quantifying climatic and anthropogenic contributions to streamflow changes: A case study in a typical semi-arid North China basin. Environ. Model. Softw. 2020, 128, 104704. [Google Scholar] [CrossRef]
- Souissi, D.; Zouhri, L.; Hammami, S.; Msaddek, M.H.; Zghibi, A.; Dlala, M. GIS-Based MCDM—AHP Modeling for Flood Susceptibility Mapping of Arid Areas, Southeastern Tunisia. Geocarto Int. 2020, 35, 991–1017. [Google Scholar] [CrossRef]
- Dano, U.L.; Balogun, A.-L.; Matori, A.-N.; Wan Yusouf, K.; Abubakar, I.R.; Said Mohamed, M.A.; Aina, Y.A.; Pradhan, B. Flood Susceptibility Mapping Using GIS-Based Analytic Network Process: A Case Study of Perlis, Malaysia. Water 2019, 11, 615. [Google Scholar] [CrossRef]
- Pal, S.C.; Chakrabortty, R.; Malik, S.; Das, B. Application of Forest Canopy Density Model for Forest Cover Mapping Using LISS-IV Satellite Data: A Case Study of Sali Watershed, West Bengal. Model. Earth Syst. Environ. 2018, 4, 853–865. [Google Scholar] [CrossRef]
- Khosravi, K.; Pourghasemi, H.R.; Chapi, K.; Bahri, M. Flash Flood Susceptibility Analysis and Its Mapping Using Different Bivariate Models in Iran: A Comparison between Shannon’s Entropy, Statistical Index, and Weighting Factor Models. Environ. Monit. Assess 2016, 188, 656. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An Ensemble Prediction of Flood Susceptibility Using Multivariate Discriminant Analysis, Classification and Regression Trees, and Support Vector Machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef]
- Malik, S.; Chandra Pal, S.; Chowdhuri, I.; Chakrabortty, R.; Roy, P.; Das, B. Prediction of Highly Flood Prone Areas by GIS Based Heuristic and Statistical Model in a Monsoon Dominated Region of Bengal Basin. Remote Sens. Appl. Soc. Environ. 2020, 19, 100343. [Google Scholar] [CrossRef]
- Tiryaki, M.; Karaca, O. Flood Susceptibility Mapping Using GIS and Multicriteria Decision Analysis: Saricay-Çanakkale (Turkey). Arab. J. Geosci. 2018, 11, 364. [Google Scholar] [CrossRef]
- Xi, W.; Li, G.; Moayedi, H.; Nguyen, H. A particle-based optimization of artificial neural network for earthquake-induced landslide assessment in Ludian county, China. Geomat. Nat. Hazards Risk. 2019, 10, 1750–1771. [Google Scholar] [CrossRef]
- Das, B.; Pal, S.C.; Malik, S.; Chakrabortty, R. Living with Floods through Geospatial Approach: A Case Study of Arambag C.D. Block of Hugli District, West Bengal, India. SN Appl. Sci. 2019, 1, 329. [Google Scholar] [CrossRef]
- Bui, D.T.; Moayedi, H.; Kalantar, B.; Osouli, A.; Pradhan, B.; Nguyen, H.; Rashid, A.S.A. A Novel Swarm Intelligence—Harris Hawks Optimization for Spatial Assessment of Landslide Susceptibility. Sensors 2019, 19, 3590. [Google Scholar] [CrossRef]
- Alin, A. Multicollinearity. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 370–374. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Yamani, M.; Pourghasemi, H.R.; Lombardo, L. Spatial Modelling of Gully Erosion Using Evidential Belief Function, Logistic Regression, and a New Ensemble of Evidential Belief Function–Logistic Regression Algorithm. Land Degrad. Dev. 2018, 29, 4035–4049. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Tien Bui, D. A Comparative Assessment of Decision Trees Algorithms for Flash Flood Susceptibility Modeling at Haraz Watershed, Northern Iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Han, H.; Guo, X.; Yu, H. Variable Selection Using Mean Decrease Accuracy and Mean Decrease Gini Based on Random Forest. In Proceedings of the 2016 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 26–28 August 2016; pp. 219–224. [Google Scholar]
- Keršuliene, V.; Zavadskas, E.K.; Turskis, Z. Selection of Rational Dispute Resolution Method by Applying New Step-wise Weight Assessment Ratio Analysis (Swara). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Arabameri, A.; Saha, A.; Chakrabortty, R.; Blaschke, T.; Pradhan, B.; Band, S.S. Implementation of Artificial Intelligence Based Ensemble Models for Gully Erosion Susceptibility Assessment. Remote Sens. 2020, 12, 3620. [Google Scholar] [CrossRef]
- Zolfani, S.H.; Chatterjee, P. Comparative Evaluation of Sustainable Design Based on Step-Wise Weight Assessment Ratio Analysis (SWARA) and Best Worst Method (BWM) Methods: A Perspective on Household Furnishing Materials. Symmetry 2019, 11, 74. [Google Scholar] [CrossRef]
- Stanujkic, D.; Karabasevic, D.; Zavadskas, E.K. A Framework for the Selection of a Packaging Design Based on the SWARA Method. Eng. Econ. 2015, 26, 181–187. [Google Scholar] [CrossRef]
- Vafaeipour, M.; Hashemkhani Zolfani, S.; Morshed Varzandeh, M.H.; Derakhti, A.; Keshavarz Eshkalag, M. Assessment of Regions Priority for Implementation of Solar Projects in Iran: New Application of a Hybrid Multi-Criteria Decision Making Approach. Energy Convers. Manag. 2014, 86, 653–663. [Google Scholar] [CrossRef]
- Smusz, S.; Kurczab, R.; Bojarski, A.J. A Multidimensional Analysis of Machine Learning Methods Performance in the Classification of Bioactive Compounds. Chemom. Intell. Lab. Syst. 2013, 128, 89–100. [Google Scholar] [CrossRef]
- Kukreja, M.; Johnston, S.A.; Stafford, P. Comparative Study of Classification Algorithms for Immunosignaturing Data. BMC Bioinform. 2012, 13, 139. [Google Scholar] [CrossRef]
- Tran, Q.C.; Minh, D.D.; Jaafari, A.; Al-Ansari, N.; Minh, D.D.; Van, D.T.; Nguyen, D.A.; Tran, T.H.; Ho, L.S.; Nguyen, D.H.; et al. Novel Ensemble Landslide Predictive Models Based on the Hyperpipes Algorithm: A Case Study in the Nam Dam Commune, Vietnam. Appl. Sci. 2020, 10, 3710. [Google Scholar] [CrossRef]
- Deeb, Z.A.; Devine, T.; Geng, Z. Randomized Decimation Hyperpipes. Citeseer 2010. Available online: http://www.csee.wvu.edu/~timm/tmp/r7.pdf (accessed on 5 September 2020).
- Vapnik, V.; Golowich, S.E.; Smola, A. Support Vector Method for Function Approximation, Regression Estimation, and Signal Processing. In Advances in Neural Information Processing Systems 9; MIT Press: Cambridge, MA, USA, 1996; pp. 281–287. [Google Scholar]
- Lu, C.-J.; Lee, T.-S.; Chiu, C.-C. Financial Time Series Forecasting Using Independent Component Analysis and Support Vector Regression. Decis. Support Syst. 2009, 47, 115–125. [Google Scholar] [CrossRef]
- Li, D.; Simske, S. Example Based Single-Frame Image Super-Resolution by Support Vector Regression. J. Pattern Recognit. Res. 2010, 5, 104–118. [Google Scholar] [CrossRef]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the Effects of Training Data Selection on the Landslide Susceptibility Mapping: A Comparison between Support Vector Machine (SVM), Logistic Regression (LR) and Artificial Neural Networks (ANN). Geomat. Nat. Hazards Risk 2018, 9, 49–69. [Google Scholar] [CrossRef]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet Support Vector Machine-Based Prediction Model of Dam Deformation. Mech. Syst. Signal Process. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Wang, J.; Li, L.; Niu, D.; Tan, Z. An Annual Load Forecasting Model Based on Support Vector Regression with Differential Evolution Algorithm. Appl. Energy 2012, 94, 65–70. [Google Scholar] [CrossRef]
- Wang, H.; Moayedi, H.; Kok Foong, L. Genetic algorithm hybridized with multilayer perceptron to have an economical slope stability design. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Moayedi, H.; Khari, M.; Bahiraei, M.; Kok Foong, L.; Bui, D.T. Spatial assessment of landslide risk using two novel integrations of neuro-fuzzy system and metaheuristic approaches; Ardabil Province, Iran. Geomat. Nat. Hazards Risk 2020, 11, 230–258. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, K.; van Beek, L.P.; Tian, X.; Bogaard, T.A. Physically-based landslide prediction over a large region: Scaling low-resolution hydrological model results for high-resolution slope stability assessment. Environ. Model. Softw. 2020, 124, 104607. [Google Scholar] [CrossRef]
- Nguyen, H.; Mehrabi, M.; Kalantar, B.; Moayedi, H.; Abdullahi, M.M. Potential of hybrid evolutionary approaches for assessment of geo-hazard landslide susceptibility mapping. Geomat. Nat. Hazards Risk 2019, 10, 1667–1693. [Google Scholar] [CrossRef]
- Liu, Y.-X.; Yang, C.-N.; Sun, Q.-D.; Wu, S.-Y.; Lin, S.-S.; Chou, Y.-S. Enhanced embedding capacity for the SMSD-based data-hiding method. Signal Process. Image Commun. 2019, 78, 216–222. [Google Scholar] [CrossRef]
- Zhao, C.; Li, J. Equilibrium Selection under the Bayes-Based Strategy Updating Rules. Symmetry 2020, 12, 739. [Google Scholar] [CrossRef]
- Xiong, Q.; Zhang, X.; Wang, W.-F.; Gu, Y. A Parallel Algorithm Framework for Feature Extraction of EEG Signals on MPI. Comput. Math. Methods Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q. Research on Road Traffic Situation Awareness System Based on Image Big Data. IEEE Intell. Syst. 2019, 35, 18–26. [Google Scholar] [CrossRef]
- Fu, X.; Yang, Y. Modeling and analysis of cascading node-link failures in multi-sink wireless sensor networks. Reliab. Eng. Syst. Saf. 2020, 197, 106815. [Google Scholar] [CrossRef]
- Fu, X.; Pace, P.; Aloi, G.; Yang, L.; Fortino, G. Topology Optimization Against Cascading Failures on Wireless Sensor Networks Using a Memetic Algorithm. Comput. Netw. 2020, 177, 107327. [Google Scholar] [CrossRef]
- Zenggang, X.; Zhiwen, T.; Xiaowen, C.; Xue-min, Z.; Kaibin, Z.; Conghuan, Y. Research on Image Retrieval Algorithm Based on Combination of Color and Shape Features. J. Signal Process. Syst. 2019, 1–8. [Google Scholar] [CrossRef]
- Zuo, C.; Sun, J.; Li, J.; Asundi, A.; Chen, Q. Wide-field high-resolution 3d microscopy with fourier ptychographic diffraction tomography. Opt. Lasers Eng. 2020, 128, 106003. [Google Scholar] [CrossRef]
- Long, Q.; Wu, C.; Wang, X. A system of nonsmooth equations solver based upon subgradient method. Appl. Math. Comput. 2015, 251, 284–299. [Google Scholar] [CrossRef]
- Zhu, J.; Shi, Q.; Wu, P.; Sheng, Z.; Wang, X. Complexity analysis of prefabrication contractors’ dynamic price competition in mega projects with different competition strategies. Complexity 2018. [Google Scholar] [CrossRef]
- Ahmadlou, M.; Karimi, M.; Alizadeh, S.; Shirzadi, A.; Parvinnejhad, D.; Shahabi, H.; Panahi, M. Flood Susceptibility Assessment Using Integration of Adaptive Network-Based Fuzzy Inference System (ANFIS) and Biogeography-Based Optimization (BBO) and BAT Algorithms (BA). Geocarto Int. 2019, 34, 1252–1272. [Google Scholar] [CrossRef]
- Malik, S.; Pal, S.C.; Sattar, A.; Singh, S.K.; Das, B.; Chakrabortty, R.; Mohammad, P. Trend of Extreme Rainfall Events Using Suitable Global Circulation Model to Combat the Water Logging Condition in Kolkata Metropolitan Area. Urban Clim. 2020, 32, 100599. [Google Scholar] [CrossRef]

| Data Type | Data Source | Time Period | Spatial Data or Map | Resolution or Scale |
|---|---|---|---|---|
| Topographical aheet (73 m) | Survey of India | 1979 | Basin boundary | Representative fraction (RF) = 1:250,000, polygon |
| Shuttle radar topography mission (SRTM) digital elevation model (DEM) | USGS Earth Explorer (https://earthexplorer.usgs.gov) | 2016 | Elevation, TWI, SPI, and distance to river | 30 m × 30 m spatial resolution, grid |
| European Space Agency (ESA) earth online | European Space Agency (ESA) earth online Sentinel 2A Multispectral Instrument (MSI) images (Relative Orbit: 33 Tile Identifier: 45QWG and 45QXG) | 16 March 2017 | LULC and NDVI | 10 m × 10 m spatial resolution, grid |
| Soil map of West Bengal | NBSS and LUP Regional Centre, Kolkata | 1991 | Soil types | RF = 1:5,000,000, Polygon |
| Monthly rainfall data | India Meteorological Department (IMD) (https://www.indiawaterportal.org) | 1984–2018 | Rainfall | Grid |
| Historical spatial flood data | Multi-hazard district disaster management plan, Birbhum (http://www.birbhum.gov.in/DMD/MH_DM_Plan_Birbhum_2017.pdf), Google Earth Image and field survey | 2017–2018 | Flood inventory | 15 m × 15 m spatial resolution, Point |
| Soil Symbol | Taxonomic Name | Soil Characteristics |
|---|---|---|
| W040 | Fine, Vertic Ochraqualfs Fine, Aeric Haplaquepts | Very deep, poorly drained, fine cracking soils occurring on level to nearly level low lying alluvial plain with loamy surface. Associated with very deep, poorly drained, fine soils. |
| W043 | Fine, Typic Ochraqualfs Fine, Vertic Ochraqualfs | Very deep, poorly drained, fine soils occurring on very gently sloping low lying alluvial plain with loamy surface. Associated with very deep, poorly drained, fine cracking soils. |
| W044 | Fine, Vertic Haplaquepts Fine, Aeric Haplaquepts | Very deep, poorly drained, fine cracking soils occurring on level to nearly level low lying alluvial plain with clayey surface and moderate flooding. Associated with very deep, poorly drained, fine soils. |
| W047 | Very fine, Aeric Haplaquepts Fine loamy, Typic Ustochrepts | Very deep, poorly drained, fine soils occurring on level to nearly level now lying alluvial plain with clayey surface and severe flooding. Associated with very deep, moderately well drained, fine loamy soils. |
| W065 | Fine loamy, Typic Ustifluvents Typic Ustifluvents | Very deep, moderately well drained, fine loamy soils occurring on very gently sloping flood plain with loamy surface, moderate erosion, and moderate flooding. Associated with very deep, well drained, sandy soils. |
| W094 | Fine loamy, Typic Haplustalfs Fine loamy, Typic Ustochrepts | Deep, well drained, loamy soils occurring on very gently sloping to undulating plain with loamy surface, and moderate erosion. Associated with deep, moderately well drained, loamy soils. |
| W095 | Loamy, Lithic Ustochrepts Loamy, Lithic Haplustalfs | Shallow, moderately well drained, coarse loamy soils occurring on gently sloping to undulating plain with gravelly loam surface and moderate erosion. Associated with drained, gravelly loamy soils. |
| W0103 | Fine loamy, Rhodic Paleustalfs Fine, Typic Rhodustalfs | Very deep, well drained, fine loamy soils occurring on very gently sloping to undulating plateau with loamy surface, and moderate erosion. Associated with very deep, moderately well drained, fine soils. |
| Flood Conditioning Factors | Tolerance(TOL) | Variance Inflation Factor (VIF) |
|---|---|---|
| Land use and land cover | 0.856 | 1.169 |
| Soil | 0.493 | 2.029 |
| Rainfall | 0.743 | 1.345 |
| NDVI | 0.807 | 1.239 |
| Distance to river | 0.969 | 1.032 |
| Elevation | 0.529 | 1.890 |
| TWI | 0.663 | 1.508 |
| SPI | 0.671 | 1.491 |
| Flood Conditioning Factors | Average Merit (AM) |
|---|---|
| LULC | 0.66 |
| Soil | 0.43 |
| Rainfall | 0.84 |
| NDVI | 0.28 |
| Distance to river | 0.91 |
| Elevation | 0.18 |
| TWI | 0.36 |
| SPI | 0.54 |
| Flood Causative Factors | Class | Number of Pixel (%) | Number of Flood (%) | SWARA Weight | Flood Causative Factors | Class | Number of Pixel (%) | Number of Flood (%) | SWARA Weight |
|---|---|---|---|---|---|---|---|---|---|
| LULC | Swamps | 2.4 | 1.62 | 0.09 | Distance to River (Meter) | 200 m | 7.65 | 18.92 | 0.23 |
| Water Body | 1.07 | 0.54 | 0.07 | 400 m | 7.06 | 24.86 | 0.32 | ||
| Arenaceous Area | 0.47 | 0 | 0 | 600 m | 6.66 | 12.43 | 0.17 | ||
| Aquatic Spume | 0.47 | 1.62 | 0.45 | 800 m | 6.36 | 10.81 | 0.16 | ||
| Agriculture Land | 29.18 | 35.14 | 0.16 | 1000 m | 6.1 | 5.95 | 0.09 | ||
| Fallow Land | 8.09 | 7.57 | 0.12 | Above 1000 m | 66.16 | 27.03 | 0.04 | ||
| Agriculture Fallow | 57.99 | 53.51 | 0.12 | Total | 100 | 100 | 1 | ||
| Dense Forest | 0.01 | 0 | 0 | Elevation (Meter) | 4.000–34.000 m | 19.84 | 51.89 | 0.52 | |
| Degraded Forest | 0.32 | 0 | 0 | 34.001–48.000 m | 19.95 | 22.7 | 0.23 | ||
| Total | 100 | 100 | 1 | 48.001–61.000 m | 30.06 | 18.92 | 0.12 | ||
| Soil Type | Urban Area | 0.65 | 0 | 0 | 61.001–77.000 m | 16.46 | 2.16 | 0.03 | |
| W040 | 39.54 | 38.38 | 0.08 | 77.001–97.000 m | 9.16 | 3.78 | 0.08 | ||
| W043 | 28.36 | 22.7 | 0.07 | 97.001–142.000 m | 4.53 | 0.54 | 0.02 | ||
| W044 | 0.6 | 2.7 | 0.37 | Total | 100 | 100 | 1 | ||
| W047 | 5.59 | 16.76 | 0.25 | TWI | 7.767–10.406 | 41.78 | 43.78 | 0.18 | |
| W065 | 5.64 | 12.97 | 0.19 | 10.407–12.061 | 21.92 | 24.32 | 0.19 | ||
| W094 | 13.81 | 5.95 | 0.04 | 12.062–13.491 | 16.73 | 13.51 | 0.14 | ||
| W095 | 1.72 | 0 | 0 | 13.492–15.498 | 11.99 | 11.89 | 0.17 | ||
| W0103 | 4.09 | 0.54 | 0.01 | 15.499–18.530 | 5.87 | 4.86 | 0.14 | ||
| Total | 100 | 100 | 1 | 18.530–24.188 | 1.71 | 1.62 | 0.17 | ||
| Rainfall (In mm) | 380.28–383.79 | 1.5 | 7.03 | 0.52 | Total | 100 | 100 | 1 | |
| 383.80–385.92 | 16.24 | 8.65 | 0.06 | SPI | 0–3.705 | 21.49 | 15.68 | 0.1 | |
| 385.93–387.12 | 20.25 | 16.76 | 0.09 | 3.706–6.500 | 29.84 | 23.24 | 0.11 | ||
| 387.13–388.28 | 24.66 | 24.86 | 0.11 | 6.501–9.611 | 27.57 | 27.03 | 0.14 | ||
| 388.29–389.52 | 22.93 | 36.22 | 0.17 | 9.612–12.458 | 12.59 | 21.08 | 0.23 | ||
| 389.53–392.07 | 14.42 | 6.49 | 0.05 | 12.459–16.676 | 6.46 | 9.73 | 0.21 | ||
| Total | 100 | 100 | 1 | 16.677–28.277 | 2.05 | 3.24 | 0.22 | ||
| Total | 100 | 100 | 1 | ||||||
| NDVI | −0.329 | 1.76 | 1.08 | 0.11 | |||||
| 0.102–0.207 | 9.74 | 8.11 | 0.15 | ||||||
| 0.208–0.269 | 20.4 | 13.51 | 0.12 | ||||||
| 0.270–0.330 | 25.6 | 24.86 | 0.17 | ||||||
| 0.331–0.395 | 27.23 | 32.43 | 0.21 | ||||||
| 0.395–0.552 | 15.27 | 20 | 0.23 | ||||||
| Total | 100 | 100 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, A.; Pal, S.C.; Arabameri, A.; Blaschke, T.; Panahi, S.; Chowdhuri, I.; Chakrabortty, R.; Costache, R.; Arora, A. Flood Susceptibility Assessment Using Novel Ensemble of Hyperpipes and Support Vector Regression Algorithms. Water 2021, 13, 241. https://doi.org/10.3390/w13020241
Saha A, Pal SC, Arabameri A, Blaschke T, Panahi S, Chowdhuri I, Chakrabortty R, Costache R, Arora A. Flood Susceptibility Assessment Using Novel Ensemble of Hyperpipes and Support Vector Regression Algorithms. Water. 2021; 13(2):241. https://doi.org/10.3390/w13020241
Chicago/Turabian StyleSaha, Asish, Subodh Chandra Pal, Alireza Arabameri, Thomas Blaschke, Somayeh Panahi, Indrajit Chowdhuri, Rabin Chakrabortty, Romulus Costache, and Aman Arora. 2021. "Flood Susceptibility Assessment Using Novel Ensemble of Hyperpipes and Support Vector Regression Algorithms" Water 13, no. 2: 241. https://doi.org/10.3390/w13020241
APA StyleSaha, A., Pal, S. C., Arabameri, A., Blaschke, T., Panahi, S., Chowdhuri, I., Chakrabortty, R., Costache, R., & Arora, A. (2021). Flood Susceptibility Assessment Using Novel Ensemble of Hyperpipes and Support Vector Regression Algorithms. Water, 13(2), 241. https://doi.org/10.3390/w13020241








