Improving Thermal Distribution in Water-Cooled PV Modules and Its Effect on RO Permeate Recovery
Abstract
1. Introduction
2. Materials and Methods
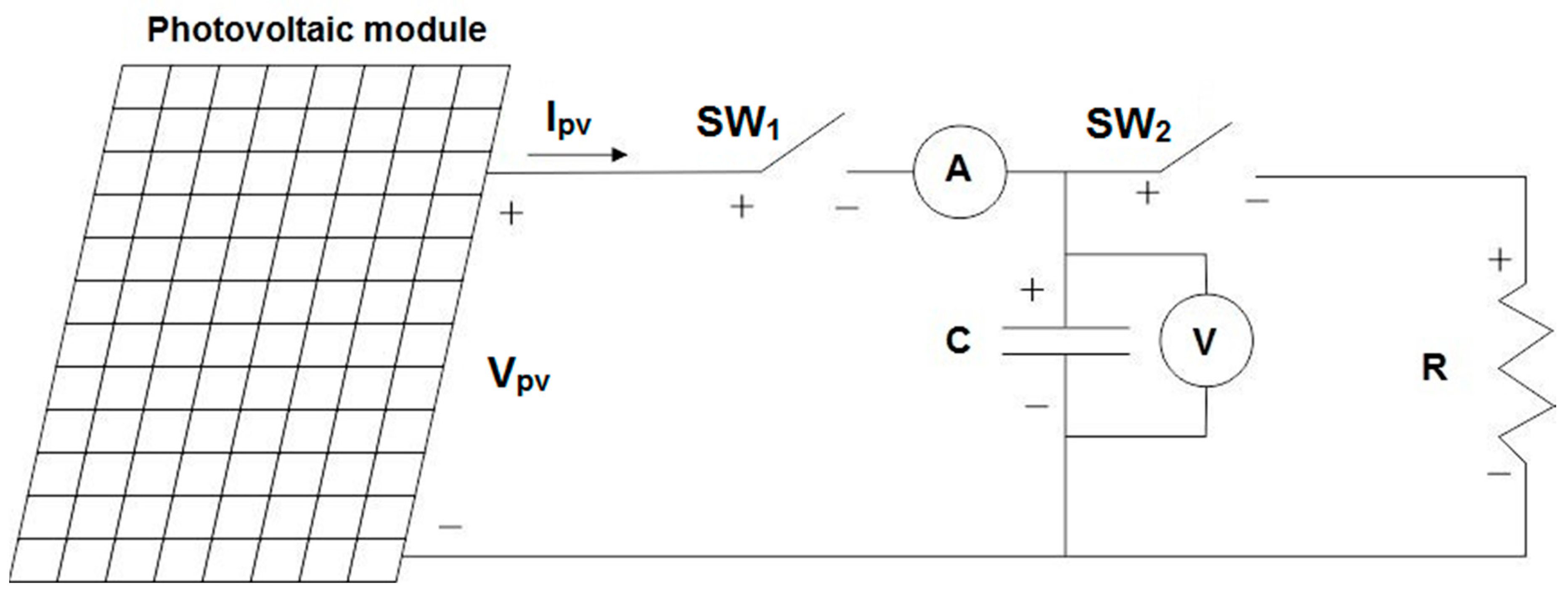
2.1. Characterisation of the PV Module
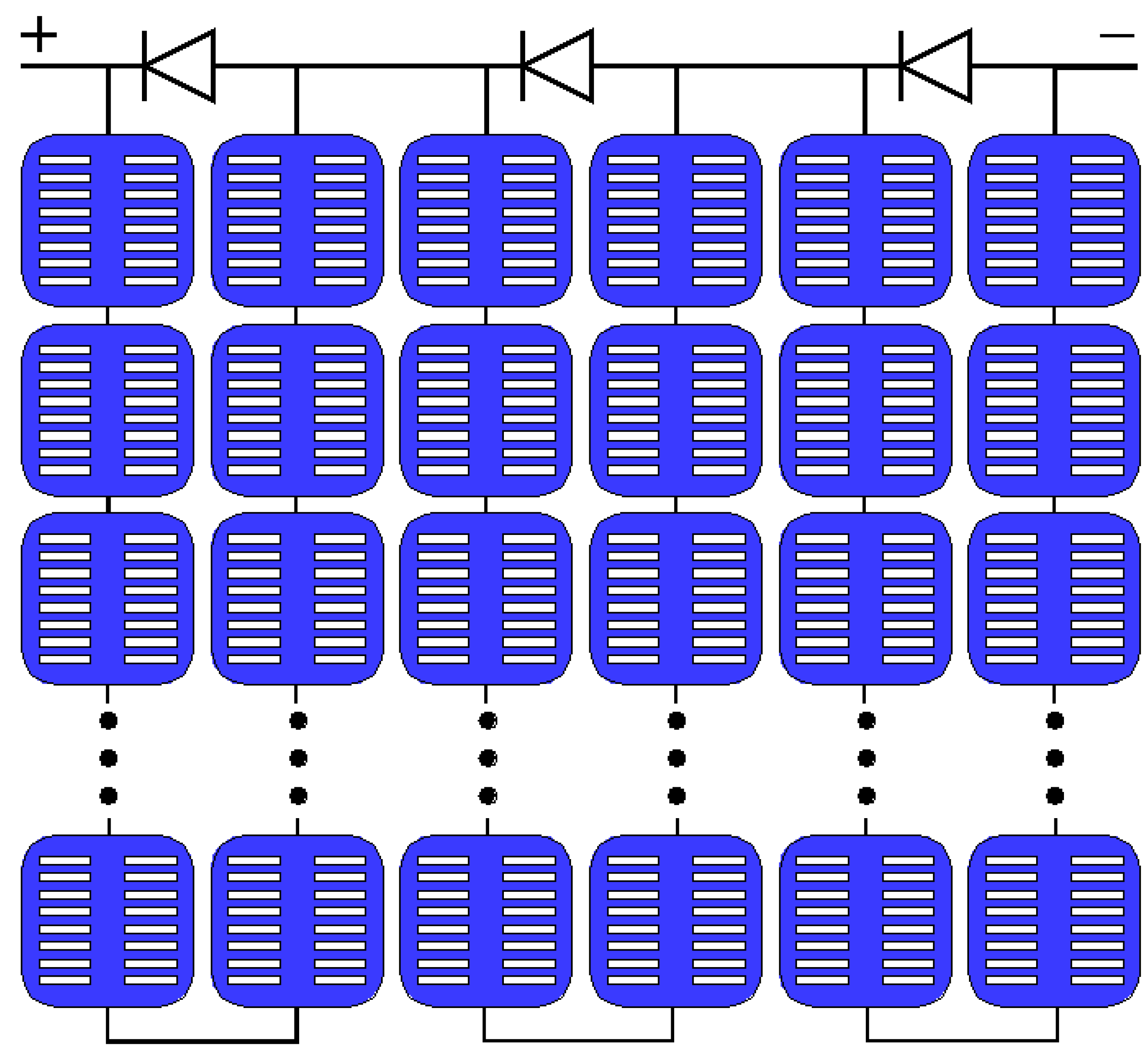
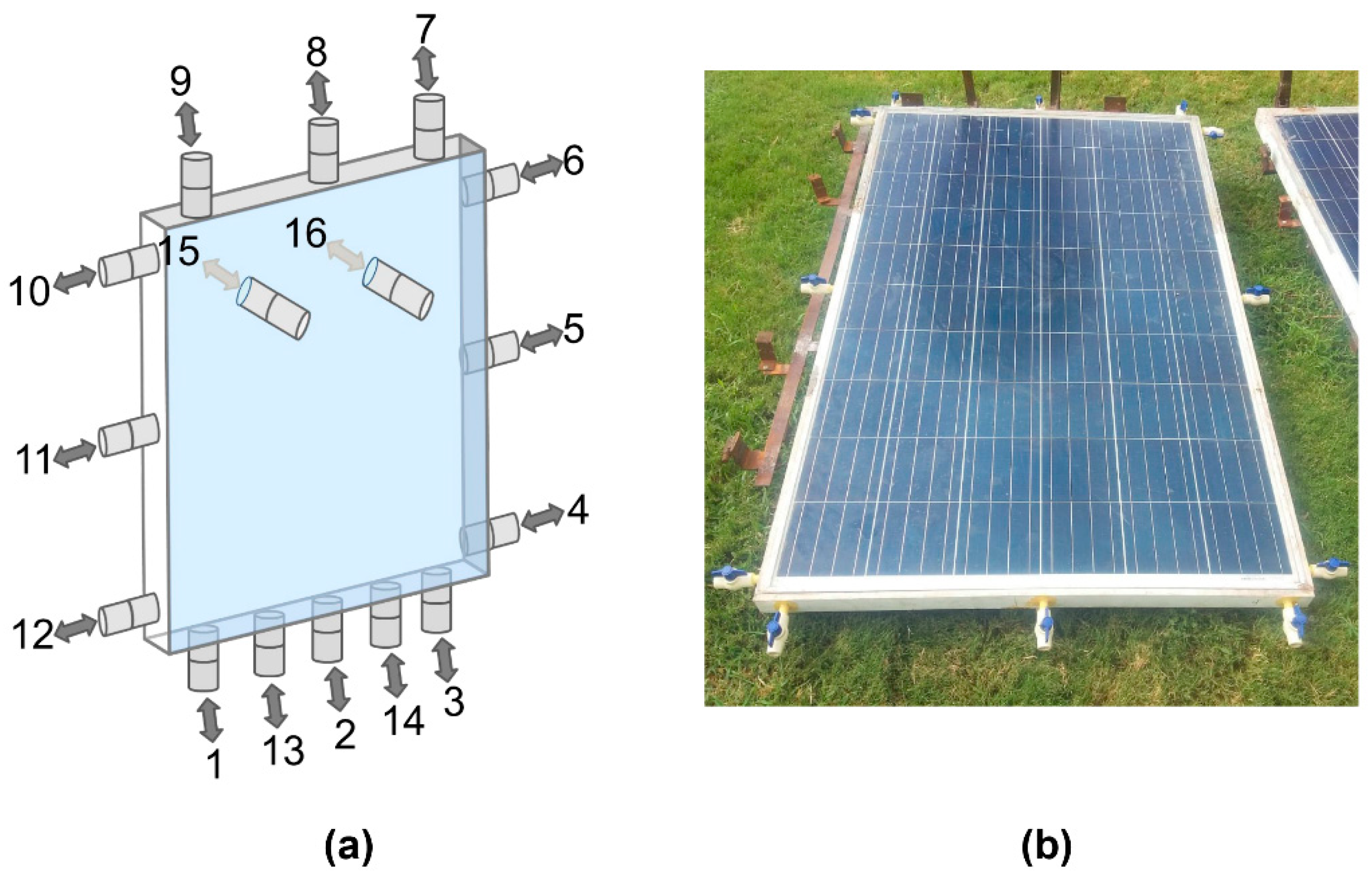
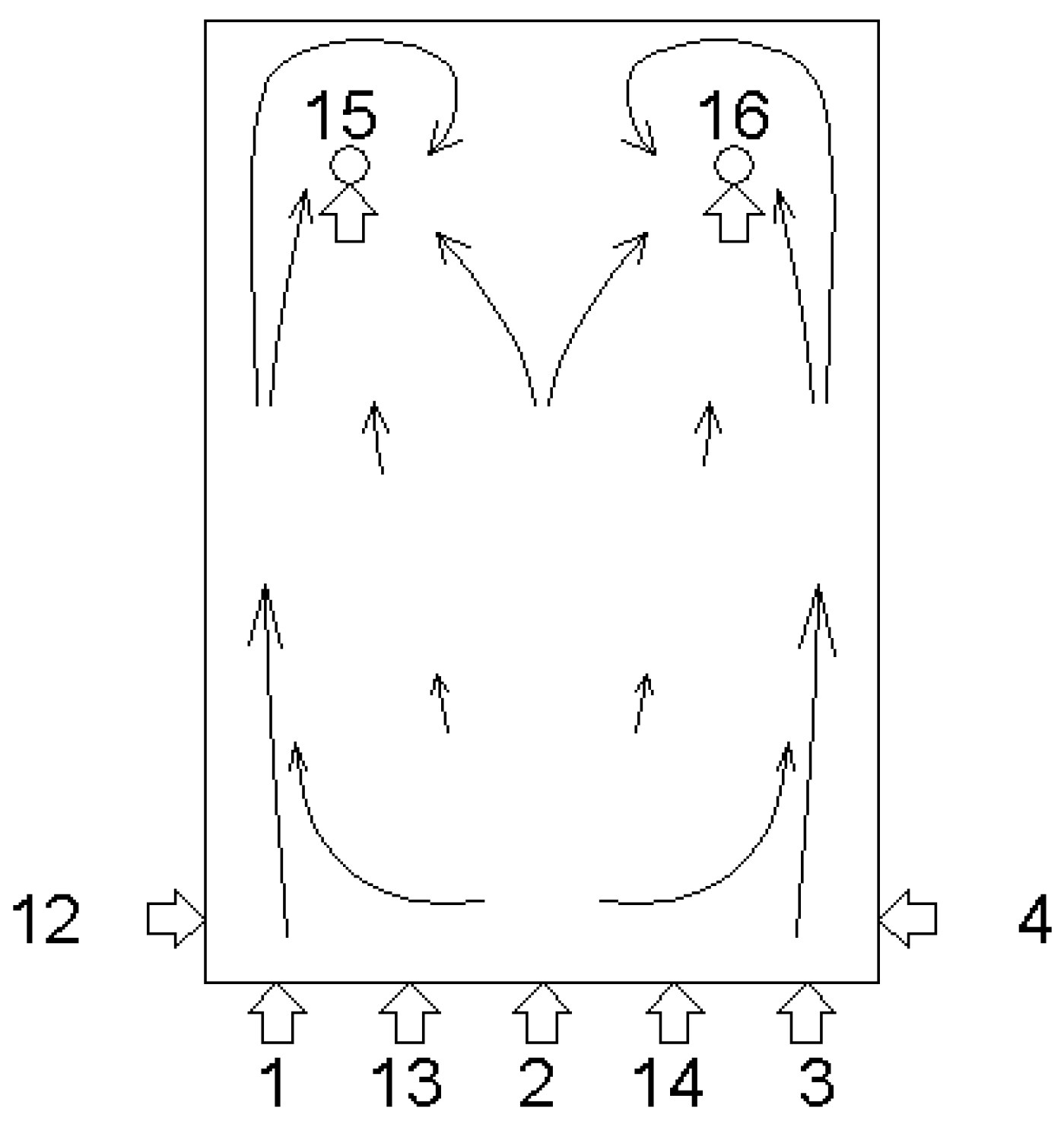
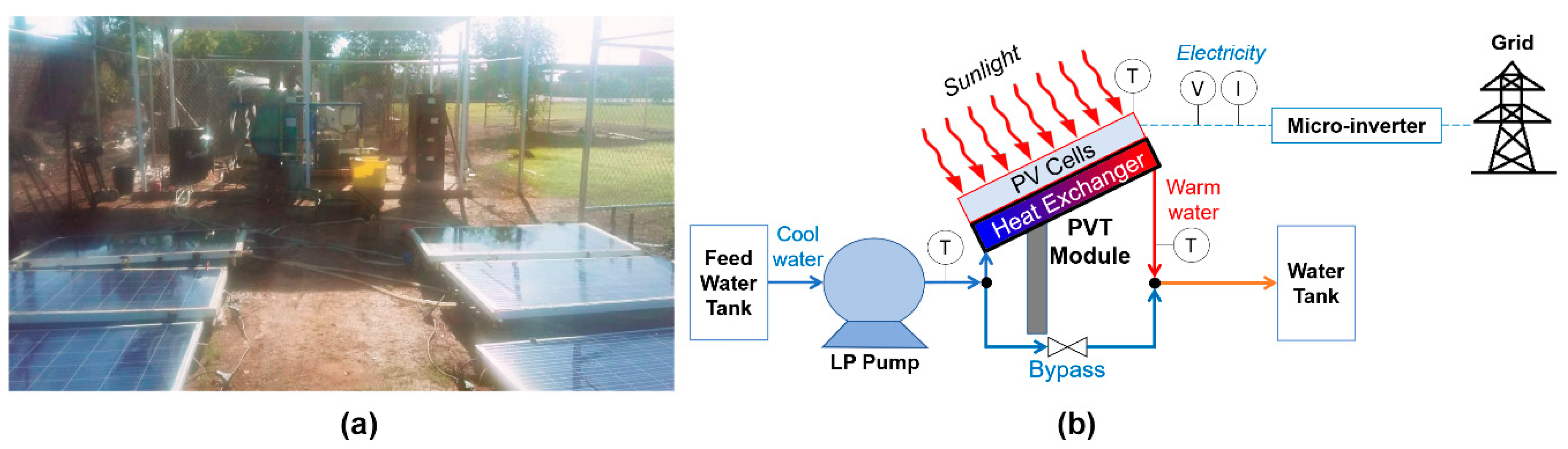
2.2. PVT Module Design
2.3. PVT Module Performance Analysis
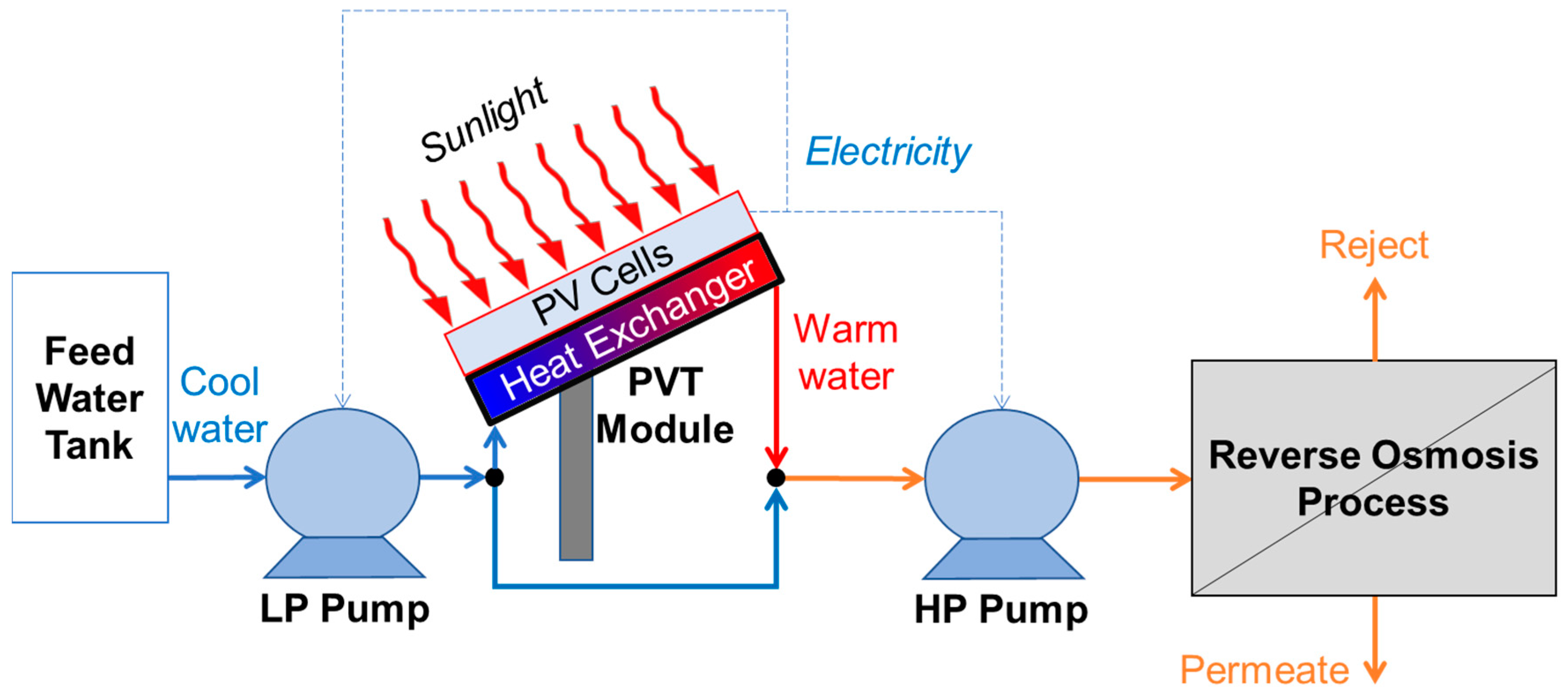
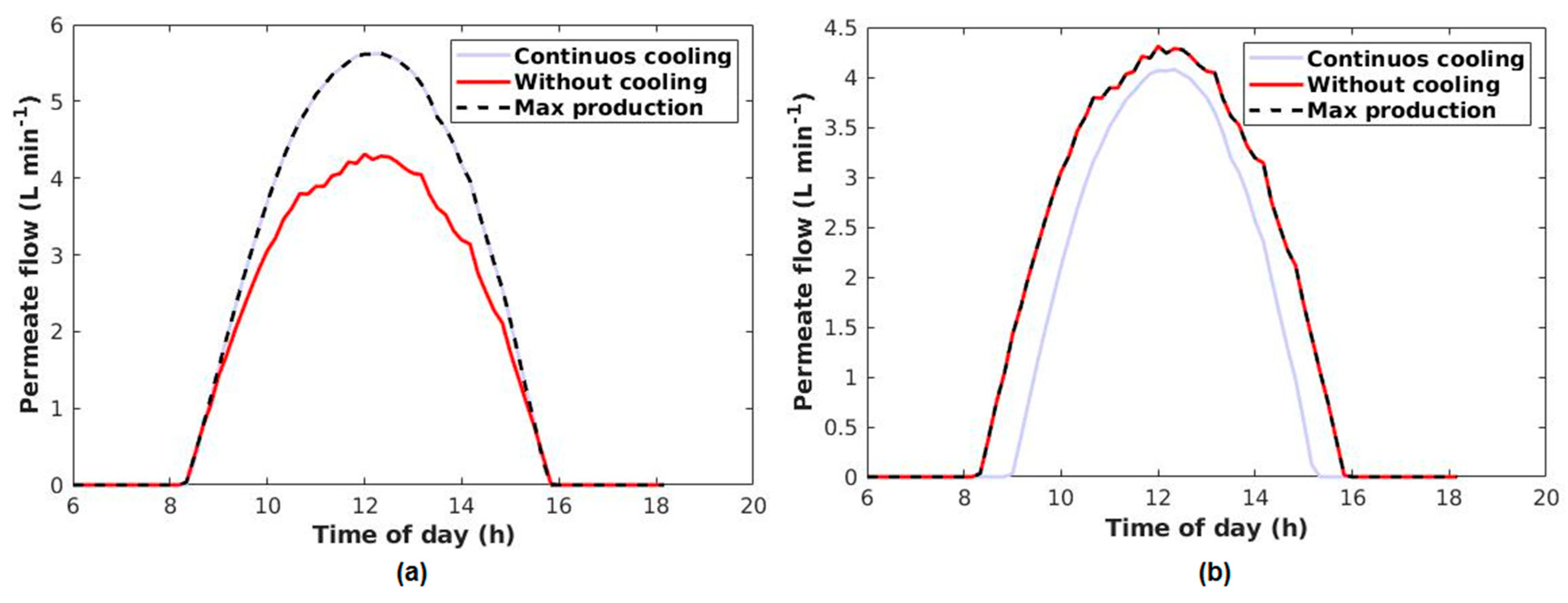
2.4. PVT-RO Simulation
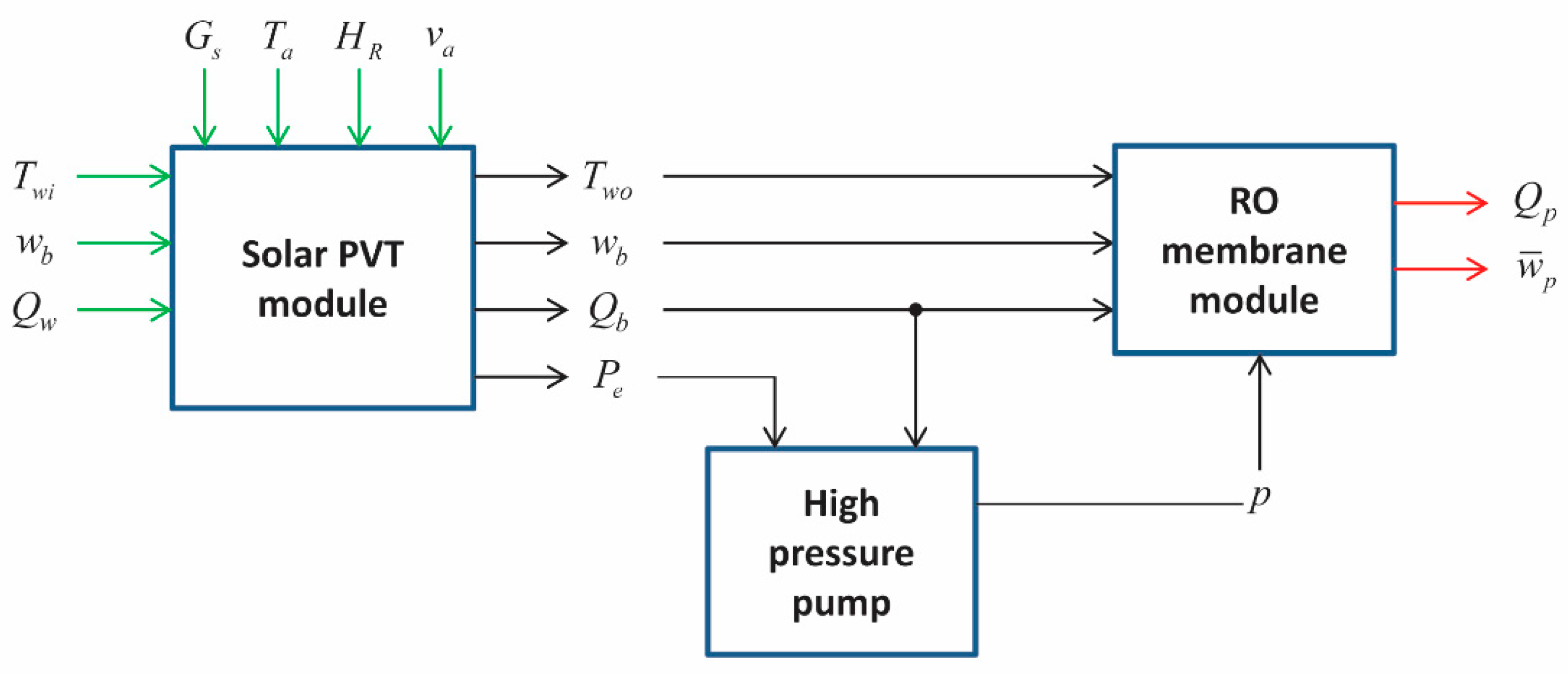
2.4.1. Solar PVT Module
2.4.2. HP Pump
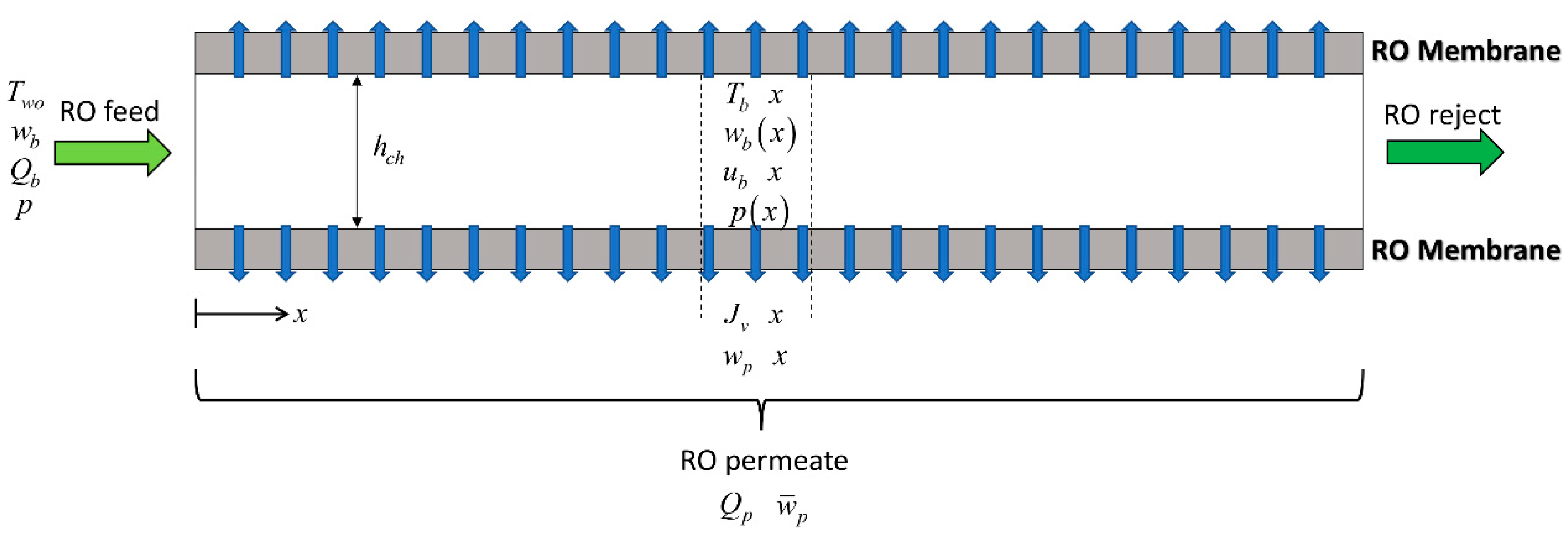
2.4.3. RO Membrane Module
3. Results and Discussion
3.1. PV Module Characterisation
3.2. Experimental Results of the PV Module Cooling Configurations
3.3. PVT-RO Modelling Results
4. Conclusions
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Variables | Description | Units |
| Am | Membrane area | m2 |
| APV | Active area of PVT module | m2 |
| Apa | Area of the PVT module in contact with the air | m2 |
| Apx | Contact area of PVT module with cooling water | m2 |
| Cpw | Heat capacity of cooling water | J kg−1 K−1 |
| D | Solute diffusivity | m2 s−1 |
| dh | Hydraulic diameter | m |
| Ee | Useful electrical energy produced over one day | W h |
| EPV | Rate of energy input to the PVT module | W |
| Ew | Rate of energy input to the cooling water | W |
| f | Fanning friction factor | - |
| FF | Fill factor | - |
| fθ | Angular dependence of solar absorptance | - |
| Gbeam | Beam solar irradiation | W m−2 |
| Gdif | Diffuse solar irradiation | W m−2 |
| Gs | Total solar irradiation | W m−2 |
| ha | Wind heat transfer coefficient | W m−2 K−1 |
| hch | RO membrane feed channel height | m |
| Ho | Extraterrestrial radiation on a horizontal surface | W m−2 |
| HR | Relative humidity | % |
| ΔHp,tm | Transmembrane pressure-enthalpy change | J kg−1 |
| ΔHT,tm | Transmembrane temperature-enthalpy change | J kg−1 |
| ΔHs,r | Specific enthalpy change of solution for NaCl at reference conditions | J kg−1 |
| Isc | Short-circuit current | A |
| Jv | Local volumetric permeate flux | m s−1 |
| kmt | Mass transfer coefficient on the membrane surface | m s−1 |
| kt | Hourly clearness index | - |
| L | RO module length | m |
| Ms | Molar mass of NaCl | kg mol−1 |
| Pe | Electric power available for the high-presure pump | W |
| Peo | Electric power output from the PVT module | W |
| PLP | Electric power required by the low-pressure pump | W |
| p | Pressure | Pa |
| pb | Pressure along feed channel fluid in RO module | Pa |
| pp | Permeate pressure | Pa |
| ΔpPVT | Pressure drop across the PVT heat exchanger | Pa |
| Δptm | Transmembrane pressure difference | Pa |
| Pr | Prandtl number | - |
| Qb | Volumetric flow rate in the feed channel of the RO module | m3 s−1 |
| Qp | Volumetric flow rate of RO permeate | m3 s−1, L min−1 |
| Qw | Cooling water volumetric flow rate | m3 s−1, L min−1 |
| qa | Rate of heat removal from the PVT module by convective heat transfer with the wind | W |
| qr | Rate of heat removal from the PVT module radiative heat transfer with the sky | W |
| qs | Rate of solar energy absorption by the PVT module | W |
| qw | Rate of heat removal from the PVT module by forced convection with cooling water | W |
| qx | Heat exchanged between PVT module and cooling water | W |
| Rg | Universal gas constant | J mol−1 K−1 |
| Rint | RO membrane intrinsic salt rejection | - |
| Rm | Hydraulic resistance of RO membrane | m−1 |
| Robs | Observed salt rejection for RO membrane module | - |
| Re | Reynolds number | - |
| Sc | Schmidt number | - |
| Sh | Sherwood number | - |
| T | Temperature | °C, K |
| Ta | Ambient temperature | °C, K |
| Tb | Temperature along feed channel in RO module | °C, K |
| Tdp | Dew point temperature | °C |
| TPV | PV module temperature | °C, K |
| TPV,max | Maximum PV module temperature | °C |
| Tr | Reference temperature | °C |
| Tsky | Sky temperature | K |
| Twi | Temperature of cooling water at PVT module inlet | °C |
| Two | Temperature of cooling water at PVT module outlet | °C |
| ΔTlm | Logarithmic mean temperature difference between PV module and cooling water | K |
| U | Overall heat transfer coefficient for cooling water heat exchange | W m−2 K |
| ub | Bulk feed flow velocity in membrane module | m s−1 |
| V | Voltage | V |
| va | Wind speed | m s−1 |
| Voc | Open-circuit voltage | V |
| Volp | Permeate volume produced over one day | m3 |
| W | Power | W |
| wb | Salinity mass fraction along feed channel fluid in RO module | - |
| wp | Salinity mass fraction of RO permeate | - |
| Greek Symbols | Description | Units |
| α | PV module solar absorptivity | - |
| β | Angle of incidence between the solar beam irradiation and the horizontal plane | ° |
| Г | Concentration polarisation modulus | - |
| ε | PV module emissivity | - |
| ϵ | Void fraction in feed channel of RO module | - |
| ∆η | Efficiency drop of PVT module | % |
| η | Electrical efficiency of PVT module | % |
| ηc | Electrical efficiency of PVT module under forced convective cooling | % |
| ηLP | Energy efficiency of the low-pressure pump | % |
| ηu | Electrical efficiency of PV module at uniform temperature | % |
| φ | Osmotic coefficient | - |
| μ | Fluid viscosity | Pa s |
| πm | Osmotic pressure on the feed side of the RO membrane surface | Pa |
| πp | Osmotic pressure on the permeate side of the RO membrane surface | Pa |
| θ | Angle of incidence between the solar beam irradiation and the PV module | ° |
| ρ | Density | kg m−3 |
| ρp | Density of the RO permeate | kg m−3 |
| ρw | Density of water | kg m−3 |
| σ | Stefan-Boltzmann constant | W m−2 K−4 |
| σT | Standard deviation of the PV module temperature distribution | K |
Abbreviations
| A | Oscilloscope current sensing probe |
| C | Capacitor |
| HP | High-pressure |
| LP | Low-pressure |
| ODE | Ordinary differential equation |
| PV | Photovoltaic |
| PVC | Polyvinyl chloride |
| PVT | Photovoltaic-thermal |
| R | Resistor |
| RO | Reverse osmosis |
| SW1 | Load capacitor switch 1 |
| SW2 | Load resistor switch 2 |
| V | Oscilloscope voltage sensing probe |
Appendix A
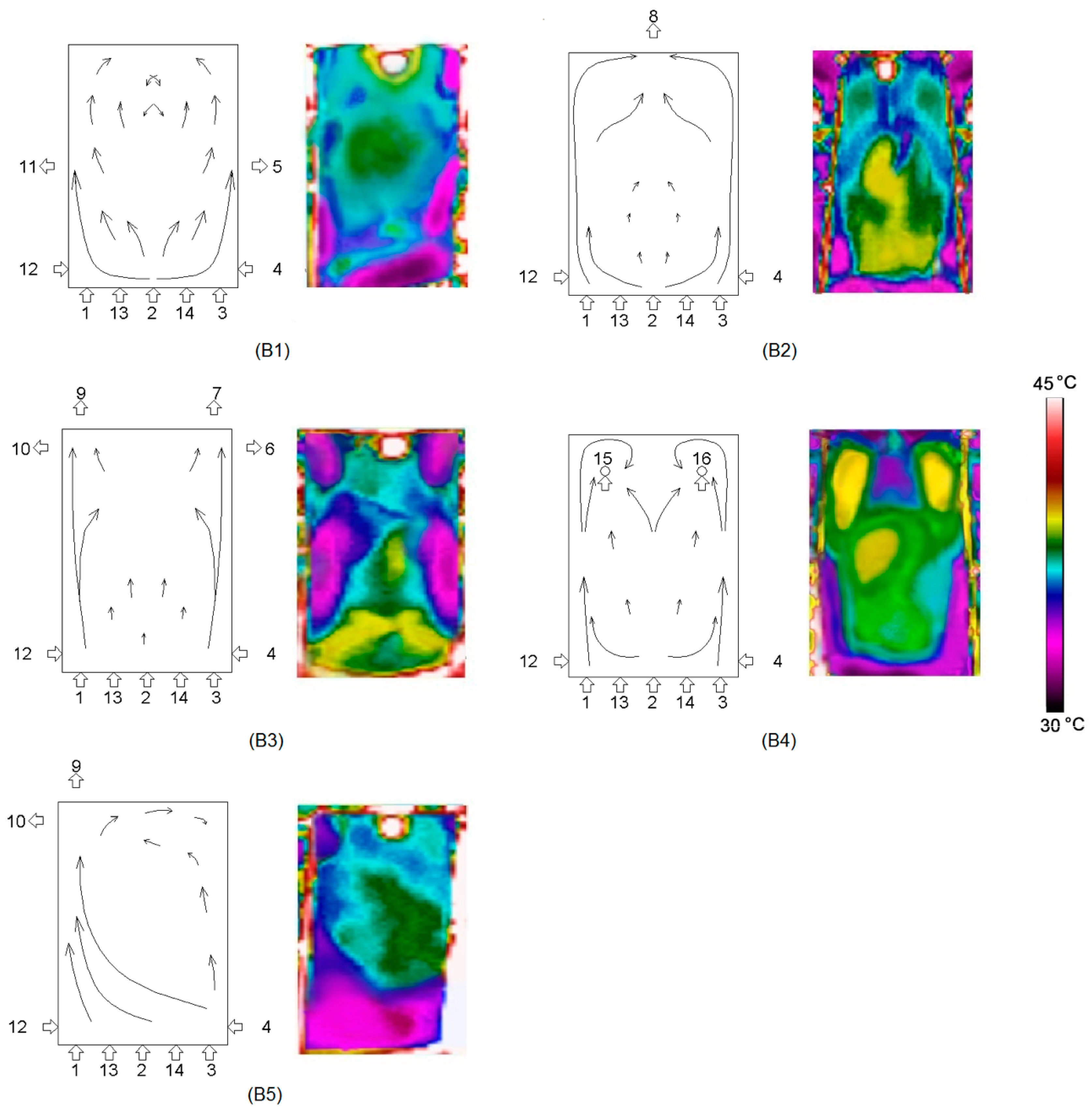
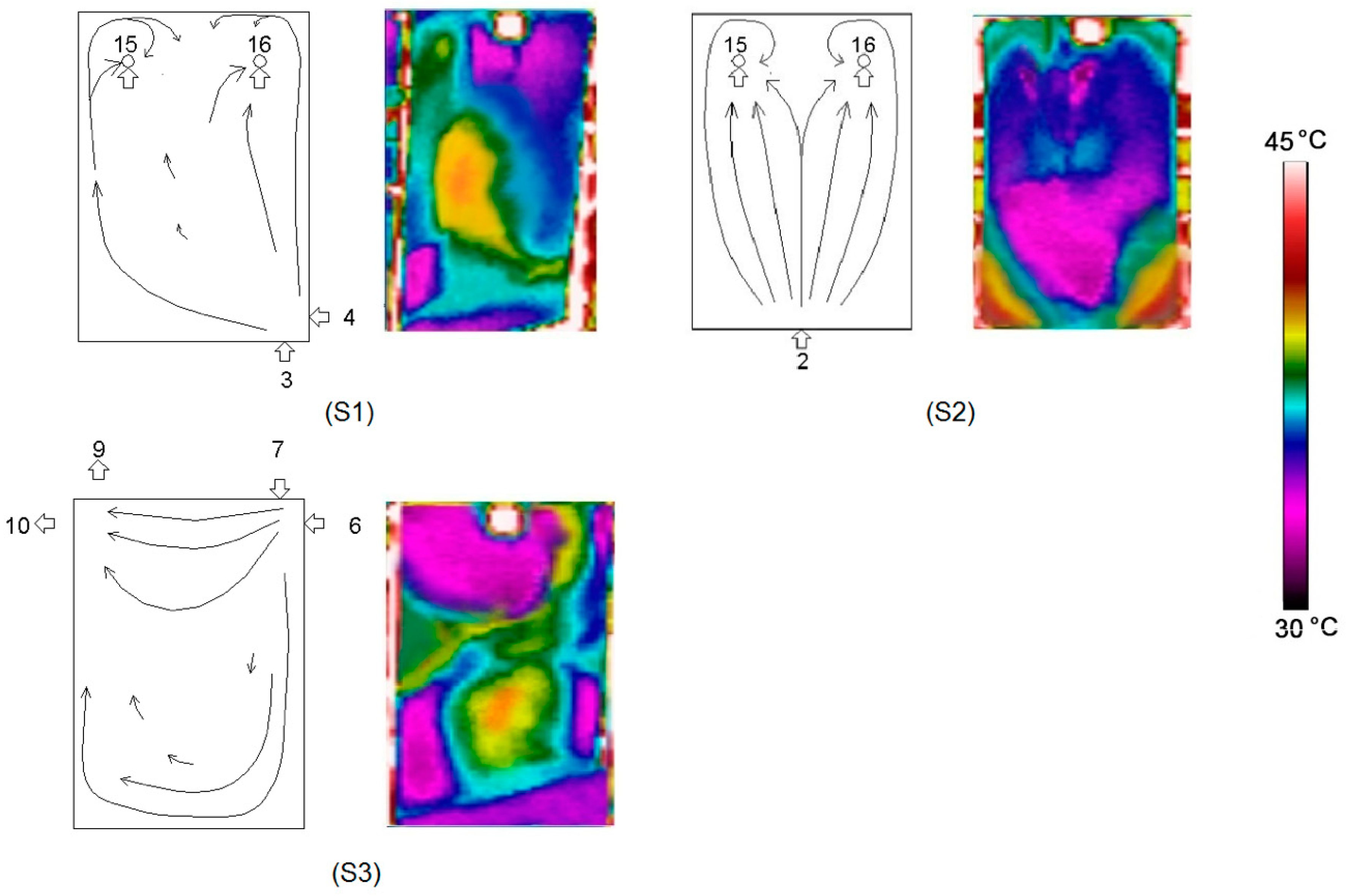
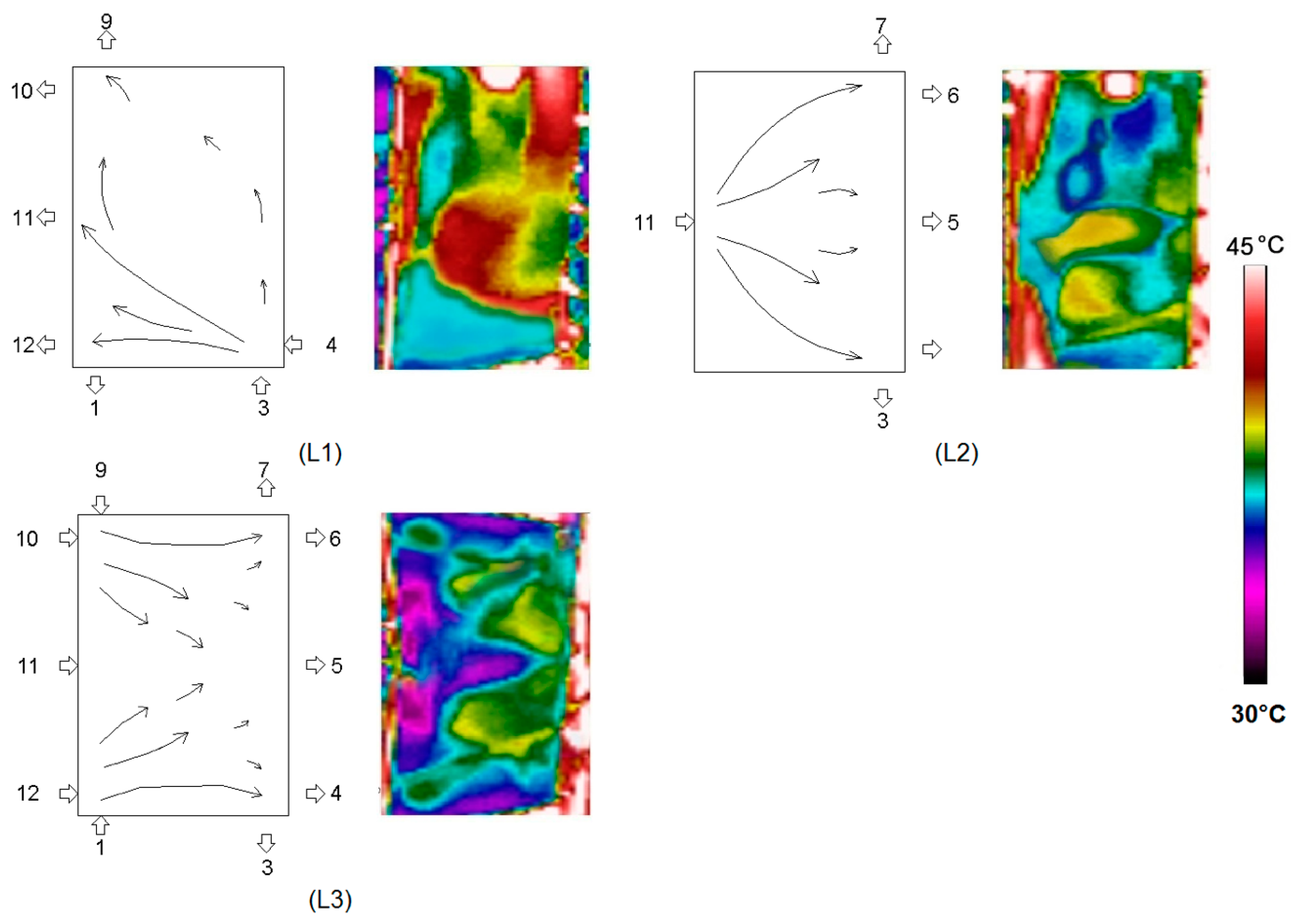
Appendix B
Appendix C
| Coefficient | Value |
|---|---|
| a0,1 | −301.03 |
| a1,1 | 35.872 |
| a2,1 | −2.6886 |
| a3,1 | 1.4446 |
| a4,1 | −1.75 × 10−5 |
| a5,1 | −6.5214 × 10−2 |
| a0,2 | 105.90 |
| a1,2 | −6.6648 |
| a2,2 | 1.2169 |
| a3,2 | 1.2325 × 10−2 |
| a4,2 | 1.24 × 10−7 |
| a5,2 | −1.1288 × 10−4 |
Appendix D
| Time of Day (h) | Gs (W m−2) | HR (%) | Ta (°C) | va (m s−1) |
|---|---|---|---|---|
| 6–7 | 316.66 | 57.07 | 31.71 | 1.491 |
| 7–8 | 528.33 | 47.81 | 33.65 | 1.574 |
| 8–9 | 715.00 | 41.85 | 35.11 | 1.542 |
| 9–10 | 853.33 | 35.33 | 36.74 | 1.238 |
| 10–11 | 936.66 | 38.37 | 37.11 | 1.395 |
| 11–12 | 973.33 | 37.52 | 37.43 | 1.283 |
| 12–13 | 936.66 | 29.94 | 38.53 | 1.059 |
| 13–14 | 836.66 | 27.36 | 38.97 | 1.113 |
| 14–15 | 686.66 | 26.47 | 39.48 | 0.959 |
| 15–16 | 495.00 | 30.79 | 38.96 | 0.995 |
| 16–17 | 275.00 | 38.06 | 37.16 | 1.112 |
| Time of Day (h) | Gs (W m−2) | HR (%) | Ta (°C) | va (m s−1) |
|---|---|---|---|---|
| 6–7 | 4.83 | 82.11 | 21.50 | 0.000 |
| 7–8 | 132.16 | 79.26 | 22.47 | 0.041 |
| 8–9 | 358.33 | 66.87 | 24.99 | 0.403 |
| 9–10 | 553.33 | 56.10 | 27.07 | 0.973 |
| 10–11 | 702.66 | 48.40 | 28.90 | 1.120 |
| 11–12 | 785.00 | 39.29 | 31.04 | 0.809 |
| 12–13 | 805.66 | 35.10 | 32.11 | 1.118 |
| 13–14 | 756.33 | 33.17 | 32.60 | 0.871 |
| 14–15 | 646.50 | 30.58 | 33.55 | 0.908 |
| 15–16 | 473.83 | 30.54 | 33.44 | 1.286 |
| 16–17 | 226.00 | 36.00 | 32.31 | 1.540 |
| 17–18 | 22.83 | 41.08 | 30.17 | 1.508 |
| Time of Day (h) | Gs (W m−2) | HR (%) | Ta (°C) | va (m s−1) |
|---|---|---|---|---|
| 6–7 | 0.00 | 87.66 | 10.04 | 0.000 |
| 7–8 | 9.50 | 88.05 | 9.87 | 0.000 |
| 8–9 | 143.00 | 87.51 | 10.75 | 0.211 |
| 9–10 | 373.00 | 78.96 | 13.24 | 1.517 |
| 10–11 | 534.16 | 65.64 | 16.16 | 1.259 |
| 11–12 | 644.00 | 51.78 | 18.58 | 1.302 |
| 12–13 | 685.66 | 41.61 | 20.65 | 1.363 |
| 13–14 | 660.16 | 32.71 | 21.76 | 1.246 |
| 14–15 | 569.00 | 26.25 | 22.57 | 1.246 |
| 15–16 | 412.33 | 24.67 | 23.19 | 1.042 |
| 16–17 | 186.66 | 24.42 | 22.91 | 1.193 |
| 17–18 | 11.00 | 38.23 | 20.59 | 0.869 |
| Configuration | Cooling Water Flow Rate, Qw (L min−1) | |||
|---|---|---|---|---|
| 1 | 2 | 1 | 2 | |
| PVT Average Outlet Water Temperature, Two (°C) | ||||
| 24 July 2018 | 20 October 2019 | |||
| B1 | 35.8 ± 2.7 | 32.1 ± 1.3 | 26.3 ± 2.4 | 22.6 ± 1.4 |
| B2 | 32.9 ± 1.6 | 30.6 ± 0.7 | 23.3 ± 1.7 | 21.5 ± 0.8 |
| B3 | 33.8 ± 2.0 | 31.6 ± 1.1 | 24.0 ± 2.1 | 22.3 ± 1.2 |
| B4 | 32.1 ± 1.3 | 31.3 ± 1.0 | 22.7 ± 1.4 | 22.1 ± 1.1 |
| B5 | 33.0 ± 1.7 | 31.1 ± 0.9 | 23.4 ± 1.8 | 21.9 ± 1.0 |
| S1 | 32.8 ± 1.6 | 31.1 ± 0.9 | 23.3 ± 1.7 | 21.9 ± 1.0 |
| S2 | 34.1 ± 2.1 | 31.7 ± 1.1 | 24.2 ± 2.2 | 22.3 ± 1.2 |
| S3 | 32.3 ± 1.4 | 31.4 ± 1.1 | 22.9 ± 1.5 | 22.2 ± 1.4 |
| L1 | 34.5 ± 2.2 | 32.3 ± 1.4 | 24.6 ± 2.3 | 22.8 ± 1.4 |
| L2 | 32.8 ± 1.6 | 31.6 ± 1.1 | 23.3 ± 1.7 | 22.3 ± 1.2 |
| L3 | 32.3 ± 1.4 | 31.1 ± 0.9 | 22.9 ± 1.5 | 21.9 ± 1.0 |
References
- Pandey, V.P.; Shrestha, S. Evolution of the nexus as a policy and development discourse. Water-Energy-Food Nexus Princ. Pract. 2017, 1, 11–20. [Google Scholar] [CrossRef]
- Cairns, R.; Krzywoszynska, A. Anatomy of a buzzword: The emergence of ‘the water-energy-food nexus’ in UK natural resource debates. Environ. Sci. Policy 2016, 64, 164–170. [Google Scholar] [CrossRef]
- Armendáriz-Ontiveros, M.M.; Álvarez-Sánchez, J.; Dévora-Isiordia, G.E.; García, A.; Fimbres Weihs, G.A. Effect of seawater variability on endemic bacterial biofouling of a reverse osmosis membrane coated with iron nanoparticles (FeNPs). Chem. Eng. Sci. 2020, 223, 115753. [Google Scholar] [CrossRef]
- Cherif, H.; Belhadj, J. Environmental Life Cycle Analysis of Water Desalination Processes. In Sustainable Desalination Handbook; Elsevier: Amsterdam, The Netherlands, 2018; pp. 527–559. [Google Scholar] [CrossRef]
- Leijon, J.; Salar, D.; Engström, J.; Leijon, M.; Boström, C. Variable renewable energy sources for powering reverse osmosis desalination, with a case study of wave powered desalination for Kilifi, Kenya. Desalination 2020, 494, 114669. [Google Scholar] [CrossRef]
- Khan, M.A.M.; Rehman, S.; Al-Sulaiman, F.A. A hybrid renewable energy system as a potential energy source for water desalination using reverse osmosis: A review. Renew. Sustain. Energy Rev. 2018, 97, 456–477. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhengming, Z.; Yuan, L. A review of renewable energy technologies integrated with desalination systems. Renew. Sustain. Energy Rev. 2009, 13, 2245–2262. [Google Scholar] [CrossRef]
- Rezk, H.; Sayed, E.T.; Al-Dhaifallah, M.; Obaid, M.; El-Sayed, A.H.M.; Abdelkareem, M.A.; Olabi, A.G. Fuel cell as an effective energy storage in reverse osmosis desalination plant powered by photovoltaic system. Energy 2019, 175, 423–433. [Google Scholar] [CrossRef]
- Elmaadawy, K.; Kotb, K.M.; Elkadeem, M.R.; Sharshir, S.W.; Dán, A.; Moawad, A.; Liu, B. Optimal sizing and techno-enviro-economic feasibility assessment of large-scale reverse osmosis desalination powered with hybrid renewable energy sources. Energy Convers. Manag. 2020, 224, 113377. [Google Scholar] [CrossRef]
- Mostafaeipour, A.; Qolipour, M.; Rezaei, M.; Babaee-Tirkolaee, E. Investigation of off-grid photovoltaic systems for a reverse osmosis desalination system: A case study. Desalination 2019, 454, 91–103. [Google Scholar] [CrossRef]
- Schies, A.; Went, J.; Heidtmann, C.; Eisele, M.; Kroemke, F.; Schmoch, H.; Vetter, M. Operating control strategies and dimensioning of photovoltaic powered reverse osmosis desalination plants without batteries. Desalination Water Treat. 2010, 21, 131–137. [Google Scholar] [CrossRef]
- Raval, H.D.; Maiti, S. Ultra-low energy reverse osmosis with thermal energy recovery from photovoltaic panel cooling and TFC RO membrane modification. Desalination Water Treat. 2016, 57, 4303–4312. [Google Scholar] [CrossRef]
- Siecker, J.; Kusakana, K.; Numbi, B. A review of solar photovoltaic systems cooling technologies. Renew. Sustain. Energy Rev. 2017, 79, 192–203. [Google Scholar] [CrossRef]
- Luque, A.; Sala, G.; Arboiro, J. Electric and thermal model for non-uniformly illuminated concentration cells. Sol. Energy Mater. Sol. Cells 1998, 51, 269–290. [Google Scholar] [CrossRef]
- Royne, A.; Dey, C.J.; Mills, D.R. Cooling of photovoltaic cells under concentrated illumination: A critical review. Sol. Energy Mater. Sol. Cells 2005, 86, 451–483. [Google Scholar] [CrossRef]
- Bahaidarah, H.M.; Baloch, A.A.; Gandhidasan, P. Uniform cooling of photovoltaic panels: A review. Renew. Sustain. Energy Rev. 2016, 57, 1520–1544. [Google Scholar] [CrossRef]
- Zhang, C.; Shen, C.; Wei, S.; Wang, Y.; Lv, G.; Sun, C. A review on recent development of cooling technologies for photovoltaic modules. J. Therm. Sci. 2020, 29, 1410–1430. [Google Scholar] [CrossRef]
- Raval, H.D.; Maiti, S.; Mittal, A. Computational fluid dynamics analysis and experimental validation of improvement in overall energy efficiency of a solar photovoltaic panel by thermal energy recovery. J. Renew. Sustain. Energy 2014, 6, 033138. [Google Scholar] [CrossRef]
- Jin, X.; Jawor, A.; Kim, S.; Hoek, E.M.V. Effects of feed water temperature on separation performance and organic fouling of brackish water RO membranes. Desalination 2009, 239, 346–359. [Google Scholar] [CrossRef]
- Monjezi, A.A.; Chen, Y.; Vepa, R.; Kashyout, A.E.-H.B.; Hassan, G.; Fath, H.E.-B.; Kassem, A.E.-W.; Shaheed, M.H. Development of an off-grid solar energy powered reverse osmosis desalination system for continuous production of freshwater with integrated photovoltaic thermal (PVT) cooling. Desalination 2020, 495, 114679. [Google Scholar] [CrossRef]
- Spertino, F.; Ahmad, J.; Ciocia, A.; Di Leo, P.; Murtaza, A.F.; Chiaberge, M. Capacitor charging method for I–V curve tracer and MPPT in photovoltaic systems. Sol. Energy 2015, 119, 461–473. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard, J.H.; Zubair, S.M. Thermophysical properties of seawater: A review of existing correlations and data. Desalination Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Sun, H.; Feistel, R.; Koch, M.; Markoe, A. New equations for density, entropy, heat capacity, and potential temperature of a saline thermal fluid. Deep Sea Res. Part I Oceanogr. Res. Pap. 2008, 55, 1304–1310. [Google Scholar] [CrossRef]
- Isdale, J.D.; Morris, R. Physical properties of sea water solutions: Density. Desalination 1972, 10, 329–339. [Google Scholar] [CrossRef]
- Gosset, E. Another differences calculus based on standar desviation and confidence interval. Stat. Ref. 1917, 26, 66–72. [Google Scholar]
- Kaiser, H.F. An index of factorial simplicity. Psychometrika 1974, 39, 31–36. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Toh, K.Y.; Liang, Y.Y.; Lau, W.J.; Fimbres Weihs, G.A. The techno-economic case for coupling advanced spacers to high-permeance RO membranes for desalination. Desalination 2020, 491, 114534. [Google Scholar] [CrossRef]
- Bartholomew, T.V.; Mauter, M.S. Computational framework for modeling membrane processes without process and solution property simplifications. J. Membr. Sci. 2019, 573, 682–693. [Google Scholar] [CrossRef]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers, 6th ed.; McGraw-Hill: New York, NY, USA, 2010; p. 968. [Google Scholar]
- Kedem, O.; Katchalsky, A. Thermodynamic Analysis of the Permeability of Biological Membranes to Non-Electrolytes. Biochim. Biophys. Acta 1958, 27, 229. [Google Scholar] [CrossRef]
- FILMTEC. FILMTEC 8” Brackish Water RO Element Specifications. In Product Information; FilmTec Corporation, Ed.; FILMTEC: Minneapolis, MN, USA, 1988; Volume 609-00616-0808. [Google Scholar]
- Schock, G.; Miquel, A. Mass transfer and pressure loss in spiral wound modules. Desalination 1987, 64, 339–352. [Google Scholar] [CrossRef]
- Sivertsen, E.; Holt, T.; Thelin, W.R. Concentration and Temperature Effects on Water and Salt Permeabilities in Osmosis and Implications in Pressure-Retarded Osmosis. Membranes 2018, 8, 39. [Google Scholar] [CrossRef]
- Boland, J.; Ridley, B.; Brown, B. Models of diffuse solar radiation. Renew. Energy 2008, 33, 575–584. [Google Scholar] [CrossRef]
- Ridley, B.; Boland, J.; Lauret, P. Modelling of diffuse solar fraction with multiple predictors. Renew. Energy 2010, 35, 478–483. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Sherwood, T.K. The Properties of Gases and Liquids, 3rd ed.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Chong, T.H.; Wong, F.S.; Fane, A.G. Enhanced concentration polarization by unstirred fouling layers in reverse osmosis: Detection by sodium chloride tracer response technique. J. Membr. Sci. 2007, 287, 198–210. [Google Scholar] [CrossRef]
- Armendáriz-Ontiveros, M.M.; García García, A.; de los Santos Villalobos, S.; Fimbres Weihs, G.A. Biofouling performance of RO membranes coated with Iron NPs on graphene oxide. Desalination 2019, 451, 45–58. [Google Scholar] [CrossRef]
- Liang, Y.Y.; Fimbres Weihs, G.A.; Wiley, D.E. Comparison of oscillating flow and slip velocity mass transfer enhancement in spacer-filled membrane channels: CFD analysis and validation. J. Membr. Sci. 2020, 593, 117433. [Google Scholar] [CrossRef]
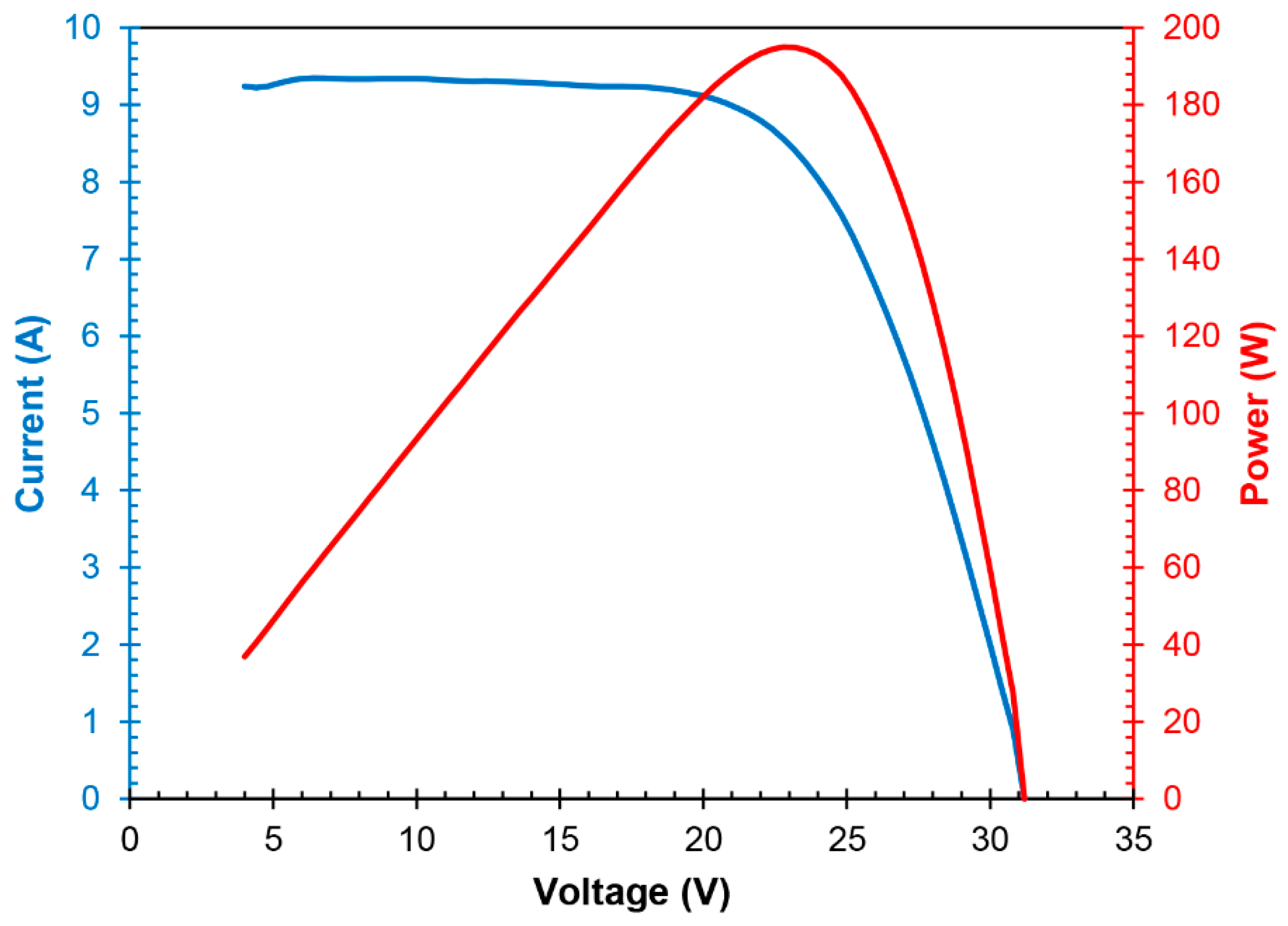
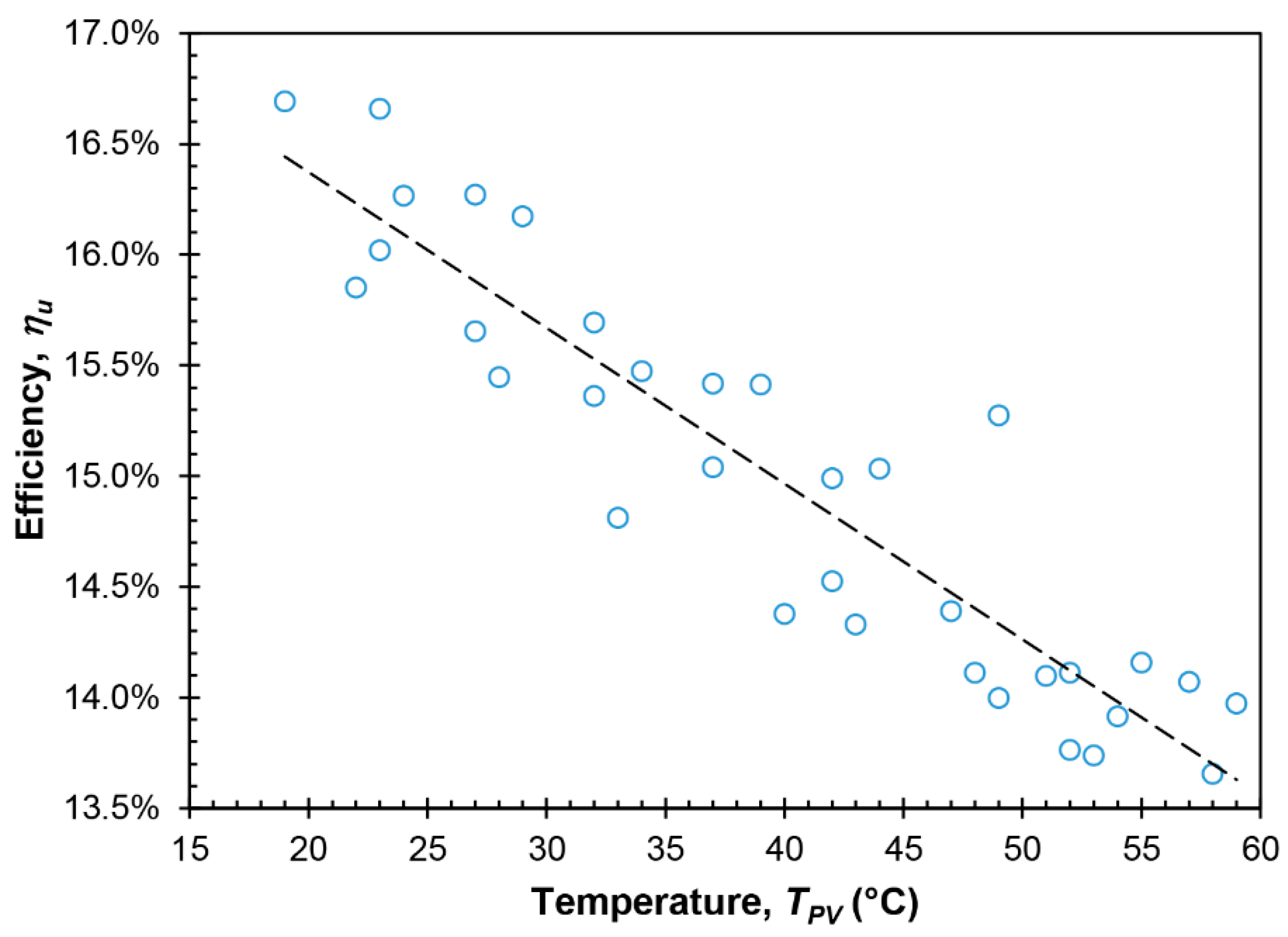
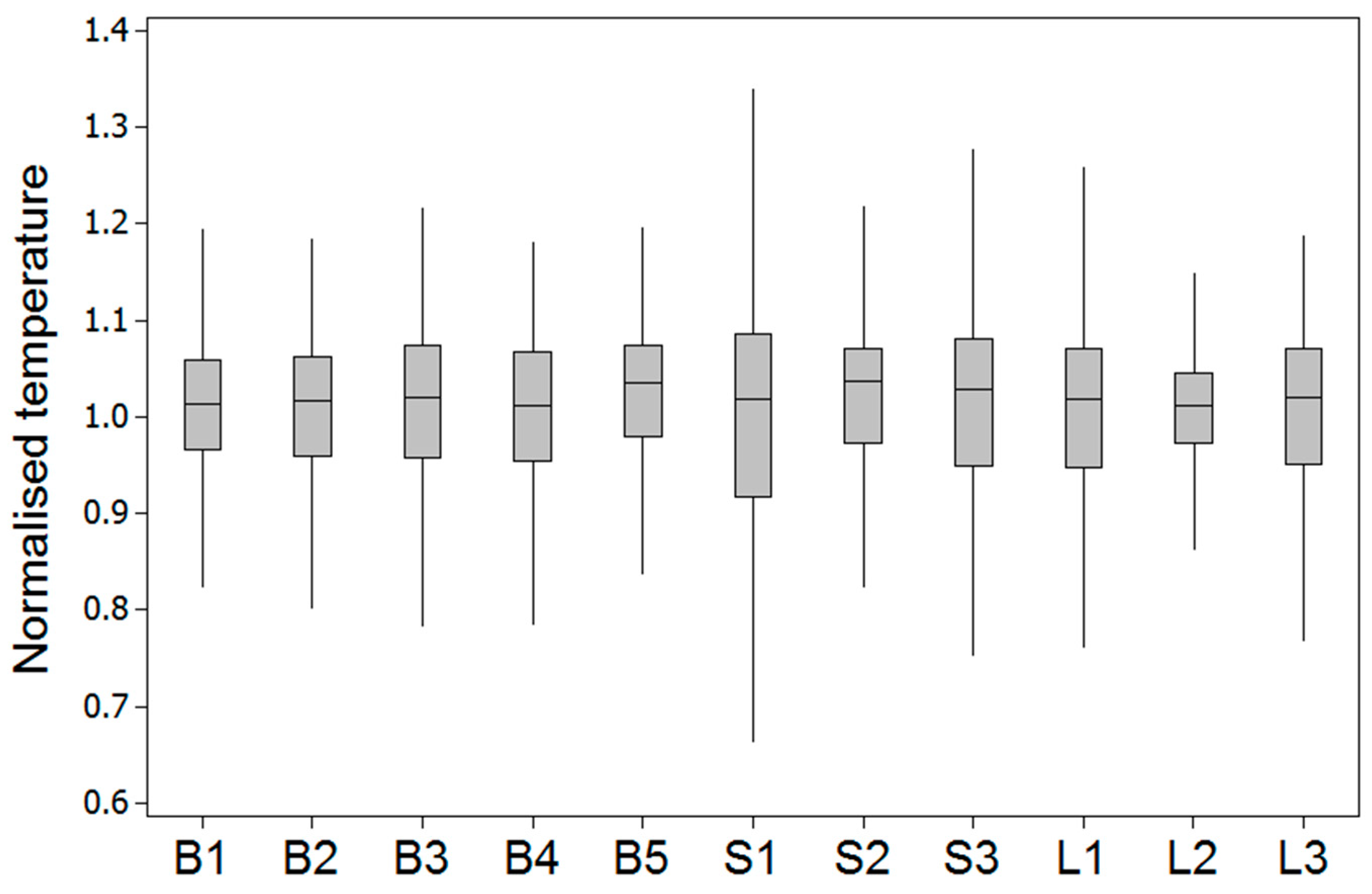
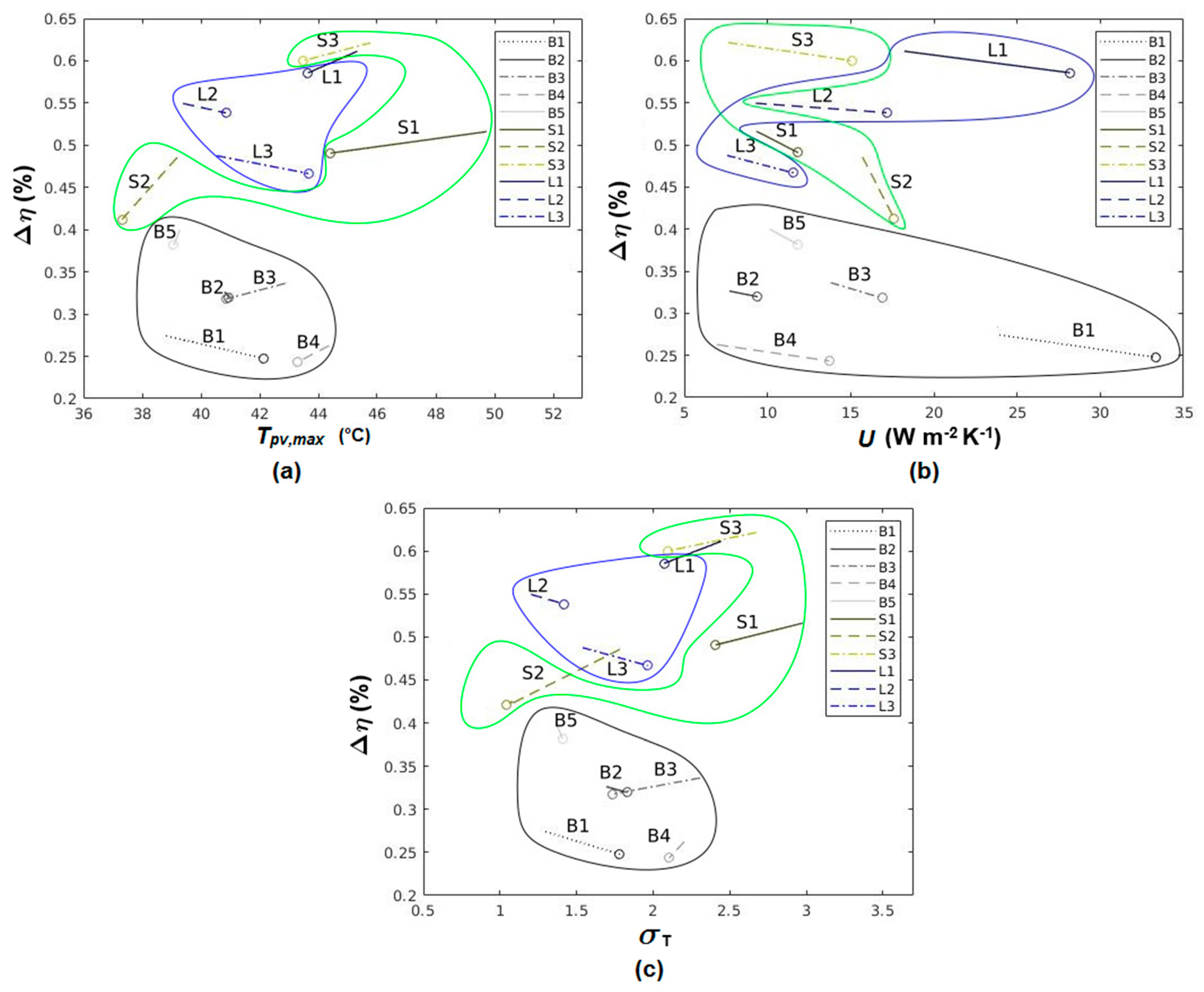
| Parameter | Value | Units |
|---|---|---|
| Rated power | 270 | W |
| Rated voltage | 31.12 | V |
| Rated current | 8.71 | A |
| Short circuit current (Icc) | 9.25 | A |
| Open circuit voltage (Voc) | 38.21 | V |
| Efficiency (η) | 16.60 | % |
| Fill factor (FF) | 0.766 | - |
| Dimensions | 1640 × 992 × 35 | mm |
| Effective area (APV) | 1.47 | m2 |
| Operating temperature | −40 to 85 | °C |
| Configuration | Inlet (s) | Outlet (s) |
|---|---|---|
| B1 | 1, 2, 3, 4, 12, 13, 14 | 5, 11 |
| B2 | 1, 2, 3, 4, 12, 13, 14 | 8 |
| B3 | 1, 2, 3, 4, 12, 13, 14 | 6, 7, 9, 10 |
| B4 | 1, 2, 3, 4, 12, 13, 14 | 15, 16 |
| B5 | 1, 2, 3, 4, 12, 13, 14 | 9, 10 |
| S1 | 3, 4 | 15, 16 |
| S2 | 2 | 15, 16 |
| S3 | 6, 7 | 9, 10 |
| L1 | 3, 4 | 1, 9, 10, 11, 12 |
| L2 | 11 | 3, 4, 5, 6, 7 |
| L3 | 1, 9, 10, 11, 12 | 3, 4, 5, 6, 7 |
| Parameter | Value | Units |
|---|---|---|
| Membrane length [32] | 0.955 | m |
| Membrane area [32] | 2.8 | m2 |
| Feed channel height (hch) [33] | 0.77 | mm |
| Feed channel void fraction () [33] | 0.89 | mm |
| Feed channel hydraulic diameter (dh) [33] | 0.95 | mm |
| PV module area (Ap) | 1.52 | m2 |
| Cooling water film thickness | 0.027 | m |
| Cooling water inlet temperature (Twi) | 25 | °C |
| Number of PVT modules | 4 | modules |
| Cooling water inlet salinity (wb) | 500 | ppm |
| Total water flow (Qb) | 8 | L min−1 |
| Pearson Correlation Coefficient between Δη and: | ||||
|---|---|---|---|---|
| Configuration | Qw | U | σT | TPV,max |
| B1 | −0.57 | 0.67 | −0.27 | −0.82 |
| B2 | −0.50 | 0.31 | 0.59 | 0.58 |
| B3 | −0.62 | 0.05 | 0.70 | 0.83 |
| B4 | −0.73 | −0.50 | −0.45 | −0.40 |
| B5 | −0.31 | −0.68 | −0.29 | −0.28 |
| S1 | −0.83 | −0.46 | −0.34 | −0.15 |
| S2 | −0.93 | −0.22 | 0.21 | 0.04 |
| S3 | −0.35 | −0.68 | 0.53 | 0.31 |
| L1 | −0.51 | −0.20 | 0.64 | 0.52 |
| L2 | −0.79 | −0.67 | 0.16 | 0.40 |
| L3 | −0.48 | −0.18 | −0.92 | 0.90 |
| Overall | −0.10 | −0.07 | 0.18 | 0.22 |
| Scenario | Volp (m3) | Ee (Wh) | wp (ppm) | Volp (m3) | Ee (Wh) | wp (ppm) | Volp (m3) | Increase (%) | Volp (m3) | Increase (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| WithoutCooling | 1.296 | 884 | 4.3 | ||||||||
| Scenario | Continuous Cooling | Max Production | |||||||||
| Qw | 1 L min−1 | 2 L min−1 | 1 L min−1 | 2 L min−1 | |||||||
| B1 | 1.650 | 913 | 8.4 | 1.002 | 636 | 8.1 | 1.650 | 27.5% | 1.296 | - | |
| B2 | 1.452 | 879 | 6.2 | 0.834 | 603 | 6.3 | 1.458 | 12.6% | 1.296 | - | |
| B3 | 1.506 | 888 | 6.8 | 0.936 | 622 | 7.2 | 1.506 | 16.4% | 1.296 | - | |
| B4 | 1.404 | 872 | 5.8 | 0.906 | 614 | 6.9 | 1.410 | 9.2% | 1.296 | - | |
| B5 | 1.440 | 875 | 6.3 | 0.888 | 617 | 6.8 | 1.440 | 11.5% | 1.296 | - | |
| S1 | 1.410 | 869 | 6.1 | 0.906 | 627 | 6.8 | 1.416 | 9.7% | 1.296 | - | |
| S2 | 1.512 | 888 | 7.0 | 0.966 | 635 | 7.2 | 1.518 | 17.3% | 1.296 | - | |
| S3 | 1.422 | 874 | 6.0 | 0.930 | 626 | 7.0 | 1.428 | 10.5% | 1.296 | - | |
| L1 | 1.512 | 882 | 7.1 | 1.026 | 649 | 7.8 | 1.512 | 17.0% | 1.296 | - | |
| L2 | 1.398 | 866 | 6.1 | 0.954 | 634 | 7.2 | 1.410 | 9.0% | 1.296 | - | |
| L3 | 1.356 | 857 | 5.8 | 0.882 | 618 | 6.8 | 1.368 | 5.9% | 1.296 | - | |
| Scenario | Volp (m3) | Ee (Wh) | wp (ppm) | Volp (m3) | Ee (Wh) | wp (ppm) | Volp (m3) | Increase (%) | Volp (m3) | Increase (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Without Cooling | 2.784 | 1247 | 20.4 | ||||||||
| Scenario | Continuous Cooling | Max Production | |||||||||
| Qw | 1 L min−1 | 2 L min−1 | 1 L min−1 | 2 L min−1 | |||||||
| B1 | 3.240 | 1336 | 39.4 | 2.508 | 1054 | 23.1 | 3.240 | 16.5% | 2.838 | 1.9% | |
| B2 | 3.000 | 1265 | 30.4 | 2.148 | 983 | 16.8 | 3.006 | 8.2% | 2.784 | - | |
| B3 | 3.066 | 1281 | 32.9 | 2.352 | 1017 | 19.7 | 3.078 | 10.6% | 2.784 | - | |
| B4 | 2.958 | 1261 | 29.2 | 2.304 | 1010 | 19.3 | 2.970 | 6.8% | 2.784 | - | |
| B5 | 2.988 | 1260 | 30.0 | 2.256 | 1002 | 18.2 | 2.994 | 7.8% | 2.784 | - | |
| S1 | 2.958 | 1252 | 29.0 | 2.286 | 1012 | 18.5 | 2.976 | 7.0% | 2.784 | - | |
| S2 | 3.096 | 1293 | 34.7 | 2.430 | 1041 | 21.4 | 3.102 | 11.6% | 2.790 | 0.3% | |
| S3 | 3.054 | 1306 | 36.4 | 2.454 | 1054 | 23.1 | 3.066 | 10.1% | 2.814 | 1.3% | |
| L1 | 3.060 | 1269 | 31.6 | 2.478 | 1041 | 20.8 | 3.072 | 10.4% | 2.808 | 1.0% | |
| L2 | 2.934 | 1242 | 27.7 | 2.352 | 1019 | 19.2 | 2.946 | 6.0% | 2.784 | 0.0% | |
| L3 | 2.850 | 1218 | 24.5 | 2.184 | 986 | 16.7 | 2.874 | 3.4% | 2.784 | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki Valenzuela, M.F.; Sánchez Soto, F.; Armendáriz-Ontiveros, M.M.; Sosa-Tinoco, I.M.; Fimbres Weihs, G.A. Improving Thermal Distribution in Water-Cooled PV Modules and Its Effect on RO Permeate Recovery. Water 2021, 13, 229. https://doi.org/10.3390/w13020229
Suzuki Valenzuela MF, Sánchez Soto F, Armendáriz-Ontiveros MM, Sosa-Tinoco IM, Fimbres Weihs GA. Improving Thermal Distribution in Water-Cooled PV Modules and Its Effect on RO Permeate Recovery. Water. 2021; 13(2):229. https://doi.org/10.3390/w13020229
Chicago/Turabian StyleSuzuki Valenzuela, Mario F., Fernando Sánchez Soto, María Magdalena Armendáriz-Ontiveros, Ian M. Sosa-Tinoco, and Gustavo A. Fimbres Weihs. 2021. "Improving Thermal Distribution in Water-Cooled PV Modules and Its Effect on RO Permeate Recovery" Water 13, no. 2: 229. https://doi.org/10.3390/w13020229
APA StyleSuzuki Valenzuela, M. F., Sánchez Soto, F., Armendáriz-Ontiveros, M. M., Sosa-Tinoco, I. M., & Fimbres Weihs, G. A. (2021). Improving Thermal Distribution in Water-Cooled PV Modules and Its Effect on RO Permeate Recovery. Water, 13(2), 229. https://doi.org/10.3390/w13020229









