A Critical Review of Methods for Analyzing Freshwater Eutrophication
Abstract
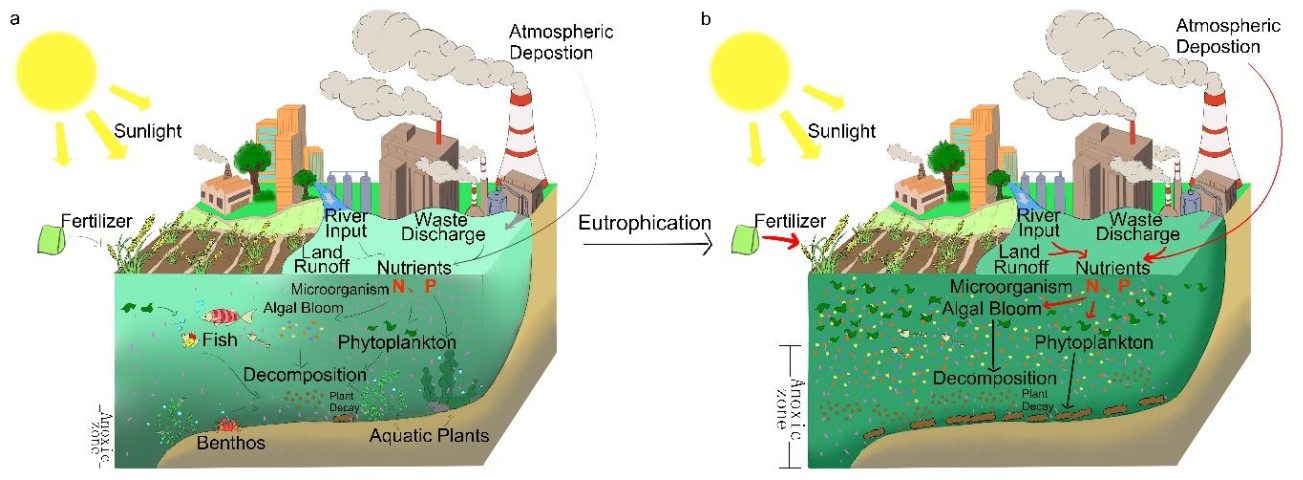
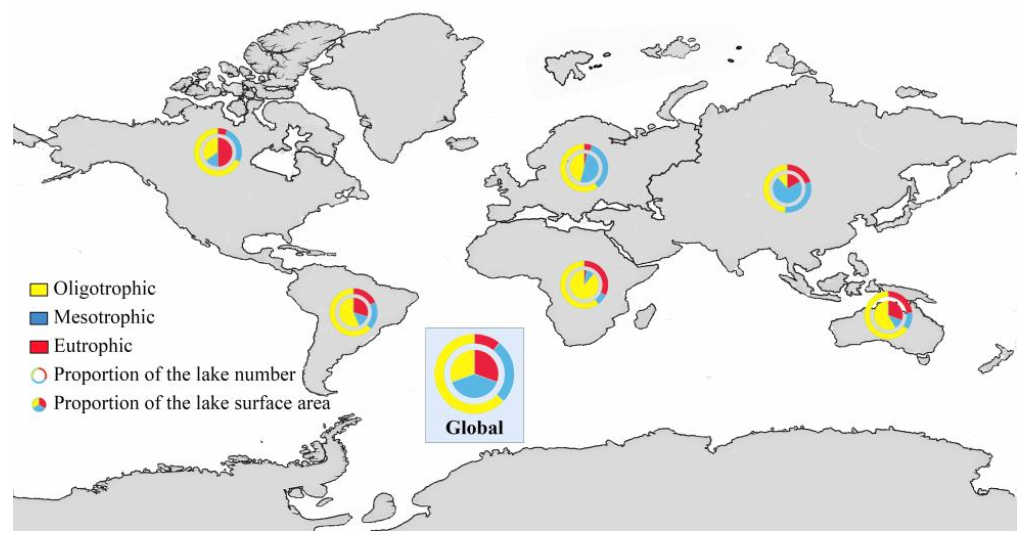
1. Introduction
2. Methods
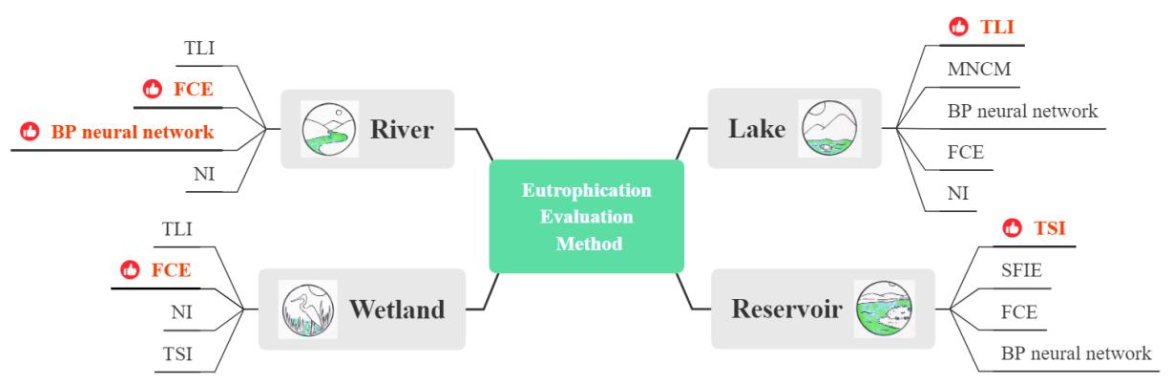
3. Globally Applied Methods for Determining the Eutrophication Status of Waters
3.1. Methods Based on Mathematical Calculations
3.1.1. The Single Factor Index Evaluation (SFIE) Method
3.1.2. Formula Scoring (SCO) Method
3.1.3. The Algal Dominant Species Evaluation Method
3.1.4. The Nemerow Index (NI)
3.1.5. The Trophic Level Index (TLI) Method
3.1.6. The Trophic State Index (TSI) Method: Carlson Index
3.1.7. Stochastic Assessment Method (Empirical Frequency)
3.2. Methods Based on Models
3.2.1. The Fuzzy Comprehensive Evaluation (FCE) Method
3.2.2. The Back Propagation (BP) Neural Network
3.2.3. The One-Dimensional Normal Cloud Model (ONCM) Method
3.2.4. The Multidimensional Normal Cloud Model (MNCM) Method
3.3. Methods Based on Spectral Imaging
3.3.1. Remote Sensing
3.3.2. Multiple Equipment
4. Methods Best Suited to Describe the Degree of Eutrophication
4.1. The TLI Method for Lake Eutrophication
4.2. The TSI Method for Reservoir Eutrophication
4.3. The BP Neural Network or the FCE Method for River Eutrophication
4.4. The FCE Method for Freshwater Wetland Eutrophication
5. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moal, L.M.; Gascuel, O.C.; Ménesguen, A.; Souchon, Y.; Étrillard, C.; Levain, A.; Moatar, F.; Pannard, A.; Souchu, P.; Lefebvre, A.; et al. Eutrophication: A new wine in an old bottle? Sci. Total Environ. 2019, 651, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Schneider, S.C.; Biberdžić, V.; Braho, V.; Gjoreska, B.B.; Cara, M.; Dana, Z.; Đurašković, P.; Eriksen, T.E.; Hjermann, D.; Imeri, A.; et al. Littoral eutrophication indicators are more closely related to nearshore land use than to water nutrient concentrations: A critical evaluation of stressor-response relationships. Sci. Total Environ. 2019, 748, 141193. [Google Scholar] [CrossRef] [PubMed]
- Gibson, G.; Carlson, R.; Simpson, J.; Smeltzer, E.; Gerritson, J.; Chapra, S.; Heiskary, S.; Jones, J.; Kennedy, R. Nutrient Criteria Technical Guidance Manual—Lakes and Reservoirs; Protection Agency: Washington, DC, USA, 2000; pp. 9-1–9-17. Available online: https://www.epa.gov/nutrient-policy-data/nutrient-criteria-technical-guidance-manuals (accessed on 1 April 2000).
- European Commission. The EU Water Framework Directive; Publications Office of the European Union: Luxembourg, 2015. [Google Scholar] [CrossRef]
- Lu, H.S.; Cao, X.Q.; Zhaori, G.T.; Wang, Y.; Cheng, J.G. Research progress of water eutrophication control. Sci. Technol. Consult. Her. 2012, 11, 11. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, L.L.; Zhou, Y.Y.; Mao, X.Z. Eutrophication control strategies for highly anthropogenic influenced coastal waters. Sci. Total. Environ. 2020, 705, 135760. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Ecology and Environment. Bulletin of Marine Ecology and Environment Status of China in 2018; Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 2019. Available online: http://english.mee.gov.cn/Resources/Reports/bomeaesoc/201911/P020191129369234962072.pdf (accessed on 29 November 2019).
- Yu, C.X.; Li, Z.Y.; Xu, Z.H.; Yang, Z. Lake recovery from eutrophication: Quantitative response of trophic states to anthropogenic influences. Ecol. Eng. 2020, 143, 105697. [Google Scholar] [CrossRef]
- Wang, S.L.; Li, J.S.; Evangelos, S. Trophic state assessment of global inland waters using a MODIS-derived Forel-Ule index. Remote Sens. Environ. 2018, 217, 444–460. [Google Scholar] [CrossRef]
- Murphy, A.E.; Sageman, B.B.; Hollander, D.J. Eutrophication by decoupling of the marine biogeochemical cycles of C, N, and P: A mechanism for the Late Devonian mass extinction. Geology 2000, 28, 427–430. [Google Scholar] [CrossRef]
- Pearl, H.W.; Huisman, J. Blooms like it hot. Science 2008, 20, 57–58. [Google Scholar] [CrossRef]
- Vollenweider, R.A. Scientific fundamentals of the eutrophication of lakes and flowing waters, with particular reference to nitrogen and phosphorous as factors in eutrophication. OECD Rep. Water Manag. Res. 1968, 159. [Google Scholar] [CrossRef]
- Caspers, H. OECD: Eutrophication of Waters. Monitoring, Assessment and Control; Organisation for Economic Co-Operation and Development: Paris, France, 1982; p. 154. [Google Scholar] [CrossRef]
- Farley, M. Eutrophication in fresh waters: An international review. In Encyclopedia of Lakes and Reservoirs; Springer: Dordrecht, The Netherlands, 2012; pp. 258–270. ISBN 978-1-4020-5616-1. [Google Scholar]
- Aurea, M.; Francisco, J.; Lino, J. Water artificial circulation for eutrophication control. Math. Control Relat. Fields 2018, 8, 277–313. [Google Scholar] [CrossRef]
- Yang, X.E.; Wu, X.; Hao, H.L. Mechanisms and assessment of water eutrophication. J. Zhejiang Univ. Sci. B 2008, 9, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.M.; Zhang, X.; Wu, Y.F. Eutrophication assessment based on the cloud matter element model. Int. J. Environ. Res. Public Health 2020, 17, 334. [Google Scholar] [CrossRef] [PubMed]
- Channar, A.G.; Rind, A.M.; Mastoi, G.M.; Almani, K.F.; Lashari, K.H.; Qurishi, M.A.; Mahar, N. Comparative study of water of Manchhar lake with drinking water quality standard of World Health Organization. Am. J. Environ. Prot. 2014, 3, 68–72. [Google Scholar] [CrossRef]
- Zeng, G.S.; Hu, C.; Zou, S.M.; Zhang, L. BP neural network model for predicting the mechanical performance of a foamed wood-fiber reinforced thermoplastic starch composite. Polym. Compos. 2019, 40, 3923–3928. [Google Scholar] [CrossRef]
- Wang, D.X. Water quality evaluation of Xinyang section of Huaihe River mainstream based on single factor evaluation method. Henan Water Resour. South North Water. Divers. 2015, 12, 93–94. [Google Scholar]
- Hu, Z.D. Application of pollution index method based on dynamic combination weight to water quality evaluation. IOP Conf. Ser. Earth Environ. Sci. 2018, 153, 1427–1433. [Google Scholar] [CrossRef]
- Yan, B.Z.; Sun, J.; An, N. Groundwater quality assessment method based on Stochastic Forest model. Hydropower. Energy.Sci. 2019, 37, 66–69. [Google Scholar]
- Zhai, K. Application of improved water quality index assessment method in water quality assessment of reservoirs. Guizhou Agric. Sci. 2010, 38, 232–234. [Google Scholar] [CrossRef]
- Shang, B.X.; LÜ, Z.L.; Li, J.N.; Li, T.Q. Application of fuzzy mathematics and single factor index in water quality evaluation. J. China Inst. Environ. Manag. 2013, 5, 1–4. [Google Scholar] [CrossRef]
- Luo, F.; Wu, G.R.; Wang, C. Application of Nemerow pollution index method and single factor evaluation method in water quality evaluation. Environ. Sustain. Dev. 2016, 41, 87–89. [Google Scholar] [CrossRef]
- Shu, J.H. Evaluation of lake Eutrophication degree in China. Environ. Pollut. Control 1990, 5, 2–7, 47. [Google Scholar]
- Shu, J.H. Evaluation of eutrophication degree of main lakes in China. J. Ocean Limnol. 1993, 6, 616–620. Available online: http://159.226.73.51/handle/332005/9591 (accessed on 1 November 1993).
- Wang, M.C.; Liu, X.Q.; Zhang, J.H. Evaluation method and classification standard of lake eutrophication. J. China Environ. Monit. 2002, 5, 47–49. [Google Scholar] [CrossRef]
- Cairns, J.; Dickson, K.L.; Lanza, G.R.; Almeida, S.P.; Balzo, D.D. Coherent optical spatial filtering of diatoms in water pollution monitoring. Arch. Mikrobiol. 1972, 83, 141–146. [Google Scholar] [CrossRef]
- Yan, H.; Huang, Y.; Wang, G. Water eutrophication evaluation based on rough set and petri nets: A case study in Xiangxi-River, Three Gorges Reservoir. Ecol. Indic. 2016, 69, 463–472. [Google Scholar] [CrossRef]
- Zhao, W.; Li, H.; Xu, Q.J. Analysis of succession of dominant algal species in water bloom of Yanghe Reservoir. J. Environ. Eng. 1993, 5, 101–106. [Google Scholar] [CrossRef]
- Barbieri, A.; Simona, M. Trophic evolution of Lake Lugano related to external load reduction: Changes in phosphorus and nitrogen as well as oxygen balance and biological parameters. Lakes Reserv. Res. Manag. 2001, 6, 37–47. [Google Scholar] [CrossRef]
- Alikaj, M.; Brahushi, F.; Piro, C. Assessment of trophic state in the water ecosystem of Gjirokastra district, Albania. Fresen. Environ. Bull. 2014, 23, 3308–3313. Available online: https://www.academia.edu/20816933/ASSESSMENTOFTROPHICSTATEINTHEWATERECOSYSTEMO-FGJIROKASTRADISTRICTALBANIA (accessed on 13 June 2014).
- Wei, H.Q.; Fu, F.; Zhu, Q.L.; Shi, L. The Olympic Forest Park wetland water quality monitoring and analysis. Proc. Int. Conf. Energy Environ. Prot. 2016, 2352–5401. [Google Scholar] [CrossRef]
- Ruley, J.E.; Rusch, K.A. An assessment of long-term post-restoration water quality trends in a shallow, subtropical, urban hypereutrophic lake. Ecol. Eng. 2002, 19, 265–280. [Google Scholar] [CrossRef]
- Ali, E.M.; Khairy, H.M. Environmental assessment of drainage water impacts on water quality and eutrophication level of Lake Idku, Egypt. Environ. Pollut. 2016, 216, 437–449. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Sun, L.P.; Zhong, Y. Water quality analysis and eutrophication assessment of Jinhe River. Ecol. Sci. 2015, 34, 105–110. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Li, M.; Du, Y. Distribution of nitrogen and phosphorus and eutrophication assessment in water of Guanshan Lake Wetland Park. Anhui Agric. Sci. 2018, 46, 60–62. [Google Scholar] [CrossRef]
- Zhang, R.; Gao, L.G.; Xi, B.D. Improved TLI index method and its application in the evaluation of Chaohu Lake’s nutritional status. J. Environ. Eng. 2013, 7, 2127–2133. [Google Scholar]
- Wang, D.; Zeng, D.B.; Vijay, P.S.; Xu, P.C.; Liu, D.F.; Wang, Y.K. A new model for water quality assessment. Uncertain Model. Knowl. Eng. Decis. Mak. 2016, 10, 681–685. [Google Scholar] [CrossRef]
- Stow, C.A.; Glassner-Shwayder, K.; Lee, D.; Wang, L.Z.; Arhonditsis, G.; DePinto, J.V.; Twiss, M.R. Lake Erie phosphorus targets: An imperative for active adaptive management. J. Great Lakes Res. 2020, 46, 672–676. [Google Scholar] [CrossRef]
- Jeppesen, E.; Søndergaard, M.; Kronvang, B.; Jensen, J.P.; Svendsen, L.M.; Lauridsen, T.L. Lake and catchment management in Denmark. Hydrobiologia 1999, 395, 419–432. [Google Scholar] [CrossRef]
- Parul, B.; Saurabh, M. Risk assessment and analysis of water quality in Ramgarh Lake, India. J. Integr. Sci. Technol. 2015, 3, 22–27. Available online: https://www.semanticscholar.Org/paper/Risk-assessment-and-analysis-of-water-quality-in-Barnwal-Mishra/7da797e38ac9965af68812dd391d4707dc5b663c (accessed on 25 April 2015).
- Lourantou, A.; Thome, J.P.; Goffart, A. Water quality assessment of a recently refilled reservoir: The case of Bütgenbach Reservoir, Belgium. Lake Reserv. Res. Manag. 2007, 12, 261–274. [Google Scholar] [CrossRef]
- Ghashghaie, M.; Maralan, M.R.S.; Askari, K.O.A.; Eslamian, S.; Singh, V.P. Determining the eutrophication state of Ecbatan reservoir using Carlson index. Am. J. Eng. Appl. Sci. 2018, 11, 491–500. [Google Scholar] [CrossRef][Green Version]
- Guo, S.Q.; Bu, X.Q.; Liao, J. Water quality evaluation and Eutrophication Analysis of Dawangtan reservoir in Nanning. Environ. Prot. Sci. 2019, 45, 63–68. [Google Scholar]
- Oberholster, P.J.; Botha, A.M.; Cloete, T.E. Biological and chemical evaluation of sewage water pollution in the Rietvlei nature reserve wetland area, South Africa. Environ. Pollut. 2008, 156, 184–192. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Zhai, L.; Lin, J.; Sun, C.; Fu, Z.Y. Water quality dynamics and evaluation of urban lake wetlands in Nanjing. Wetl. Sci. Manag. 2011, 7, 29–32, 39. [Google Scholar] [CrossRef]
- Romero, J.R.; Kagalou, I.; Imberger, J.; Hela, D.; Kotti, M.; Bartzokas, A.; Albanis, T.; Evmirides, N.; Karkabounas, S.; Papagiannis, J.; et al. Seasonal water quality of shallow and eutrophic Lake Pamvotis, Greece: Implications for restoration. Hydrobiologia 2002, 474, 91–105. [Google Scholar] [CrossRef]
- Fang, T.Z.; Du, Y.; Cai, S.M. Fuzzy mathematics for evaluation of eutrophic levels in Honghu Lake of Hubei Province. J. Zhejiang A & F Univ. 2008, 4, 116–120. [Google Scholar] [CrossRef]
- De, V.S. The deteriorating nutrient status of the Berg River, South Africa. Water SA 2007, 33, 659–664. [Google Scholar] [CrossRef]
- Cui, D.W. The application of MATLAB neural network in the evaluation of eutrophication degree of lakes and reservoirs—Taking the evaluation of eutrophication degree of 24 lakes in China as an example. Environ. Res. Monit. 2012, 25, 42–48. [Google Scholar]
- Yao, L.G.; Zhao, X.M.; Zhou, G.G.; Wan, Y.H.; Cai, L.M.; Hu, G.W.; Xu, Z.C. Preliminary regulating factors of spring cyanobacteria bloom in Gaozhou Reservoir, Guangdong Province. J. Lake Sci. 2011, 23, 534–540. [Google Scholar] [CrossRef]
- Guan, B.R. Evaluation of Nemero’s pollution index. Environ. Sci. 1979, 4, 67–71. [Google Scholar]
- Wu, Y.Q.; Gao, R.L.; Yang, J.Z. Prediction of coal and gas outburst: A method based on the BP neural network optimized by GASA. Process Saf. Environ. Prot. 2019, 133, 64–72. [Google Scholar] [CrossRef]
- Jiang, L.Y.; Li, Q.Z.; Liu, L. Evaluation of and control schemes for current eutrophication of land-scape lakes in Kaifeng City, Henan Province. J. Landsc. Res. 2012, 4, 57–60. [Google Scholar]
- Carlson, R.E. A trophic state index for lakes. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef]
- Zou, W.; Zhu, G.W.; Cai, Y.J.; Vilmi, A.; Xu, H.; Zhu, M.Y.; Gong, Z.J.; Zhang, Y.L.; Qin, B.Q. Relationships between nutrient, chlorophyll a and Secchi depth in lakes of the Chinese Eastern Plains ecoregion: Implications for eutrophication management. J. Environ. Manag. 2020, 260, 109923. [Google Scholar] [CrossRef]
- Li, B.C. Application comparison of different water quality assessment methods in river water quality assessment. Reg. Govern. 2019, 28, 69–71. [Google Scholar]
- Awo, M.E.; Fonge, B.A.; Tabot, P.T.; Akoachere, J.T.K. Water quality of the volcanic crater lake, Lake Barombi Kotto, in Cameroon. Afr. J. Aquat. Sci. 2020, 45, 401–411. [Google Scholar] [CrossRef]
- Tian, H. Application of Carlson TSI index in the study of water quality eutrophication in Yanghe Reservoir. Water Sci. Eng. Technol. 2001, 5, 23–24. [Google Scholar] [CrossRef]
- Ansa-Asare, O.D.; Asante, K.A. A comparative study of the nutrient status of two reservoirs in southeast Ghana. Lake Reserv. Res. Manag. 2010, 3, 205–217. [Google Scholar] [CrossRef]
- Ji, B.; Liang, J.C.; Chen, R. Bacterial eutrophic index for potential water quality evaluation of a freshwater ecosystem. Environ. Sci. Pollut. R. 2020, 27, 32449–32455. [Google Scholar] [CrossRef]
- Xie, P.; Li, H.Q.; Ye, A.Z. A lake eutrophication stochastic assessment method by using empirical frequency curve and its verification. J. Lake Sci. 2004, 16, 371–376. [Google Scholar] [CrossRef]
- Liu, X.; Du, G.S.; Zhang, H. Phytoplankton and nutrient degree of water in Miyun Reservoir. Res. Environ. Sci. 2003, 16, 27–29. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Liang, C. Application of fuzzy matter-element model based on coefficients of entropy in comprehensive evaluation of water quality. J. Hydraul. Eng. 2005, 36, 1057–1061. [Google Scholar] [CrossRef]
- Cheng, J.L.; Wang, L.Q.; Ji, G.H. Eutrophication evaluation of landscape waters in ten urban parks in Shanghai. J. Shanghai Ocean Univ. 2009, 18, 435–442. [Google Scholar]
- Wang, Y.Y.; Wang, B.G. Fuzzy evaluation method of scouring stability on soil subgrade slope. J. Highw. Transp. 2005, 18, 24–29. [Google Scholar] [CrossRef]
- Chen, S.Y.; Guo, Y. Fuzzy variable set method for comprehensive evaluation of water quality. Water Res. Prot. 2005, 6, 23–26. [Google Scholar] [CrossRef]
- Zhang, H.; Li, W.J.; Miao, P.P.; Sun, B.W.; Kong, F.Q. Risk grade assessment of sudden water pollution based on analytic hierarchy process and fuzzy comprehensive evaluation. Environ. Sci. Pollut. R. 2020, 27, 469–481. [Google Scholar] [CrossRef]
- Zhao, H.F.; Qiu, W.H.; Wang, X.Z. Fuzzy integrative evaluation method of the risk factor. Syst. Eng. Theory Pract. 1997, 7, 95–98, 125. [Google Scholar] [CrossRef]
- Fang, T.Z.; Du, Y.; Cai, S.M.; Chen, B.; Jiang, Y.S. Application of fuzzy mathematics in eutrophication evaluation of Honghu Lake. J. Zhejiang A & F Univ. 2008, 25, 517–521. [Google Scholar] [CrossRef]
- Yue, C.Y.; Sun, T.; Xie, J.F. The remote sensing image geometrical model of bp neural network. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2020, XLII-3/W10, 381–386. [Google Scholar] [CrossRef]
- Kolehmainen, M.; Martikainen, H.; Ruuskanen, J. Neural networks and periodic components used in air quality forecasting. Atmos. Environ. 2001, 35, 815–825. [Google Scholar] [CrossRef]
- Shen, Y.Y.; Wang, Y.; Huang, X.F.; Xu, J.C. Application of BP-RBF neural network model in water eutrophication assessment of urban landscape. J. Digit. Technol. Appl. 2012, 7, 47–49. [Google Scholar] [CrossRef]
- Wei, S.; Chen, C.H. A carbon price prediction model based on secondary decomposition algorithm and optimized back propagation neural network. J. Clean. Prod. 2019, 243, 118671. [Google Scholar] [CrossRef]
- Soepangkat, B.; Norcahyo, R.; Effendi, M.K.; Pramujati, B. Multi-response optimization of carbon fiber reinforced polymer (CFRP) drilling using back propagation neural network-particle swarm optimization (BPNN-PSO). Eng. Sci. Technol. 2019, 23, 700–713. [Google Scholar] [CrossRef]
- Zhou, S.; Shen, C.Y.; Zhang, L.L. Dual-optimized adaptive Kalman filtering algorithm based on BP neural network and variance compensation for laser absorption spectroscopy. Opt. Express 2019, 27, 31874. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Pan, Z.F.; Tan, J.; Tian, H. Assessment of water quality by firefly algorithm based on BP neural network model. South North Water Transf. Water Sci. Technol. 2020, 18, 104–110. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Zhang, W.; Luo, Z.B. Ultrasonic characterization of thermal barrier coatings porosity through BP neural network optimizing Gaussian process regression algorithm. Ultrasonics 2019, 100, 105981. [Google Scholar] [CrossRef]
- Ghose, D.K.; Panda, S.S.; Swain, P.C. Prediction of water table depth in western region, Orissa using BPNN and RBFN neural networks. J. Hydrol. 2010, 394, 296–304. [Google Scholar] [CrossRef]
- Xiao, J.Z. Study on Water Quality Evaluation Model Based on BP Neural Network. Master’s Thesis, Nanchang University, Jiangxi, China, 2020. [Google Scholar] [CrossRef]
- Cai, H.Y.; Du, R.Z.; Tian, J.F. Research of trust model based on multidimensional trust cloud. J. Comput. Appl. 2012, 32, 5–133. [Google Scholar] [CrossRef]
- Richard, A.; Anthes, A. A cumulus parameterization scheme utilizing a one-dimensional cloud model. J. Mon. Weather Rev. 1977, 105, 270. [Google Scholar] [CrossRef]
- Mouftah, H.T.; Guennoun, M.; Khanafer, M. Priority-based CCA periods for efficient and reliable communications in wireless sensor networks. Wirel. Sens. Netw. 2012, 4, 45–51. [Google Scholar] [CrossRef]
- Zeng, D.B.; Wang, D.; Ding, H. The comparison between multidimensional normal cloud model method and several other methods for water eutrophication evaluation. J. Nanjing Univ. 2015, 1, 67–72. [Google Scholar] [CrossRef]
- Li, D.Y. AI research and development in the network age. CAAI Trans. Intell. Syst. 2009, 4, 1–6. [Google Scholar] [CrossRef]
- Zeng, D.B. Evaluation Method of Water Eutrophication Based on Multidimensional Normal Cloud Model. Master’s Thesis, Nanjing University, Nanjing, China, 2015. Available online: https://kns.cnki.net/kcms/download.aspx?filename=yEFTlt2QFtiRwwUcqNmQOljbpFHO44melhzSENFaGpnUZRTWmhFZ2RDbJJHWKNWUysSM0IEb0hWTCRmYpFUTiR0LjJ3ROJXYws2c5IHNo9SVaBXQ5MVNZtUb4EVWxU3U2RWWLtCW3pGRBhUV6dXVrp2YFdFc4pUQ&dflag=nhdown&dflag=cajdown&tablename=CMFD201601 (accessed on 27 May 2015).
- Wang, J.L.; Fu, Z.S.; Qiao, H.X.; Liu, F.X. Assessment of eutrophication and water quality in the estuarine area of Lake Wuli, Lake Taihu, China. Sci. Total. Environ. 2019, 650, 1392–1402. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.N.; Gao, J.F.; Yin, H.B.; Liu, C.S.; Xia, T.; Wang, J.; Huang, Q. Remote sensing estimation of the total phosphorus concentration in a large lake using band combinations and regional multivariate statistical modeling techniques. J. Environ. Manag. 2015, 151, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.M. Application progress of remote sensing technology in ecological environment monitoring and law enforcement. Min. Metall. Eng. 2020, 40, 165–168, 173. [Google Scholar] [CrossRef]
- Peppa, M.; Vasilakos, C.; Kavroudakis, D. Eutrophication monitoring for lake Pamvotis, Greece, using sentinel-2 data. ISPRS Int. J. Geo-Inf. 2020, 9, 143. [Google Scholar] [CrossRef]
- Kiage, L.M.; Walker, N.D. Using NDVI from MODIS to monitor duckweed bloom in Lake Maracaibo, Venezuela. Water Resour. Manag. 2009, 23, 1125–1135. [Google Scholar] [CrossRef]
- Wang, X.J.; Ma, T. Monitoring and evaluation of water quality in Taihu Lake by remote sensing technology. Environ. Sci. 2000, 6, 65–68. [Google Scholar] [CrossRef]
- Rostom, N.G.; Shalaby, A.A.; Issa, Y.M.; Afifi, A.A. Evaluation of Mariut Lake water quality using hyperspectral remote sensing and laboratory works. Egypt. J. Remote Sens. Space Sci. 2017, 20, S39–S48. [Google Scholar] [CrossRef]
- Ding, C.J.; Song, S.; Feng, Y.B.; Chen, X. Design of stereo atmospheric environment monitoring system based on UAV. Transducer Microsyst. Technol. 2020, 39, 62–65, 69. [Google Scholar] [CrossRef]
- Fang, E.Z.; Zhou, Z.L.; Gui, C.Y. Principles and applications of underwater gliders. Def. Sci. Technol. Ind. 2020, 8, 66–68. Available online: http://kns.cnki.net/kcms/detail/detail.aspx?FileName=ZGBG202008020&DbName=CJFQ2020 (accessed on 1 August 2020).
- Jia, Y.I.; Schmid, C.; Yin, B.Q.; Elke, Z. Toxicological and ecotoxicological evaluation of the water quality in a large and eutrophic freshwater lake of China. Sci. Total Environ. 2019, 667, 809–820. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.C.; Li, M. Research on controller based on multidimensional normal cloud model. Ind. Control Comput. 2014, 27, 77–78. [Google Scholar] [CrossRef]
- Bao, G.Q.; Yin, L.; Yu, J.L. Evaluation of eutrophication of Heihe river based on comprehensive nutrition state index and BP neural network. Bull. Soil Water Conserv. 2018, 38, 264–269. [Google Scholar] [CrossRef]
- Rao, J.G.; Zhang, T.; Rao, X.W. Water quality evaluation of Qingshan national wetland park based on nutrition state index and grey pattern recognition model. Hubei Agric. Sci. 2019, 58, 39–43. [Google Scholar] [CrossRef]
- Zhang, K.S.; Wan, J.Y.; Liu, S. Application of BP neural network in lake water quality assessment. J. Yangtze Univ. Med. V 2004, 1, 28–30. [Google Scholar] [CrossRef]
- Huang, W.Y.; Shu, J.H.; Wu, Y.G. Eutrophication evaluation of main reservoirs in China. Environ. Prot. Technol. 1997, 2, 12–16. [Google Scholar]
- Yang, G.; Liu, H.Z.; Zhu, K.; Liu, D.S. The inversion analysis for mechanical parameters of dam based on the artificial fish swarm algorithm. Appl. Mech. Mater. 2013, 416, 1786–1790. [Google Scholar] [CrossRef]
- Luo, F.; Wu, G.R. Analysis of reservoir water quality based on single factor evaluation method and ratio method. Resour. Econ. Environ. Prot. 2018, 195, 91–98. [Google Scholar]
- Zheng, G.C.; Ma, P.F. Comprehensive evaluation of water quality of Xinlicheng Reservoir Based on cloud model method. Water Conserv. Tech. Superv. 2019, 3, 124–127. [Google Scholar] [CrossRef]
- Lin, Z.J. Eutrophication assessment and control of water quality of Shanmei Reservoir in Quanzhou. Dam Saf. 2014, 2, 31–31. [Google Scholar] [CrossRef]
- Qiu, D.L. Comparison of influence of different water quality evaluation methods on trend analysis of reservoir water quality. Guangdong Water Resour. Hydropower 2018, 7, 13–15. [Google Scholar]
- Li, F.; Qiu, Z.Z.; Zhang, J.D.; Liu, C.Y. Temporal variation of major nutrients and probabilistic eutrophication evaluation based on stochastic-fuzzy method in Honghu Lake, Middle China. Sci. China Technol. Sci. 2019, 62, 417–426. [Google Scholar] [CrossRef]
- Chen, Y.H. Discussion on evaluation method of river eutrophication degree. New Technol. New Prod. China 2016, 1, 144. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zhang, Y. Application of improved BP neural network in eutrophication evaluation of Baiyangdian Lake. South North Water Divers. Water Conserv. Technol. 2012, 10, 90–92. Available online: http://qikan.cqvip.com/Qikan/Article/Detail?id=43100428 (accessed on 1 July 2012).
- Xia, F.; Hu, S.; Gong, Z.J. Comparative study on the application of different water quality assessment methods-Taking Danjiangkou Reservoir as an example. Yangtze River 2017, 48, 11–15. [Google Scholar] [CrossRef]
- Yu, H.X.; He, P.; Zhao, J.J. Eutrophication assessment and control of Xixi Wetland Park. J. Wuhan Inst. Technol. 2011, 33, 50–53. [Google Scholar] [CrossRef]
- Luo, S.Q.; Jia, Z.S. Application of improved Nemero index method in water quality evaluation of Dongfanghong wetland. J. Nat. Sci. Heilongjiang Univ. 2018, 35, 19–25. [Google Scholar] [CrossRef]
- Liu, Y.Q. Analysis of water eutrophication: Causes, prevention principles and measures. Technol. Wind 2018, 3, 126–126. [Google Scholar] [CrossRef]
| Evaluation Method (Criteria) | Water | Nutrient (N) (mg/L) | Nutrient (P) (mg/L) | Chl-a 9 (μg/L) | Documented Eutrophication | Reference |
|---|---|---|---|---|---|---|
| NI 1 | Lugano Lake, Switzerland | NA 10 | TP 4: 0.140 | NA | Hyper-eutrophic (1960~2001) | [32] |
| Viroi Lake, Albania | NH4+: 0.090 NO3−: 0.670 | NA | NA | Eutrophic (2013~2014) | [33] | |
| Olympic Forest Park wetland, China | TN 5: 0.300~2.100 | TP: 0.040~0.180 | NA | Light-eutrophic (2016) | [34] | |
| TLI 2 | City Park Lake, Louisiana, USA | TN: 0.682 | TP: 0.330 | 35.1 | Eutrophic (2000~2001) | [35] |
| Idku Lake, Egypt | NA | PO43−: 0.200~0.430 | 39.9~104.2 | Hyper-eutrophic (2016) | [36] | |
| Jinhe River, China | TN: 0.240~8.340 | TP: 0.019~0.490 | 1.6~92.7 | Eutrophic (2007~2011) Hyper-eutrophic (2012~2014) Middle-eutrophic (2015) | [37] | |
| Guanshan Wetland, China | TN: 0.520~2.200 | TP: 0.019~1.040 | 1.0~37.0 | Light-eutrophic (2014~2016) | [38] | |
| Improved TLI | Chaohu Lake, China | TN: 1.500~2.680 | TP: 0.150~0.230 | 13.2~21.9 | Light-eutrophic (2000~2006) Middle-eutrophic (2007~2017) | [39] |
| TSI 3 | Erie Lake, USA | NA | TP: 0.115 | 58.0 | Blue-green algae bloom (1965~1979) Declined quality (1995~2004) | [40,41] |
| Lyng Lake, Danish | TN: 2.400 | TP: 0.370 | 73.0 | Hyper-eutrophic (1999) | [42] | |
| Ramgarh Lake, India | NA | NA | NA | Hyper-eutrophic (2015) | [43] | |
| Bütgenbach Reservoir, Belgium | NH4⁺: 0~0.480 | PO43−: 0~0.110 | 0~39.4 | Hyper-eutrophic (2007) | [44] | |
| Ecbatan Reservoir, Egypt | TN: 2.200 | TP: 0.075 | 5.8 | Middle-eutrophic (2018) | [45] | |
| Dawangtan Reservoir, China | NH4⁺−N: 0.180~0.710 TN: 0.820~2.760 | TP: 0.020~0.090 | NA | Middle-eutrophic (2019) | [46] | |
| TSI | Rietvlei nature reserve wetland, South Africa | TN: 0.358~6.000 | TP: 0.081~0.371 | NA | Middle-eutrophic (2005~2006) | [47] |
| Xuanwu Wetland, China | TN: 2.010~2.110 | TP: 0.160~0.310 | NA | Hyper-eutrophic (2011) | [48] | |
| FCE 6 | Pamvotis Lake, Northwest Greece | NH4⁺: 0.250 NO3−: 0.560 | NA | NA | Eutrophic (2002) | [49] |
| Honghu Lake, China | TN: 1.410 | TP: 0.065 | 2.6~3.7 | Middle-eutrophic (2005~2006) | [50] | |
| Berg River, South Africa | TN: 2.170 | TP: 0.700 | NA | Hyper-eutrophic (2007) | [51] | |
| BP neural network 7 | Dianshan Lake, China | TN: 1.086 | TP: 0.029 | 3.0 | Light-eutrophic (2011) | [52] |
| Gaozhou Reservoir, China | TN: 0.358 | TP: 0.046 | 1.4 | Mesotrophic (2011) | [53] | |
| OECD 8 classification | Wastwater | NO3−: 0.352 | TP: 0.003 | 0.8 | Ultra-oligotrophic | [14] |
| Ennerdale Water | NO3−: 0.333 | TP: 0.008 | 1.05 | Oligotrophic | [14] | |
| Buttermere | NO3−: 0.175 | TP: 0.004 | 1.43 | Oligotrophic | [14] | |
| Crummock Water | NO3−: 0.193 | TP: 0.007 | 2.075 | Oligotrophic | [14] | |
| Coniston Water | NO3−: 0.365 | TP: 0.008 | 3.585 | Oligotrophic | [14] | |
| Derwentwater | NO3−: 0.199 | TP: 0.015 | 3.275 | Mesotrophic | [14] | |
| Grasmere | NO3−: 0.253 | TP: 0.016 | 5.655 | Mesotrophic | [14] | |
| Loweswater | NO3−: 0.529 | TP: 0.013 | 7.68 | Mesotrophic | [14] | |
| Bassenthwaite Lake | NO3−: 0.384 | TP: 0.022 | 6.37 | Mesotrophic | [14] | |
| Ullswater | NO3−: 0.254 | TP: 0.012 | 5.44 | Mesotrophic | [14] | |
| Blelharn Tarn | NO3−: 0.827 | TP: 0.039 | 18.345 | Eutrophic | [14] | |
| Esthwaite Water | NO3−: 0.695 | TP: 0.031 | 22.355 | Eutrophic | [14] |
| Method | Parameter | Classification | Reference | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SCO 1 | CODMn (mg/L) | TN (mg/L) | TP (mg/L) | SD (m) | Chl-a (mg/L) | Score | [26] | |||
| ≤0.15 | ≤0.020 | ≤0.001 | ≥10.0 | ≤0.0005 | ≤10 | Oligotrophic | ||||
| >0.15, ≤0.3 | >0.020, ≤0.030 | >0.001, ≤0.0025 | <10.0, ≥8.0 | >0.0005, ≤0.0010 | >10, ≤20 | |||||
| >0.3, ≤0.4 | >0.030, ≤0.050 | >0.0025, ≤0.005 | <8.0, ≥5.0 | >0.0010, ≤0.0020 | >20, ≤30 | Mesotrophic | ||||
| >0.4, ≤2.0 | >0.050. ≤0.300 | >0.005, ≤0.025 | <5.0, ≥1.5 | >0.0020, ≤0.0040 | >30, ≤40 | Eutrophic | ||||
| >2.0, ≤4.0 | >0.050, ≤0.300 | >0.025, ≤0.050 | <1.5, ≥1.0 | >0.0040, ≤0.0100 | >40, ≤50 | Light-eutrophic | ||||
| >4.0, ≤8.0 | >0.300, ≤0.800 | >0.025, ≤0.050 | <1.0, ≥0.5 | >0.0100, ≤0.0260 | >50, ≤60 | Mid-eutrophic | ||||
| >8.0, ≤18.0 | >0.800, ≤2.000 | >0.050, ≤0.200 | <0.5, ≥0.4 | >0.0260, ≤0.0650 | >60, ≤70 | |||||
| >18.0, ≤25.0 | >2.000, ≤6.000 | >0.200, ≤0.600 | <0.4, ≥0.3 | >0.0650, ≤0.1600 | >70, ≤80 | Hyper-eutrophic | ||||
| >25.0, ≤40.0 | >6.000, ≤9.000 | >0.600, ≤0.900 | <0.3, ≥0.2 | >0.1600, ≤0.4000 | >80, ≤90 | |||||
| >60.0 | >14.000 | >1.300 | <0.12 | >1.0000 | >90, ≤100 | |||||
| TLI (Σ) 2 | CODMn (mg/L) | TN (mg/L) | TP (mg/L) | SD (m) | Chl-a (mg/L) | TLI | [89] | |||
| ≤0.15 | ≤0.02 | ≤0.001 | ≥10.0 | ≤0.0005 | ≤30 | Oligotrophic | ||||
| >0.15, ≤0.40 | >0.02, ≤0.05 | >0.001, ≤0.004 | <10.0, ≥5.0 | >0.0005, ≤0.0010 | ||||||
| >0.40, ≤1.00 | >0.05, ≤0.10 | >0.004, ≤0.010 | <5.0, ≥3.0 | >0.0010, ≤0.0020 | >30, ≤50 | Mesotrophic | ||||
| >1.00, ≤2.00 | >0.10, ≤0.30 | >0.010, ≤0.030 | <3.0, ≥1.5 | >0.0020, ≤0.0040 | ||||||
| >2.00, ≤4.00 | >0.30, ≤0.50 | >0.030, ≤0.050 | <1.5, ≥1.0 | >0.0040, ≤0.0100 | ||||||
| >4.00, ≤8.00 | >0.50, ≤1.00 | >0.050, ≤0.100 | <1.0, ≥0.5 | >0.0100, ≤0.0300 | >50, ≤60 | Light-eutrophic | ||||
| >8.00, ≤10.00 | >1.00, ≤2.00 | >0.100, ≤0.200 | <0.5, ≥0.4 | >0.0300, ≤0.0640 | >60, ≤70 | Mid-eutrophic | ||||
| >10.00, ≤25.00 | >2.00, ≤6.00 | >0.200, ≤0.600 | <0.4, ≥0.3 | >0.0640, ≤0.1600 | ||||||
| >40.00 | >9.00 | >0.900 | <0.2 | >0.4000 | >70 | Hyper-eutrophic | ||||
| TSIM 3 | TSIM (TP) | TSIM (SD) | TSIM (Chl-a) | [61] | ||||||
| ≤2.0 | ≤4.4 | ≤24.6 | Oligotrophic | |||||||
| >2.0, ≤11.9 | >4.4, ≤18.2 | >24.6, ≤32.2 | Mesotrophic | |||||||
| >11.9, ≤35.1 | >18.2, ≤42.1 | >32.2, ≤39.7 | Eutrophic | |||||||
| >35.1, ≤45.2 | >42.1, ≤50.1 | >39.7, ≤47.6 | Light-eutrophic | |||||||
| >45.2, ≤65.2 | >50.1, ≤68.3 | >47.6, ≤70.2 | Mid-eutrophic | |||||||
| >65.2 | >68.3 | >70.2 | Hyper-eutrophic | |||||||
| Empirical Frequency | CODMn (mg/L) | TN (mg/L) | TP (mg/L) | SD (m) | Chl-a (mg/L) | Empirical Frequency | [64] | |||
| ≤0.3 | ≤0.030 | ≤0.0025 | ≥10.0 | ≤0.001 | ≤14.3 | Oligotrophic | ||||
| >0.3, ≤0.4 | >0.030, ≤0.050 | >0.0025, ≤0.0050 | <10.0, ≥5.0 | >0.001, ≤0.002 | >0.4, ≤28.6 | Mesotrophic | ||||
| >0.4, ≤2.0 | >0.050, ≤0.300 | >0.0050, ≤0.0250 | <5.0, ≥1.5 | >0.002, ≤0.004 | >0.4, ≤42.9 | Eutrophic | ||||
| >2.0, ≤4.0 | >0.300, ≤0.500 | >0.0250, ≤0.0500 | <1.5, ≥1.0 | >0.004, ≤0.010 | >0.4, ≤57.1 | Light-eutrophic | ||||
| >10.0, ≤25.0 | >2.000, ≤6.000 | >0.2000, ≤0.6000 | <0.4, ≥0.3 | >0.065, ≤0.160 | >71.4, ≤85.7 | Mid-eutrophic | ||||
| >25.0 | >6.000 | >0.6000 | <0.3 | >0.160 | >85.7 | Hyper-eutrophic | ||||
| FCE 4 | DO (mg/L) | BOD5 (mg/L) | CODMn (mg/L) | NH3-N(mg/L) | Cyanogen (mg/L) | As (mg/L) | Cr (mg/L) | F (mg/L) | [66] | |
| ≥8.0 | ≤3.0 | ≤15.0 | ≤0.5 | ≤0.005 | ≤0.05 | ≤0.01 | ≤1.0 | Class I | ||
| <8.0, ≥6.0 | ≤3.0 | ≤15.0 | ≤0.5 | >0.005, ≤0.050 | ≤0.05 | >0.01, ≤0.05 | ≤1.0 | Class II | ||
| <6.0, ≥5.0 | >3.0, ≤4.0 | >15.0, ≤20.0 | >0.5, ≤10.0 | >0.050, ≤0.200 | >0.05, ≤0.20 | >0.01, ≤0.05 | ≤1.0 | Class IV | ||
| <5.0, ≥3.0 | >4.0, ≤6.0 | >20.0, ≤30.0 | >1.0, ≤2.0 | >0.200 | >0.20 | >0.01, ≤0.05 | >1.0, ≤1.5 | Class IV | ||
| <1.0 | >10.0 | >40.0 | >2.0 | >0.200 | >0.20 | >0.10 | >1.5 | Class V | ||
| BP neural network | CODMn (mg/L) | TN (mg/L) | TP (mg/L) | Chl-a (mg/L) | value | [75] | ||||
| ≤0.3 | ≤0.03 | ≤0.0025 | ≤0.001 | 0 ≤ y < 1 | Oligotrophic | |||||
| >0.3, ≤0.4 | >0.03, ≤0.05 | >0.0030, ≤0.0050 | >0.001, ≤0.005 | 1 ≤ y < 2 | Mesotrophic | |||||
| >0.4, ≤2.0 | >0.05, ≤0.30 | >0.0050, ≤0.0300 | >0.005, ≤0.025 | 2 ≤ y < 3 | Eutrophic | |||||
| >2.0, ≤4.0 | >0.30, ≤0.50 | >0.0300, ≤0.0500 | >0.025, ≤0.050 | 3 ≤ y < 4 | Light-eutrophic | |||||
| >4.0, ≤10.0 | >0.50, ≤2.00 | >0.0500, ≤0.2000 | >0.050, ≤0.500 | 4 ≤ y < 5 | Mid-eutrophic | |||||
| >10.0 | >2.00 | >0.2000 | >0.500 | y ≥ 5 | Hyper-eutrophic | |||||
| Ex 7 | En 8 | He 9 | [88] | |||||||
| ONCM 5 | ≥15.0 | 5.0 | 0.01 | C1 | ||||||
| <15.0, ≥7.5 | 5.0 | 0.01 | C2 | |||||||
| <7.5, ≥3.8 | 5.0 | 0.01 | C3 | |||||||
| MNCM 6 | <3.8, ≥1.3 | 5.0 | 0.01 | C4 | ||||||
| <1.3, ≥0.7 | 5.0 | 0.01 | C5 | |||||||
| <0.2 | 5.0 | 0.01 | C6 | |||||||
| Monitoring Parameters | SS 1 (mg/L) | SD 2 (m) | DO 3 (mg/L) | CODMn 4 (mg/L) | BOD5 5 (mg/L) | TN 6 (mg/L) | TP 7 (mg/L) | Reference |
|---|---|---|---|---|---|---|---|---|
| Monitoring parameters AVG 8 | 37.53 | 0.33 | 8.83 | 4.05 | 2.07 | 4.39 | 1.30 | [95] |
| Radiation data MW 9/(cm2·SR 10) | TM1 11 | TM2 | TM3 | TM4 | TM5 | TM6 | TM7 | |
| Radiation data AVG | 0.687 | 0.554 | 0.267 | 0.033 | 0.010 | 0.086 | 0.002 | |
| Monitoring parameters | T (°C) | pH | TUB 12 (NTU) | HDO 13 (% Sat.) | Chl (μg/L) | [96] | ||
| 17.3~20.9 | 7.5~8.9 | 18.5~110.0 | 18.9~207.6 | 4.79~219.1 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, M.; Dong, J.; Yang, H.; Van Zwieten, L.; Lu, H.; Alshameri, A.; Zhan, Z.; Chen, X.; Jiang, X.; et al. A Critical Review of Methods for Analyzing Freshwater Eutrophication. Water 2021, 13, 225. https://doi.org/10.3390/w13020225
Zhang Y, Li M, Dong J, Yang H, Van Zwieten L, Lu H, Alshameri A, Zhan Z, Chen X, Jiang X, et al. A Critical Review of Methods for Analyzing Freshwater Eutrophication. Water. 2021; 13(2):225. https://doi.org/10.3390/w13020225
Chicago/Turabian StyleZhang, Yan, Mingxuan Li, Jiefeng Dong, Hong Yang, Lukas Van Zwieten, Hui Lu, Aref Alshameri, Zihan Zhan, Xin Chen, Xueding Jiang, and et al. 2021. "A Critical Review of Methods for Analyzing Freshwater Eutrophication" Water 13, no. 2: 225. https://doi.org/10.3390/w13020225
APA StyleZhang, Y., Li, M., Dong, J., Yang, H., Van Zwieten, L., Lu, H., Alshameri, A., Zhan, Z., Chen, X., Jiang, X., Xu, W., Bao, Y., & Wang, H. (2021). A Critical Review of Methods for Analyzing Freshwater Eutrophication. Water, 13(2), 225. https://doi.org/10.3390/w13020225








