On the Rainfall Triggering of Phlegraean Fields Volcanic Tremors
Abstract
1. Introduction
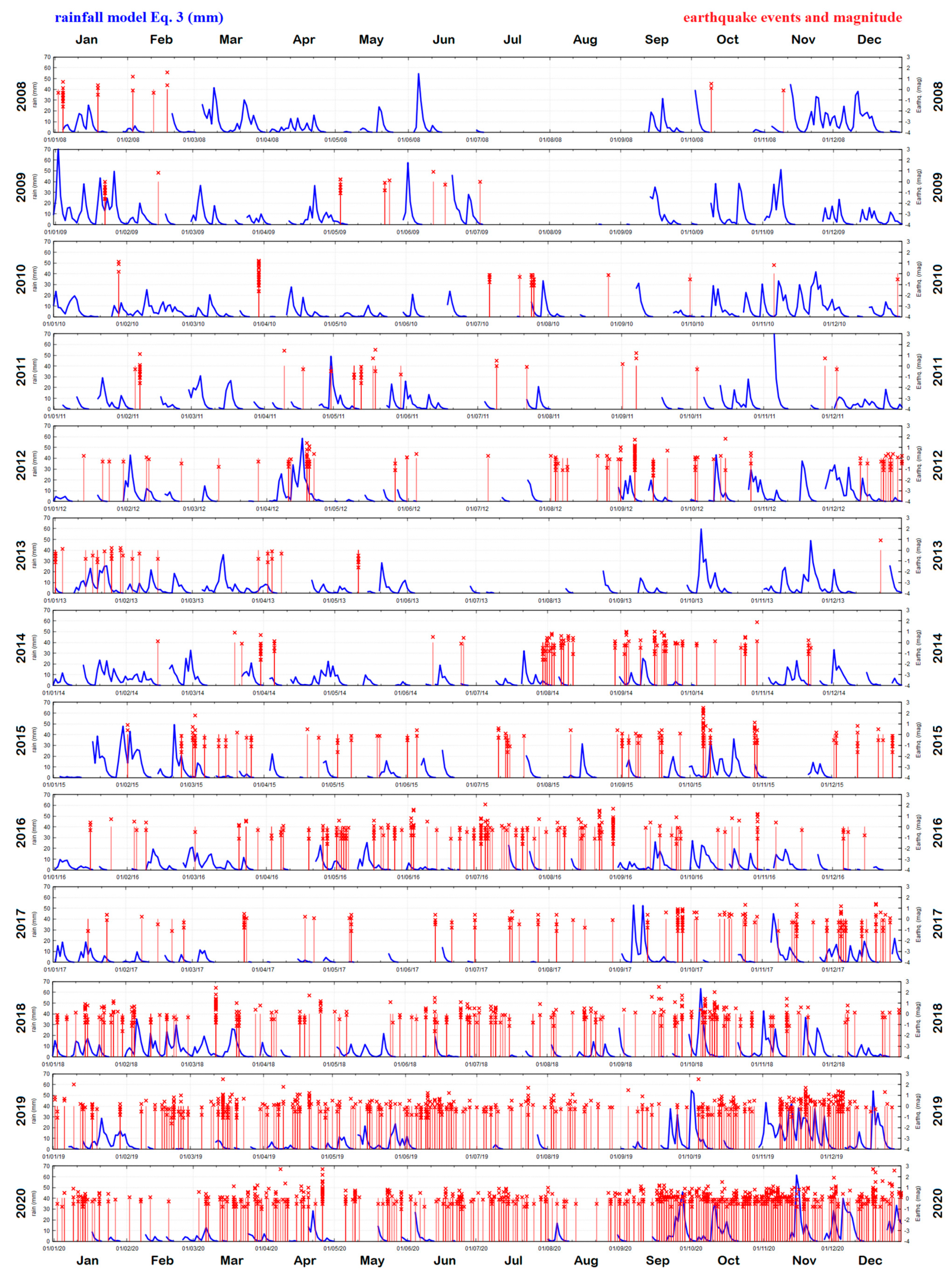
2. Data
3. Methods
- (1)
- R = 0.2 mm and τ = 1 day;
- (2)
- R = 0.1 mm and τ = 1 day;
- (3)
- R = 0.2 mm and τ = 2 day;
- (4)
- R = 0.1 mm and τ = 2 day.
- the number of days for each year (DY);
- the number of wet days (WD) as defined by Equation (3) with the threshold R;
- the number of days when earthquakes occur (DE);
- the number of wet days when earthquakes occur (WDE);
- the total number of earthquakes (E);
- the total number of earthquakes that occur during wet days (EWD).
- the probability of having random earthquakes with no relation with wet days (Rand = WD divided by DY), which is our null hypothesis to be tested;
- the measured probability of having a seismic day during a wet day (WEQD = WDE divided by DE);
- the measured probability of having an earthquake during a wet day (WEQ = EWD divided by E).
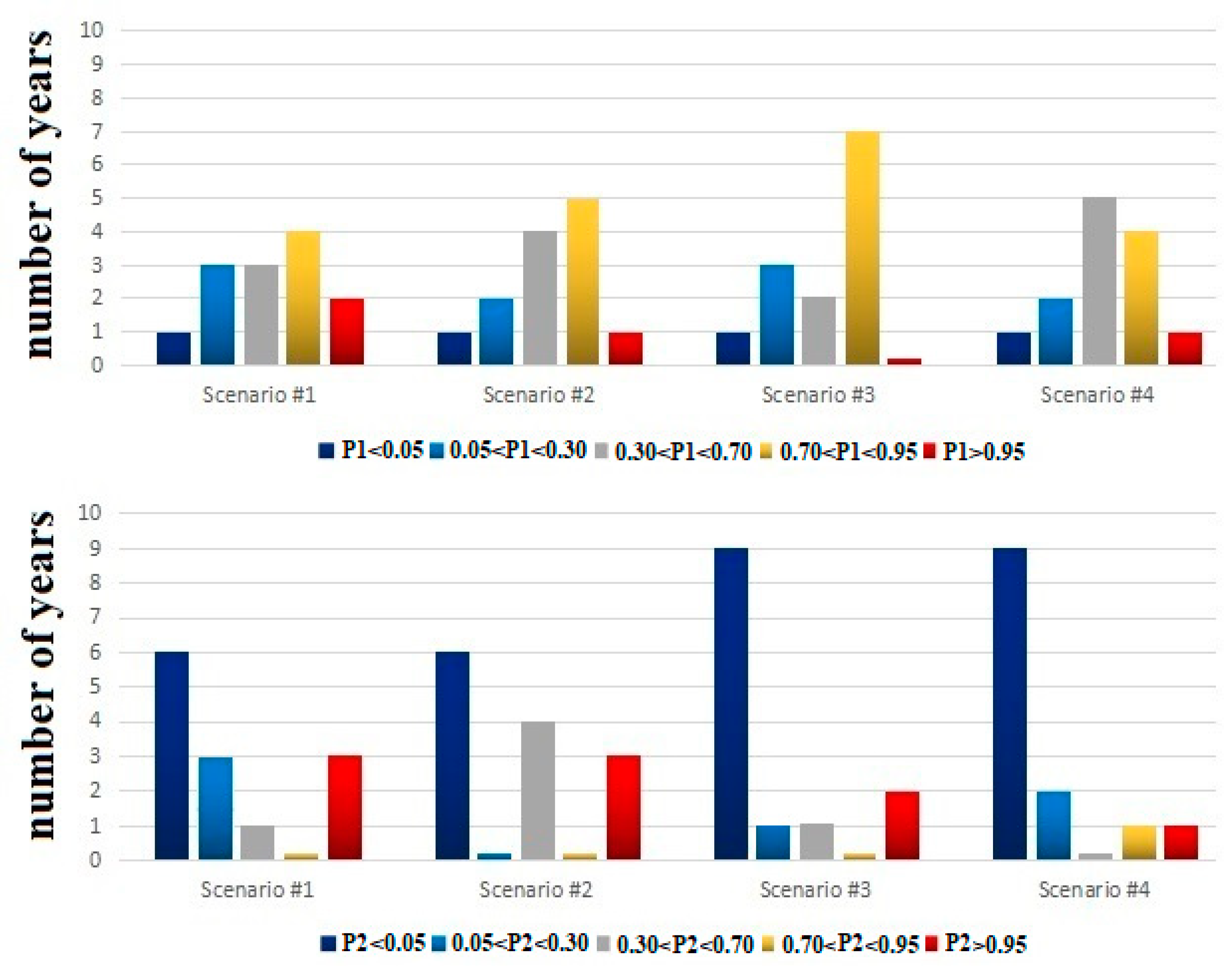
4. Results
- Scenario #1: R = 0.2 mm and τ = 1 day. P2 ≤ 0.05 for 6 years (2008, 2009, 2012, 2014, 2015, and 2017), 0.05 < P2 ≤ 0.30 for 3 other years (2018, 2019 and 2020), while P2 ≥ 0.95 for three years (2010, 2011 and 2016);
- Scenario #2: R = 0.1 mm and τ = 1 day. P2 ≤ 0.05 for 6 years (2008, 2009, 2012, 2014, 2015, and 2018) while P2 ≥ 0.95 for just 3 years (2010, 2011 and 2016);
- Scenario #3: R = 0.2 mm and τ = 2 day. P2 ≤ 0.05 for 9 years (2008, 2009, 2011, 2012, 2013, 2014, 2017, 2018, and 2019), while P2 ≥ 0.95 for just 2 years (2010, 2016);
- Scenario #4: R = 0.1 mm and τ = 2 day. P2 ≤ 0.05 for 9 years (2008, 2009, 2010, 2011, 2012, 2013, 2014, 2017, and 2019), 0.05 < P2 ≤ 0.30 for 2 years (2018 and 2020), while P2 ≥ 0.95 for just one year (2016).
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
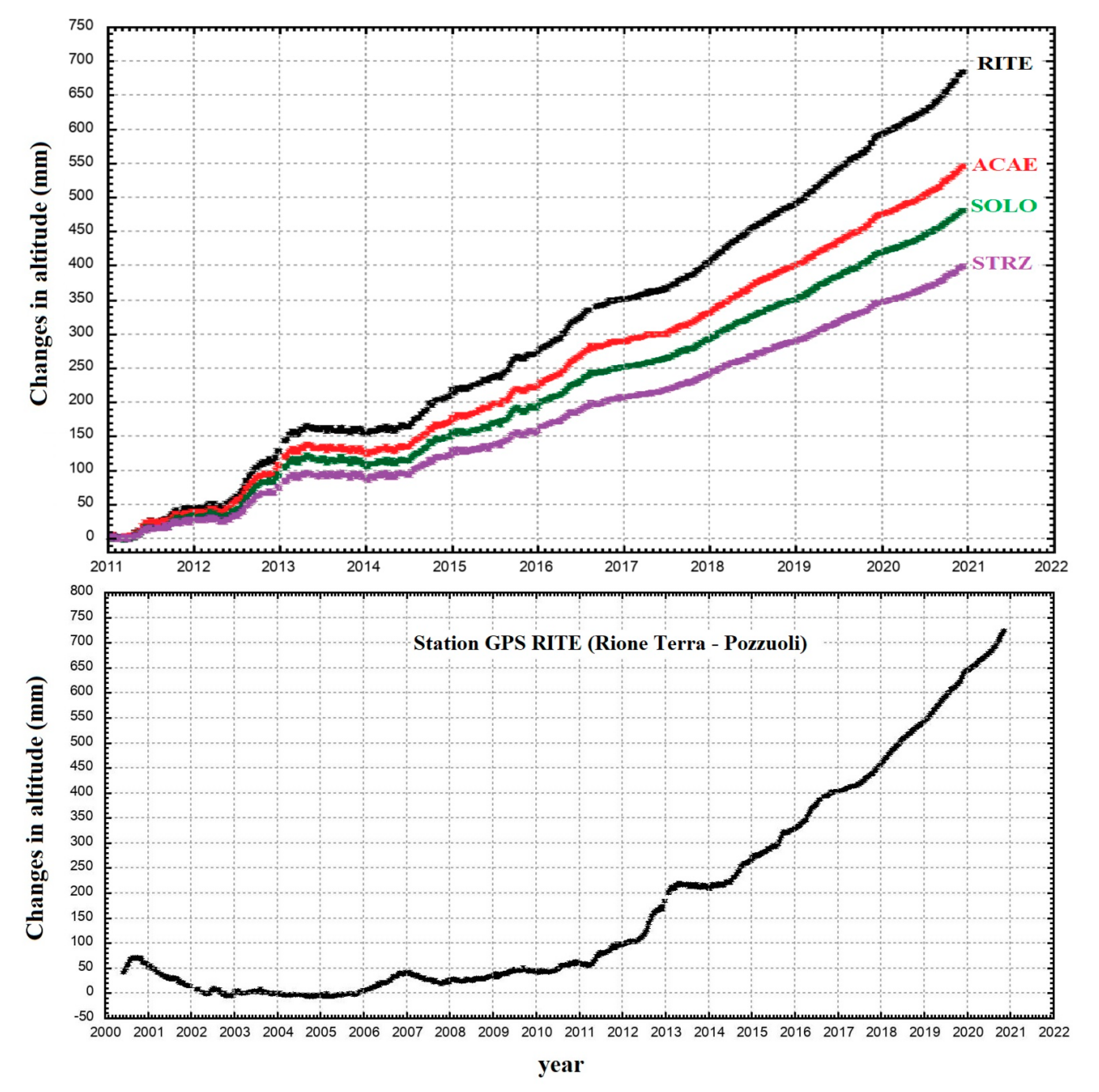
Appendix B
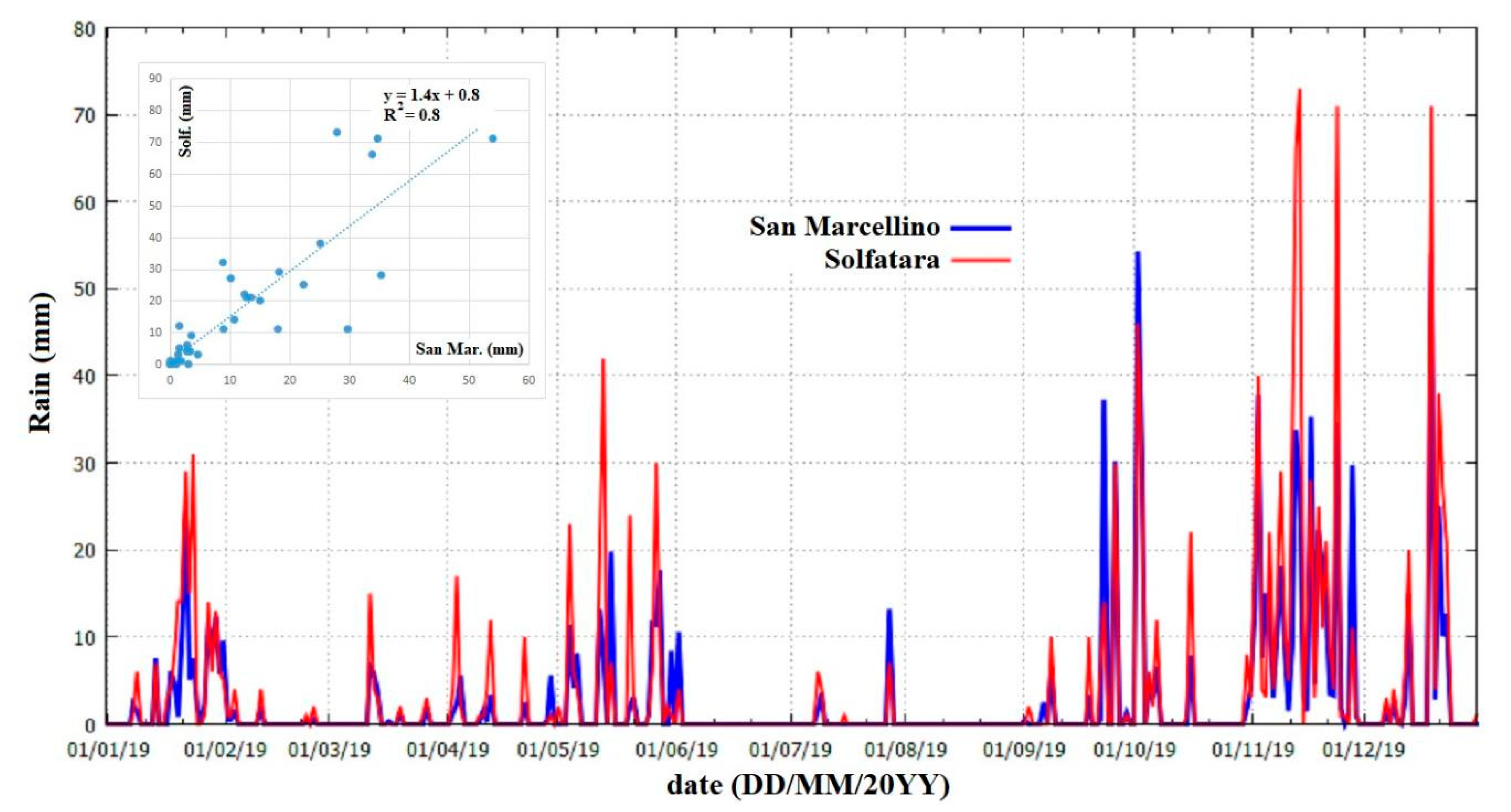
References
- Charlton, D.; Kilburn, C.; Edwards, S. Volcanic unrest scenarios and impact assessment at Campi Flegrei caldera, Southern Italy. J. Appl. Volcanol. 2020, 9, 7. [Google Scholar]
- De Vivo, B.; Belkin, H.; Rolandi, G. Vesuvius, Campi Flegrei, and Campanian Volcanism; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- De Vivo, B.; Rolandi, G. Volcanological risk associated with Vesuvius and Campi Flegrei. In Vesuvius, Campi Flegrei, and Campanian Volcanism; De Vivo, B., Belkin, H.E., Rolandi, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 17, pp. 471–493. [Google Scholar]
- Palumbo, A. Influence of external tidal and meteorological forces on the bradyseismic phenomenon in the Phlegraean Fields. Il Nuovo Cimento C 1985, 8, 538–551. [Google Scholar] [CrossRef]
- Mazzarella, A.; Palumbo, A. Does the solar cycle modulate seismic and volcanic activity? J. Volc. Geoth. Res. 1989, 39, 89–93. [Google Scholar] [CrossRef]
- Mastin, L.G. Can rain cause volcanic eruptions? In U.S.G.S., Open-File Report; US Geological Survey: Reston, VA, USA, 1993; pp. 93–445. Available online: https://pubs.usgs.gov/of/1993/0445/ (accessed on 30 November 2020).
- Mastin, L.G. Explosive tephra emissions at Mount St. Helens, 1989–1991: The violent escape of magmatic gas following storms? Geol. Soc. Am. Bull. 1994, 106, 175–185. [Google Scholar]
- Neuberg, J. External modulation of volcanic activity. Geophys. J. Int. 2000, 142, 232–240. [Google Scholar] [CrossRef]
- Violette, S.; De Marsily, G.; Carbonnel, J.P.; Goblet, P.; Ledoux, E.; Tijani, S.M.; Vouille, G. Can rainfall trigger volcanic eruptions? A mechanical stress model of an active volcano: ‘Piton de la Fournaise’, Reunion Island. Terra Nova 2001, 13, 18–24. [Google Scholar]
- Matthews, A.J.; Barclay, J.; Carn, S.; Thompson, G.; Alexander, J.; Herd, R.; Williams, C. Rainfall-induced volcanic activity on Montserrat. Geoph. Res. Lett. 2002, 29, 1644. [Google Scholar] [CrossRef]
- Matthews, A.J.; Barclay, J. A thermodynamical model for rainfall triggered volcanic dome collapse. Geoph. Res. Lett. 2004, 31, L05614. [Google Scholar] [CrossRef]
- Matthews, A.J.; Barclay, J.; Johnstone, J. The fast response of volcano-seismic activity to intense precipitation: Triggering of primary volcanic activity by rainfall at Soufrière Hills Volcano, Montserrat. J. Volcanol. Geoth. Res. 2009, 184, 405–415. [Google Scholar]
- Hainzl, S.; Kraft, T.; Wassermann, J.; Igel, H.; Schmedes, E. Evidence for rainfall-triggered earthquakes activity. Geophys. Res. Lett. 2006, 33, L19303. [Google Scholar]
- Miller, S.A. Note on rain-triggered earthquakes and their dependence on karst geology. Geophys. J. Int. 2008, 173, 334–338. [Google Scholar] [CrossRef]
- Farquharson, J.I.; Amelung, F. Extreme rainfall triggered the 2018 rift eruption at Kīlauea Volcano. Nature 2020, 580, 491–495. [Google Scholar] [CrossRef] [PubMed]
- Dana, J.D. Characteristics of Volcanoes: With Contributions of Facts and Principles from the Hawaiian Islands; Dodd, Mead and Co.: New York, NY, USA, 1891. [Google Scholar]
- Banks, N.G.; Mora, H.; Tryggvaso, E. Deformation monitoring at Nevado del Ruiz, Colombia—October 1985—March 1988. J. Volcanol. Geoth. Res. 1990, 41, 269–295. [Google Scholar] [CrossRef]
- Barclay, J.; Alexander, J.; Sušnik, J. Rainfall-induced lahars in the Belham Valley, Montserrat, West Indies. J. Geol. Soc. 2007, 164, 815–827. [Google Scholar]
- Smithsonian Institution. Guagua Pichincha (Ecuador): Phreatic explosion kills two scientists: Bull. Glob. Volcanism Netw. 1993, 18, 2.
- Guest, J.; Murray, J.; Kilburn, C.; Lopes, R. Eruptions on Mount Etna during 1979. Earthq. Inf. Bull. 1980, 12, 154–160. [Google Scholar]
- Mazzarella, A.; Scafetta, N. Evidences for higher nocturnal seismic activity at the Mt. Vesuvius. J. Volc. Geoth. Res. 2016, 321, 102–113. [Google Scholar] [CrossRef]
- Scafetta, N.; Mazzarella, A. Cultural noise and the night-day asymmetry of the seismic activity recorded at the Bunker-East (BKE) Vesuvian Station. J. Volc. Geoth. Res. 2018, 349, 117–127. [Google Scholar] [CrossRef]
- Cannatelli, C.; Spera, F.J.; Bodnar, R.J.; Lima, A.; De Vivo, B. Ground movement (bradyseism) in the Campi Flegrei volcanic area: A review. In Vesuvius, Campi Flegrei, and Campanian Volcanism; De Vivo, B., Belkin, H.E., Rolandi, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Chapter 15; pp. 407–433. [Google Scholar]
- De Vivo, B.; Lima, A. A hydrothermal model for ground movements (bradyseism) at Campi Flegrei, Italy. In Volcanism in the Campania Plain: Vesuvius, Campi Flegrei and Ignimbrites; De Vivo, B., Ed.; Developments in Volcanology 9; Elsevier: Amsterdam, The Netherlands, 2006; pp. 289–317. [Google Scholar]
- Bodnar, R.J.; Cannatelli, C.; De Vivo, B.; Lima, A.; Belkin, H.E.; Milia, A. Quantitative model for magma degassing and ground deformation (bradyseism) at Campi Flegrei, Italy: Implications for future eruptions. Geology 2007, 35, 791–794. [Google Scholar]
- Lima, A.; De Vivo, B.; Spera, F.J.; Bodnar, R.J.; Milia, A.; Nunziata, C.; Belkin, H.E.; Cannatelli, C. Thermodynamic model for the uplift and deflation episodes (bradyseism) associated with magmatic-hydrothermal activity at the Campi Flegrei active volcanic center (Italy). Earth Sci. Rev. 2009, 97, 44–58. [Google Scholar] [CrossRef]
- Calò, M.; Tramelli, A. Anatomy of the Campi Flegrei caldera using Enhanced Seismic Tomography Models. Sci. Rep. 2018, 8, 16254. [Google Scholar] [CrossRef] [PubMed]
- Petrosino, S.; Cusano, P.; Madonia, P. Tidal and hydrological periodicities of seismicity reveal new risk scenarios at Phlegraean Area caldera. Sci. Rep. 2018, 8, 13808. [Google Scholar] [CrossRef] [PubMed]
- Fortelli, A.; Scafetta, N.; Mazzarella, A. Nowcasting and real-time monitoring of heavy rainfall events inducing flash-floods: An application to Phlegraean area (Central-Southern Italy). Nat. Hazards 2019, 97, 861–889. [Google Scholar] [CrossRef]
- Ausilio, C. Phlegraean Area, allarme trivellazioni: Scatenate fumarole alte dieci metri. Vesuvius Live, 15 June 2020. Available online: https://www.vesuviolive.it/ultime-notizie/343822-agnano-trivellazioni-fumarole/ (accessed on 30 November 2020).
- Contessa, L. Progetto GEOGRID e Trivellazioni ad Agnano: Interviene l’Osservatorio Vesuviano. Cronaca Flegrea, Rione Terra News, 15 June 2020. Available online: https://www.cronacaflegrea.it/progetto-geogrid-e-trivellazioni-ad-agnano-interviene-losservatorio-vesuviano/ (accessed on 30 November 2020).
- Whitaker, S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Media 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Liu, C.; Evett, J.B. Soils and Foundations; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications: Mineola, NY, USA, 1972. [Google Scholar]
- Zollo, A.; Maercklin, N.; Vassallo, M.; Dello Iacono, D.; Virieux, J.; Gasparini, P. Seismic reflections reveal a massive melt layer feeding Campi Flegrei caldera. Geophys. Res. Lett. 2008, 35, L12306. [Google Scholar] [CrossRef]
- Piochi, M.; Kilburn, C.R.J.; Di Vito, M.A.; Mormone, A.; Tramelli, A.; Troise, C.; De Natale, G. The volcanic and geothermally active Campi Flegrei caldera: An integrated multidisciplinary image of its buried structure. Int. J. Earth Sci. 2014, 103, 401–421. [Google Scholar] [CrossRef]
- De Martino, P.; Tammaro, U.; Obrizzo, F. GPS time series at Campi Flegrei caldera (2000–2013). Ann. Geophys. 2014, 57, S0213. [Google Scholar]
- Palumbo, A.; Mazzarella, A. Mean sea level variations and their practical applications. J. Geophys. Res. 1982, 87(C6), 4249–4256. [Google Scholar] [CrossRef]
- Pasculli, A.; Sciarra, N.; Esposito, L.; Esposito, A.W. Effects of wetting and drying cycles on mechanical properties of pyroclastic soils. Catena 2017, 156, 113–123. [Google Scholar] [CrossRef]
- Troiano, A.; Isaia, R.; Di Giuseppe, M.G.; Tramparulo, F.D.A.; Vitale, S. Deep Electrical Resistivity Tomography for a 3D picture of the most active sector of Campi Flegrei caldera. Sci. Rep. 2019, 9, 15124. [Google Scholar] [CrossRef]
- Bruno, P.P.G.; Ricciardi, G.P.; Petrillo, Z.; Di Fiore, V.; Troiano, A.; Chiodini, G. Geophysical and hydrogeological experiments from a shallow hydrothermal system at Solfatara Volcano, Campi Flegrei, Italy: Response to caldera unrest. J. Geophys. Res. 2007, 112, B06201. [Google Scholar] [CrossRef]
- Bernardinetti, S.; Bruno, P.P.G. The Hydrothermal System of Solfatara Crater (Campi Flegrei, Italy) Inferred from Machine Learning Algorithms. Front. Earth Sci. 2019, 7, 286. [Google Scholar] [CrossRef]
- Caliro, S.; Chiodini, G.; Paonita, A. Geochemical evidences of magma dynamics at Campi Flegrei (Italy). Geochim. Cosmochim. Acta 2014, 132, 1–15. [Google Scholar] [CrossRef]
- Shapiro, S.A.; Patzig, R.; Rothert, E.; Rindschwentner, J. Triggering of seismicity by pore-pressure perturbations: Permeability-related signatures of the phenomenon. In Thermo-Hydro-Mechanical Coupling in Fractured Rock (1051–1066); Birkhäuser: Basel, Switzerland, 2003. [Google Scholar]
- De Bottis, D.G. Istoria dei Vari incendi del Monte Vesuvio; Stamperia Regale: Napoli, Italy, 1786. [Google Scholar]
- Della Torre, G.M. Storia e Fenomeni del Vesuvio; Raimondi Editore: Napoli, Italy, 1755. [Google Scholar]
- Palumbo, N.; Mazzarella, A. Rainfall Statistical Properties in Naples. Monthly Weather Rev. 1980, 108, 1041–1045. [Google Scholar] [CrossRef]
| Year | DY | WD | DE | WDE | E | EWD | Rand (%) | WEQD (%) | P1 | WEQ (%) | P2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2008 | 366 | 195 | 8 | 3 | 53 | 46 | 53 | 38 | (0.70 ≤ p < 0.95) | 87 | (p ≤ 0.05) |
| 2009 | 365 | 204 | 8 | 3 | 162 | 155 | 56 | 38 | (0.70 ≤ p < 0.95) | 96 | (p ≤ 0.05) |
| 2010 | 365 | 237 | 10 | 6 | 124 | 19 | 65 | 60 | (0.30 < p < 0.70) | 15 | (p ≥ 0.95) |
| 2011 | 365 | 187 | 17 | 5 | 59 | 10 | 51 | 29 | (p ≥ 0.95) | 17 | (p ≥ 0.95) |
| 2012 | 366 | 183 | 47 | 26 | 225 | 186 | 50 | 55 | (0.05 < p ≤ 0.30) | 83 | (p ≤ 0.05) |
| 2013 | 365 | 212 | 18 | 14 | 47 | 27 | 58 | 78 | (p ≤ 0.05) | 57 | (0.30 < p < 0.70) |
| 2014 | 365 | 219 | 38 | 22 | 155 | 106 | 60 | 58 | (0.30 < p < 0.70) | 68 | (p ≤ 0.05) |
| 2015 | 365 | 178 | 44 | 20 | 175 | 108 | 49 | 45 | (0.30 < p < 0.70) | 62 | (p ≤ 0.05) |
| 2016 | 366 | 208 | 78 | 38 | 288 | 104 | 57 | 49 | (0.70 ≤ p < 0.95) | 36 | (p ≥ 0.95) |
| 2017 | 365 | 154 | 54 | 25 | 180 | 87 | 42 | 46 | (0.05 < p ≤ 0.30) | 48 | (p ≤ 0.05) |
| 2018 | 365 | 227 | 107 | 60 | 375 | 241 | 62 | 56 | (0.70 ≤ p < 0.95) | 64 | (0.05 < p ≤ 0.30) |
| 2019 | 365 | 194 | 180 | 87 | 592 | 322 | 53 | 48 | (p ≥ 0.95) | 54 | (0.05 < p ≤ 0.30) |
| 2020 | 366 | 165 | 209 | 97 | 776 | 364 | 45 | 46 | (0.05 < p ≤ 0.30) | 47 | (0.05 < p ≤ 0.30) |
| all | 4749 | 2563 | 818 | 406 | 3211 | 1775 | 54 | 50 | 55 |
| Year | DY | WD | DE | WDE | E | EWD | Rand (%) | WEQD (%) | P1 | WEQ (%) | P2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2008 | 366 | 211 | 8 | 4 | 53 | 47 | 58 | 50 | (0.30 < p < 0.70) | 89 | (p ≤ 0.05) |
| 2009 | 365 | 217 | 8 | 3 | 162 | 155 | 59 | 38 | (0.70 ≤ p < 0.95) | 96 | (p ≤ 0.05) |
| 2010 | 365 | 258 | 10 | 7 | 124 | 20 | 71 | 70 | (0.30 < p < 0.70) | 16 | (p ≥ 0.95) |
| 2011 | 365 | 205 | 17 | 5 | 59 | 10 | 56 | 29 | (p ≥ 0.95) | 17 | (p ≥ 0.95) |
| 2012 | 366 | 203 | 47 | 31 | 225 | 195 | 55 | 66 | (0.05 < p ≤ 0.30) | 87 | (p ≤ 0.05) |
| 2013 | 365 | 225 | 18 | 15 | 47 | 28 | 62 | 83 | (p ≤ 0.05) | 60 | (0.30 < p < 0.70) |
| 2014 | 365 | 235 | 38 | 25 | 155 | 115 | 64 | 66 | (0.30 < p < 0.70) | 74 | (p ≤ 0.05) |
| 2015 | 365 | 200 | 44 | 22 | 175 | 112 | 55 | 50 | (0.70 ≤ p < 0.95) | 64 | (p ≤ 0.05) |
| 2016 | 366 | 228 | 78 | 44 | 288 | 118 | 62 | 56 | (0.70 ≤ p < 0.95) | 41 | (p ≥ 0.95) |
| 2017 | 365 | 173 | 54 | 26 | 180 | 88 | 47 | 48 | (0.30 < p < 0.70) | 49 | (0.30 < p < 0.70) |
| 2018 | 365 | 247 | 107 | 66 | 375 | 272 | 68 | 62 | (0.70 ≤ p < 0.95) | 73 | (p ≤ 0.05) |
| 2019 | 365 | 210 | 180 | 97 | 592 | 345 | 58 | 54 | (0.70 ≤ p < 0.95) | 58 | (0.30 < p < 0.70) |
| 2020 | 366 | 180 | 209 | 106 | 776 | 381 | 49 | 51 | (0.05 < p ≤ 0.30) | 49 | (0.30 < p < 0.70) |
| all | 4749 | 2792 | 818 | 451 | 3211 | 1886 | 59 | 55 | 59 |
| Year | DY | WD | DE | WDE | E | EWD | Rand (%) | WEQD (%) | P1 | WEQ (%) | P2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2008 | 366 | 248 | 8 | 5 | 53 | 49 | 68 | 63 | (0.30 < p < 0.70) | 92 | (p ≤ 0.05) |
| 2009 | 365 | 260 | 8 | 5 | 162 | 157 | 71 | 63 | (0.70 ≤ p < 0.95) | 97 | (p ≤ 0.05) |
| 2010 | 365 | 293 | 10 | 7 | 124 | 20 | 80 | 70 | (0.70 ≤ p < 0.95) | 16 | (p ≥ 0.95) |
| 2011 | 365 | 264 | 17 | 11 | 59 | 51 | 72 | 65 | (0.70 ≤ p < 0.95) | 86 | (p ≤ 0.05) |
| 2012 | 366 | 255 | 47 | 37 | 225 | 203 | 70 | 79 | (0.05 < p ≤ 0.30) | 90 | (p ≤ 0.05) |
| 2013 | 365 | 267 | 18 | 17 | 47 | 46 | 73 | 94 | (p ≤ 0.05) | 98 | (p ≤ 0.05) |
| 2014 | 365 | 292 | 38 | 32 | 155 | 136 | 80 | 84 | (0.05 < p ≤ 0.30) | 88 | (p ≤ 0.05) |
| 2015 | 365 | 253 | 44 | 26 | 175 | 122 | 69 | 59 | (0.70 ≤ p < 0.95) | 70 | (0.30 < p < 0.70) |
| 2016 | 366 | 280 | 78 | 56 | 288 | 148 | 77 | 72 | (0.70 ≤ p < 0.95) | 51 | (p ≥ 0.95) |
| 2017 | 365 | 215 | 54 | 35 | 180 | 122 | 59 | 65 | (0.05 < p ≤ 0.30) | 68 | (p ≤ 0.05) |
| 2018 | 365 | 293 | 107 | 82 | 375 | 314 | 80 | 77 | (0.70 ≤ p < 0.95) | 84 | (p ≤ 0.05) |
| 2019 | 365 | 254 | 180 | 122 | 592 | 445 | 70 | 68 | (0.70 ≤ p < 0.95) | 75 | (p ≤ 0.05) |
| 2020 | 366 | 226 | 209 | 130 | 776 | 490 | 62 | 62 | (0.30 < p < 0.70) | 63 | (0.05 < p ≤ 0.30) |
| all | 4749 | 3400 | 818 | 565 | 3211 | 2303 | 72 | 69 | 72 |
| Year | DY | WD | DE | WDE | E | EWD | Rand (%) | WEQD (%) | P1 | WEQ (%) | P2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2008 | 366 | 262 | 8 | 6 | 53 | 50 | 72 | 75 | (0.30 < p < 0.70) | 94 | (p ≤ 0.05) |
| 2009 | 365 | 270 | 8 | 5 | 162 | 157 | 74 | 63 | (0.70 ≤ p < 0.95) | 97 | (p ≤ 0.05) |
| 2010 | 365 | 312 | 10 | 8 | 124 | 117 | 85 | 80 | (0.30 < p < 0.70) | 94 | (p ≤ 0.05) |
| 2011 | 365 | 278 | 17 | 12 | 59 | 52 | 76 | 71 | (0.70 ≤ p < 0.95) | 88 | (p ≤ 0.05) |
| 2012 | 366 | 274 | 47 | 38 | 225 | 204 | 75 | 81 | (0.05 < p ≤ 0.30) | 91 | (p ≤ 0.05) |
| 2013 | 365 | 280 | 18 | 17 | 47 | 46 | 77 | 94 | (p ≤ 0.05) | 98 | (p ≤ 0.05) |
| 2014 | 365 | 302 | 38 | 32 | 155 | 136 | 83 | 84 | (0.30 < p < 0.70) | 88 | (p ≤ 0.05) |
| 2015 | 365 | 269 | 44 | 28 | 175 | 124 | 74 | 64 | (0.70 ≤ p < 0.95) | 71 | (0.70 ≤ p < 0.95) |
| 2016 | 366 | 297 | 78 | 57 | 288 | 149 | 81 | 73 | (p ≥ 0.95) | 52 | (p ≥ 0.95) |
| 2017 | 365 | 234 | 54 | 38 | 180 | 143 | 64 | 70 | (0.05 < p ≤ 0.30) | 79 | (p ≤ 0.05) |
| 2018 | 365 | 314 | 107 | 87 | 375 | 328 | 86 | 81 | (0.70 ≤ p < 0.95) | 87 | (0.05 < p ≤ 0.30) |
| 2019 | 365 | 270 | 180 | 131 | 592 | 473 | 74 | 73 | (0.30 < p < 0.70) | 80 | (p ≤ 0.05) |
| 2020 | 366 | 245 | 209 | 139 | 776 | 531 | 67 | 67 | (0.30 < p < 0.70) | 68 | (0.05 < p ≤ 0.30) |
| all | 4749 | 3607 | 818 | 598 | 3211 | 2510 | 76 | 73 | 78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scafetta, N.; Mazzarella, A. On the Rainfall Triggering of Phlegraean Fields Volcanic Tremors. Water 2021, 13, 154. https://doi.org/10.3390/w13020154
Scafetta N, Mazzarella A. On the Rainfall Triggering of Phlegraean Fields Volcanic Tremors. Water. 2021; 13(2):154. https://doi.org/10.3390/w13020154
Chicago/Turabian StyleScafetta, Nicola, and Adriano Mazzarella. 2021. "On the Rainfall Triggering of Phlegraean Fields Volcanic Tremors" Water 13, no. 2: 154. https://doi.org/10.3390/w13020154
APA StyleScafetta, N., & Mazzarella, A. (2021). On the Rainfall Triggering of Phlegraean Fields Volcanic Tremors. Water, 13(2), 154. https://doi.org/10.3390/w13020154






