Supervised Machine Learning for Estimation of Total Suspended Solids in Urban Watersheds
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Source
2.2. Data Preprocessing
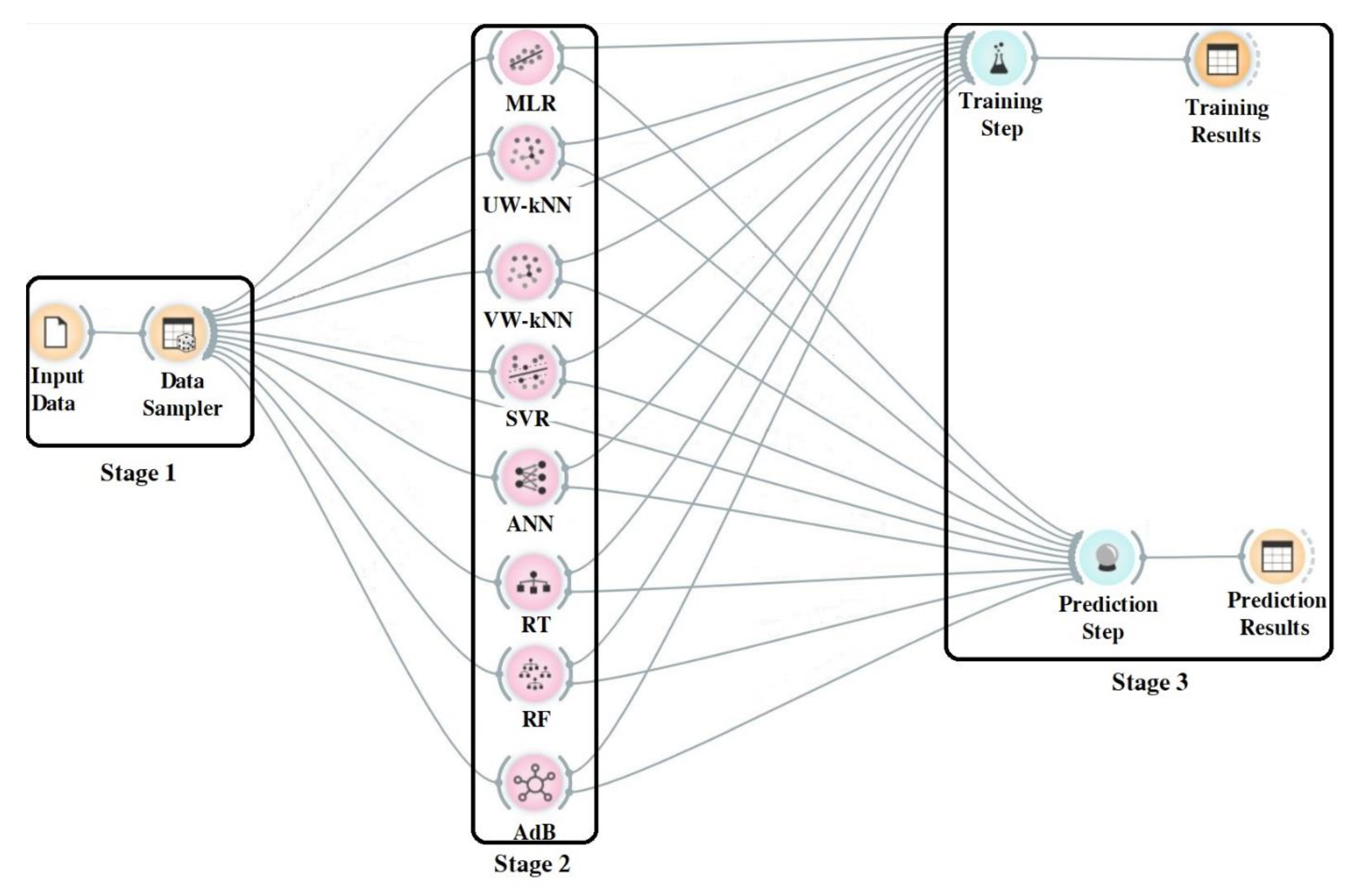
2.3. ML Model Structure
2.4. Machine Learning (ML) Methods
2.4.1. Single-Model ML Methods
- Linear Regression (LR)
- 2.
- k-Nearest Neighbor (kNN)
- 3.
- Support Vector Regression (SVR)
- 4.
- Artificial Neural Network (ANN)
- 5.
- Regression Tree (RT)
2.4.2. Ensemble-Model ML Methods
- Bagging Ensemble Models
- 2.
- Boosting Ensemble Models
3. Results
3.1. Training and Prediction Steps
3.2. Single ML Algorithm
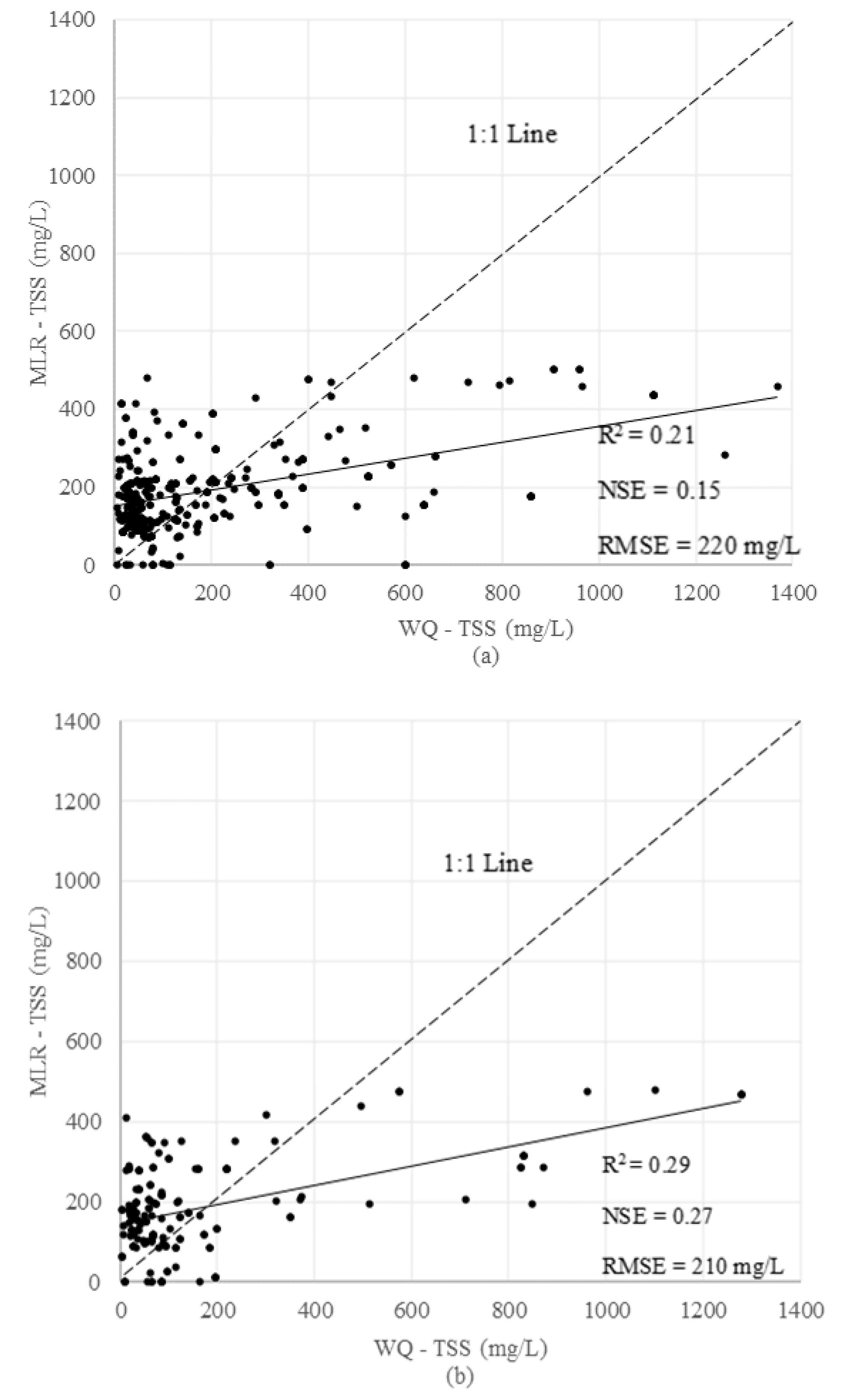
3.2.1. Multiple Linear Regression (MLR)
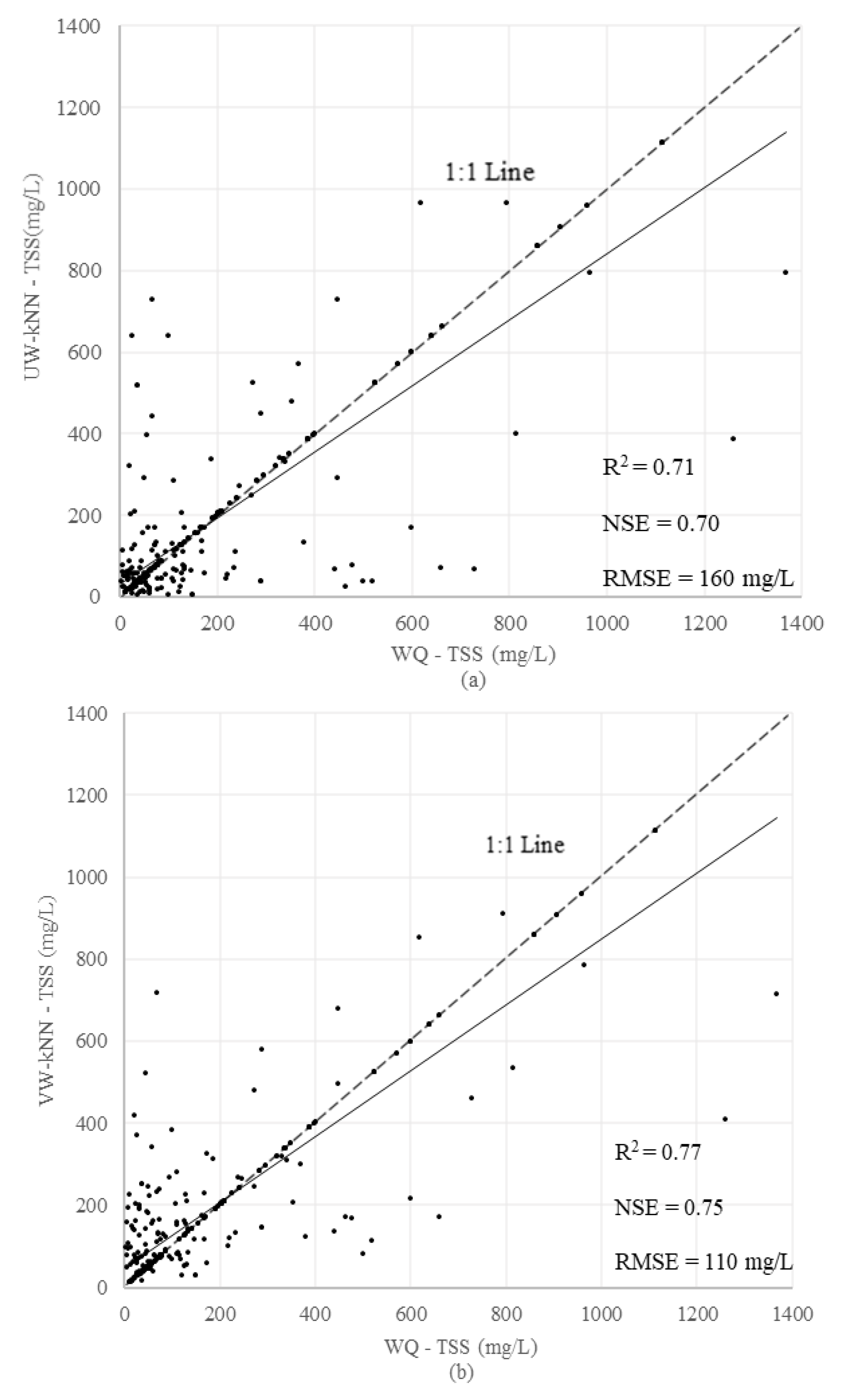
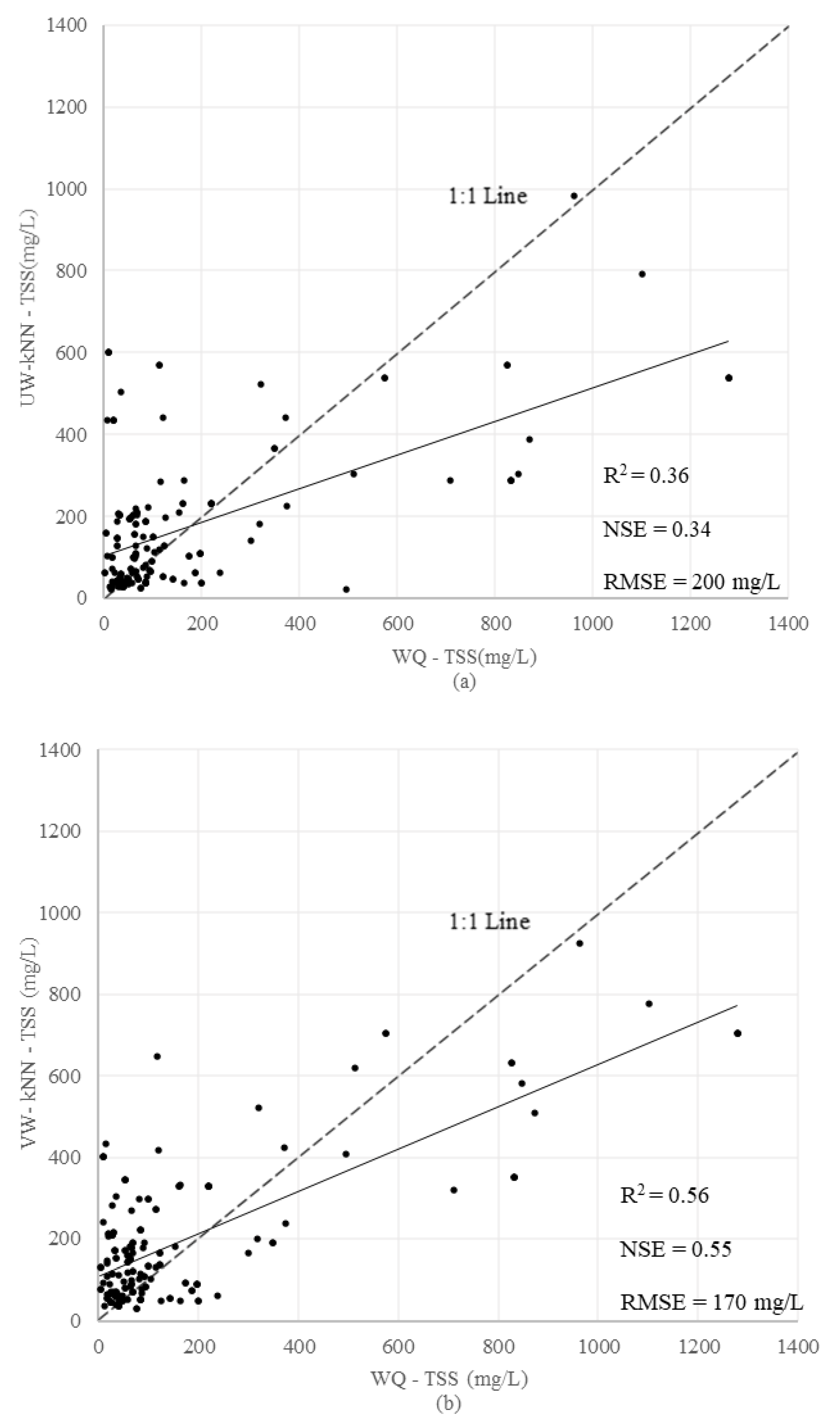
3.2.2. k-Nearest Neighbors (kNN)
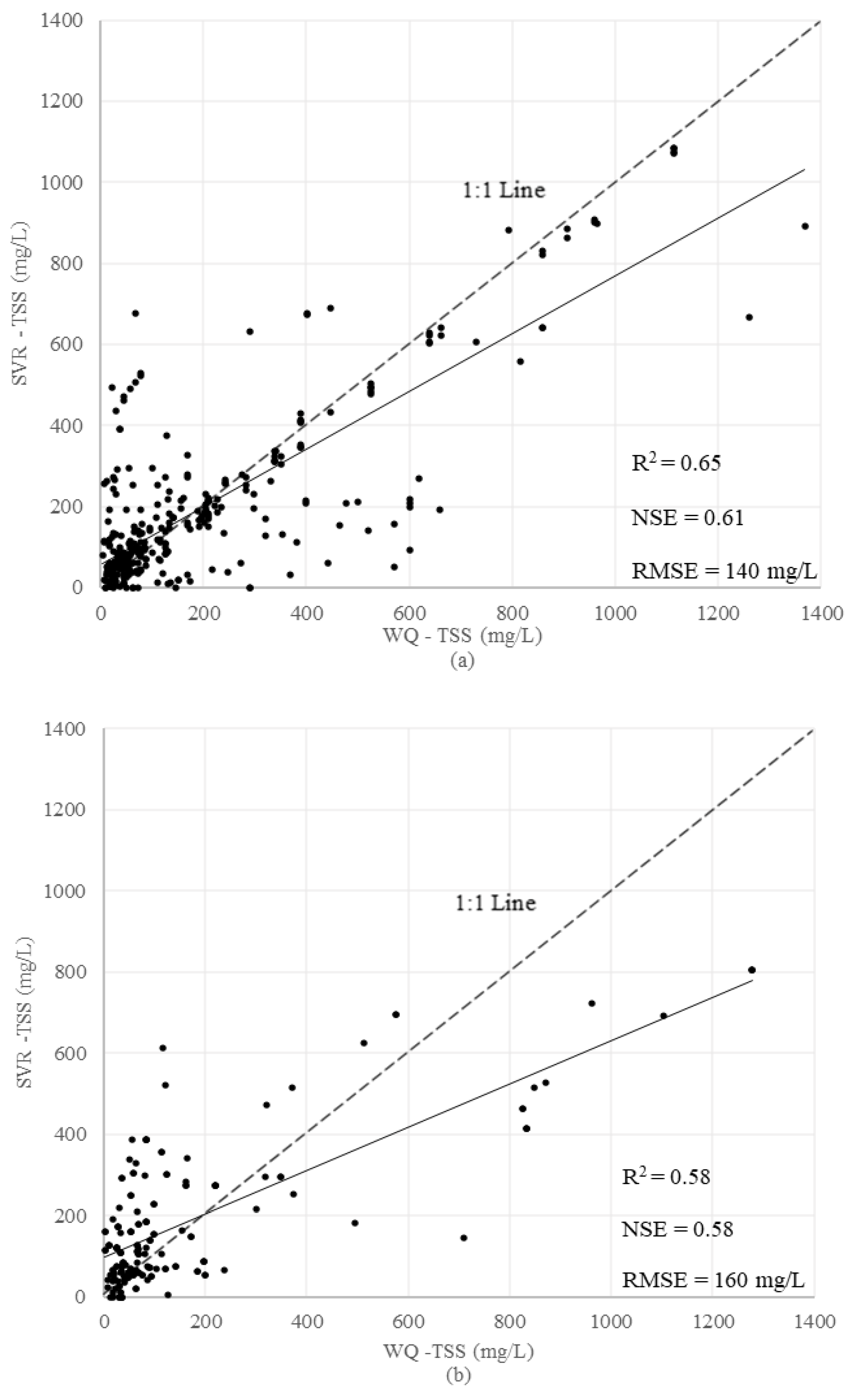
3.2.3. Support Vector Regression (SVR)
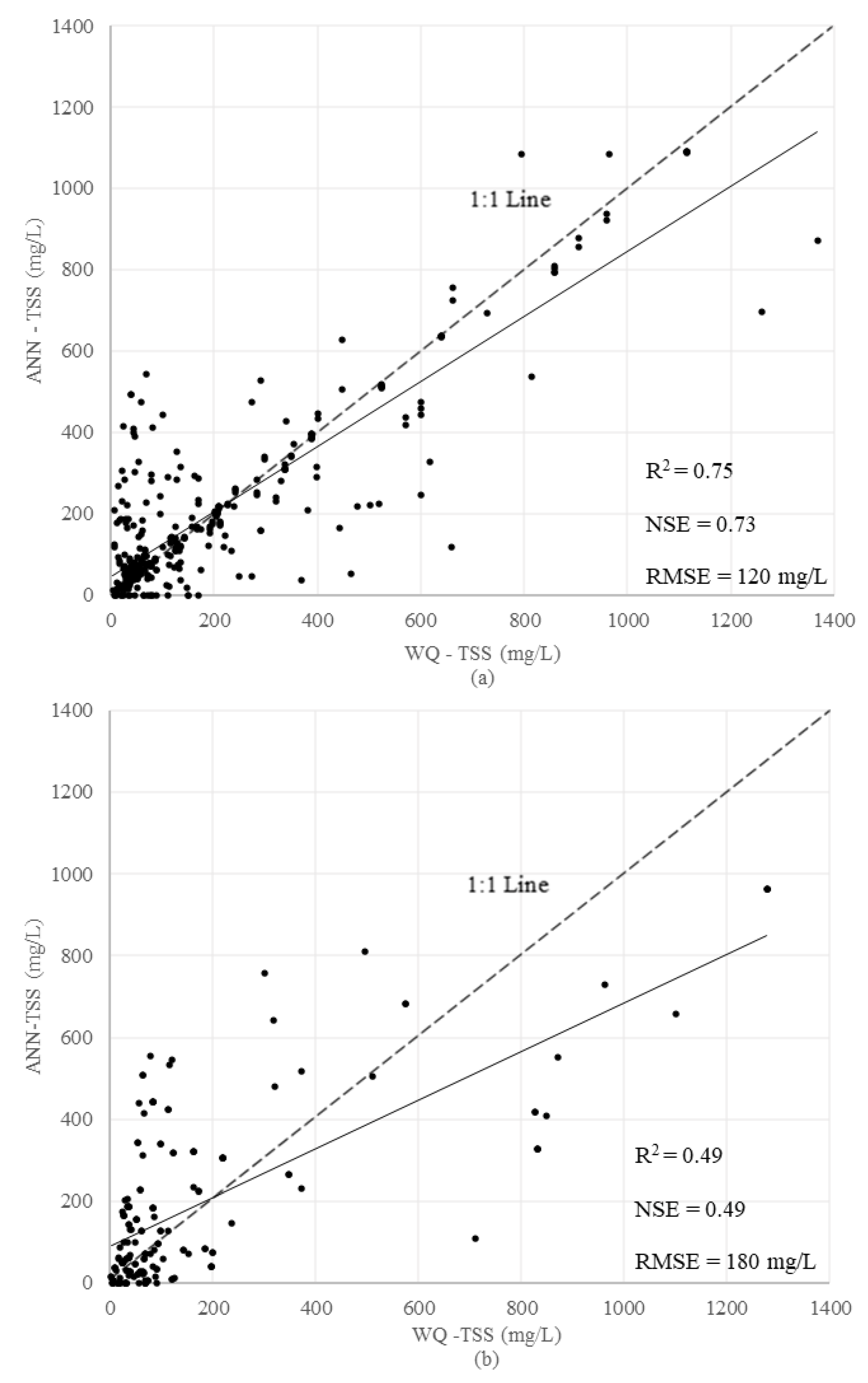
3.2.4. Artificial Neural Network (ANN)
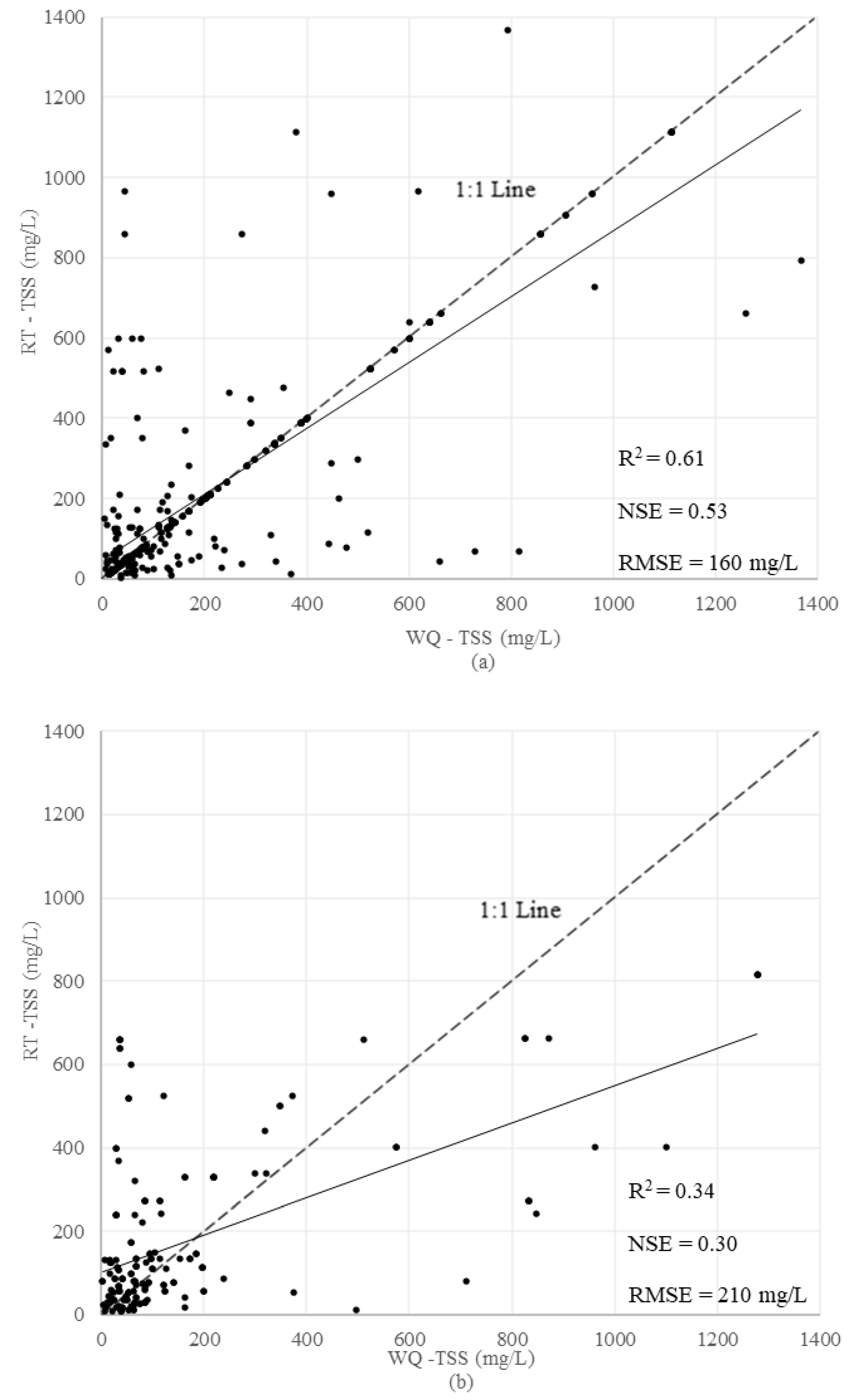
3.2.5. Regression Tree (RT)
3.3. Ensemble Modeling
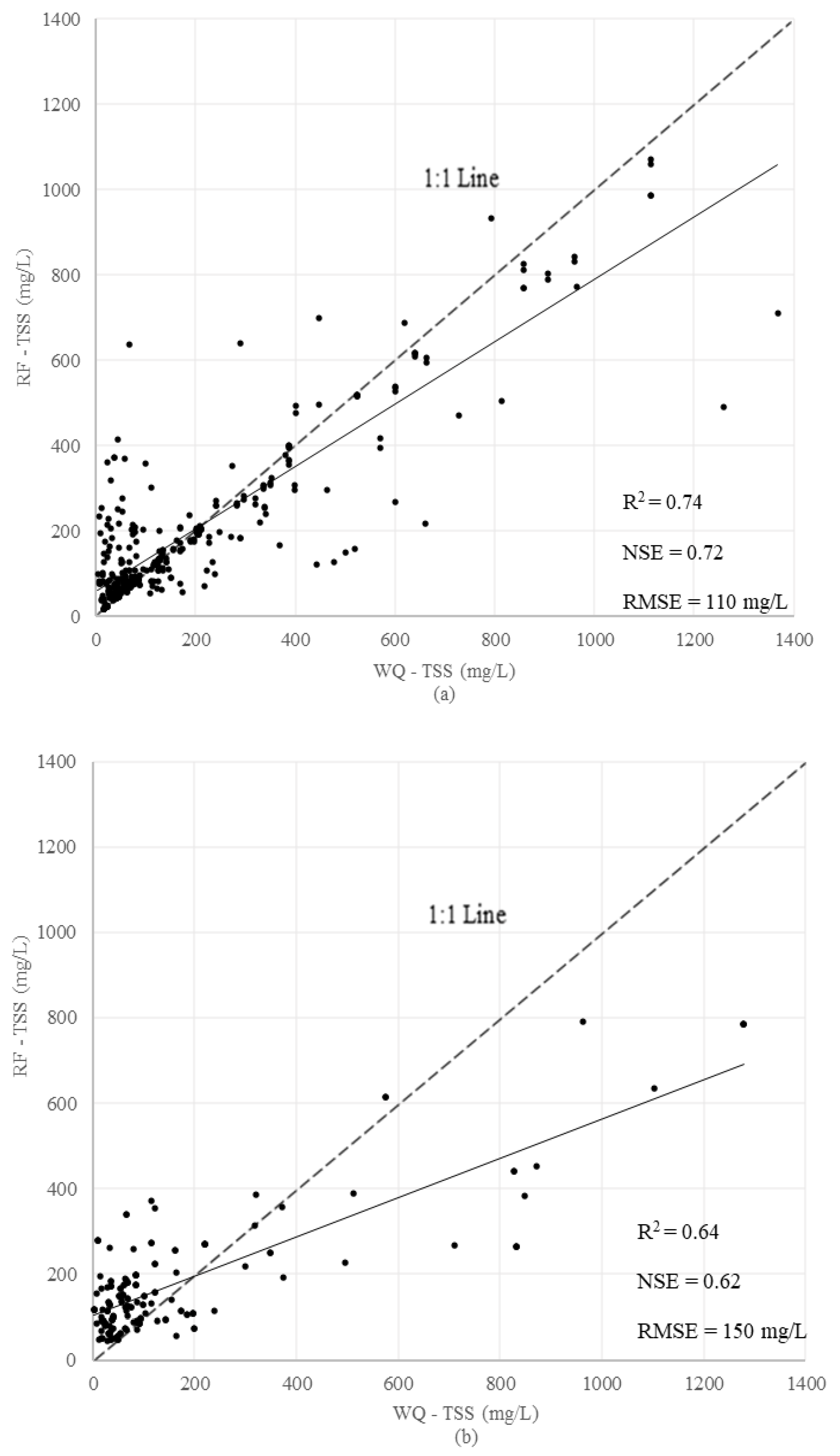
3.3.1. Bagging Model—Random Forest (RF)
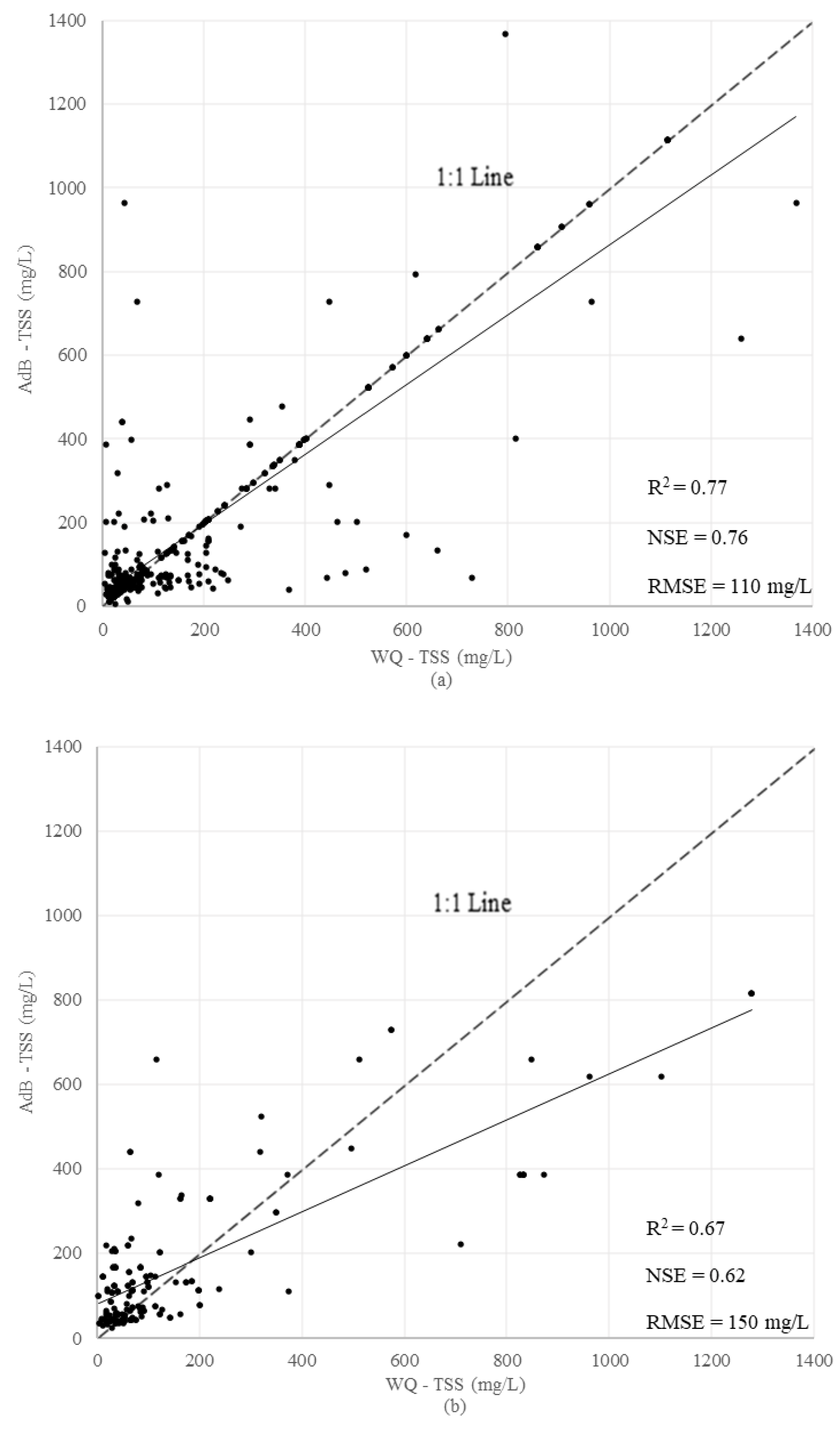
3.3.2. Boosting Model—Adaptive Boosting (AdB)
4. Discussion
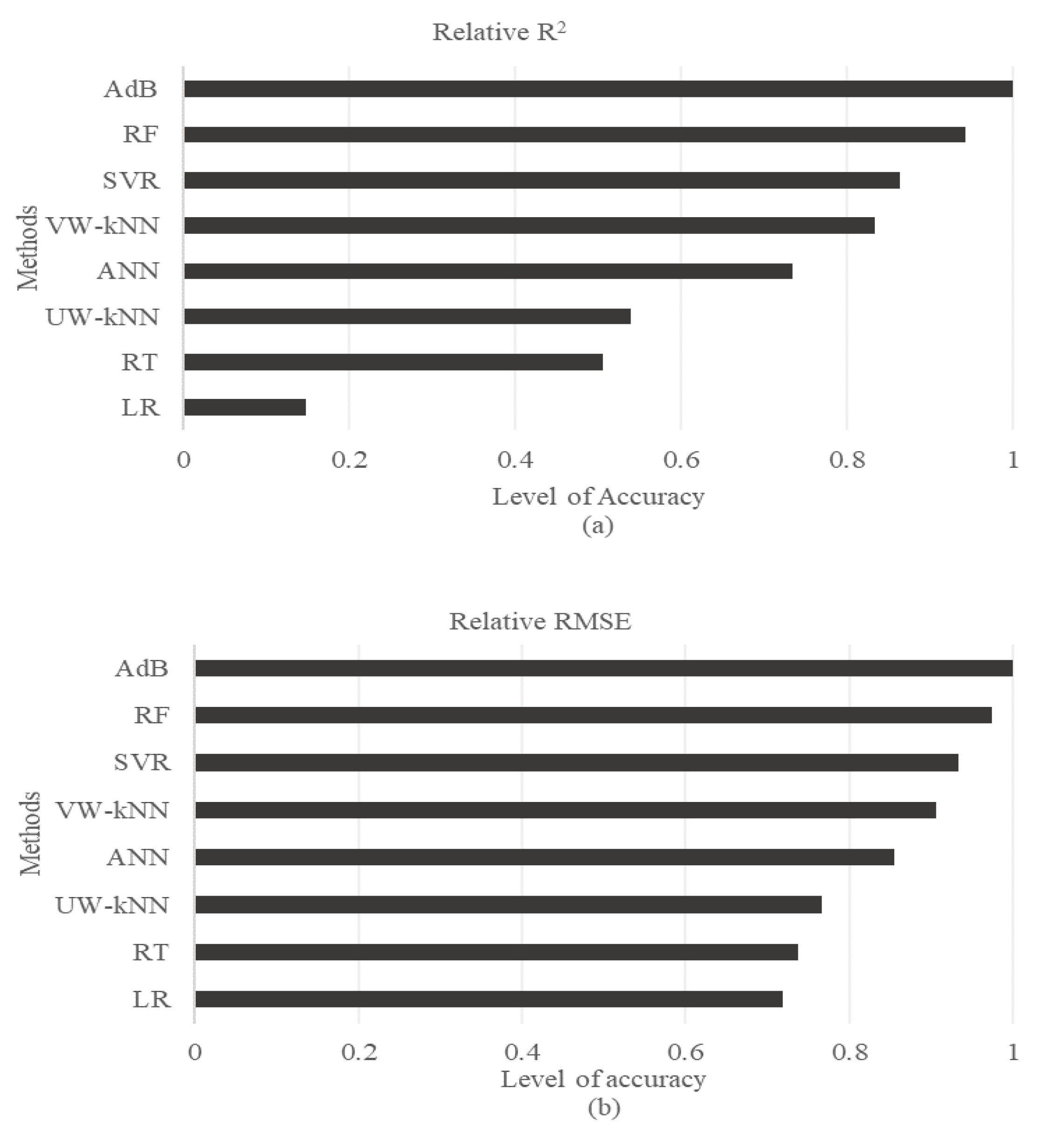
4.1. Single, Bagging, and Boosting Models
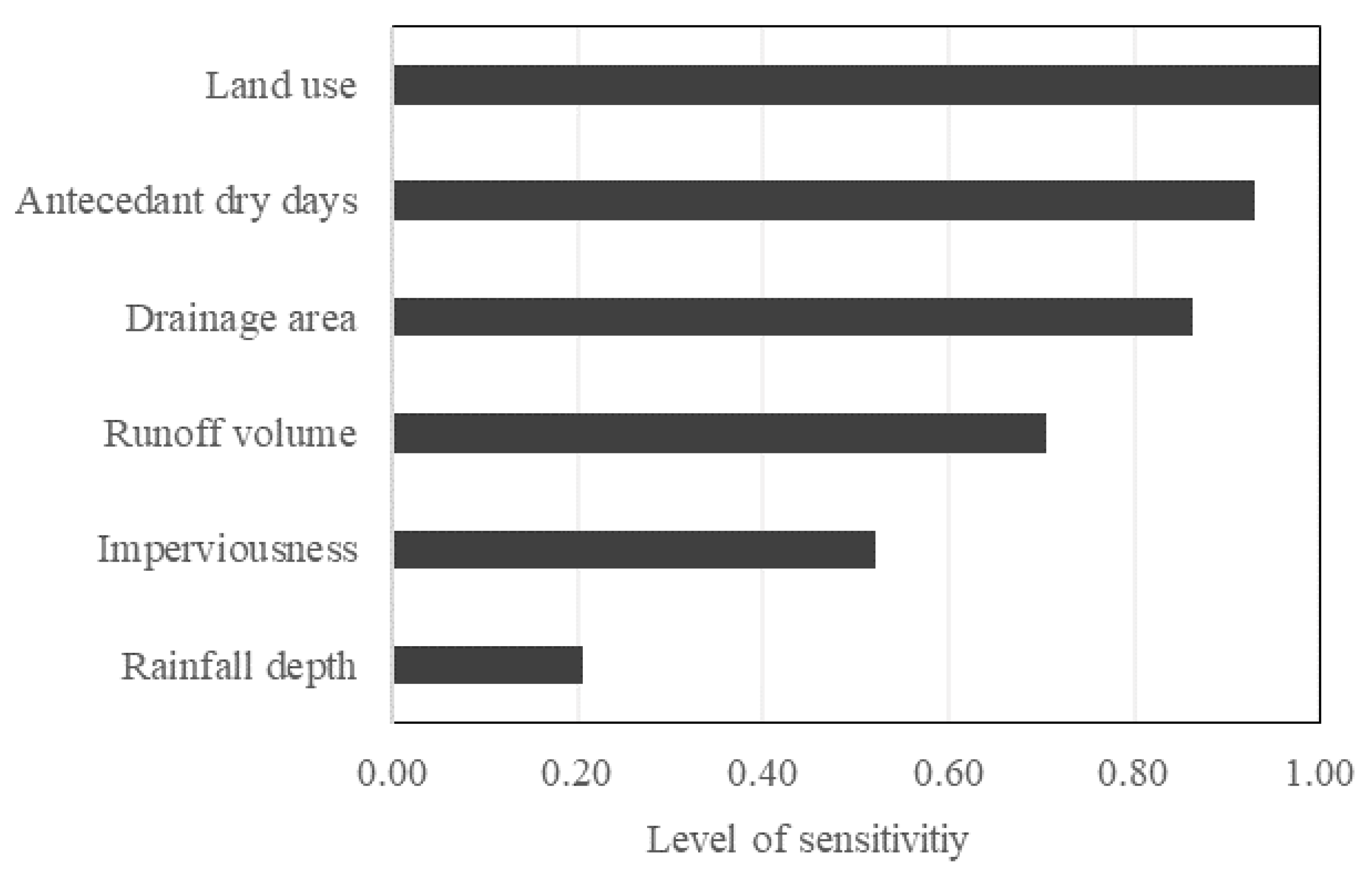
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Danades, A.; Pratama, D.; Anggraini, D.; Anggriani, D. Comparison of accuracy level K-nearest neighbor algorithm and support vector machine algorithm in classification water quality status. In Proceedings of the 2016 6th International Conference on System Engineering and Technology (ICSET), Bandung, Indonesia, 3–4 October 2016; pp. 137–141. [Google Scholar]
- Bedient, P.B.; Lambert, J.L.; Springer, N.K. Stormwater pollutant load-runoff relationships. J. Water Pollut. Control Fed. 1980, 52, 2396–2404. [Google Scholar]
- Jeung, M.; Baek, S.; Beom, J.; Cho, K.H.; Her, Y.; Yoon, K. Evaluation of random forest and regression tree methods for estimation of mass first flush ratio in urban catchments. J. Hydrol. 2019, 575, 1099–1110. [Google Scholar] [CrossRef]
- Patil, S.S.; Barfield, B.J.; Wilber, G.G. Turbidity modeling based on the concentration of total suspended solids for stormwater runoff from construction and development sites. In Proceedings of the World Environmental and Water Resources Congress 2011, Palm Springs, CA, USA, 22–26 May 2011; pp. 477–486. [Google Scholar]
- Peters, J.; De Baets, B.; Verhoest, N.E.C.; Samson, R.; Degroeve, S.; De Becker, P.; Huybrechts, W. Random forests as a tool for ecohydrological distribution modelling. Ecol. Model. 2007, 207, 304–318. [Google Scholar] [CrossRef]
- Young, B.N.; Hathaway, J.M.; Lisenbee, W.A.; He, Q. Assessing the runoff reduction potential of highway swales and WinSLAMM as a predictive tool. Sustainability 2018, 10, 2871. [Google Scholar] [CrossRef]
- Pitt, R. WinSLAMM Instruction. 2013. Available online: http://www.winslamm.com/docs/WinSLAMM%20Model%20Algorithms%20v7.pdf (accessed on 10 December 2020).
- Bachhuber, J.A.; Mattfield, K. Quantifying Urban Stormwater Pollutant Loads and Management Costs Within the Lower Fox River Basin. Proc. Water Environ. Fed. 2009, 2009, 600–605. [Google Scholar] [CrossRef]
- Pitt, R. Calibration of WinSLAMM. Available online: http://winslamm.com/docs/WinSLAMM%20calibration%20Sept (accessed on 9 February 2020).
- Rossman, L.A.; Dickinson, R.E.; Schade, T.; Chan, C.C.; Burgess, E.; Sullivan, D.; Lai, F.-H. SWMM 5-the Next Generation of EPA’s Storm Water Management Model. J. Water Manag. Model. 2004, 16, 339–358. [Google Scholar] [CrossRef]
- Zoppou, C. Review of urban storm water models. Environ. Model. Softw. 2001, 16, 195–231. [Google Scholar] [CrossRef]
- Niazi, M.; Nietch, C.; Maghrebi, M.; Jackson, N.; Bennett, B.R.; Tryby, M.; Massoudieh, A. Storm water management model: Performance review and gap analysis. J. Sustain. Water Built Environ. 2017, 3, 04017002. [Google Scholar] [CrossRef]
- Charbeneau, R.J.; Barrett, M.E. Evaluation of methods for estimating stormwater pollutant loads. Water Environ. Res. 1998, 70, 1295–1302. [Google Scholar] [CrossRef]
- Tu, M.-C.; Smith, P. Modeling pollutant buildup and washoff parameters for SWMM based on land use in a semiarid urban watershed. Water Air Soil Pollut. 2018, 229, 121. [Google Scholar] [CrossRef]
- Azari, B.; Tabesh, M. Optimal design of stormwater collection networks considering hydraulic performance and BMPs. Int. J. Environ. Res. 2018, 12, 585–596. [Google Scholar] [CrossRef]
- Moeini, M.; Zahraie, B. Monthly Water Balance Modeling By Linking Hydro-Climatologic And Tank Groundwater Balance Models. Iran Water Resour. Res. 2018, 14, 59–70. [Google Scholar]
- Chang, F.-J.; Guo, S. Advances in hydrologic forecasts and water resources management. Water 2020, 12, 1819. [Google Scholar] [CrossRef]
- Chang, F.-J.; Hsu, K.; Chang, L.-C. Flood Forecasting Using Machine Learning Methods; MDPI: Basel, Switzerland, 2019. [Google Scholar]
- Hu, J.-H.; Tsai, W.-P.; Cheng, S.-T.; Chang, F.-J. Explore the relationship between fish community and environmental factors by machine learning techniques. Environ. Res. 2020, 184, 109262. [Google Scholar] [CrossRef]
- Kao, I.-F.; Zhou, Y.; Chang, L.-C.; Chang, F.-J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Kashani, A.R.; Gandomi, M.; Camp, C.V.; Gandomi, A.H. Optimum design of shallow foundation using evolutionary algorithms. Soft Comput. 2020, 24, 6809–6833. [Google Scholar] [CrossRef]
- Liang, J.; Li, W.; Bradford, S.A.; Šimůnek, J. Physics-Informed Data-Driven Models to Predict Surface Runoff Water Quantity and Quality in Agricultural Fields. Water 2019, 11, 200. [Google Scholar] [CrossRef]
- May, D.B.; Sivakumar, M. Prediction of urban stormwater quality using artificial neural networks. Environ. Model. Softw. 2009, 24, 296–302. [Google Scholar] [CrossRef]
- Álvarez-Cabria, M.; Barquín, J.; Peñas, F.J. Modelling the spatial and seasonal variability of water quality for entire river networks: Relationships with natural and anthropogenic factors. Sci. Total Environ. 2016, 545, 152–162. [Google Scholar] [CrossRef]
- Guimarães, T.T.; Veronez, M.R.; Koste, E.C.; Souza, E.M.; Brum, D.; Gonzaga, L.; Mauad, F.F. Evaluation of regression analysis and neural networks to predict total suspended solids in water bodies from unmanned aerial vehicle images. Sustainability 2019, 11, 2580. [Google Scholar] [CrossRef]
- Ahmed, U.; Mumtaz, R.; Anwar, H.; Shah, A.A.; Irfan, R.; García-Nieto, J. Efficient water quality prediction using supervised Machine Learning. Water 2019, 11, 2210. [Google Scholar] [CrossRef]
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; De Marinis, G. Machine learning algorithms for the forecasting of wastewater quality indicators. Water 2017, 9, 105. [Google Scholar] [CrossRef]
- Karamouz, M.; Mojahedi, S.A.; Ahmadi, A. Interbasin water transfer: Economic water quality-based model. J. Irrig. Drain. Eng. 2010, 136, 90–98. [Google Scholar] [CrossRef]
- Maestre, A.; Pitt, R.E.; Williamson, D. Nonparametric statistical tests comparing first flush and composite samples from the national stormwater quality database. J. Water Manag. Model. 2004. [Google Scholar] [CrossRef]
- Pitt, R.; Maestre, A.; Morquecho, R. The National Stormwater Quality Database (NSQD, Version 1.1). In Proceedings of the 1st Annual Stormwater Management Research Symposium Proceedings, Orlando, FL, USA, 16 February 2004; pp. 13–51. [Google Scholar]
- Maestre, A.; Pitt, R.E. Identification of significant factors affecting stormwater quality using the national stormwater quality database. J. Water Manag. Model. 2006, 13, 287–326. [Google Scholar] [CrossRef]
- Aiken, L.S.; West, S.G.; Pitts, S.C.; Baraldi, A.N.; Wurpts, I.C. Multiple linear regression. In Handbook of Psychology, 2nd ed.; Wiley Online Library: Hoboken, NJ, USA, 2012; Volume 2. [Google Scholar]
- McCarthy, D.T.; Hathaway, J.M.; Hunt, W.F.; Deletic, A. Intra-event variability of Escherichia coli and total suspended solids in urban stormwater runoff. Water Res. 2012, 46, 6661–6670. [Google Scholar] [CrossRef] [PubMed]
- Azizi, K.; Attari, J.; Moridi, A. Estimation of discharge coefficient and optimization of Piano Key Weirs. In Labyrinth and Piano Key Weirs III–PKW 2017; CRC Press: Boca Raton, FL, USA, 2017; p. 213. [Google Scholar]
- Barnes, K.B.; Morgan, J.; Roberge, M. Impervious Surfaces and the Quality of Natural and Built Environments; Department of Geography and Environmental Planning, Towson University: Towson, MD, USA, 2001. [Google Scholar]
- Brodie, I.M.; Dunn, P.K. Suspended particle characteristics in storm runoff from urban impervious surfaces in Toowoomba, Australia. Urban Water J. 2009, 6, 137–146. [Google Scholar] [CrossRef]
- Uygun, B.Ş.; Albek, M. Determination effects of impervious areas on urban watershed. Environ. Sci. Pollut. Res. 2015, 22, 2272–2286. [Google Scholar] [CrossRef]
- Pizarro, J.; Vergara, P.M.; Morales, J.L.; Rodríguez, J.A.; Vila, I. Influence of land use and climate on the load of suspended solids in catchments of Andean rivers. Environ. Monit. Assess. 2014, 186, 835–843. [Google Scholar] [CrossRef]
- Gong, Y.; Liang, X.; Li, X.; Li, J.; Fang, X.; Song, R. Influence of rainfall characteristics on total suspended solids in urban runoff: A case study in Beijing, China. Water 2016, 8, 278. [Google Scholar] [CrossRef]
- King, J.K.; Blanton, J.O. Model for predicting effects of land-use changes on the canal-mediated discharge of total suspended solids into tidal creeks and estuaries. J. Environ. Eng. 2011, 137, 920–927. [Google Scholar] [CrossRef]
- Shakya, S.; Tamaddun, K.A.; Stephen, H.; Ahmad, S. Urban Runoff and Pollutant Reduction by Retrofitting Green Infrastructure in Storm Water Management System. In Proceedings of the World Environmental and Water Resources Congress 2011, Palm Springs, CA, USA, 22–26 May 2019; pp. 93–104. [Google Scholar]
- Karathanasis, A.D.; Potter, C.L.; Coyne, M.S. Vegetation effects on fecal bacteria, BOD, and suspended solid removal in constructed wetlands treating domestic wastewater. Ecol. Eng. 2003, 20, 157–169. [Google Scholar] [CrossRef]
- Al Hasan, M.; Chaoji, V.; Salem, S.; Zaki, M. Link prediction using supervised learning. In Proceedings of the SDM06: Workshop on Link Analysis, Counter-Terrorism and Security, Bethesda, MD, USA, 19 April 2006; pp. 798–805. [Google Scholar]
- Hardt, M.; Price, E.; Srebro, N. Equality of opportunity in supervised learning. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3315–3323. [Google Scholar]
- Springenberg, J.T. Unsupervised and semi-supervised learning with categorical generative adversarial networks. arXiv 2015, arXiv:1511.06390. [Google Scholar]
- Tan, M.; Le, Q.V. Efficientnet: Rethinking model scaling for convolutional neural networks. arXiv 2019, arXiv:1905.11946. [Google Scholar]
- Solomatine, D.P.; Maskey, M.; Shrestha, D.L. Eager and lazy learning methods in the context of hydrologic forecasting. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 4847–4853. [Google Scholar]
- Wei, C.-C. Comparing lazy and eager learning models for water level forecasting in river-reservoir basins of inundation regions. Environ. Model. Softw. 2015, 63, 137–155. [Google Scholar] [CrossRef]
- García-Callejas, D.; Araújo, M.B. The effects of model and data complexity on predictions from species distributions models. Ecol. Model. 2016, 326, 4–12. [Google Scholar] [CrossRef]
- Yao, Y.; Xiao, Z.; Wang, B.; Viswanath, B.; Zheng, H.; Zhao, B.Y. Complexity vs. performance: Empirical analysis of machine learning as a service. In Proceedings of the 17th ACM SIGCOMM Internet Measurement Conference (IMC 2017), London, UK, 1–3 November 2017; pp. 384–397. [Google Scholar]
- Li, P.; Zha, Y.; Shi, L.; Tso, C.-H.M.; Zhang, Y.; Zeng, W. Comparison of the use of a physical-based model with data assimilation and machine learning methods for simulating soil water dynamics. J. Hydrol. 2020, 584, 124692. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 821. [Google Scholar]
- Marill, K.A. Advanced statistics: Linear regression, part II: Multiple linear regression. Acad. Emerg. Med. 2004, 11, 94–102. [Google Scholar] [CrossRef]
- Almeida, A.M.d.; Castel-Branco, M.M.; Falcao, A.C. Linear regression for calibration lines revisited: Weighting schemes for bioanalytical methods. J. Chromatogr. B 2002, 774, 215–222. [Google Scholar] [CrossRef]
- Shojaeizadeh, A.; Geza, M.; McCray, J.; Hogue, T.S. Site-scale integrated decision support tool (i-DSTss) for stormwater management. Water 2019, 11, 2022. [Google Scholar] [CrossRef]
- Liang, J.; Yang, Q.; Sun, T.; Martin, J.D.; Sun, H.; Li, L. MIKE 11 model-based water quality model as a tool for the evaluation of water quality management plans. J. Water Supply Res. Technol. AQUA 2015, 64, 708–718. [Google Scholar] [CrossRef]
- Kohli, S.; Godwin, G.T.; Urolagin, S. Sales Prediction Using Linear and KNN Regression. In Advances in Machine Learning and Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2020; pp. 321–329. [Google Scholar]
- Saini, I.; Singh, D.; Khosla, A. QRS detection using K-Nearest Neighbor algorithm (KNN) and evaluation on standard ECG databases. J. Adv. Res. 2013, 4, 331–344. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.M.R.; Arif, R.B.; Siddique, M.A.B.; Oishe, M.R. Study and observation of the variation of accuracies of KNN, SVM, LMNN, ENN algorithms on eleven different datasets from UCI machine learning repository. In Proceedings of the 2018 4th International Conference on Electrical Engineering and Information & Communication Technology (iCEEiCT), Dhaka, Bangladesh, 13–15 September 2018; pp. 124–129. [Google Scholar]
- Wang, X.; Ma, L.; Wang, X. Apply semi-supervised support vector regression for remote sensing water quality retrieving. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2757–2760. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Liu, S.; Tai, H.; Ding, Q.; Li, D.; Xu, L.; Wei, Y. A hybrid approach of support vector regression with genetic algorithm optimization for aquaculture water quality prediction. Math. Comput. Model. 2013, 58, 458–465. [Google Scholar] [CrossRef]
- Najah, A.; El-Shafie, A.; Karim, O.A.; El-Shafie, A.H. Application of artificial neural networks for water quality prediction. Neural Comput. Appl. 2013, 22, 187–201. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality—A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Fotovvati, B.; Balasubramanian, M.; Asadi, E. Modeling and Optimization Approaches of Laser-Based Powder-Bed Fusion Process for Ti-6Al-4V Alloy. Coatings 2020, 10, 1104. [Google Scholar] [CrossRef]
- Graupe, D. Principles of Artificial Neural Networks; World Scientific: Singapore, 2013; Volume 7. [Google Scholar]
- Yegnanarayana, B. Artificial Neural Networks; PHI Learning Pvt. Ltd.: New Delhi, India, 2009. [Google Scholar]
- Rizwan, J.M.; Krishnan, P.N.; Karthikeyan, R.; Kumar, S.R. Multi layer perception type artificial neural network based traffic control. Indian J. Sci. Technol. 2016, 9, 1–6. [Google Scholar] [CrossRef]
- Boughrara, H.; Chtourou, M.; Amar, C.B.; Chen, L. Facial expression recognition based on a mlp neural network using constructive training algorithm. Multimed. Tools Appl. 2016, 75, 709–731. [Google Scholar] [CrossRef]
- Sutton, C.D. Classification and regression trees, bagging, and boosting. Handb. Stat. 2005, 24, 303–329. [Google Scholar]
- Ließ, M.; Glaser, B.; Huwe, B. Uncertainty in the spatial prediction of soil texture: Comparison of regression tree and Random Forest models. Geoderma 2012, 170, 70–79. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Faradonbeh, R.S.; Amnieh, H.B.; Armaghani, D.J.; Monjezi, M. Forecasting blast-induced ground vibration developing a CART model. Eng. Comput. 2017, 33, 307–316. [Google Scholar] [CrossRef]
- Golecha, Y.S. Analyzing Term Deposits in Banking Sector by Performing Predictive Analysis Using Multiple Machine Learning Techniques. Masters Thesis, National College of Ireland, Dublin, Ireland, 2017. [Google Scholar]
- Rajadurai, H.; Gandhi, U.D. A stacked ensemble learning model for intrusion detection in wireless network. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wu, D.; Wang, H.; Seidu, R. Smart data driven quality prediction for urban water source management. Future Gener. Comput. Syst. 2020, 107, 418–432. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R news 2002, 2, 18–22. [Google Scholar]
- Ok, A.O.; Akar, O.; Gungor, O. Evaluation of random forest method for agricultural crop classification. Eur. J. Remote Sens. 2012, 45, 421–432. [Google Scholar] [CrossRef]
- Adam, E.M.; Mutanga, O.; Rugege, D.; Ismail, R. Discriminating the papyrus vegetation (Cyperus papyrus L.) and its co-existent species using random forest and hyperspectral data resampled to HYMAP. Int. J. Remote Sens. 2012, 33, 552–569. [Google Scholar] [CrossRef]
- Smith, R.G.; Majumdar, S. Groundwater Storage Loss Associated With Land Subsidence in Western United States Mapped Using Machine Learning. Water Resour. Res. 2020, 56, e2019WR026621. [Google Scholar] [CrossRef]
- Al-Stouhi, S.; Reddy, C.K. Adaptive Boosting for Transfer Learning using Dynamic Updates; Springer: Berlin/Heidelberg, Germany, 2011; pp. 60–75. [Google Scholar]
- Freund, Y.; Schapire, R.; Abe, N. A short introduction to boosting. J. Jpn. Soc. Artif. Intell. 1999, 14, 1612. [Google Scholar]
- Duan, S.; Yang, W.; Wang, X.; Mao, S.; Zhang, Y. Forecasting of grain pile temperature from meteorological factors using machine learning. IEEE Access 2019, 7, 130721–130733. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Firouzmand, M.; Charmi, M.; Hemmati, M.; Moghadam, M.; Ghorbani, Y. Blood pressure estimation from appropriate and inappropriate PPG signals using A whole-based method. Biomed. Signal Process. Control 2019, 47, 196–206. [Google Scholar] [CrossRef]
- Rojas, R. AdaBoost and the Super Bowl of Classifiers a Tutorial Introduction to Adaptive Boosting; Freie University: Berlin, Germany, 2009. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Yuan, Q.; Guerra, H.B.; Kim, Y. An investigation of the relationships between rainfall conditions and pollutant wash-off from the paved road. Water 2017, 9, 232. [Google Scholar] [CrossRef]
| Features and Target Value | Description | Unit | |
|---|---|---|---|
| Drainage area | Area contributing to discharge and pollutant loading | km2 | |
| Land use | Residential | Percent of the area under each land use category | % |
| Institutional | |||
| Commercial | |||
| Industrial | |||
| Open Space | |||
| Freeway | |||
| Imperviousness | Percent impervious | % | |
| Antecedent dry days | The number of dry days before the storm event | days | |
| Rainfall depth | Rainfall depth | mm | |
| Runoff volume | The volume of runoff during a specific event | m3 | |
| TSS | Measured TSS concentration used as a target value | mg/L | |
| Features | Drainage Area | Land Use | Imperviousness | Antecedent Dry Days | Rainfall Depth | Runoff Volume |
|---|---|---|---|---|---|---|
| Drainage Area | 1 | −0.14 | −0.04 | −0.12 | −0.07 | 0.31 |
| Land use | −0.14 | 1 | 0.09 | 0.017 | 0 | −0.08 |
| Imperviousness | −0.04 | 0.09 | 1 | 0.22 | 0.04 | −0.28 |
| Antecedent dry days | −0.12 | 0.017 | 0.22 | 1 | −0.03 | −0.03 |
| Rainfall depth | −0.07 | 0 | 0.04 | −0.03 | 1 | 0.46 |
| Runoff volume | 0.31 | −0.08 | −0.28 | −0.03 | 0.46 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moeini, M.; Shojaeizadeh, A.; Geza, M. Supervised Machine Learning for Estimation of Total Suspended Solids in Urban Watersheds. Water 2021, 13, 147. https://doi.org/10.3390/w13020147
Moeini M, Shojaeizadeh A, Geza M. Supervised Machine Learning for Estimation of Total Suspended Solids in Urban Watersheds. Water. 2021; 13(2):147. https://doi.org/10.3390/w13020147
Chicago/Turabian StyleMoeini, Mohammadreza, Ali Shojaeizadeh, and Mengistu Geza. 2021. "Supervised Machine Learning for Estimation of Total Suspended Solids in Urban Watersheds" Water 13, no. 2: 147. https://doi.org/10.3390/w13020147
APA StyleMoeini, M., Shojaeizadeh, A., & Geza, M. (2021). Supervised Machine Learning for Estimation of Total Suspended Solids in Urban Watersheds. Water, 13(2), 147. https://doi.org/10.3390/w13020147





