A New Multi-Objective Optimization Model of Water Resources Considering Fairness and Water Shortage Risk
Abstract
:1. Introduction
2. Materials and Methods
2.1. Optimization Model
2.1.1. Objective Function
2.1.2. Constraints
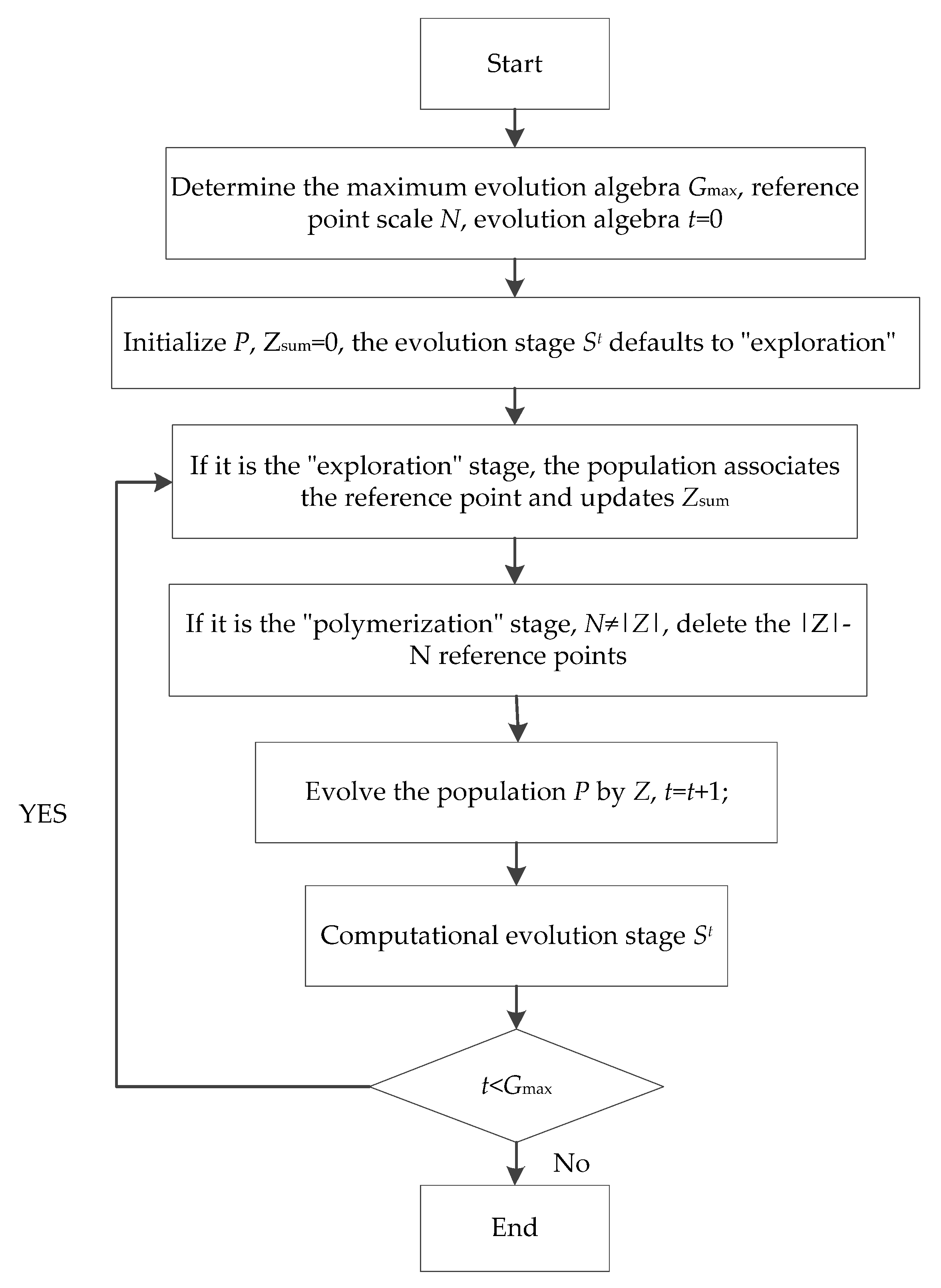
2.2. Optimization Algorithm
2.2.1. NSGA-III
2.2.2. ARNSGA-III
- 1.
- According to the population size N, select the reference point set Z divided into p in each dimension; the number of reference points is , and p satisfies .
- 2.
- Determine the evolution stage of the population according to the plan in step 1.
- 3.
- When the population is in the “exploration” stage, statistical reference point set Z is the sum of the number of associated individuals in each generation .
- 4.
- When the population just enters the “polymerization” stage, the N reference points with the largest number of associations in Z are retained according to to form a new reference point set .
2.3. HV Algorithm Test Indicators
- 1.
- Taking (,,) as the reference point in the HV evaluation index, (, ,) as each Pareto solution obtained in a certain run of an algorithm, and (, , ) and (, , ) as the diagonal of the rectangle, the area of the rectangle enclosed by each solution and the reference point is calculated.
- 2.
- Taking the union of all the rectangles calculated in step 1, the area of the figure formed is the HV value.
3. Case Study
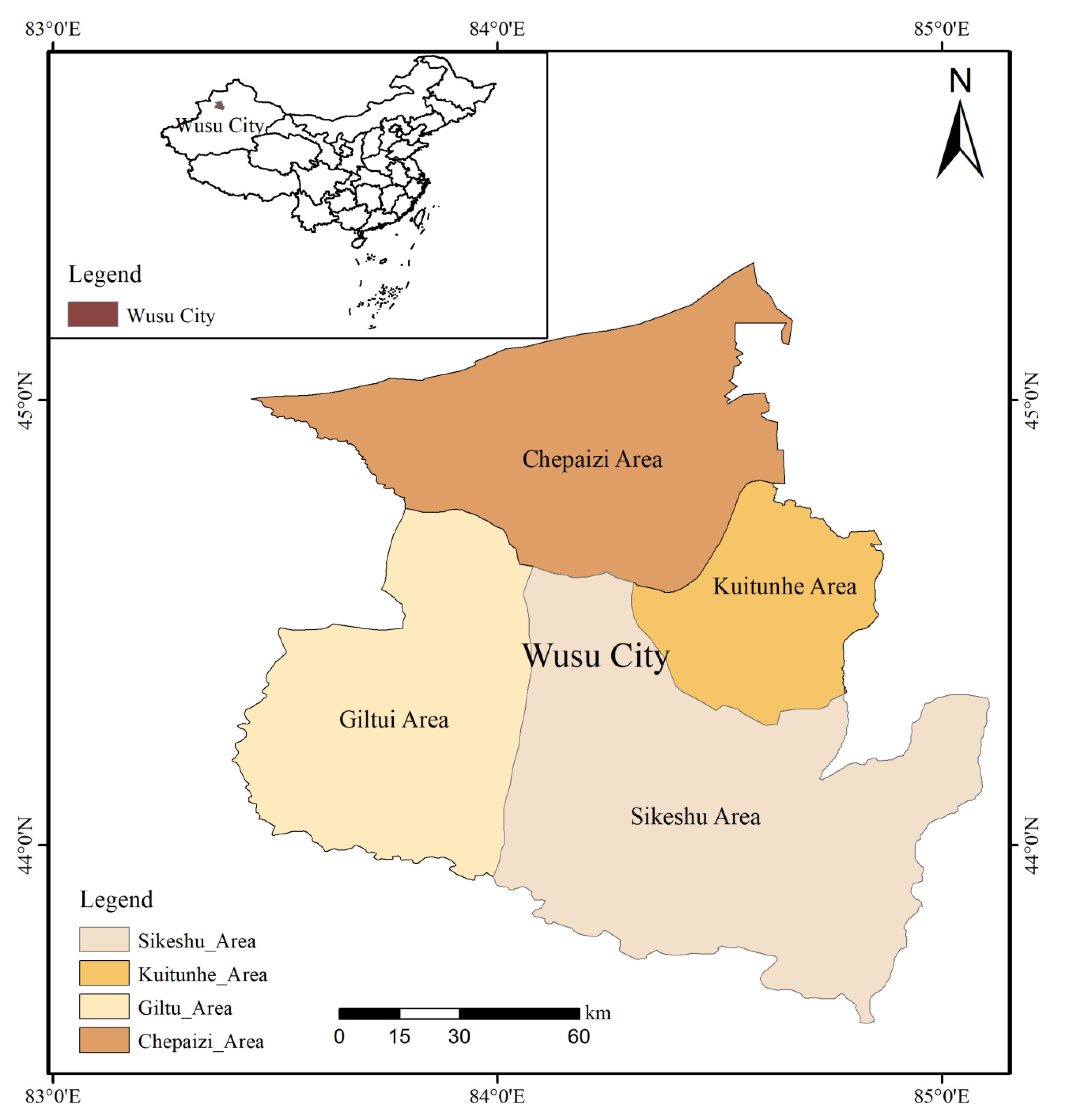
3.1. Study Area
3.2. Data
4. Results and Discussion
4.1. ARNSGA-III Instance Test
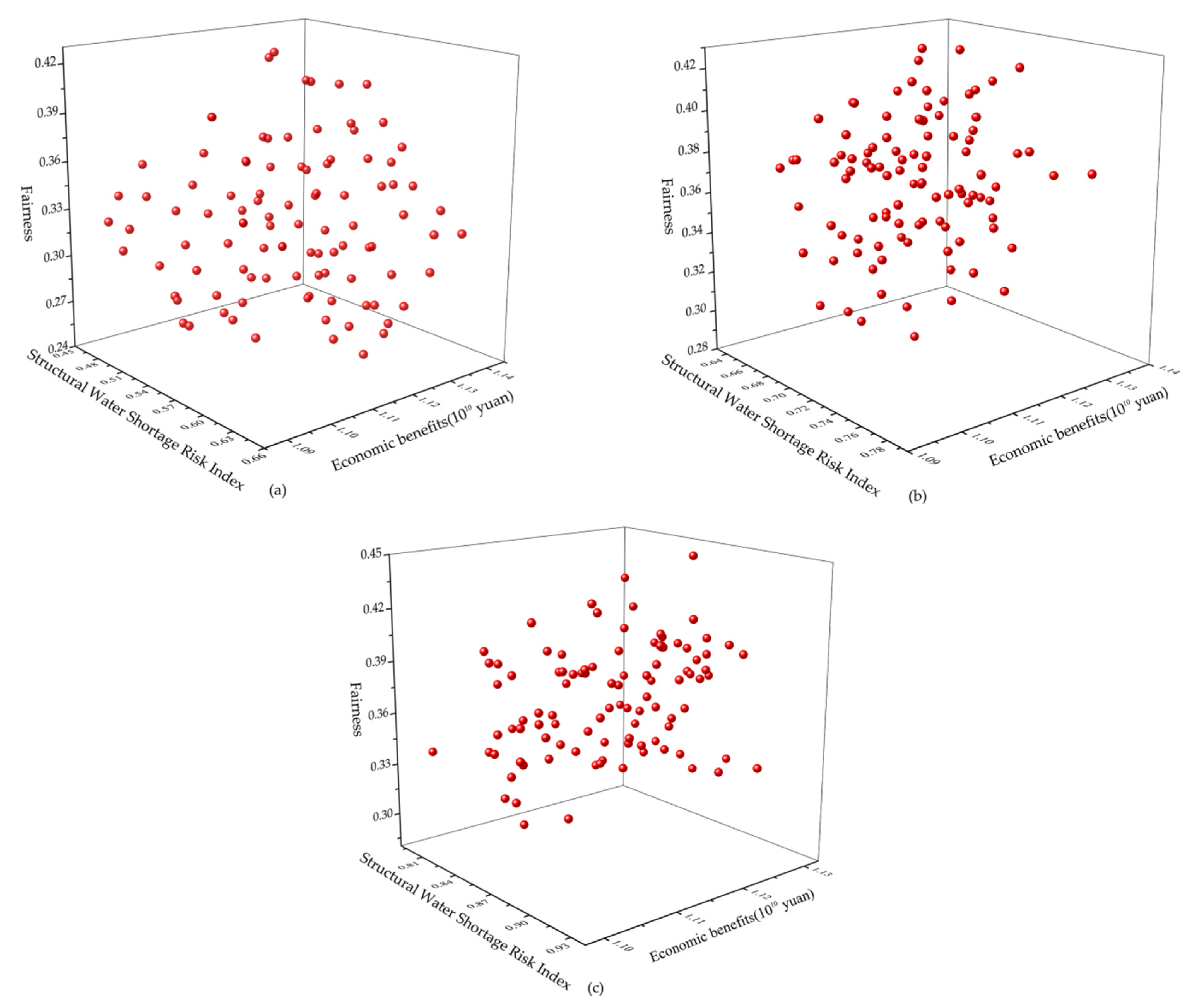
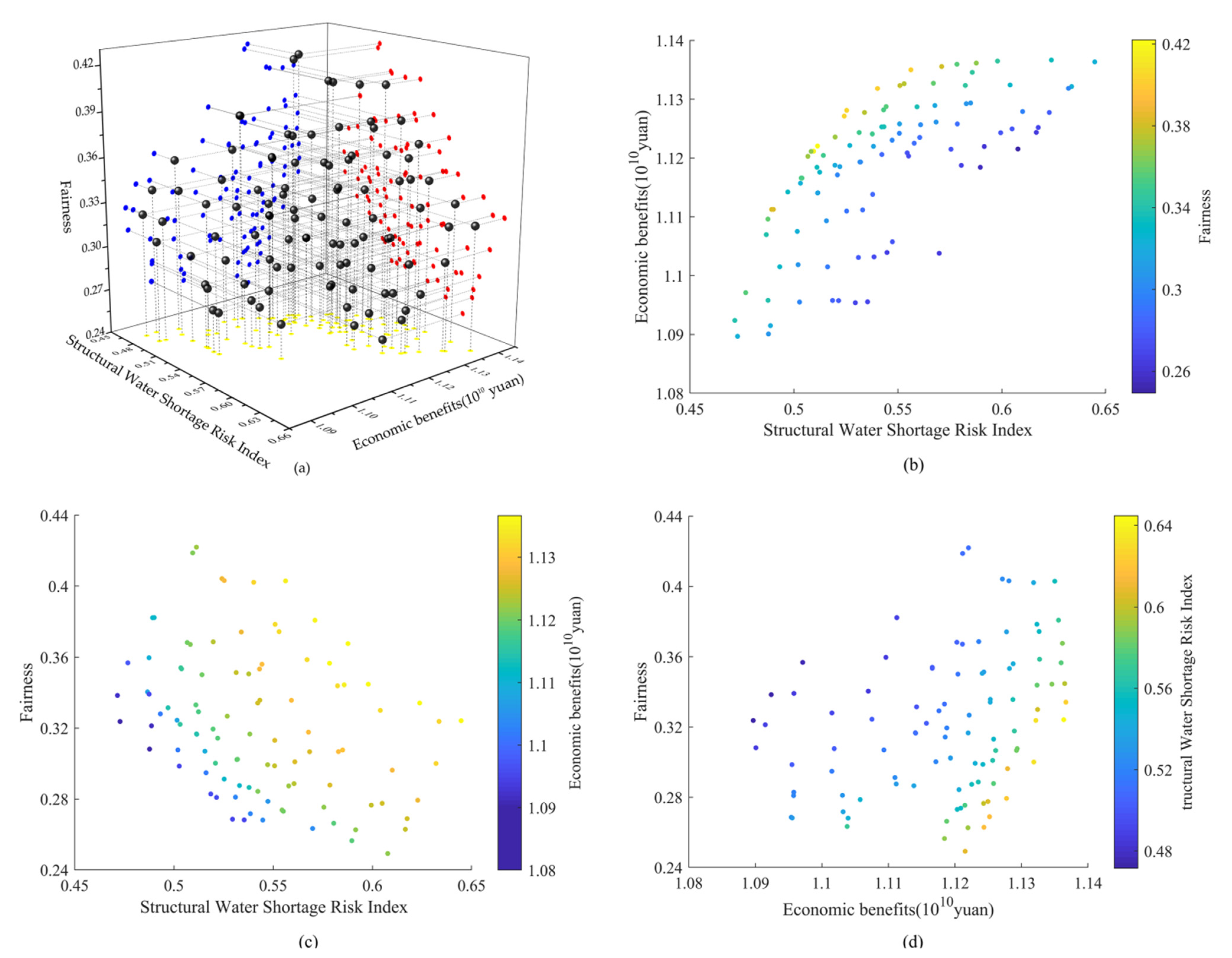
4.2. Typical Year Analysis
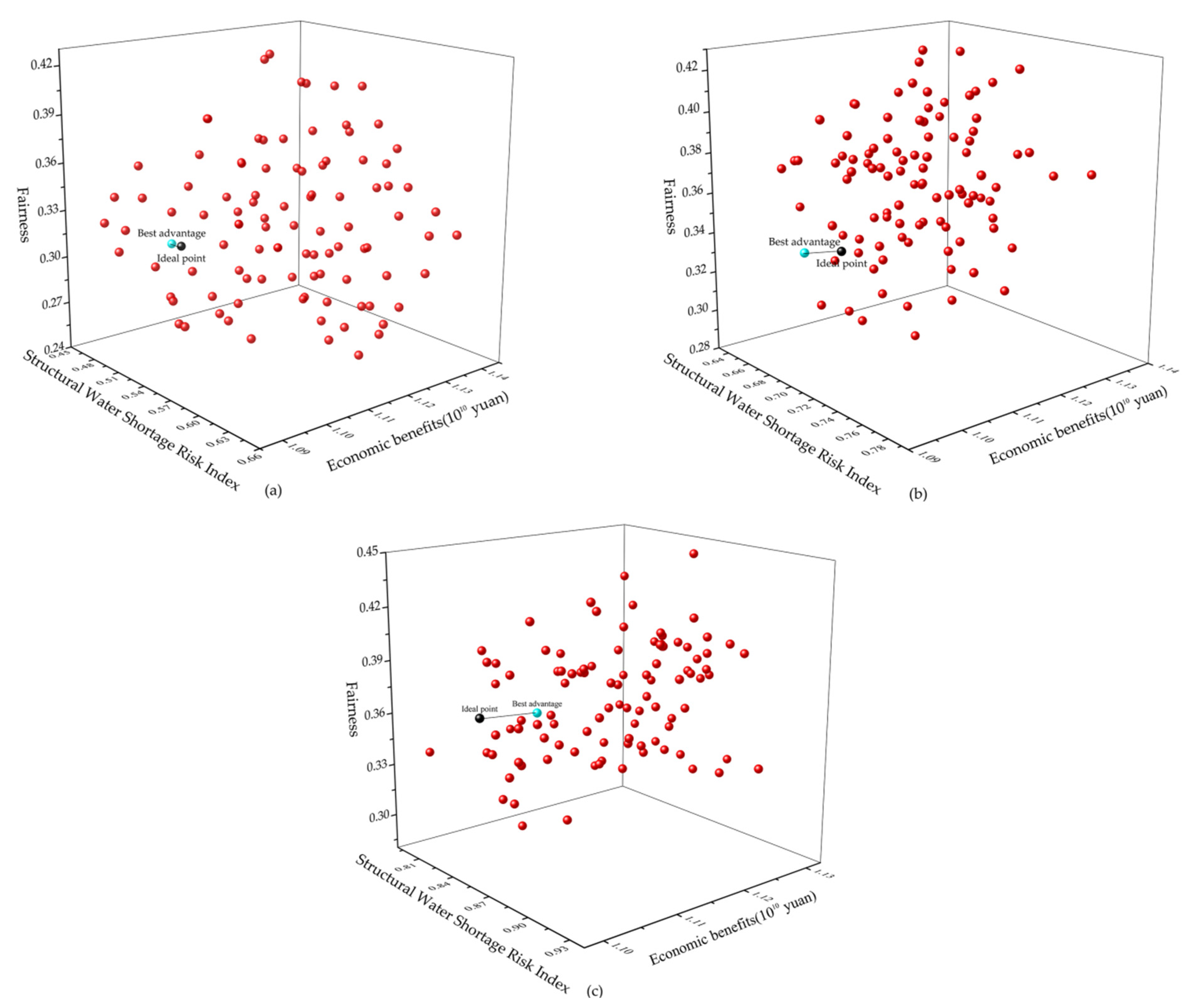
4.3. Water Resource Allocation
5. Conclusions
- 1.
- The new multi-objective optimization model, which combines the fairness of water allocation with structural water shortage risks, provides reasonable and feasible solutions for solving water conflicts caused by unfair water distribution and water shortage risks.
- 2.
- Analyzing the relationship between the objective functions reveals that there is a competitive, restrictive relationship between the three objective functions, among which the structural water shortage risk index and economic benefits have the strongest negative relationship.
- 3.
- The convergence and stability of ARNSGA-III are better than those of NSGA-III, MOSPO, and MOEA/D, which proves that ARNSGA-III has strong practicability for water resources allocation.
- 4.
- The new multi-objective optimization model has been applied to the allocation of water resources in Wusu City of China. The optimal allocation schemes of water resources in normal years, dry years, and extremely dry years are proposed, respectively. Taking the normal years as an example, the structural water shortage risk index is reduced by 0.540, economic benefits by 0.002 × 1010 yuan, and fairness is reduced by 0.472. The results show that the model is applicable in the field of water resources allocation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, Z.; Wei, C.; Yao, L.; Li, L.; Li, C. A multi-objective optimization model with conditional value-at-risk constraints for water allocation equality. J. Hydrol. 2016, 542, 330–342. [Google Scholar] [CrossRef]
- Eliasson, J. The rising pressure of global water shortages. Nat. News 2015, 517, 6. [Google Scholar] [CrossRef]
- Habibi Davijani, M.; Banihabib, M.E.; Nadjafzadeh Anvar, A.; Hashemi, S.R. Multi-Objective Optimization Model for the Allocation of Water Resources in Arid Regions Based on the Maximization of Socioeconomic Efficiency. Water Resour. Manag. 2016, 30, 927–946. [Google Scholar] [CrossRef]
- Cosgrove, W.J.; Loucks, D.P. Water management: Current and future challenges and research directions. Water Resour. Res. 2015, 51, 4823–4839. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Guo, S.; Liu, D.; Pan, Z.; Hong, X. A Fair Approach for Multi-Objective Water Resources Allocation. Water Resour. Manag. 2019, 33, 3633–3653. [Google Scholar] [CrossRef]
- Cullis, J.; Koppen, B.V. Applying the Gini Coefficient to Measure Inequality of Water Use in the Olifants River Water Management Area, South Africa; IWMI Research Report 113; IWNI: Colombo, Sri Lanka, 2009; p. 19. [Google Scholar]
- Yang, G.; Guo, P.; Huo, L.; Ren, C. Optimization of the irrigation water resources for Shijin irrigation district in north China. Agric. Water Manag. 2015, 158, 82–98. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, Y.; Yao, L.; Wei, C.; Li, C. Optimal allocation of regional water resources: From a perspective of equity-efficiency tradeoff. Resour. Conserv. Recycl. 2016, 109, 102–113. [Google Scholar] [CrossRef]
- Zhang, C.; Li, M.; Guo, P. An interval multistage joint-probabilistic chance-constrained programming model with left-hand-side randomness for crop area planning under uncertainty. J. Clean. Prod. 2017, 167, 1276–1289. [Google Scholar] [CrossRef]
- Ma, L. Data-Driven Model of the Water Use and Water Uniform-Scarcity Risk Analysis in Shiyang River. Ph.D. Thesis, Northwest Agriculture and Forestry University of Science and Technology, Xi’an, China, 2012. [Google Scholar]
- Wang, Y.; Guo, P. Irrigation water resources optimization with consideration of the regional agro-hydrological process of crop growth and multiple uncertainties. Agric. Water Manag. 2021, 245, 106630. [Google Scholar] [CrossRef]
- Gao, X.; Liu, Y.; Sun, B. Water shortage risk assessment considering large-scale regional transfers: A copula-based uncertainty case study in Lunan, China. Env. Sci. Pollut. Res. Int. 2018, 25, 23328–23341. [Google Scholar] [CrossRef]
- Fu, J.; Zhong, P.-A.; Xu, B.; Zhu, F.; Chen, J.; Li, J. Comparison of Transboundary Water Resources Allocation Models Based on Game Theory and Multi-Objective Optimization. Water 2021, 13, 1421. [Google Scholar] [CrossRef]
- Louati, M.H.; Benabdallah, S.; Lebdi, F.; Milutin, D. Application of a Genetic Algorithm for the Optimization of a Complex Reservoir System in Tunisia. Water Resour. Manag. 2011, 25, 2387–2404. [Google Scholar] [CrossRef]
- Shourian, M.; Mousavi, S.J. Performance Assessment of a Coupled Particle Swarm Optimization and Network Flow Programming Model for Optimum Water Allocation. Water Resour. Manag. 2017, 31, 4835–4853. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, X.; Zhang, X.; Li, D.; Yang, M.; Tian, J. Application of NSGA-II and Improved Risk Decision Method for Integrated Water Resources Management of Malian River Basin. Water 2019, 11, 1650. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Wang, N.; Xie, J.; Jiang, R.; Zhao, M. Optimal Scale of Urbanization with Scarce Water Resources: A Case Study in an Arid and Semi-Arid Area of China. Water 2018, 10, 1602. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Dai, C.; Qin, X.S.; Chen, Y.; Guo, H.C. Dealing with equality and benefit for water allocation in a lake watershed: A Gini-coefficient based stochastic optimization approach. J. Hydrol. 2018, 561, 322–334. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Guo, S.; Yue, Q.; Guo, P. A bi-level multi-objective linear fractional programming for water consumption structure optimization based on water shortage risk. J. Clean. Prod. 2019, 237, 117829. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Z.; Chen, Z.; Xu, Y. A self-adaptive multi-objective particles warm optimization algorithm based on swarm distribution characteristic. Control Decis. 2017, 32, 1386–1394. [Google Scholar] [CrossRef]
- Coello, C.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; pp. 1051–1056. [Google Scholar] [CrossRef]
- Qingfu, Z.; Hui, L. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Cheng, R.; Zhang, X.; Li, M.; Jin, Y. Diversity Assessment of Multi-Objective Evolutionary Algorithms: Performance Metric and Benchmark Problems [Research Frontier]. IEEE Comput. Intell. Mag. 2019, 14, 61–74. [Google Scholar] [CrossRef]
- He, Y.; Tang, X.; Peng, L.; Ju, J. Optimized selection of the solution for multi-objective optimal allocation of water resources in Fengshou Irrigation Areas of South Xinjiang. Trans. CSAE 2021, 37, 117–126. [Google Scholar] [CrossRef]
- Guo, Y.; Tian, X.; Fang, G.; Xu, Y.-P. Many-objective optimization with improved shuffled frog leaping algorithm for inter-basin water transfers. Adv. Water Resour. 2020, 138, 103531. [Google Scholar] [CrossRef]
- Xu, J.; Lv, C.; Yao, L.; Hou, S. Intergenerational equity based optimal water allocation for sustainable development: A case study on the upper reaches of Minjiang River, China. J. Hydrol. 2019, 568, 835–848. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Liu, L.; Guo, P. A fuzzy dependent-chance interval multi-objective stochastic expected value programming approach for irrigation water resources management under uncertainty. Desalin. Water Treat. 2020, 212, 17–30. [Google Scholar] [CrossRef]
- Yu, Z.; Shang, S. Multi-objective optimization method for irrigation scheduling of crop rotation system and its application in North China. J. Hydraul. Eng. 2016, 47, 1188–1196. [Google Scholar]

| Category | Irrigation Area (hm2) | Industrial Output Value (108 Yuan) | Population (104) |
|---|---|---|---|
| Kuitunhe Area | 4.78 | 47.81 | 14.71 |
| Sikeshu Area | 6.03 | 11.92 | 7.45 |
| Chepaizi Area | 1.73 | - | 1.67 |
| Jiertuhe Area | 1.27 | - | 1.22 |
| Total | 13.81 | 59.73 | 25.05 |
| Category | Agricultural (104 m3) | Industrial (104 m3) | Domestic (104 m3) | |||
|---|---|---|---|---|---|---|
| Minimum | Maximum | Minimum | Maximum | Minimum | Maximum | |
| Kuitunhe Area | 16,116 | 17,895 | 1303 | 1789 | 670 | 827 |
| Sikeshu Area | 20,031 | 21,681 | 180 | 422 | 284 | 310 |
| Chepaizi Area | 5636 | 6735 | - | - | 56 | 73 |
| Jiertuhe Area. | 4146 | 4904 | - | - | 35 | 52 |
| Algorithm | N | D | Average Value of HV | Standard Deviation of HV |
|---|---|---|---|---|
| ARNSGAIII | 3 | 12 | 44.10 | 0.33 |
| NSGAIII | 3 | 12 | 43.97 | 0.39 |
| MOPSO | 3 | 12 | 35.13 | 0.78 |
| MOEA/D | 3 | 12 | 25.56 | 1.02 |
| Category | Normal Years | Dry Years | Extremely Dry Years | ||||||
|---|---|---|---|---|---|---|---|---|---|
| f1 | f2 | f3 | f1 | f2 | f3 | f1 | f2 | f3 | |
| Min f1 | 0.47 | 1.09 | 0.34 | 0.65 | 1.10 | 0.35 | 0.80 | 1.10 | 0.34 |
| Max f2 | 0.62 | 1.14 | 0.33 | 0.77 | 1.13 | 0.37 | 0.89 | 1.13 | 0.33 |
| Max f3 | 0.61 | 1.12 | 0.25 | 0.71 | 1.11 | 0.29 | 0.84 | 1.11 | 0.30 |
| Category | Agricultural (104 m3) | Industrial (104 m3) | Domestic (104 m3) | |
|---|---|---|---|---|
| Kuitunhe Area | Normal years | 17,017 | 1376 | 675 |
| Dry years | 16,680 | 1387 | 677 | |
| Extremely dry years | 16,349 | 1392 | 680 | |
| Sikeshu Area | Normal years | 21,099 | 343 | 284 |
| Dry years | 20,751 | 344 | 280 | |
| Extremely dry years | 20,076 | 359 | 284 | |
| Chepaizi Area | Normal years | 6090 | - | 64 |
| Dry years | 6024 | - | 63 | |
| Extremely dry years | 5716 | - | 63 | |
| Jiertuhe Area | Normal years | 4465 | - | 46 |
| Dry years | 4347 | - | 48 | |
| Extremely dry years | 4174 | - | 48 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; He, Y.; Qi, P.; Chang, Z.; Jiang, M.; Dai, Z. A New Multi-Objective Optimization Model of Water Resources Considering Fairness and Water Shortage Risk. Water 2021, 13, 2648. https://doi.org/10.3390/w13192648
Tang X, He Y, Qi P, Chang Z, Jiang M, Dai Z. A New Multi-Objective Optimization Model of Water Resources Considering Fairness and Water Shortage Risk. Water. 2021; 13(19):2648. https://doi.org/10.3390/w13192648
Chicago/Turabian StyleTang, Xiaoyu, Ying He, Peng Qi, Zehua Chang, Ming Jiang, and Zhongbin Dai. 2021. "A New Multi-Objective Optimization Model of Water Resources Considering Fairness and Water Shortage Risk" Water 13, no. 19: 2648. https://doi.org/10.3390/w13192648
APA StyleTang, X., He, Y., Qi, P., Chang, Z., Jiang, M., & Dai, Z. (2021). A New Multi-Objective Optimization Model of Water Resources Considering Fairness and Water Shortage Risk. Water, 13(19), 2648. https://doi.org/10.3390/w13192648






