Turbulent Flow through Random Vegetation on a Rough Bed
Abstract
:1. Introduction
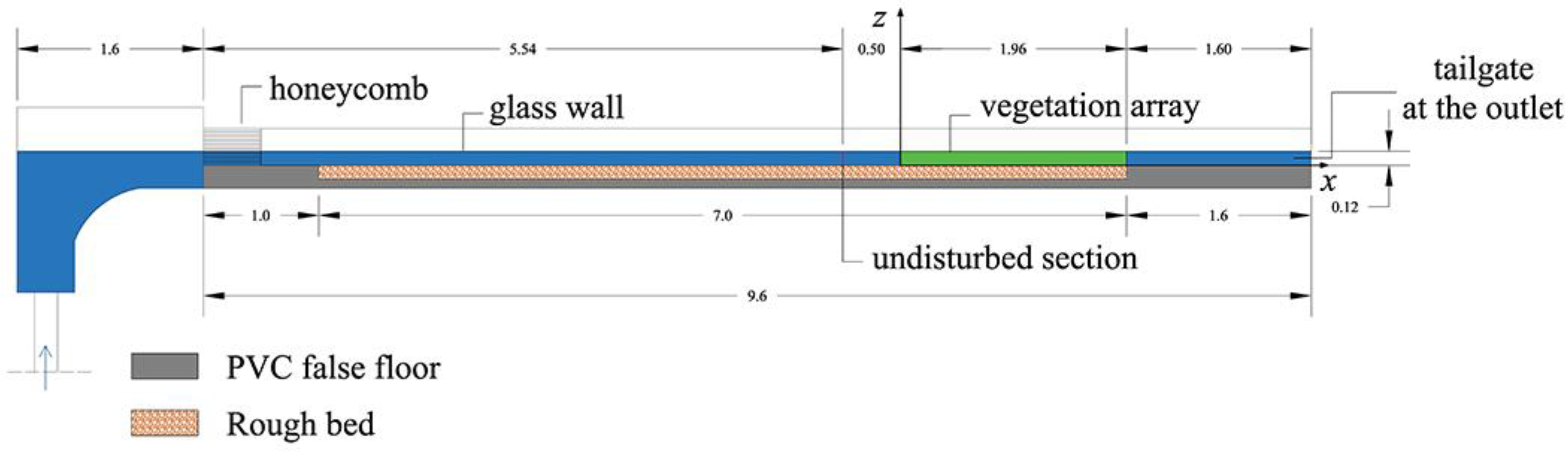
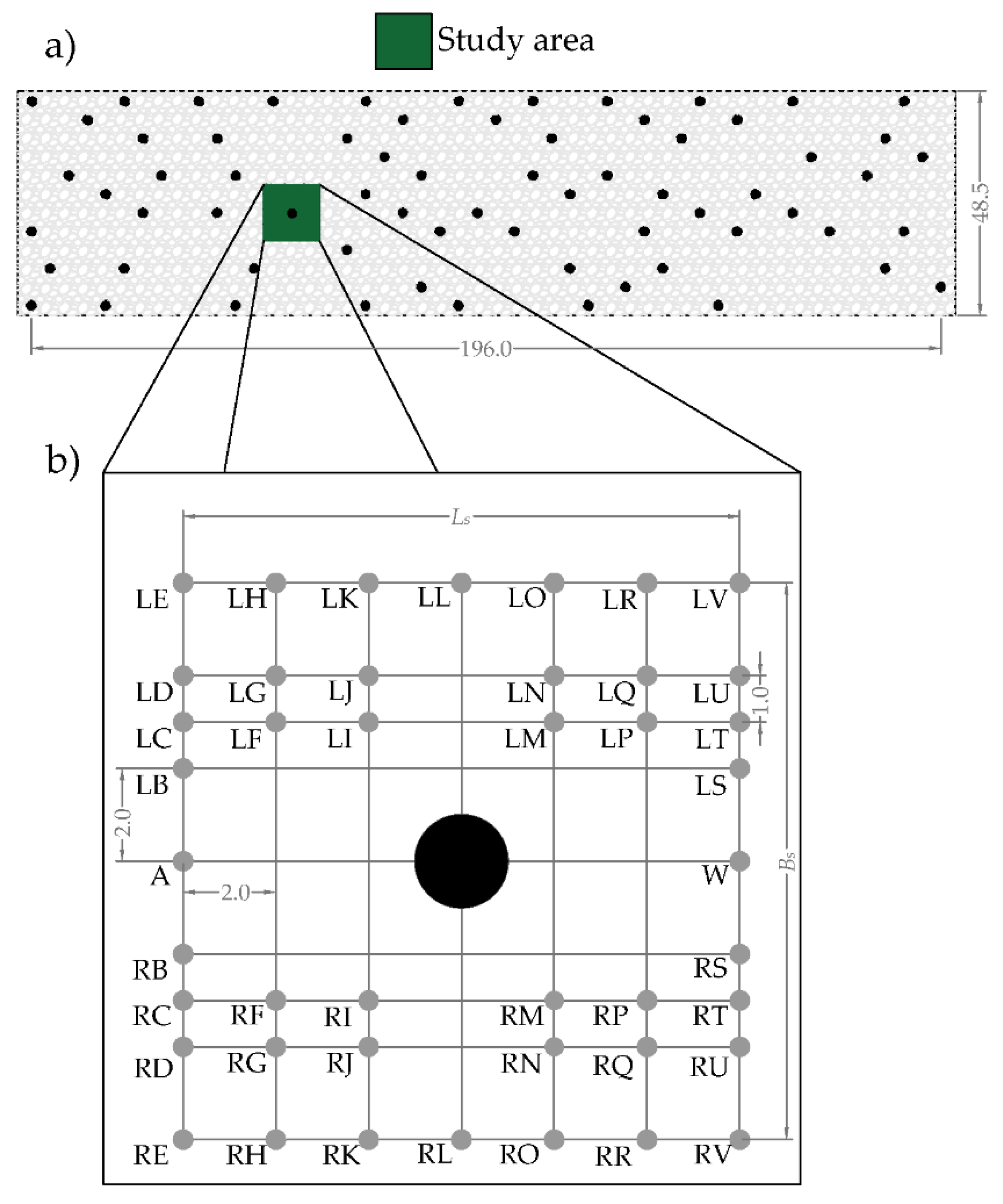
2. Laboratory Experiments and Methodology
3. Results and Discussion
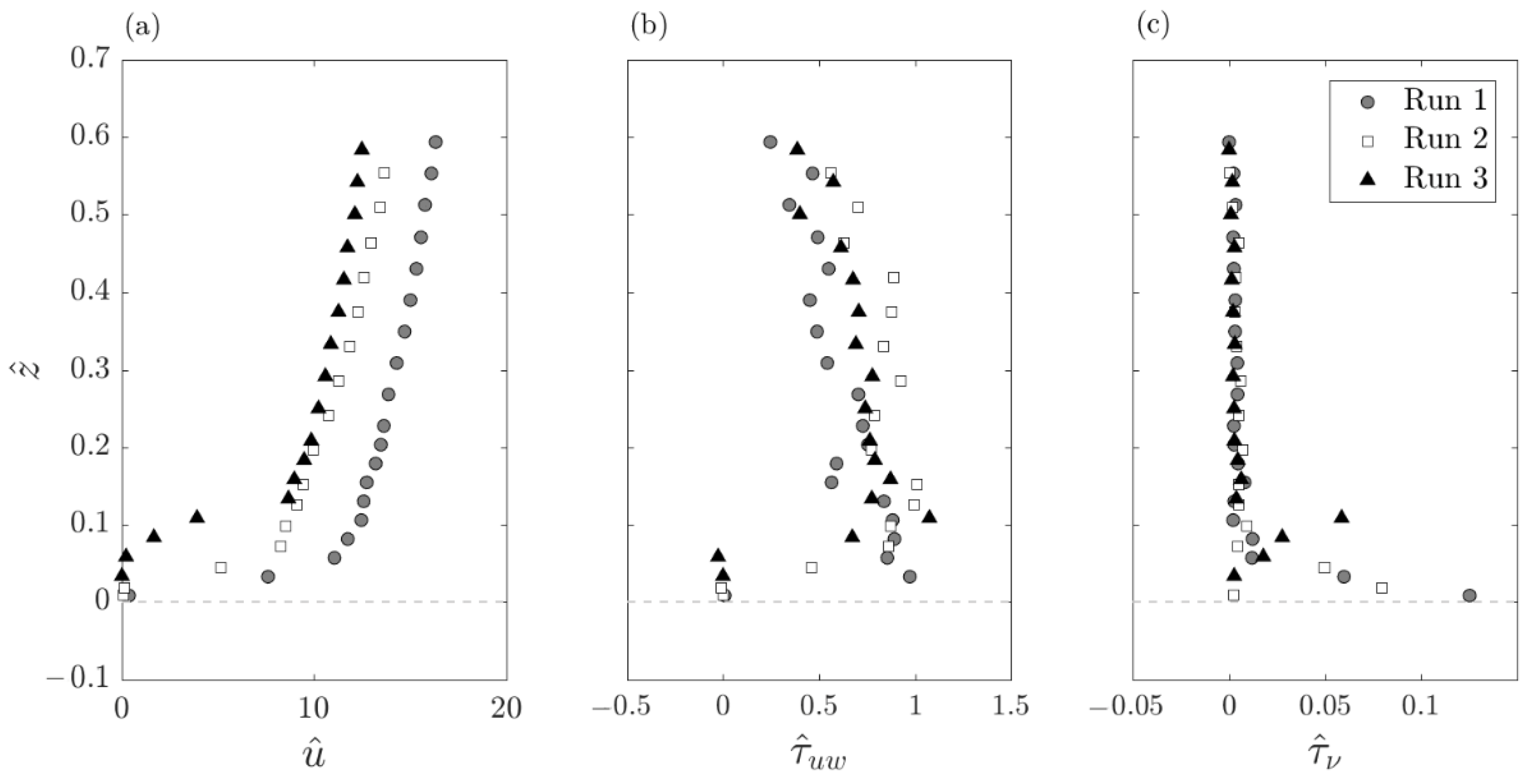
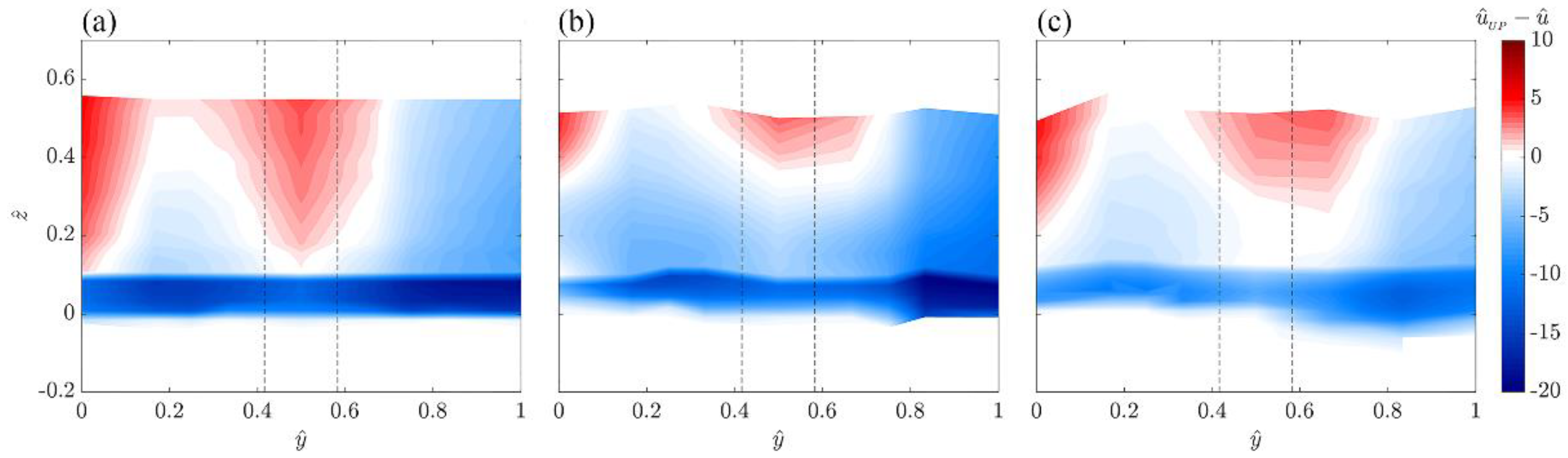
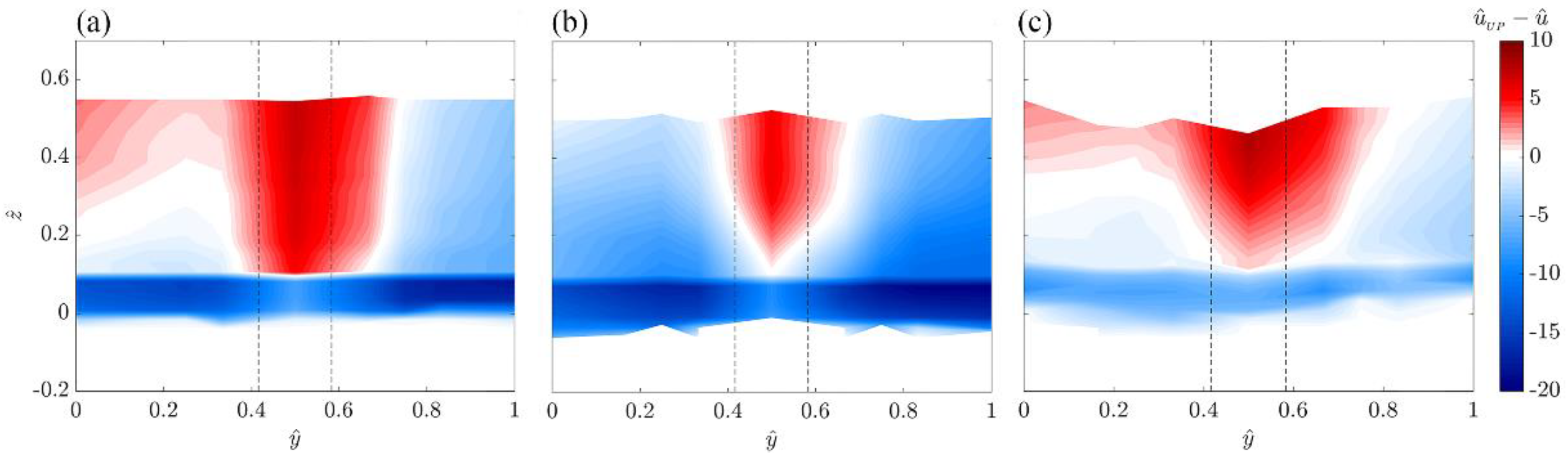
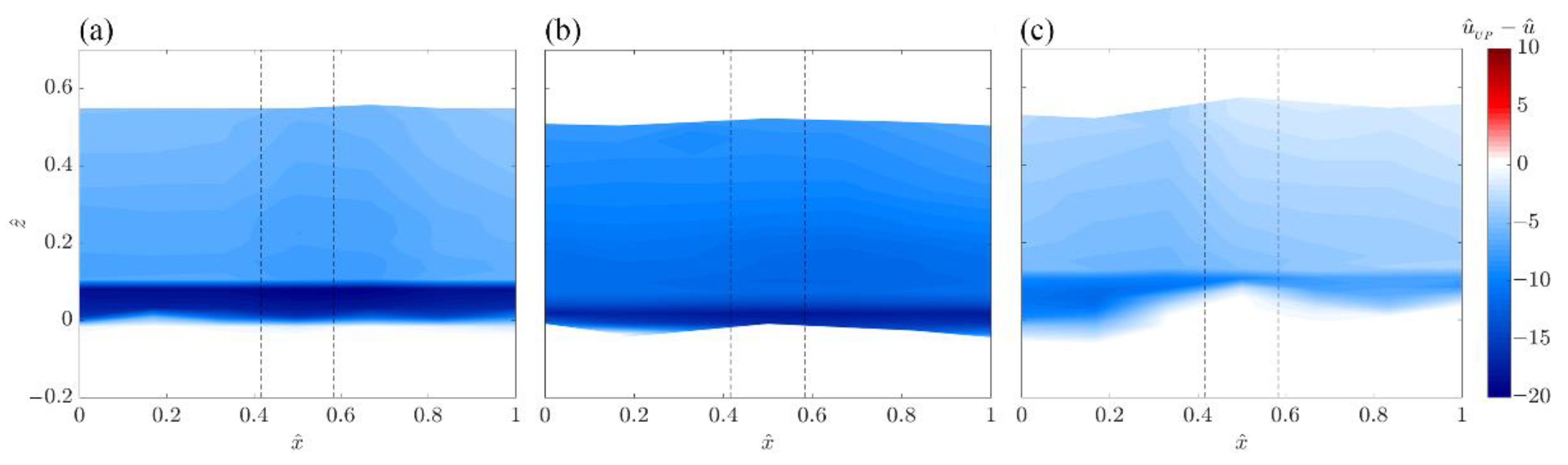
3.1. Time-Averaged Flow
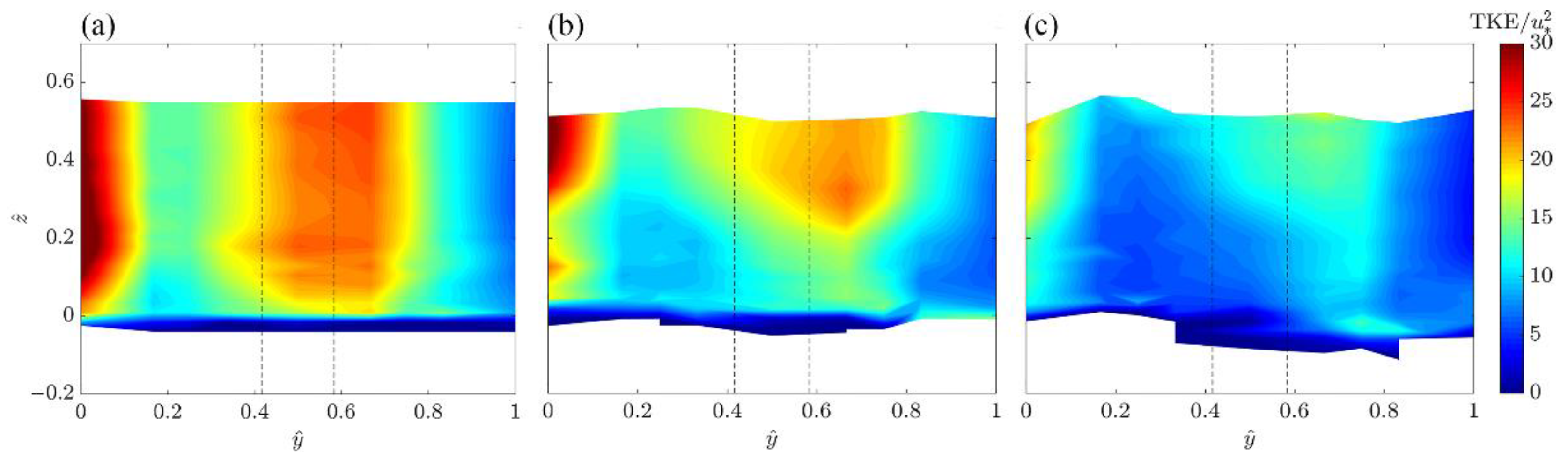
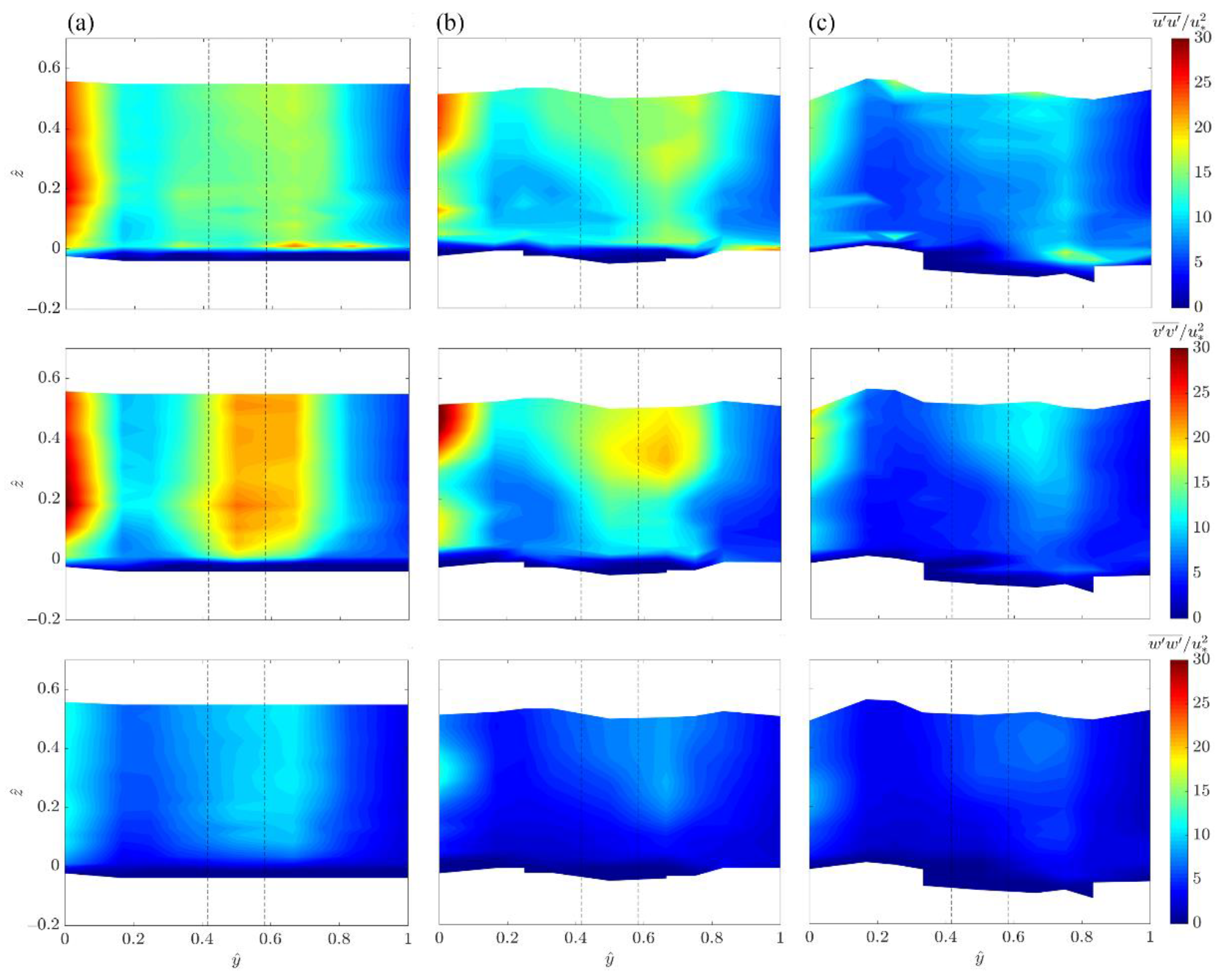
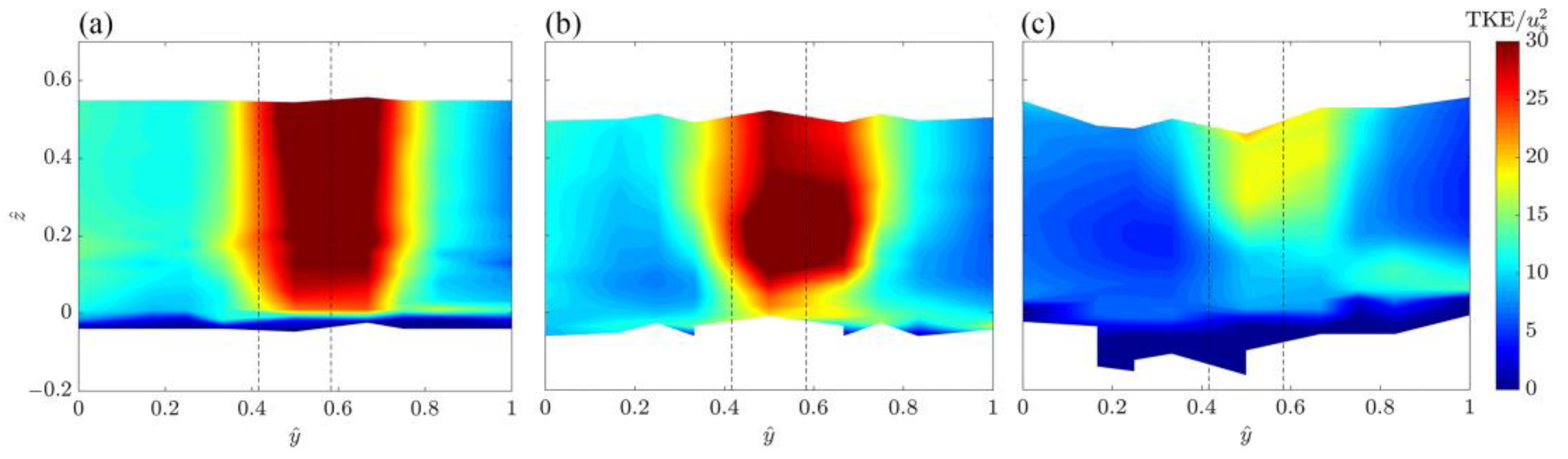
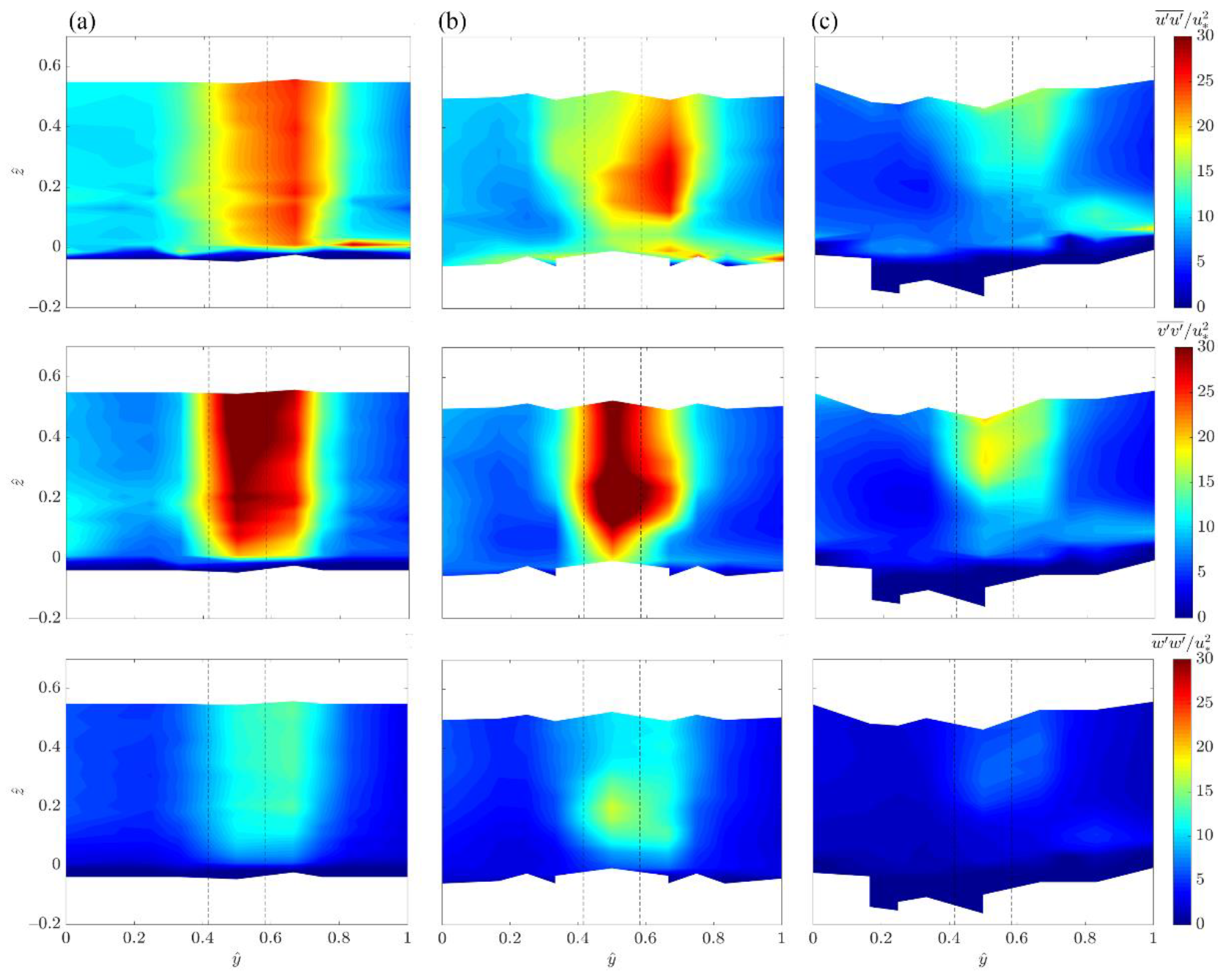
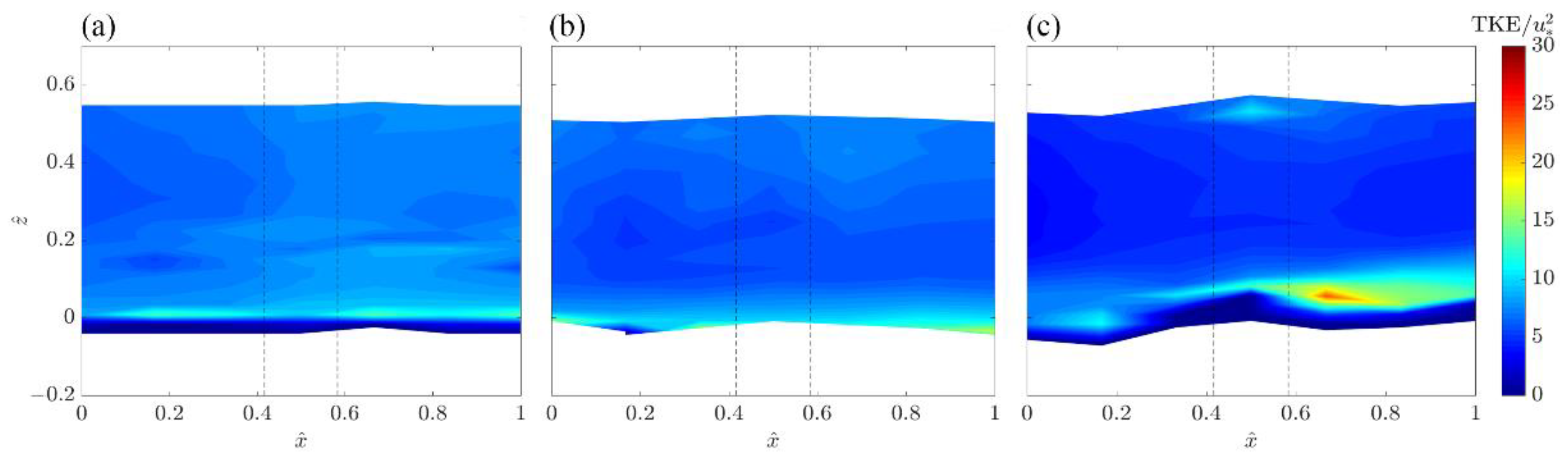
3.2. TKE and Normal Stresses
3.3. Energy Spectra
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- White, B.L.; Nepf, H.M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Meftah, M.B.; De Serio, F.; Mossa, M. Hydrodynamic behavior in the outer shear layer of partly obstructed open channels. Phys. Fluids 2014, 26, 065102. [Google Scholar] [CrossRef]
- Caroppi, G.; Gualtieri, P.; Fontana, N.; Giugni, M. Vegetated channel flows: Turbulence anisotropy at flow–rigid canopy interface. Geosciences 2018, 8, 259. [Google Scholar] [CrossRef] [Green Version]
- Rowiński, P.M.; Västilä, K.; Aberle, J.; Järvelä, J.; Kalinowska, M.B. How vegetation can aid in coping with river management challenges: A brief review. Ecohydrol. Hydrobiol. 2018, 18, 345–354. [Google Scholar] [CrossRef] [Green Version]
- Caroppi, G.; Västilä, K.; Järvelä, J.; Rowiński, P.M.; Giugni, M. Turbulence at water-vegetation interface in open channel flow: Experiments with natural-like plants. Adv. Water Resour. 2019, 127, 180–191. [Google Scholar] [CrossRef]
- Kemp, J.; Harper, D.; Crosa, G. The habitat-scale ecohydraulics of rivers. Ecol. Eng. 2000, 16, 17–29. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef] [Green Version]
- Västilä, K.; Järvelä, J. Modeling the flow resistance of woody vegetation using physically based properties of the foliage and stem. Water Resour. Res. 2014, 50, 229–245. [Google Scholar] [CrossRef]
- Nepf, H.M.; Vivoni, E.R. Flow structure in depth-limited, vegetated flow. J. Geophys. Res. Oceans 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Järvelä, J. Effect of submerged flexible vegetation on flow structure and resistance. J. Hydrol. 2005, 307, 233–241. [Google Scholar] [CrossRef]
- Li, C.W.; Xie, J. FNumerical modeling of free surface flow over submerged and highly flexible vegetation. Adv. Water Resour. 2011, 34, 468–477. [Google Scholar] [CrossRef]
- Maji, S.; Hanmaiahgari, P.R.; Balachandar, R.; Pu, J.H.; Ricardo, A.M.; Ferreira, R.M. A Review on Hydrodynamics of Free Surface Flows in Emergent Vegetated Channels. Water 2020, 12, 1218. [Google Scholar] [CrossRef]
- Ricardo, A.M.; Franca, M.J.; Ferreira, R.M. Turbulent flows within random arrays of rigid and emergent cylinders with varying distribution. J. Hydraul. Eng. 2016, 142, 04016022. [Google Scholar] [CrossRef]
- Nezu, I.; Sanjou, M. Turburence structure and coherent motion in vegetated canopy open-channel flows. J. Hydro-Environ. Res. 2008, 2, 62–90. [Google Scholar] [CrossRef]
- Yang, W.; Choi, S.U. A two-layer approach for depth-limited open-channel flows with submerged vegetation. J. Hydraul. Res. 2010, 48, 466–475. [Google Scholar] [CrossRef]
- Shimizu, Y.; Tsujimoto, T. Numerical analysis of turbulent open-channel flow over a vegetation layer using a k-ε turbulence model. J. Hydrosci. Hydraul. Eng. 1994, 11, 57–67. [Google Scholar]
- Nepf, H. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Righetti, M.; Armanini, A. Flow resistance in open channel flows with sparsely distributed bushes. J. Hydrol. 2002, 269, 55–64. [Google Scholar] [CrossRef]
- Choi, S.U.; Kang, H. Numerical investigations of mean flow and turbulence structures of partly-vegetated open-channel flows using the Reynolds stress model. J. Hydraul. Res. 2006, 44, 203–217. [Google Scholar] [CrossRef]
- Poggi, D.; Krug, C.; Katul, G.G. Hydraulic resistance of submerged rigid vegetation derived from first-order closure models. Water Resour. Res. 2009, 45, W10442. [Google Scholar] [CrossRef]
- Gualtieri, P.; De Felice, S.; Pasquino, V.; Doria, G. Use of conventional flow resistance equations and a model for the Nikuradse roughness in vegetated flows at high submergence. J. Hydrol. Hydromech. 2018, 66, 107–120. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An experimental study of flow through rigid vegetation. J. Geophys. Res. Earth Surf. 2008, 113, F04015. [Google Scholar] [CrossRef]
- De Serio, F.; Ben Meftah, M.; Mossa, M.; Termini, D. Experimental investigation on dispersion mechanisms in rigid and flexible vegetated beds. Adv. Water Resour. 2018, 120, 98–113. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Bed roughness effects on the turbulence characteristics of flows through emergent rigid vegetation. Water 2020, 12, 2401. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Anisotropy in the free stream region of turbulent flows through emergent rigid vegetation on rough bed. Water 2020, 12, 2464. [Google Scholar] [CrossRef]
- Petryk, S. Drag on Cylinders in Open Channel Flow. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1969. [Google Scholar]
- Stone, B.M.; Shen, H.T. Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraul. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef] [Green Version]
- Dey, S.; Sarkar, A. Scour downstream of an apron due to submerged horizontal jets. J. Hydraul. Eng. 2006, 132, 246–257. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; Gaudio, R. Turbulent Flow Field around Horizontal Cylinders with Scour Hole. Water 2020, 12, 143. [Google Scholar] [CrossRef] [Green Version]
- Pu, J.H.; Hussain, A.; Guo, Y.K.; Vardakastanis, N.; Hanmaiahgari, P.R.; Lam, D. Submerged flexible vegetation impact on open channel flow velocity distribution: An analytical modelling study on drag and friction. Water Sci. Eng. 2019, 12, 121–128. [Google Scholar] [CrossRef]
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Manes, C.; Pokrajac, D.; McEwan, I. Double-averaged open-channel flows with small relative submergence. J. Hydraul. Eng. 2007, 133, 896–904. [Google Scholar] [CrossRef]
- Dey, S.; Das, R. Gravel-bed hydrodynamics: Double-averaging approach. J. Hydraul. Eng. 2012, 138, 707–725. [Google Scholar] [CrossRef]
- Neill, C.R. Mean-velocity criterion for scour of coarse uniform bed material. In Proceedings of the International Association of Hydraulic Research 12th Congress, Fort Collins, CO, USA, 11–14 September 1967; pp. 46–54. [Google Scholar]
- Strom, K.B.; Papanicolaou, A.N. ADV measurements around a cluster microform in a shallow mountain stream. J. Hydraul. Eng. 2007, 133, 1379–1389. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Moghbel, R.; Gallichand, J.; Jueyi, S.U.I. Investigation of turbulence characteristics in channel with dense vegetation. Int. J. Sediment Res. 2011, 26, 269–282. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V.I. Despiking acoustic Doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Dey, S. Fluvial Hydrodynamics; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Dey, S.; Sarkar, S.; Ballio, F. Double-averaging turbulence characteristics in seeping rough-bed streams. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H. Lateral dispersion in random cylinder arrays at high Reynolds number. J. Fluid Mech. 2008, 600, 339–371. [Google Scholar] [CrossRef] [Green Version]
- Defina, A.; Bixio, A.C. Mean flow and turbulence in vegetated open channel flow. Water Resour. Res. 2005, 41, W07006. [Google Scholar] [CrossRef] [Green Version]


| Parameter (Units) | Run 1 | Run 2 | Run 3 |
|---|---|---|---|
| d50 (mm) | 1.53 | 6.49 | 17.98 |
| h (m) | 0.12 | 0.12 | 0.12 |
| Q (l/s) | 19.73 | 19.73 | 19.73 |
| U (m/s) | 0.34 | 0.34 | 0.34 |
| u* (m/s) | 0.021 | 0.022 | 0.028 |
| Uc (m/s) | 0.39 | 0.69 | 1.04 |
| S (‰) | 1.50 | 1.50 | 1.50 |
| T (°C) | 16.67 | 18.06 | 18.70 |
| ν (m 2/s) | 1.09 × 10−6 | 1.05 × 10−6 | 1.03 × 10−6 |
| Fr | 0.31 | 0.31 | 0.31 |
| Re | 37,431 | 38,857 | 39,612 |
| Re* | 59 | 272 | 978 |
| Red | 6239 | 6192 | 6602 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coscarella, F.; Penna, N.; Ferrante, A.P.; Gualtieri, P.; Gaudio, R. Turbulent Flow through Random Vegetation on a Rough Bed. Water 2021, 13, 2564. https://doi.org/10.3390/w13182564
Coscarella F, Penna N, Ferrante AP, Gualtieri P, Gaudio R. Turbulent Flow through Random Vegetation on a Rough Bed. Water. 2021; 13(18):2564. https://doi.org/10.3390/w13182564
Chicago/Turabian StyleCoscarella, Francesco, Nadia Penna, Aldo Pedro Ferrante, Paola Gualtieri, and Roberto Gaudio. 2021. "Turbulent Flow through Random Vegetation on a Rough Bed" Water 13, no. 18: 2564. https://doi.org/10.3390/w13182564
APA StyleCoscarella, F., Penna, N., Ferrante, A. P., Gualtieri, P., & Gaudio, R. (2021). Turbulent Flow through Random Vegetation on a Rough Bed. Water, 13(18), 2564. https://doi.org/10.3390/w13182564







