A Spatial Structure Variable Approach to Characterize Storm Events for Coastal Flood Hazard Assessment
Abstract
:1. Introduction
2. Critical Issues Related to Sea Storm Identification and Sampling
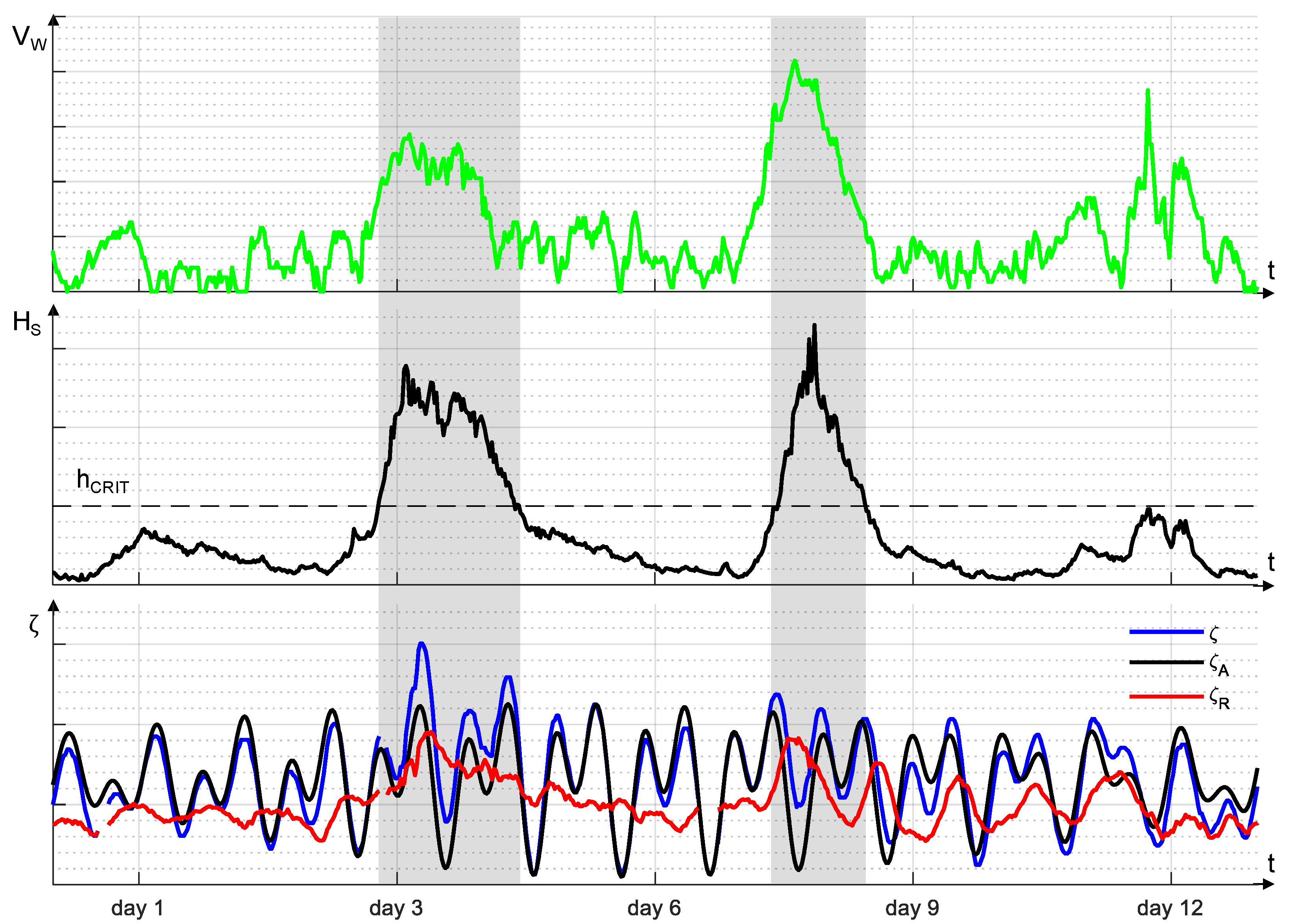
2.1. Declustering Scheme for Sea Storm Identification
2.2. Sampling Procedure within Sea Storms
- Maximum Hs and simultaneous value of ζ;
- Maximum ζ and simultaneous value of Hs;
- Maxima of Hs and ζ during the storm regardless of their concomitance.
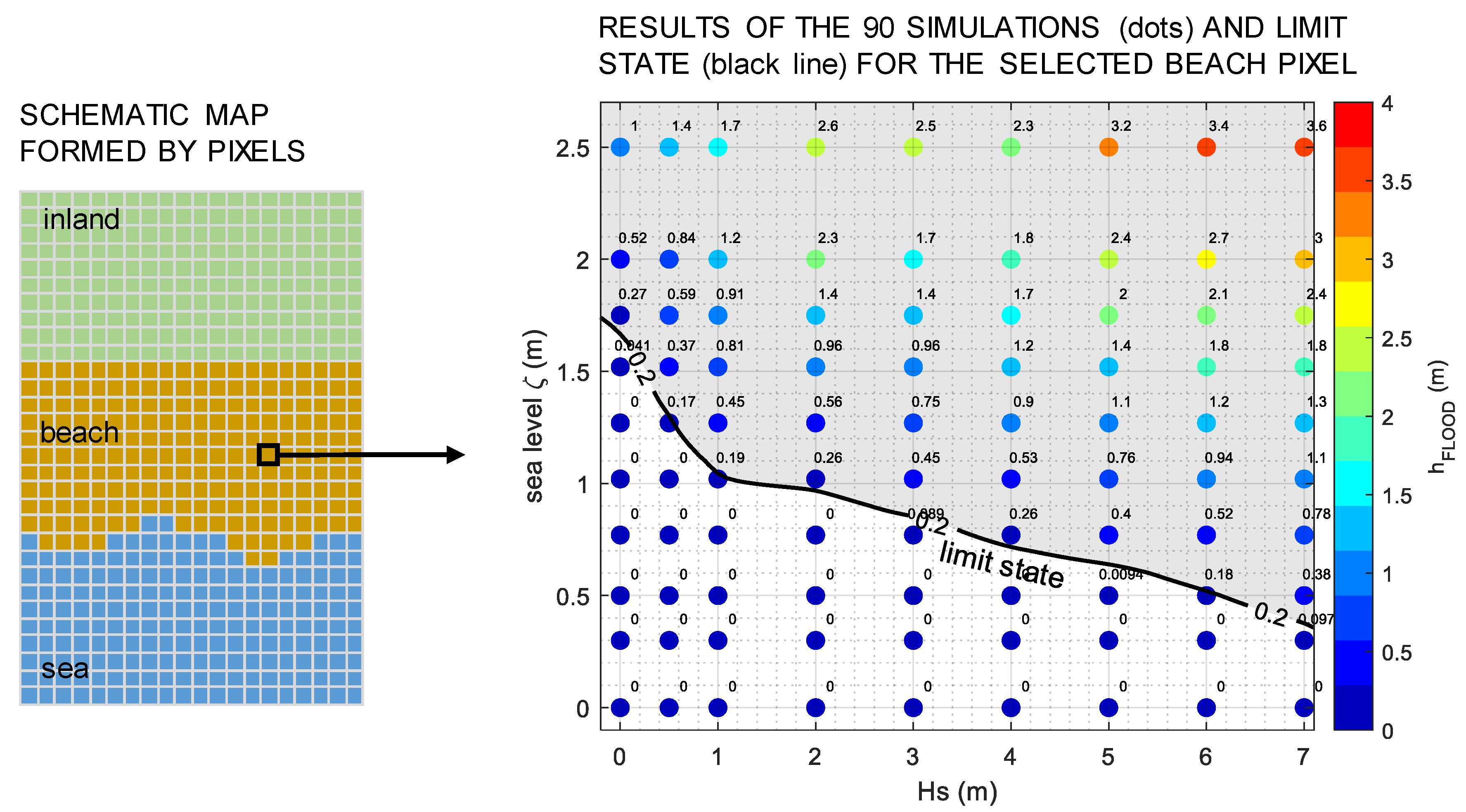
3. Case Study
Available Data
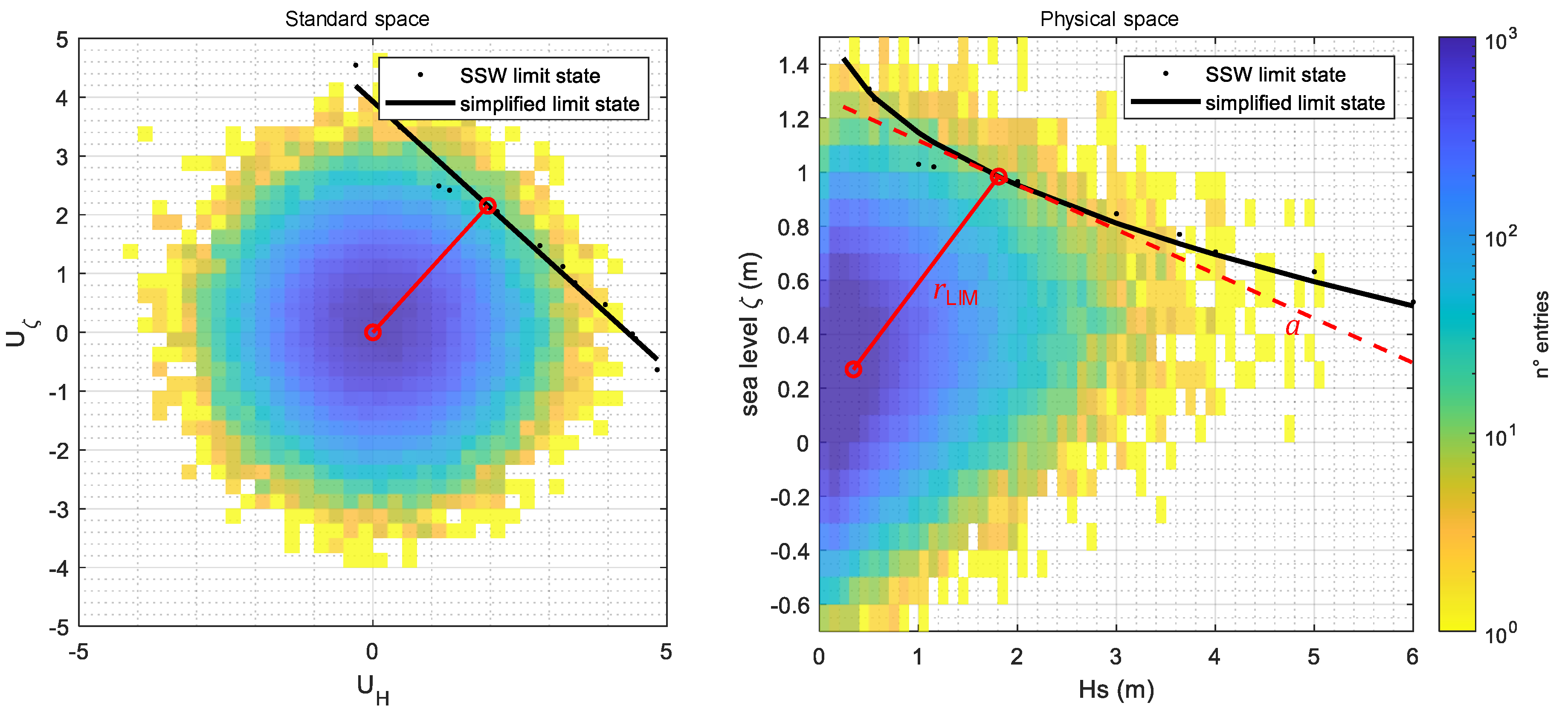
4. Results
Discussion on the October 2018 and November 2019 Events
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Coles, S.G.; Tawn, J.A. Statistical methods for multivariate extremes: An application to structural design. J. R. Stat. Soc. Ser. C Appl. Stat. 1994, 43, 1–48. [Google Scholar] [CrossRef]
- Zachary, S.; Feld, G.; Ward, G.; Wolfram, J. Multivariate extrapolation in the offshore environment. Appl. Ocean Res. 1998, 20, 273–295. [Google Scholar] [CrossRef]
- Masina, M.; Lamberti, A.; Archetti, R. Coastal flooding: A copula based approach for estimating the joint probability of water levels and waves. Coast. Eng. 2015, 97, 37–52. [Google Scholar] [CrossRef]
- Li, F.; Van Gelder, P.H.A.J.M.; Ranasinghe, R.; Callaghan, D.P.; Jongejan, R.B. Probabilistic modelling of extreme storms along the Dutch coast. Coast. Eng. 2014, 86, 1–13. [Google Scholar] [CrossRef]
- Hawkes, P.J.; Gouldby, B.P.; Tawn, J.A.; Owen, M.W. The joint probability of waves and water levels in coastal engineering design. J. Hydraul. Res. 2002, 40, 241–251. [Google Scholar] [CrossRef]
- Lerma, A.N.; Bulteau, T.; Elineau, S.; Paris, F.; Durand, P.; Anselme, B.; Pedreros, R. High-resolution marine flood modelling coupling overflow and overtopping processes: Framing the hazard based on historical and statistical approaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 207–229. [Google Scholar] [CrossRef]
- Arnoux, F.; Abadie, S.; Bertin, X.; Kojadinovic, I. Coastal flooding event definition based on damages: Case study of Biarritz Grande Plage on the French Basque coast. Coast. Eng. 2021, 166, 103873. [Google Scholar] [CrossRef]
- Favaretto, C.; Martinelli, L.; Ruol, P. Coastal flooding hazard due to overflow using a level II method: Application to the Venetian littoral. Water 2019, 11, 134. [Google Scholar] [CrossRef]
- Foti, E.; Musumeci, R.E.; Stagnitti, M. Coastal defence techniques and climate change: A review. Rend. Lincei Sci. Fis. Nat. 2020, 31, 123–138. [Google Scholar] [CrossRef]
- Di Risio, M.; Bruschi, A.; Lisi, I.; Pesarino, V.; Pasquali, D. Comparative analysis of coastal flooding vulnerability and hazard assessment at national scale. J. Mar. Sci. Eng. 2017, 5, 51. [Google Scholar] [CrossRef]
- Wahl, T.; Plant, N.G.; Long, J.W. Probabilistic assessment of erosion and flooding risk in the northern Gulf of Mexico. J. Geophys. Res. Ocean. 2016, 121, 3029–3043. [Google Scholar] [CrossRef]
- Bruun, J.T.; Tawn, J.A. Comparison of approaches for estimating the probability of coastal flooding. J. R. Stat. Soc. Ser. C Appl. Stat. 1998, 47, 405–423. [Google Scholar] [CrossRef]
- Hawkes, P.J. Joint probability analysis for estimation of extremes. J. Hydraul. Res. 2008, 46, 246–256. [Google Scholar] [CrossRef]
- Mazas, F.; Hamm, L. An event-based approach for extreme joint probabilities of waves and sea levels. Coast. Eng. 2017, 122, 44–59. [Google Scholar] [CrossRef]
- Harley, M.D. Coastal storm definition. In Coastal Storms: Processes and Impacts; Ciavola, P., Coco, G., Eds.; John Wiley and Sons: Chichester, UK, 2017; pp. 1–21. [Google Scholar]
- Boccotti, P. On coastal and offshore structure risk analysis. Excerpta Ital. Contrib. Field Hydraul. Eng. 1986, 1, 19–36. [Google Scholar]
- Mendoza, E.T.; Jimenez, J.A.; Mateo, J.; Salat, J. A coastal storms intensity scale for the Catalan sea (NW Mediterranean). Nat. Hazards Earth Syst. Sci. 2011, 11, 2453–2462. [Google Scholar] [CrossRef]
- Taylor, G.I. Diffusion by continuous movements. Proc. Lond. Math. Soc. 1922, 2, 196–212. [Google Scholar] [CrossRef]
- Pasquali, D.; Bruno, M.F.; Celli, D.; Damiani, L.; Di Risio, M. A simplified hindcast method for the estimation of extreme storm surge events in semi-enclosed basins. Appl. Ocean. Res. 2019, 85, 45–52. [Google Scholar] [CrossRef]
- Bajo, M.; Međugorac, I.; Umgiesser, G.; Orlić, M. Storm surge and seiche modelling in the Adriatic Sea and the impact of data assimilation. Q. J. R. Meteorol. Soc. 2019, 145, 2070–2084. [Google Scholar] [CrossRef]
- Favaretto, C.; Martinelli, L.; Ruol, P. A Model of Coastal Flooding Using Linearized Bottom Friction and Its Application to a Case Study in Caorle, Venice, Italy. Int. J. Offshore Polar Eng. 2019, 29, 182–190. [Google Scholar] [CrossRef]
- Favaretto, C.; Martinelli, L.; Ruol, P. Run up on Beaches through Simplified Shallow Water Model. In Proceedings of the 29th International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- Hasofer, A.M.; Lind, N.C. Exact and invariant second-moment code format. J. Eng. Mech. Div. 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Martinelli, L.; Zanuttigh, B.; Corbau, C. Assessment of coastal flooding hazard along the Emilia Romagna littoral, IT. Coast. Eng. 2010, 57, 1042–1058. [Google Scholar] [CrossRef]
- Boccotti, P. Wave Mechanics for Ocean Engineering; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific: Singapore, 2010. [Google Scholar]
- Laface, V.; Arena, F. A new equivalent exponential storm model for long-term statistics of ocean waves. Coast. Eng. 2016, 116, 133–151. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208, p. 208. [Google Scholar]
- Umgiesser, G.; Bajo, M.; Ferrarin, C.; Cucco, A.; Lionello, P.; Zanchettin, D.; Papa, A.; Tosoni, A.; Ferla, M.; Coraci, E.; et al. The prediction of floods in Venice: Methods, models and uncertainty (review article). Nat. Hazards Earth Syst. Sci. 2021, 21, 2679–2704. [Google Scholar] [CrossRef]
- Biolchi, S.; Denamiel, C.; Devoto, S.; Korbar, T.; Macovaz, V.; Scicchitano, G.; Furlani, S. Impact of the October 2018 storm Vaia on coastal boulders in the northern Adriatic Sea. Water 2019, 11, 2229. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bajo, M.; Barbariol, F.; Bastianini, M.; Benetazzo, A.; Bertotti, L.; Chiggiato, J.; Davolio, S.; Ferrarin, C.; Magnusson, L.; et al. The October 29, 2018 storm in Northern Italy—An exceptional event and its modeling. Prog. Oceanogr. 2019, 178, 102178. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bajo, M.; Barbariol, F.; Bastianini, M.; Benetazzo, A.; Bertotti, L.; Umgiesser, G. The 2019 Flooding of Venice and its implications for future predictions. Oceanography 2020, 33, 42–49. [Google Scholar] [CrossRef]
- Ruol, P.; Favaretto, C.; Volpato, M.; Martinelli, L. Flooding of Piazza San Marco (Venice): Physical Model Tests to Evaluate the Overtopping Discharge. Water 2020, 12, 427. [Google Scholar] [CrossRef]
- Ruol, P.; Martinelli, L.; Favaretto, C. Vulnerability analysis of the Venetian littoral and adopted mitigation strategy. Water 2018, 10, 984. [Google Scholar] [CrossRef]
- Tosi, L.; Teatini, P.; Strozzi, T. Natural versus anthropogenic subsidence of Venice. Sci. Rep. 2013, 3, 1–9. [Google Scholar] [CrossRef]
- ISPRA. Available online: https://annuario.isprambiente.it/ada/basic/6972 (accessed on 18 March 2020).
- Moftakhari, H.R.; AghaKouchak, A.; Sanders, B.F.; Allaire, M.; Matthew, R.A. What is nuisance flooding? Defining and monitoring an emerging challenge. Water Resour. Res. 2018, 54, 4218–4227. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Portland, OR, USA, 2007. [Google Scholar]
- De Michele, C.; Salvadori, G.; Passoni, G.; Vezzoli, R. A multivariate model of sea storms using copulas. Coast. Eng. 2007, 54, 734–751. [Google Scholar] [CrossRef]

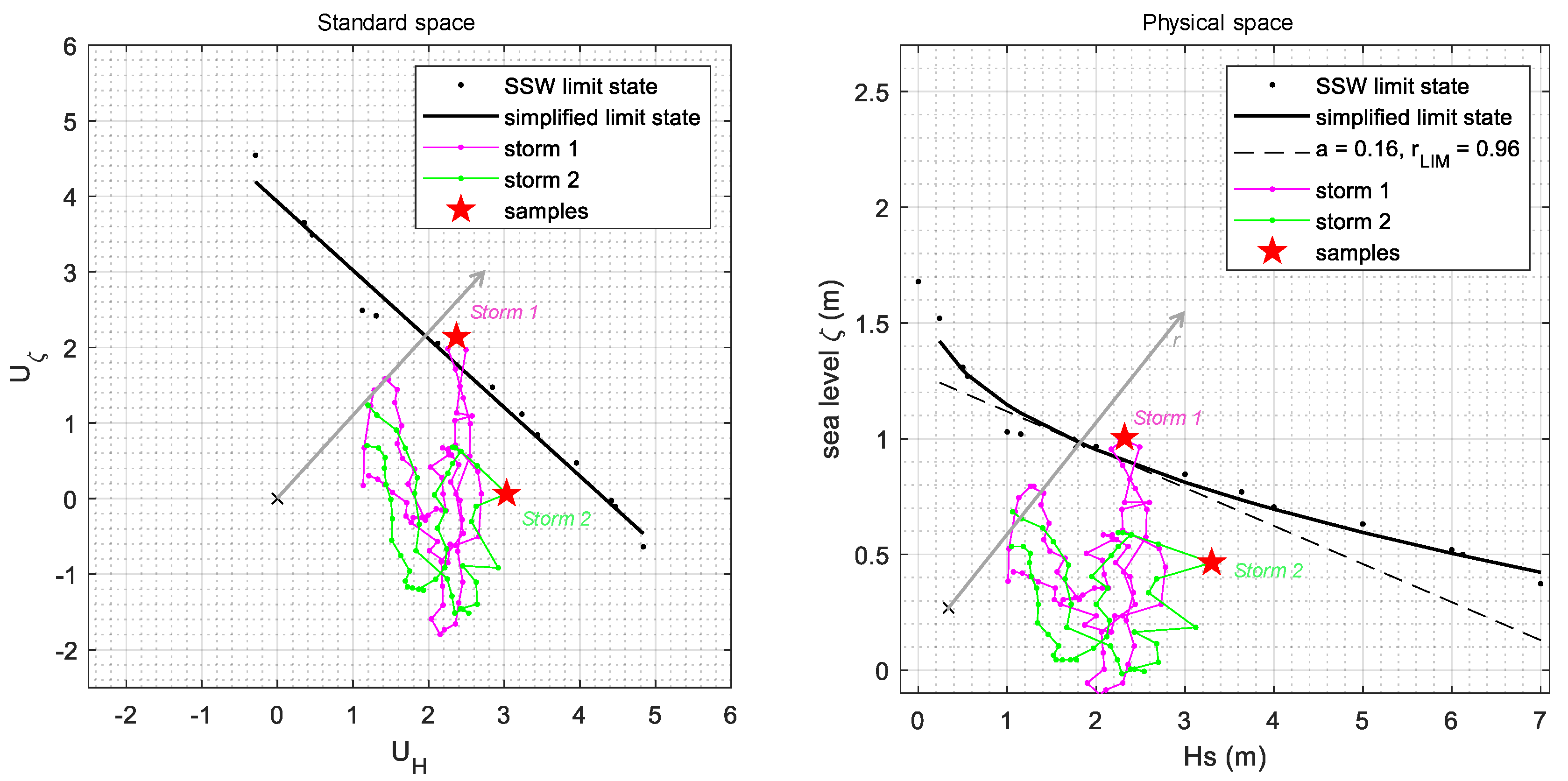

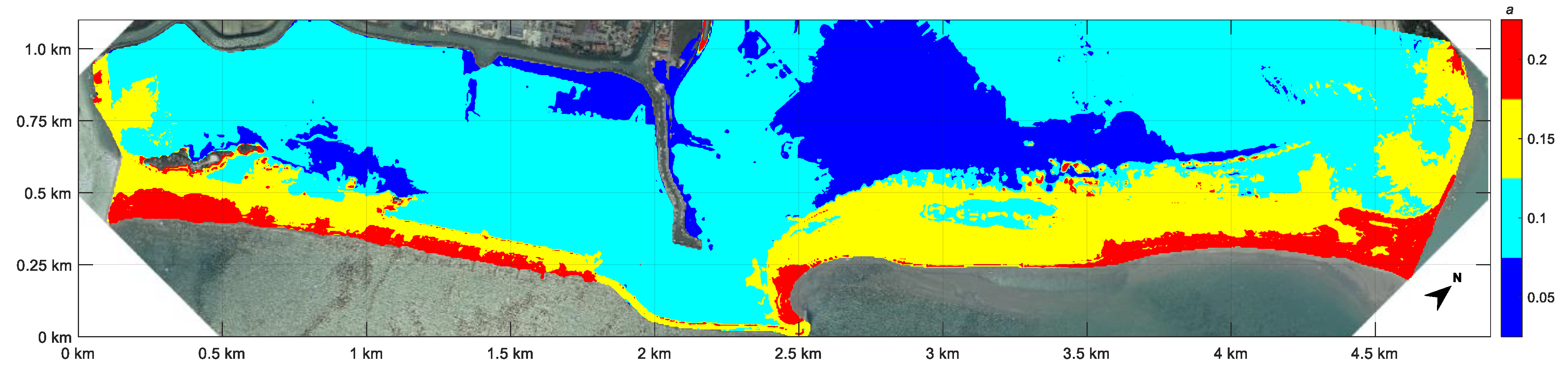
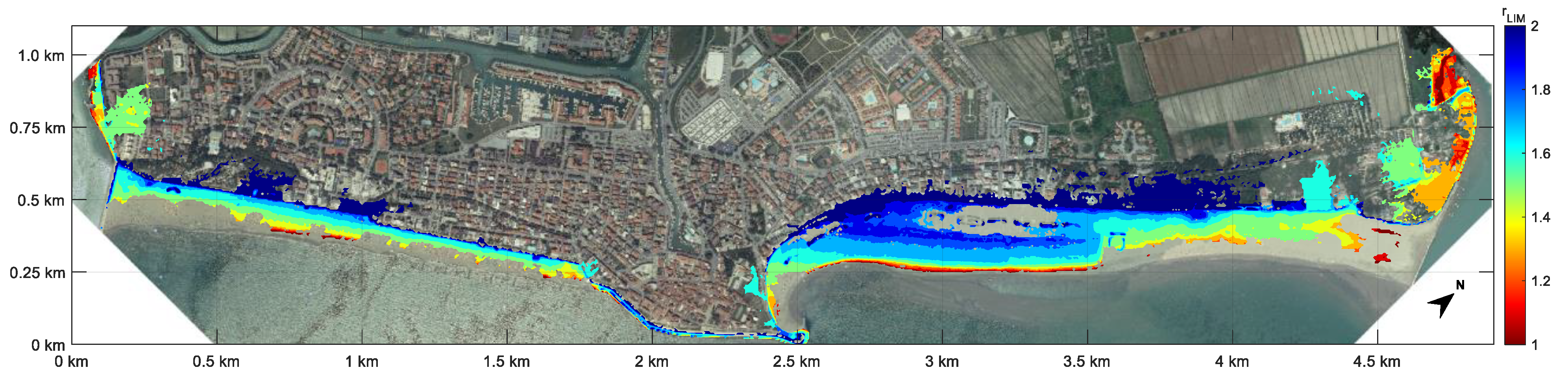
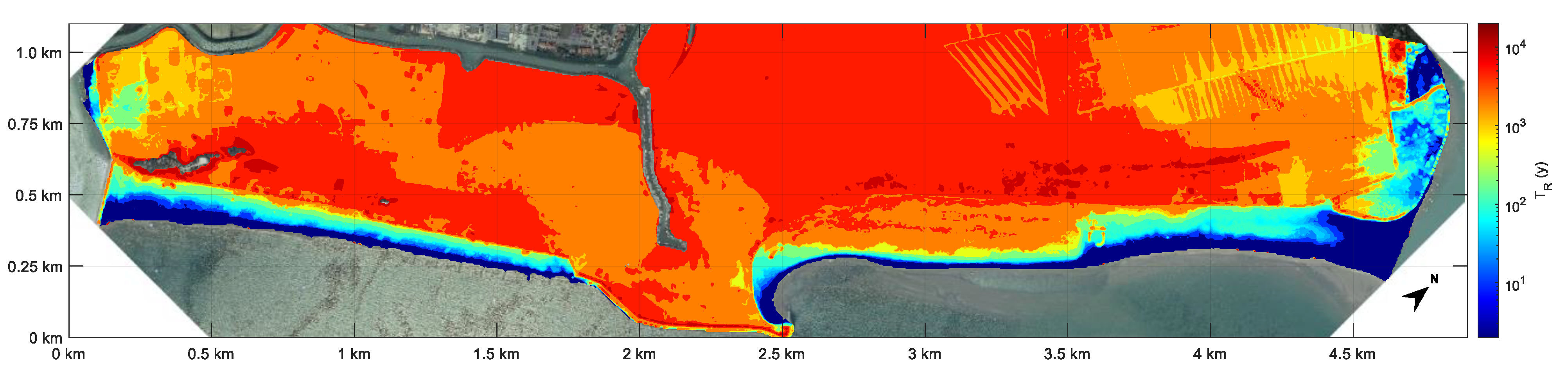


| Samples | October 2018 | November 2019 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hs (m) | ζ* (m) | r0 (m) | P (r > r0) | TR (y) =1/[λ P (r >r0)] | Hs (m) | ζ* (m) | r0 (m) | P (r > r0) | TR (y) =1/[λ P (r >r0)] | |
| a = 0 | 2.80 | 1.10 | 0.83 | 0.0887 | 6 | 2.34 | 1.42 | 1.15 | 0.0029 | 181 |
| a = 0.05 | 2.80 | 1.10 | 0.95 | 0.0770 | 7 | 2.34 | 1.42 | 1.25 | 0.0031 | 166 |
| a = 0.1 | 5.05 | 0.93 | 1.13 | 0.0455 | 11 | 2.34 | 1.42 | 1.35 | 0.0053 | 97 |
| a = 0.15 | 5.05 | 0.93 | 1.36 | 0.0217 | 24 | 2.34 | 1.42 | 1.45 | 0.0109 | 47 |
| a = 0.2 | 5.05 | 0.93 | 1.60 | 0.0125 | 41 | 2.34 | 1.42 | 1.55 | 0.0189 | 27 |
| a = 0.25 | 5.05 | 0.93 | 1.84 | 0.0079 | 66 | 2.34 | 1.42 | 1.65 | 0.0317 | 16 |
| a = 0.3 | 5.05 | 0.93 | 2.07 | 0.0078 | 66 | 2.34 | 1.42 | 1.75 | 0.0493 | 10 |
| a = 0.35 | 5.05 | 0.93 | 2.31 | 0.0084 | 62 | 2.34 | 1.42 | 1.85 | 0.0681 | 8 |
| a = 0.4 | 5.05 | 0.93 | 2.54 | 0.0108 | 48 | 2.34 | 1.42 | 1.95 | 0.0865 | 6 |
| a = 0.45 | 5.05 | 0.93 | 2.78 | 0.0096 | 54 | 2.34 | 1.42 | 2.05 | 0.1093 | 5 |
| a = 0.5 | 5.05 | 0.93 | 3.01 | 0.0110 | 47 | 2.34 | 1.42 | 2.15 | 0.1304 | 4 |
| S1: Max Hs and simultaneous ζ | 5.29 | 0.81 | - | 0.0026 | 258 | 3.16 | 0.72 | - | 0.1020 | 7 |
| S2: Max ζ and simultaneous Hs | 0.72 | 1.10 | - | 0.0377 | 13 | 2.34 | 1.42 | - | 0.0050 | 102 |
| S3: Maxima of Hs and ζ | 5.29 | 1.10 | - | 0.0024 | 91 | 3.16 | 1.42 | - | 0.0011 | 197 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Favaretto, C.; Martinelli, L.; Ruol, P. A Spatial Structure Variable Approach to Characterize Storm Events for Coastal Flood Hazard Assessment. Water 2021, 13, 2556. https://doi.org/10.3390/w13182556
Favaretto C, Martinelli L, Ruol P. A Spatial Structure Variable Approach to Characterize Storm Events for Coastal Flood Hazard Assessment. Water. 2021; 13(18):2556. https://doi.org/10.3390/w13182556
Chicago/Turabian StyleFavaretto, Chiara, Luca Martinelli, and Piero Ruol. 2021. "A Spatial Structure Variable Approach to Characterize Storm Events for Coastal Flood Hazard Assessment" Water 13, no. 18: 2556. https://doi.org/10.3390/w13182556
APA StyleFavaretto, C., Martinelli, L., & Ruol, P. (2021). A Spatial Structure Variable Approach to Characterize Storm Events for Coastal Flood Hazard Assessment. Water, 13(18), 2556. https://doi.org/10.3390/w13182556








