Comparison of Seasonal Flow Rate Change Indices Downstream of Three Types of Dams in Southern Quebec (Canada)
Abstract
:1. Introduction
2. Materials and Methods
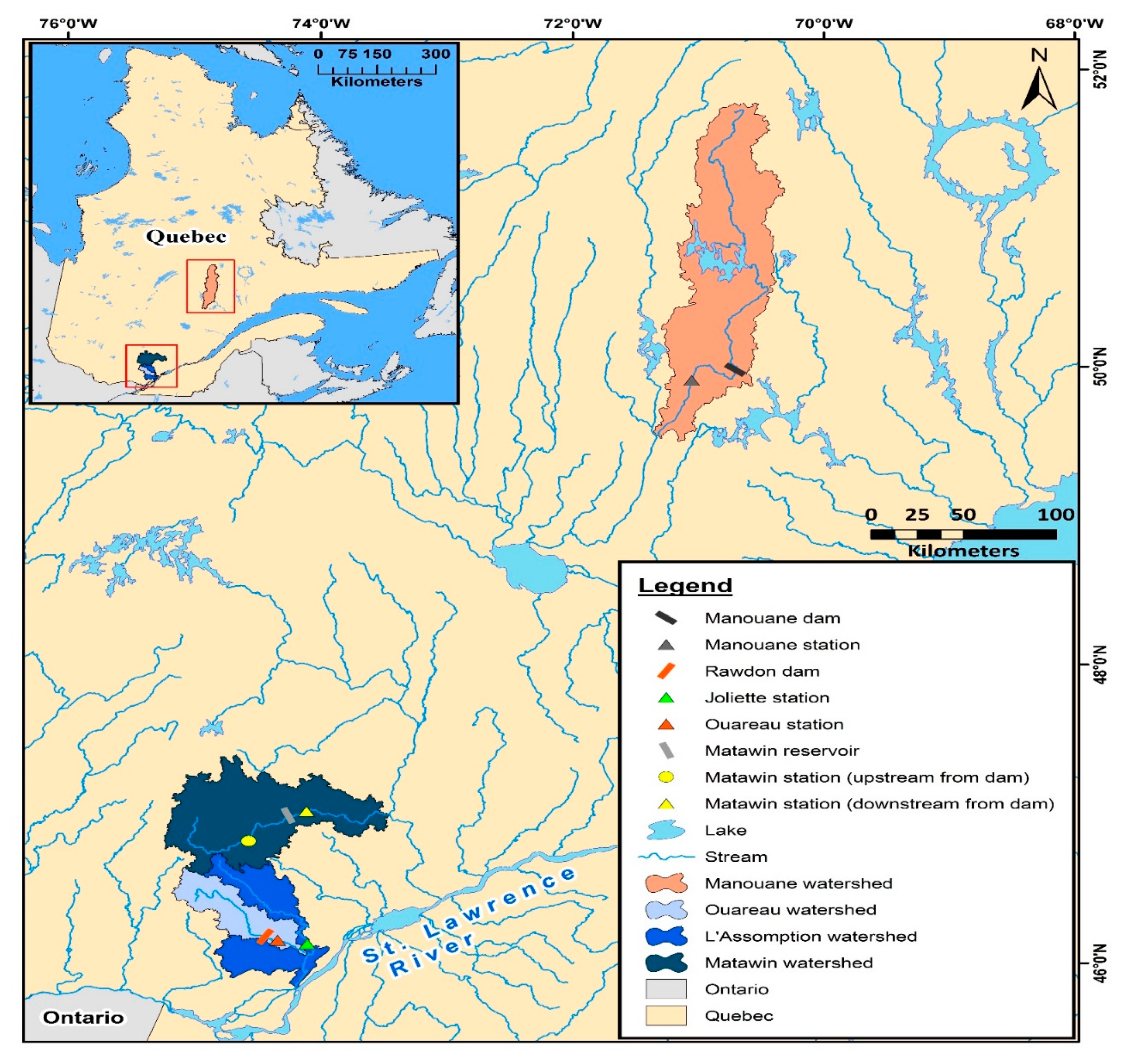
2.1. Watersheds and Data Sources
- -
- Type of dam management method or type of regulated hydrological regime. Three management methods were selected for this study: inversion, natural and diversion. The homogenization management method was not analyzed due to the absence of data measured in a natural river and downstream of a dam.
- -
- The existence of continuous flow measurements in natural rivers and downstream of a dam over a longer period of time (at least 10 years).
2.2. Definition of Hydroclimatic Variables
- -
- The series of mean daily maximum temperatures (Tmax);
- -
- The series of mean daily minimum temperatures (Tmin);
- -
- The series of daily mean temperatures (Tme);
- -
- The series of total snowfall (TSF);
- -
- The series of total rainfall (TRF);
- -
- The series of total precipitation (rain and snow, TP).
2.3. Statistical Data Analysis
- -
- In the first step, we compared the means of two CV and CI indices calculated in natural rivers and downstream of dams in the three watersheds using the Kruskal-Wallis non-parametric and parametric variance analysis (ANOVA) tests. The purpose of this step is to identify the influence of dam management methods on flow rate change index values.
- -
- The second step consisted in analyzing the temporal variability of these two indices (CI and CV) to compare their stationarity on the basis of dam management methods. We applied the Lombard test to analyze this stationarity [25,26]. The rationale for selecting this test is that it can detect abrupt or gradual breaks in means, in contrast with all other statistical tests used in hydrology. Such as with the other tests, it also helps determine the dates of such breaks. The test has already been widely described in our previous work (e.g., [27]). Given a series of independent observations where Xi is the observation taken at time It is important to assess whether the mean of this series has changed at some unknown time. To this end, one considers as a possible pattern for the mean of these observations the smooth-change model introduced by [25], where the mean of Xi is defined by:
- -
- Finally, the last step statistical analysis consisted of analyzing the correlation between the flow rate change indices and the six climatic variables in pristine (stations) rivers and downstream from dams.
3. Results
3.1. Comparison of the Mean Values of Flow Rate Change Indices in Pristine Rivers and Downstream from Dams
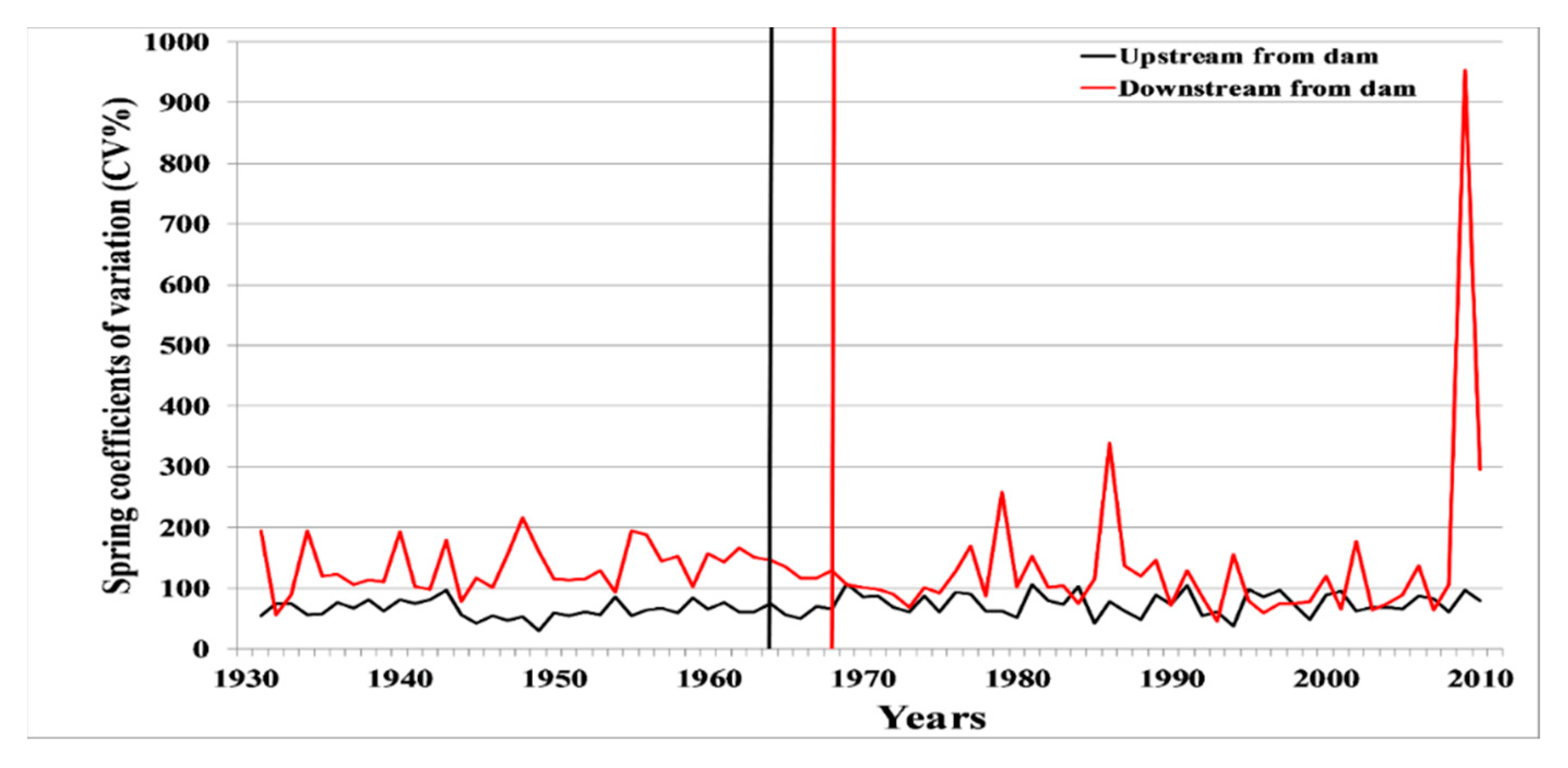
3.2. Analysis of the Temporal Variability of Flow Rate Change Indices
3.3. Analysis of the Influence of Dam Management Modes on the Relationship between Flow Rate Indices and Climate Variables
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ritcher, B.D.; Baumgartner, J.V.; Braun, D.P.; Powell, J. A spatial assessment of hydrologic alteration within a river network. Regul. Rivers Res. Manag. 1996, 14, 329–340. [Google Scholar]
- Poff, N.L.; Allan, J.D.; Bain, M.B.; Karr, J.R.; Prestegaard, K.L.; Richter, B.D.; Sparks, R.E.; Stromberg, J.C. The natural flow regime. Bioscience 1997, 47, 769–784. [Google Scholar] [CrossRef]
- Assani, A.A.; Landry, R.; Delisle, F. Effects of land use on flow rate change indices. Forests 2015, 6, 4349–4359. [Google Scholar] [CrossRef] [Green Version]
- Arthington, A.H. Environmental Flows: Saving Rivers in the Third Millennium; University of California Press: Berkeley, CA, USA, 2012. [Google Scholar]
- Richter, B.D.; Richter, H.E. Prescribing flood regimes to sustain riparian ecosystems along meandering rivers. Conserv. Biol. 2000, 14, 1467–1478. [Google Scholar] [CrossRef]
- Assani, A.A.; Simard, É.; Gravel, É.; Ibrahim, G.; Campeau, S. The impact of “Man-Made Hydrological drought” on plant species abundance in the low-flow channel downstream from the Matawin dam, Quebec. Water 2013, 5, 875–892. [Google Scholar] [CrossRef] [Green Version]
- Larned, S.T.; Datry, T.; Arscott, D.B.; Tockner, K. Emerging concepts in temporary-river ecology. Freshw. Biol. 2010, 55, 717–738. [Google Scholar] [CrossRef]
- Gebremicael, T.G.; Mohamed, Y.A.; Van Zaag, P.; Hagos, E.Y. Temporal and spatial changes of rainfall and streamflow in the Upper Tekeze-Atbara River basin, Ethiopia. Hydrol. Earth Syst. Sci. 2017, 21, 2127–2142. [Google Scholar] [CrossRef] [Green Version]
- Haas, N.A.; O’Connor, B.L.; Hayse, J.W.; Bevelhimer, M.S.; Endreny, T.A. Analysis of daily peaking and run-of-river operations with flow variability metrics, considering subdaily to seasonaly time scales. J. Am. Water Res. Assoc. 2014, 50, 1622–1640. [Google Scholar] [CrossRef]
- Li, D.N.; Long, D.; Zhao, J.S.; Lu, H.H.; Hong, Y. Observed changes in flow regimes in the Mekong River basin. J. Hydrol. 2017, 551, 217–232. [Google Scholar] [CrossRef]
- Mori, T.; Onoda, Y.; Kayaka, Y. Geographical patterns of flow-regime alterations by flood-control dams in Japan. Limnology 2018, 19, 53–67. [Google Scholar] [CrossRef]
- Peñas, F.J.; Barquin, J. Assessment of large-scale patterns of hydrological alteration caused by dams. J. Hydrol. 2019, 572, 706–718. [Google Scholar] [CrossRef]
- Moyle, P.B.; Mount, J.F. Homogenous rivers, homogenous fauna. Proc. Nat. Acad. Sci. USA 2007, 104, 5711–5712. [Google Scholar] [CrossRef] [Green Version]
- Cushman, R.M. Review of ecological effects of rapidly varying flows downstream from hydroelectric facilities. N. Am. J. Fish. Manag. 1985, 5, 330–339. [Google Scholar] [CrossRef]
- Zimmerman, J.K.H.; Letcher, B.; Nislow, K.H.; Lutz, K.A.; Magillan, J.F. Determining the effects of dams on subdaily variations in river flows at a whole-basin scale. Rivers Res. Appl. 2010, 26, 1246–1260. [Google Scholar]
- Grelsson, G. Vegetational changes on two eroding banks of a short-term regulated river reservoir in northern Sweden. N. J. Bot. 1986, 5, 581–614. [Google Scholar] [CrossRef]
- Nilsson, C.; Svedmark, M. Basic principles and ecological consequences of changing water regimes: Riparian plant communities. Environ. Manag. 2002, 30, 468–480. [Google Scholar] [CrossRef]
- Rood, S.B.; Mahoney, J.M.; Reid, D.E.; Zilm, L. Instream flows and the decline of riparian cottonwoods along the St. Mary River, Alberta. Can. J. Bot. 1995, 73, 1250–1260. [Google Scholar] [CrossRef]
- Rood, S.B.; Tabouchalnas, K.; Bradley, C.E.; Kalischuk, A.R. Influence of flow regulation on channel dynamics and riparian cottonwoods along the Bow River, Alberta. Water 1999, 7, 33–48. [Google Scholar]
- Assani, A.A.; Gravel, E.; Buffin-Bélanger, T.; Roy, A.G. Impacts des barrages sur les débits annuels minimums en fonction des régimes hydrologiques artificialisés au Québec (Canada). J. Water Sci. 2005, 18, 103–127. [Google Scholar] [CrossRef] [Green Version]
- Assani, A.A.; Stichelbout, E.; Roy, A.G.; Petit, F. Comparison of impacts of dams on the annual maximum flow characteristics in the three regulated hydrological regimes in Québec. Hydrol. Process. 2006, 20, 3485–3501. [Google Scholar] [CrossRef]
- Lajoie, F.; Assani, A.A.; Roy, A.G.; Mesfioui, M. Impacts of dams on monthly flow characteristics. The influence of watershed size and seasons. J. Hydrol. 2007, 334, 423–439. [Google Scholar] [CrossRef]
- Matteau, M.; Assani, A.A.; Mesfioui, M. Application of multivariate statistical analysis methods to the dam hydrologic impact studies. J. Hydrol. 2009, 371, 120–128. [Google Scholar] [CrossRef]
- Assani, A.A.; Buffin-Bélanger, T.; Roy, A.G. Analyse des impacts d’un barrage sur le régime hydrologique de la rivière Matawin (Québec, Canada). J. Water Sci. 2002, 15, 557–574. [Google Scholar]
- Lombard, F. Rank tests for change-point problems. Biometrika 1987, 74, 615–624. [Google Scholar] [CrossRef]
- Quessy, J.-F.; Favre, A.-C.; Saïd, M.; Champagne, M. Statistical inference in Lombard’s smooth-change model. Environmetrics 2011, 22, 882–893. [Google Scholar] [CrossRef]
- Assani, A.A. The usefulness of the Lombard method for analyzing the hydrological impacts of dams: The case of the Manouane River diversion dam, Quebec, Canada. Water 2016, 8, 410. [Google Scholar] [CrossRef] [Green Version]
- Fortier, C.; Assani, A.A.; Mesfioui, M.; Roy, A.G. Comparison of the interannual and interdecadal variability of heavy flood charactristics upstream and downstream from dams in inversed hydrologic regime: Case study of Matawin River (Québec, Canada). Rivers Res. Appl. 2011, 27, 1277–1289. [Google Scholar] [CrossRef]
- Assani, A.A.; Chauvette, L.; Campeau, S. Analysis of the Impacts of Changes in Streamflow and of Reforestation on the Morphological Evolution of the Matambin River Channel in the St. Lawrence Lowlands (Quebec, Canada); Shukla, D.P., Ed.; Geomorphology, Intech: London, UK, 2017. [Google Scholar] [CrossRef] [Green Version]
- Dubeau, S.; Assani, A.A.; Ibrahim, G.; Rodríguez, M.A. Temporal variability of streamflow and plant species abundance on islets as they relate to ENSO events downstream from an inversion-type reservoir. River Res. Appl. 2017, 33, 1411–1419. [Google Scholar] [CrossRef]
- Assani, A.A.; Leduc, S. The influence of the charactersitics of geomorphological deposits on terrestrial plant species richness in the low flow channel downstream from an inversion-tyep reservoir. Int. J. Environ. Sci. Nat. Res. 2021, 28, 556232. [Google Scholar] [CrossRef]
| Seasons | Indices | Before | After | p-Value (KW) | p-Value (t) | R (%) |
|---|---|---|---|---|---|---|
| M1 | M2 | |||||
| Fall | CI | 7.88 (4.13) | 5.21 (1.83) | 0.027 | 0.011 | −33.9 |
| CV | 55.63 (16.62) | 45.13 (12.51) | 0.041 | 0.036 | −18.9 | |
| Winter | CI | 1.82 (0.70) | 2.10 (1.84) | 0.671 | 0.594 | − |
| CV | 16.64 (10.53) | 17.06 (20.44) | 0.117 | 0.944 | − | |
| Spring | CI | 29.75 (11.29) | 28.19 (14.96) | 0.854 | 0.740 | − |
| CV | 82.52 (14.55) | 99.09 (24.24) | 0.039 | 0.032 | +20.1 | |
| Summer | CI | 6.04 (2.89) | 7.10 (3.48) | 0.421 | 0.349 | − |
| CV | 47.32 (14.14) | 48.86 (11.79) | 0.815 | 0.733 | − |
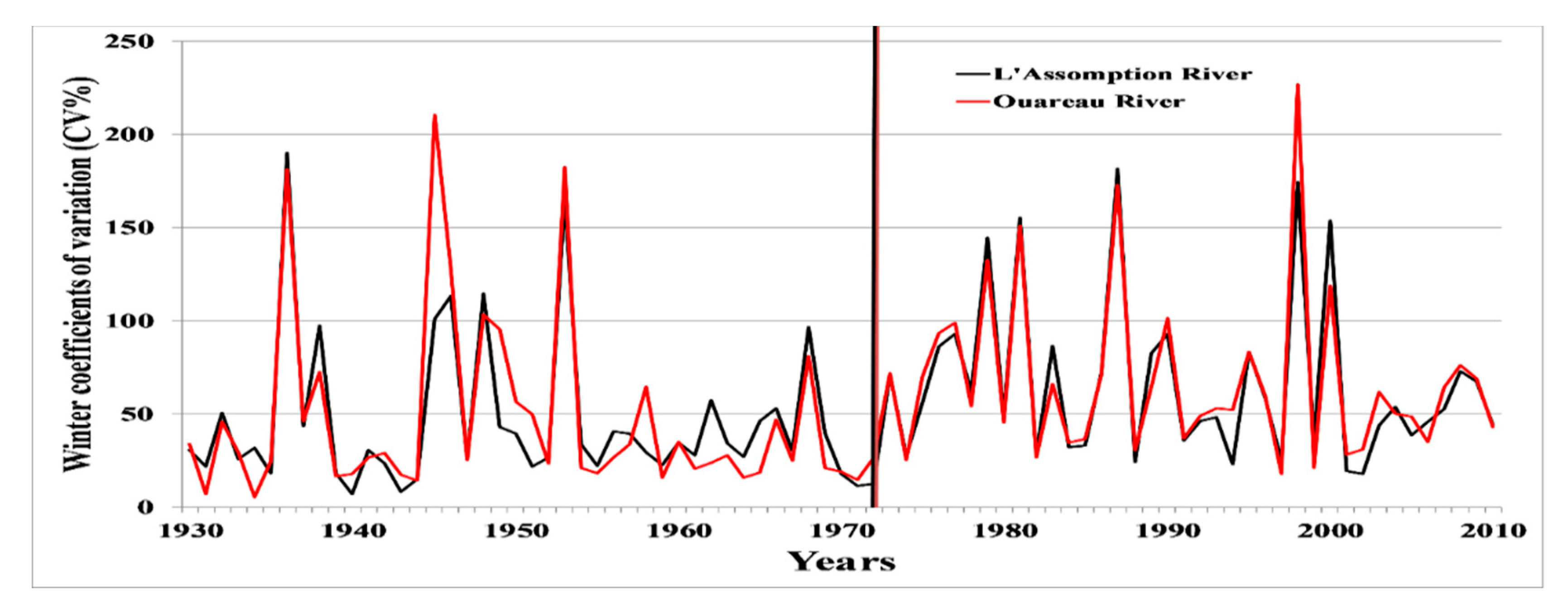
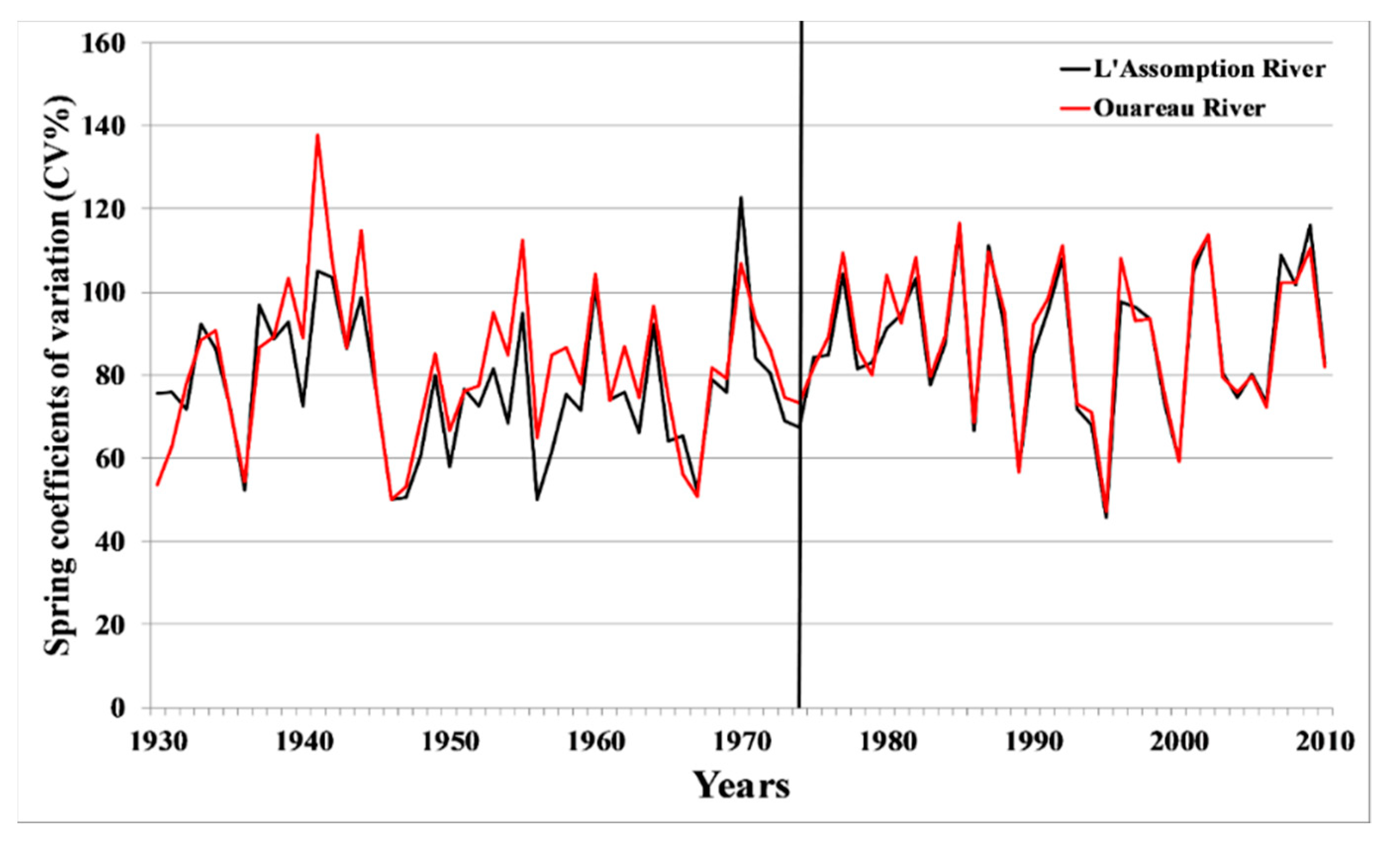
| Seasons | Indices | L’Assomption River | Ouareau River | p-Value (KW) | p-Value (t) | R (%) |
|---|---|---|---|---|---|---|
| M1 | M2 | |||||
| Fall | CI | 9.56 (7.03) | 11.26 (15.88) | 0.291 | 0.354 | − |
| CV | 53.79 (21.25) | 53.61 (18.54) | 0.879 | 0.928 | − | |
| Winter | CI | 7.35 (8.73) | 9.36 (14.66) | 0.714 | 0.747 | − |
| CV | 55.00 (42.89) | 56.42 (47.25) | 0.895 | 0.945 | − | |
| Spring | CI | 19.73 (9.32) | 26.00 (14.96) | 0.001 | 0.001 | +31.78 |
| CV | 81.84 (17.47) | 85.16 (18.27) | 0.213 | 0.239 | − | |
| Summer | CI | 9.45 (6.47) | 15.84 (20.53) | 0.049 | − | +67.62 |
| CV | 57.36 (21.94) | 59.64 (25.93) | 0.664 | 0.661 | − |
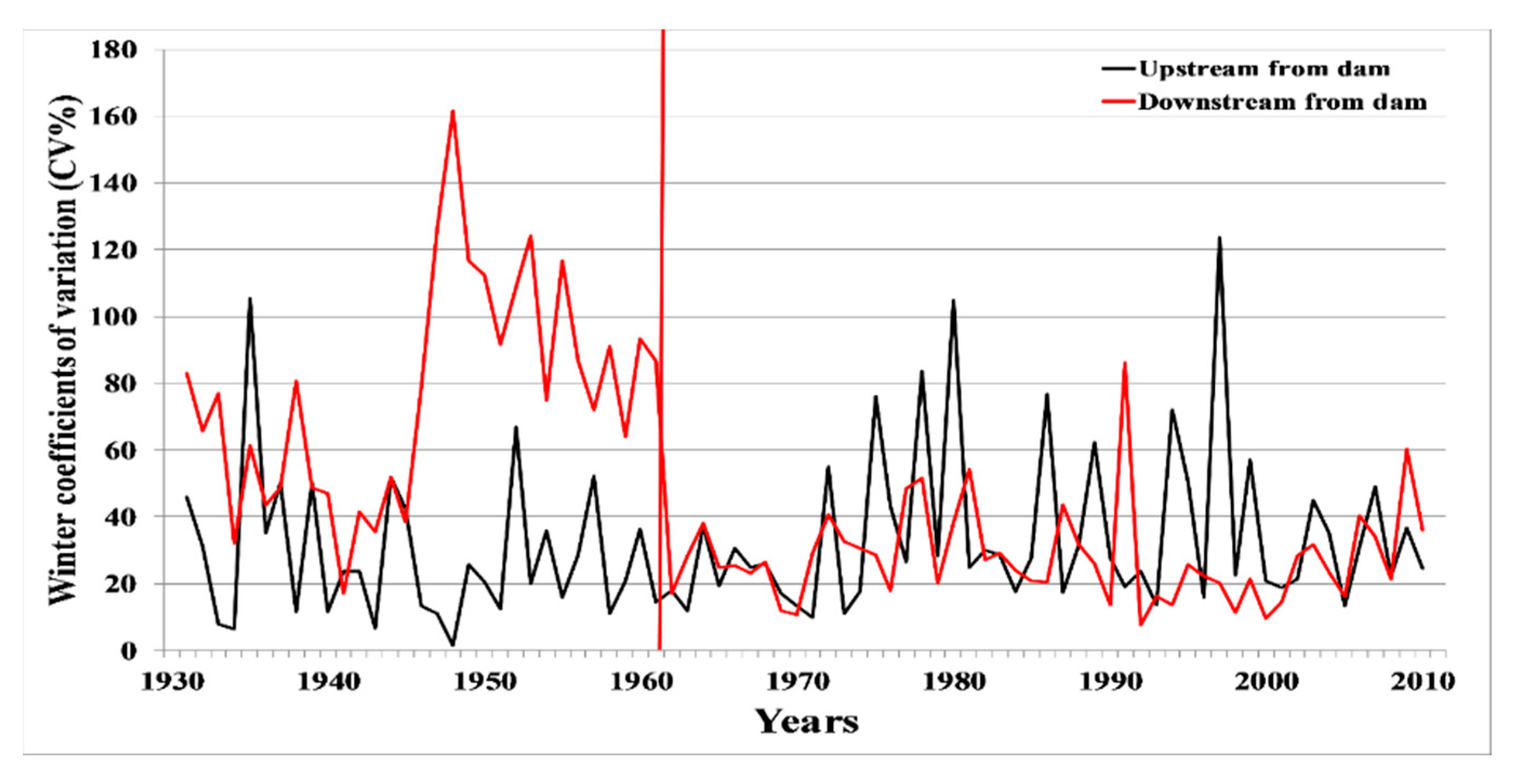
| Seasons | Indices | Upstream from Dam | Downstream from Dam | p-Value (KW) | p-Value (t) | R (%) |
|---|---|---|---|---|---|---|
| M1 | M2 | |||||
| Fall | CI | 5.02 (2.31) | 111.72 (71.74) | 0.000 | − | +2125.5 |
| CV | 40.50 (12.45) | 90.85 (40.40) | 0.000 | 0.000 | +126.84 | |
| Winter | CI | 3.52 (3.10) | 49.93 (66.37) | 0.000 | − | +1318.47 |
| CV | 32.37 (24.02) | 46.94 (33.40) | 0.000 | 0.002 | +43.28 | |
| Spring | CI | 13.61 (6.40) | 134.56 (100.16) | 0.000 | − | +888.68 |
| CV | 69.90 (17.20) | 135.17 (105.88) | 0.000 | 0.000 | +933.38 | |
| Summer | CI | 7.22 (3.95) | 93.09 (63.03) | 0.000 | 0.000 | +1189.34 |
| CV | 52.93 (17.37) | 94.03 (30.72) | 0.000 | 0.000 | +77.65 |
| Seasons | CI | CV | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L’Assomption River | Ouareau River | L’Assomption River | Ouareau River | |||||||||
| Sn | T1/T2 | R (%) | Sn | T1/T2 | R (%) | Sn | T1/T2 | R (%) | Sn | T1/T2 | R (%) | |
| Fall | 0.0099 | - | − | 0.0024 | − | − | 0.0045 | − | − | 0.0006 | − | − |
| Winter | 0.0940 | 1951/52 | −41.46 | 0.0569 | 1973/74 | −2.27 | 0.0594 | 1971/72 | −41.36 | 0.0745 | 1971/72 | −42.01 |
| Spring | 0.0688 | 1994/95 | −27.08 | 0.0052 | − | − | 0.0498 | 1973/74 | −13.04 | 0.0244 | − | − |
| Summer | 0.0688 | 1994/95 | −70.56 | 0.1410 | 1976/97 | −78.50 | 0.1062 | 1994/95 | −50.08 | 0.1420 | 1982/85 | −52.84 |
| Seasons | CI | CV | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Upstream from dam | Downstream from Dam | Upstream from Dam | Downstream from Dam | |||||||||
| Sn | T1/T2 | R (%) | Sn | T1/T2 | R (%) | Sn | T1/T2 | R (%) | Sn | T1/T2 | R (%) | |
| Fall | 0.0770 | 1961/62 | −33.64 | 0.1173 | 1982/83 | +48.30 | 0.0472 | 1986/87 | −27.03 | 0.3150 | 1959/72 | +46.21 |
| Winter | 0.0819 | 1970/71 | −52.44 | 0.3079 | 1958/68 | +80.26 | 0.0316 | − | − | 0.3020 | 1960/61 | +59.76 |
| Spring | 0.0207 | − | − | 0.0886 | 1981/82 | +37.00 | 0.0699 | 1963/64 | −16.67 | 0.0546 | 1967/68 | 0.32 |
| Summer | 0.1009 | 1992/96 | −82.82 | 0.2728 | 1986/87 | +58.94 | 0.0894 | 1993/94 | −31.83 | 0.0144 | − | − |
| Fall | Winter | Spring | Summer | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L’Assomption River | Ouareau River | L’Assomption River | Ouareau River | L’Assomption River | Ouareau River | L’Assomption River | Ouareau River | |||||||||
| CI | CV | CI | CV | CI | CV | CI | CV | CI | CV | CI | CV | CI | CV | CI | CV | |
| Tmax | 0.063 | −0.031 | 0.088 | 0.032 | 0.251 | 0.305 | 0.280 | 0.319 | 0.401 | 0.415 | 0.230 | 0.366 | 0.107 | 0.103 | 0.076 | 0.035 |
| Tmin | 0.156 | 0.091 | 0.140 | 0.086 | 0.305 | 0.319 | 0.263 | 0.316 | 0.314 | 0.317 | 0.175 | 0.229 | 0.046 | 0.120 | 0.272 | 0.181 |
| Tmoy | 0.129 | 0.040 | 0.135 | 0.071 | 0.308 | 0.340 | 0.292 | 0.333 | 0.383 | 0.402 | 0.209 | 0.324 | 0.109 | 0.013 | 0.366 | 0.172 |
| TRF | 0.502 | 0.425 | 0.388 | 0.408 | 0.586 | 0.645 | 0.447 | 0.532 | −0.168 | −0.175 | −0.105 | −0.231 | 0.134 | 0.124 | 0.236 | 0.266 |
| TSF | −0.105 | −0.196 | −0.059 | −0.198 | −0.132 | −0.201 | −0.239 | −0.207 | 0.163 | 0.076 | 0.086 | 0.000 | − | − | − | − |
| TP | 0.313 | 0.217 | 0.329 | 0.226 | 0.343 | 0.311 | 0.164 | 0.228 | −0.118 | −0.118 | −0.074 | −0.195 | 0.134 | 0.124 | 0.238 | 0.266 |
| Fall | Winter | Spring | Summer | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Upstrteam | Downstream | Upstrteam | Downstream | Upstrteam | Downstream | Upstrteam | Downstream | |||||||||
| CI | CV | CI | CV | CI | CV | CI | CV | CI | CV | CI | CV | CI | CV | CI | CV | |
| Tmax | −0.029 | 0.052 | 0.203 | 0.041 | 0.030 | 0.029 | 0.054 | −0.060 | −0.023 | 0.010 | −0.206 | 0.092 | 0.242 | 0.193 | −0.175 | 0.034 |
| Tmin | 0.013 | 0.012 | 0.101 | 0.203 | 0.066 | 0.126 | 0.184 | 0.080 | −0.043 | −0.019 | −0.118 | −0.118 | 0.131 | 0.142 | −0.022 | 0.073 |
| Tmoy | −0.012 | 0.030 | 0.177 | 0.118 | 0.035 | 0.073 | 0.129 | 0.022 | −0.031 | 0.003 | −0.150 | −0.001 | 0.223 | 0.190 | −0.109 | 0.056 |
| TRF | 0.232 | 0.216 | −0.210 | 0.009 | 0.211 | 0.280 | −0.030 | −0.020 | 0.141 | 0.281 | 0.317 | −0.531 | −0.161 | −0.111 | −0.046 | −0.128 |
| TSF | 0.075 | 0.113 | −0.065 | −0.143 | −0.275 | −0.279 | 0.134 | 0.253 | 0.077 | 0.065 | 0.193 | 0.016 | − | − | − | − |
| TP | 0.271 | 0.272 | −0.189 | −0.040 | −0.148 | −0.125 | 0.124 | 0.234 | 0.165 | 0.299 | 0.343 | −0.515 | −0.163 | −0.113 | −0.046 | −0.129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delisle, F.; Assani, A.A. Comparison of Seasonal Flow Rate Change Indices Downstream of Three Types of Dams in Southern Quebec (Canada). Water 2021, 13, 2555. https://doi.org/10.3390/w13182555
Delisle F, Assani AA. Comparison of Seasonal Flow Rate Change Indices Downstream of Three Types of Dams in Southern Quebec (Canada). Water. 2021; 13(18):2555. https://doi.org/10.3390/w13182555
Chicago/Turabian StyleDelisle, Francis, and Ali Arkamose Assani. 2021. "Comparison of Seasonal Flow Rate Change Indices Downstream of Three Types of Dams in Southern Quebec (Canada)" Water 13, no. 18: 2555. https://doi.org/10.3390/w13182555
APA StyleDelisle, F., & Assani, A. A. (2021). Comparison of Seasonal Flow Rate Change Indices Downstream of Three Types of Dams in Southern Quebec (Canada). Water, 13(18), 2555. https://doi.org/10.3390/w13182555







