Operation Rule Derivation of Hydropower Reservoirs by Support Vector Machine Based on Grey Relational Analysis
Abstract
:1. Introduction
2. Deterministic Reservoir Operation Optimization Model
2.1. Objective Function
2.2. Operation Constraints
2.3. Optimization Method
3. Derivation Rule Method
Support Vector Machine (SVM)
4. Using Grey Relational Analysis to Quantify the Influence of Input Vectors and Evolution Index
4.1. Grey Relational Analysis
4.2. Evolution Index
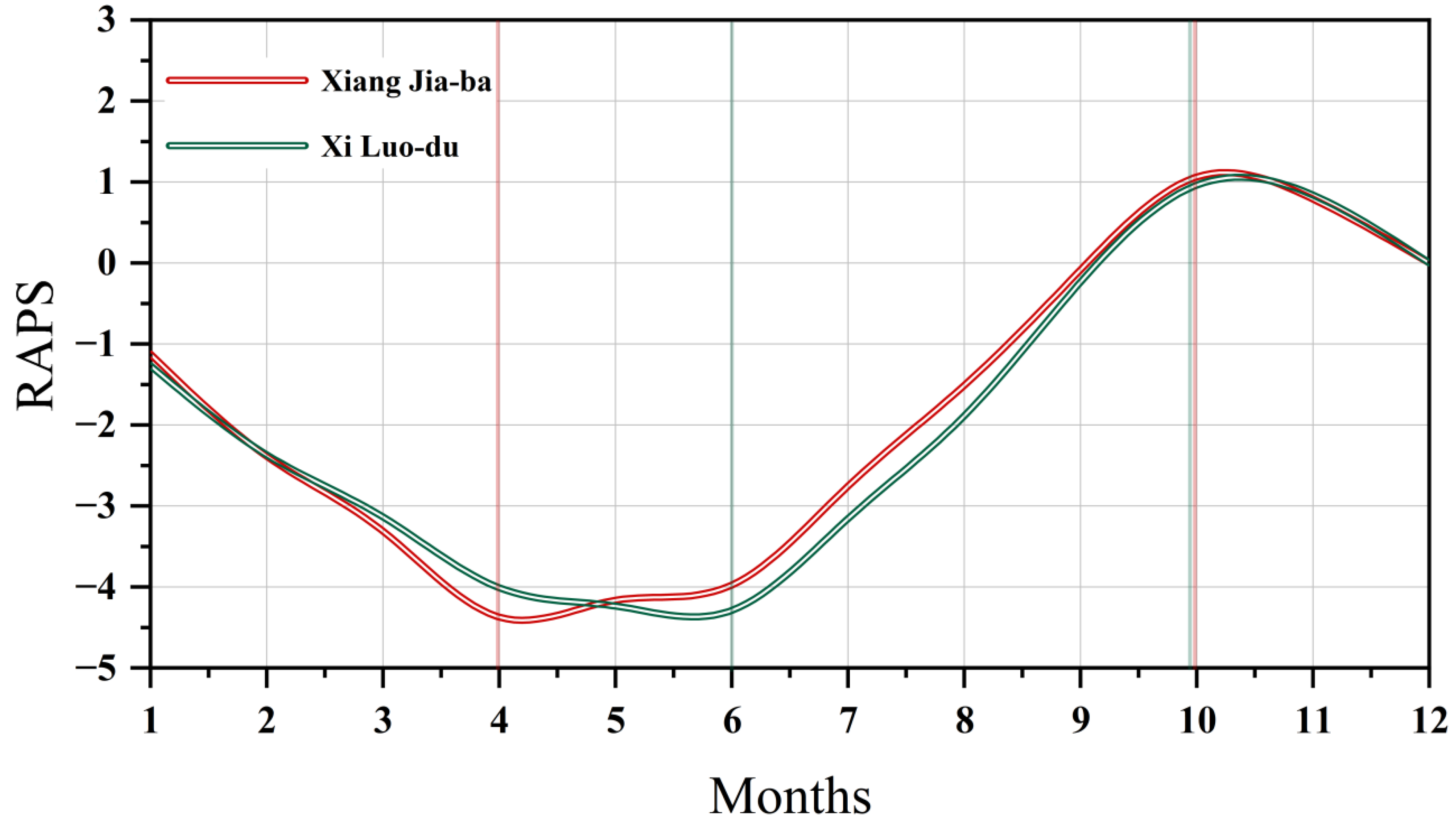
4.3. Rescaled Adjusted Partial Sums
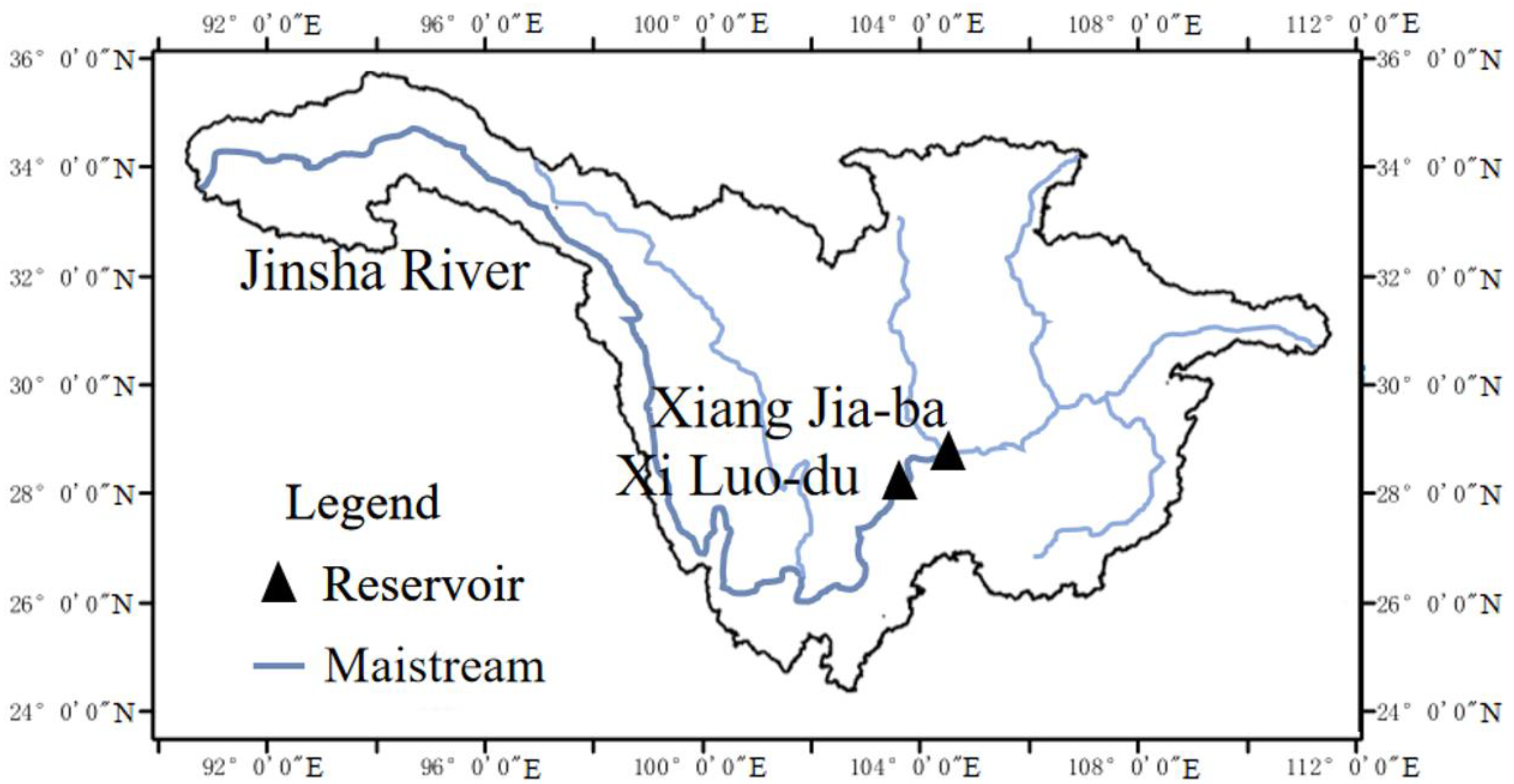
5. Case Study
5.1. Correlation Analysis in the GRA
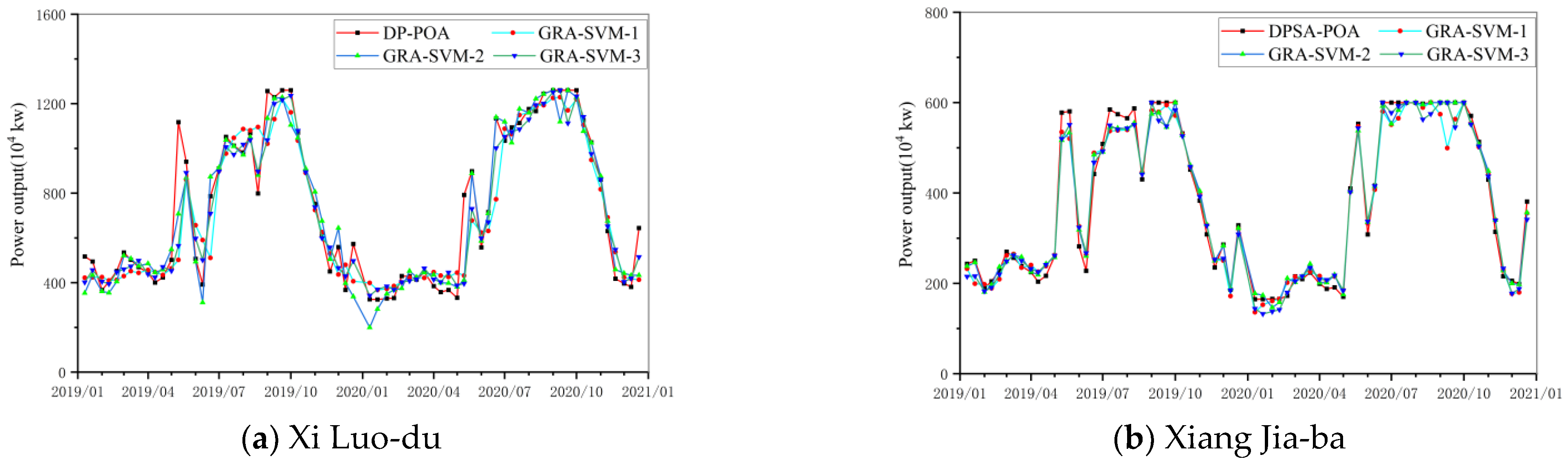
5.2. Operating Rules Derivation and Results Discussion
6. Conclusions
- (1)
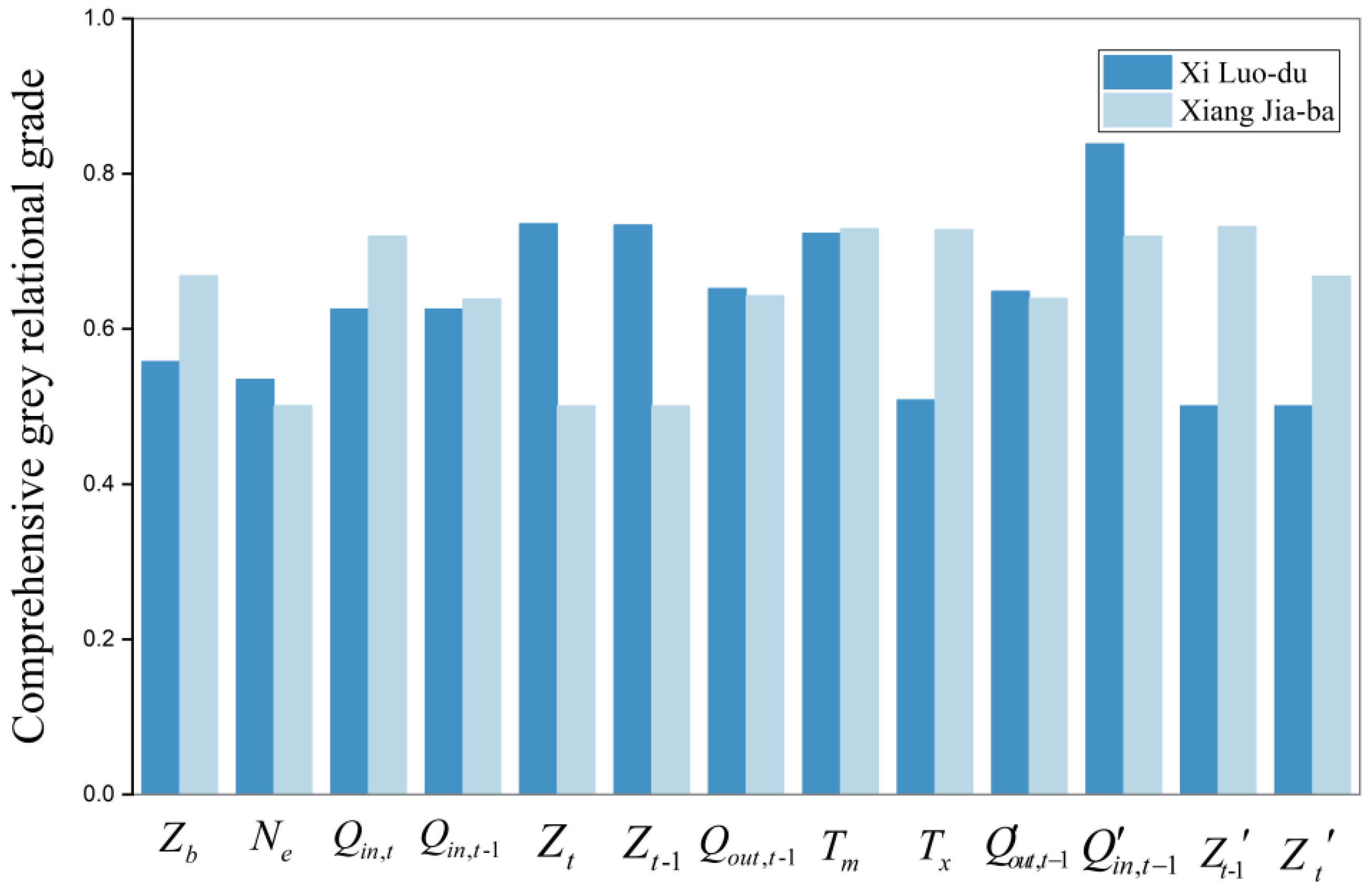
- The simulation results indicate that the significant correlation factor and potential correlation factors can improve the fitting accuracy. For correlation factor, the larger the grey relational grade is, the better the fitting accuracy will be.
- (2)
- Among the three GRA-SVM schemes, GRA-SVM-2 has the best fitting accuracy and the absolute error of hydropower generation are 2.57 and 0.42, respectively. Therefore, in practical application, as many related factors (comprehensive grey relational grade is more than 0.5) should be selected as possible.
- (3)
- The GRA quantifies the importance of each correlation factor, which may as the input of the SVM model. Among the water conservancy between Xi Luo-du and Xiang Jia-ba considering the backwater effect, the relevant data of adjacent hydropower station plays an important role to improve accuracy.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, Z.-K.; Niu, W.-J.; Wang, W.-C.; Zhou, J.-Z.; Cheng, C.-T. A mixed integer linear programming model for unit commitment of thermal plants with peak shaving operation aspect in regional power grid lack of flexible hydropower energy. Energy 2019, 175, 618–629. [Google Scholar] [CrossRef]
- Ming, B.; Liu, P.; Guo, S.; Zhang, X.; Feng, M.; Wang, X. Optimizing utility-scale photovoltaic power generation for integration into a hydropower reservoir by incorporating long- and short-term operational decisions. Appl. Energy 2017, 204, 432–445. [Google Scholar] [CrossRef]
- Catalao, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Hydro energy systems management in Portugal: Profit-based evaluation of a mixed-integer nonlinear approach. Energy 2011, 36, 500–507. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Cheng, C.-T.; Lund, J.R. Optimizing Hydropower Reservoirs Operation via an Orthogonal Progressive Optimality Algorithm. J. Water Resour. Plan. Manag. 2018, 144, 04018001. [Google Scholar] [CrossRef]
- Chang, J.-X.; Bai, T.; Huang, Q.; Yang, D.-W. Optimization of Water Resources Utilization by PSO-GA. Water Resour. Manag. 2013, 27, 3525–3540. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, P.-F.; Wang, C.; Qian, J.; Hou, J. Combined Monthly Inflow Forecasting and Multiobjective Ecological Reservoir Operations Model: Case Study of the Three Gorges Reservoir. J. Water Resour. Plan. Manag. 2017, 143, 05017004. [Google Scholar] [CrossRef]
- Zhao, T.; Cai, X.; Lei, X.; Wang, H. Improved Dynamic Programming for Reservoir Operation Optimization with a Concave Objective Function. J. Water Resour. Plan. Manag. ASCE 2012, 138, 590–596. [Google Scholar] [CrossRef]
- Philbrick, C.R.; Kitanidis, P.K. Limitations of deterministic optimization applied to reservoir operations. J. Water Resour. Plan. Manag. 1999, 125, 135–142. [Google Scholar] [CrossRef]
- Madani, K. Hydropower licensing and climate change: Insights from cooperative game theory. Adv. Water Resour. 2011, 34, 174–183. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W. Prediction of rainfall time series using modular soft computing methods. Eng. Appl. Artif. Intell. 2013, 26, 997–1007. [Google Scholar] [CrossRef] [Green Version]
- Young, G.K. Finding reservoir operating rules. J. Hydraul. Div. 1967, 93, 297–321. [Google Scholar] [CrossRef]
- Ji, C.; Su, X.; Zhou, T. Study on the optimal operating rules for cascade hydropower stations based on output allocation model. J. Hydroelectr. Eng. 2010, 30, 26–31. [Google Scholar]
- Yang, P.; Ng, T.L. Fuzzy Inference System for Robust Rule-Based Reservoir Operation under Nonstationary Inflows. J. Water Resour. Plan. Manag. 2017, 143, 04016084. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Aboutalebi, M.; Ashofteh, P.-S.; Loaiciga, H.A. Real-time reservoir operation using data mining techniques. Environ. Monit. Assess. 2018, 190, 594. [Google Scholar] [CrossRef]
- Chau, K.W. Particle swarm optimization training algorithm for ANNs in stage prediction of Shing Mun River. J. Hydrol. 2006, 329, 363–367. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.-C.; Xu, D.-M.; Chau, K.-W.; Chen, S.-Y. Improved annual rainfall-runoff forecasting using PSO-SVM model based on EEMD. J. Hydroinform. 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Hsu, C.W.; Lin, C.J. A simple decomposition method for support vector machines. Mach. Learn. 2002, 46, 291–314. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.-T.; Feng, Z.-K.; Niu, W.-J.; Liao, S.-L. Heuristic Methods for Reservoir Monthly Inflow Forecasting: A Case Study of Xinfengjiang Reservoir in Pearl River, China. Water 2015, 7, 4477–4495. [Google Scholar] [CrossRef]
- Ullah, K.; Garg, H.; Mahmood, T.; Jan, N.; Ali, Z. Correlation coefficients for T-spherical fuzzy sets and their applications in clustering and multi-attribute decision making. Soft Comput. 2020, 24, 1647–1659. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Chan, J.W.K.; Tong, T.K.L. Multi-criteria material selections and end-of-life product strategy: Grey relational analysis approach. Mater. Des. 2007, 28, 1539–1546. [Google Scholar] [CrossRef]
- Kuo, Y.-Y.; Yang, T.-H.; Huang, G.-W. The use of grey relational analysis in solving multiple attribute decision-making problems. Comput. Ind. Eng. 2008, 55, 80–93. [Google Scholar] [CrossRef]
- Tosun, N. Determination of optimum parameters for multi-performance characteristics in drilling by using grey relational analysis. Int. J. Adv. Manuf. Technol. 2006, 28, 450–455. [Google Scholar] [CrossRef]
- Wei, G.-W. Gray relational analysis method for intuitionistic fuzzy multiple attribute decision making. Expert Syst. Appl. 2011, 38, 11671–11677. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Cheng, X.; Wang, J.-Y.; Wang, S.; Song, Z.-G. An effective three-stage hybrid optimization method for source-network-load power generation of cascade hydropower reservoirs serving multiple interconnected power grids. J. Clean. Prod. 2020, 246, 119035. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Wang, S.; Cheng, C.-T.; Jiang, Z.-Q.; Qin, H.; Liu, Y. Developing a successive linear programming model for head-sensitive hydropower system operation considering power shortage aspect. Energy 2018, 155, 252–261. [Google Scholar] [CrossRef]
- Niu, W.-J.; Feng, Z.-K.; Feng, B.-F.; Min, Y.-W.; Cheng, C.-T.; Zhou, J.-Z. Comparison of Multiple Linear Regression, Artificial Neural Network, Extreme Learning Machine, and Support Vector Machine in Deriving Operation Rule of Hydropower Reservoir. Water 2019, 11, 88. [Google Scholar] [CrossRef] [Green Version]
- Pan, Z.; Chen, L.; Teng, X. Research on joint flood control operation rule of parallel reservoir group based on aggregation-decomposition method. J. Hydrol. 2020, 590, 125479. [Google Scholar] [CrossRef]
- Dong, S. Multi class SVM algorithm with active learning for network traffic classification. Expert Syst. Appl. 2021, 176, 114885. [Google Scholar] [CrossRef]
- Geng, D.; Alkhachroum, A.; Melo Bicchi, M.A.; Jagid, J.R.; Cajigas, I.; Chen, Z.S. Deep learning for robust detection of interictal epileptiform discharges. J. Neural Eng. 2021, 18, 056015. [Google Scholar] [CrossRef] [PubMed]
- Deng, J. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Garbrecht, J.; Fernandez, G.P. Visualization of trends and fluctuations in climatic records. J. Am. Water Resour. Assoc. 1994, 30, 297–306. [Google Scholar] [CrossRef]
- Bonacci, O.; Bonacci, D.; Roje-Bonacci, T. Different air temperature changes in continental and Mediterranean regions: A case study from two Croatian stations. Theor. Appl. Climatol. 2021, 145, 1333–1346. [Google Scholar] [CrossRef]
- Sajid, T.; Tanveer, S.; Sabir, Z.; Guirao, J.L.G. Impact of Activation Energy and Temperature-Dependent Heat Source/Sink on Maxwell-Sutterby Fluid. Math. Probl. Eng. 2020, 2020, 5251804. [Google Scholar]
- Markovinovic, D.; Kranjcic, N.; Durin, B.; Orsulic, O.B. Identifying the Dynamics of the Sea-Level Fluctuations in Croatia Using the RAPS Method. Symmetry 2021, 13, 289. [Google Scholar] [CrossRef]
- Qiu, H.; Chen, L.; Zhou, J.; He, Z.; Zhang, H. Risk analysis of water supply-hydropower generation-environment nexus in the cascade reservoir operation. J. Clean. Prod. 2021, 283, 124239. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Dai, L.; Huang, K.; Zha, G. Risk assessment of multireservoir joint flood control system under multiple uncertainties. J. Flood Risk Manag. 2021, e12740. [Google Scholar] [CrossRef]
- Wu, Y.; Fang, H.; Huang, L.; Ouyang, W. Changing runoff due to temperature and precipitation variations in the dammed Jinsha River. J. Hydrol. 2020, 582, 124500. [Google Scholar] [CrossRef]

| Reservoirs | Xi Luo-Du | Xiang Jia-Ba |
|---|---|---|
| Flood control water level (m) | 560 | 370 |
| Normal pool level (m) | 600 | 380 |
| Dead water level (m) | 540 | 370 |
| Flood storage (billion m3) | 46.50 | 9.03 |
| Regulating storage (billion m3) | 64.60 | 9.03 |
| Regulation ability | Seasonal | Seasonal |
| Power Capacity (MW) | 12,600 | 6400 |
| Firm output (MW) | 3850 | 2009 |
| Reservoirs | Xi Luo-Du | Xiang Jia-Ba | ||||
|---|---|---|---|---|---|---|
| Grey Relational Grade | Absolute | Relative | Comprehensive | Absolute | Relative | Comprehensive |
| Zb | 0.61 | 0.50 | 0.56 | 0.83 | 0.50 | 0.67 |
| Ne | 0.57 | 0.50 | 0.53 | 0.50 | 0.50 | 0.50 |
| Zt−1 | 0.96 | 0.51 | 0.73 | 0.50 | 0.50 | 0.50 |
| Zt | 0.96 | 0.51 | 0.74 | 0.50 | 0.50 | 0.50 |
| Qin,t−1 | 0.73 | 0.52 | 0.63 | 0.72 | 0.56 | 0.64 |
| Qin,t | 0.73 | 0.52 | 0.63 | 0.77 | 0.66 | 0.72 |
| Qout,t−1 | 0.79 | 0.51 | 0.65 | 0.78 | 0.51 | 0.64 |
| Tm | 0.94 | 0.51 | 0.72 | 0.96 | 0.50 | 0.73 |
| Tx | 0.52 | 0.50 | 0.51 | 0.96 | 0.50 | 0.73 |
| 0.78 | 0.51 | 0.65 | 0.77 | 0.51 | 0.64 | |
| 0.78 | 0.89 | 0.84 | 0.77 | 0.66 | 0.72 | |
| 0.50 | 0.50 | 0.50 | 0.94 | 0.52 | 0.73 | |
| 0.50 | 0.50 | 0.50 | 0.82 | 0.52 | 0.67 | |
| Reservoirs | Xi Luo-Du | Xiang Jia-Ba | ||||
|---|---|---|---|---|---|---|
| Methods | GRA-SVM-1 | GRA-SVM-2 | GRA-SVM-3 | GRA-SVM-1 | GRA-SVM-2 | GRA-SVM-3 |
| R | 0.918 | 0.961 | 0.953 | 0.990 | 0.994 | 0.992 |
| RMSE | 134.63 | 94.33 | 103.73 | 26.51 | 21.32 | 23.42 |
| MAE | 87.87 | 57.54 | 60.94 | 20.18 | 15.73 | 18.75 |
| Methods | Conventional Operation | DP-POA | GRA-SVM-1 | GRA-SVM-2 | GRA-SVM-3 | |||
|---|---|---|---|---|---|---|---|---|
| Assessment Index | Generation (108 kWh) | Generation (108 kWh) | Generation (108 kWh) | Gap (%) | Generation (108 kWh) | Gap (%) | Generation (108 kWh) | Gap (%) |
| Xi Luo-du | 1115.46 | 1230.66 | 1183.43 | 3.84 | 1199.10 | 2.57 | 1192.19 | 3.13 |
| Xiang Jia-ba | 578.36 | 638.37 | 626.87 | 1.80 | 635.68 | 0.42 | 626.93 | 1.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zhou, J.; Qiu, H.; Li, J.; Zhang, Q. Operation Rule Derivation of Hydropower Reservoirs by Support Vector Machine Based on Grey Relational Analysis. Water 2021, 13, 2518. https://doi.org/10.3390/w13182518
Zhu Y, Zhou J, Qiu H, Li J, Zhang Q. Operation Rule Derivation of Hydropower Reservoirs by Support Vector Machine Based on Grey Relational Analysis. Water. 2021; 13(18):2518. https://doi.org/10.3390/w13182518
Chicago/Turabian StyleZhu, Yuxin, Jianzhong Zhou, Hongya Qiu, Juncong Li, and Qianyi Zhang. 2021. "Operation Rule Derivation of Hydropower Reservoirs by Support Vector Machine Based on Grey Relational Analysis" Water 13, no. 18: 2518. https://doi.org/10.3390/w13182518





