Simulating Rainfall Interception by Caatinga Vegetation Using the Gash Model Parametrized on Daily and Seasonal Bases
Abstract
1. Introduction
2. Materials and Methods
2.1. Meteorological and Rainfall Measurements
2.2. Sparse Gash Model Parametrized on Daily and Seasonal Bases
2.3. Estimation of Meteorological and Canopy Parameters
2.4. Validation Analysis
2.5. Statistical and Sensitivity Analyses
3. Results
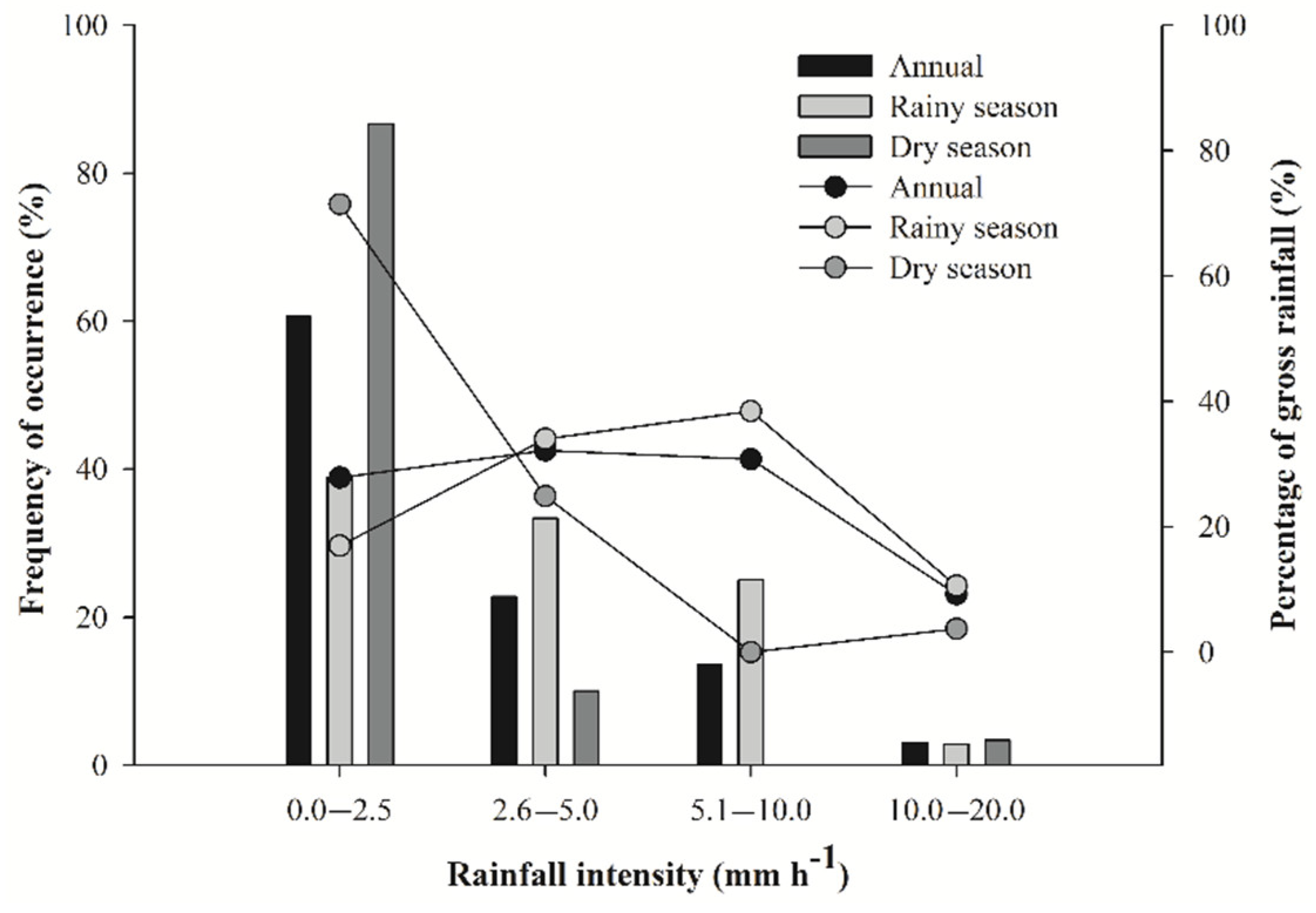
3.1. Rainfall Partitioning
3.2. Model Parameters
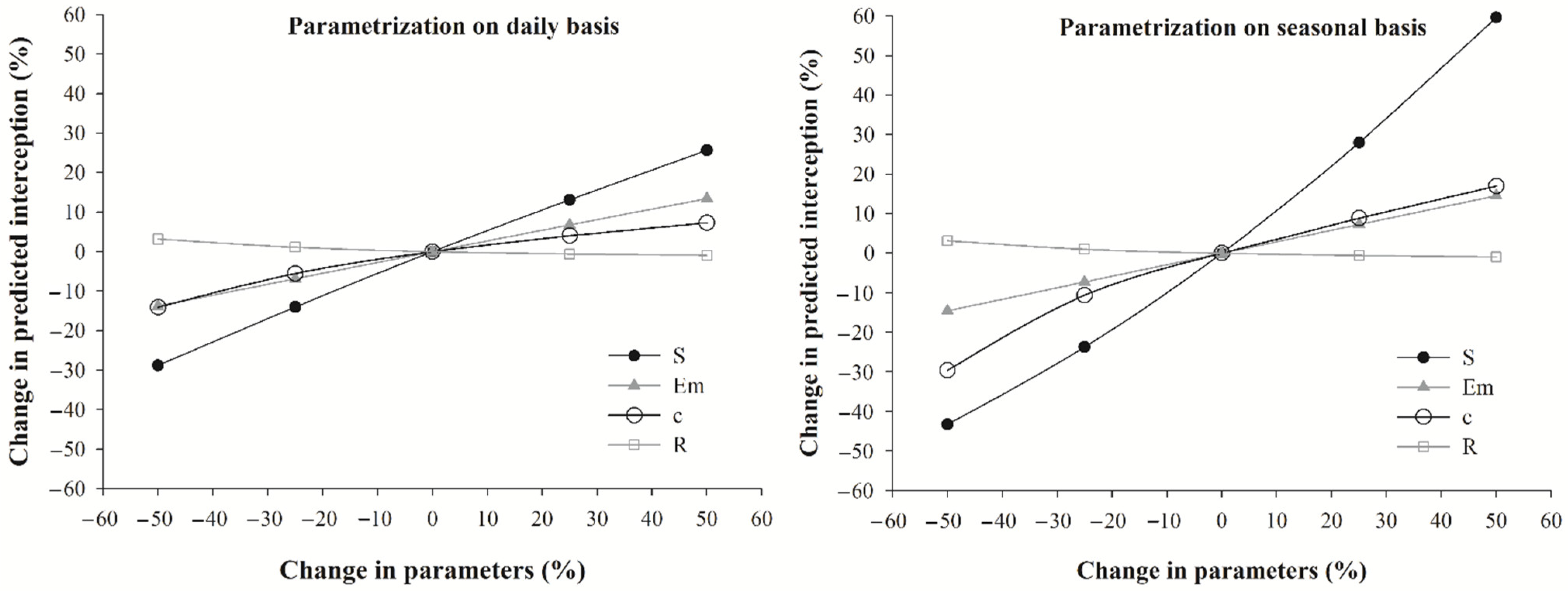
3.3. Sensitivity Analyses
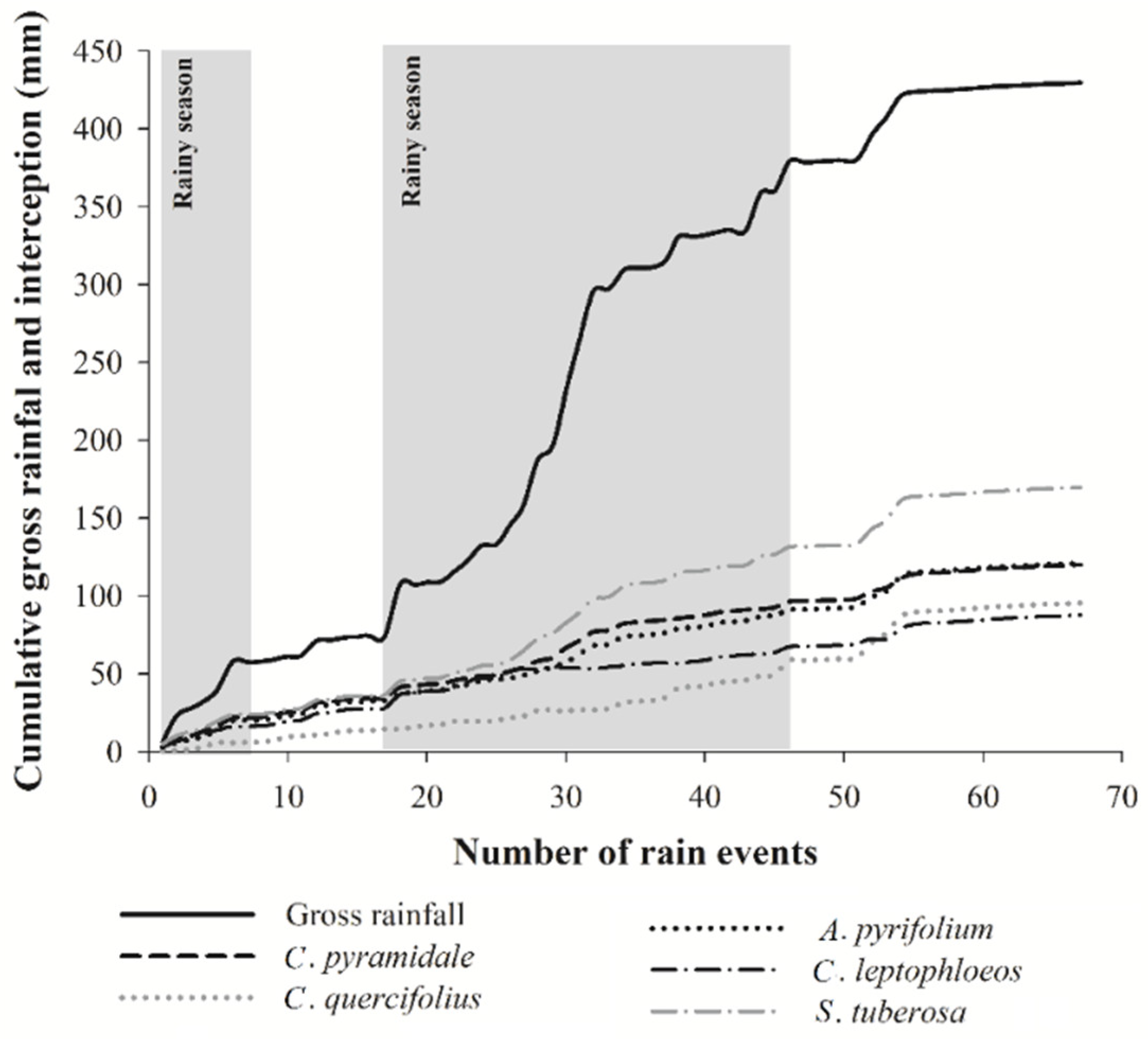
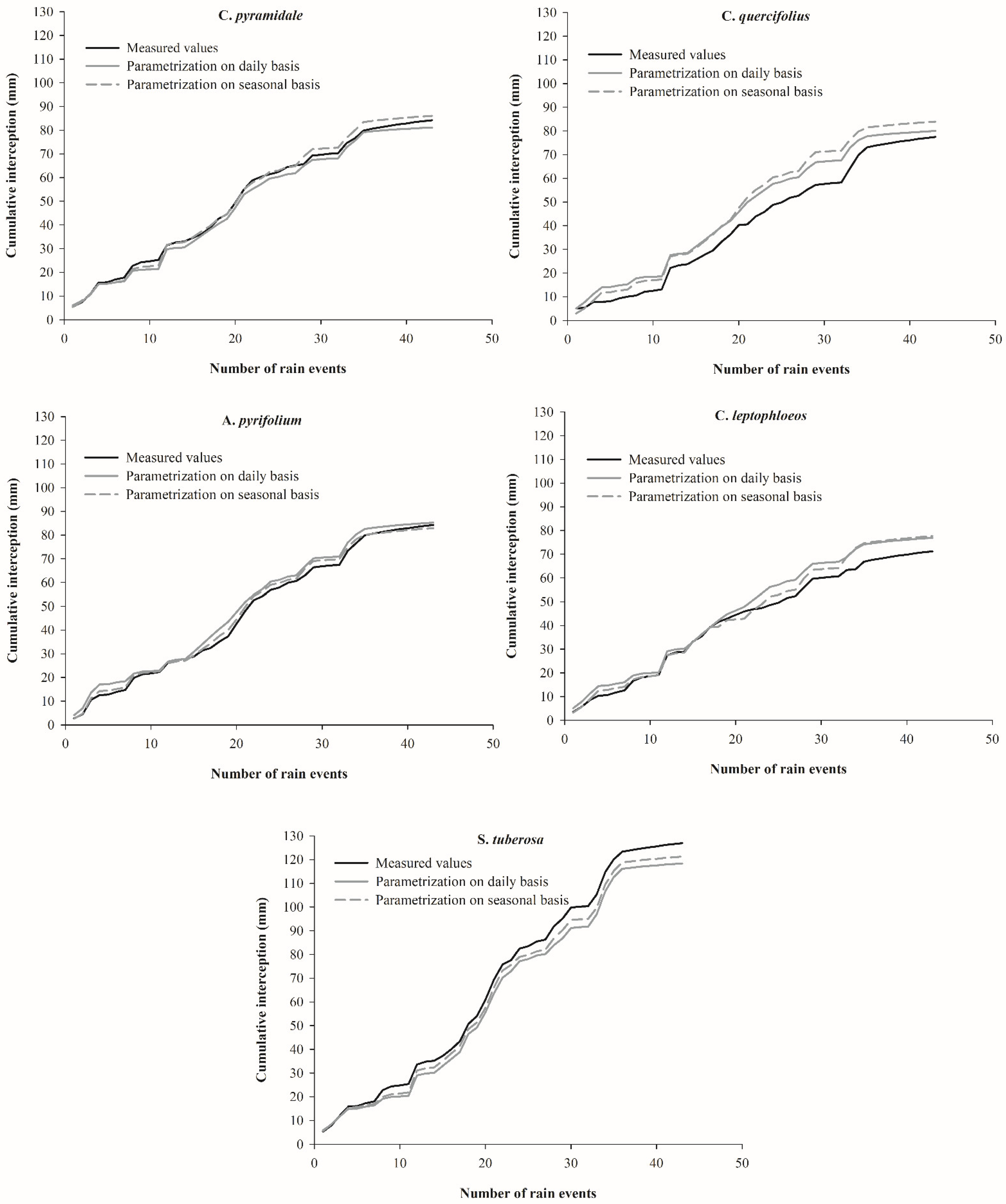
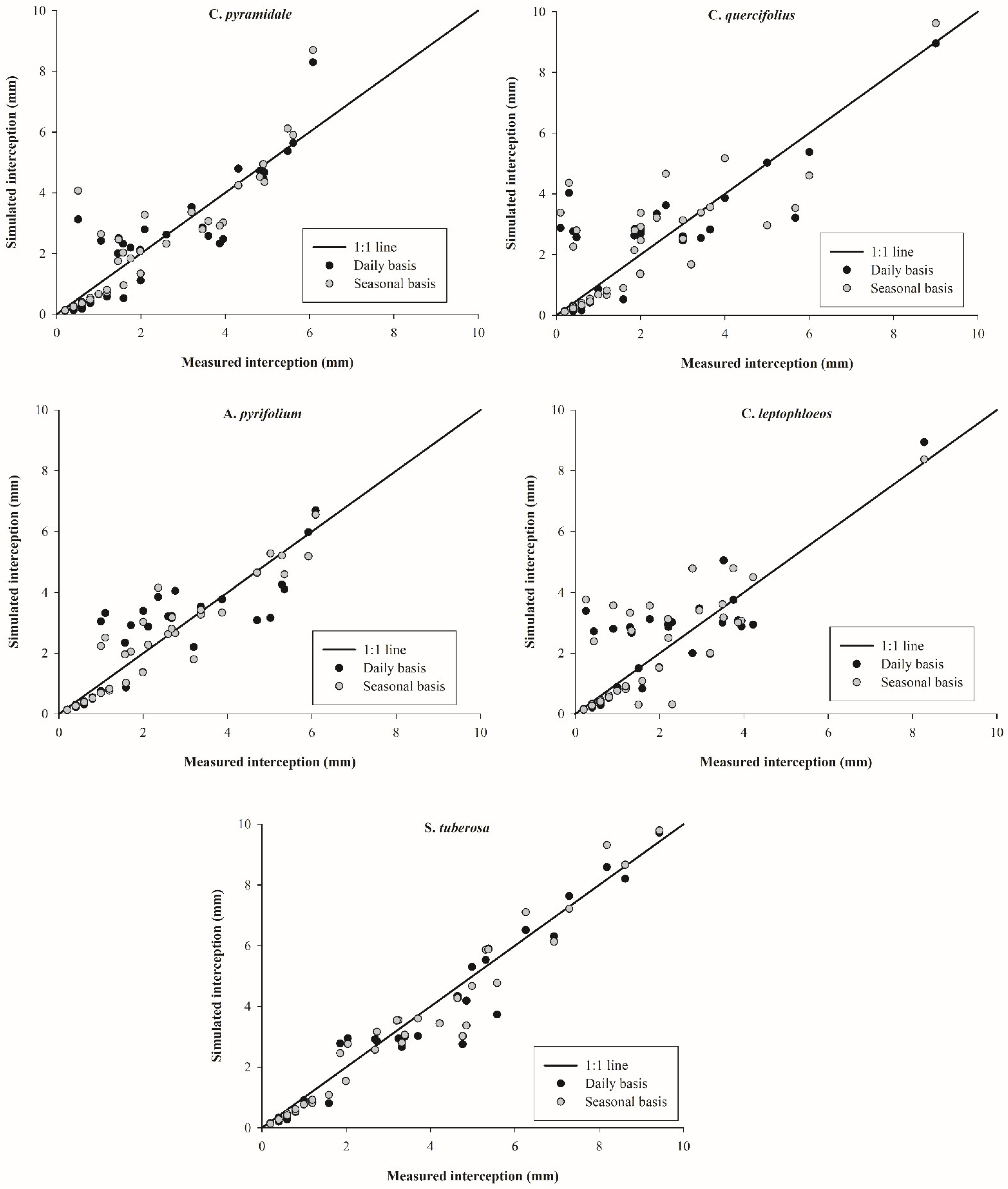
3.4. Rainfall Interception Simulations
4. Discussion
4.1. Rainfall Partitioning
4.2. Model Parameters
4.3. Rainfall Interception Simulations
4.4. Limitations and Constraints
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Brasil, J.B.; Andrade, E.M.; Queiroz Palácio, H.A.; Medeiros, P.H.A.; Santos, J.C.N. Characteristics of precipitation and the process of interception in a seasonally dry tropical forest. J. Hydrol. 2018, 19, 307–317. [Google Scholar] [CrossRef]
- Hassan, S.M.T.; Ghimire, C.P.; Lubczynski, M.W. Remote sensing upscaling of interception loss from isolated oaks: Sardon catchment case study, Spain. J. Hydrol. 2017, 555, 489–505. [Google Scholar] [CrossRef]
- Pypker, T.G.; Tarasoff, C.S.; Koh, H.S. Assessing the efficacy of two in direct methods for quantifying canopy variables associated with interception loss of rainfall in temperate hardwood forests. Open J. Mod. Hydrol. 2012, 2, 29–40. [Google Scholar] [CrossRef]
- Rutter, A.J.; Morton, A.J.; Robins, P.C. A predictive model of rainfall interception in forests. II. Generalization of the model and comparison with observations in some coniferous and hardwoods stands. J. Appl. Ecol. 1975, 12, 367–380. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, Y.; Xu, L.; Xiong, W.; Yu, P.; Gao, J.; Zhang, L. Fraction of incident rainfall within the canopy of a pure stand of Pinus armandii with revised Gash model in the Liupan Mountains of China. J. Hydrol. 2010, 385, 44–50. [Google Scholar] [CrossRef]
- Calder, I.R. A stochastic model of rainfall interception. J. Hydrol. 1986, 89, 65–71. [Google Scholar] [CrossRef]
- Link, T.E.; Unsworth, M.; Marks, D. The dynamics of rainfall interception by a seasonal temperate rainforest. Agric. For. Meteorol. 2004, 124, 171–191. [Google Scholar] [CrossRef]
- Fathizadeh, O.; Hosseini, S.M.; Keim, R.F.; Boloorani, A.D. A seasonal evaluation of the reformulated Gash interception model for semiarid deciduous oak forest stands. For. Ecol. Manag. 2018, 409, 601–613. [Google Scholar] [CrossRef]
- Gash, J.H.C.; Lloyd, C.R.; Lachaud, G. Estimating sparse forest rainfall interception with an analytical model. J. Hydrol. 1995, 170, 79–86. [Google Scholar] [CrossRef]
- Steidle Neto, A.J.; Ribeiro, A.; Lopes, D.C.; Sacramento Neto, O.B.; Souza, W.G.; Santana, M.O. Simulation of rainfall interception of canopy and litter in Eucalyptus plantation in tropical climate. For. Sci. 2012, 58, 54–60. [Google Scholar] [CrossRef]
- Su, L.; Zhao, C.; Xu, W.; Xie, Z. Modelling interception loss using the revised Gash model: A case study in a mixed evergreen and deciduous broadleaved forest in China. Ecohydrology 2016, 9, 1580–1589. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Bruijnzeel, L.A. Modelling rainfall interception by vegetation of variable density using an adapted analytical model. Part 1. Model description. J. Hydrol. 2001, 247, 230–238. [Google Scholar] [CrossRef]
- Lopes, D.C.; Steidle Neto, A.J.; Queiroz, M.G.; Souza, L.S.B.; Zolnier, S.; Silva, T.G.F. Sparse Gash model applied to seasonal dry tropical forest. J. Hydrol. 2020, 590, 125497. [Google Scholar] [CrossRef]
- Medeiros, P.H.A.; Araujo, J.C.; Bronstert, A. Interception measurements and assessment of Gash model performance for a tropical semiarid region. Rev. Ciênc. Agron. 2009, 40, 165–174. [Google Scholar] [CrossRef]
- Silva, A.C.F.; Souto, J.S.; Santana, J.A.S.; Souto, P.C.; Nascimento, J.A.M. Distribution of rainwater by species of caatinga vegetation. Afr. J. Agric. Res. 2018, 13, 2239–2248. [Google Scholar] [CrossRef]
- Queiroz, M.G.; Silva, T.G.F.; Zolnier, S.; Souza, C.A.A.; Souza, L.S.B.; Araújo, G.N.; Jardim, A.M.R.F.; Moura, M.S.B. Partitioning of rainfall in a seasonal dry tropical forest. Ecohydrol. Hydrobiol. 2020, 20, 230–242. [Google Scholar] [CrossRef]
- Machado, I.C.S.; Barros, L.M.; Sampaio, E.V.S.B. Phenology of Caatinga species at Serra Talhada, PE, Northeastern Brazil. Biotropica 1997, 29, 57–68. [Google Scholar] [CrossRef]
- Vieira, R.D.S.P.; Tomasella, J.; Alvalá, R.C.S.; Sestini, M.F.; Affonso, A.G.; Rodriguez, D.A.; Barbosa, A.A.; Cunha, A.P.M.A.; Valles, G.F.; Crepani, E.; et al. Identifying areas susceptible to desertification in the Brazilian northeast. Solid Earth 2015, 6, 347–360. [Google Scholar] [CrossRef]
- Queiroz, M.G.; Silva, T.G.F.; Zolnier, S.; Souza, C.A.A.; Souza, L.S.B.; Steidle Neto, A.J.; Araújo, G.G.L.; Ferreira, W.P.M. Seasonal patterns of deposition litterfall in a seasonal dry tropical forest. Agric. For. Meteorol. 2019, 279, 107712. [Google Scholar] [CrossRef]
- Gash, J.H.C. An analytical model of rainfall interception by forests. Q. J. R. Meteorol. Soc. 1979, 105, 43–55. [Google Scholar] [CrossRef]
- Muzylo, A.; Llorens, P.; Valente, F.; Keizer, J.J.; Domingo, F.; Gash, J.H.C. A review of rainfall interception modelling. J. Hydrol. 2009, 350, 191–206. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Li, X.Y.; Jiang, Z.Y.; Li, D.Q.; Lin, H. Modelling of rainfall partitioning by a deciduous shrub using a variable parameters Gash model. Ecohydrology 2018, 11, e2011. [Google Scholar] [CrossRef]
- Sadeghi, S.M.M.; Attarod, P.; Van Stan II, J.T.; Pypker, T.G.; Dunkerley, D. Efficiency of the reformulated Gash’s interception model in semiarid afforestations. Agric. For. Meteorol. 2015, 201, 76–85. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; Luo, Y.; Shao, M.; Jia, X. The modelling of rainfall interception in growing and dormant seasons for a pine plantation and a black locust plantation in semi-arid Northwest China. J. Hydrol. 2019, 577, 123849. [Google Scholar] [CrossRef]
- Lima, A.L.A.; Rodal, M.J.N. Phenology and wood density of plants growing in the semi-arid region of northeastern Brazil. J. Arid Environ. 2010, 74, 1363–1373. [Google Scholar] [CrossRef]
- Lins Neto, E.M.F.; Almeida, A.L.S.; Peroni, N.; Castro, C.C.; Albuquerque, U.P. Phenology of Spondias tuberosa Arruda (Anacardiaceae) under different landscape management regimes and a proposal for a rapid phenological diagnosis using local knowledge. J. Ethnobiol. Ethnomed. 2013, 9, 10. [Google Scholar] [CrossRef]
- Moura, V.G.M. Sazonalidade Fenológica e Aspectos Funcionais de Espécies Lenhosas da Caatinga: Acompanhamento com Camera Hemisférica e in Loco. Master’s Thesis, Universidade Federal Rural de Pernambuco, Recife, Brazil, 2018. [Google Scholar]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; Gonçalves, J.L.M.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Norman, J.M.; Jarvis, P.G. Photosynthesis in Sitka Spruce (Picea Sitchensis (Bong.) Carr.). III. Measurements of Canopy Structure and Interception of Radiation. J. Appl. Ecol. 1974, 11, 375–398. [Google Scholar] [CrossRef]
- Pokovai, K.; Fodor, N. Adjusting Ceptometer Data to Improve Leaf Area Index Measurements. Agronomy 2019, 9, 866. [Google Scholar] [CrossRef]
- Bryant, M.L.; Bhat, S.; Jacobs, J.M. Measurements and modeling of throughfall variability for five forest communities in the southeastern US. J. Hydrol. 2005, 312, 95–108. [Google Scholar] [CrossRef]
- Lloyd, C.R.; Gash, J.H.C.; Shuttleworth, W.J. The measurement and modelling of rainfall interception by Amazonian rain forest. Agric. For. Meteorol. 1998, 43, 277–294. [Google Scholar] [CrossRef]
- Pereira, F.L.; Gash, J.H.C.; David, J.S.; David, T.S.; Monteiro, P.R.; Valente, F. Modelling interception loss from evergreen oak Mediterranean savannas: Application of a tree-based modelling approach. Agric. For. Meteorol. 2009, 149, 680–688. [Google Scholar] [CrossRef]
- Bäse, F.; Elsenbeer, H.; Neill, C.; Krusche, A.V. Differences in throughfall and net precipitation between soybean and transitional tropical forest in the southern Amazon, Brazil. Agric. Ecosyst. Environ. 2012, 159, 19–28. [Google Scholar] [CrossRef]
- Levia, D.F.; Frost, E.E. A review and evaluation of stemflow literature in the hydrologic and biogeochemical cycles of forested and agricultural ecosystems. J. Hydrol. 2003, 274, 1–29. [Google Scholar] [CrossRef]
- He, Z.-B.; Yang, J.J.; Du, J.; Zhao, W.-Z.; Liu, H.; Chang, X.X. Spatial variability of canopy interception in a spruce forest of the semiarid mountain regions of China. Agric. For. Meteorol. 2014, 188, 58–63. [Google Scholar] [CrossRef]
- Murakami, S. Application of three canopy interception models to a young stand of Japanese cypress and interpretation in terms of interception mechanism. J. Hydrol. 2007, 342, 305–319. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- Valente, F.; David, J.S.; Gash, J.H.C. Modelling interception loss for two sparse eucalypt and pine forests in central Portugal using reformulated Rutter and Gash analytical models. J. Hydrol. 1997, 190, 141–162. [Google Scholar] [CrossRef]
- Oyarzún, R.; Stöckle, C.; Wu, J.; Whiting, M. In field assessment on the relationship between photosynthetic active radiation (PAR) and global solar radiation transmittance through discontinuous canopies. Chil. J. Agric. Res. 2011, 71, 122–131. [Google Scholar] [CrossRef][Green Version]
- Cuartas, L.A.; Tomasella, J.; Nobre, A.D.; Hodnett, M.G.; Waterloo, M.J.; Múnera, J.C. Interception water-partitioning dynamics for a pristine rainforest in Central Amazonia: Marked differences between normal and dry years. Agric. For. Meteorol. 2007, 145, 69–83. [Google Scholar] [CrossRef]
- Motahari, M.; Attarod, P.; Pypker, T.G.; Etemad, V.; Shirvany, A. Rainfall interception in a Pinus eldarica plantation in a semiarid climate zone: An application of the Gash model. J. Agric. Sci. Technol. 2013, 15, 981–994. [Google Scholar]
- Véliz-Chávez, C.; Mastachi-Loza, C.A.; González-Sosa, E.; Becerril-Piña, R.; Ramos-Salinas, N.M. Canopy storage implications on interception loss modelling. Am. J. Plant Sci. 2014, 5, 3032–3048. [Google Scholar] [CrossRef]
- Klaasen, W.; Bosveld, F.; Water, E. Water storage and evaporation as constituents of rainfall interception. J. Hydrol. 1998, 212–213, 36–50. [Google Scholar] [CrossRef]
- Lopes, D.C.; Steidle Neto, A.J.; Vasco Júnior, R. Comparison of equilibrium models for grain aeration. J. Stored Prod. Res. 2015, 60, 11–18. [Google Scholar] [CrossRef]
- Návar, J. Fitting rainfall interception models to forest ecosystems of Mexico. J. Hydrol. 2017, 548, 458–470. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Ferreira, D.F. Sisvar: A computer statistical analysis system. Ciên. Agrotecnol. 2011, 35, 1039–1042. [Google Scholar] [CrossRef]
- Jackson, N.A. Measured and modelled rainfall interception loss from an agroforestry system in Kenya. Agric. For. Meteorol. 2000, 100, 323–336. [Google Scholar] [CrossRef]
- Amorim, I.L.D.; Sampaio, E.V.D.S.B.; Araújo, E.D.L. Phenology of woody species in the Caatinga of Seridó, RN, Brazil. Rev. Árvore 2009, 33, 491–499. [Google Scholar] [CrossRef]
- Jiao, L.; Lu, N.; Sun, G.; Ward, E.J.; Fu, B. Biophysical controls on canopy transpiration in a black locust (Robinia pseudoacacia) plantation on the semi-arid Loess Plateau, China. Ecohydrology 2016, 9, 1068–1081. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Tian, A.; Liu, Y.; Ashley, A.W.; Wang, Y.; Zuo, H.; Pengtao, Y.; Xiong, W.; Xu, L. Characteristics of canopy interception and its simulation with a revised Gash model for a larch plantation in the Liupan Mountains, China. J. For. Res. 2018, 29, 187–198. [Google Scholar] [CrossRef]
- Santos, J.C.N.; Andrade, E.M.; Medeiros, P.H.A.; Guerreiro, M.J.S.; Palácio, H.A.Q. Effect of Rainfall Characteristics on Runoff and Water Erosion for Different Land Uses in a Tropical Semiarid Region. Water Resour. Manag. 2017, 31, 173–185. [Google Scholar] [CrossRef]
- Linhoss, A.C.; Siegert, C.M. A comparison of five forest interception models using global sensitivity and uncertainty analysis. J. Hydrol. 2016, 538, 109–116. [Google Scholar] [CrossRef]
- Sun, X.; Onda, Y.; Kato, H. Incident rainfall partitioning and canopy interception modelling for an abandoned Japanese cypress stand. J. For. Res. 2014, 19, 317–328. [Google Scholar] [CrossRef]
| Scientific Name | DBH (m) | NS (-) | H (m) | CPA (m2) | N (-) |
|---|---|---|---|---|---|
| C. pyramidale | 0.08 | 3 | 4.9 | 19.4 | 415 |
| C. quercifolius | 0.13 | 2 | 6.5 | 33.7 | 35 |
| A. pyrifolium | 0.07 | 3 | 4.1 | 12.5 | 280 |
| C. leptophloeos | 0.15 | 1 | 5.5 | 64.7 | 10 |
| S. tuberosa | 0.21 | 5 | 4.9 | 99.9 | 10 |
| Interception Component | Seasonal Basis | Daily Basis |
|---|---|---|
| For m storms insufficient to saturate the canopy (PG ≤ PS) | ||
| Evaporation from the whole canopy (IC) | cy PGi | ci PGi |
| For n storms sufficient to saturate the canopy (PG > PS) | ||
| Wetting up of canopy (IW) | n cy (PSy − Scy) | ci (PSi − Sci) |
| Wet canopy evaporation during storms (IS) | (PGi − PSy) | (PGi − PSi) |
| Evaporation after storms cease (IA) | n cy Scy | ci Sci |
| Classes (mm) | |||||
|---|---|---|---|---|---|
| 0.0–5.0 | 5.1–10.0 | 10.1–20.0 | 20.1–30.0 | 30.1–40.0 | |
| Annual Analysis | |||||
| NE (-) | 43 (65.2%) | 7 (10.6%) | 10 (15.2%) | 2 (3.0%) | 4 (6.1%) |
| CGR (mm) | 46.0 | 53.9 | 144.9 | 52.2 | 132.5 |
| PGR (%) | 10.7 | 12.6 | 33.7 | 12.1 | 30.9 |
| Rainy Season | |||||
| NE (-) | 18 (50.0%) | 6 (16.7%) | 6 (16.7%) | 2 (5.6%) | 4 (11.1%) |
| CGR (mm) | 27.3 | 45.0 | 86.8 | 52.2 | 132.5 |
| PGR (%) | 7.9 | 13.1 | 25.3 | 15.2 | 38.6 |
| Dry Season | |||||
| NE (-) | 25 (83.3%) | 1 (3.3%) | 4 (13.3%) | 0 (0.0%) | 0 (0.0%) |
| CGR (mm) | 18.7 | 9.0 | 58.1 | 0.0 | 0.0 |
| PGR (%) | 21.8 | 10.5 | 67.7 | 0.0 | 0.0 |
| Classes (mm) | |||||
|---|---|---|---|---|---|
| 0.0–5.0 | 5.1–10.0 | 10.1–20.0 | 20.1–30.0 | 30.1–40.0 | |
| Annual Analysis (I:GR—%) | |||||
| C. pyramidale | 82.1 | 34.4 | 25.0 | 8.6 | 17.3 |
| C. quercifolius | 78.1 | 11.3 | 32.7 | 12.0 | 1.1 |
| A. pyrifolium | 80.5 | 37.0 | 28.2 | 9.7 | 13.7 |
| C. leptophloeos | 80.2 | 35.7 | 17.0 | 1.3 | 6.9 |
| S. tuberosa | 87.0 | 46.2 | 42.3 | 24.7 | 23.1 |
| Rainy Season (I:GR—%) | |||||
| C. pyramidale | 41.4 | 25.3 | 14.1 | 8.6 | 17.3 |
| C. quercifolius | 37.4 | 10.4 | 9.0 | 12.0 | 1.1 |
| A. pyrifolium | 39.8 | 27.7 | 13.2 | 9.7 | 13.7 |
| C. leptophloeos | 39.8 | 28.4 | 8.1 | 1.3 | 6.9 |
| S. tuberosa | 46.3 | 37.4 | 20.5 | 24.7 | 23.1 |
| Dry Season (I:GR—%) | |||||
| C. pyramidale | 40.7 | 9.1 | 10.9 | 0.0 | 0.0 |
| C. quercifolius | 40.7 | 1.0 | 23.7 | 0.0 | 0.0 |
| A. pyrifolium | 40.7 | 9.3 | 15.1 | 0.0 | 0.0 |
| C. leptophloeos | 40.7 | 7.3 | 8.9 | 0.0 | 0.0 |
| S. tuberosa | 40.7 | 8.8 | 21.8 | 0.0 | 0.0 |
| Vegetation | Sc (mm) | L (mm2 mm−2) | Ec/R (-) | Em (mm h−1) | c (-) | PS (mm) |
|---|---|---|---|---|---|---|
| Daily Basis | ||||||
| C. pyramidale | 2.3–3.4 | 0.4–1.6 | 0.04–0.83 | 0.20–0.85 | 0.29–0.72 | 2.8–5.4 |
| C. quercifolius | 1.7–4.4 | 0.5–4.0 | 0.04–0.79 | 0.21–0.94 | 0.27–0.94 | 2.3–4.9 |
| A. pyrifolium | 2.8–4.0 | 0.9–2.0 | 0.03–0.79 | 0.19–0.80 | 0.52–0.80 | 3.3–4.6 |
| C. leptophloeos | 1.9–4.4 | 0.9–4.0 | 0.03–0.86 | 0.20–0.89 | 0.48–0.95 | 2.2–4.8 |
| S. tuberosa | 1.8–4.8 | 0.8–7.0 | 0.03–0.83 | 0.20–0.85 | 0.46–0.97 | 2.1–5.0 |
| Seasonal Basis (Rainy Season) | ||||||
| C. pyramidale | 2.30 (±0.2) | 1.04 (±0.3) | 0.16 (±0.2) | 0.40 (±0.11) | 0.67 (±0.1) | 2.50 |
| C. quercifolius | 2.85 (±0.6) | 1.82 (±0.7) | 0.17 (±0.2) | 0.44 (±0.12) | 0.68 (±0.2) | 3.13 |
| A. pyrifolium | 2.58 (±0.3) | 1.44 (±0.2) | 0.15 (±0.2) | 0.38 (±0.10) | 0.69 (±0.1) | 2.79 |
| C. leptophloeos | 2.89 (±0.5) | 2.02 (±0.6) | 0.14 (±0.1) | 0.42 (±0.12) | 0.76 (±0.10) | 3.12 |
| S. tuberosa | 2.97 (±0.6) | 2.22 (±0.8) | 0.14 (±0.2) | 0.40 (±0.12) | 0.77 (±0.12) | 3.19 |
| Seasonal Basis (Dry Season) | ||||||
| C. pyramidale | 2.10 (±0.2) | 0.85 (±0.3) | 0.27 (±0.2) | 0.38 (±0.16) | 0.60 (±0.1) | 2.45 |
| C. quercifolius | 2.49 (±0.4) | 1.30 (±0.6) | 0.31 (±0.2) | 0.42 (±0.18) | 0.56 (±0.2) | 2.98 |
| A. pyrifolium | 2.45 (±0.3) | 1.28 (±0.2) | 0.24 (±0.2) | 0.36 (±0.15) | 0.64 (±0.1) | 2.78 |
| C. leptophloeos | 2.55 (±0.4) | 1.59 (±0.5) | 0.25 (±0.1) | 0.40 (±0.17) | 0.68 (±0.1) | 2.93 |
| S. tuberosa | 2.56 (±0.4) | 1.69 (±0.6) | 0.24 (±0.2) | 0.38 (±0.15) | 0.68 (±0.1) | 2.92 |
| Vegetation | a (-) | b (-) | R2 (-) | MBE (mm) | d (-) | E (-) |
|---|---|---|---|---|---|---|
| Daily Basis | ||||||
| S. tuberosa | 0.99 | −0.19 | 0.96 | −0.20 | 0.99 | 0.95 |
| C. leptophloeos | 0.93 | 0.26 | 0.72 | 0.13 | 0.92 | 0.66 |
| A. pyrifolium | 0.90 | 0.22 | 0.77 | 0.02 | 0.94 | 0.75 |
| C. quercifolius | 0.82 | 0.39 | 0.69 | 0.06 | 0.91 | 0.66 |
| C. pyramidale | 1.01 | −0.10 | 0.83 | −0.07 | 0.97 | 0.79 |
| Seasonal Basis | ||||||
| S. tuberosa | 1.02 | −0.20 | 0.96 | −0.13 | 0.99 | 0.96 |
| C. leptophloeos | 0.93 | 0.26 | 0.66 | 0.15 | 0.89 | 0.53 |
| A. pyrifolium | 0.98 | 0.01 | 0.90 | −0.03 | 0.97 | 0.89 |
| C. quercifolius | 0.82 | 0.46 | 0.65 | 0.15 | 0.90 | 0.59 |
| C. pyramidale | 1.03 | −0.02 | 0.82 | 0.04 | 0.95 | 0.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, D.C.; Steidle Neto, A.J.; Silva, T.G.F.; Souza, L.S.B.; Zolnier, S.; Souza, C.A.A. Simulating Rainfall Interception by Caatinga Vegetation Using the Gash Model Parametrized on Daily and Seasonal Bases. Water 2021, 13, 2494. https://doi.org/10.3390/w13182494
Lopes DC, Steidle Neto AJ, Silva TGF, Souza LSB, Zolnier S, Souza CAA. Simulating Rainfall Interception by Caatinga Vegetation Using the Gash Model Parametrized on Daily and Seasonal Bases. Water. 2021; 13(18):2494. https://doi.org/10.3390/w13182494
Chicago/Turabian StyleLopes, Daniela C., Antonio José Steidle Neto, Thieres G. F. Silva, Luciana S. B. Souza, Sérgio Zolnier, and Carlos A. A. Souza. 2021. "Simulating Rainfall Interception by Caatinga Vegetation Using the Gash Model Parametrized on Daily and Seasonal Bases" Water 13, no. 18: 2494. https://doi.org/10.3390/w13182494
APA StyleLopes, D. C., Steidle Neto, A. J., Silva, T. G. F., Souza, L. S. B., Zolnier, S., & Souza, C. A. A. (2021). Simulating Rainfall Interception by Caatinga Vegetation Using the Gash Model Parametrized on Daily and Seasonal Bases. Water, 13(18), 2494. https://doi.org/10.3390/w13182494