A Deterministic Topographic Wetland Index Based on LiDAR-Derived DEM for Delineating Open-Water Wetlands
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Methods for Existing Wetland Delineation
2.2.1. Normalized Difference Vegetation Index (NDVI)
2.2.2. Normalized Difference Water Index (NDWI)
2.2.3. Topographic Wetness Index (TWI)
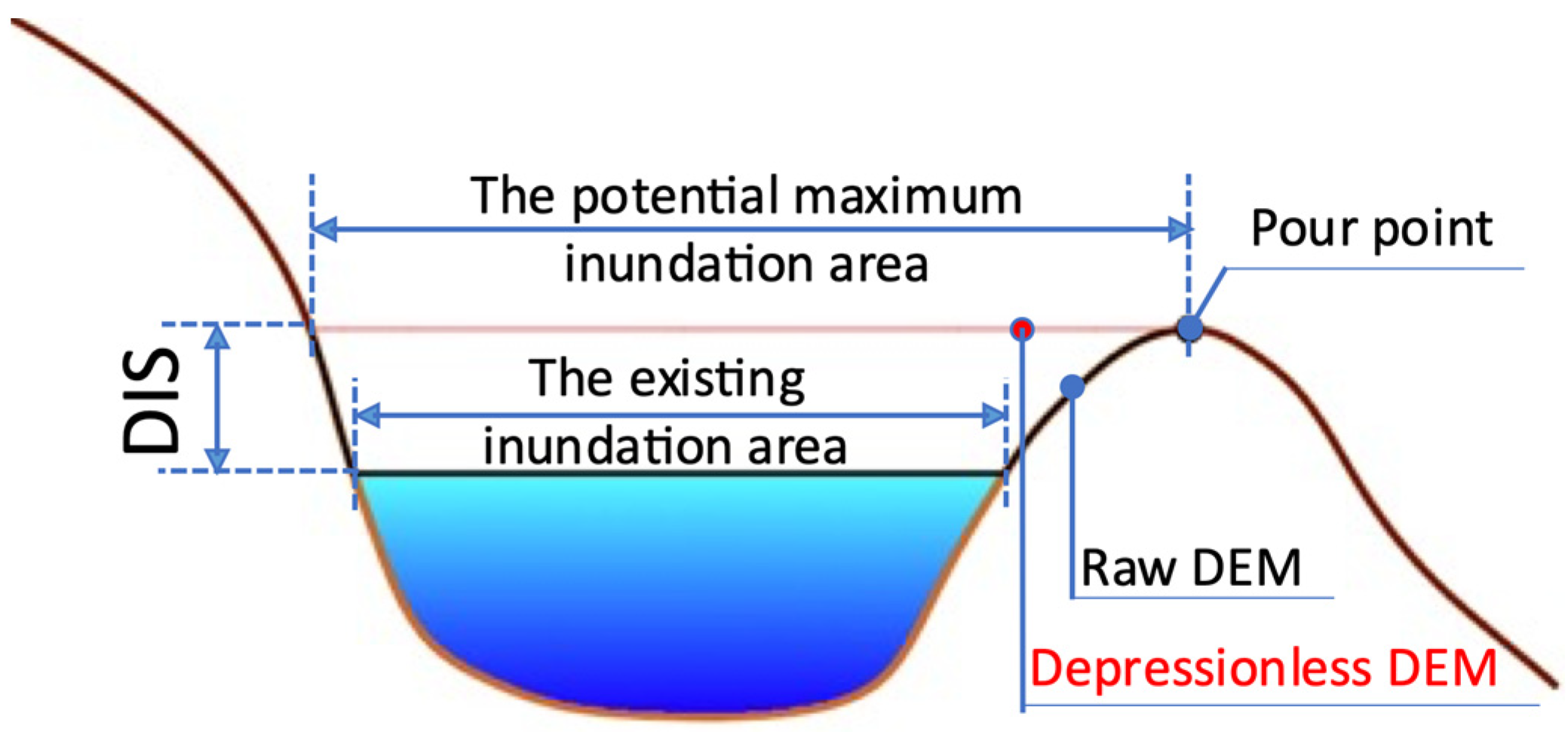
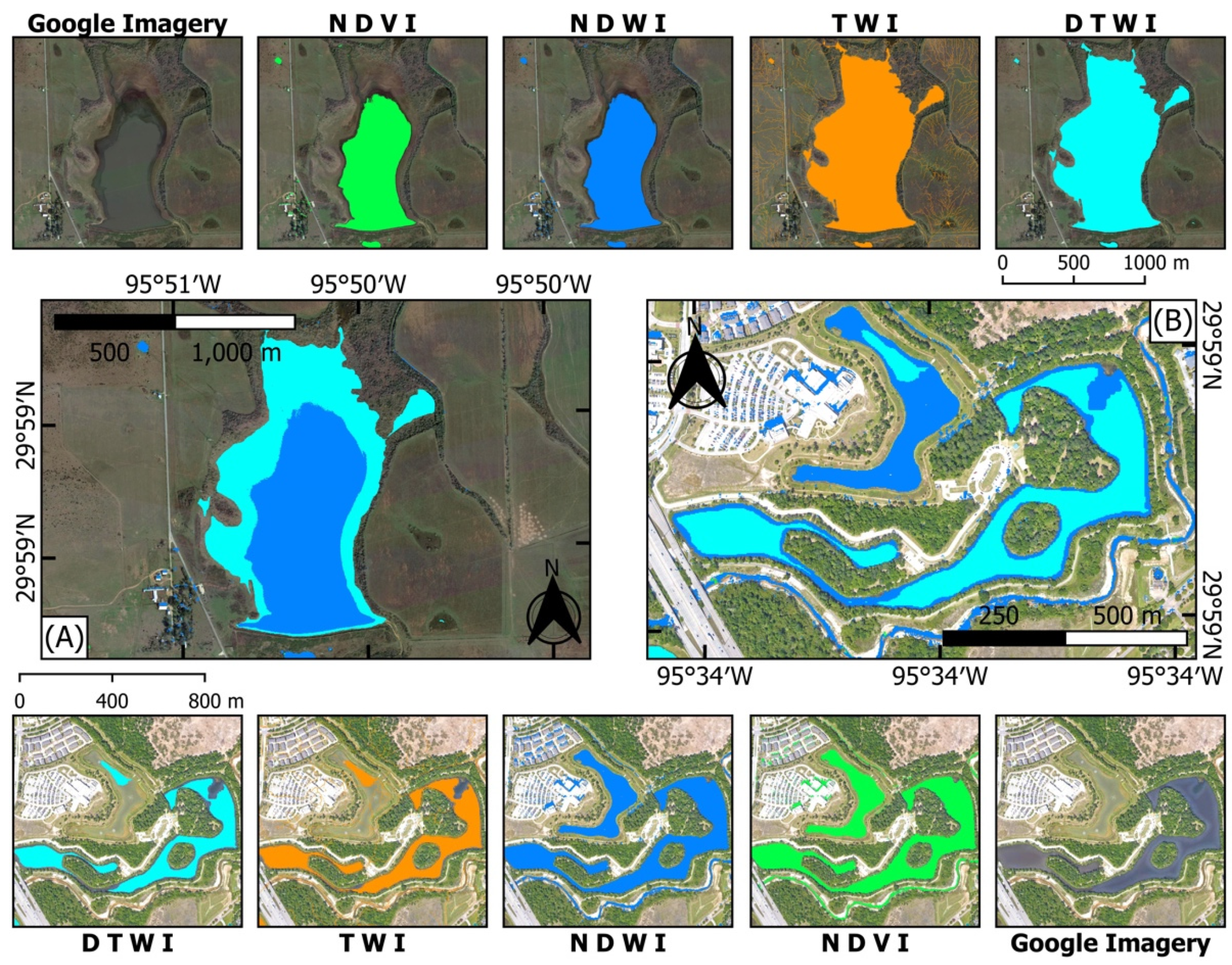
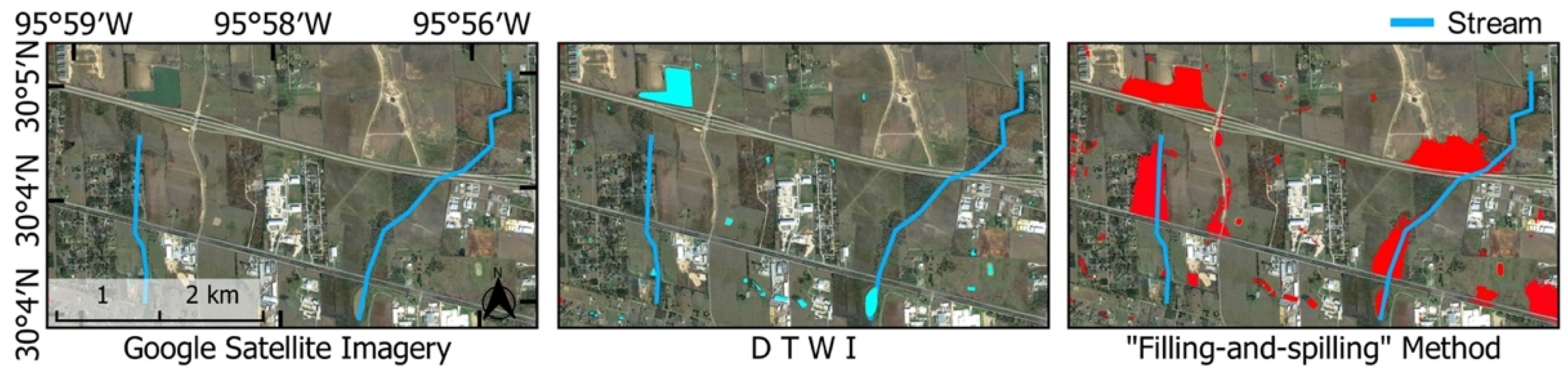
2.2.4. Deterministic Topographic Wetland Index (DTWI)
- The water surface in open-water wetlands tends to be in a horizontal plane as water velocity is extremely slow (standing water bodies).
- The local slope of the water surface () is 0 on the LiDAR-derived DEM. This is because LiDAR point clouds show voids in the areas where water bodies occur, and the missing elevation data can be interpolated from a single elevation value obtained from the land edge of the water body.
- The topography should have depression areas that allow water to be detained in the wetlands. Therefore, open-water wetlands should form where the DIS is greater than 0.
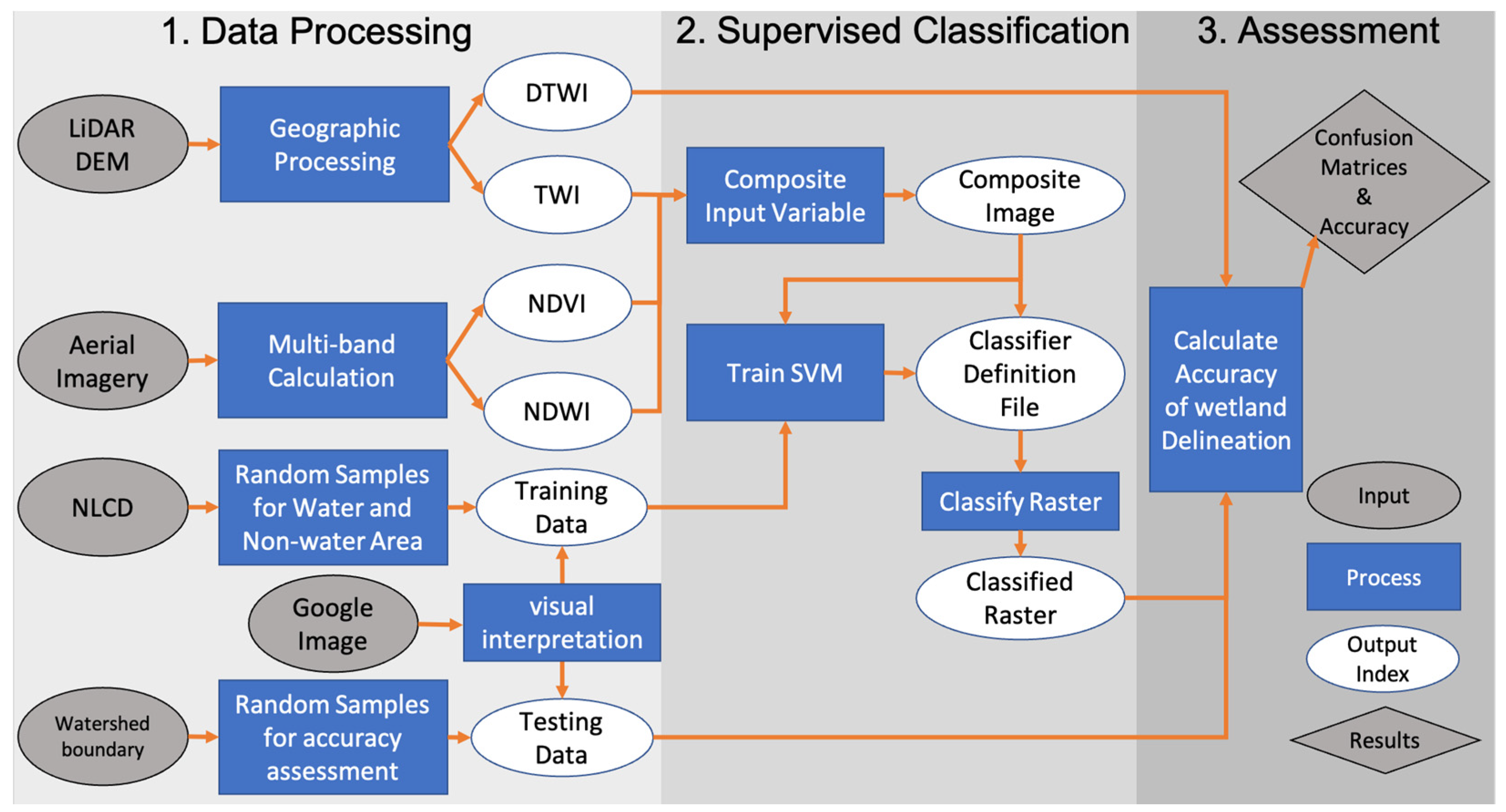
2.3. Input Datasets and Data Preprocessing
3. Results and Discussion
3.1. The Existing Wetland Delineation
3.2. The Accuracy Assessment
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lewis, J.; William, M. Wetlands Explained: Wetland Science, Policy, and Politics in America; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Bullock, A.; Acreman, M. The role of wetlands in the hydrological cycle. Hydrol. Earth Syst. Sci. 2003, 7, 358–389. [Google Scholar] [CrossRef] [Green Version]
- Fausold, C.J.; Lilieholm, R.J. The Economic Value of Open Space: A Review and Synthesis. Environ. Manag. 1999, 23, 307–320. [Google Scholar] [CrossRef]
- Godschalk, D.; Beatley, T.; Berke, P.; Brower, D.; Kaiser, E.J. Natural Hazard Mitigation: Recasting Disaster Policy and Planning; Island Press: Washington, DC, USA, 1998. [Google Scholar]
- Nivitzki, R. Effects of Lakes and Wetlands on Floodflows and Base Flows in Selected Northern and Eastern States. In Proceedings of the Conference Wetlands of the Chesapeake, Easton, MD, USA, 9–11 April 1985; pp. 143–154. [Google Scholar]
- Leon, A.S.; Tang, Y.; Qin, L.; Chen, D. A MATLAB framework for forecasting optimal flow releases in a multi-storage system for flood control. Environ. Model. Softw. 2020, 125, 104618. [Google Scholar] [CrossRef]
- Tang, Y.; Leon, A.S.; Kavvas, M.L. Impact of Size and Location of Wetlands on Watershed-Scale Flood Control. Water Resour. Manag. 2020, 34, 1693–1707. [Google Scholar] [CrossRef]
- Tang, Y.; Leon, A.S.; Kavvas, M.L. Impact of Dynamic Storage Management of Wetlands and Shallow Ponds on Watershed-scale Flood Control. Water Resour. Manag. 2020, 34, 1305–1318. [Google Scholar] [CrossRef]
- Sørensen, R.; Zinko, U.; Seibert, J. On the calculation of the topographic wetness index: Evaluation of different methods based on field observations. Hydrol. Earth Syst. Sci. 2006, 10, 101–112. [Google Scholar] [CrossRef] [Green Version]
- McKergow, L.A.; Gallant, J.C.; Dowling, T.I. Modelling Wetland Extent Using Terrain Indices, Lake Taupo, NZ. In Proceedings of the MODSIM07—Land, Water and Environmental Management: Integrated Systems for Sustainability, Proceedings, Christchurch, New Zealand, 10–13 December 2007; pp. 1335–1341. [Google Scholar]
- O’Neil, G.L.; Goodall, J.; Watson, L.T. Evaluating the potential for site-specific modification of LiDAR DEM derivatives to improve environmental planning-scale wetland identification using Random Forest classification. J. Hydrol. 2018, 559, 192–208. [Google Scholar] [CrossRef]
- Lidzhegu, Z.; Ellery, W.; Mantel, S.; Hughes, D. Delineating wetland areas from the cut-and-fill method using a Digital Elevation Model (DEM). S. Afr. Geogr. J. 2020, 102, 97–115. [Google Scholar] [CrossRef]
- Melesse, A.M.; Weng, Q.; Thenkabail, P.S.; Senay, G.B. Remote Sensing Sensors and Applications in Environmental Resources Mapping and Modelling. Sensors 2007, 7, 3209–3241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Y.; Dong, J.; Xiao, X.; Xiao, T.; Yang, Z.; Zhao, G.; Zou, Z.; Qin, Y. Open Surface Water Mapping Algorithms: A Comparison of Water-Related Spectral Indices and Sensors. Water 2017, 9, 256. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Granger, J.E.; Mohammadimanesh, F.; Salehi, B.; Brisco, B.; Homayouni, S.; Gill, E.; Huberty, B.; Lang, M. Meta-Analysis of Wetland Classification Using Remote Sensing: A Systematic Review of a 40-Year Trend in North America. Remote Sens. 2020, 12, 1882. [Google Scholar] [CrossRef]
- Wu, Q. GIS and Remote Sensing Applications in Wetland Mapping and Monitoring. Compr. Geogr. Inf. Syst. 2018, 3, 140–157. [Google Scholar] [CrossRef]
- Worstell, B.B.; Poppenga, S.K.; Evans, G.A.; Prince, S. Lidar Point Density Analysis: Implications for Identifying Water Bodies; US Geological Survey: Reston, VA, USA, 2014.
- Toscano, G.; Acharjee, P.; McCormick, C.; Devarajan, V. Water Surface Elevation Calculation Using LiDAR Data. In Proceedings of the ASPRS Conference, Tampa, FL, USA, 4–8 May 2015. [Google Scholar]
- Bochow, M.; Heim, B.; Küster, T.; Rogaß, C.; Bartsch, I.; Segl, K.; Reigber, S.; Kaufmann, H. On the use of airborne imaging spectroscopy data for the automatic detection and delineation of surface water bodies. In Remote Sensing of Planet Earth; InTech: London, UK, 2012; pp. 1–22. [Google Scholar]
- Jahncke, R.; Leblon, B.; Bush, P.; LaRocque, A. Mapping wetlands in Nova Scotia with multi-beam RADARSAT-2 Polarimetric SAR, optical satellite imagery, and Lidar data. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 139–156. [Google Scholar] [CrossRef]
- Ozesmi, S.L.; Bauer, M.E. Satellite remote sensing of wetlands. Wetl. Ecol. Manag. 2002, 10, 381–402. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Jenkins, D.G.; McCauley, L.A. GIS, SINKS, FILL, and Disappearing Wetlands: Unintended Consequences in Algorithm Development and Use. In Proceedings of the 2006 ACM Symposium on Applied Computing, Dijon, France, 23–27 April 2006; Association for Computing Machinery: New York, NY, USA, 2006; pp. 277–282. [Google Scholar]
- Wu, Q.; Lane, C.R.; Wang, L.; Vanderhoof, M.; Christensen, J.R.; Liu, H. Efficient Delineation of Nested Depression Hierarchy in Digital Elevation Models for Hydrological Analysis Using Level-Set Method. JAWRA J. Am. Water Resour. Assoc. 2019, 55, 354–368. [Google Scholar] [CrossRef]
- Chapelle, O.; Haffner, P.; Vapnik, V.N. Support vector machines for histogram-based image classification. IEEE Trans. Neural Netw. 1999, 10, 1055–1064. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Rokach, L.; Maimon, O. Top-Down Induction of Decision Trees Classifiers—A Survey. IEEE Trans. Syst. Man, Cybern. Part C Appl. Rev. 2005, 35, 476–487. [Google Scholar] [CrossRef] [Green Version]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef] [Green Version]
- Thapa, A.; Bradford, L.; Strickert, G.; Yu, X.; Johnston, A.; Watson-Daniels, K. “Garbage in, Garbage Out” Does Not Hold True for Indigenous Community Flood Extent Modeling in the Prairie Pothole Region. Water 2019, 11, 2486. [Google Scholar] [CrossRef] [Green Version]
- Teague, A. Development of a Distributed Water Quality Model Using Advanced Hydrologic Simulation. Ph.D. Thesis, Rice University, Houston, TX, USA, August 2011. [Google Scholar]
- Leon, A.S.; Verma, V. Towards Smart and Green Flood Control: Remote and Optimal Operation of Control Structures in a Network of Storage Systems for Mitigating Floods. In Proceedings of the World Environmental and Water Resources Congress 2019, Pittsburgh, PA, USA, 19–23 May 2019; pp. 177–189. [Google Scholar]
- Wu, Q.; Lane, C.R. Delineation and Quantification of Wetland Depressions in the Prairie Pothole Region of North Dakota. Wetlands 2016, 36, 215–227. [Google Scholar] [CrossRef]
- Gleason, R.A.; Tangen, B.A.; Laubhan, M.K.; Kermes, K.E.; Euliss, N.H., Jr. Estimating Water Storage Capacity of Existing and Potentially Restorable Wetland Depressions in a Subbasin of the Red River of the North; USGS Northern Prairie Wildlife Research Center: Jamestown, ND, USA, 2007; p. 89.
- Golden, H.E.; Lane, C.; Amatya, D.M.; Bandilla, K.W.; Kiperwas, H.R.; Knightes, C.D.; Ssegane, H. Hydrologic connectivity between geographically isolated wetlands and surface water systems: A review of select modeling methods. Environ. Model. Softw. 2014, 53, 190–206. [Google Scholar] [CrossRef]
- Verma, V.; Bian, L.; Rojali, A.; Ozecik, D.; Leon, A. A Remotely Controlled Framework for Gravity-Driven Water Release in Shallow and Not Shallow Storage Ponds. In Proceedings of the World Environmental and Water Resources Congress 2020, Henderson, NV, USA, 17–21 May 2020; American Society of Civil Engineers (ASCE): Reston, VG, USA, 2020; pp. 12–22. [Google Scholar]
- Qin, L.; Leon, A.S.; Bian, L.-L.; Dong, L.-L.; Verma, V.; Yolcu, A. A Remotely-Operated Siphon System for Water Release from Wetlands and Shallow Ponds. IEEE Access 2019, 7, 157680–157687. [Google Scholar] [CrossRef]
- Narumalani, S.; Jensen, J.R.; Burkhalter, S.; Althausen, J.D.; Mackey, H.E., Jr. Aquatic Macrophyte Modeling Using GIS and Logistic Multiple Regression. Photogramm. Eng. Remote Sens. 1997, 63, 41–49. [Google Scholar]
- Melesse, A.M.; Jordan, J.D.; Graham, W.D. Enhancing Land Cover Mapping using Landsat Derived Surface Temperature and NDVI. In Proceedings of the World Water and Environmental Resources, Orlando, FL, USA, 20–24 May 2001; pp. 1–7. [Google Scholar]
- Hui, Y.; Rongqun, Z.; Xianwen, L. Classification of Wetland from TM Imageries Based on Decision Tree. WSEAS Trans. Inf. Sci. Appl. 2009, 6, 1155–1164. [Google Scholar]
- Lane, C.R.; Liu, H.; Autrey, B.C.; Anenkhonov, O.A.; Chepinoga, V.V.; Wu, Q. Improved Wetland Classification Using Eight-Band High Resolution Satellite Imagery and a Hybrid Approach. Remote Sens. 2014, 6, 12187–12216. [Google Scholar] [CrossRef] [Green Version]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Beven, K. Runoff Production and Flood Frequency in Catchments of Order n: An Alternative Approach. In Climate Change Impacts on Water Resources; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1986; pp. 107–131. [Google Scholar]
- Infascelli, R.; Faugno, S.; Pindozzi, S.; Boccia, L.; Merot, P. Testing Different Topographic Indexes to Predict Wetlands Distribution. Procedia Environ. Sci. 2013, 19, 733–746. [Google Scholar] [CrossRef] [Green Version]
- Esri Find Areas at Risk of Flooding in a Cloudburst: Use ModelBuilder to Analyze Drainage Problems When Extreme Rainfall Hits Denmark. Available online: https://learn.arcgis.com/en/projects/find-areas-at-risk-of-flooding-in-a-cloudburst/ (accessed on 30 December 2020).
- Antonić, O.; Hatic, D.; Pernar, R. DEM-based depth in sink as an environmental estimator. Ecol. Model. 2001, 138, 247–254. [Google Scholar] [CrossRef]
- Wu, Q.; Lane, C.R.; Li, X.; Zhao, K.; Zhou, Y.; Clinton, N.; DeVries, B.; Golden, H.; Lang, M.W. Integrating LiDAR data and multi-temporal aerial imagery to map wetland inundation dynamics using Google Earth Engine. Remote Sens. Environ. 2019, 228, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Liu, H. An efficient method for identifying and filling surface depressions in digital elevation models for hydrologic analysis and modelling. Int. J. Geogr. Inf. Sci. 2006, 20, 193–213. [Google Scholar] [CrossRef]
- Uuemaa, E.; Hughes, A.O.; Tanner, C.C. Identifying Feasible Locations for Wetland Creation or Restoration in Catchments by Suitability Modelling Using Light Detection and Ranging (LiDAR) Digital Elevation Model (DEM). Water 2018, 10, 464. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Xie, C.; Fang, X.; Zhang, L. Combining Pixel- and Object-Based Machine Learning for Identification of Water-Body Types From Urban High-Resolution Remote-Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2097–2110. [Google Scholar] [CrossRef]
- Karasiak, N. Dzetsaka Qgis Classification Plugin 2016. Available online: https://github.com/nkarasiak/dzetsaka (accessed on 9 September 2021).
- Karasiak, N.; Perbet, P. Remote Sensing of Distinctive Vegetation in Guiana Amazonian Park. QGIS Appl. Agric. For. 2018, 2, 215–245. [Google Scholar] [CrossRef]
- Sejati, A.W.; Buchori, I.; Kurniawati, S.; Brana, Y.C.; Fariha, T.I. Quantifying the impact of industrialization on blue carbon storage in the coastal area of Metropolitan Semarang, Indonesia. Appl. Geogr. 2020, 124, 102319. [Google Scholar] [CrossRef]
- Cohen’s Kappa. Available online: https://en.wikipedia.org/wiki/Cohen%27s_kappa (accessed on 9 September 2021).
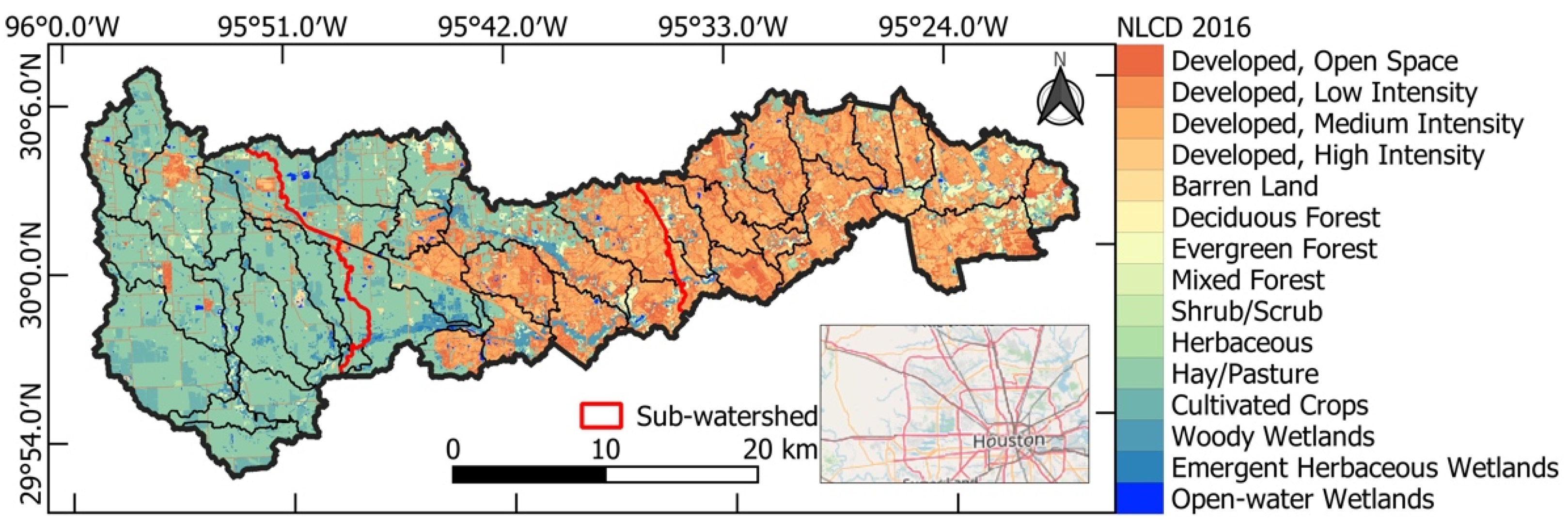


| Dataset | Band | Original Resolution | Resample Resolution | Acquisition Date | Custodian | Use in the Study |
|---|---|---|---|---|---|---|
| NLCD | 30 m | 30 m | 2016 | United States Geological Survey | To generate the training samples rapidly and roughly. Before the training samples used for supervised classification, their accuracy will be modified by Google satellite images, if necessary. | |
| NAIP | B: 435–496 nm | 0.6 m | 2 m | 2018 December | To calculate NDWI and NDVI for wetland delineation. | |
| G: 525–585 nm | ||||||
| R: 619–651 nm | ||||||
| NIR: 808–882 nm | ||||||
| LiDAR derived DEM | 1.5 m | 2 m | 2018 October | Texas Natural Resources Information System | To calculate TWI and DTWI. | |
| Google Satellite Imagery | N.A. | N.A. | 2015 November | Google Earth | As primary ground truth data reference for visual interpretation of the generated testing samples and the comparison of the calculated results. | |
| 2017 February | ||||||
| 2019 April | ||||||
| 2021 January |
| Index | Training Algorithm | Training | Validation | Kappa | Classified Accuracy |
|---|---|---|---|---|---|
| NDVI | SVM | 70% | 30% | 0.955 | 97.74% |
| NDWI | 0.943 | 97.17% | |||
| TWI | 0.811 | 90.57% |
| Predict Class | Positive | Negative | Accuracy Assessment | |||
|---|---|---|---|---|---|---|
| Actual Class | Positive | Negative | Positive | Negative | Kappa Coefficient | Overall Accuracy |
| Output Case | T.P. | F.P. | F.N. | T.N. | ||
| Normalized Difference Vegetation Index | ||||||
| November 2015 | 120 | 170 | 30 | 9680 | 0.536 | 98.00% |
| February 2017 | 106 | 187 | 51 | 9656 | 0.460 | 97.62% |
| April 2019 | 106 | 155 | 45 | 9694 | 0.505 | 98.00% |
| January 2021 | 133 | 172 | 72 | 9623 | 0.510 | 97.56% |
| Normalized Difference Water Index | ||||||
| November 2015 | 121 | 268 | 29 | 9582 | 0.437 | 97.03% |
| February 2017 | 106 | 286 | 51 | 9557 | 0.372 | 96.63% |
| April 2019 | 108 | 239 | 43 | 9610 | 0.432 | 97.18% |
| January 2021 | 130 | 258 | 75 | 9537 | 0.423 | 96.69% |
| Topographic Wetness Index | ||||||
| November 2015 | 115 | 542 | 35 | 9308 | 0.267 | 94.23% |
| February 2017 | 109 | 591 | 48 | 9252 | 0.235 | 93.61% |
| April 2019 | 95 | 595 | 56 | 9254 | 0.206 | 93.49% |
| January 2021 | 129 | 542 | 76 | 9253 | 0.272 | 93.82% |
| Deterministic Topographic Wetland Index | ||||||
| November 2015 | 105 | 39 | 45 | 9811 | 0.710 | 99.16% |
| February 2017 | 99 | 49 | 58 | 9794 | 0.644 | 98.93% |
| April 2019 | 85 | 54 | 66 | 9795 | 0.580 | 98.80% |
| January 2021 | 114 | 38 | 91 | 9757 | 0.632 | 98.71% |
| Overall Accuracy Assessment for 4-year ground truth samples | ||||||
| NDVI | 465 | 684 | 198 | 38,653 | 0.503 | 97.80% |
| NDWI | 465 | 1051 | 198 | 38,286 | 0.413 | 96.88% |
| TWI | 448 | 2270 | 215 | 37,067 | 0.245 | 93.79% |
| DTWI | 403 | 180 | 260 | 39,157 | 0.641 | 98.90% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, L.; Melesse, A.M.; Leon, A.S.; Verma, V.; Yin, Z. A Deterministic Topographic Wetland Index Based on LiDAR-Derived DEM for Delineating Open-Water Wetlands. Water 2021, 13, 2487. https://doi.org/10.3390/w13182487
Bian L, Melesse AM, Leon AS, Verma V, Yin Z. A Deterministic Topographic Wetland Index Based on LiDAR-Derived DEM for Delineating Open-Water Wetlands. Water. 2021; 13(18):2487. https://doi.org/10.3390/w13182487
Chicago/Turabian StyleBian, Linlong, Assefa M. Melesse, Arturo S. Leon, Vivek Verma, and Zeda Yin. 2021. "A Deterministic Topographic Wetland Index Based on LiDAR-Derived DEM for Delineating Open-Water Wetlands" Water 13, no. 18: 2487. https://doi.org/10.3390/w13182487
APA StyleBian, L., Melesse, A. M., Leon, A. S., Verma, V., & Yin, Z. (2021). A Deterministic Topographic Wetland Index Based on LiDAR-Derived DEM for Delineating Open-Water Wetlands. Water, 13(18), 2487. https://doi.org/10.3390/w13182487








