1. Introduction
During the summer months, increased atmospheric heating leads to many reservoirs stratifying as increased surface heating creates temperature differences in the water column [
1,
2]. Reservoir stratification is defined as when there is a temperature gradient within the water column [
3]. Thermally stratified water bodies are stable and mixing is suppressed [
4]; these physical effects can have considerable influence on the biological, chemical, and general ecosystem processes of the water body [
5]. Correspondingly, summer stratification directly affects the water quality within reservoirs [
6] via processes including benthic sediment oxygen demand and decomposition of organic matter which consume oxygen from the hypolimnion. When stratification persists for long enough, the inhibition of oxygen supply to the hypolimnion results in oxygen depletion and may result in hypoxic conditions (i.e., the near absence of oxygen at <2 mgL
dissolved oxygen). Whether a water body is hypoxic or not drives many critical biogeochemical processes including trace metal transport, phytoplankton dynamics, and the carbon cycle [
3,
7,
8,
9].
Artificial destratification (i.e., mixing) is often used in lakes and reservoirs to overcome negative effects of summer stratification [
10]. A popular method used is bubble plumes [
11]. The reported success of bubble plumes in reservoir management has been varied, suggesting that there is a lack of guidance regarding best operational practice [
12]. Bubble plumes are usually installed at the deepest point of the water column and force compressed air into the bottom water, which rises and forms a plume [
13]. Bubble plumes work to destratify the water column as the rising bubbles entrain the surrounding denser hypolimnion water. The denser water is then raised into the lighter epilimnion, promoting mixing [
14]. This allows aeration via both atmospheric gas exchange and directly from the produced bubbles [
15]. Many water utilities use bubble plume destratification systems to ultimately improve source water quality prior to draw-off [
16]. A minimum airflow of 9.2 m
3 min
km
has been given as a threshold to ensure total destratification of a reservoir via these plumes [
17,
18]. The aim of destratification systems such as bubble plumes is to reduce cyanobacteria biomass and minimise concentrations of trace metals, such as soluble manganese, entering the water treatment works to improve the sustainability of treatment and reduce costs to the consumers [
16,
18]. Oxygenation of the hypolimnion has been shown to decrease concentrations of soluble reduced forms [
19] of iron and manganese [
20] which are released from sediments under low-oxygen conditions [
21]. Additional mixing can affect phytoplankton by increasing the mixed depth to below the photic zone, thereby reducing irradiance which has been shown to reduce cyanobacteria blooms [
22].
Currently, increased greenhouse gases (GHG), such as methane (CH
4) and carbon dioxide (CO
2) [
23], are leading to a rapid rise in global temperatures. It has been shown that inland waters (e.g., reservoirs) may account for ∼18% of CH
4 emissions globally [
24,
25]. With existing trends, future GHG release will further contribute to global temperature rise and its consequences. Climate change influences inland water bodies via alterations to air temperature and precipitation [
26]. This introduces new elements that threaten to exacerbate water-quality issues related to reservoir stratification [
27]. For many reservoirs, there will be alterations to the timing of stratification, potentially forming earlier and destratifying later, leading to enhanced periods of hypolimnetic anoxia and subsequent release of deleterious chemical species from the sediment [
27,
28,
29]. This directly affects carbon fluxes and long-term dissolved organic matter trends by extending anoxic periods in the hypolimnion [
27]. Rising global temperatures and increased anthropogenic eutrophication of freshwater systems are likely to promote favourable growth conditions for cyanobacteria. Increased water column stability can favour bloom-forming or positively buoyant species of cyanobacteria, some of which may produce taste and odour compounds or cyanotoxins and result in a deterioration in source water quality [
30].
Prolonged stratification seasons predicted with climate change will require destratification systems to be efficient in both current and future climates. In addition, more stable water columns (i.e., stronger stratification) will be increasingly likely, which will require greater energy input from destratification systems to successfully mix lakes and reservoirs [
28]. However, the relationship between increased temperature and stratification stability is not a linear effect and stratification can be strongly influenced by water-body morphometry and volume [
5]. To date, research has largely focused on the effects of artificial mixing on source water quality in current climates. In this novel study, modelled future climate scenarios were used to estimate how effective current destratification systems are likely to be in the future.
During June 2017, much of western Europe was struck by a heatwave. Record-breaking temperatures were recorded across many countries, including the UK. On 21 June, temperatures in the UK reached 34.5 °C; at the time, this was the hottest June since 1976 [
31]. Such heatwaves have been shown to cause strong stratification events in shallow polymictic lakes; several of which are similar in depth to the study site, Blagdon Lake, located in the southwestern UK [
32].
This study presents in situ observations of temperature in the shallow, aerated Blagdon Lake during the 2017 heatwave. These observations are used as the basis for the development of a 3D hydrodynamic model, via the widely used AEM3D [
33,
34,
35,
36,
37] which is available publicly with a yearly licence, to capture effects of extreme events on stratification such as the 2017 summer heatwave. With this calibrated model and down-scaled hourly future forcing data, this study examines how effective bubble plumes will be under future climate scenarios. Results show that existing issues with reservoir mixing interventions will likely continue into the future and managers will need to consider future proofing options.
2. Materials and Methods
2.1. Study Site
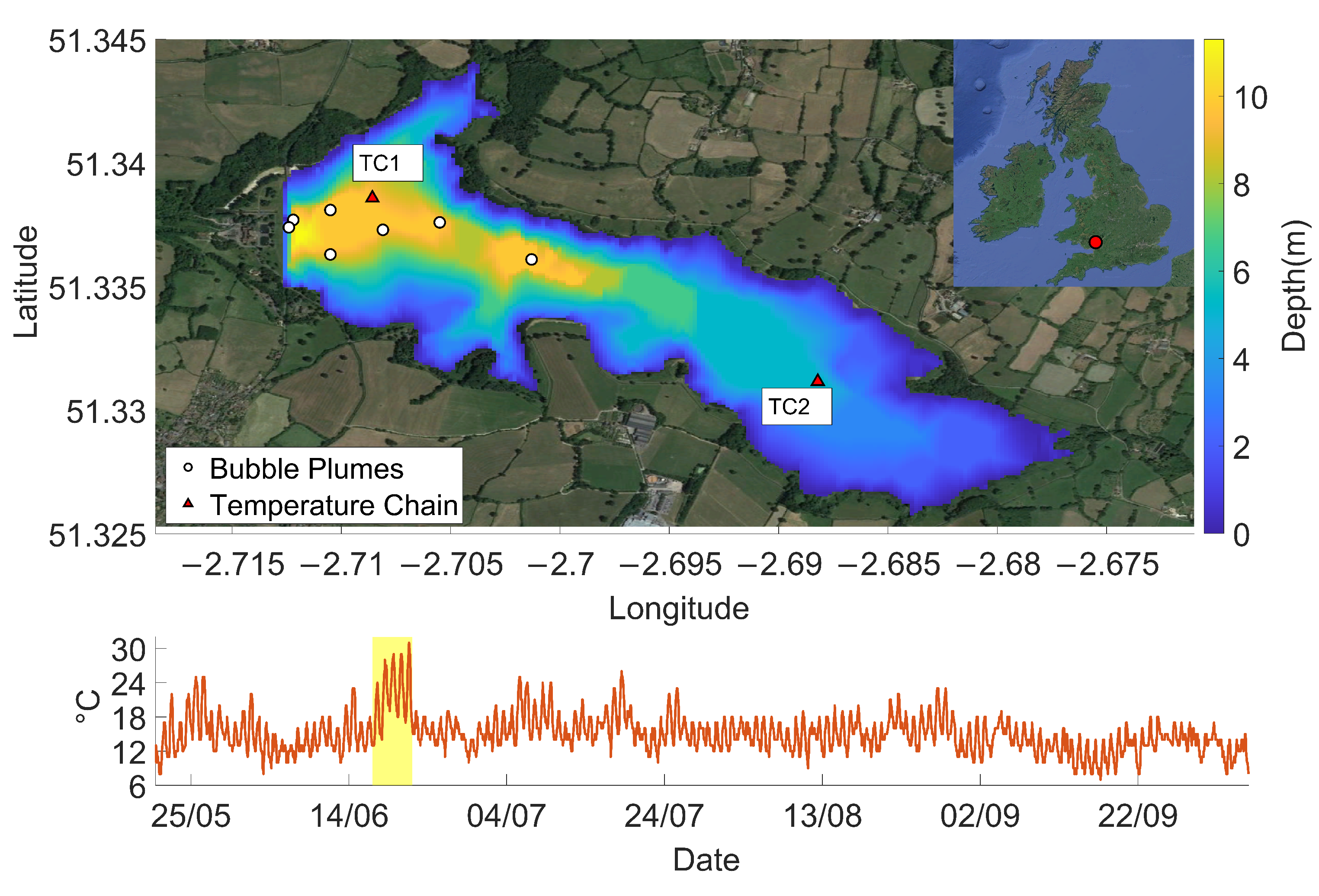
Blagdon Lake is a shallow drinking water reservoir, located in Somerset, England, and operated by Bristol Water Plc. The reservoir has a surface area of 1.78 km
2 with a mean depth of 4.75 m and a maximum depth of approximately 12 m (
Figure 1). The lake was created when the River Yeo was dammed in 1905. Several small streams feed into Blagdon and these inflows have a combined catchment area of 21.8 km
2.
Artificial destratification was first implemented in Blagdon in the 1970s and since 2007 there have been seven bubble plumes installed (
Figure 1). The bubble plumes are typically operated from April to September each year with the aim of destratifying the reservoir during the summer. Specifically, the bubble plumes were installed at Blagdon to address problems with soluble manganese concentrations and phytoplankton cell counts at the draw-off. Initially, five of the bubble plumes were positioned at 200 m, 250 m, 400 m, 600 m, and 850 m away from the draw-off tower at the dam. An additional two bubble plumes were placed nearer the draw-off tower to reduce soluble manganese concentrations entering the treatment plant. The bubble plumes contain no moving parts and have a 2-meter pipe containing a helical structure where compressed air bubbles can mix with the bottom water and generate a vertical plume that rises to the surface. These bubble plumes have a reported airflow of 0.011 m
3s
(Bristol Water pers. Comms).
Per data collected by Bristol Water, the bubble plumes appear to have reduced concentrations of soluble manganese at the Blagdon draw-off tower, with a 91.6% reduction from 2007 to 2008 of maximum observed soluble manganese. However, the effects of bubble plumes on phytoplankton cell counts at Blagdon, in particular cyanobacteria, appear less successful. Bloom-forming cyanobacteria are positively buoyant and have specific adaptations, such as gas vacuoles, that provide a competitive advantage under stratified conditions. Generally, the frequency of high counts of bloom-forming cyanobacteria at the Blagdon draw-off have increased since 2006. In 2014, for example, cyanobacteria cell counts at the draw-off exceeded 20,000 cells mL
on twelve occasions and peaked at 125,038 cells mL
, which related to a Microcystis bloom. On 26 June 2017, counts of Microcystis were elevated at the Blagdon draw-off, following the heatwave. Data provided by Bristol Water indicate that bubble plumes are not fully effective at reducing the buoyancy advantage of bloom-forming cyanobacteria during warm periods [
38].
2.2. Observation Methodology
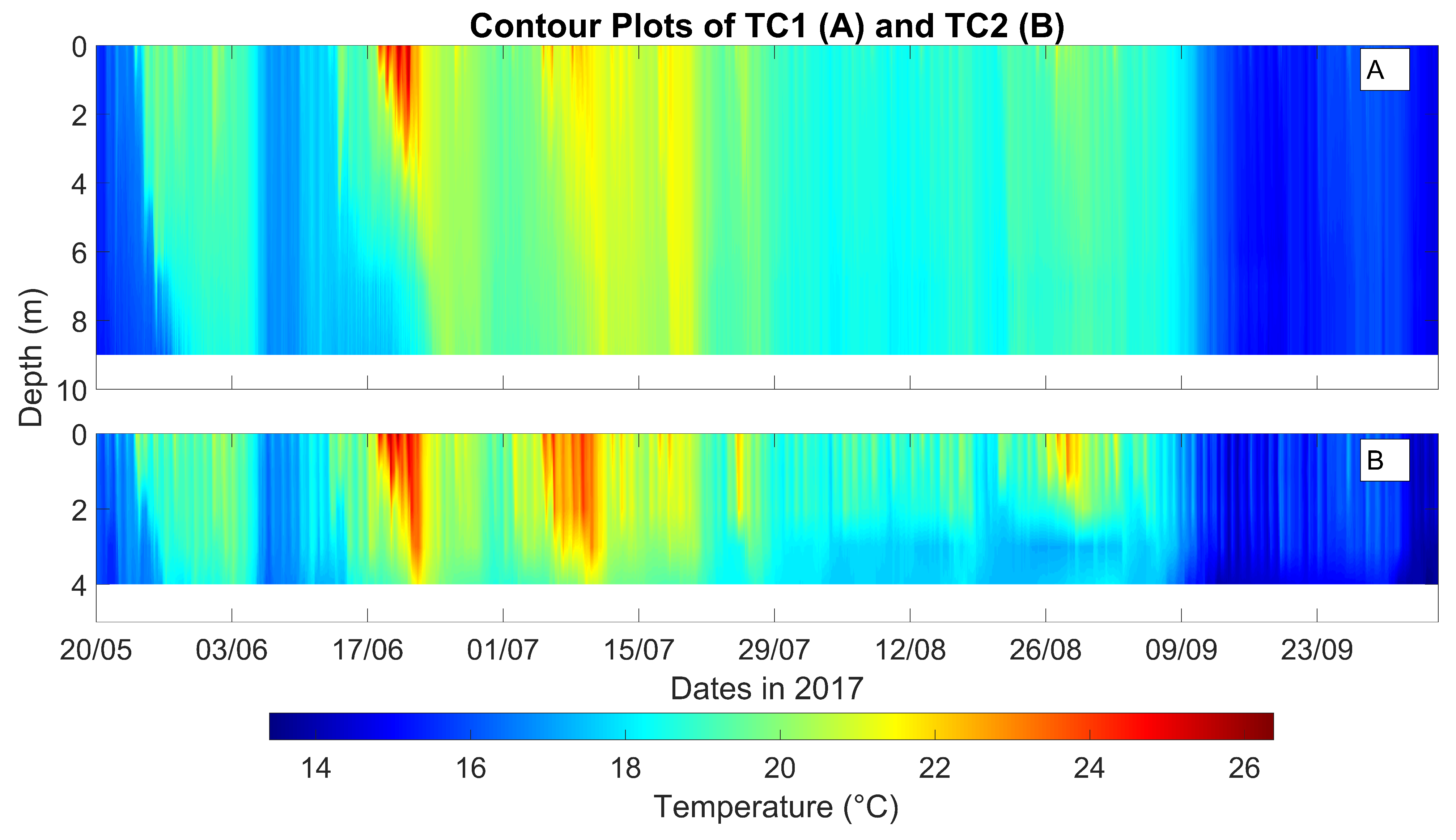
From 20th May to 5th October 2017, two temperature chains were deployed in Blagdon Lake to better understand the thermal regime in the reservoir over this time period. Each of the two chains were set at one-metre resolution and recorded data every ten minutes. One chain was placed in the deeper part of the reservoir (at depth of approximately 9 m), located within the zone immediately influenced by the bubble plumes located at latitude 51.33858 and longitude −2.70858; this chain is hereby referred to as temperature chain 1 (TC1). Per instructions from the water utility, this chain was placed as close as allowed to this intake zone. In order to evaluate the spatial extent of bubble plume mixing, the other temperature chain was placed further away in the shallower (at depth of approximately 5 m), non-aerated section of the reservoir located at latitude 51.33116 and at longitude −2.688. This shallower chain is referred to as temperature chain 2 (TC2). Over the 2017 observation period, a series of Secchi depths were also taken within Blagdon Lake at various points along the bubble plume transect; see
Figure 1.
2.3. Data
2.3.1. Boundary Condition Data
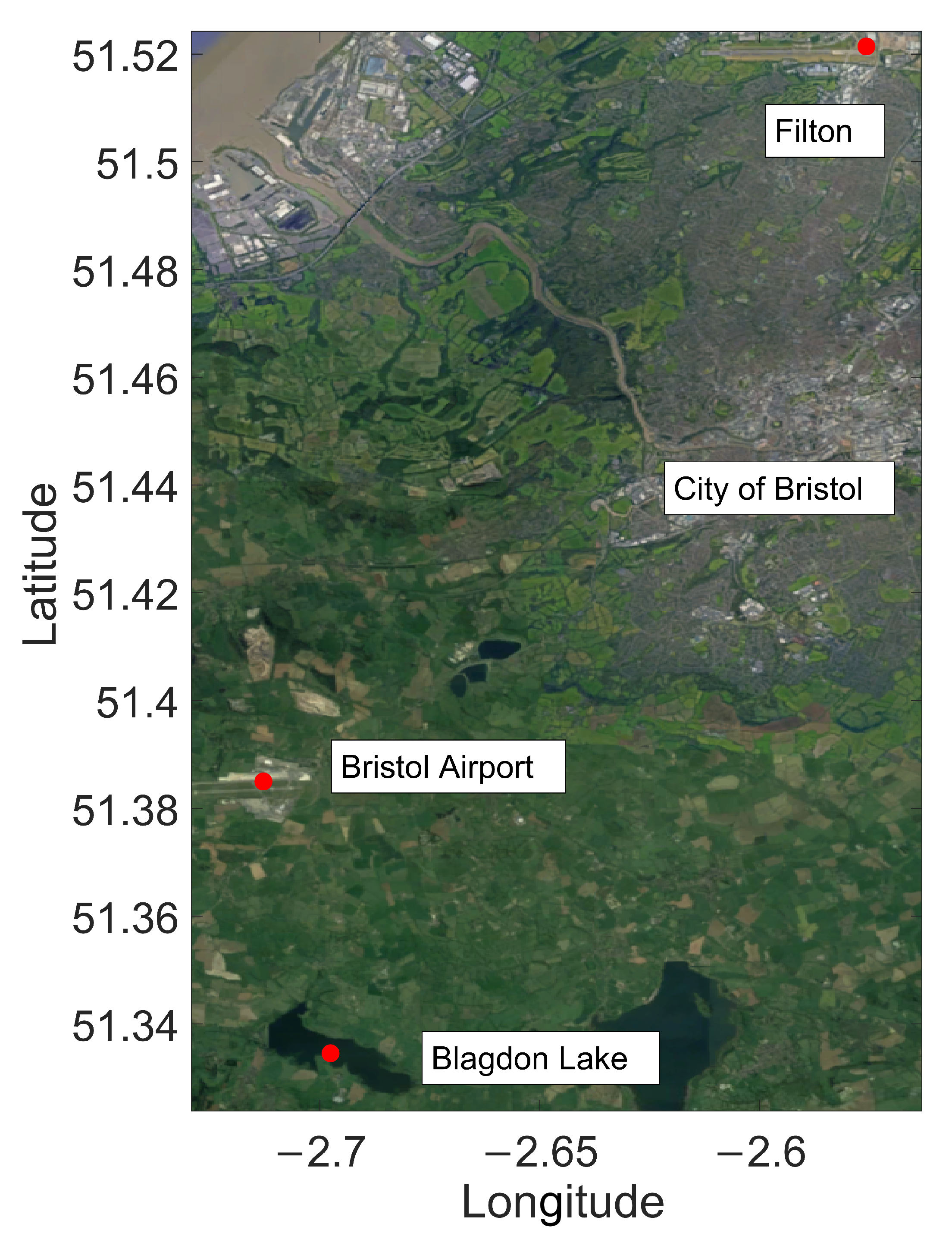
To cover the forcing requirements of AEM3D, eight meteorological inputs were used. These include solar radiation (Wm
), cloud cover (decimal), air temperature (°C), atmospheric pressure (Pascals), precipitation (mday
), wind speed (ms
), wind direction (°) and relative humidity (decimal). Information about wind, air temperature, cloud cover and atmospheric pressure was taken from the weather station at Bristol Airport, which is proximal (around 5 km) to Blagdon Lake. Precipitation, solar radiation and relative humidity were sourced from the Filton weather station; this station is further from the lake (20 km) but offers a more comprehensive suite of measured variables than available for Bristol Airport. Weather station positions relative to Blagdon Lake are shown in
Figure 2. The Met Office MIDAS Open UK Land Surface Stations Data was used to gather relative humidity, solar radiation and precipitation [
39]. Remaining weather variables were sourced from the sub-daily Met Office Hadley Centre’s Integrated Surface Database [
40,
41,
42,
43]. Whilst the most proximal sources were considered, the lack of direct meteorological data is a limitation that was taken into account in the evaluation of results but not considered a critical detriment. Mass balance information for the calibration and validation periods were sourced from outflow and reservoir capacity provided by Bristol Water. This calculated inflow was then separated between the six stream inflows into the lake, namely the Yeo, Butcombe, Rickford, Ubley, Copse and Holt Farm; the weighting applied to each inflow was based on the percentage of the lake’s catchment each tributary contributed. Forcing data related to the seven bubble plumes installed in the reservoir was based on their 0.011 m
3s
flow rate. Modelling was focused on characterising the summer season to cover time periods when stratification was most likely to occur; as such, the bubble plumes were assumed to be on throughout the simulations.
2.3.2. Future Meteorological Data
Future forcing data were sourced from the UK Climate Projection 2018 (UKCP18) project which was designed to help inform adaptions as a result of climactic change [
44]. The UKCP18 made use of models from the Coupled Model Intercomparison Project Phase 5 (CMIP5). These data sets were taken from regional climate model projections for the future climate of the UK extending from a 100-year period from 1981 to 2080 [
45]. The climate projections were considered for the highest GHG emission scenario used by the IPCC, the representative pathway 8.5 (RCP 8.5). This representative pathway, named for the projected radiative forcing of 8.5 Wm
by 2100, predicts a future where high energy demand and high GHG emissions occur with little to no climate change policies to counteract this, thereby worsening climate change; due to this RCP 8.5 is considered the “worst case” scenario [
46,
47]. These projections were done using the UK Met Office’s Hadley Centre Global Environmental model (HadGEM3), a coupled atmosphere-ocean climate model [
48].
Twelve UKCP18 climate scenarios were down-scaled from twelve different HadGEM3-GC3.05 simulations from a grid size of 60 km to a higher resolution of 12 km via the HadREM3-GA705 model covering much of the British Isles on the Ordnance Survey’s British National Grid [
45]. The dataset has several separate projections of future climates that were used to force the future model runs; the scenarios used were 1, 4–13 and 15 since these had the required variables. These twelve scenarios offer distinct projections of climate variability due to climate change over the British Isles until 2080. From these projections, the following data were sourced at daily values with the following units: downwards shortwave radiation (Wm
), northerly wind speed (ms
), easterly wind speed (ms
), relative humidity (%), cloud cover (%), atmospheric pressure (Pascals), precipitation (mmday
), maximum temperature (°C), and minimum temperature (°C) [
44]. The future years consist of 360-day years, with twelve 30-day months. As this date format was incompatible with the model set-up, some days were repeated for an additional day after their occurrence or needed to be treated differently to get the climate scenarios into a standard date format. Depending on whether there was a leap year or not, one or two days were moved from February to later months. The final days of July, August, October and December were repeated; additionally, during a leap year May also had a repeated final day. This was done to space out repeated days throughout the year. Future model runs of Blagdon lake did not consider inflows or outflows. The HadGEM3 projects used were notably warmer than other CMIP5 model runs, though all were within the IPCC’s stated range for future warming. This may contribute to higher water temperature being predicted by model runs [
45].
2.4. Future Weather Down-Scaling
Predicted future data were obtained as daily values; in order to get sub-daily values, these data sets needed to be down-scaled temporally. The down-scaled methodology was evaluated using observed weather data, where daily averages of the observed data were produced before applying the various methods used in the down-scaling; this was also used to calibrate several of the required parameters. Down-scaling results were compared with the original observations. Numerous approaches were used for down-scaling, which will be detailed in the following sections. The data sets are openly available [
49].
2.4.1. Temperature
The temporal down-scaling of air temperature data was done by using maximum and minimum temperature for any single given day in the future. These are all measured in °C. As air temperature follows a diurnal pattern related to the day-night cycle, air temperature can be described numerically with a sine function and an exponential function based on the time of day. The daytime air temperature function is described by the equation:
where
Ta(t) describes the air temperature at time
t.
Tn(max) and
Tn(min) denote the daily maximum and minimum temperatures for any given day. The
S(t) refers to the following sine pattern at time
t:
DL is the day length at the field site in hours; this required the times of sunrise and sunset to be known.
SM defines the time of solar maximum and
P is the delay between the time of
SM and the
Tn(max). These are all measured in hours.
For periods after sunset, the temperature is instead measured as an exponential decline curve based on the sunset temperature from the current day down to lowest temperature of the next day. This curve is based on lowest temperatures occurring just before dawn. The night temperature function can be written as:
Tt and
t maintain the same definitions as previous; these are measured as °C and hours.
Tss and
ss refer to the temperature and time of the day’s sunset, respectively; these are measured as °C and hours.
Tn+1(min) is the minimum temperature the following day.
is a time coefficient, in hours, that is calibrated for the field site using observational weather data and selecting the
value that produced the smallest error and bias towards underestimation or overestimation. Prior to using this method with modelled future data, it was calibrated for the field site with observed data [
50].
2.4.2. Relative Humidity
Relative Humidity (
RH) was calculated as a decimal, from the ratios of actual vapour pressure in air (
VPA) and the saturated vapour pressure (
es). These are measured in kPa [
50]. Equations used treat
RH as a percentage; these can be calculated with the following equations:
Ta and
Td are the air temperature and dew-point temperature measured in °C. As these are a function of temperature,
RH also follows a diurnal pattern. In order to down-scale this
RH, the initial daily value of
Ta and the initial daily value of
RH were used to produce a daily
Td. This was done numerically with the following rearranged equation based on Equations (4)–(6). This produced two separate estimations for
VPA, one made by subbing in various values for
Td within a sensible temperature range for the UK (−10 °C to 30 °C), then subtracting the two estimations. The chosen
Td value was based on the result closest to zero.
Once this daily
Td was estimated, a final
VPA was calculated with the dew-point value.
es was calculated with the sub-daily modeled
Ta and from these, an estimated sub-daily
RH on the same time step was calculated using Equation (6). At times, this equation produced results of greater than 100%; these values were ignored and set to 100% as beyond this limit the model will not accept the forcing data [
50].
2.4.3. Downwards Shortwave Radiation
The diurnal solar radiation pattern was based on the total global radiation, denoted as
Rsum; this value was calculated by multiplying the daily modelled incoming radiation (in units of watts) by the number of seconds in a day to joules. From this total insolation, sub-daily values were estimated with a sine function [
50]. Hourly incoming solar radiation (
Rt) was estimated as a function of solar declination (°), solar elevation (°), latitude (°), and day length (hours), as defined by the following set of Equations (9)–(12) [
50]. Solar declination, denoted by
, was calculated via the following equation [
51]:
where
n is the day number. Seasonal offset and amplitude of the sine wave,
SD and
CD, respectively, were calculated with the following equations:
L is the latitude of the site in question. These can then be used to obtain the sine of the solar elevation,
sin β, as calculated by:
The solar maximum,
SM, and the time of day,
t, are in hours. For this method of estimation of solar radiation, a linear increase of the atmospheric transmissivity with the sine of solar height was assumed.
Rt can then be calculated with the following equation:
C is a meteorological variable characterising dependence of transmissivity on solar height equal to about 0.4 [
52] and
DBSE is the integral of solar radiation from sunrise to sunset. This then produces an
Rt in a sine pattern; periods at night when the insolation was below zero were adjusted to zero values [
50].
2.4.4. Longwave Radiation
Downwards long-wave radiation (
Ld) was chosen to be down-scaled, as opposed to down-scaling cloud cover, as
Ld is more diurnal due to being a function of
Ta. The Stefan-Boltzmann equation presented below is traditionally used to determine long-wave radiation [
53]:
Eeff is effective emissivity (dimensionless),
Teff is the temperature from the atmosphere (measured in K within the equation) above and
is the Stefan-Boltzmann constant (5.670367 × 10
kg s
k
). The parameterisation of
Ld normally uses surface
Ta and humidity measurements. Initially, the effective emissivity of a clear sky was needed. The Angstrom equation from 1918 was used to calculate clear sky emissivity as it has been shown to estimate
Ld on a clear day [
53]:
where
eclr is the clear sky emissivity (dimensionless) and
ea is vapour pressure. After the clear sky emissivity was calculated, an additional equation was used to calculate emissivity based on cloud cover. This was based on the Unsworth and Monteith equation from 1975 [
54] as this is established as performing well for estimating cloud cover influence. These values of cloud cover, taken as a decimal, were obtained from daily predicated values from the twelve future climate scenarios considered [
53].
Cf is the value of cloud cover. This was kept constant throughout the day using the daily value from future modelled weather data predictions. This was then placed into Equation (13) along with the daily down-scaled
Ta to produce a time series of sub-daily
Ld.
2.4.5. Wind Speed and Direction
Wind speed varies both cyclically and randomly in time. This often forms as random variance around a more regular diurnal cycle relating to atmospheric pressure and geostrophic wind. The deterministic approach is to use a wave function that varies from a minimum to a maximum wind speed over the course of the day [
55].
Wind direction (°) and wind speed (ms
) were considered together, with wind speed down-scaled first and the wind direction calculated from that. With one wind value available for each day, an applicable method was used [
56]. Firstly, wind speed was considered in its eastward and northward elements. These were then both down-scaled assuming a cosine function for wind speed, where maximum wind speed occurs later in the day and lower wind speed occurs earlier on in the day. These are based on the following equation [
56]:
Wt references to wind speed at time
t.
Wa is the average wind speed.
Hmax is a time of maximum wind, as estimated from the observed wind speed. This was found to occur at midday. These sub-daily northward and eastward wind speeds were then used to calculate geostrophic wind speed and wind direction [
56].
2.4.6. Air Pressure
When comparing observed values with their daily averaged values, it was found that daily variations of air pressure were minor when compared to timescales longer than a day. Due to this, a daily average of observed values was considered sufficient for down-scaling. Air pressure is measured in Pascals.
2.4.7. Precipitation
Rain in the study region is prone to periodic spikes in rainfall at shifting times. Due to this, a static rate across the entire day was used to capture general periods of high and low rainfall. As such, a daily average of observed values was considered sufficient for down-scaling. Precipitation rate is measured in mday.
2.5. Down-Scaling Performance
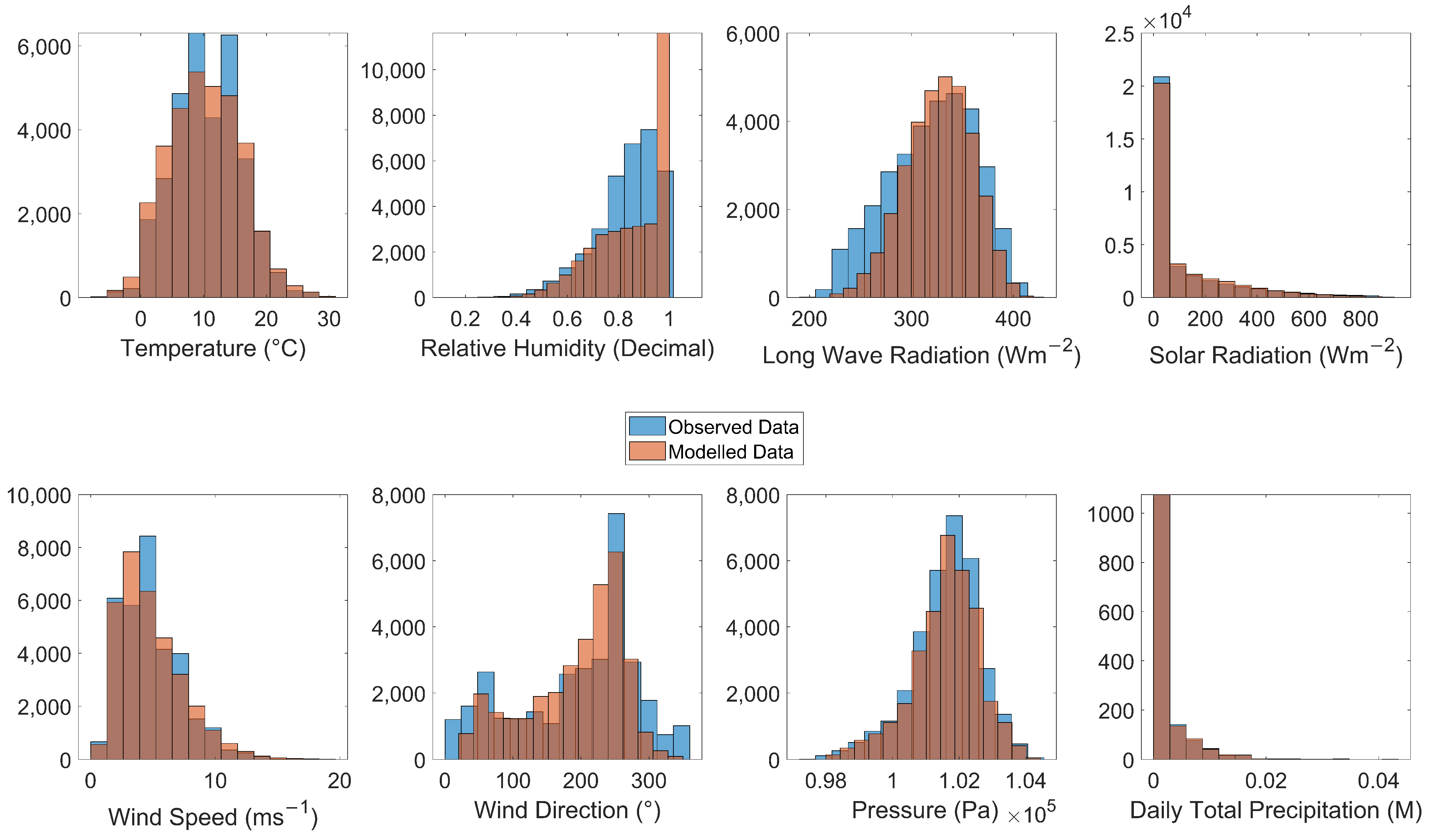
The performance of these methods based on modern weather can be seen in
Figure 3 and
Table 1. The down-scaled temperature produced deviations more regularly from mode temperature towards the minimum and maximum. The root mean squared error (RMSE) produced an error of 1.6 °C. Errors were introduced in winter months when the sinusoidal temperature pattern was less dominating, when the down-scaled temperature always assumes a sinusoidal pattern. Error was also introduced during the night as warmer nights can have colder temperature allocated to them if a colder temperature occurred within the day. However, there is a high coefficient of correlation at 0.96, showing the method appropriately captured sub-daily patterns.
Down-scaled
RH overestimations occurred at higher humidity. When the cut-off filter of over 1 was applied, this overestimation was downplayed but is still evident in
Figure 3. At lower
RH, the down-scaled method performed much better. The RMSE from a time series comparison is 0.09; this is improved by placing a cap on humidity values. The correlation coefficient of 0.78 shows sufficient capturing of the general temporal trends.
Downwards Ld was the only meteorological factor where proximal observed data was not available so was not included in the down-scaling method. Due to this, Ta, Cf and RH were used instead as a proxy. The calculated values based on observations will be referred to as the “observed Ld” for simplicity. Both observed and modelled Ld centred around the same modal value, but the modelled had a narrower range of values with a lower maximum value and a higher minimum value. Modelled Ld under-predicted the frequency of lower values. The RMSE of 26.87 Wm and a coefficient of correlation of 0.8 show that they capture the overall pattern sufficiently.
Solar radiation is among the best performing down-scaled methods within the study. The modelled solar radiation under-predicted times of no short-wave radiation, likely due to the hourly time step obfuscating exact times of sunrise and sunset. The method has a comparatively low RMSE of 53.54 Wm and a high coefficient of correlation of 0.95. Differences may primarily be effects of Cf on solar radiation which is not considered within the down-scaling.
Wind speed methodology produced a similar range of results, but the centre of the down-scaled wind speed frequency was lower. However, there is a general agreement of the frequency for the other speeds. The RMSE is large compared to other meteorological elements at 2 ms. The correlation coefficient was also the weakest, at 0.66. These results suggest that, despite a similar range and frequency of values on a similar time scale, the method does not perform as well at capturing hourly wind speeds compared to other meteorological parameters.
Down-scaled wind direction matches the mode wind direction at 270° within the observations and captures another small frequency peak around 90°. The down-scaled method does not represent northerly winds well (around 0°). There is a large RMSE of 55.2° and the coefficient of correlation is 0.79. The down-scaled values captured the frequency spread of wind direction well but did not perform as well on hourly comparisons.
Surface pressure has a comparatively low RMSE of 253.52 Pa; this down-scaled parameter had the highest correlation coefficient of 0.97. Due to using an average of the air pressure, as it does not vary massively over a daily time period, agreement was very close.
When considering the performance of down-scaled precipitation, daily total precipitation was used. The down-scaling worked remarkably well with a RMSE within a rounding error of 0 and coefficient of correlation of 1.
Across all the down-scaled meteorological factors, there was found to be suitable agreement between observed and down-scaled weather parameters. All shared a similar range of values capturing the variability experienced, and many had low RMSE and high correlation. Thus, the down-scaled parameters were considered to sufficiently represent the required modelling needs.
2.6. AEM3D
2.6.1. Model Description
AEM3D, a coupled 3D model of hydrodynamics and ecology, was used for this study. This model is established for considering various hydro-environments and capturing many related physical and biogeochemical processes [
33,
35,
37,
57], though this study only focused on physical process modelling. It has often been employed in reservoir studies [
33], including the evaluation of dammed rivers [
36] and reservoirs of various sizes [
35]. The model allows for the prediction of mixing requirements [
36], temperature arrangements [
36] and management methods [
35]. The volume of research done shows that the model has a wide range of applicability [
33,
34,
35,
36,
37]. This model works by coupling ELCOM and CAEDYM routines [
33] which enables AEM3D to be a hydrodynamic model and/or fully coupled with a biogeochemistry module [
33,
35]. The model uses a z-grid system [
57]. The solver for the hydrodynamics, ELCOM, solves in 3D with hydrostatic, Boussinesq, Reynolds-averaged, unsteady, viscous Naiver-Stokes equations [
33]. For the vertical turbulence closure of Reynolds stresses, and corresponding turbulent fluxes, a 1D mixed layer model is utilized [
34]. The biogeochemical element, CAEDYM, includes an array of algorithms to incorporate various production and cycling processes [
33]; specifically, this module contains descriptions for primary production, secondary production, oxygen dynamics and nutrient cycling [
34]. When new wet cells, i.e., cells within the model where water is present, are filled, as a default the surrounding cells are averaged to inform these new cells. Options exist such that non-temperature factors can be set to zero instead as the new wet cell fills. When water level drop is sufficient, wet cells will empty of water and convert to dry cells [
57]. AEM3D also includes a module that simulates bubble plumes, allowing for characterisation of aeration-induced mixing in Blagdon Lake for the current study [
57].
2.6.2. Model Set-Up
For running model calibration and validation, the full length of observations from 20th May to 6th October 2017 was used. For the future runs, focus was placed on the summer stratification period and 20th May through the end of August was considered, performed at five-year intervals from 2030 to 2080. This was done to capture a sufficient period during which the lake exhibited ephemeral stratification, whilst also optimising computational time. Measured 2017 temperature chain data on 20th May were used as initial conditions for each model run, though future results were processed using data from June onwards. The domain chosen for the model used grid cells with 25-m sides and with 1-m height in the vertical for the more stable epilimnion and hypolimnion; 0.5 m was used in the vertical to capture the more dynamic metalimnion zone. These regions within the model domain were estimated based on observed temperatures.
Secchi depth (
ZSD in m) casts obtained during the 2017 observation period were used to establish a range of possible light attenuation (
K) estimates based on the Poole and Arkins (1929) formulation [
58].
To best match the dynamics of the measured data, inflows were included in the model for calibration. Some editing of the inflow boundary conditions was required. Stream inflows ultimately needed to be routed from the edge of the reservoir into its deeper region since, with varying water levels, inflows set directly to the reservoir shoreline become invalid; as the water level dropped, these wet cells become dry. Due to the shape of Blagdon, some of the inflow streams cannot be directly routed to the deeper sections of the reservoir so were ultimately moved to new locations, proximal to the actual position but with a more direct path to the lake’s interior in order to facilitate long-term simulations that capture the varying water levels. Though used for model calibration, once the model was validated inflows were not included in future-prediction model runs for the sake of minimising error related to uncertainty in estimating changes in demand for water and stream inflows.
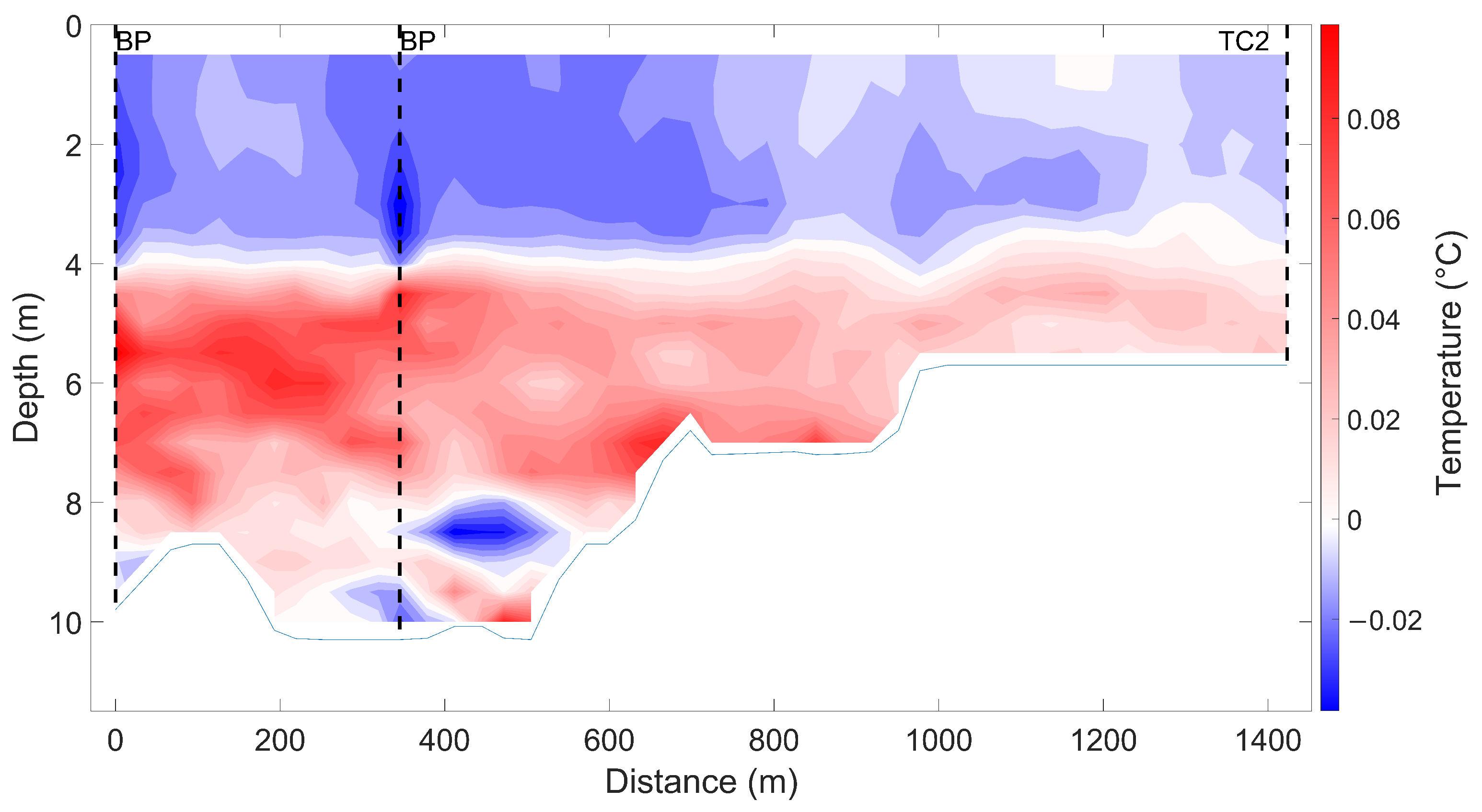
Bubble plumes were assigned to grid cells within the model domain closest to their actual locations in the reservoir (
Figure 1). Due to the long-term operation of bubble plumes in Blagdon Lake, reaching back over four decades, there is no available data for the natural mixing regime during the summer stratification period. This means that quantifying the actual influence of the bubble plumes on the mixing regimes compared to the natural regime is difficult. To quantify the bubble plumes’ effect on the reservoir, a series of model runs were done with the bubble plume module within the model turned on and off.
Figure 4 shows model run results and highlights that the bubble plumes had minimal influence on the physical mixing regime within the model. A localized mixing effect and increased heat transference are shown around the bubble plume at 350 m from the dam, suggesting the model underestimated the bubble plumes’ influence and/or they have a limited effect. The airflow of the mixers in Blagdon lake is estimated to at 2.57 m
3 min
km
, below the given threshold of 9.2 m
3 min
km
, suggesting they might not be as effective as recommended by design standards.
2.7. Calibration and Validation
2.7.1. Performance Criteria
For calibration and validation of the model developed and used for this study, the RMSE between the observed values and the modelled outputs were calculated. For this operation, temperature was chosen as the evaluated parameter as it is the most representative of the overall physical environment of the reservoir.
n represents the number of considered points,
is the modelled data and
x is the observed data.
Mean bias error (MBE) will be considered when analysing the performance of stability calculations to understand how well the model captures the mixing. This is shown in the equation below which uses the same definitions as Equation (18).
2.7.2. Approach
For calibration and validation of the model, the 2017 observed temperatures were used; TC1 and TC2 modelled locations were based on their real-world locations, shown in
Figure 1. The calibration period used was from the start of temperature measurements, May 20th, to the end of June. The first recorded temperatures were used as initial conditions. The remaining observation period was used for validation. Based on sensitivity analysis runs, wind stress coefficient, heat transfer coefficient and albedo (defined by the fraction of incident solar radiation reflected back [
59]) were chosen as model calibration parameters. Light attenuation was also used as a calibration parameter. A series of automated model runs varying these values was undertaken where MATLAB was used to alter the values and re-run the model. Albedo and the heat transfer coefficient have been used for model calibration in similar work [
35]. The base values for heat transfer and wind stress coefficients within the model are both 0.0013; these coefficients were varied along a similar range from 0.001 to 0.0016. Albedo was varied from 8%, the model’s base value, to 6%, based on northern altitude lakes [
60]. Light attenuation was calculated from the Poole equation based on a range of Secchi depths taken from the site, 2 m to 5 m, and the established ratios between the various light attenuation factors contained within the base setup of the model were adjusted accordingly. The runs with the lowest RMSE were chosen to use for validation and used for model runs considering future climates.
2.8. Schmidt Stability
Schmidt stability is a widely used indicator of a water body’s resistance to mixing, commonly used with both observed and simulated temperatures [
61,
62,
63,
64,
65,
66]. Schmidt stability describes the amount of mechanical work needed per unit surface area to mix a stratified water column into a homogeneous state [
67]. According to Schmidt stability theory, larger values denote strong stratification and near-zero values indicate an isothermal, fully mixed structure [
62]. Schmidt stability (
S), measured in Jm
, is described in Equation (20) [
68].
Area (m2) is represented by A0 for surface area and Az for surface area at depthz (m). ρz stands for the density (kgm) at any given depth, where ρ* is the volume-weighted mean density within the water column. The depth at which this mean density occurred is denoted by z* (m). Gravity-induced acceleration is indicated by g (ms).
Acknowledged downsides to
S analysis include that, primarily, it is limited by a 1D assumption which simplifies both the stratification and the final homogeneous state of the full water column. This 1D calculation, which commonly uses measurements taken from the deepest point within a reservoir [
66,
69], can be problematic in larger water bodies or reservoirs where there are large mass-balance changes for which horizontal heterogeneity cannot be assumed.
S was used to diagnose when stratification was present and was not present. A threshold was based on 10% of the maximum daily S of the observed summer, 28.26 Jm. This placed the threshold at 2.83 Jm; this will be used when considering the results.
2.9. Mann-Kendall Trend Test
The Mann–Kendall trend test [
70,
71] allows for distinguishing statistically significant trends, both increasing and decreasing, over a temporal data set. This statistical test has often been used to examine trends within hydrology and meteorological time series and has been used within studies looking at climate change effects [
72,
73]. In this study, a significance level of
= 0.05 was considered, with the analysis being done in MATLAB.
4. Discussion
In situ observations, displayed in
Figure 5, show that Blagdon Lake will stratify during a heatwave such as that observed in June 2017. Furthermore, other stratification events were also observed in May, July and August 2017 when considering the entire reservoir. This shows that the bubble plumes were not able to prevent stratification within the reservoir over the duration of the summer. It should be noted, however, that the bubble plumes have been considered largely successful at reducing soluble manganese concentrations in the Blagdon in-take water to the treatment plant.
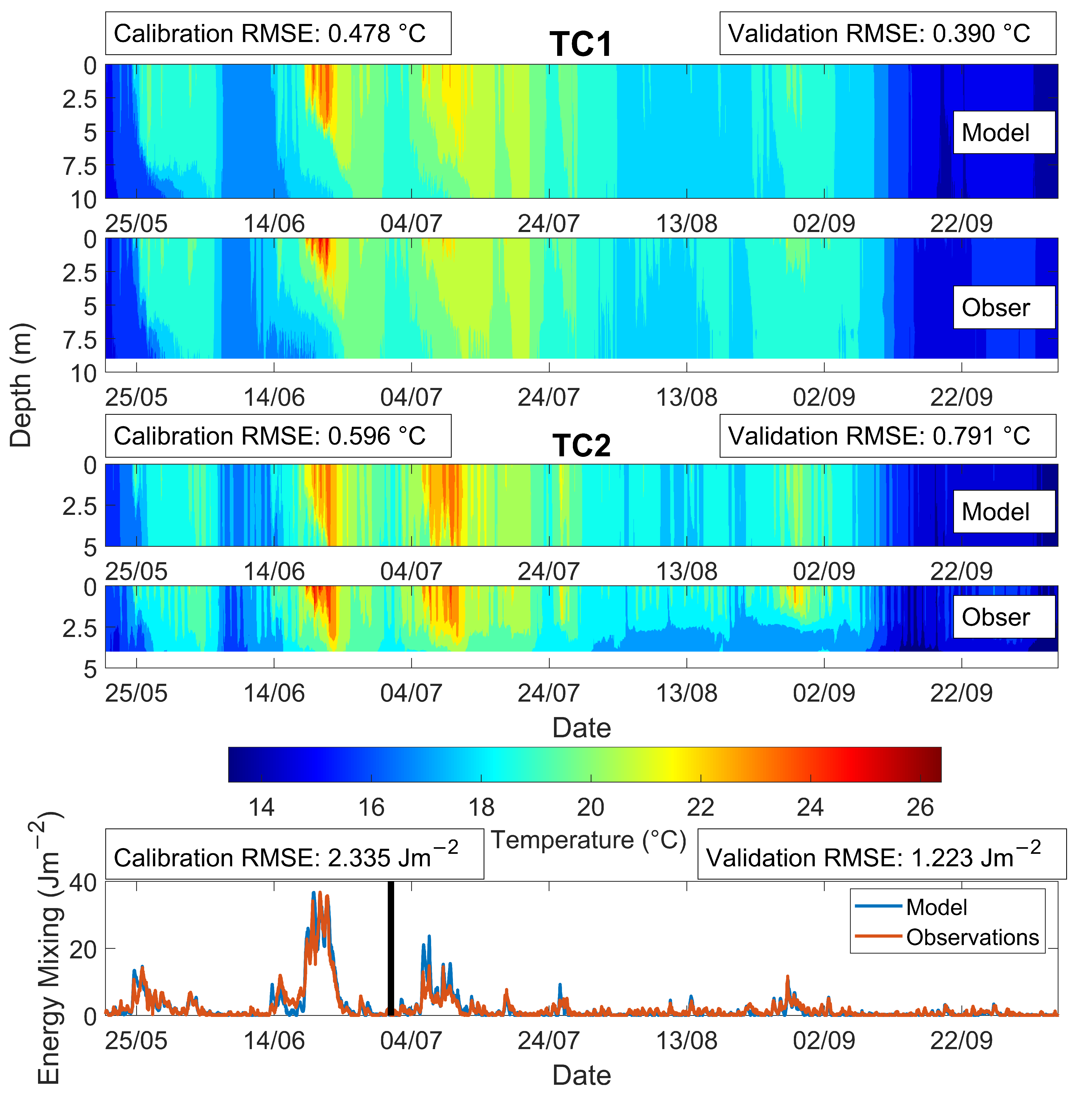
As shown from the results in
Figure 6, this study provides a robust example of the effectiveness of the AEM3D model for simulating hydrodynamic environments. Even with indirect forcing, the model was able to represent ephemeral stratification within a shallow reservoir. The model does remarkably well at resolving the energy requirements to mix the reservoir. Results also showed that the developed model appropriately characterised the thermal structure and much of the mixing/stratification within the reservoir.
There were mixed results based on the methodology for down-scaling daily meteorological factors into hourly datasets. Some factors with stronger diurnal patterns such as
Ta,
RH and solar radiation produced much closer agreement (
Figure 3). There were less accurate fits for wind where this diurnal pattern is much less prevalent. Nevertheless, all the down-scaled parameters had strong correlation coefficients shown in
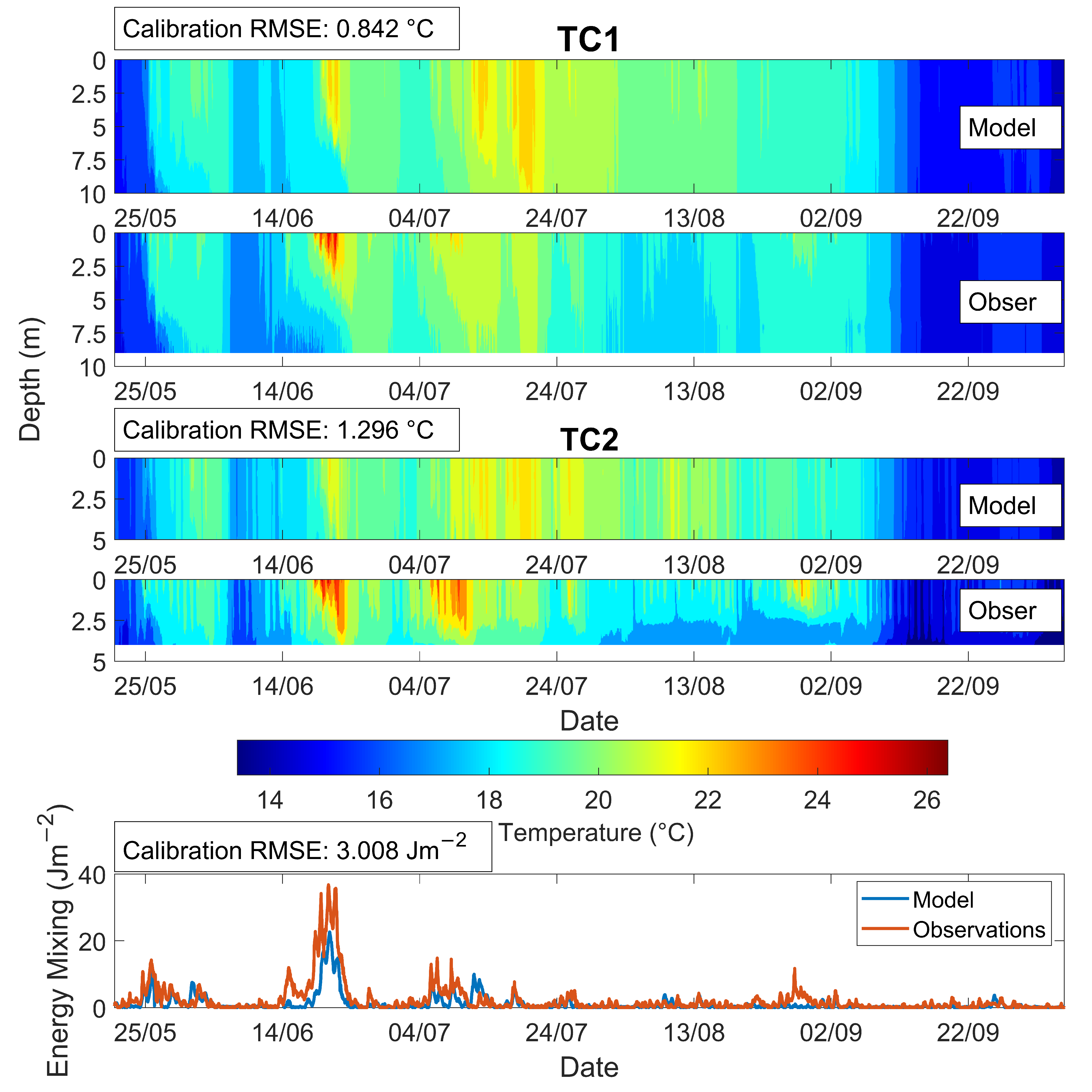
Table 1. Methods were selected that made use of the available future modelled weather; this is one area that could be improved upon, e.g., if a more diverse future data set was to be used. When the down-scaled forcing data were used for forcing, the model produced results in line with in situ lake temperature measurements (
Figure 7). The shift in time of the warmest daily temperature might delay the estimate for lake temperature maximum. This may limit the model applicability to resolve issues on smaller time steps. However, the reasonable temperature error and correlation in energy requirements over the length of the simulation, seen in
Figure 7, show it is applicable when discussing trends over the course of the year. Additionally, the model was found to underestimate the stability (
S in
Figure 7), capturing 47% of the mean energy requirement during the June heatwave. The down-scaled run underestimated the surface water temperature during this heatwave but performed better during other stratified periods. This should be considered when interpreting the results.
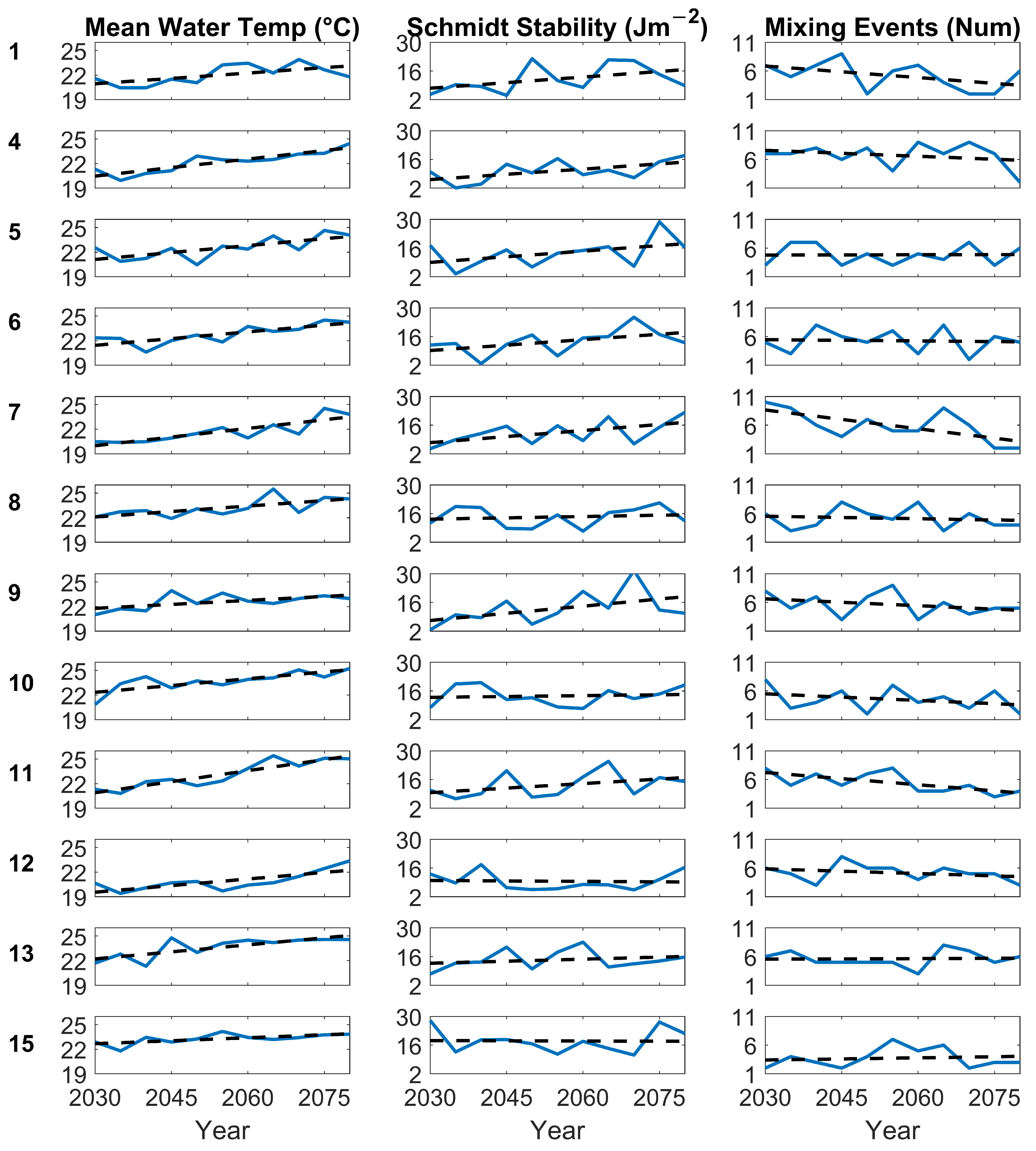
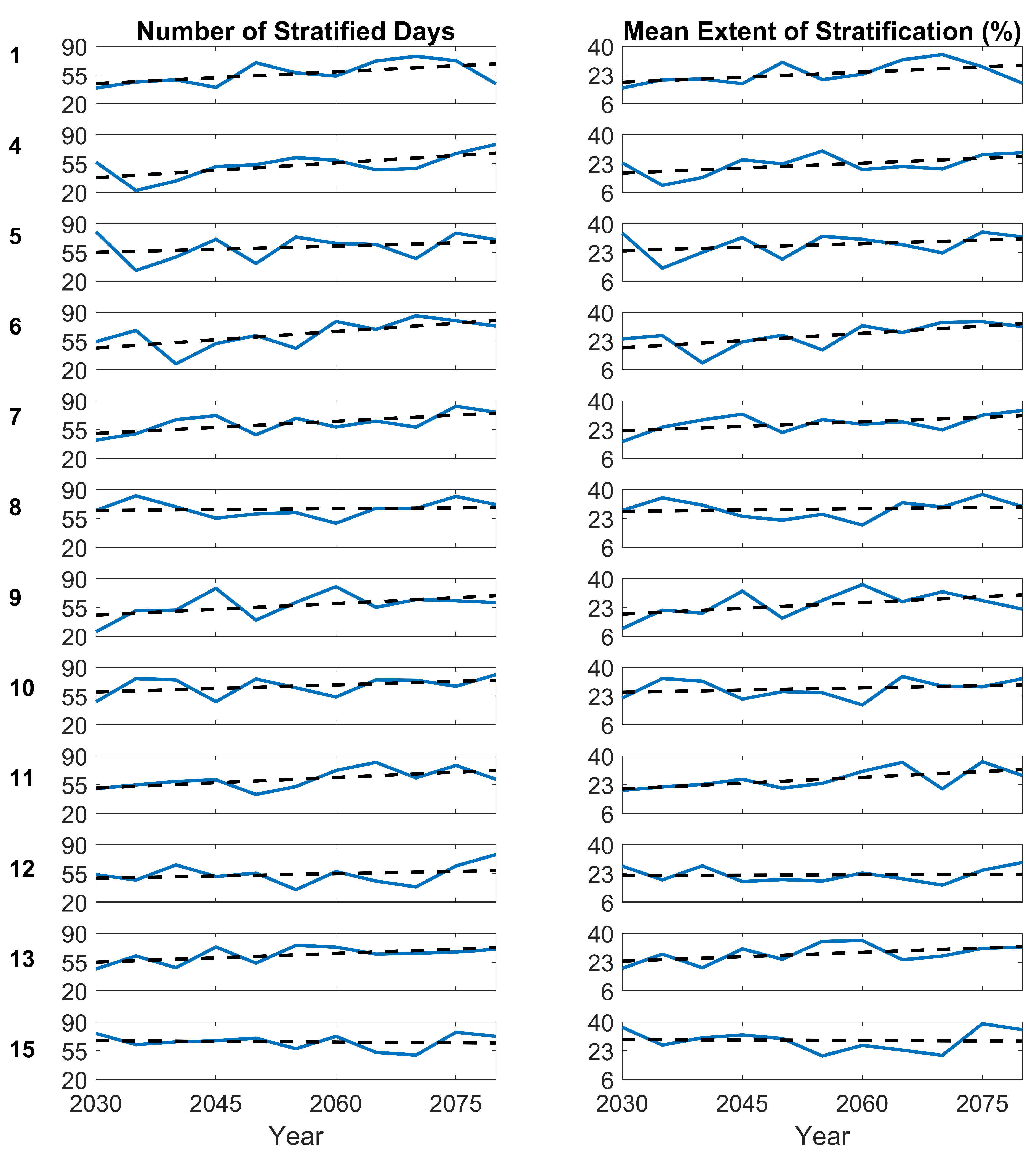
Despite the increased heat content within the reservoir (
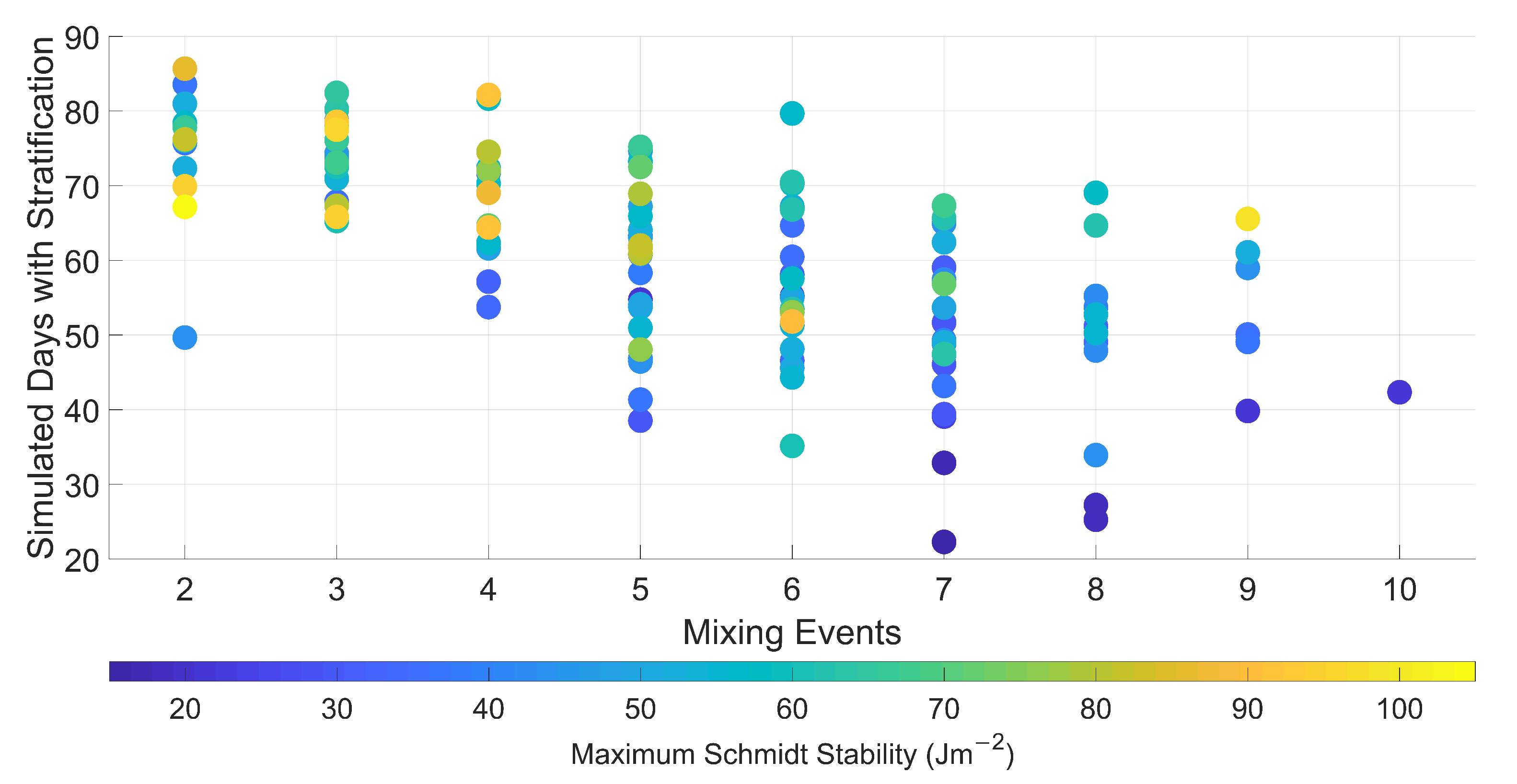
Figure 9), the lake maintained polymixis and mixed numerous times over the modelled summers, though scenarios 7 and 11 showed a statistically significant decreasing trend of mixing events. As these scenarios were modelled over summer periods, the model is possibly missing shorter stratification events before and/or after the summer and a true monomictic regime cannot be confirmed. Additionally, there are a few runs that stand out as outliers, where a more monomictic nature with higher
S and a lower number of mixing events, is displayed during the simulation period (
Figure 10). The model did highlight some evidence of increased extent and length of stratification (
Table 3 and
Figure 9) as scenarios 6 and 11 showed evidence of a statistically significant trends in these factors. Other studies have provided some evidence of polymictic lakes stratifying for longer periods [
74,
75,
76]. There was no statistically significant trend for increasing energy requirements to mix the reservoir, though most of the scenarios showed a positive trend. It should be noted that the actual energy requirement is likely underestimated, as seen in
Figure 7.
Across all runs, none remained well mixed throughout the simulation period, with some stratified periods always remaining present. This is highlighted in
Figure 10 where all the model runs had
S above the chosen threshold of 2.83 Jm
during the simulation, supporting the view that, in the future, the reservoir will continue to be at risk of stratification and the associated water quality impacts. It is thought that the current ephemeral stratification persists as the increased atmospheric heating is not sufficient to stabilise the water column enough to prevent mixing. Thus, when mixing occurs the increased heat content is mixed down into the hypolimnion; as such, when the next stratification event occurs, the relative temperature difference between the epilimnion and hypolimnion is not meaningful different to conditions experienced in the present and hence the stability does not meaningfully increase with time.
Model runs for this study were performed based on the RCP 8.5 climate projection, which projects an increase in GHG production from the present and is often considered the “worst case” scenario for climate change, with the temperature increase reaching 4.3 °C by 2100. With a continuation of the current stratification regime under this “worst case” scenario, this would imply any results based on modelling using less-extreme temperature increases will also show little to no modification to the current stratification regime.
The use of discontinuous runs means that the model results will not take the retention of heat from previous years into account. This was primarily done to optimise the available computational times. The amount of heat retained year to year cannot be quantified as observations are not sufficiently long enough. However, the reservoir has a dynamic outflow and the residence time is around 315 to 430 days. As the reservoir can completely flush in less than a year, this yearly heat retention may not be a significant issue.
The results of the study indicate that the bubble plume mixer arrangement, as currently operated within the Blagdon Lake, will continue to be unable to prevent stratification moving forwards, as shown by summer 2017 heatwave data in
Figure 5 and future model results in
Figure 10. Results suggest than an artificial mixing system that can effectively prevent stratification from developing during current conditions will likely also be effective at preventing stratification for several decades. Additionally, with scenarios 6 and 11 showing an increase in the areal extent of stratification, it is possible that some alterations to the areal extent of mixing via bubble plumes might need to be considered.
Ultimately, the results here demonstrate that modelling is an effective tool for predicting whether existing reservoir aeration systems are currently effective and if they are likely to remain so in the future. While stratification does not meaningfully change under the modeled future scenarios, the over-heating of the reservoir may pose other concerns. Conditions may start to favour algal growth at higher temperatures; this may require additional management focus and adapted strategies in order to counteract this potential future water quality threat. Furthermore, increased water temperature may cause shifts in microbial communities, corresponding oxygen consumption and biogeochemical cycling (e.g., trace metal release from sediments) [
77].
5. Conclusions
A shallow drinking water reservoir, artificially mixed by bubble plumes, was observed for summer 2017 and, using the 3D hydrodynamic model AEM3D, modeled with down-scaled hourly future climate data. The calibrated model did well at representing the shallow lake based on a summer of observations with a RMSE of 0.53 °C. In situ measurements from 2017 and supporting model results highlight that, despite the operation of bubble plumes, the reservoir still stratified during the summer. Supporting source water quality data suggest that the plumes have been successful at addressing issues related to soluble manganese but not cyanobacteria blooms.
Twelve climate scenarios from RCP 8.5, often thought to be the worst-case scenario prediction, were considered using 5-year intervals from 2030 to 2080. These were down-scaled using various sub-daily methods which exhibited mixed results. Using the bubble plume arrangement at Blagdon, eight of these scenarios showed statistically significant trends of increasing mean water temperature increasing with the warming climate. On average, across all the scenarios this increase is around 2.7 °C between 2030 and 2080. Only two scenarios showed a statistically significant trend of decreasing mixing events and no scenarios showed a meaningful trend of changing energy requirements to mix the reservoir. The majority of the evidence suggests that, while the reservoir warmed, the present stratification regime will likely continue with no significant climate-induced changes to the current stratification regimes. Though some scenarios showed some evidence of gradual shift to monomitic conditions, scenarios 6 and 11 showed a significant increase in the extent (between 0.2 and 0.3 % of the reservoir per year) and length of stratification (between 0.4 and 0.7 days per year).
The results show that under the current bubble plume arrangement and operation, issues with stratification will remain; every model run showed the presence of stratification, with maximum S of 15 Jm or greater. To prevent further stratification-related issues with source water quality, reservoir managers need to consider what mitigation options might be required to be more effective in the future. Here, in situ observations demonstrated that bubble plumes are currently not fully effective and, under modelled scenarios, their ineffectiveness will likely continue. The bubble plumes are currently being operated below the given threshold of airflow of 9.2 m3 min km for total mixing; targeting this threshold could be a better approach for future proofing. Modelling can be an effective tool for reservoir managers to proactively assess the effectiveness of current reservoir management schemes as well as necessary mitigation in the future. This approach will support evidence-based decisions on whether further mitigation and/or enhancement of current management strategies are required.
Future work could examine similar aeration systems in future climates to see how these will perform in comparison to results obtained for Blagdon Lake. Consideration should be placed on how to improve best practice for such artificial destratification systems to safeguard against future water quality risk. A wider range of climate scenarios could also be considered to establish a broader scope of possible responses to future climatic change.