1. Introduction
Due to its high population density, South Korea has only one-sixth of the world’s average water available per capita and suffers from deterioration of water resource quality, floods, and droughts due to significant variance in yearly regional and seasonal precipitation [
1]. In particular, islands and mountainous areas suffer from annual water shortages that require the use of emergency water supplies with restrictions on water usage. These shortages are due to low water inflow, specifically on tributary streams with delayed investment in infrastructure, causing an increase in damage of water-related natural disasters [
1,
2]. To overcome these issues, Korea has constructed multipurpose dams to manage water resources. However, climate change significantly increases the probability of water-related disasters (e.g., floods and droughts) and adds to the uncertainty of water resource management [
2]. Consequently, climate change alters dam inflow patterns, adding difficulties to water supply and water resource utilization plans [
3]. According to Jung et al. [
4], researchers previously used conceptual and physical hydrologic models to predict the water level or inflow rate of the dam; however, these models must include meteorological and geological data, and prediction accuracy varies based on the number of parameters. In addition, conceptual and physical hydrologic models require constant verification and adjustment of each input parameter, causing an increase in simulation time and reducing the overall time to prepare for a natural disaster. Researchers have used various models, such as the Hydrological Simulation Program—Fortran [
5], the watershed-scale Long-Term Hydrologic Impact Assessment Model [
6], and the Soil and Water Assessment Tool (SWAT) [
7], to predict the river discharge and dam inflow rate.
In the case of the Soyang River, some areas of the watershed are located in North Korea, resulting in insufficient hydrological data for prediction, and SWAT does not yield accurate inflow rate predictions. Furthermore, the Soyang Dam, a multipurpose dam that controls water supply and generates power for the Seoul metropolitan area, is located on the Soyang River. To overcome the lack of accurate hydrological data to predict the Soyang River Multipurpose Dam inflow, researchers have used data-driven models [
8,
9,
10,
11,
12,
13,
14,
15,
16]. The proposed model not only can predict the inflow rate without detailed hydrological data but also outperforms the existing algorithms [
8,
9]. We believe that our model can be applied to other dams that do not have sufficient hydrological data for predicting the inflow rate.
Data-driven models are capable of repeatedly learning the complex nonlinear relationships between input and output data to produce highly predictive performance, regardless of the conceptual and physical characteristics. Researchers worldwide use data-driven models for various applications, such as decoding clinical biomarker space of COVID-19 [
17], water quality prediction [
18], and pipe-break rate prediction [
19]. Researchers attempt to use data-driven models for various hydrological predictions, such as MARS [
20,
21,
22,
23,
24], DENFIS [
25], LSTM-ALO [
26], and LSSVR-GSA [
27]. MARS uses forward and backward step to add and remove piecewise linear functions to fit the model. However, there is performance degradation if data contain too many variables. To get the best result, MARS requires variable selection [
20,
21,
22,
23,
24]. DENFIS requires prior assumptions about data and needs domain knowledge to set predefined parameters. Yuan et al. [
26] claim that LSTM-ALO can find the optimal hyperparameter with an ant-lion optimizer. However, the model uses a variable to predict the runoff. Adnan et al. [
27] claim that the gravitation search algorithm (GSA) will help to find the optimal value for the least square support vector regressor (LSSVR). LSSVR is a modified version of the support vector regressor (SVR) that reduces the complexity of the optimization program [
24]. Even though LSSVR-GSA outperforms LSSVR, there was no mention that implementing GSA would reduce the overall training time.
In the case of inflow rate prediction, researchers used SVR [
10,
11,
12], Comb_ML [
9], multivariate adaptive regression splines (MARS) [
28], random forest [
9,
10,
11,
12,
13], and gradient boosting [
9,
11,
14]. In addition, deep learning models, such as multilayer perceptron regressors (MLP) [
9,
10,
13], recurrent neural networks (RNNs) [
8], and LSTM [
15,
16], as the models for inflow rate predictions. These models have proven to be highly effective in predicting inflow rates, but they do not have the ability to capture input data’s long-term dependencies and summarize the data.
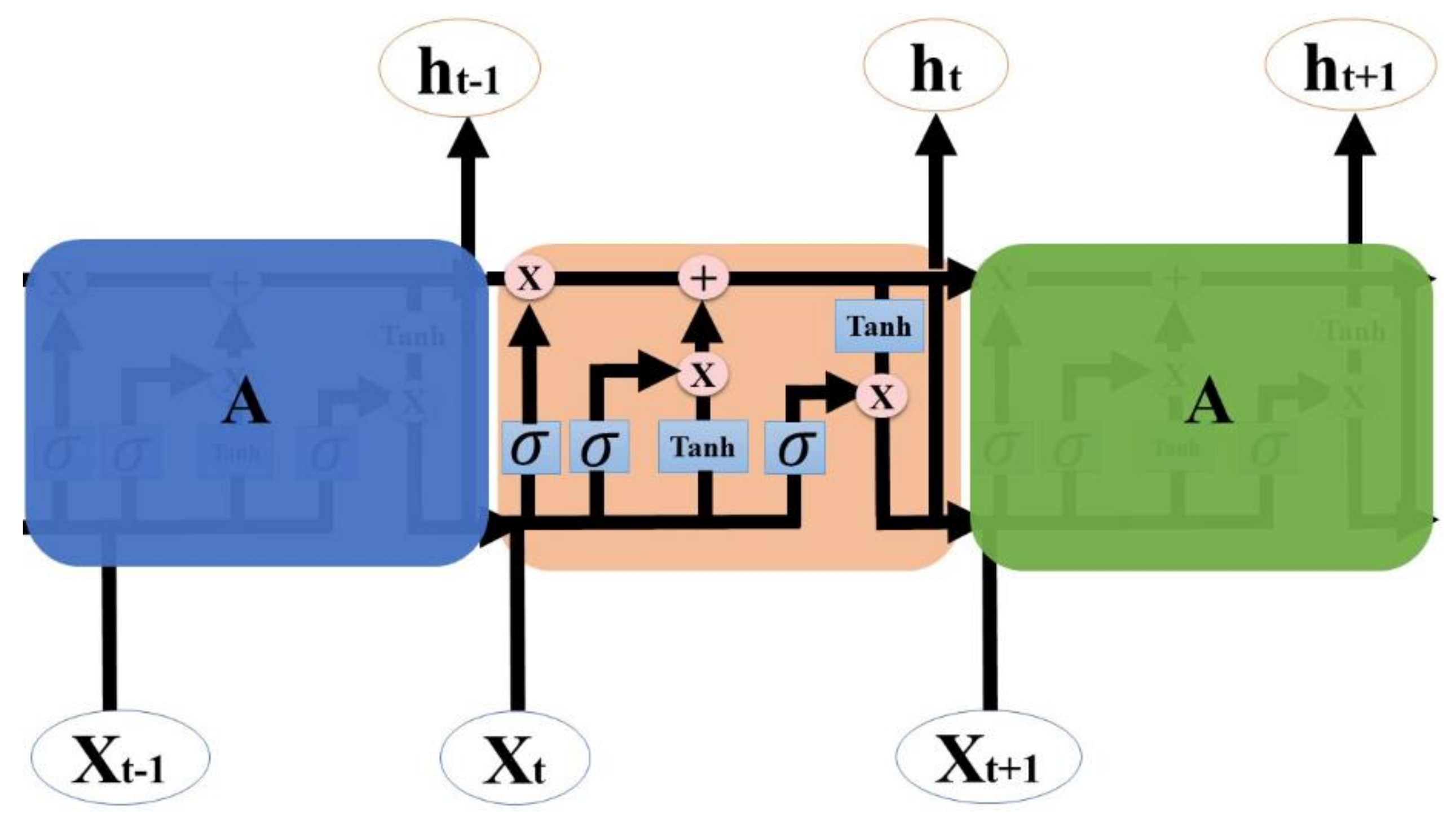
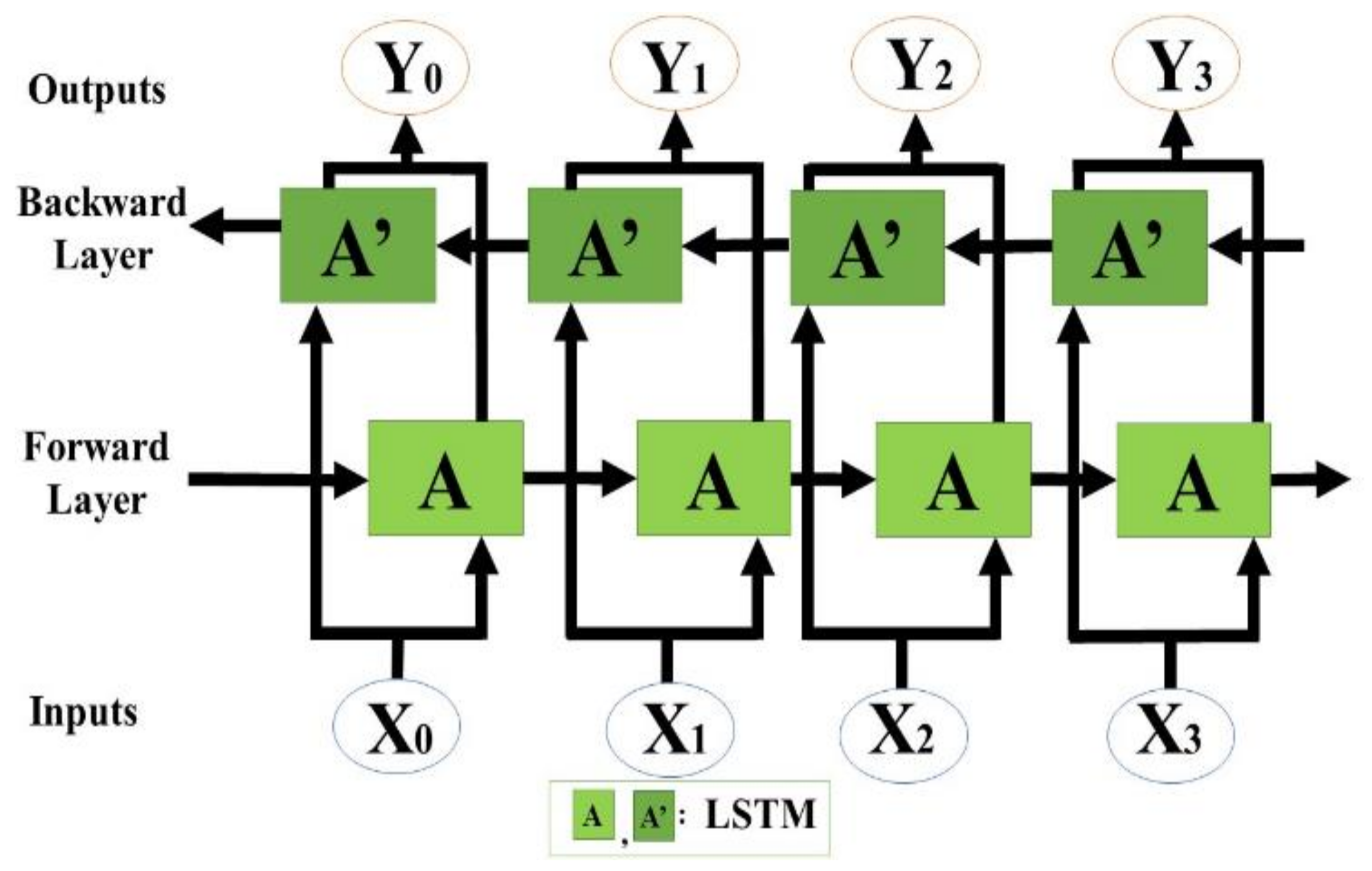
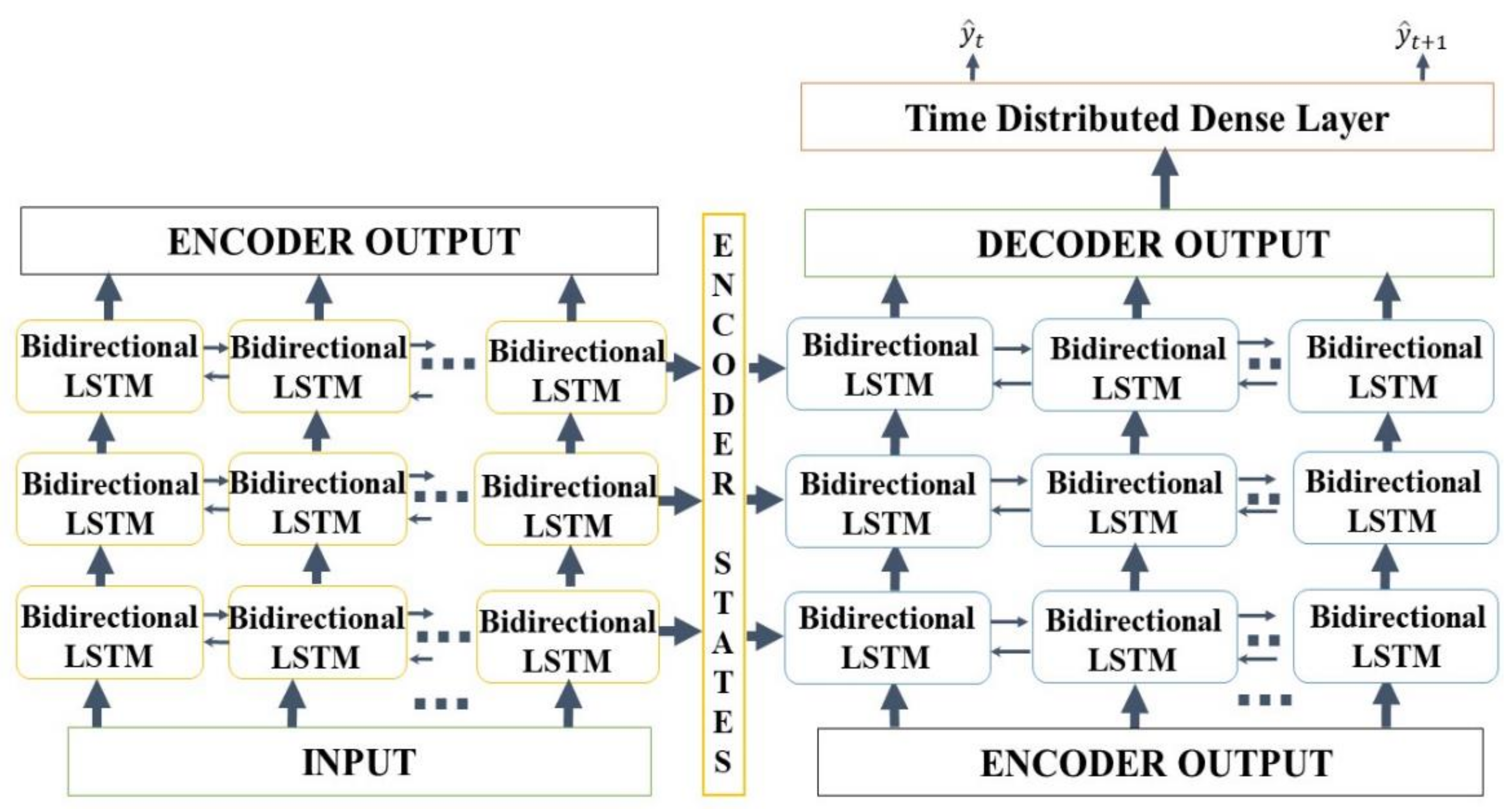
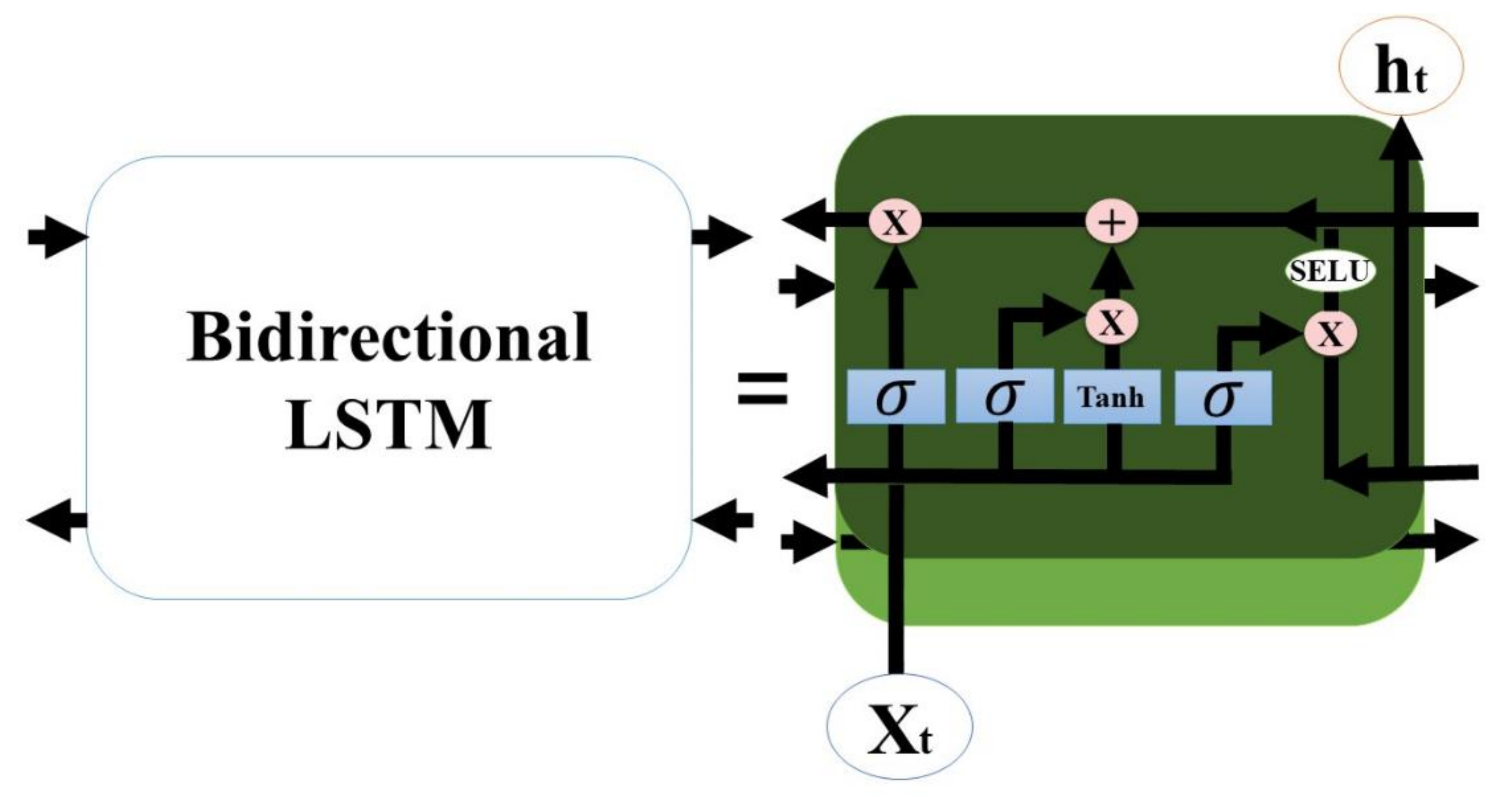
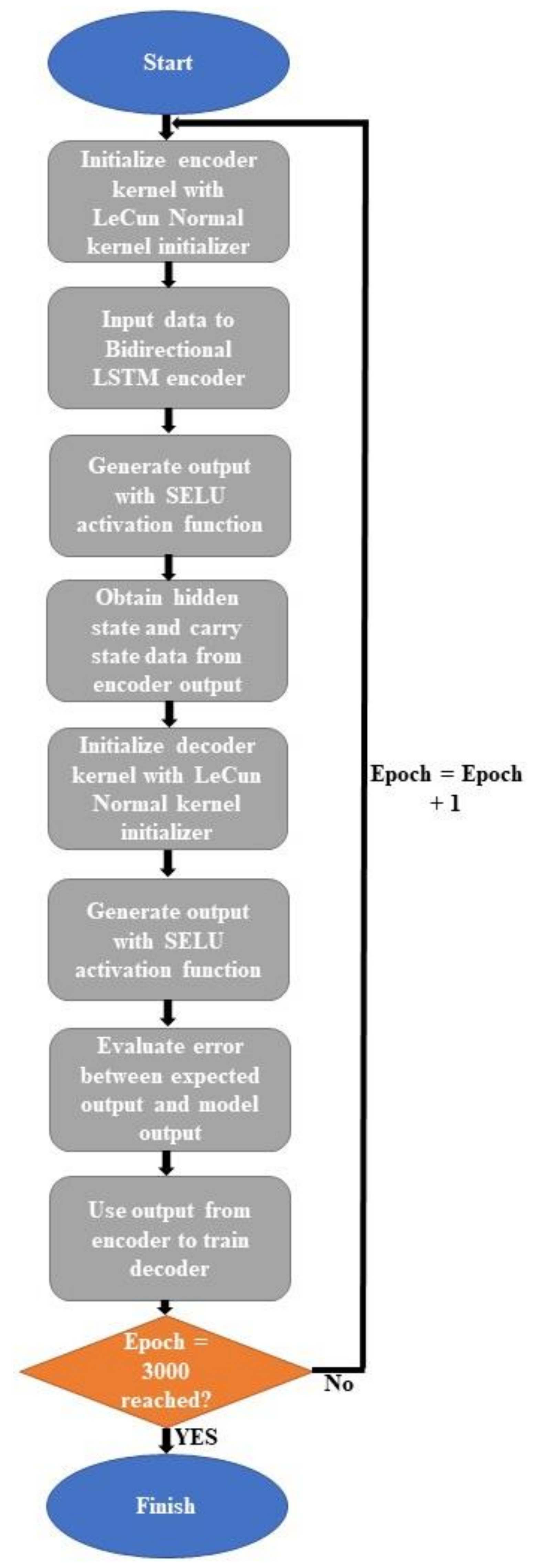
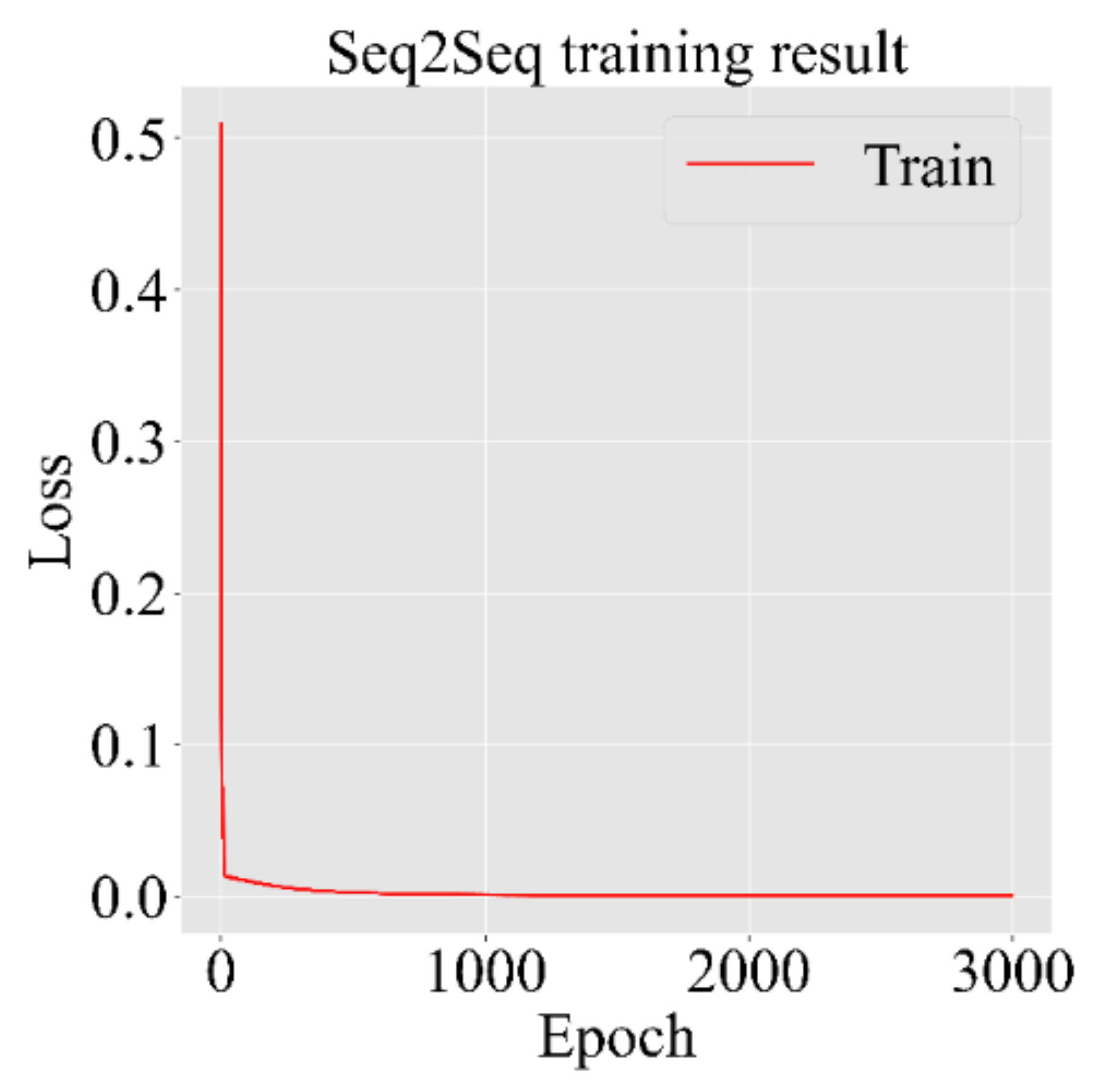
We propose an end-to-end model that consists of a Seq2Seq algorithm incorporated with bi-directional LSTM and a scaled exponential linear unit (SELU) activation function to predict the inflow rate over a period of two days. Then we evaluate and compare the model with other algorithms. The Seq2Seq model consists of an encoder and decoder. First, the encoder summarizes the information of the input sequence. Then the decoder uses the summarized information for prediction. We use LSTM for both an encoder and a decoder. LSTM consists of gating units to handle sequential data and learns long-term dependencies. In addition, we incorporated bidirectionality with LSTM to extract extra information about complex relationships between present and past data. Lastly, we change the activation function of LSTM from tanh to SELU with LeCun normal kernel initializers to stabilize the training process despite the presence of abnormally high and low inflow rates. We did not use any decomposition method because we believe bidirectional LSTM can extract information from flooding and drought events, and SELU activation function helps to stabilize the training process with the abnormal inflow rates. Our model proves that predicting the inflow rate is possible without using detailed hydrological data.
In this article, we construct some commonly used machine learning models to compare the prediction accuracy with the proposed model. Then, we evaluate the result of the proposed model by using a discrepancy ratio. We propose a deep learning algorithm that surpasses the prediction accuracy of the existing algorithms, such as RNN [
8] and Comb-ML [
9], in predicting the inflow rate of the Soyang Multipurpose Dam for a period of two days. We also compared the prediction accuracy of our model with those of the existing machine learning models.
The contributions of this study are as follows:
We developed an end-to-end model capable of summarizing input data for inflow rate forecasting.
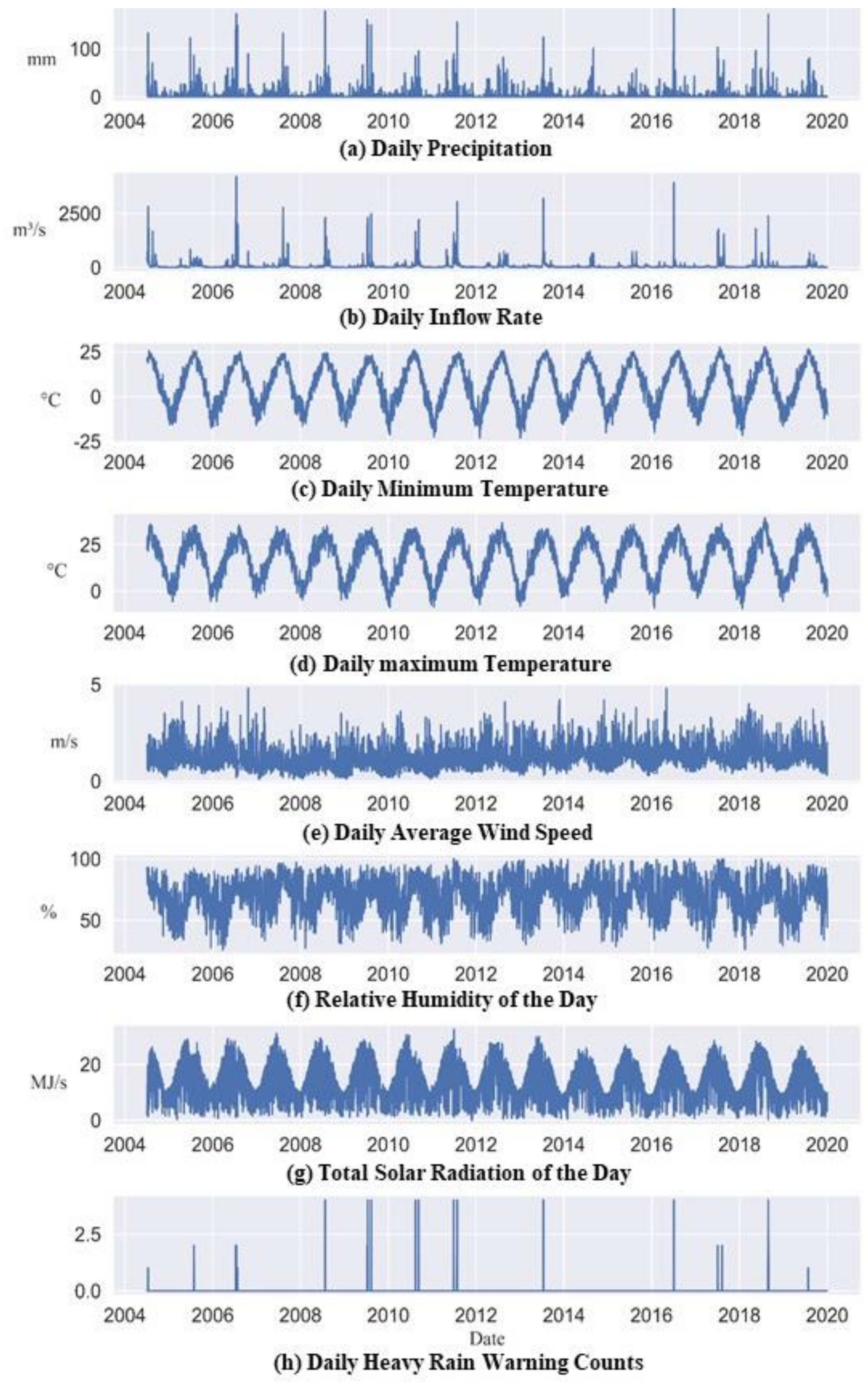
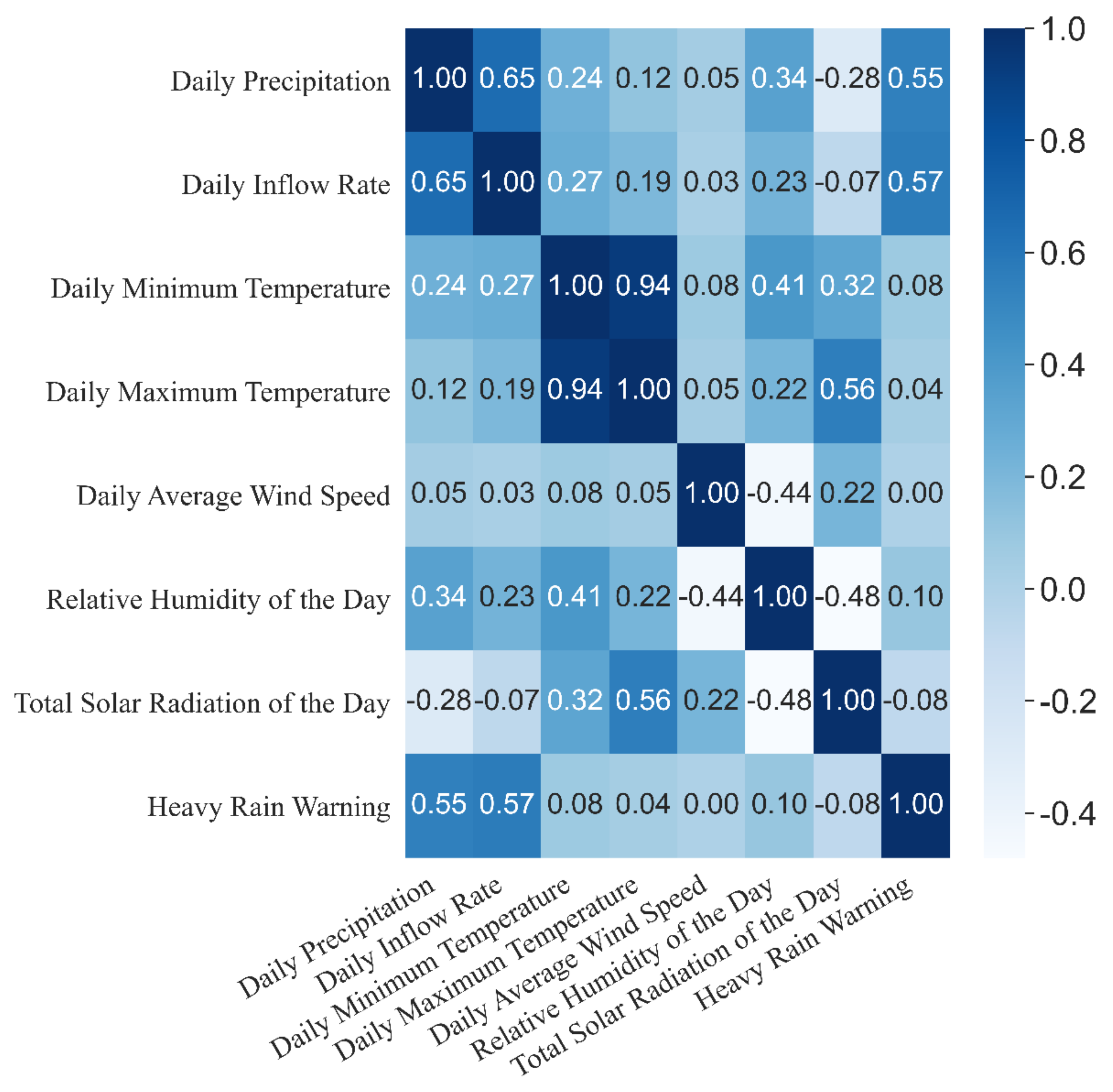
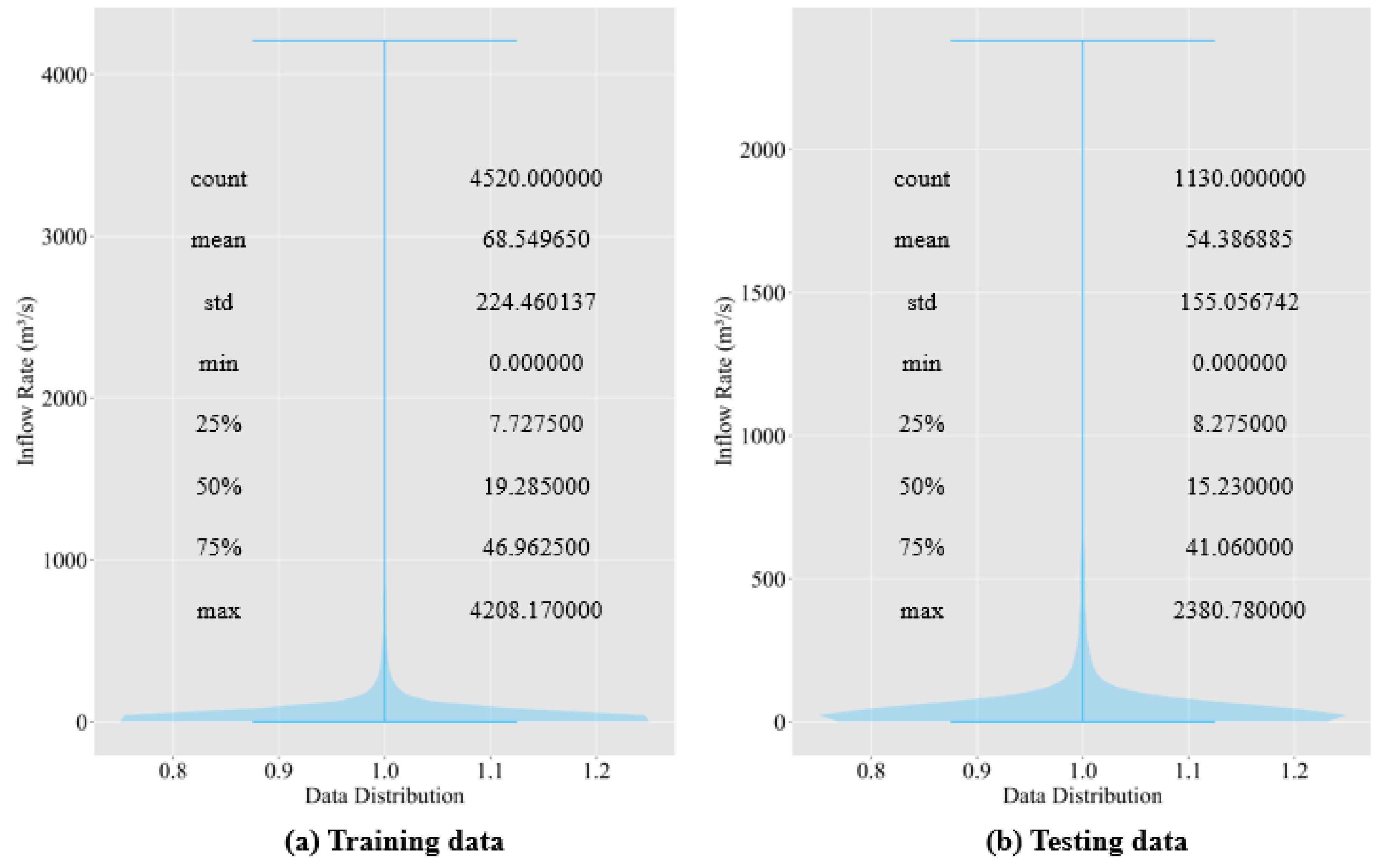
Unlike previous research, we only used nearly 15 years of weather warning data, along with the meteorological and dam inflow rate data.
Our Seq2Seq model used bidirectional LSTMs, SELU activation function, and LeCun normal kernel initializer to stabilize the training process and outperformed the baseline models in most accuracy criteria.
5. Conclusions
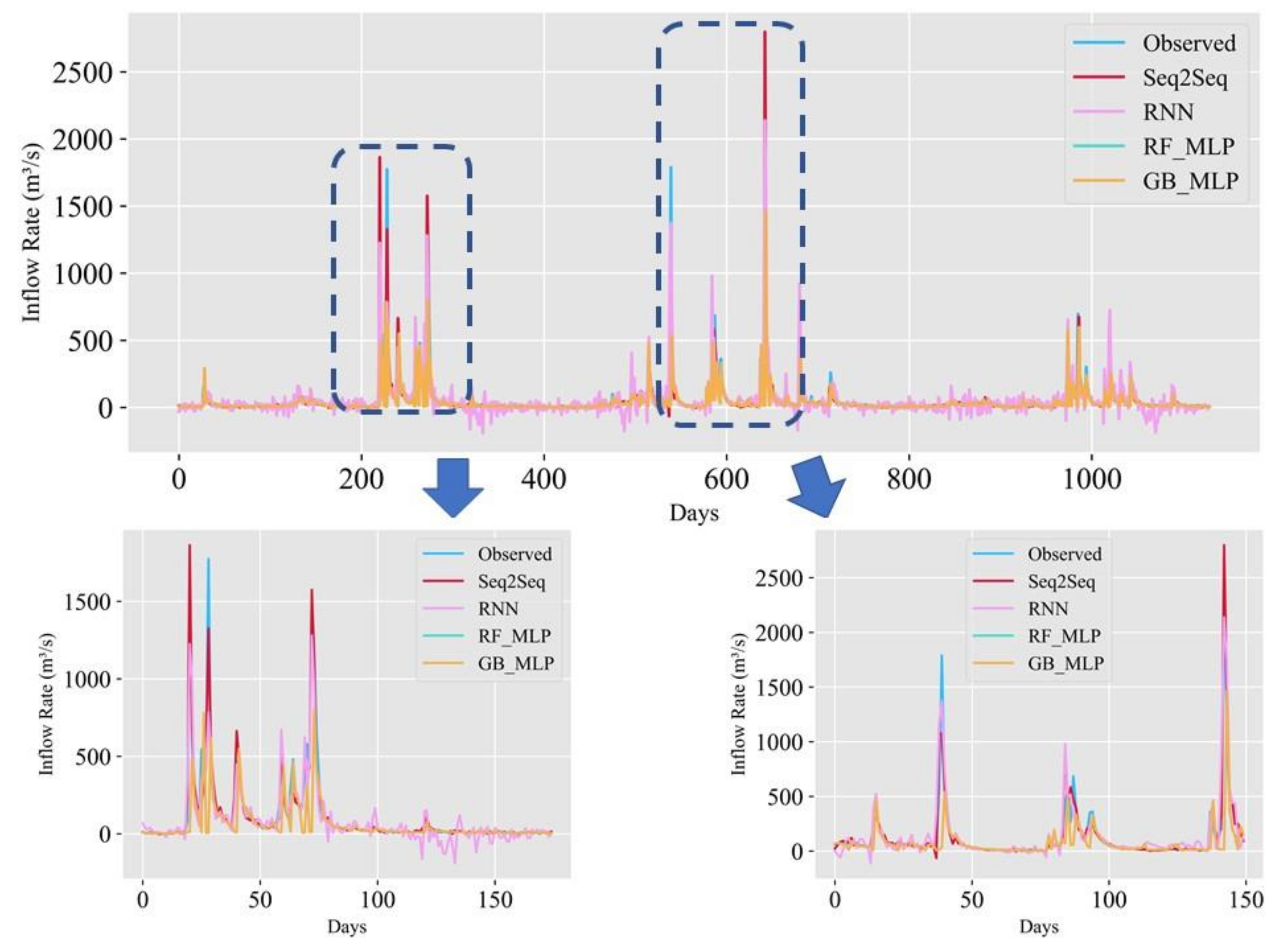
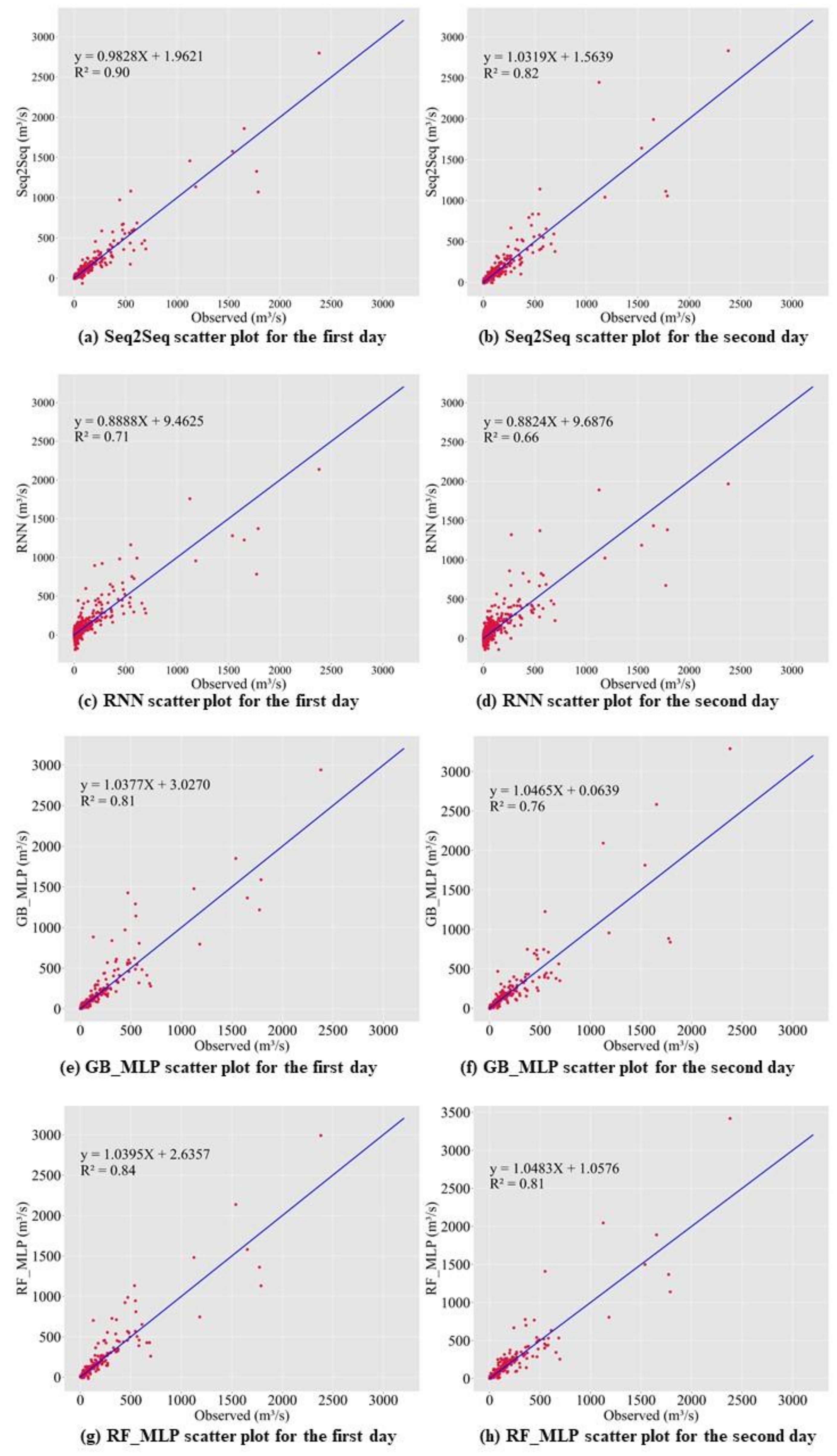
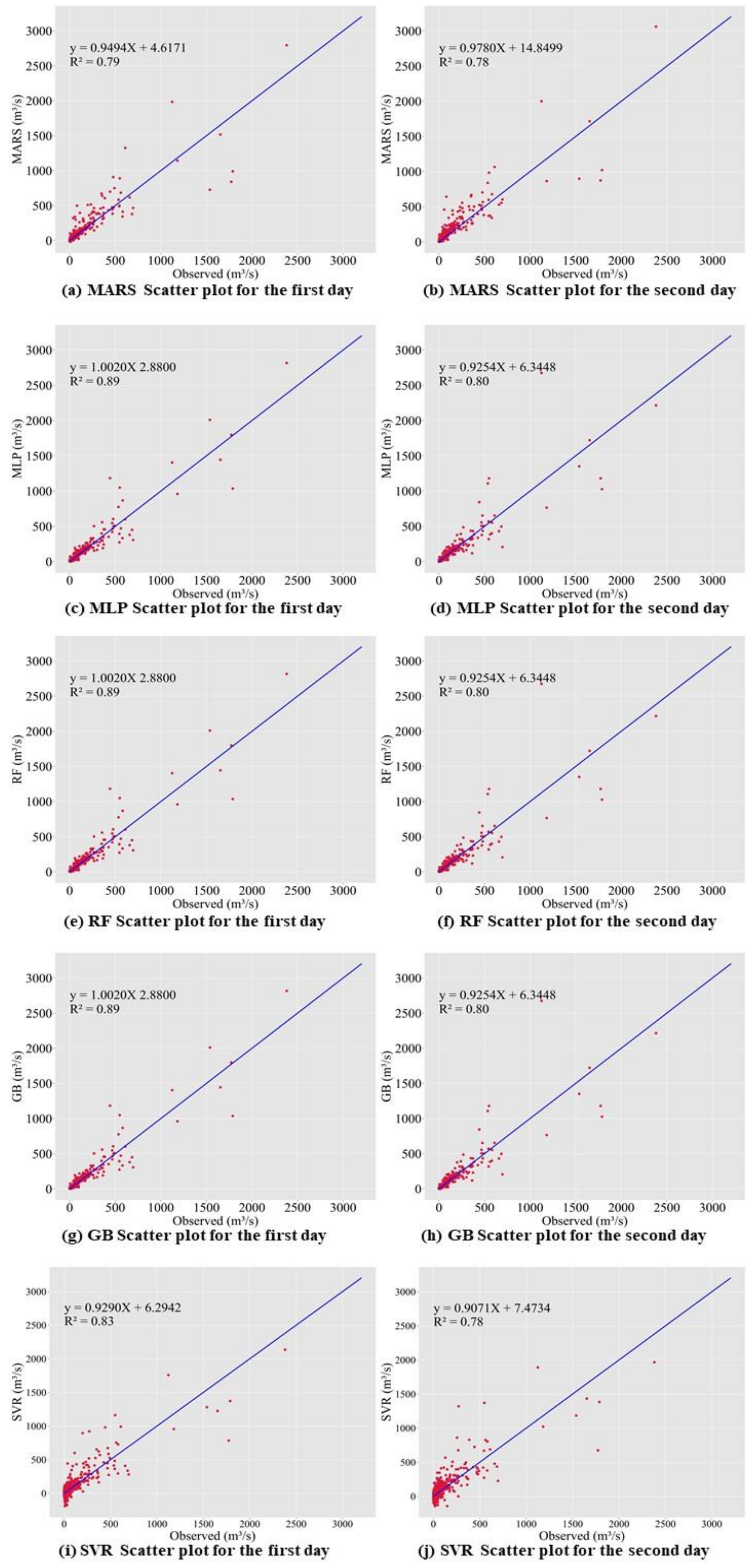
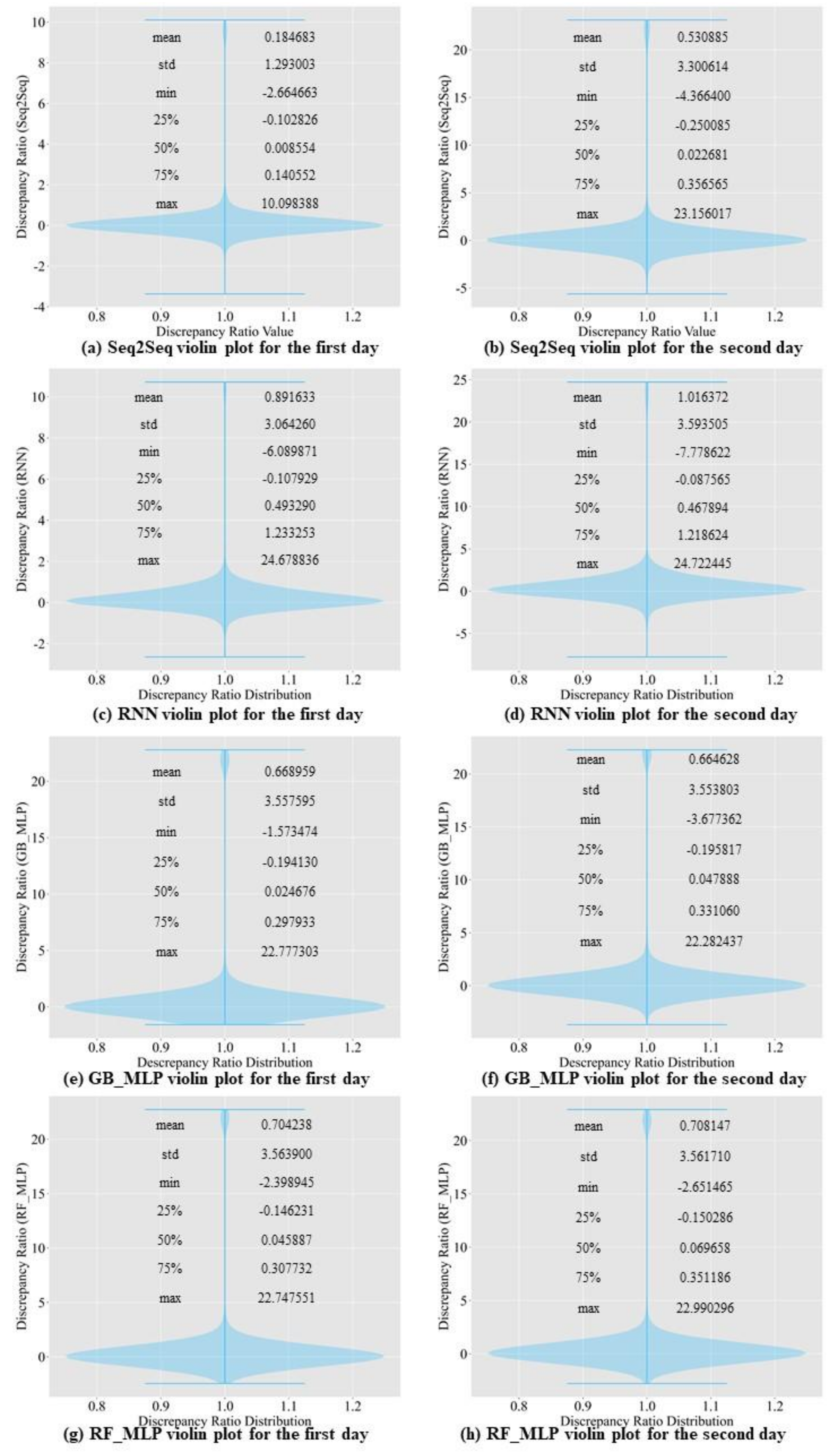
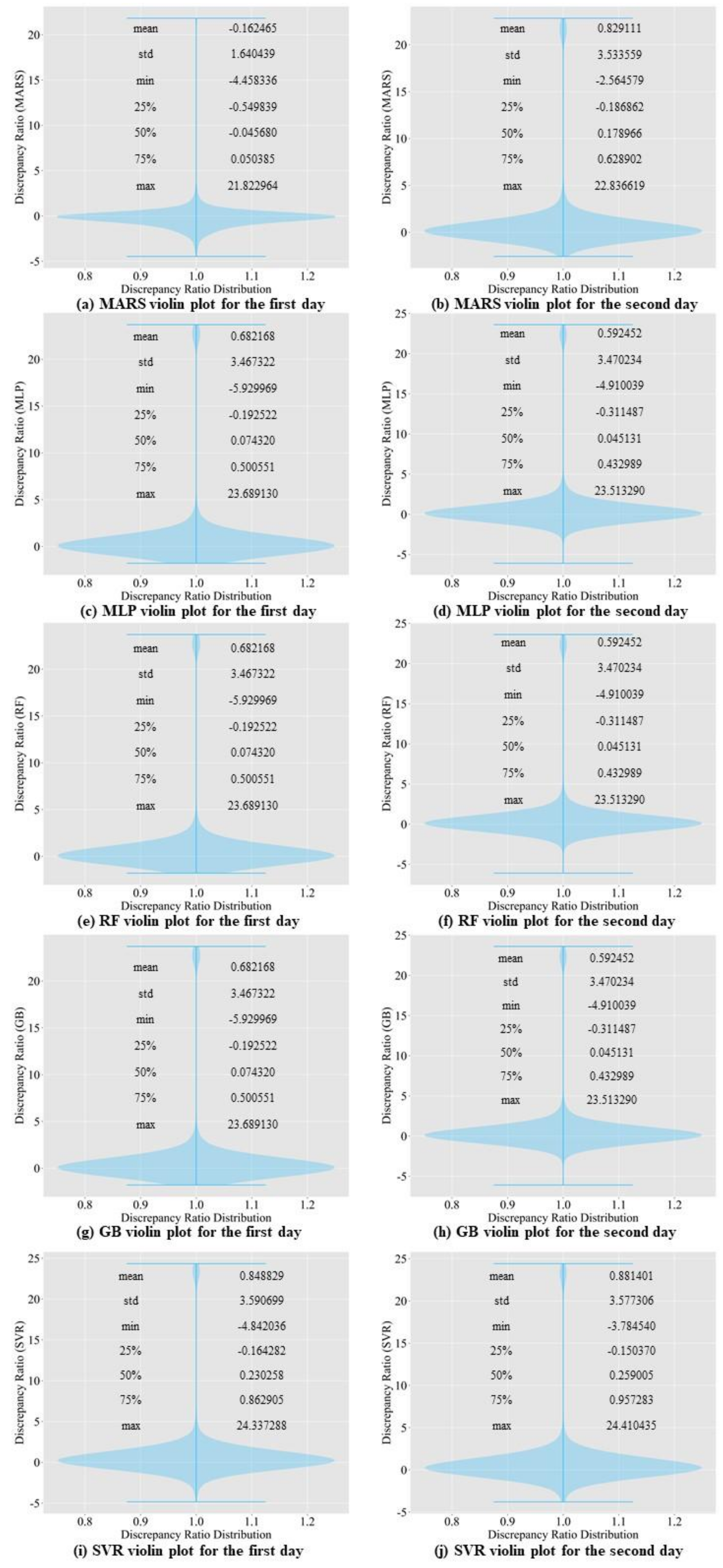
In this study, we propose a model that outperforms models from other studies. In addition, we set models from other studies as baseline models, namely MLP, random forest regressor, gradient boosting regressor, Comb-ML, and RNN models. We performed a grid search to determine the optimal hyperparameters for each model. Comb-ML combines an MLP model with an ensemble model, but its prediction performance was not better than that of the MLP model. The MLP model has the highest prediction accuracy, whereas RNN is the least accurate predictive model. The RNN model did not have the ability to retain important information for the prediction task. Therefore, the RNN uses all information without distinguishing critical information to predict the inflow rate. The prediction accuracy of our sequence-to-sequence model outperforms those of all baseline models. Only the next day’s MAE value for our model was higher than that of the MLP.
We propose the use of the SELU activation function with the LeCun normal kernel initializer for bidirectional LSTM to improve the prediction accuracy. This combination allowed stable training with self-normalizing features. Consequently, the model can accurately predict the inflow rate under extreme weather conditions, such as flooding and drought. In addition, bidirectional LSTM allows the model to learn the relationship from past to present and present to past. Therefore, the model requires more input information and predicts inflow more accurately than the baseline models.
Three cases were included in the ablation study. The first case involved removing the bidirectionality of the LSTM. The prediction accuracy decreased. The second case involved changing the SELU activation function to tanh. We observed a performance degradation in the inflow prediction. In the last case, warning data were excluded from training. The model returned less accurate predictions without the warning data. In conclusion, the ablation study proves that the bidirectionality of LSTM, a change in activation function, and the addition of warning data all contribute to the prediction accuracy.
The findings of this research show that the Seq2Seq model can be effective in predicting the inflow rate. Unlike physically based models, our model does not require detailed hydrological data for predicting the inflow rate. Therefore, our model is suitable for dams with lacking hydrological data. We also need to experiment with dams that contain abundant hydrological data to compare our model with physically based models. Lastly, we need to see how the Seq2Seq model performs if we include hydrological data to predict the inflow rate.