Predicting Inflow Rate of the Soyang River Dam Using Deep Learning Techniques
Abstract
1. Introduction
- We developed an end-to-end model capable of summarizing input data for inflow rate forecasting.
- Unlike previous research, we only used nearly 15 years of weather warning data, along with the meteorological and dam inflow rate data.
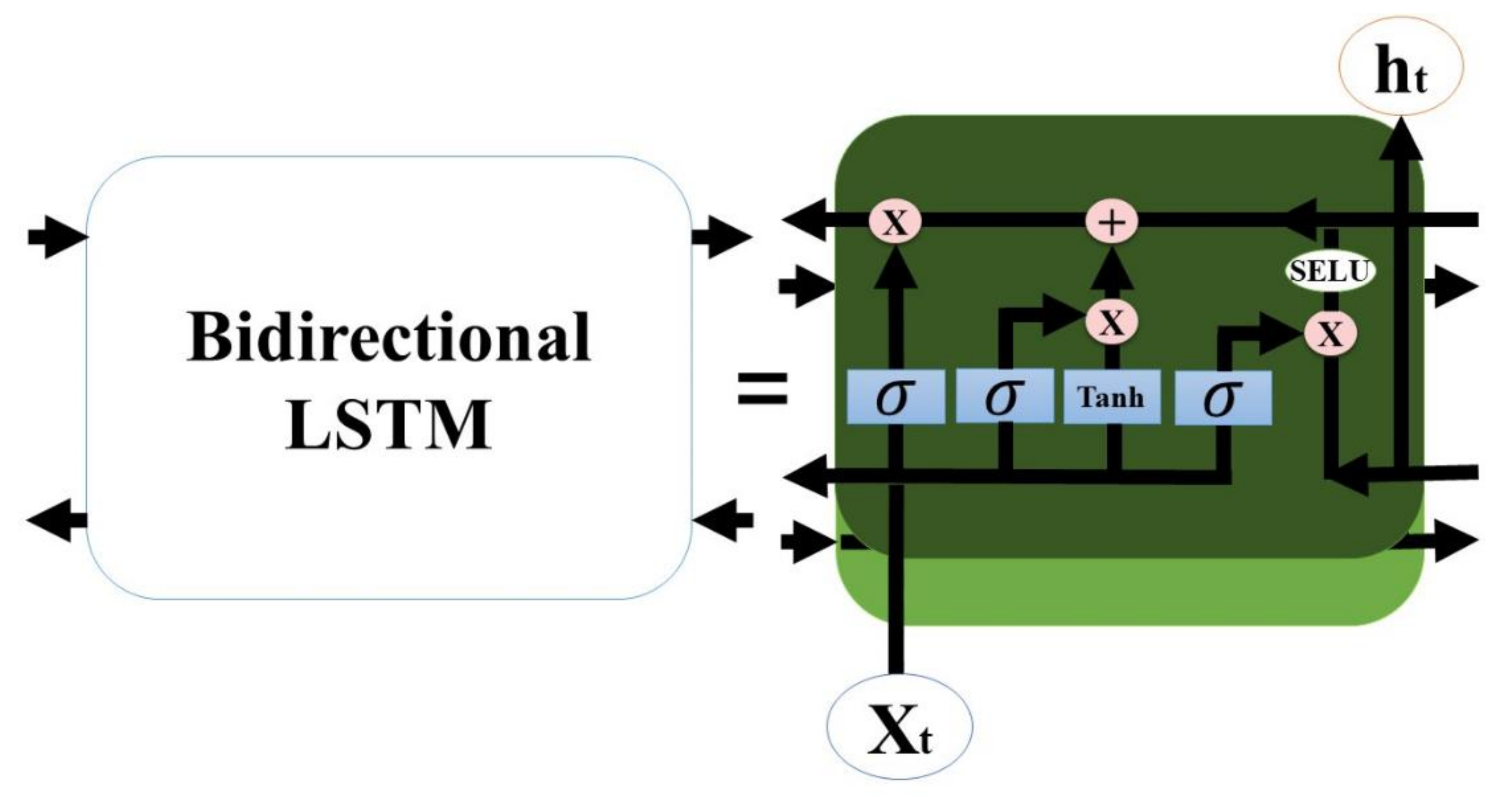
- Our Seq2Seq model used bidirectional LSTMs, SELU activation function, and LeCun normal kernel initializer to stabilize the training process and outperformed the baseline models in most accuracy criteria.
2. Materials and Methods
2.1. Study Area
2.2. Data Description
2.3. Background
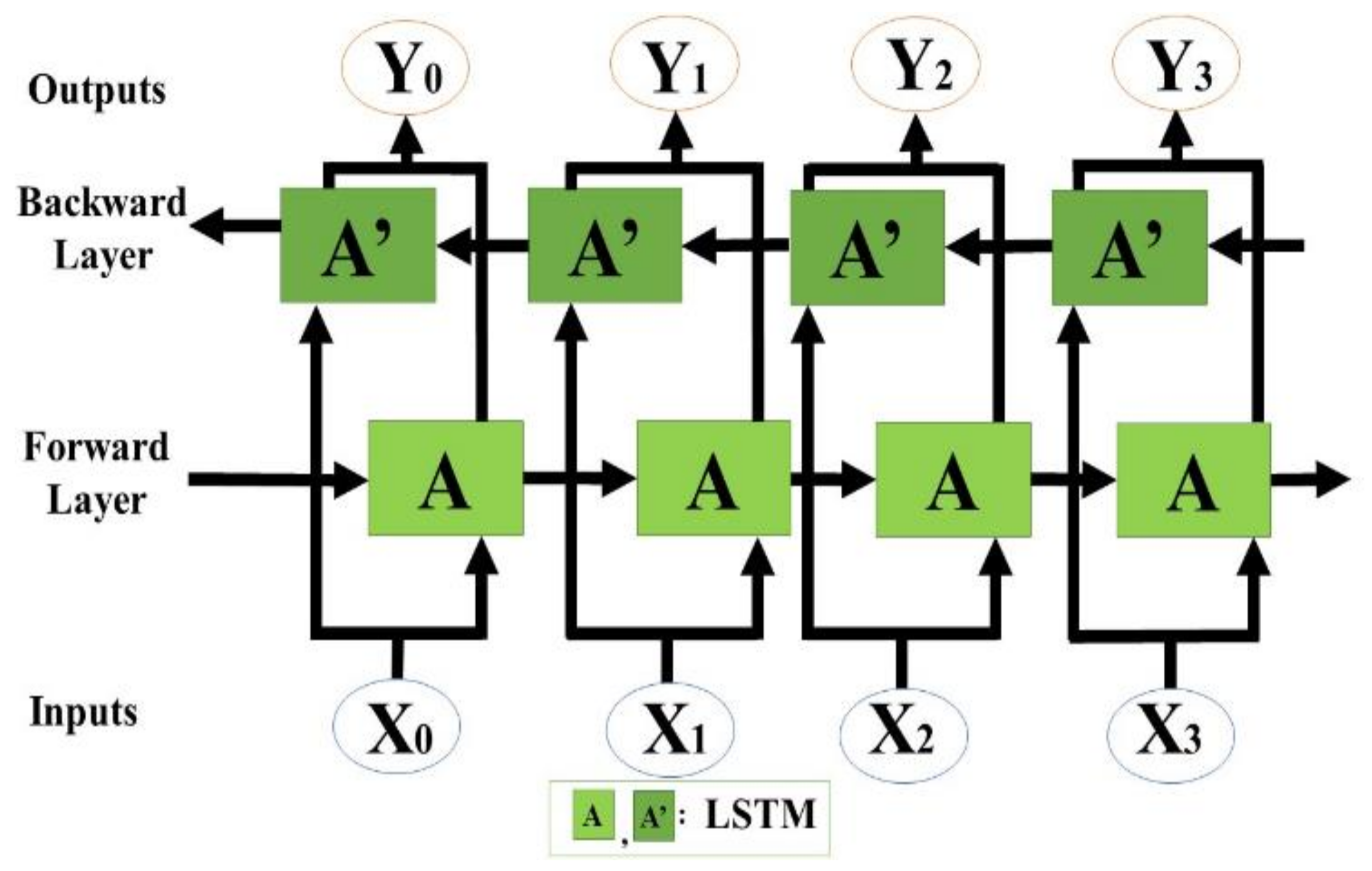
2.3.1. Bidirectional LSTM
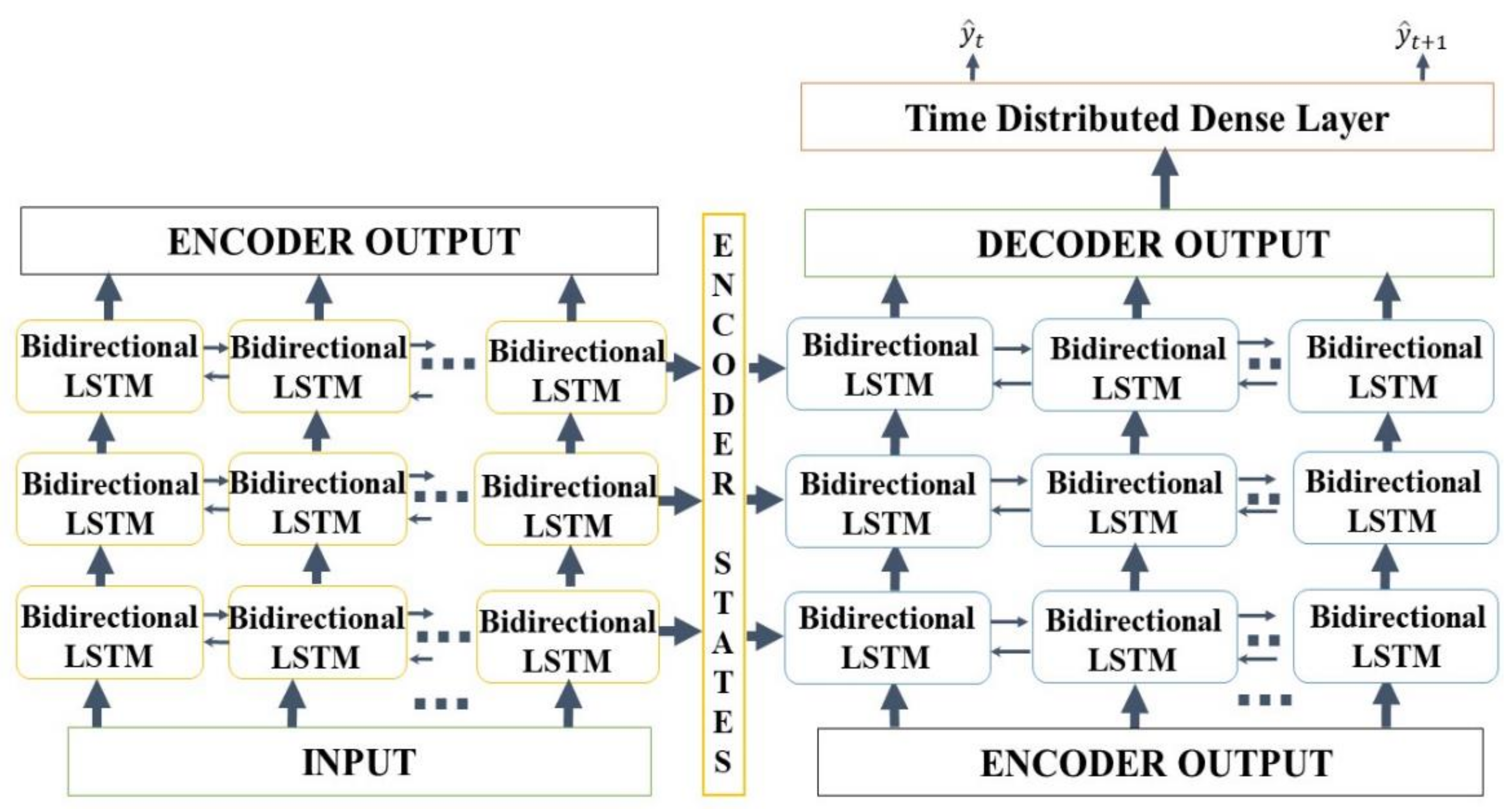
2.3.2. Seq2Seq Model
2.4. Experimental Setup
2.4.1. SVR (Baseline)
2.4.2. Random Forest Regressor (Baseline)
2.4.3. Gradient Boosting Regressor (Baseline)
2.4.4. Multilayer Perceptron Regressor (Baseline)
2.4.5. Comb-ML (Baseline)
2.4.6. RNN (Baseline)
2.4.7. MARS (Baseline)
2.4.8. Seq2Seq Model
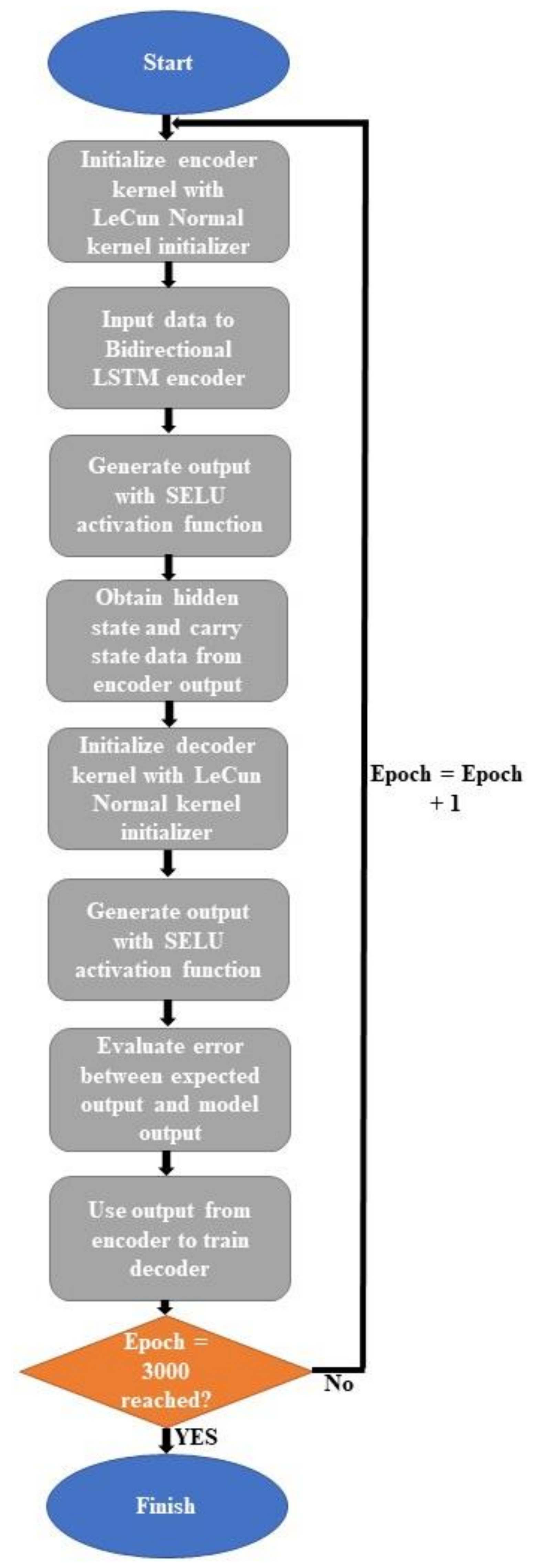
| Algorithm 1: Seq2Seq Training Procedure. | |
| Input: Weather data for the last seven days and forecasted rainfall | |
| Output: Predicted inflow rate for t and t + 1 | |
| 1: | For Epoch = Epoch + 1 to 3000 do |
| 2: | Initialize encoder kernel with LeCun Normal kernel initializer |
| 3: | Generate encoder output with SELU activation function |
| 3: | Obtain hidden and carry state data from encoder output |
| 4: | Initialize decoder with LeCun Normal kernel initializer |
| 5: | Generate decoder output with SELU activation function |
| 6: | Evaluate error between expected output and the model output with mean squared error |
3. Results
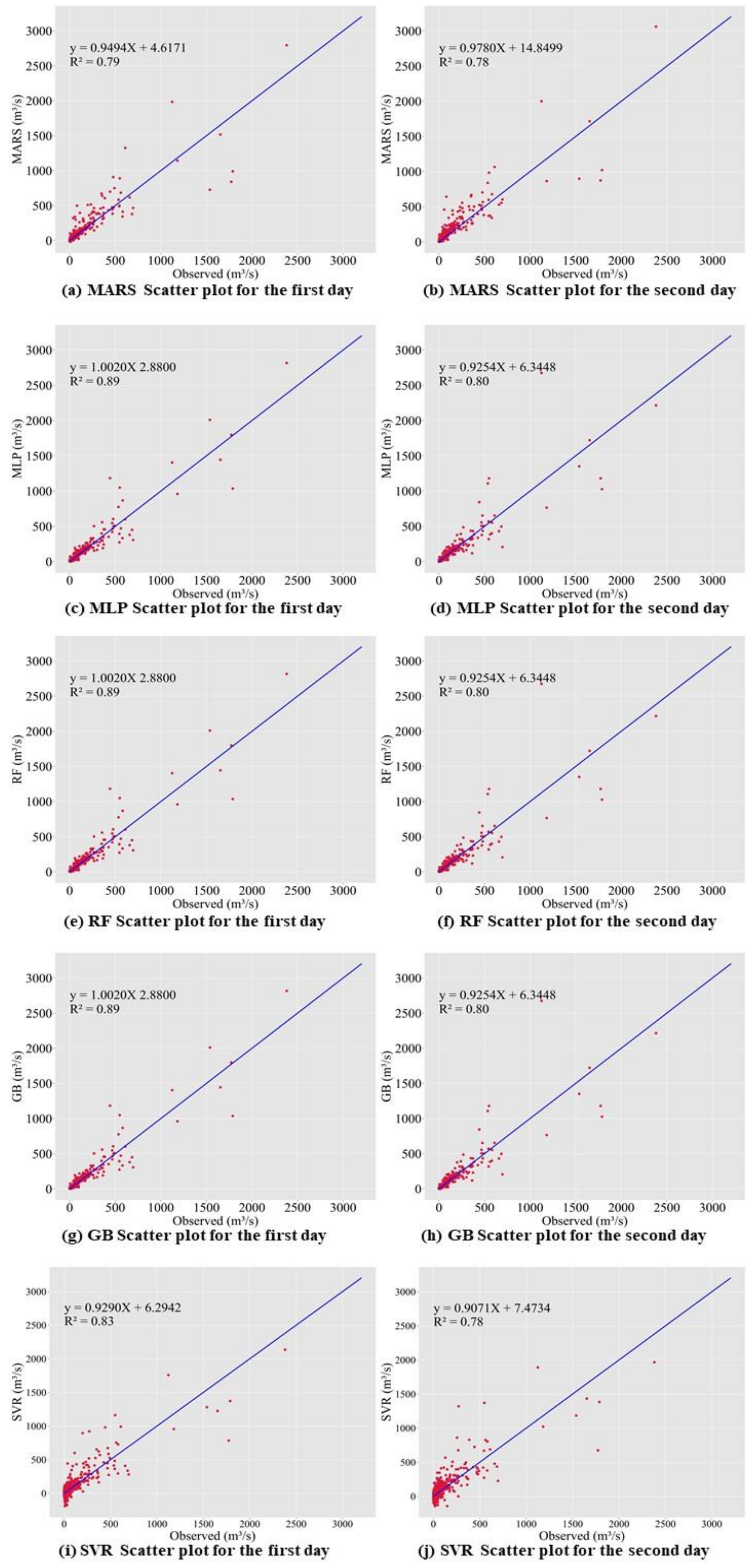
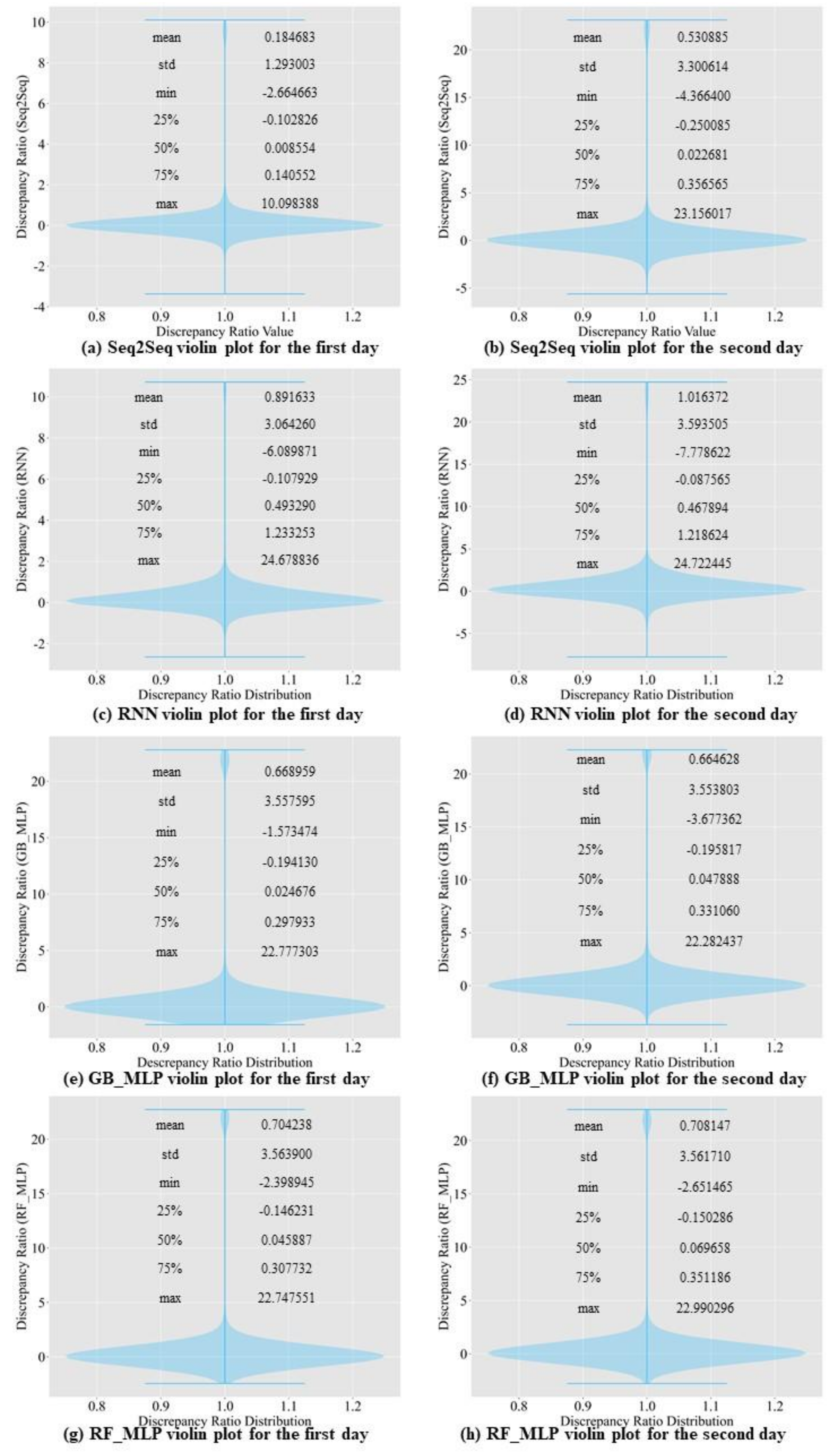
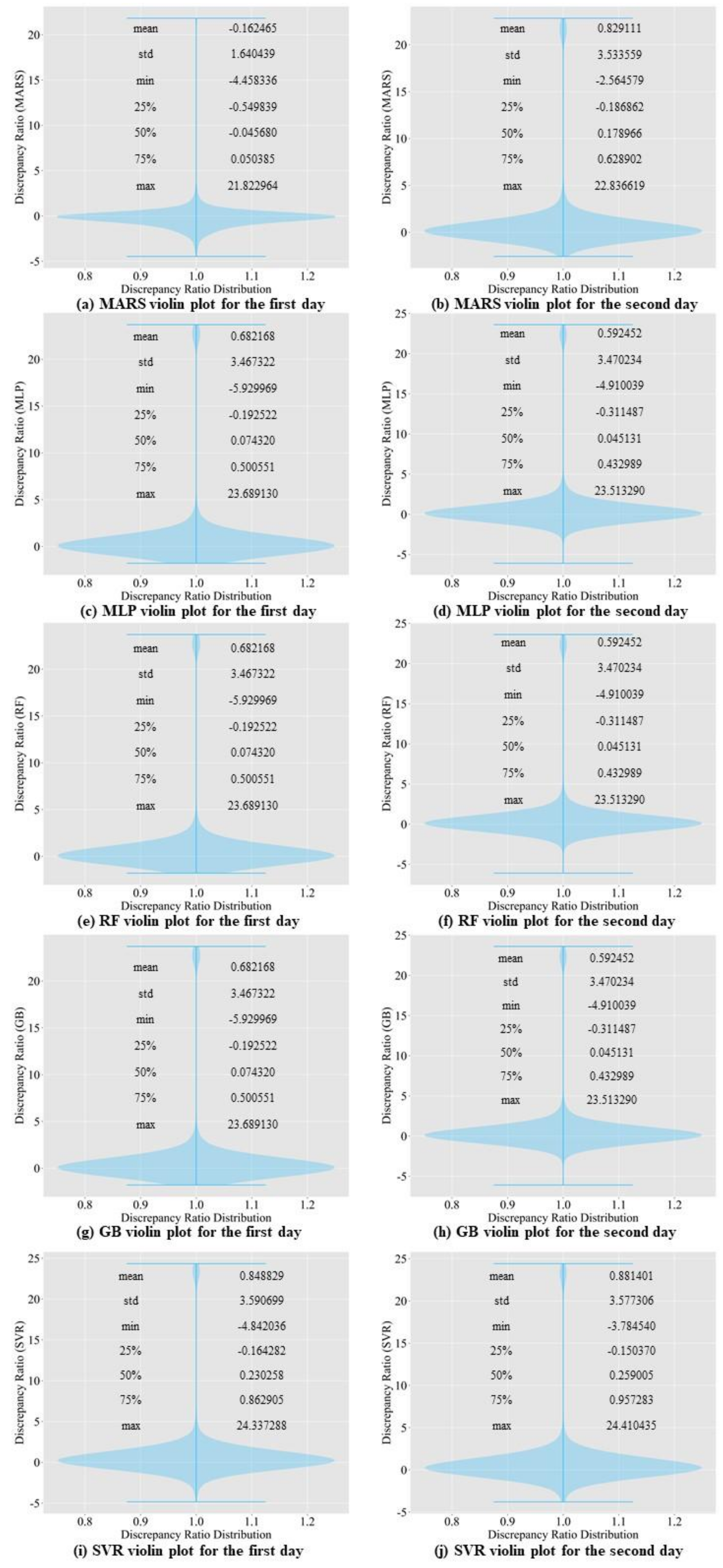
3.1. Comparison of Prediction Accuracy among Baseline Models
3.2. Comparison of Prediction Accuracy between Baseline Models and the Proposed Model
3.3. Ablation Study
4. Discussion
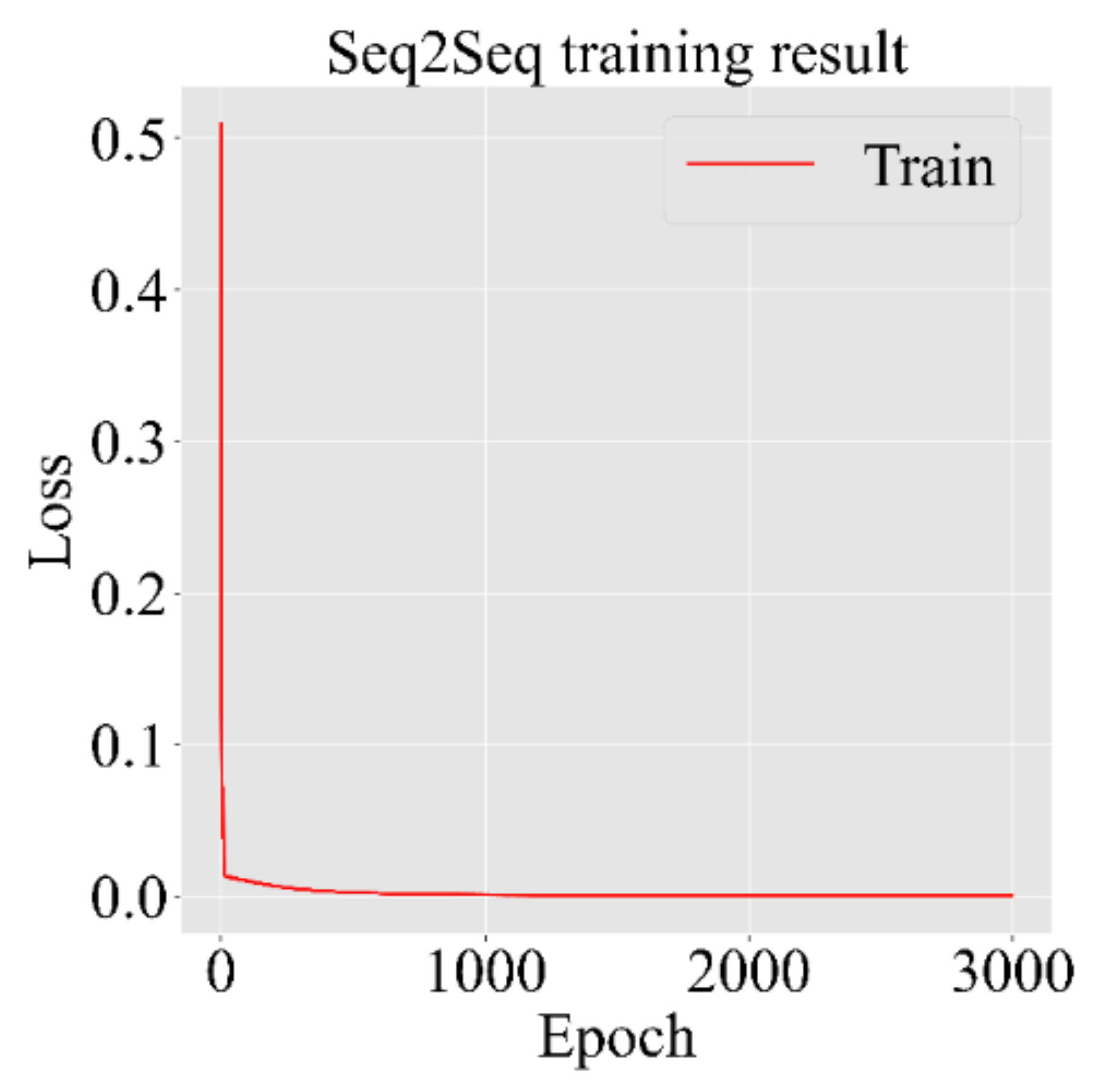
4.1. Seq2Seq Training Result
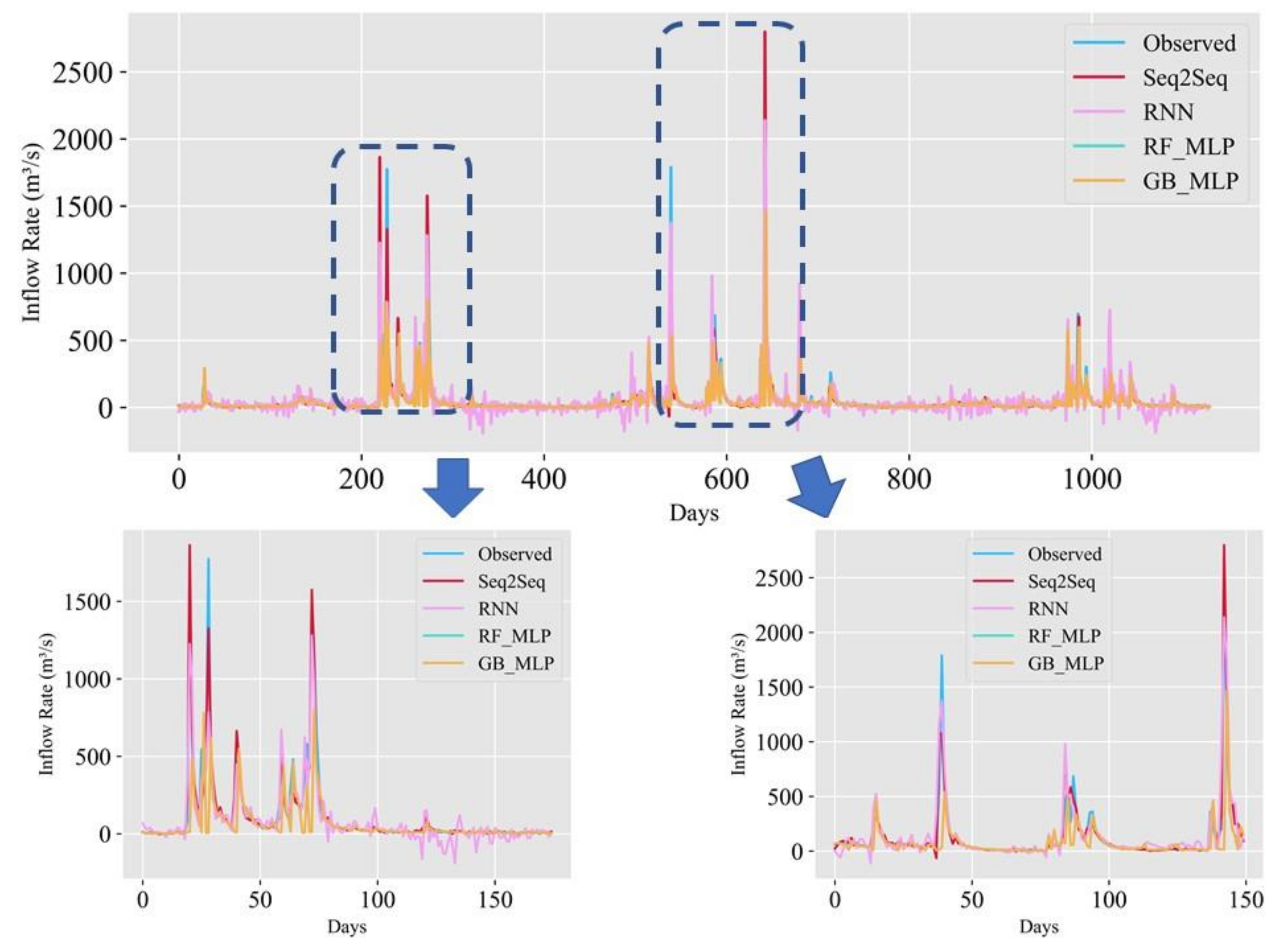
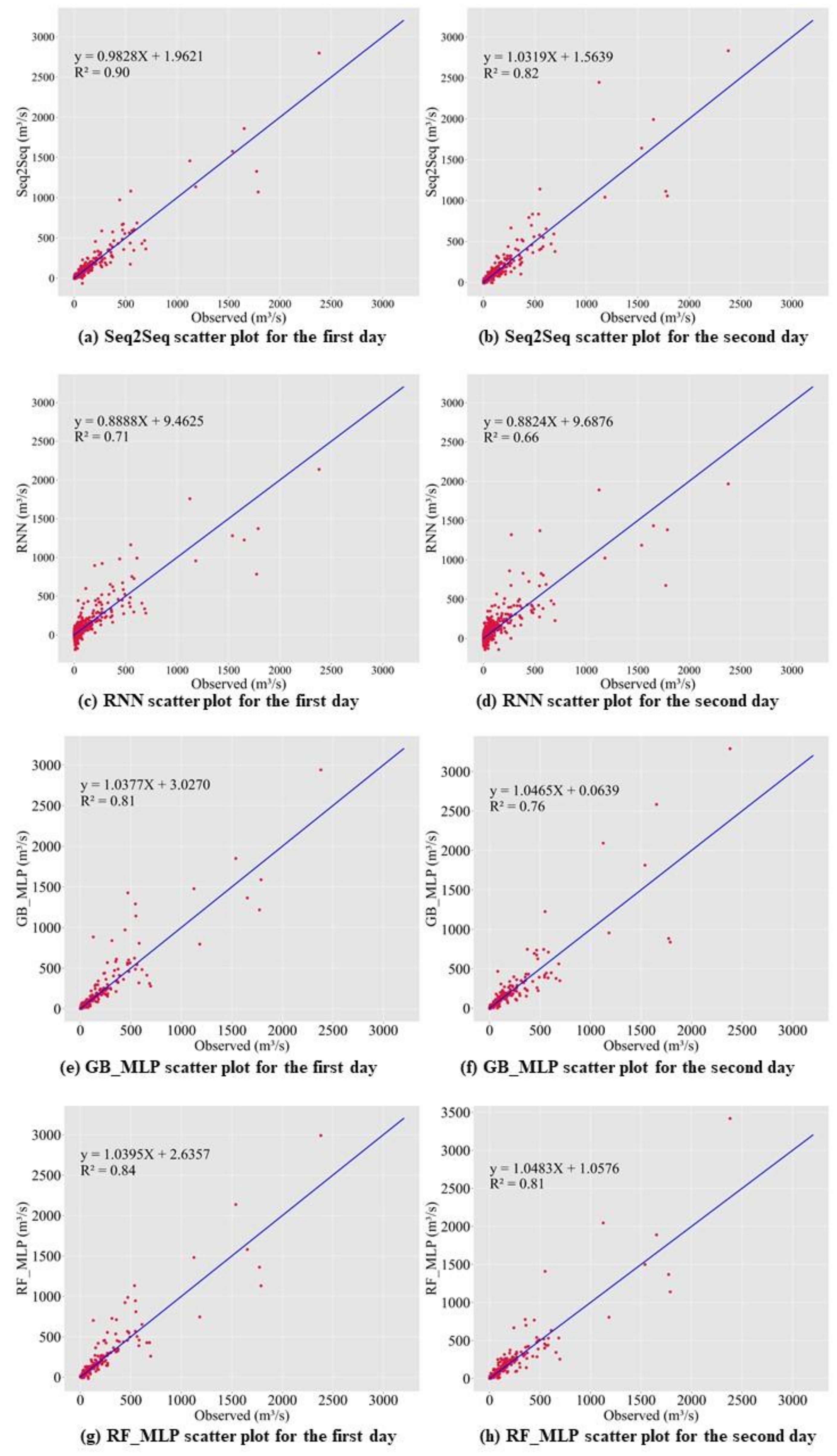
4.2. Results of Prediction Accuracy Comparison
4.3. Ablation Study Analysis
4.4. Seq2Seq Model’s Performance Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, J. Practical method for the 21st century water crisis using IWARM. J. Water Policy Econ. 2015, 24, 47–58. [Google Scholar]
- Shift in Water Resource Management Paradigm. K-water. 2012. Available online: https://www.kwater.or.kr/gov3/sub03/annoView.do?seq=1209&cate1=7&s_mid=54 (accessed on 6 September 2021).
- Park, J.Y.; Kim, S.J. Potential impacts of climate change on the reliability of water and hydropower supply from a multipurpose dam in South Korea. J. Am. Water Resour. Assoc. 2014, 50, 1273–1288. [Google Scholar] [CrossRef]
- Jung, S.; Lee, D.; Lee, K. “Prediction of River Water Level Using Deep-Learning Open Library. J. Korean Soc. Hazard Mitig. 2018, 18, 135. [Google Scholar] [CrossRef]
- Stern, M.; Flint, L.; Minear, J.; Flint, A.; Wright, S. Characterizing changes in streamflow and sediment supply in the Sacramento River Basin, California, using hydrological simulation program—FORTRAN (HSPF). Water 2016, 8, 432. [Google Scholar] [CrossRef]
- Ryu, J.; Jang, W.S.; Kim, J.; Choi, J.D.; Engel, B.A.; Yang, J.E.; Lim, K.J. Development of a watershed-scale long-term hydrologic impact assessment model with the asymptotic curve number regression equation. Water 2016, 8, 153. [Google Scholar] [CrossRef]
- Nyeko, M. Hydrologic modelling of data scarce basin with SWAT Model: Capabilities and limitations. Water Resour. Manag. 2015, 29, 81–94. [Google Scholar] [CrossRef]
- Park, M.K.; Yoon, Y.S.; Lee, H.H.; Kim, J.H. Application of recurrent neural network for inflow prediction into multi-purpose dam basin. J. Korea Water Resour. Assoc. 2018, 51, 1217–1227. [Google Scholar]
- Hong, J.; Lee, S.; Bae, J.H.; Lee, J.; Park, W.J.; Lee, D.; Kim, J.; Lim, K.J. Development and Evaluation of the Combined Machine Learning Models for the Prediction of Dam Inflow. Water 2020, 12, 2927. [Google Scholar] [CrossRef]
- Babei, M.; Ehsanzadeh, E. Artificial Neural Network and Support Vector Machine Models for Inflow Prediction of Dam Reservoir (Case Study: Zayandehroud Dam Reservoir). Water Resour. Manag. 2019, 33, 2203–2218. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Y.; Wu, L.; Chen, G.; Wang, L.; Qin, H. Comparison of support vector regression and extreme gradient boosting for decomposition-based data-driven 10-day streamflow forecasting. J. Hydrol. 2020, 582, 124293. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, R.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
- Seo, Y.; Choi, E.; Yeo, W. Reservoir Water Level Forecasting Using Machine Learning Models. J. Korean Soc. Agric. Eng. 2017, 59, 97–110. [Google Scholar]
- Liao, S.; Liu, Z.; Liu, B.; Cheng, C.; Jin, X. Multistep-ahead daily inflow forecasting using the ERA-nterim reanalysis data set based on gradient-boosting regression trees. Hydrol. Earth Syst. Sci. 2020, 24, 2343–2363. [Google Scholar] [CrossRef]
- Le, X.-H.; Ho, H.V.; Lee, G.; Jung, S. Ap plication of long short-term memory (LSTM) neural network for flood forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Mok, J.Y.; Choi, J.H.; Moon, Y. Prediction of multipurpose dam inflow using deep learning. J. Korea Water Resour. Assoc. 2020, 53, 97–105. [Google Scholar]
- Saberi-Movahed, F.; Mohammadifard, M.; Mehrpooya, A.; Rezaei-Ravari, M.; Berahmand, K.; Rostami, M.; Karami, S.; Najafzadeh, M.; Hajinezhad, D.; Jamshidi, M.; et al. Decoding Clinical Biomarker Space of COVID-19: Exploring Matrix Factorization-based Feature Selection Methods. medRxiv 2021, preprint, 1–51. [Google Scholar]
- Najafzadeh, M.; Niazmardi, S. A Novel Multiple-Kernel Support Vector Regression Algorithm for Estimation of Water Quality Parameters. Nat. Resour. Res. 2021, 17, 1–15. [Google Scholar]
- Amiri-Ardakani, Y.; Najafzadeh, M. Pipe Break Rate Assessment While Considering Physical and Operational Factors: A Methodology based on Global Positioning System and Data-Driven Techniques. Water Resour. Manag. 2021, in press. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; El-Shafie, A.; Zounemat-Kermani, M.; Kisi, O. Prediction of Suspended Sediment Load Using Data-Driven Models. Water 2019, 11, 2060. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Parmar, K.S.; Soni, K.; Kisi, O. Modeling monthly streamflow in mountainous basin by MARS, GMDHNN and DENFIS using hydroclimatic data. Neural Comput. Appl. 2020, 33, 2853–2871. [Google Scholar] [CrossRef]
- Adnan, R.M.; Khosravinia, P.; Karimi, B.; Kisi, O. Prediction of hydraulics performance in drain envelopes using Kmeans based multivariate adaptive regression spline. Appl. Soft Comput. J. 2020, 100, 2021. [Google Scholar]
- Adnan, R.M.; Liang, Z.; Trajkovic, S.; Zounemat-Kermani, M.; Li, B.; Kisi, O. Daily streamflow prediction using optimally pruned extreme learning machine. J. Hydrol. 2019, 577, 123981. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Heddam, S.; Zounemat-Kermani, M.; Kisi, O.; Li, B. Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydro-meteorological data as inputs. J. Hydrol. 2020, 586, 124371. [Google Scholar] [CrossRef]
- Kwin, C.T.; Talei, A.; Alaghmand, S.; Chua, L.H. Rainfall-runoff modeling using Dynamic Evolving Neural Fuzzy Inference System with online learning. Procedia Eng. 2016, 154, 1103–1109. [Google Scholar] [CrossRef][Green Version]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Adnan, R.M. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Adnan, R.M.; Yuan, X.; Kisi, O.; Anam, R. Improving Accuracy of River Flow Forecasting Using LSSVR with Gravitational Search Algorithm. Adv. Meteorol. 2017, 2017, 1–23. [Google Scholar] [CrossRef]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine learning methods for empirical streamflow simulation: A comparison of model accuracy, interpretability, and uncertainty in seasonal watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef]
- Korea National Committee on Large Dams. Available online: http://www.kncold.or.kr/eng/ds4_1.html (accessed on 15 March 2021).
- Dam Operation Status. Available online: https://www.water.or.kr/realtime/sub01/sub01/dam/.hydr.do?seq=1408&p_group_seq=1407&menu_mode=2 (accessed on 15 March 2021).
- Korea Meteorological Administration (KMA). Available online: http://kma.go.kr/home/index.jsp (accessed on 12 January 2021).
- Weather Warning Status. Available online: http://www.kma.go.kr/HELP/html/help_wrn001.jsp (accessed on 12 January 2021).
- Woo, W.; Moon, J.; Kim, N.W.; Choi, J.; Kim, K.S.; Park, Y.S.; Jang, W.S.; Lim, K.J. Evaluation of SATEEC Daily R Module using Daily Rainfall. J. Korean Soc. Water Environ. 2010, 26, 841–849. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Persio, L.D.; Honchar, O. Analysis of Recurrent Neural Networks for Short-Term. AIP Conf. 2017, 1906, 190006. [Google Scholar]
- Althelaya, K.A.; El-Alfy, E.S.M.; Mohammed, S. Evaluation of Bidirectional LSTM for Short- and Long-Term Stock Market Prediction. In Proceedings of the International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 3–5 April 2018; pp. 151–156. [Google Scholar]
- Suyskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 2, pp. 3104–3112. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; pp. 278–282. [Google Scholar]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras & Tensorflow; O’Reilly: Sebastopol, CA, USA, 2020; pp. 254–255. [Google Scholar]
- Schapire, R.E. A Brief Introduction to Boosting. In Proceedings of the 16th International Joint Conference on Artificial Intelligence (IJCAI), Stockholm, Sweden, 31 July–6 August 1999; pp. 1401–1406. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations; MIT Press: Cambridge, MA, USA, 1987; pp. 318–362. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Py-Earth. Available online: https://contrib.scikit-learn.org/py-earth/content.html# (accessed on 12 August 2021).
- Klambauer, G.; Unterthiner, T.; Mayr, A. Self-Normalizing Neural Networks. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 972–981. [Google Scholar]
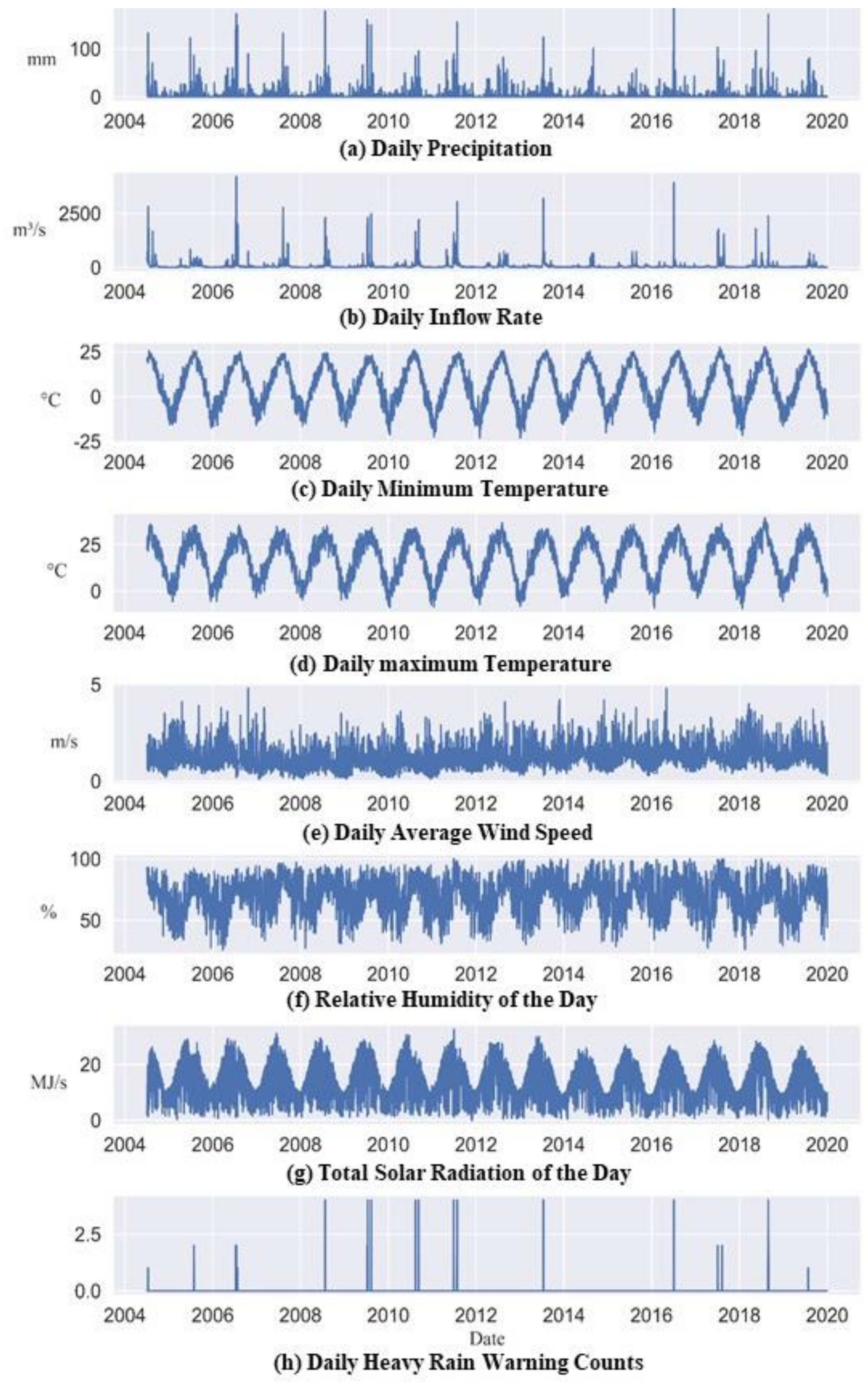
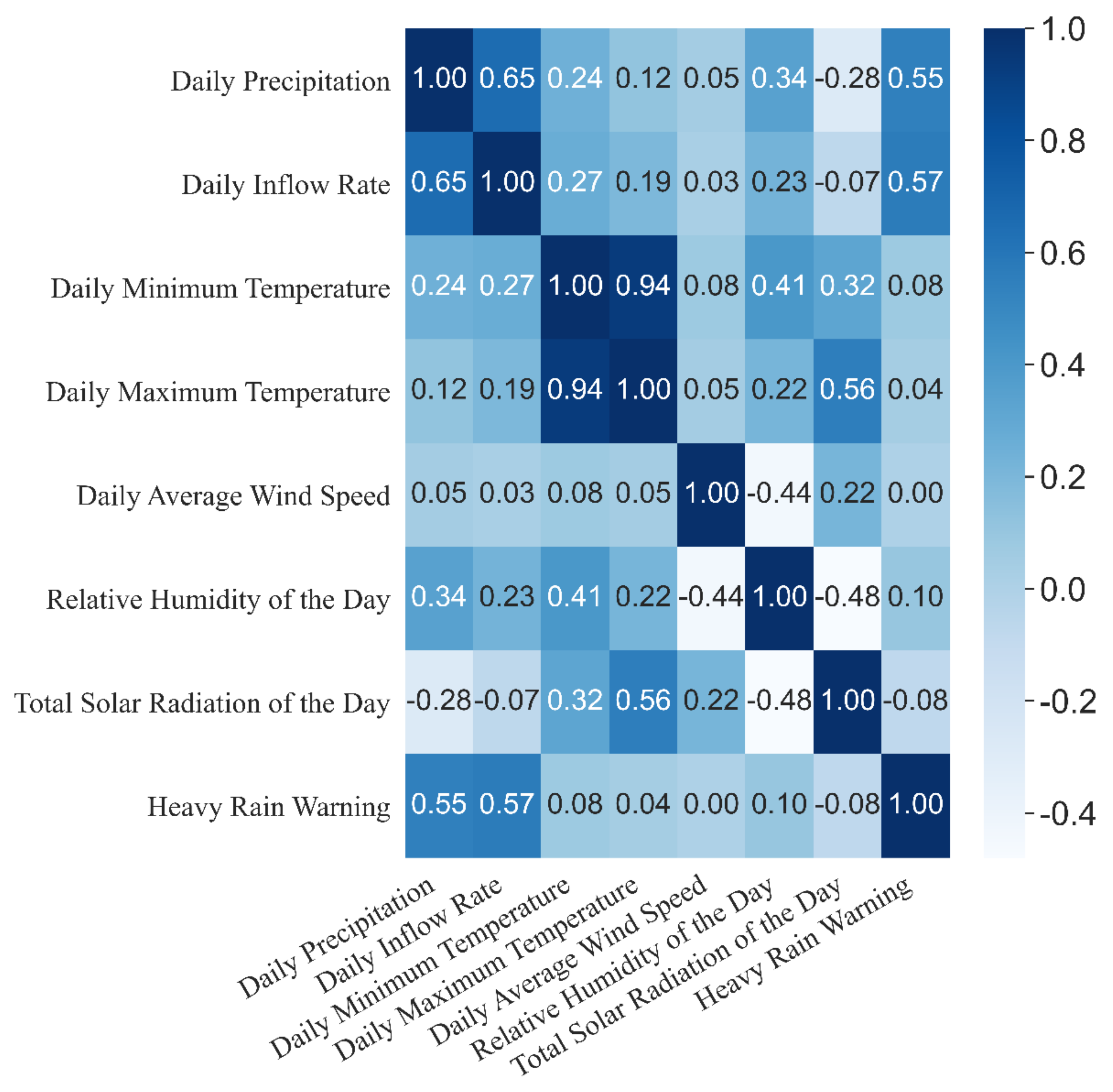
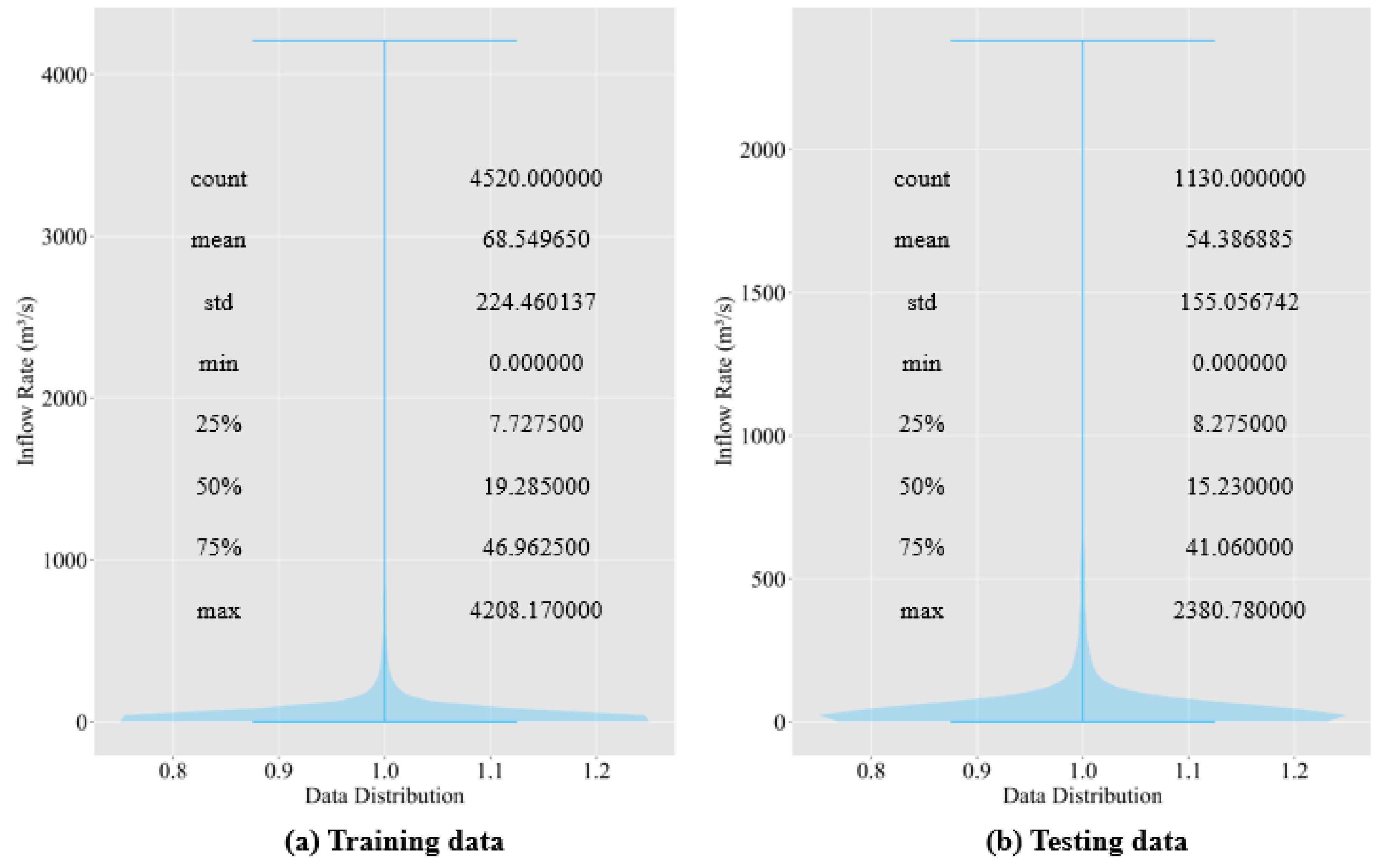
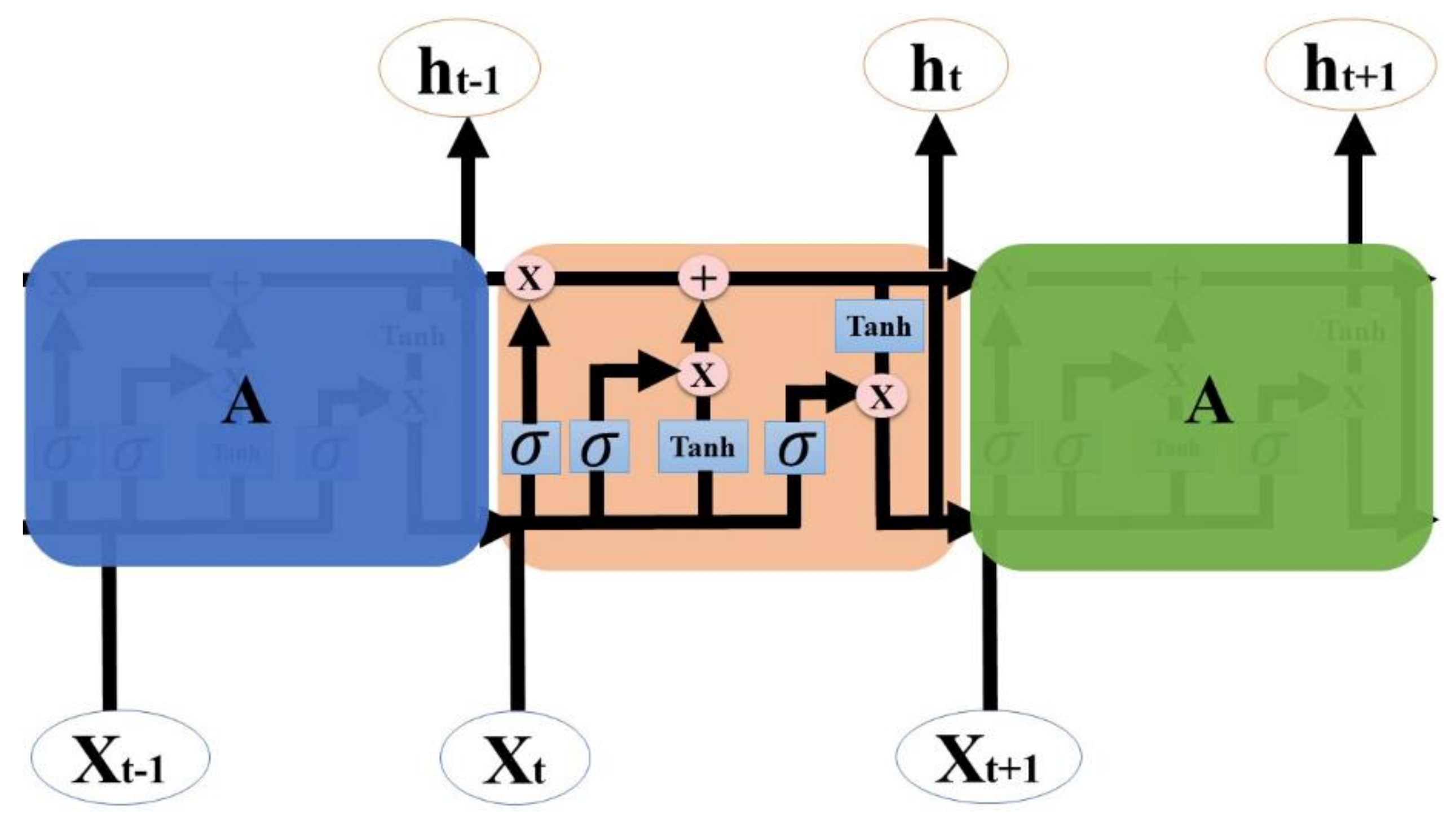
| Input Variable | Output Variable | |
|---|---|---|
| Weather data for the last seven days | Inflow (t − 7) | |
| Inflow (t − 6) | ||
| Inflow (t − 1) | ||
| min_temperature (t − 7), min_temperature (t − 6), min_temperature (t − 1) | ||
| max_temperature (t − 7), max_temperature (t − 6), max_temperature (t − 1) | ||
| precipitation (t − 7), | ||
| precipitation (t − 6), | ||
| precipitation (t − 1) | ||
| wind (t − 7), | Inflow of the day: Inflow (t), | |
| wind (t − 6), | Inflow of the next day: Inflow (t + 1) | |
| wind (t − 1) | ||
| solar_radiation (t − 7), solar_radiation (t − 6), olar_radiation (t − 1) | ||
| humidity (t − 7) | ||
| humidity (t − 6) | ||
| humidity (t − 1) | ||
| heavy_rain_warn (t − 7), heavy_rain_warn (t − 6) | ||
| heavy_rain_warn (t − 1) | ||
| Forecasted data | precipitation (t) | |
| precipitation (t + 1) |
| Hyperparameter | Value |
|---|---|
| kernel | poly, rbf |
| degree | 2, 3, 4, 5 |
| gamma | scale, auto |
| Hyperparameter | Value |
|---|---|
| n_estimators | 100, 200, 500 |
| max_features | 2, 3, 4, 5 |
| criterion | mse, mae |
| Hyperparameter | Value |
|---|---|
| loss | ls, lad, huber, quantile |
| learning_rate | 0.1, 0.01, 0.001 |
| n_estimators | 100, 200, 300 |
| criterion | friedman_mse, mse. mae |
| Hyperparameter | Value |
|---|---|
| hidden_layer_sizes | (30, 30, 30), (50, 50, 50), (100, 100) |
| activation | Identity, logistic, tanh, relu |
| solver | lbfgs, sgd, adam |
| batch_size | 32, 64, 128 |
| learning_rate | Constant, invscaling, adaptive |
| shuffle | True, False |
| Hyperparameter | Value |
|---|---|
| Learning rate | 0.1, 0.01, 0.001 |
| Batch size | 64, 128, 256 |
| Hyperparameter | Value |
|---|---|
| Learning rate | 0.1, 0.01, 0.001 |
| Batch size | 64, 128, 256 |
| Number of output units | |
| per bidirectional LSTM | 59,100,118,177 |
| Baseline Model | Prediction Time | RMSE | MAE | NSE |
|---|---|---|---|---|
| RNN | T | 100.34 | 53.51 | 0.78 |
| T + 1 | 104.08 | 55.05 | 0.77 | |
| MLP | T | 53.49 | 16.74 | 0.94 |
| T + 1 | 59.89 | 16.95 | 0.93 | |
| SVR | T | 63.78 | 26.06 | 0.92 |
| T + 1 | 73.12 | 28.80 | 0.89 | |
| Random Forest Regressor | T | 66.63 | 15.76 | 0.91 |
| T + 1 | 58.21 | 15.95 | 0.93 | |
| Gradient Boosting Regressor | T | 76.90 | 16.71 | 0.90 |
| T + 1 | 64.78 | 17.21 | 0.93 | |
| Comb -ML (RF_MLP) | T | 69.79 | 16.44 | 0.92 |
| T + 1 | 71.01 | 16.80 | 0.92 | |
| Comb -ML (GB_MLP) | T | 69.39 | 16.73 | 0.92 |
| T + 1 | 71.17 | 16.97 | 0.92 | |
| MARS | T | 71.68 | 21.88 | 0.907 |
| T + 1 | 73.37 | 25.48 | 0.902 |
| MLP | Support Vector Regressor | ||
|---|---|---|---|
| Hyperparameter | Value | Hyperparameter | Value |
| activation | logistic | degree | 2 |
| batch_size | 32 | gamma | auto |
| Hidden_layer_size | (100, 100, 100) | kernel | poly |
| learning_rate | constant | ||
| shuffle | False | ||
| solver | lbfgs | ||
| Random Forest Regressor | Gradient Boosting Regressor | ||
| Hyperparameter | Value | Hyperparameter | Value |
| criterion | mse | criterion | mse |
| max_features | auto | learning_rate | 0.1 |
| n_estimators | 100 | loss | ls |
| n_estimators | 300 | ||
| RNN | |||
| Hyperparameter | Value | ||
| Batch Size | 64 | ||
| Learning rate | 0.1 | ||
| Our Proposed Model | |
|---|---|
| Hyperparameter | Value |
| Batch size | 256 |
| Learning rate | 0.001 |
| Number of output units per bidirectional LSTM | 177 |
| Sequence-to-Sequence Model (Our Model) | MLP | |||||
|---|---|---|---|---|---|---|
| RMSE | MAE | NSE | RMSE | MAE | NSE | |
| T | 44.17 | 14.94 | 0.96 | 53.49 | 16.74 | 0.94 |
| T + 1 | 58.59 | 17.11 | 0.94 | 59.89 | 16.95 | 0.93 |
| Sequence-to-Sequence Model (Unidirectional LSTM) | Sequence-to-Sequence Model (Control) | |||||
|---|---|---|---|---|---|---|
| RMSE | MAE | NSE | RMSE | MAE | NSE | |
| T | 54.90 | 16.23 | 0.94 | 44.17 | 14.94 | 0.96 |
| T + 1 | 74.12 | 19.29 | 0.90 | 58.59 | 17.11 | 0.94 |
| Sequence-to-Sequence Model (Activation Function: Tanh) | Sequence-to-Sequence Model (Control) | |||||
|---|---|---|---|---|---|---|
| RMSE | MAE | NSE | RMSE | MAE | NSE | |
| T | 58.38 | 15.62 | 0.94 | 44.17 | 14.94 | 0.96 |
| T + 1 | 61.04 | 17.03 | 0.94 | 58.59 | 17.11 | 0.94 |
| Sequence-to-Sequence Model (No Warning Data) | Sequence-to-Sequence Model (Control) | |||||
|---|---|---|---|---|---|---|
| RMSE | MAE | NSE | RMSE | MAE | NSE | |
| T | 54.19 | 14.57 | 0.95 | 44.17 | 14.94 | 0.96 |
| T + 1 | 60.67 | 16.59 | 0.94 | 58.59 | 17.11 | 0.94 |
| Models | Metrics | |||
|---|---|---|---|---|
| RMSE | MAE | NSE | ||
| Our model (Seq2Seq) | T | 44.17 | 14.94 | 0.96 |
| T + 1 | 58.59 | 17.11 | 0.94 | |
| Comb-ML (RF_MLP) | T | 69.79 | 16.44 | 0.92 |
| T + 1 | 71.01 | 16.80 | 0.92 | |
| Comb-ML (RF_MLP) | T | 69.39 | 16.73 | 0.92 |
| T + 1 | 71.17 | 16.97 | 0.92 | |
| RNN | T | 100.34 | 53.51 | 0.78 |
| T + 1 | 104.08 | 55.05 | 0.77 | |
| Sequence-to-Sequence Model (Our Model) | RNN | |||||
|---|---|---|---|---|---|---|
| RMSE | MAE | NSE | RMSE | MAE | NSE | |
| T | 44.17 | 14.94 | 0.96 | 100.34 | 53.51 | 0.78 |
| T + 1 | 58.59 | 17.11 | 0.94 | 104.08 | 55.05 | 0.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kim, J. Predicting Inflow Rate of the Soyang River Dam Using Deep Learning Techniques. Water 2021, 13, 2447. https://doi.org/10.3390/w13172447
Lee S, Kim J. Predicting Inflow Rate of the Soyang River Dam Using Deep Learning Techniques. Water. 2021; 13(17):2447. https://doi.org/10.3390/w13172447
Chicago/Turabian StyleLee, Sangwon, and Jaekwang Kim. 2021. "Predicting Inflow Rate of the Soyang River Dam Using Deep Learning Techniques" Water 13, no. 17: 2447. https://doi.org/10.3390/w13172447
APA StyleLee, S., & Kim, J. (2021). Predicting Inflow Rate of the Soyang River Dam Using Deep Learning Techniques. Water, 13(17), 2447. https://doi.org/10.3390/w13172447






