Towards a High Order Convergent ALE-SPH Scheme with Efficient WENO Spatial Reconstruction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Arbitrary Lagrangian–Eulerian Riemann-Based SPH
- A Riemann solver, that can be exact or approximate;
- A reconstruction procedure to infer the values of mass and momentum fluxes at the midpoint of the pair, for both the left (L) and the right (R) states of the Riemann problem.
2.2. Rusanov Flux
2.3. High-Order Polynomial Weighted Essentially Non-Oscillatory Reconstruction
2.4. Corrected SPH Estimation of Derivatives
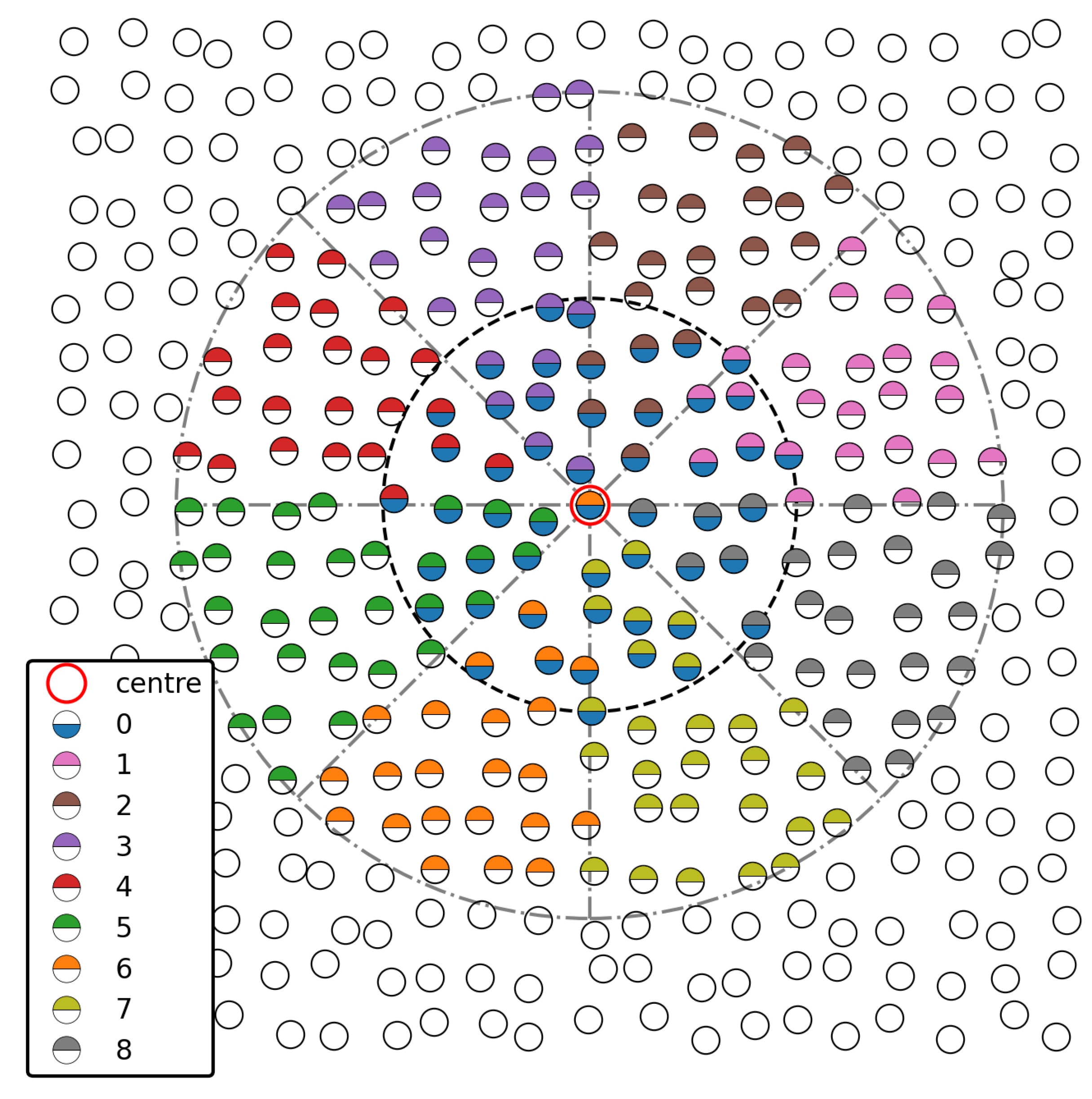
Generation of polynomials for the Weighted Essentially Non-Oscillatory Reconstruction
3. Results and Discussion
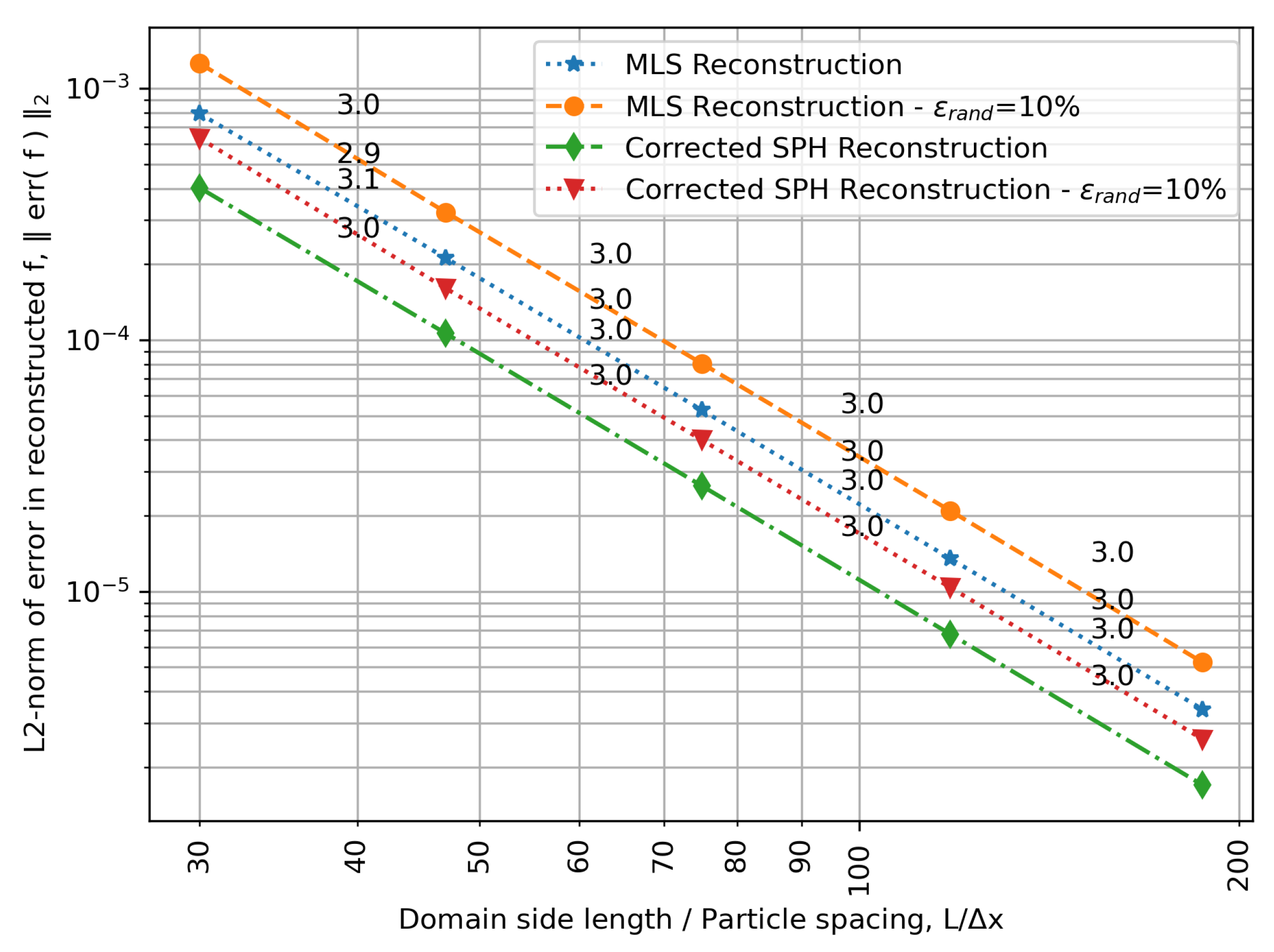
3.1. Moving Least-Squares vs. Corrected SPH Interpolation for the Generation of Reconstruction Polynomials
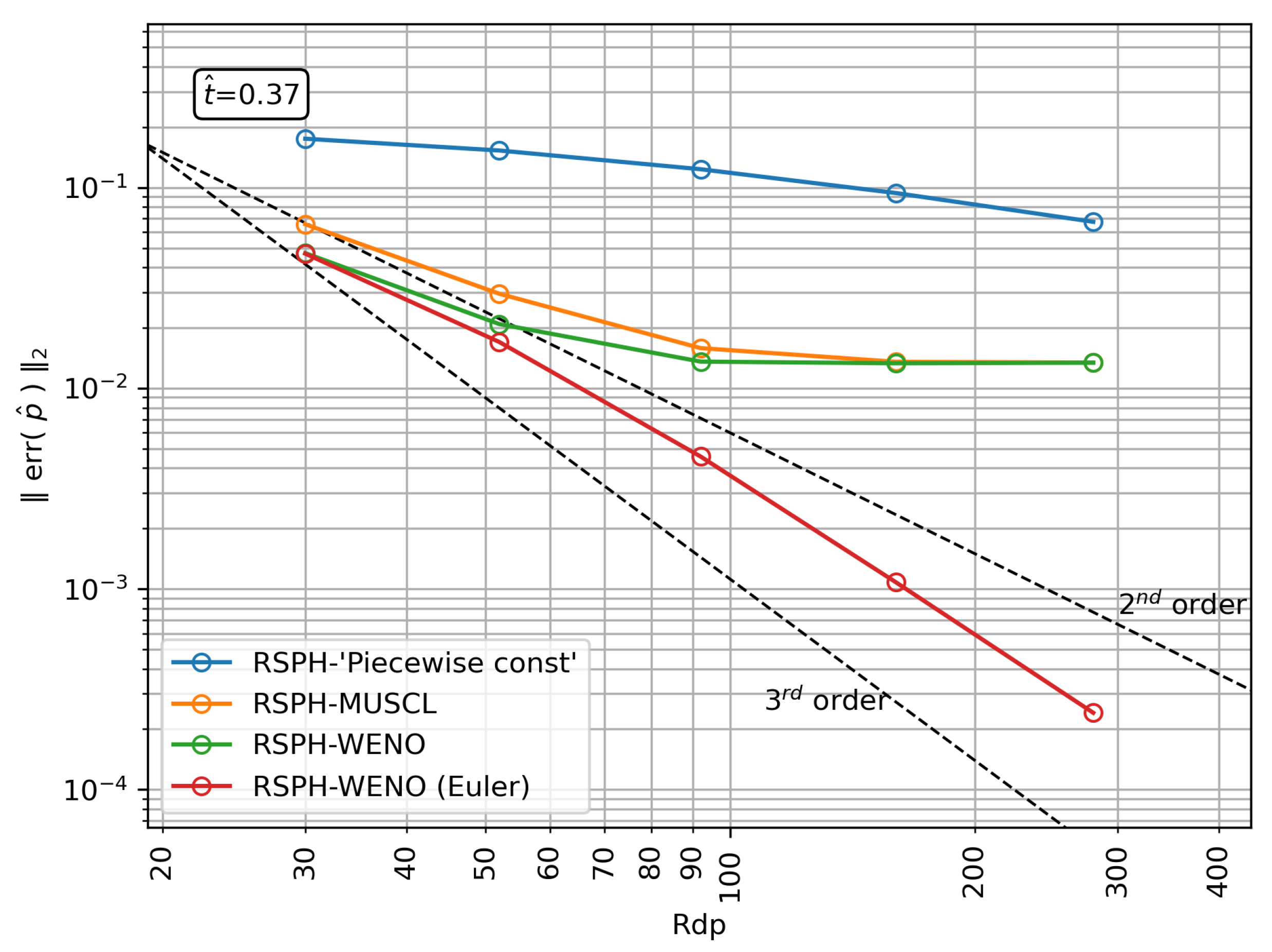
3.2. Weakly Compressible 2D Vortex
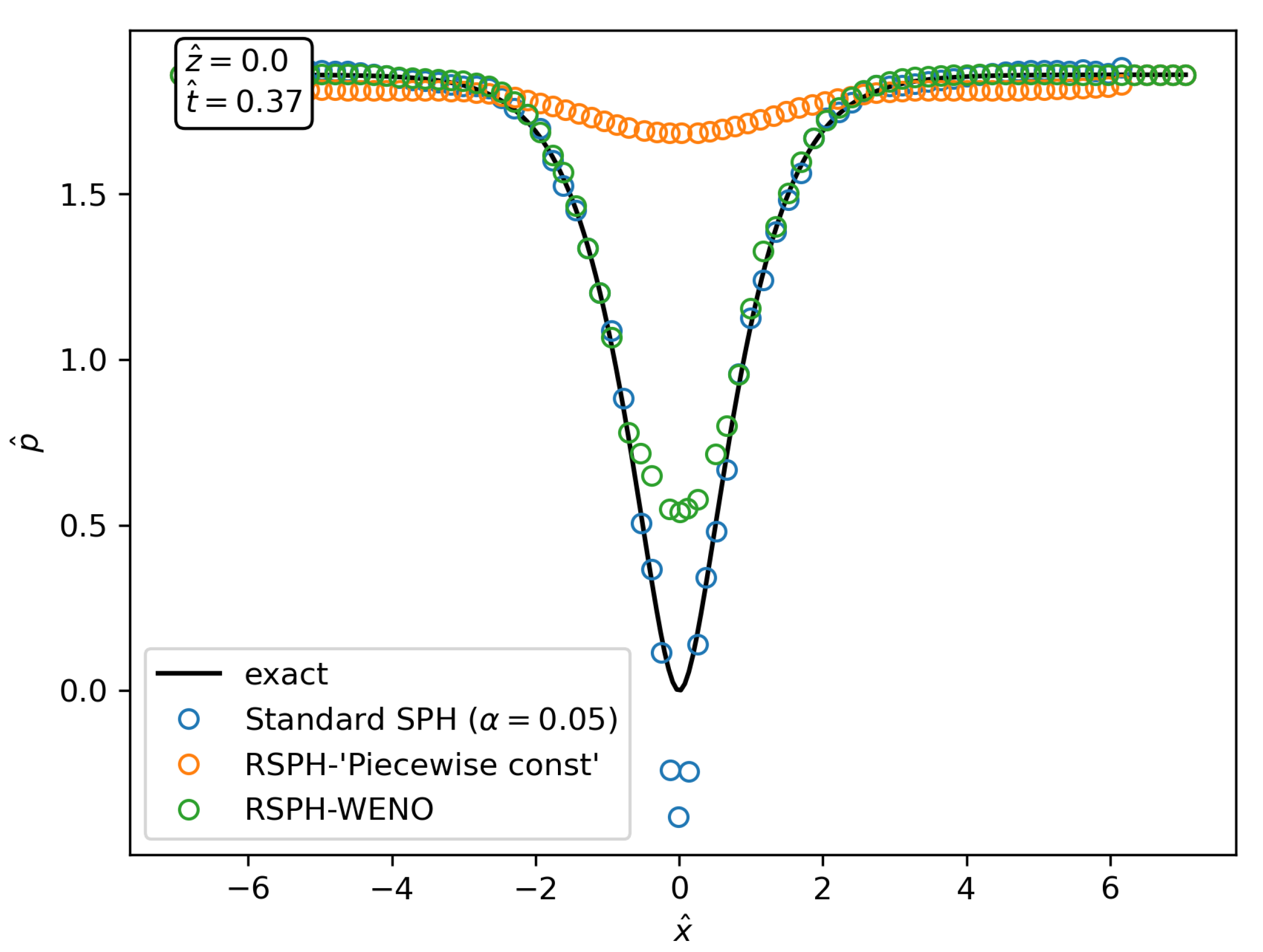
- RSPH with a piece-wise constant reconstruction. This is the less accurate scheme due to the very large diffusion introduced by the Riemann problem with a trivial reconstruction.
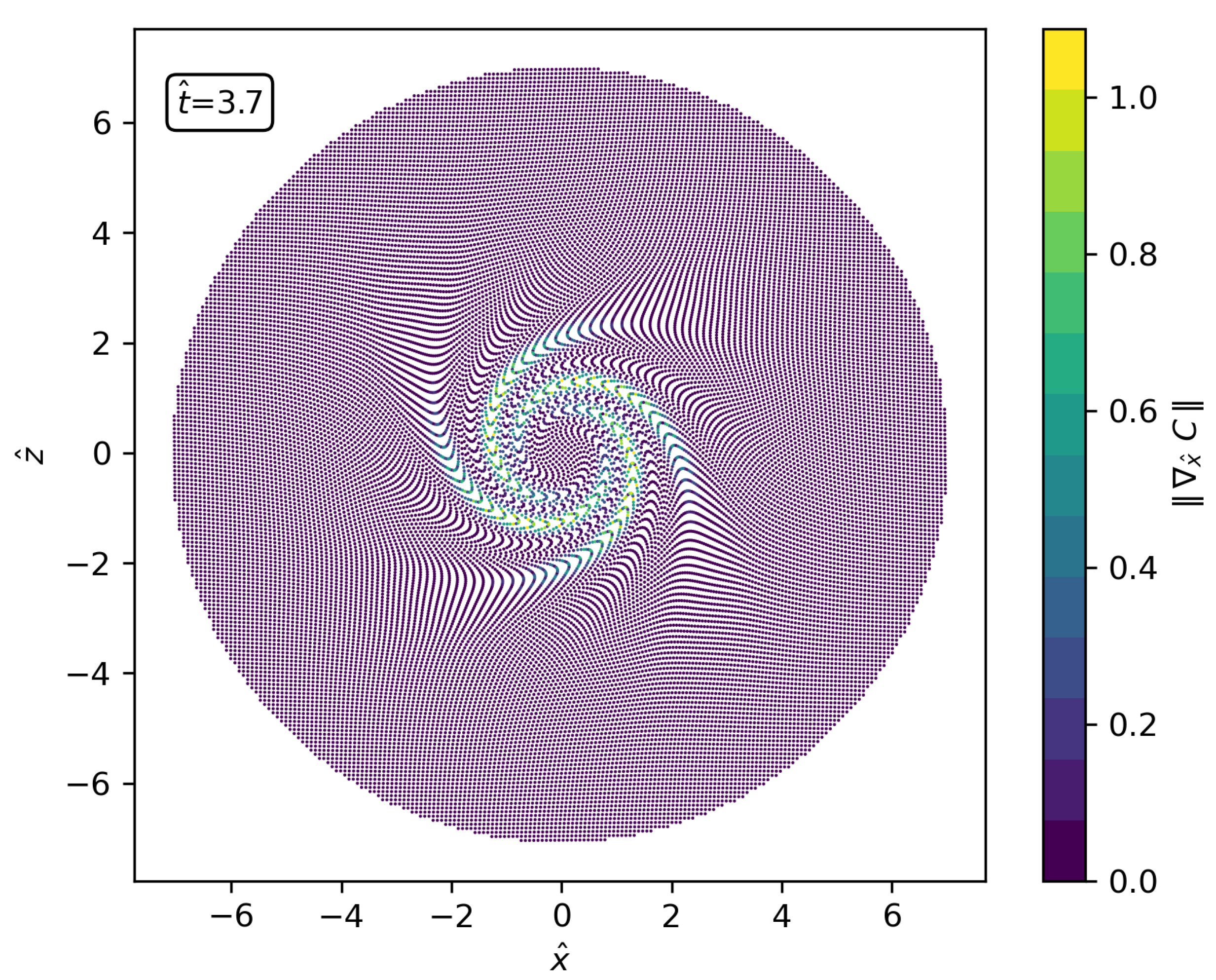
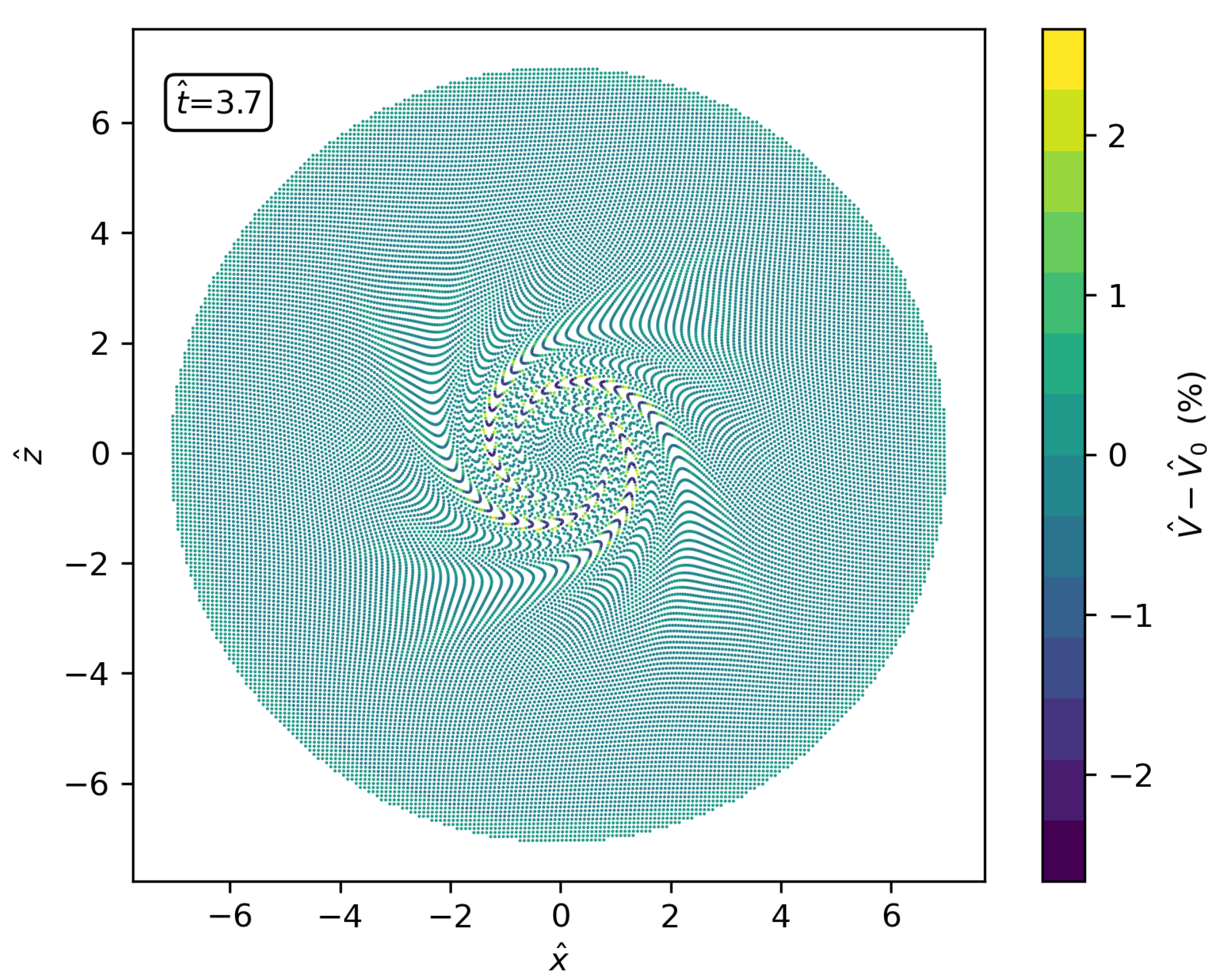
- RSPH with a MUSCL reconstruction. Uses linear reconstructions based on gradients estimated by standard SPH operators, with slope limiters (to prevent oscillatory fields) as first depicted by [30]. The MUSCL reconstruction improves the accuracy of the scheme to the point that anisotropic distributions (like the ones displayed in Figure 4 for the RSPH-WENO scheme) appear, especially for high resolutions. The result is an increase in the discretization error that saturates the decrease in the global error.
- RSPH with WENO reconstruction: The high-order spatial reconstruction further improves the accuracy of the trajectories described by the particles which, in conjunction with the usage of standard divergence SPH operators in Equations (5) and (6), ruins the beneficial effect of the high-order reconstruction.
- RSPH with WENO reconstruction and Eulerian transport. In these simulations, particles remain fixed on the vertices of a Cartesian grid (). Hence, the gradient of partition of unity is exactly zero in the whole field, unleashing the full potential of the WENO reconstruction to reach a maximum convergence rate of ∼2.7. Considering that the theoretical convergence for the second order reconstructing polynomials used is third order, this result suggests that the overall convergence of the scheme is guided by the order of the WENO polynomials.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SPH | Smoothed Particle Hydrodynamics |
| WEC | Wave Energy Converters |
| LES | Large Eddy Simulation |
| SPHERIC | SPH rEsearch and engineeRing |
| MLS | Moving least-squares |
| ALE | Arbitrary Lagrangian–Eulerian |
| WENO | Weighted Essentially Non-Oscillatory |
| ADER | Arbitrary DERivative |
| MOOD | Multi-dimensional Optimal Order Detection |
| LABFM | Local Anisotropic Basis Function Method |
| GPU | Graphics Processing Unit |
| CFL | Courant–Friedrichs–Lewy |
| RSPH | Riemann-based SPH |
References
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Shadloo, M.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Violeau, D. Fluid Mechanics and the SPH Method: Theory and Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar] [CrossRef]
- Lind, S.J.; Rogers, B.D.; Stansby, P.K. Review of smoothed particle hydrodynamics: Towards converged Lagrangian flow modelling. Proc. R. Soc. A 2020, 476. [Google Scholar] [CrossRef]
- Bottelli, D.N. Application of Smoothed Particle Hydrodynamics (SPH) for preliminary hydraulic design of Water-WasterWater Works. In Proceedings of the 14th International SPHERIC Workshop, Exeter, UK, 25–27 June 2019. [Google Scholar]
- Rentschler, M.; Marongiu, J.C.; Neuhauser, M.; Parkinson, E. Overview of SPH-ALE applications for hydraulic turbines in ANDRITZ Hydro. J. Hydrodyn. 2018, 30, 114–121. [Google Scholar] [CrossRef]
- Novak, G.; Domínguez, J.M.; Tafuni, A.; Silva, A.T.; Pengal, P.; Četina, M.; Žagar, D. 3-D Numerical Study of a Bottom Ramp Fish Passage Using Smoothed Particle Hydrodynamics. Water 2021, 13, 1595. [Google Scholar] [CrossRef]
- O’Connor, J.; Rogers, B.D. A fluid–structure interaction model for free-surface flows and flexible structures using smoothed particle hydrodynamics on a GPU. J. Fluids Struct. 2021, 104, 103312. [Google Scholar] [CrossRef]
- Green, M.D.; Zhou, Y.; Dominguez, J.M.; Gesteira, M.G.; Peiró, J. Smooth particle hydrodynamics simulations of long-duration violent three-dimensional sloshing in tanks. Ocean Eng. 2021, 229, 108925. [Google Scholar] [CrossRef]
- Quartier, N.; Ropero-Giralda, P.; Domínguez, J.M.; Stratigaki, V.; Troch, P. Influence of the Drag Force on the Average Absorbed Power of Heaving Wave Energy Converters Using Smoothed Particle Hydrodynamics. Water 2021, 13, 384. [Google Scholar] [CrossRef]
- Altomare, C.; Tafuni, A.; Domínguez, J.M.; Crespo, A.J.C.; Gironella, X.; Sospedra, J. SPH Simulations of Real Sea Waves Impacting a Large-Scale Structure. J. Mar. Sci. Eng. 2020, 8, 826. [Google Scholar] [CrossRef]
- Di Mascio, A.; Antuono, M.; Colagrossi, A.; Marrone, S. Smoothed particle hydrodynamics method from a large eddy simulation perspective. Phys. Fluids 2017, 29, 035102. [Google Scholar] [CrossRef]
- Antuono, M.; Marrone, S.; Di Mascio, A.; Colagrossi, A. Smoothed particle hydrodynamics method from a large eddy simulation perspective. Generalization to a quasi-Lagrangian model. Phys. Fluids 2021, 33, 15102. [Google Scholar] [CrossRef]
- Vacondio, R.; Altomare, C.; De Leffe, M.; Hu, X.; Le Touzé, D.; Lind, S.; Marongiu, J.C.; Marrone, S.; Rogers, B.D.; Souto-Iglesias, A. Grand challenges for Smoothed Particle Hydrodynamics numerical schemes. Comput. Part. Mech. 2021, 8, 575–588. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Quinlan, N.J.; Basa, M.; Lastiwka, M. Truncation error in mesh-free particle methods. Int. J. Numer. Methods Eng. 2006, 66, 2064–2085. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM National Conference, New York, NY, USA, 27–29 August 1968; ACM Press: New York, NY, USA, 1968; pp. 517–524. [Google Scholar] [CrossRef]
- Randles, P.W.; Libersky, L.D. Smoothed Particle Hydrodynamics: Some recent improvements and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 375–408. [Google Scholar] [CrossRef]
- Bonet, J.; Kulasegaram, S. Correction and stabilization of smooth particle hydrodynamics methods with applications in metal forming simulations. Int. J. Numer. Methods Eng. 2000, 47, 1189–1214. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Sibilla, S. An algorithm to improve consistency in Smoothed Particle Hydrodynamics. Comput. Fluids 2015, 118, 148–158. [Google Scholar] [CrossRef]
- Dilts, G.A. Moving least-squares-particle hydrodynamics I. Consistency and stability. Int. J. Numer. Methods Eng. 1999, 44, 1115–1155. [Google Scholar] [CrossRef]
- Chaniotis, A.K.; Poulikakos, D.; Koumoutsakos, P. Remeshed smoothed particle hydrodynamics for the simulation of viscous and heat conducting flows. J. Comput. Phys. 2002, 182, 67–90. [Google Scholar] [CrossRef] [Green Version]
- Monaghan, J.J. On the Problem of Penetration in Particle Methods. J. Comput. Phys. 1989, 82, 1–15. [Google Scholar] [CrossRef]
- Lind, S.J.; Xu, R.; Stansby, P.K.; Rogers, B.D. Incompressible smoothed particle hydrodynamics for free-surface flows: A generalised diffusion-based algorithm for stability and validations for impulsive flows and propagating waves. J. Comput. Phys. 2012, 231, 1499–1523. [Google Scholar] [CrossRef]
- Lind, S.; Stansby, P. High-order Eulerian incompressible smoothed particle hydrodynamics with transition to Lagrangian free-surface motion. J. Comput. Phys. 2016, 326, 290–311. [Google Scholar] [CrossRef]
- Fourtakas, G.; Vacondio, R.; Rogers, B.D. An arbitrary Lagrangian–Eulerian weakly compressible SPH formulation by means of iterative diffusion-based particle shifting. In Proceedings of the 14th International SPHERIC Workshop, University of, Exeter, Exeter, UK, 25–27 June 2019. [Google Scholar]
- Vila, J.P. On particle weighted methods and Smooth Particle Hydrodynamics. Math. Model. Methods Appl. Sci. 1999, 09, 161–209. [Google Scholar] [CrossRef]
- Avesani, D.; Dumbser, M.; Bellin, A. A new class of Moving-Least-Squares WENO–SPH schemes. J. Comput. Phys. 2014, 270, 278–299. [Google Scholar] [CrossRef]
- Avesani, D.; Dumbser, M.; Vacondio, R.; Righetti, M. An alternative SPH formulation: ADER-WENO-SPH. Comput. Methods Appl. Mech. Eng. 2021, 382, 113871. [Google Scholar] [CrossRef]
- Vergnaud, A.; Oger, G.; Le Touzé, D. A higher order SPH scheme based on WENO reconstructions for two-dimensional problems. In Proceedings of the 14th International SPHERIC Workshop, University of, Exeter, Exeter, UK, 25–27 June 2019. [Google Scholar]
- Zhang, C.; Xiang, G.M.; Wang, B.; Hu, X.Y.; Adams, N.A. A weakly compressible SPH method with WENO reconstruction. J. Comput. Phys. 2019, 392, 1–18. [Google Scholar] [CrossRef]
- Eirís, A.; Ramírez, L.; Fernández-Fidalgo, J.; Couceiro, I.; Nogueira, X. SPH-ALE Scheme for Weakly Compressible Viscous Flow with a Posteriori Stabilization. Water 2021, 13, 245. [Google Scholar] [CrossRef]
- Nasar, A.M.; Fourtakas, G.; Lind, S.J.; Rogers, B.D.; Stansby, P.K.; King, J.R. High-order velocity and pressure wall boundary conditions in Eulerian incompressible SPH. J. Comput. Phys. 2021, 434, 109793. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Fourtakas, G.; Altomare, C.; Canelas, R.B.; Tafuni, A.; García-Feal, O.; Martínez-Estévez, I.; Mokos, A.; Vacondio, R.; Crespo, A.J.C.; et al. DualSPHysics: From fluid dynamics to multiphysics problems. Comput. Part. Mech. 2021. [Google Scholar] [CrossRef]
- English, A.; Domínguez, J.M.; Vacondio, R.; Crespo, A.J.C.; Stansby, P.K.; Lind, S.J.; Chiapponi, L.; Gómez-Gesteira, M. Modified dynamic boundary conditions (mDBC) for general-purpose smoothed particle hydrodynamics (SPH): Application to tank sloshing, dam break and fish pass problems. Comput. Part. Mech. 2021. [Google Scholar] [CrossRef]
- King, J.R.; Lind, S.J.; Nasar, A.M. High order difference schemes using the local anisotropic basis function method. J. Comput. Phys. 2020, 415, 109549. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Avesani, D.; Herrera, P.; Chiogna, G.; Bellin, A.; Dumbser, M. Smooth Particle Hydrodynamics with nonlinear Moving-Least-Squares WENO reconstruction to model anisotropic dispersion in porous media. Adv. Water Resour. 2015, 80, 43–59. [Google Scholar] [CrossRef]
- Avesani, D.; Dumbser, M.; Chiogna, G.; Bellin, A. An alternative smooth particle hydrodynamics formulation to simulate chemotaxis in porous media. J. Math. Biol. 2017, 74, 1037–1058. [Google Scholar] [CrossRef] [Green Version]
- Bunch, J.R.; Hopcroft, J.E. Triangular Factorization and Inversion by Fast Matrix Multiplication. Math. Comput. 1974, 28, 231–236. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in Fortran, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Vacondio, R.; Rogers, B. Consistent Iterative shifting for SPH methods. In Proceedings of the 12th International SPHERIC Workshop, Universidade de Vigo, Ourense, Spain, 13–15 June 2017. [Google Scholar]
- Oger, G.; Marrone, S.; Le Touzé, D.; de Leffe, M. SPH accuracy improvement through the combination of a quasi-Lagrangian shifting transport velocity and consistent ALE formalisms. J. Comput. Phys. 2016, 313, 76–98. [Google Scholar] [CrossRef]
| Riemann-Based Scheme | CPU Time / CPU Time Standard SPH |
|---|---|
| MUSCL | 2.5 |
| WENO | 10.9 |
| SPH Scheme | CPU time / CPU Time Standard SPH | ||
|---|---|---|---|
| Standard SPH () | 160 | 0.020532 | 1 |
| WENO-RSPH | 52 | 0.020878 | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antona, R.; Vacondio, R.; Avesani, D.; Righetti, M.; Renzi, M. Towards a High Order Convergent ALE-SPH Scheme with Efficient WENO Spatial Reconstruction. Water 2021, 13, 2432. https://doi.org/10.3390/w13172432
Antona R, Vacondio R, Avesani D, Righetti M, Renzi M. Towards a High Order Convergent ALE-SPH Scheme with Efficient WENO Spatial Reconstruction. Water. 2021; 13(17):2432. https://doi.org/10.3390/w13172432
Chicago/Turabian StyleAntona, Rubén, Renato Vacondio, Diego Avesani, Maurizio Righetti, and Massimiliano Renzi. 2021. "Towards a High Order Convergent ALE-SPH Scheme with Efficient WENO Spatial Reconstruction" Water 13, no. 17: 2432. https://doi.org/10.3390/w13172432








