River Runoff Modelling and Hydrological Drought Assessment Based on High-Resolution Brightness Temperatures in Mainland China
Abstract
:1. Introduction
2. Study Areas and Data
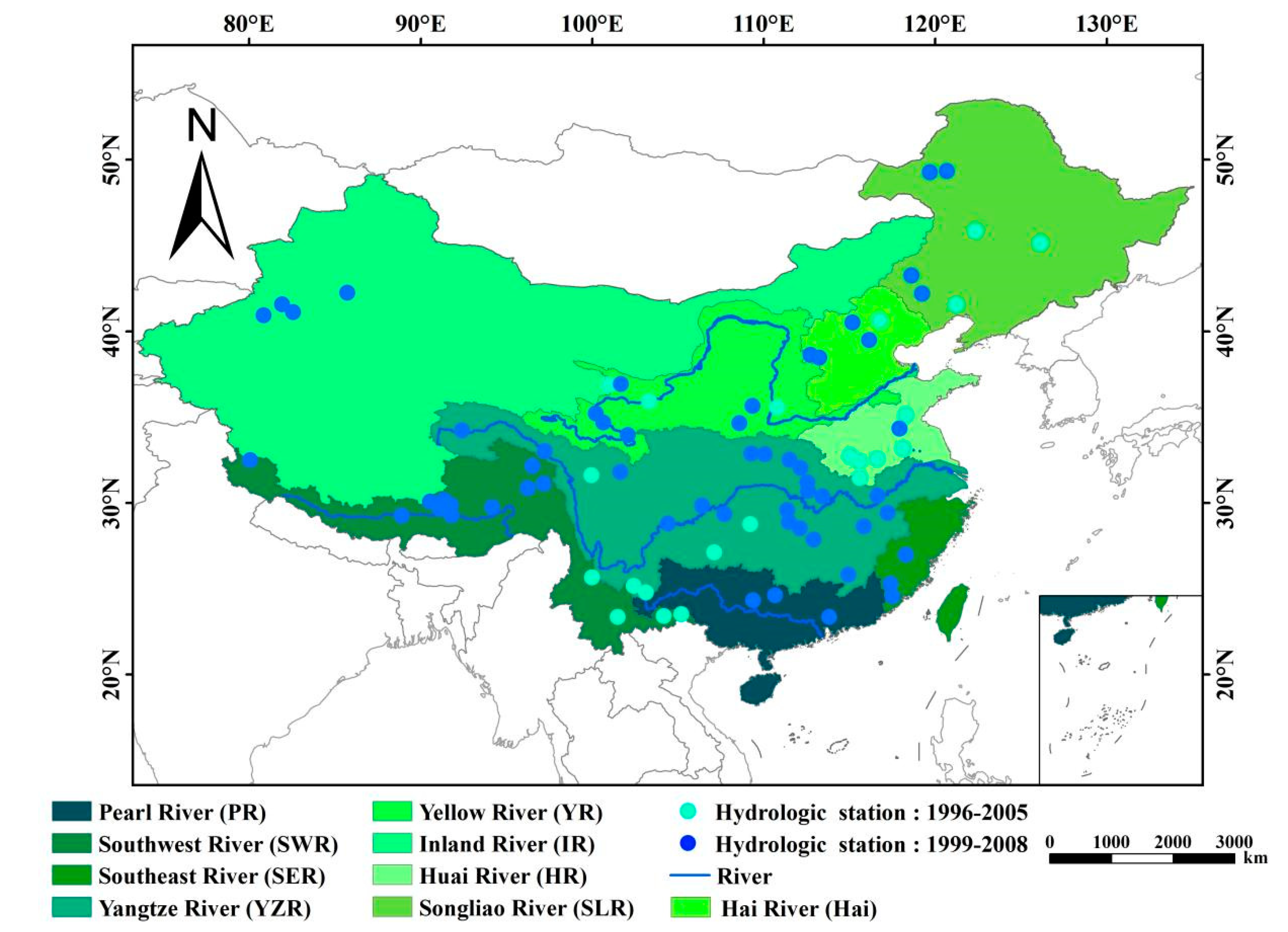
2.1. Study Areas
2.2. Data
2.2.1. Hydrological Data
2.2.2. Remote Sensing Data
2.2.3. Reference Data
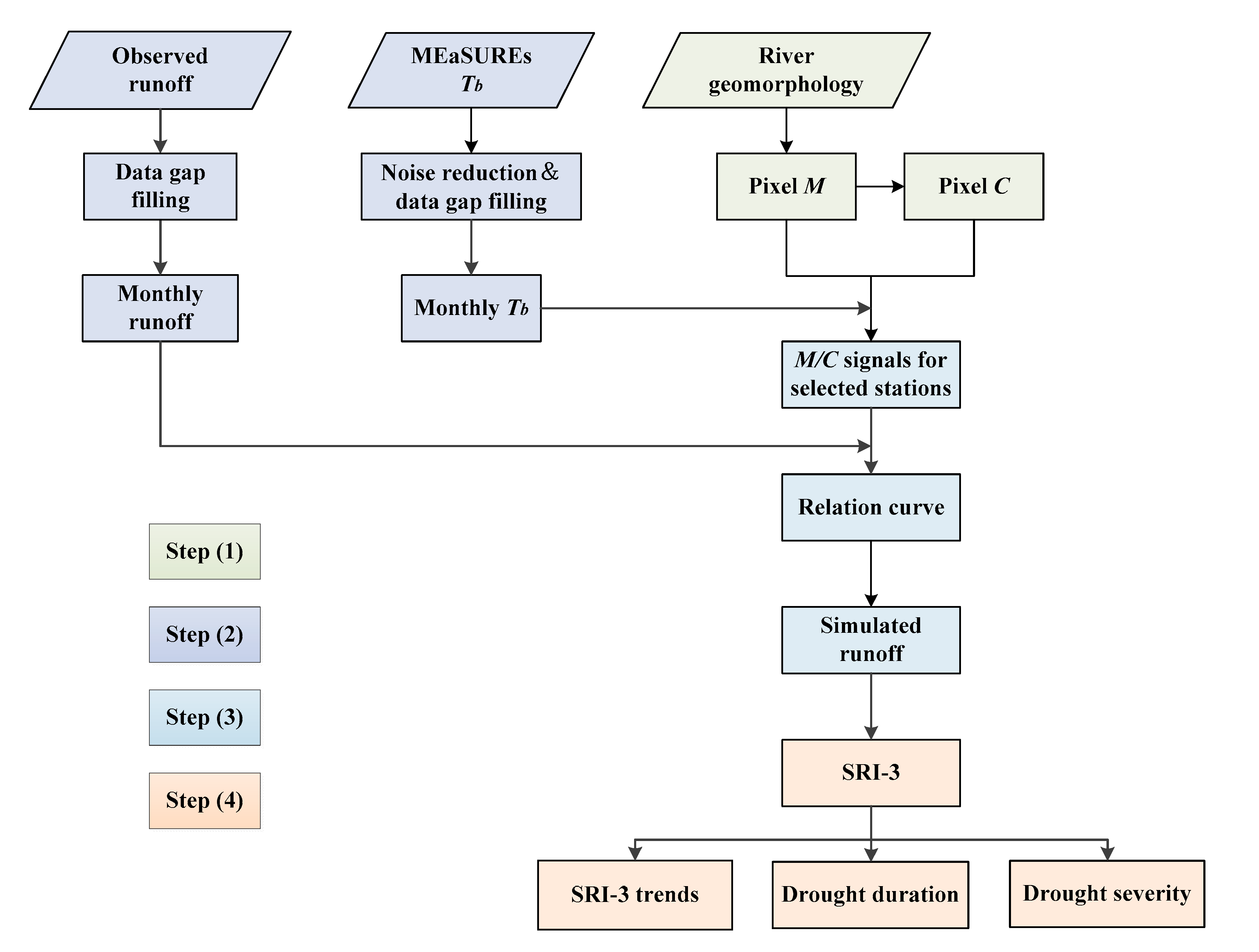
3. Methods
3.1. Processing Steps for Tb Data
3.2. Building a Runoff Simulation Model
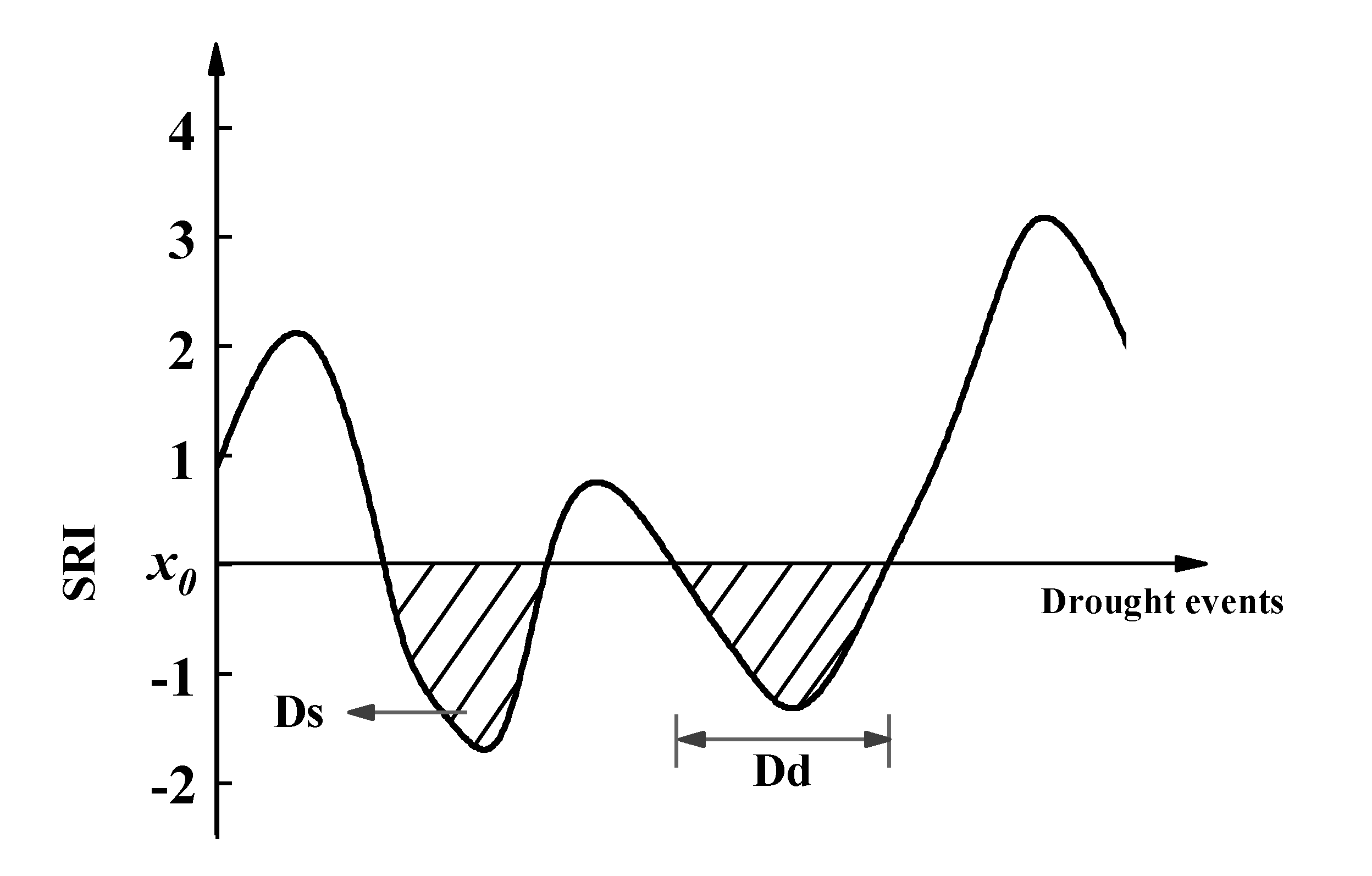
3.3. SRI Calculation and Run Theory
3.4. Statistical Metrics
4. Results
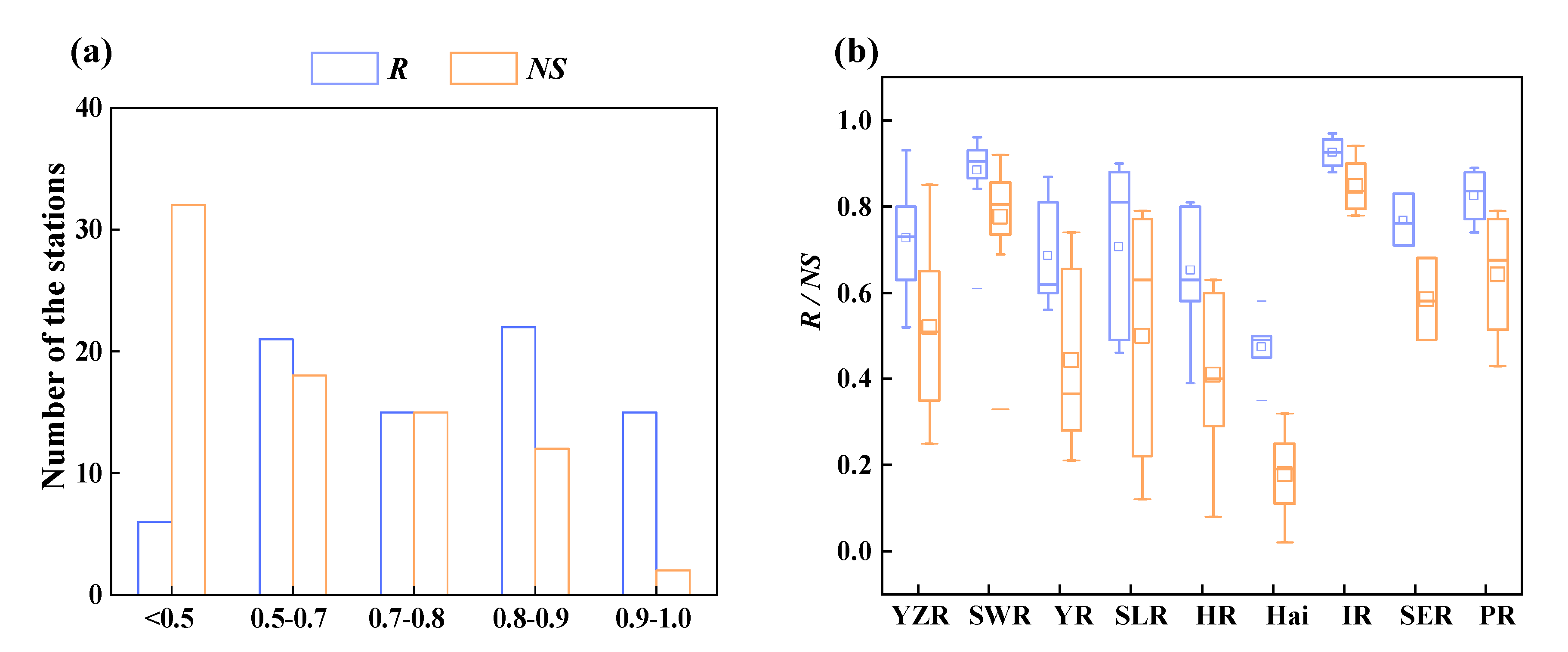
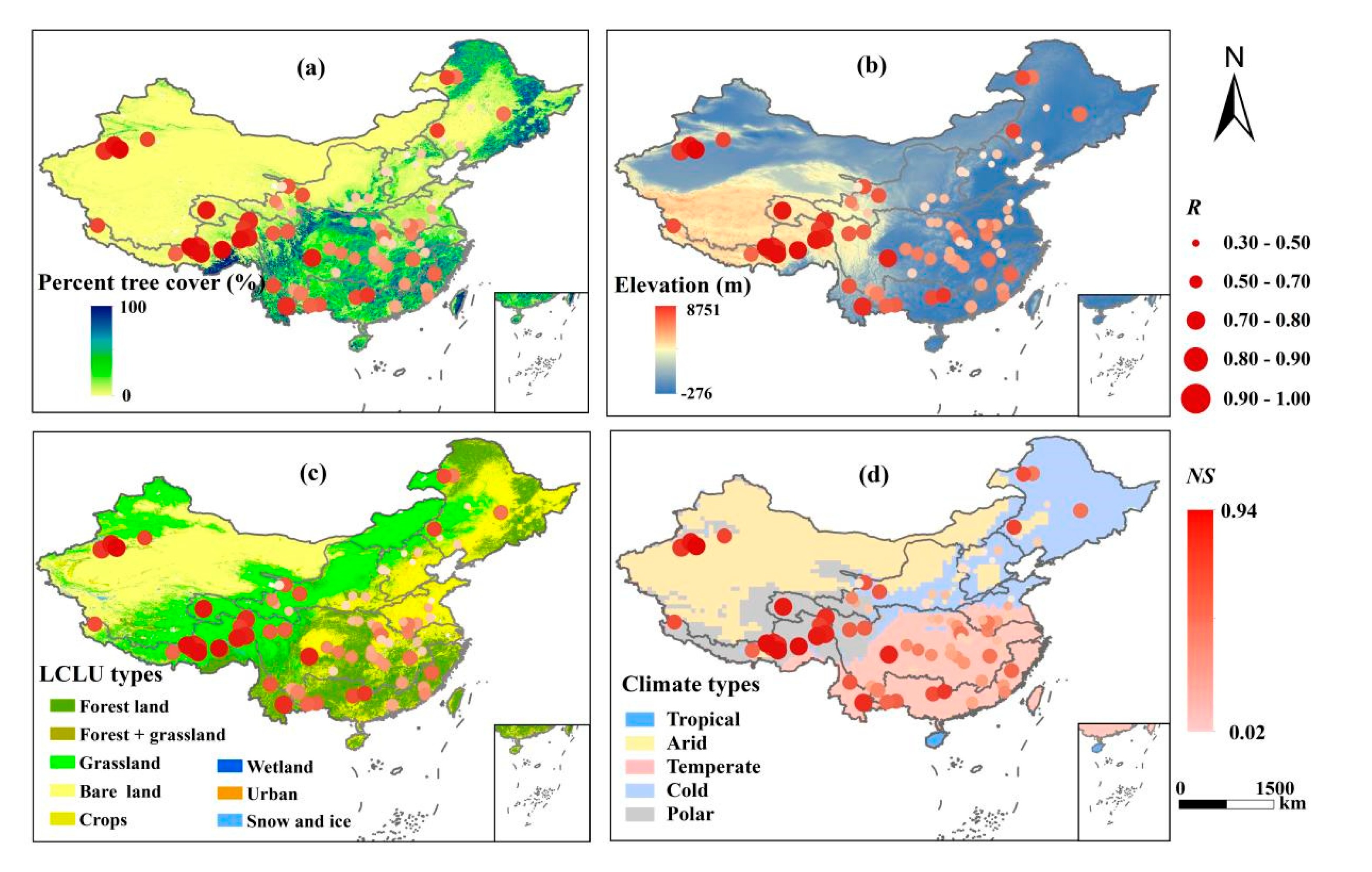
4.1. Runoff Simulation Results Obtained by the M/C Signal Method
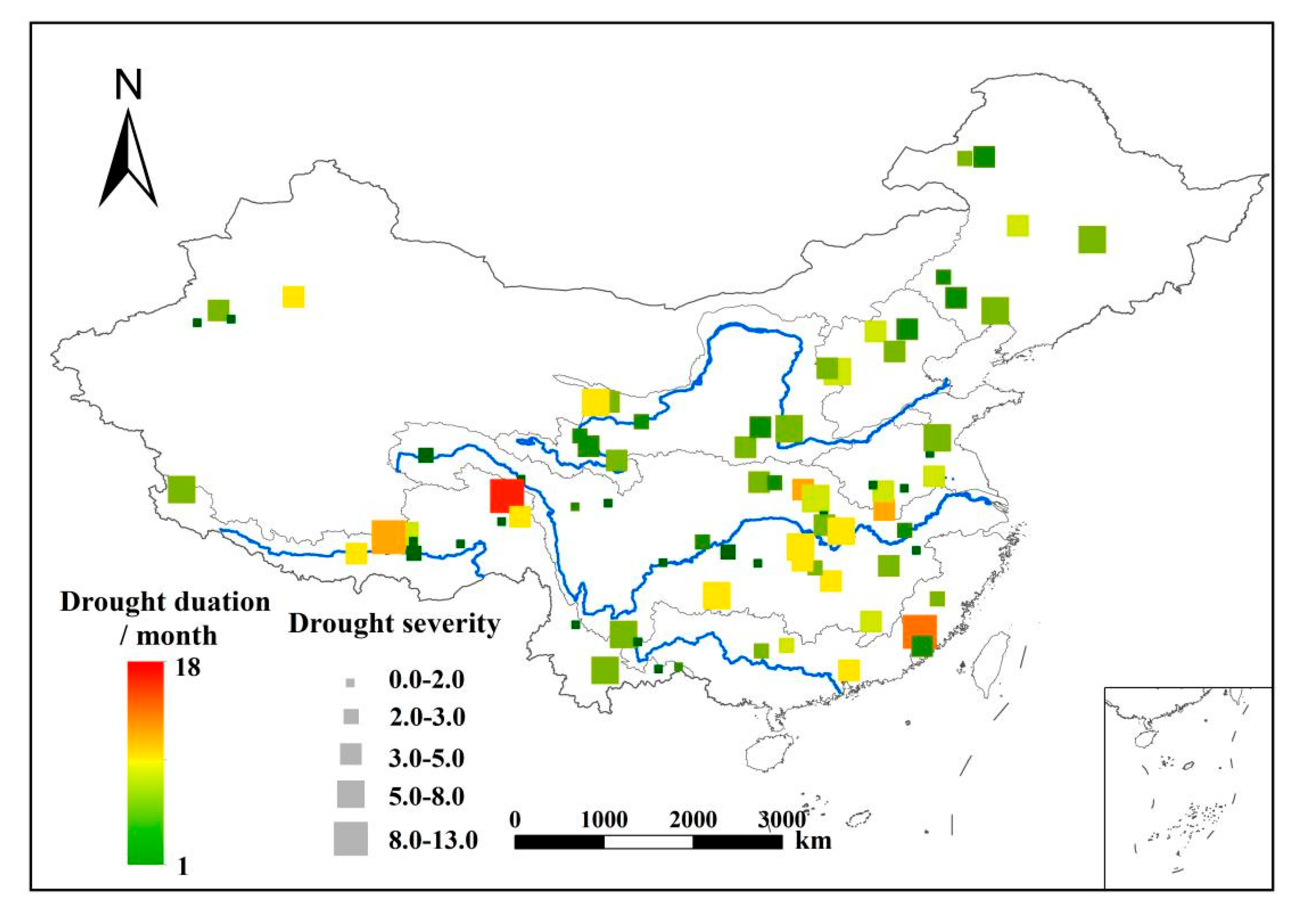
4.2. Hydrological Drought Assessment Based on Simulated Runoff
5. Discussion
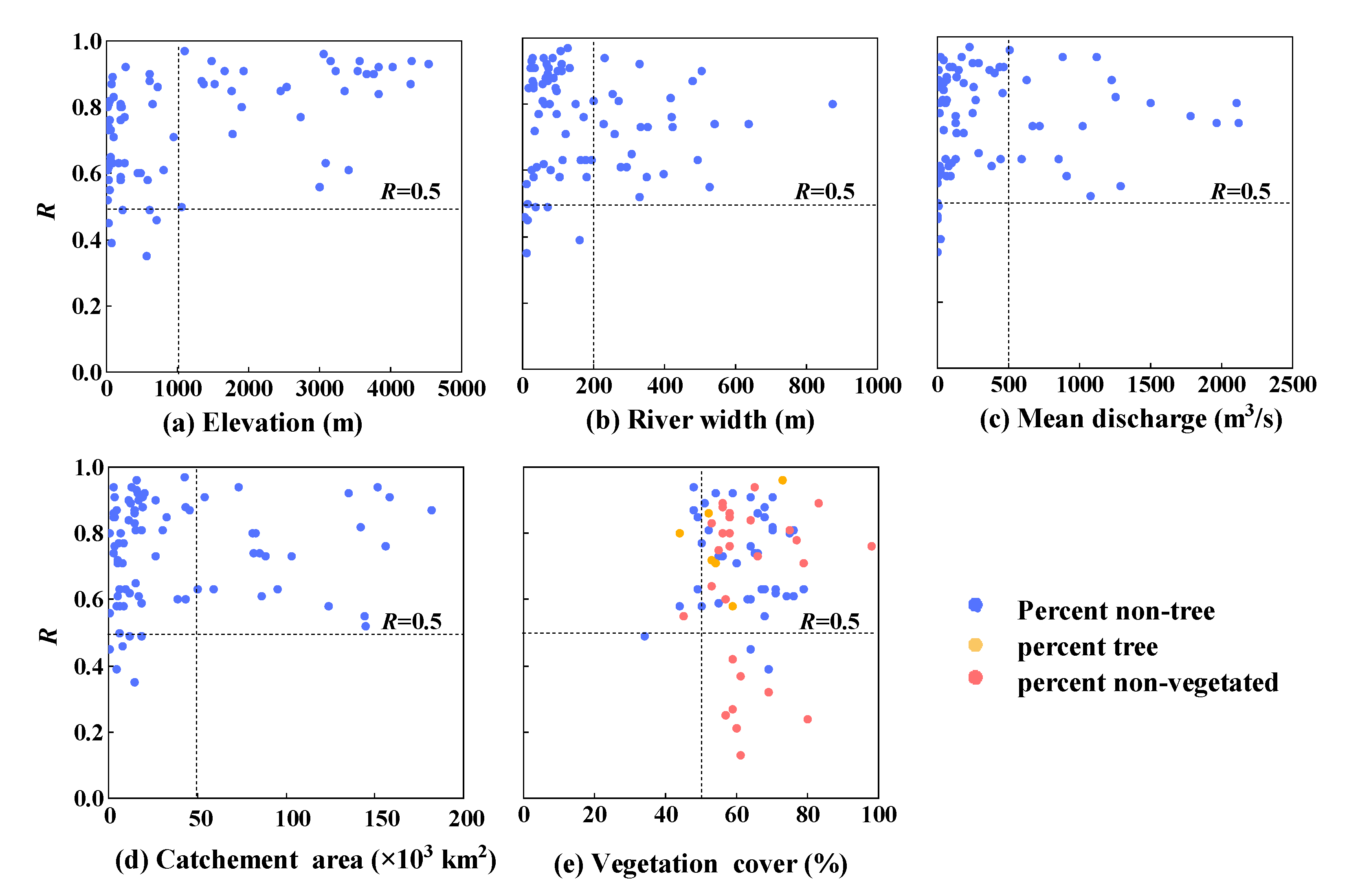
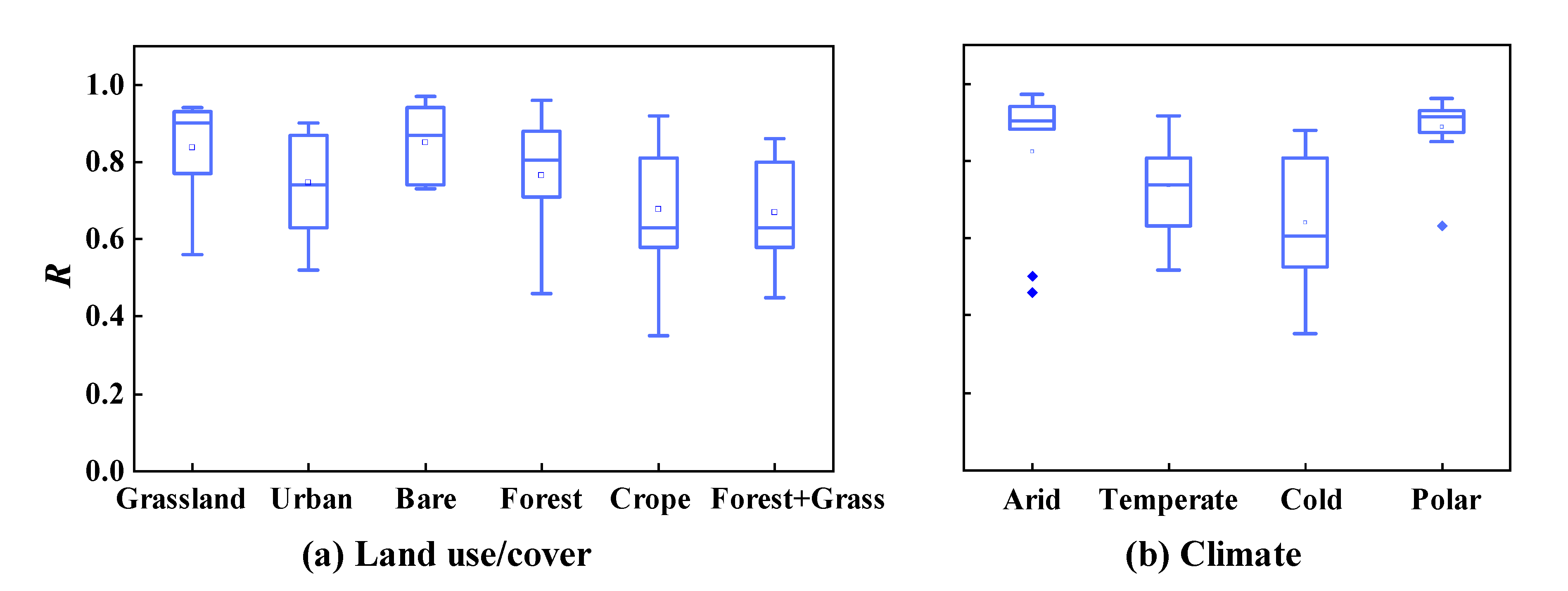
5.1. Influencing Factors of Runoff Simulation Based on the M/C Signal Method
5.2. Drought Assessment Based on Remote Sensing
6. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schubert, S.D.; Stewart, R.E.; Wang, H.; Barlow, M.; Berbery, E.H.; Cai, W.; Hoerling, M.P.; Kanikicharla, K.K.; Koster, R.D.; Lyon, B.; et al. Global meteorological drought: A synthesis of current understanding with a focus on SST Drivers of precipitation deficits. J. Clim. 2016, 29, 3989–4019. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Ionita, M.; Nagavciuc, V.; Kumar, R.; Rakovec, O. On the curious case of the recent decade, mid-spring precipitation deficit in central Europe. NPJ Clim. Atmos. Sci. 2020, 3, 1–10. [Google Scholar] [CrossRef]
- Ionita, M.; Dima, M.; Nagavciuc, V.; Scholz, P.; Lohmann, G. Past megadroughts in central Europe were longer, more severe and less warm than modern droughts. Commun. Earth Environ. 2021, 2, 53887. [Google Scholar] [CrossRef]
- Kim, T.; Jehanzaib, M. Drought Risk Analysis, Forecasting and Assessment under Climate Chang. Water-Sui 2020, 12, 1862. [Google Scholar]
- Zhuguo, M.; Congbin, F. Interannual characteristics of the surface hydrological variables over the arid and semi-arid areas of northern China. Glob. Planet. Chang. 2003, 37, 189–200. [Google Scholar]
- Leng, G.; Tang, Q.; Rayburg, S. Climate change impacts on meteorological, agricultural and hydrological droughts in China. Glob. Planet. Chang. 2015, 126, 23–34. [Google Scholar] [CrossRef]
- Barriopedro, D.; Gouveia, C.M.; Trigo, R.M.; Wang, L. The 2009/10 Drought in China: Possible Causes and Impacts on Vegetation. J. Hydrometeorol. 2012, 13, 1251–1267. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Xu, H.; Liu, D. Features of the extremely severe drought in the east of Southwest China and anomalies of atmospheric circulation in summer 2006. Acta Meteorol. Sin. 2011, 25, 176–187. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, L.; Feng, Z.; Li, P. Detecting effects of the recent drought on vegetation in southwestern China. J. Resour. Ecol. 2012, 3, 43–49. [Google Scholar]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Yang, H.; Li, Z.; Qin, Y.; Shen, Y. Spatio-temporal variation of drought in China during 1961–2012: A climatic perspective. J. Hydrol. 2015, 526, 253–264. [Google Scholar] [CrossRef]
- Fendeková, M.; Gauster, T.; Labudová, L.; Vrablíková, D.; Danáčová, Z.; Fendek, M.; Pekárová, P. Analysing 21st century meteorological and hydrological drought events in Slovakia. J. Hydrol. Hydromech. 2018, 66, 393–403. [Google Scholar] [CrossRef] [Green Version]
- Vasiliades, L.; Loukas, A.; Liberis, N. A water balance derived drought index for Pinios River Basin, Greece. Water Resour. Manag. 2011, 25, 1087–1101. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kieist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Welford, M.; Hollinger, S.; Isard, S. A new soil moisture drought index for predicting crop yields. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 187–190. [Google Scholar]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Zhang, X.; Wang, X.; Hao, Z.; Singh, V.P.; Hao, F. Propagation from meteorological drought to hydrological drought under the impact of human activities: A case study in northern China. J. Hydrol. 2019, 579, 124147. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, Y.; Chen, Y.; Bai, Y.; Zhang, L.; Zhang, Q. Hydrological drought risk assessment using a multidimensional Copula function approach in arid inland basins, China. Water-Sui 2020, 12, 1888. [Google Scholar] [CrossRef]
- Gu, L.; Chen, J.; Yin, J.; Xu, C.; Chen, H. Drought hazard transferability from meteorological to hydrological propagation. J. Hydrol. 2020, 585, 124761. [Google Scholar] [CrossRef]
- Liu, X.; Wang, S.; Zhou, Y.; Wang, F.; Li, W.; Liu, W. Regionalization and spatiotemporal variation of drought in China based on standardized precipitation evapotranspiration index (1961–2013). Adv. Meteorol. 2015, 2015, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Guo, S.; Gu, L.; Zeng, Z.; Liu, D.; Chen, J.; Shen, Y.; Xu, C. Blending multi-satellite, atmospheric reanalysis and gauge precipitation products to facilitate hydrological modelling. J. Hydrol. 2021, 593, 125878. [Google Scholar] [CrossRef]
- Tang, G.; Long, D.; Hong, Y.; Gao, J.; Wan, W. Documentation of multifactorial relationships between precipitation and topography of the Tibetan Plateau using spaceborne precipitation radars. Remote Sens. Environ. 2018, 208, 82–96. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Lawrence Dingman, S.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Anderson, M.C.; Eichinger, W.E.; Entekhabi, D.; Hornbuckle, B.K.; Houser, P.R.; Katul, G.G.; Kustas, W.P.; Norman, J.M.; Peters-Lidard, C.; et al. A remote sensing observatory for hydrologic sciences: A genesis for scaling to continental hydrology. Water Resour. Res. 2006, 42, W7301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Hong, Y.; Wang, X.; Gourley, J.J.; Gao, J.; Vergara, H.J.; Yong, B. Assimilation of passive microwave streamflow signals for improving flood forecasting: A first study in Cubango River Basin, Africa. Appl. Earth Obs. Remote Sens. 2013, 6, 2375–2390. [Google Scholar] [CrossRef]
- Zeng, Z.; Gan, Y.; Kettner, A.J.; Yang, Q.; Zeng, C.; Brakenridge, G.R.; Hong, Y. Towards high resolution flood monitoring: An integrated methodology using passive microwave brightness temperatures and Sentinel synthetic aperture radar imagery. J. Hydrol. 2020, 582, 124377. [Google Scholar] [CrossRef]
- Zaji, A.H.; Bonakdari, H.; Gharabaghi, B. Remote sensing satellite data preparation for simulating and forecasting river discharge. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3432–3441. [Google Scholar] [CrossRef]
- Huang, Q.; Long, D.; Du, M.; Zeng, C.; Li, X.; Hou, A.; Hong, Y. An improved approach to monitoring Brahmaputra River water levels using retracked altimetry data. Remote Sens. Environ. 2018, 211, 112–128. [Google Scholar] [CrossRef]
- McFarland, M.J.; Miller, R.L.; Neale, C.M.U. Land surface temperature derived from the SSM/I passive microwave brightness temperatures. IEEE Trans. Geosci. Remote Sens. 1990, 28, 839–845. [Google Scholar] [CrossRef]
- Alley, R.; Jentoft-Nilsen, M. Algorithm Theoretical Basis Document for: Brightness Temperature; Jet Propulsion Laboratory: Pasadena, CA, USA, 1999. [Google Scholar]
- Brakenridge, G.R.; Cohen, S.; Kettner, A.J.; De Groeve, T.; Nghiem, S.V.; Syvitski, J.P.M.; Fekete, B.M. Calibration of satellite measurements of river discharge using a global hydrology model. J. Hydrol. 2012, 475, 123–136. [Google Scholar] [CrossRef]
- Brakenridge, G.R.; Nghiem, S.V.; Anderson, E.; Chien, S. Space-based measurement of river runoff. Trans. Am. Geophys. Union 2005, 86, 185–188. [Google Scholar] [CrossRef] [Green Version]
- Brakenridge, G.R.; Nghiem, S.V.; Anderson, E.; Mic, R. Orbital microwave measurement of river discharge and ice status. Water Resour. Res. 2007, 43, W4405. [Google Scholar] [CrossRef]
- van Dijk, A.I.J.M.; Brakenridge, G.R.; Kettner, A.J.; Beck, H.E.; De Groeve, T.; Schellekens, J. River gauging at global scale using optical and passive microwave remote sensing. Water Resour. Res. 2016, 52, 6404–6418. [Google Scholar] [CrossRef]
- Revilla-Romero, B.; Thielen, J.; Salamon, P.; De Groeve, T.; Brakenridge, G.R. Evaluation of the satellite-based Global Flood Detection System for measuring river discharge: Influence of local factors. Hydrol. Earth Syst. Sci. 2014, 18, 4467–4484. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Lang, X.; Jiang, D. Köppen climate zones in China over the last 21,000 years. J. Geophys. Res. Atmos. 2021, 126, e2020JD034310. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, J.; Li, H. Drought and flood monitoring of the Liao River Basin in Northeast China using extended GRACE data. Remote Sens. 2018, 8, 1168. [Google Scholar] [CrossRef] [Green Version]
- Brodzik, M.J.; Long, D.G.; Hardman, M.A.; Paget, A.; Armstrong, R. MEaSUREs Calibrated Enhanced-Resolution Passive Microwave Daily EASE-Grid 2.0 Brightness Temperature ESDR, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2020. [Google Scholar]
- Brodzik, M.J.; Hardman, M.A.; Long, D.G. Leveraging metadata conventions to improve usability of an EASE-Grid 2.0 passive microwave data product. Int. Geosci. Remote Sens. Symp. 2017, 5197–5200. [Google Scholar] [CrossRef]
- Long, D.G.; Stroeve, J. Enhanced-Resolution SSM/I and AMSR-E Daily Polar Brightness Temperatures; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 2011. [Google Scholar]
- Johnson, M.T.; Ramage, J.; Troy, T.J.; Brodzik, M.J. Snowmelt detection with calibrated, Enhanced--Resolution Brightness Temperatures (CETB) in Colorado Watersheds. Water Resour. Res. 2020, 1, e2018WR024542. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, G2004. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, D.; O’Loughlin, F.; Trigg, M.A.; Miller, Z.F.; Pavelsky, T.M.; Bates, P.D. Development of the Global Width Database for Large Rivers. Water Resour. Res. 2014, 50, 3467–3480. [Google Scholar] [CrossRef]
- Chen, J.; Ban, Y.; Li, S. China: Open access to Earth land-cover map. Nature 2014, 7523, 434. [Google Scholar]
- DiMiceli, C.; Carroll, M.; Sohlberg, R.; Kim, D.; Kelly, M.; Townshend, J. MOD44B MODIS/Terra Vegetation Continuous Fields Yearly L3 Global 250 m SIN Grid V006; NASA EOSDIS Land Processes DAAC: Washington, DC, USA, 2015. [Google Scholar]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Peel, M.C.; Finlayson, B.L.; Mcmahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. Discuss. 2007, 5, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Rees, W.; Peellikkap, P.P. Principles of remote sensing. In Remote Sensing of Glaciers; Taylor & Francis: Abingdon, UK, 2009. [Google Scholar]
- Brakenridge, G.R.; De Grove, T. Satellite River Discharge and Runoff Measurements: Technical Summary; University of Colorado: Boulder, CO, USA, 2013. [Google Scholar]
- Khan, S.I.; Hong, Y.; Vergara, H.J.; Gourley, J.J.; Brakenridge, G.R.; De Groeve, T.; Flamig, Z.L.; Policelli, F.; Yong, B. Microwave satellite data for hydrologic modeling in ungauged basins. Trans. Geosci. Remote Sens. 2012, 4, 663–667. [Google Scholar] [CrossRef]
- Zelenhasić, E.; Salvai, A. A method of streamflow drought analysis. Water Resour. Reacher. 1987, 1, 156. [Google Scholar] [CrossRef]
- Wu, R.; Zhang, J.; Bao, Y.; Guo, E. Run theory and Copula-based drought risk analysis for Songnen Grassland in northeastern China. Sustainability 2019, 11, 6032. [Google Scholar] [CrossRef] [Green Version]
- Kwak, J.; Kim, S.; Jung, J.; Singh, V.P.; Lee, D.R.; Kim, H.S. Assessment of meteorological drought in Korea under climate Chang. Adv. Meteorol. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Guttman, N.B. Accepting the Standardized Precipitation Index: A calculation algorithm. J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Mei, Y.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Evaluating Satellite Precipitation Error Propagation in Runoff Simulations of Mountainous Basins. J. Hydrometeorol. 2016, 17, 1407–1423. [Google Scholar] [CrossRef]
- Ehsan Bhuiyan, M.A.; Nikolopoulos, E.I.; Anagnostou, E.N.; Polcher, J.; Albergel, C.; Dutra, E.; Fink, G.; Martínez-de La Torre, A.; Munier, S. Assessment of precipitation error propagation in multi-model global water resource reanalysis. Hydrol. Earth Syst. Sci. 2019, 23, 1973–1994. [Google Scholar] [CrossRef] [Green Version]
- De Groeve, T. Flood monitoring and mapping using passive microwave remote sensing in Namibia. Geomat. Nat. Hazards Risk 2010, 1, 19–35. [Google Scholar] [CrossRef]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Elsevier Science: New York, NY, USA, 1994. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Bjerklie, D.M. Estimating the bankfull velocity and discharge for rivers using remotely sensed river morphology information. J. Hydrol. 2007, 341, 144–155. [Google Scholar] [CrossRef]
- Tian, H.; Iqbal, M. Utilizing a new soil effective temperature scheme and archived satellite microwave brightness temperature data to estimate surface soil moisture in the Nagqu region, Tibetan Plateau of China. J. Arid Land 2018, 10, 84–100. [Google Scholar] [CrossRef] [Green Version]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating discharge in rivers using remotely sensed hydraulic information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- Moffitt, C.B.; Hossain, F.; Adler, R.F.; Yilmaz, K.K.; Pierce, H.F. Validation of a TRMM-based global Flood Detection System in Bangladesh. Int. J. Appl. Earth Obs. 2011, 13, 165–177. [Google Scholar] [CrossRef]
- Yao, N.; Zhao, H.; Li, Y.; Biswas, A.; Feng, H.; Liu, F.; Pulatov, B. National-scale variation and propagation characteristics of meteorological, agricultural, and hydrological droughts in China. Remote Sens. 2020, 12, 3407. [Google Scholar] [CrossRef]
- Yu, M.; Li, Q.; Hayes, M.J.; Svoboda, M.D.; Heim, R.R. Are droughts becoming more frequent or severe in China based on the Standardized Precipitation Evapotranspiration Index: 1951–2010? Int. J. Climatol. 2014, 34, 545–558. [Google Scholar] [CrossRef]
- Zhai, J.; Su, B.; Krysanova, V.; Vetter, T.; Gao, C.; Jiang, T. Spatial variation and trends in PDSI and SPI indices and their relation to streamflow in 10 large regions of China. J. Clim. 2010, 23, 649–663. [Google Scholar] [CrossRef]
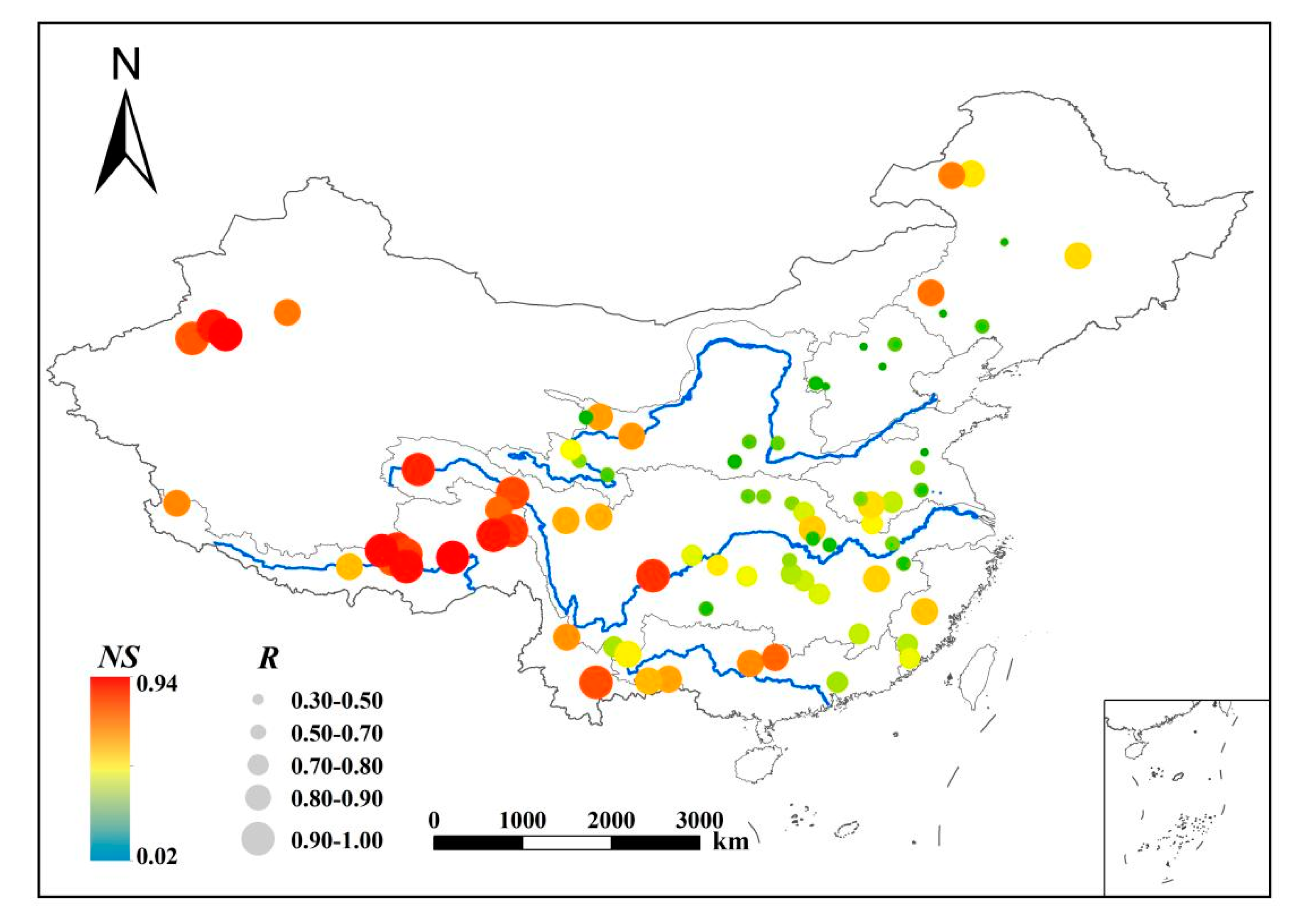
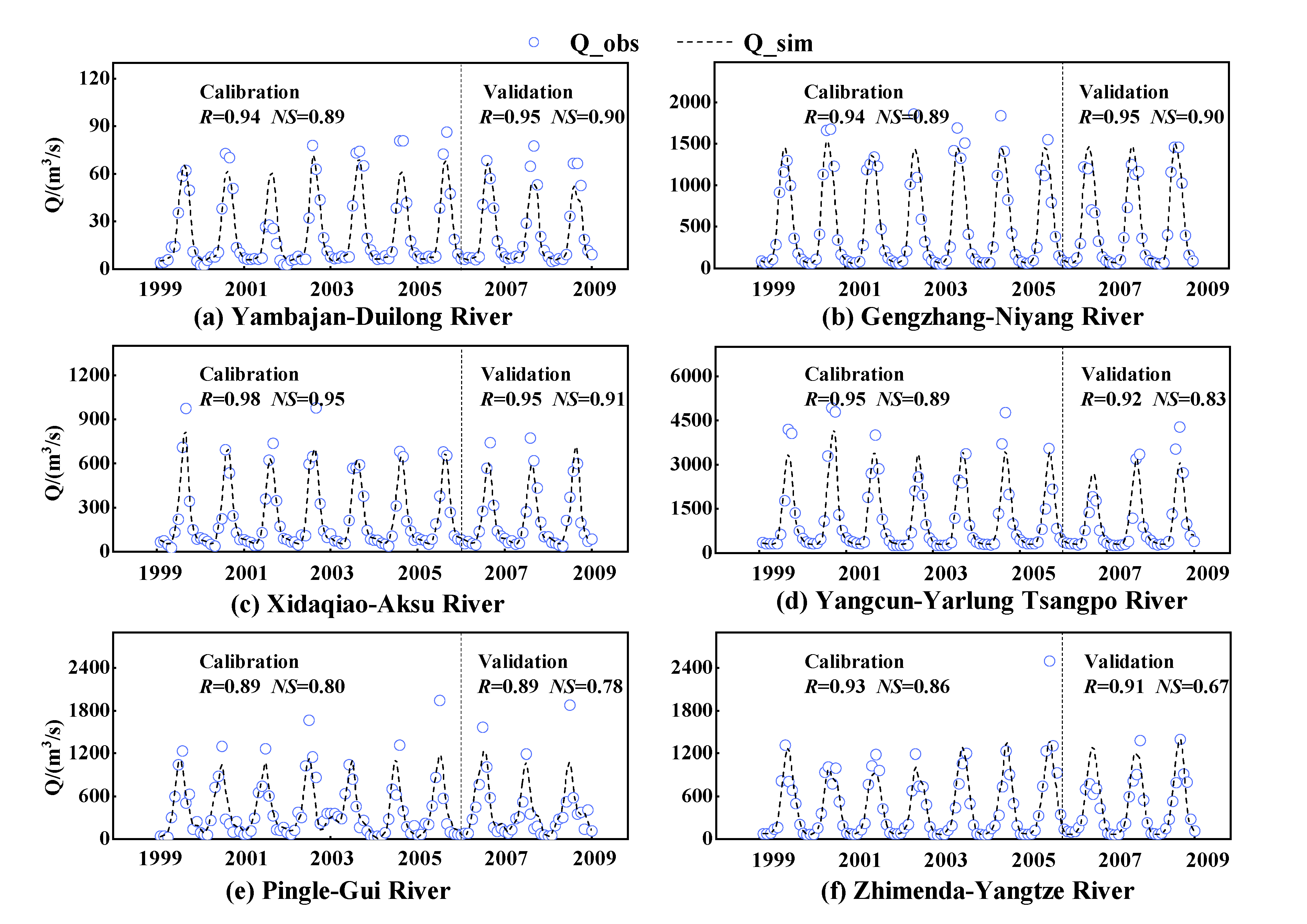
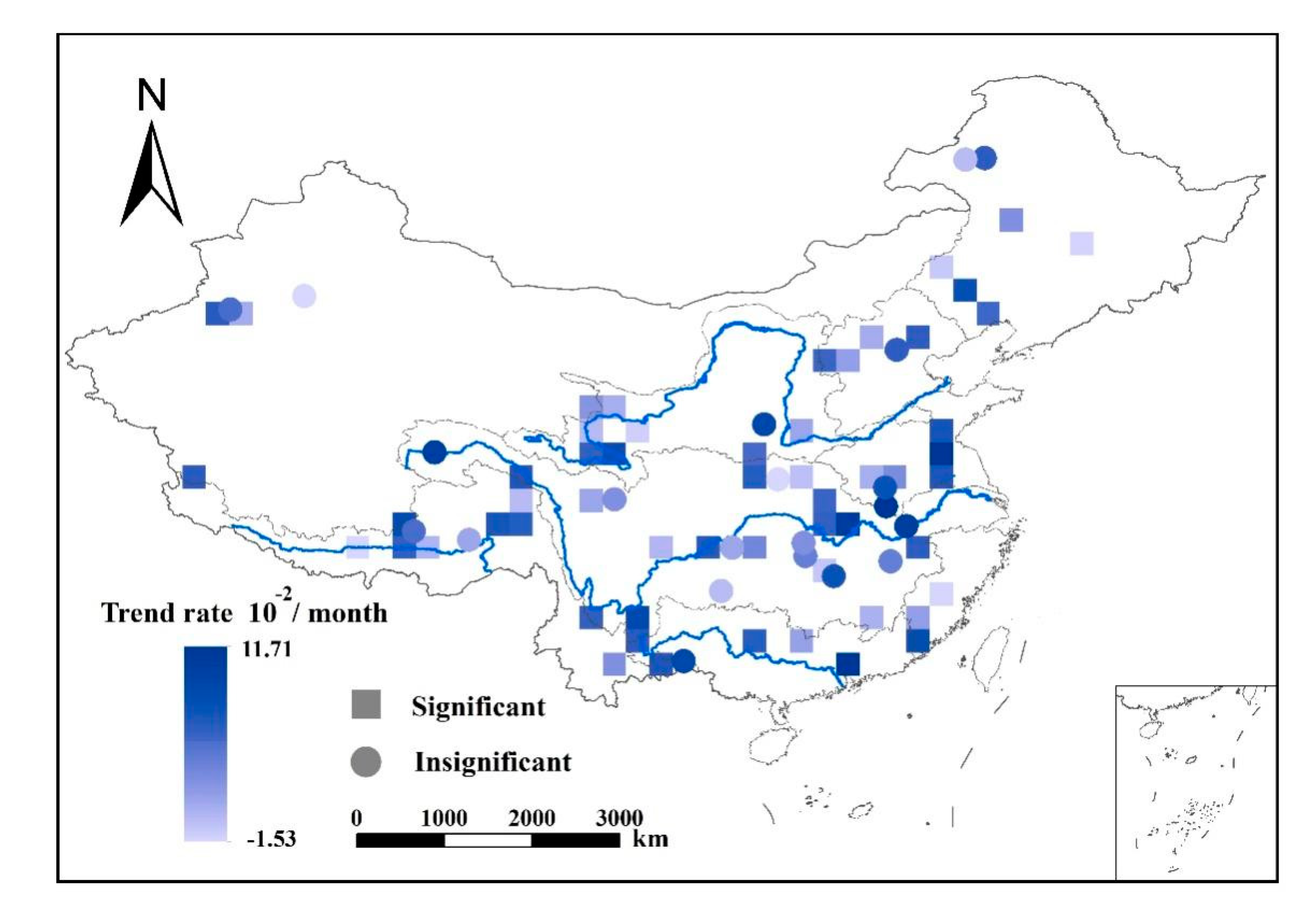
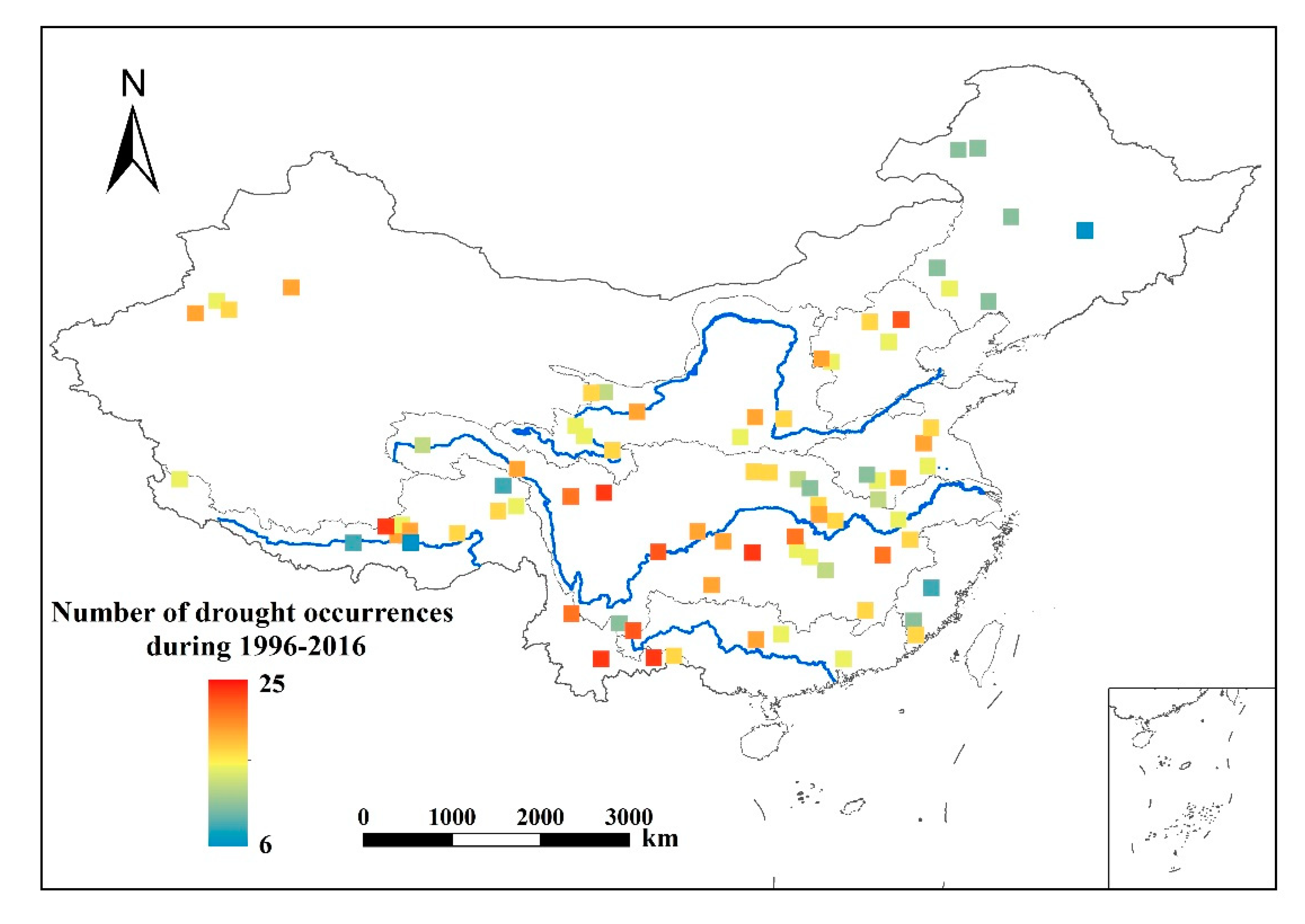
| Basin | YZR | YR | PR | SWR | HR | SER | Hai | SLR | IR | |
|---|---|---|---|---|---|---|---|---|---|---|
| Climate | Tropical | |||||||||
| Arid | 2 | 1 | 2 | 4 | ||||||
| Temperate | 21 | 7 | 4 | 4 | 5 | 3 | ||||
| Cold | 2 | 2 | 4 | 5 | ||||||
| Polar | 4 | 2 | 7 | |||||||
| LULC | Grassland | 4 | 5 | 6 | ||||||
| Forest + grassland | 4 | 1 | 2 | 2 | 2 | 2 | ||||
| Crops | 5 | 2 | 2 | 2 | 5 | 3 | ||||
| Urban | 6 | 2 | 1 | 1 | 1 | |||||
| Forest land | 3 | 3 | 3 | 5 | ||||||
| Bare land | 3 | 1 | 3 | |||||||
| Mean discharge (m3/s) | <100 | 6 | 7 | 1 | 6 | 3 | 5 | 7 | ||
| 100–500 | 6 | 1 | 2 | 6 | 2 | 3 | 4 | |||
| >500 | 13 | 1 | 1 | 3 | 2 | |||||
| Catchment area (×103 km2) | <10 | 7 | 5 | 2 | 4 | 2 | 2 | 3 | 1 | |
| 10–50 | 5 | 3 | 2 | 7 | 2 | 1 | 2 | 6 | 4 | |
| >100 | 13 | 1 | 4 | 3 | ||||||
| Topography | Fist terrace | 4 | 6 | 11 | 3 | |||||
| Second terrace | 8 | 3 | 1 | 4 | 1 | 3 | 4 | |||
| Third terrace | 13 | 3 | 7 | 4 | 4 | |||||
| Data Period | 1996–2005 | 4 | 3 | 1 | 4 | 6 | 1 | 3 | ||
| 1999–2008 | 21 | 6 | 3 | 11 | 1 | 3 | 4 | 4 | 4 | |
| Total | 25 | 9 | 4 | 15 | 7 | 3 | 5 | 7 | 4 | |
| Basin | Increasing Trend | Percentage (%) | Decreasing Trend | Percentage (%) |
|---|---|---|---|---|
| YZR | 12/25 * | 48.0 | 13/25 | 52.0 |
| YR | 3/7 | 37.5 | 5/7 | 62.5 |
| PR | 3/4 | 75.0 | 1/4 | 25.0 |
| SWR | 9/16 | 56.3 | 7/16 | 43.8 |
| SER | 1/3 | 33.3 | 2/3 | 66.7 |
| HR | 4/7 | 57.1 | 3/7 | 42.9 |
| Hai | 2/5 | 40.0 | 3/5 | 60.0 |
| SLR | 2/7 | 28.6 | 5/7 | 71.4 |
| IR | 2/4 | 40.0 | 2/4 | 40.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, X.; Zeng, Z.; Yuan, Z.; Huo, J.; Wang, Y.; Xu, J. River Runoff Modelling and Hydrological Drought Assessment Based on High-Resolution Brightness Temperatures in Mainland China. Water 2021, 13, 2429. https://doi.org/10.3390/w13172429
Qu X, Zeng Z, Yuan Z, Huo J, Wang Y, Xu J. River Runoff Modelling and Hydrological Drought Assessment Based on High-Resolution Brightness Temperatures in Mainland China. Water. 2021; 13(17):2429. https://doi.org/10.3390/w13172429
Chicago/Turabian StyleQu, Xing, Ziyue Zeng, Zhe Yuan, Junjun Huo, Yongqiang Wang, and Jijun Xu. 2021. "River Runoff Modelling and Hydrological Drought Assessment Based on High-Resolution Brightness Temperatures in Mainland China" Water 13, no. 17: 2429. https://doi.org/10.3390/w13172429
APA StyleQu, X., Zeng, Z., Yuan, Z., Huo, J., Wang, Y., & Xu, J. (2021). River Runoff Modelling and Hydrological Drought Assessment Based on High-Resolution Brightness Temperatures in Mainland China. Water, 13(17), 2429. https://doi.org/10.3390/w13172429





