Machine Learning-Based Prediction of Chlorophyll-a Variations in Receiving Reservoir of World’s Largest Water Transfer Project—A Case Study in the Miyun Reservoir, North China
Abstract
:1. Introduction
2. Materials and Methods
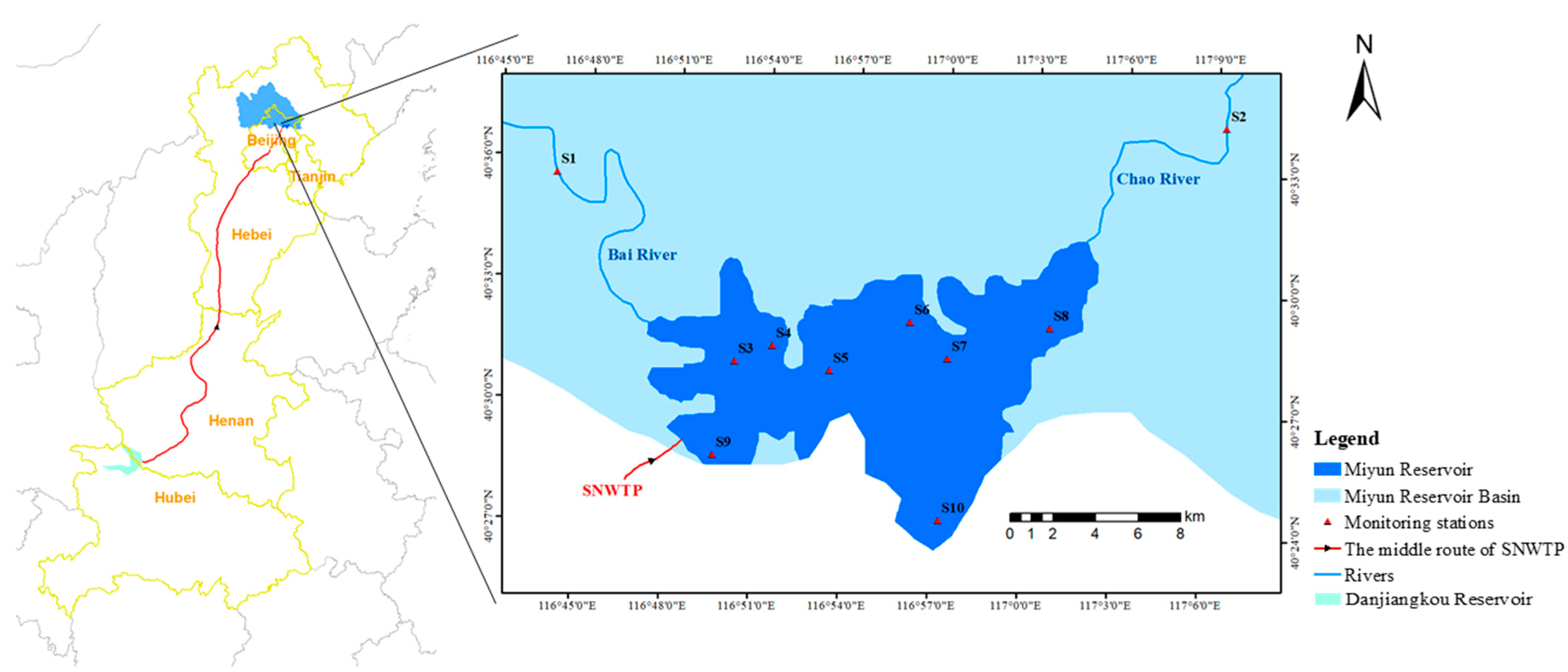
2.1. Study Area and Data Source
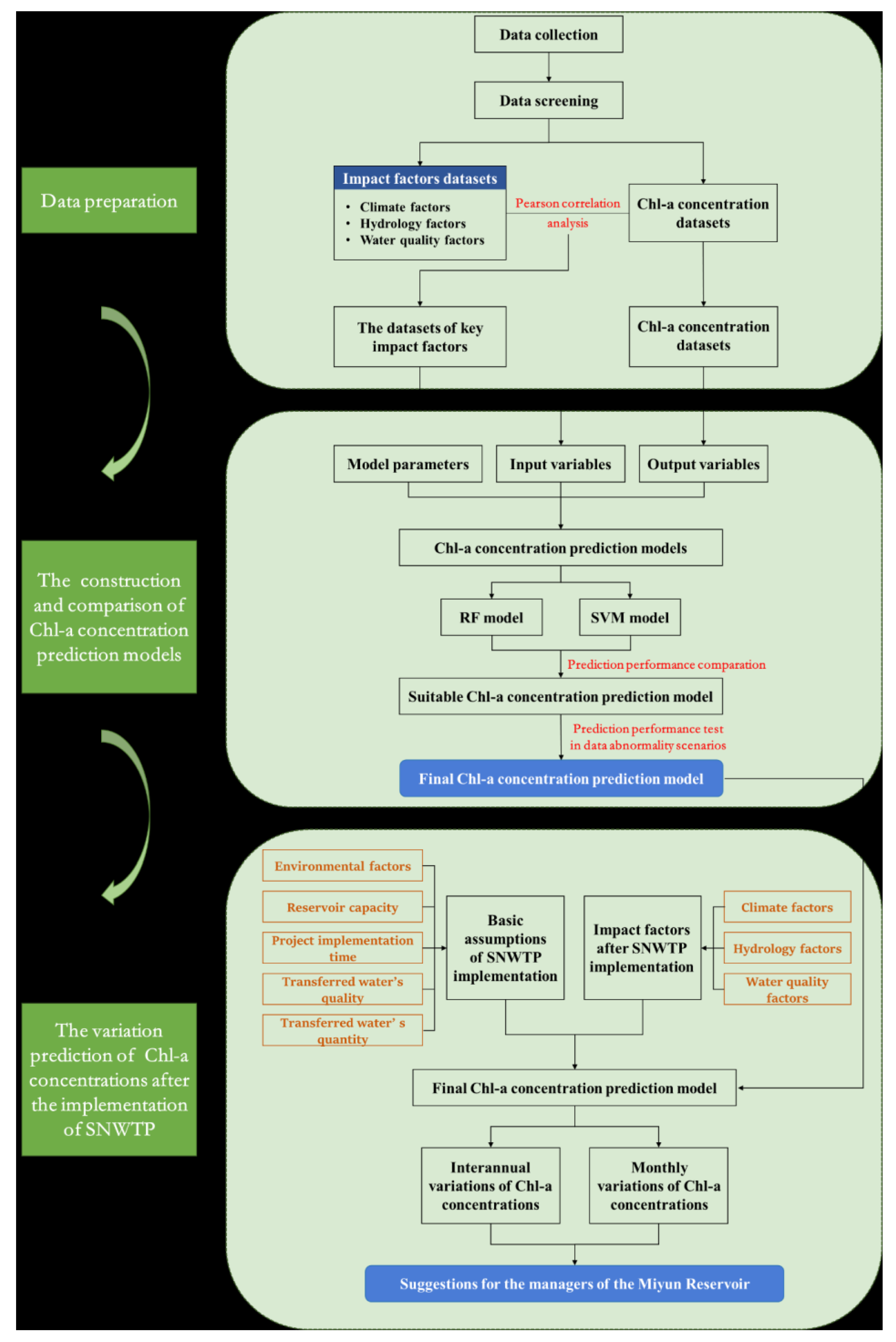
2.2. Technical Roadmap for Predicting Chl-a Variations in the Receiving Reservoir of Water Transfer Project
2.3. Model Construction
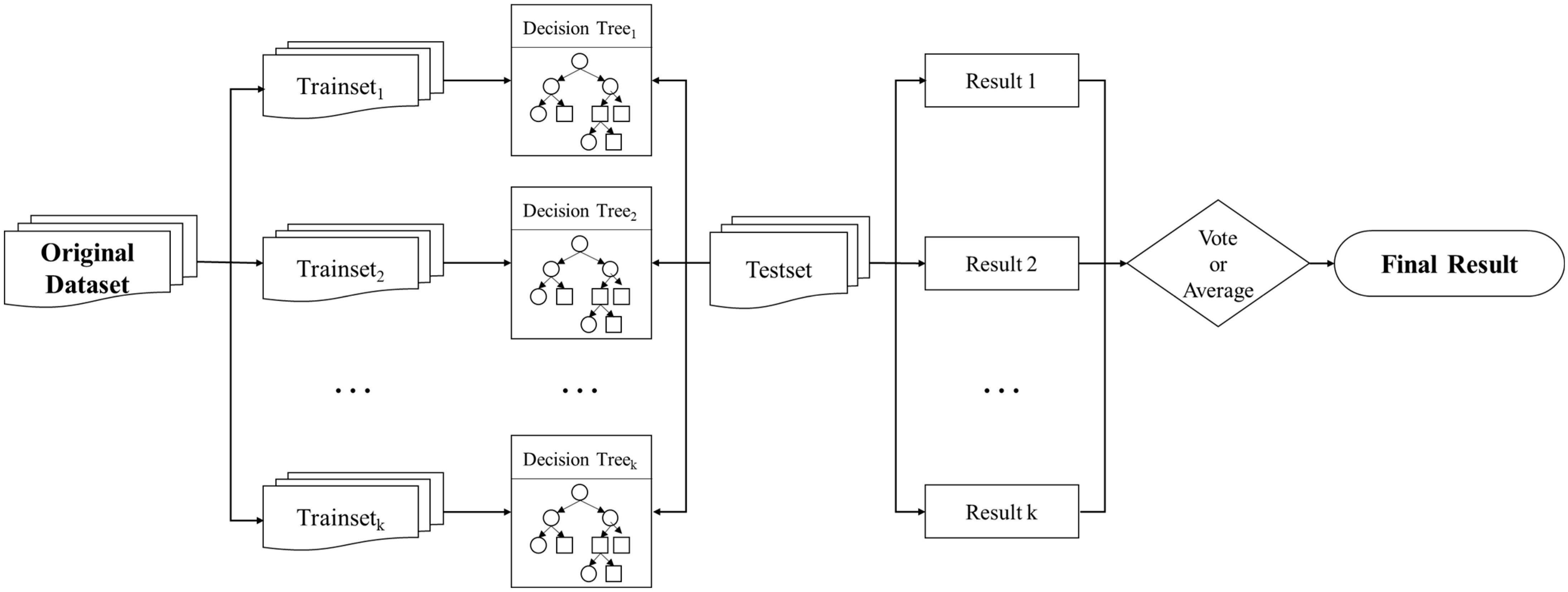
2.3.1. Model Principle
2.3.2. Chl-a Prediction Model Development
2.3.3. Assessment Metrics of Model Prediction Performance
3. Results
3.1. Prediction Performances of Two Machine Learning Models
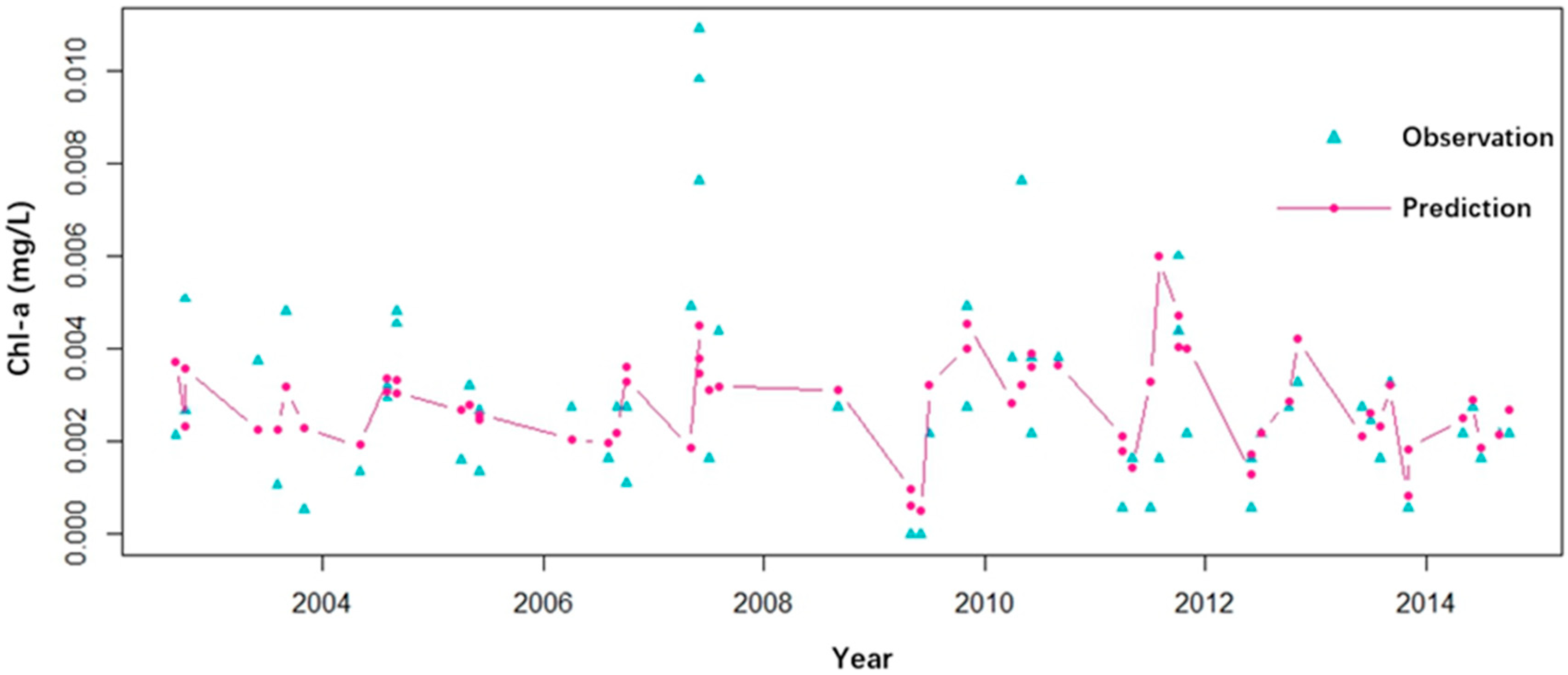
3.1.1. Comparation of SVM and RF Models
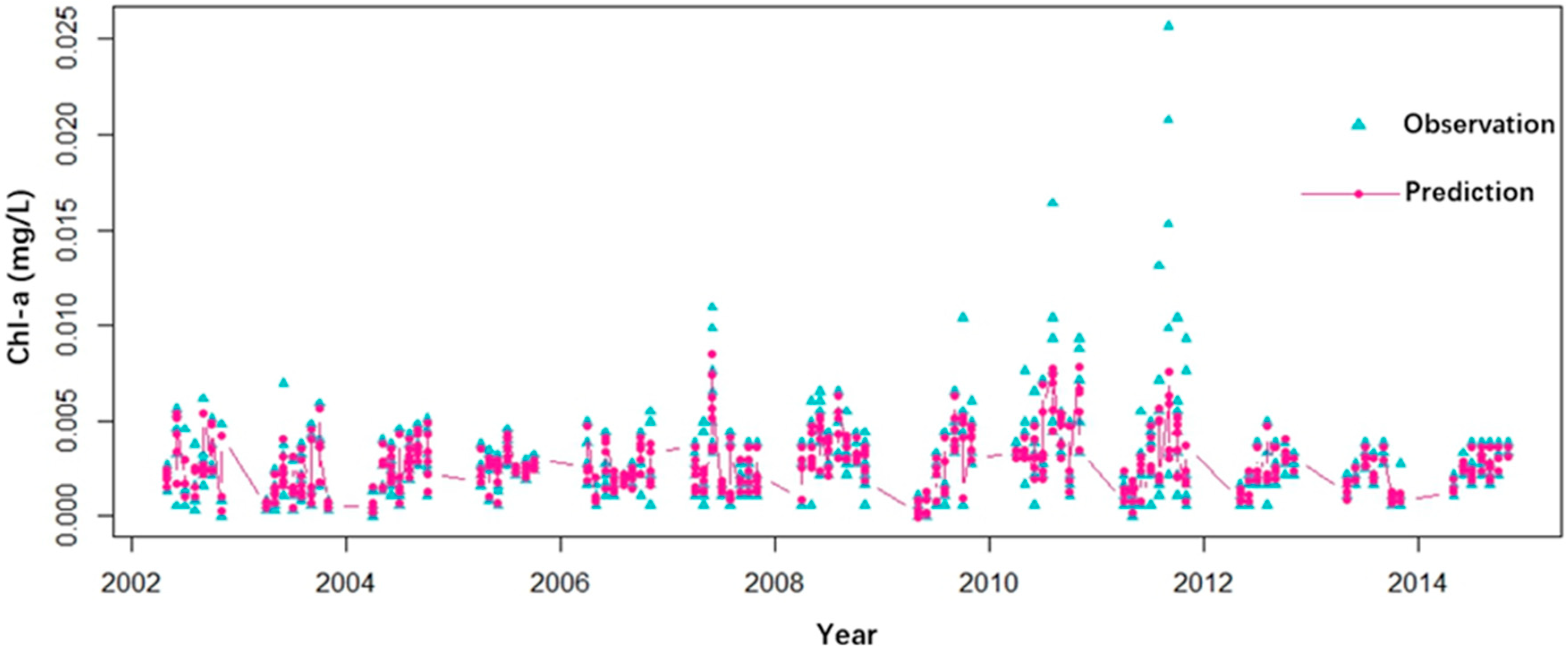
3.1.2. Robustness Analysis of RF Model
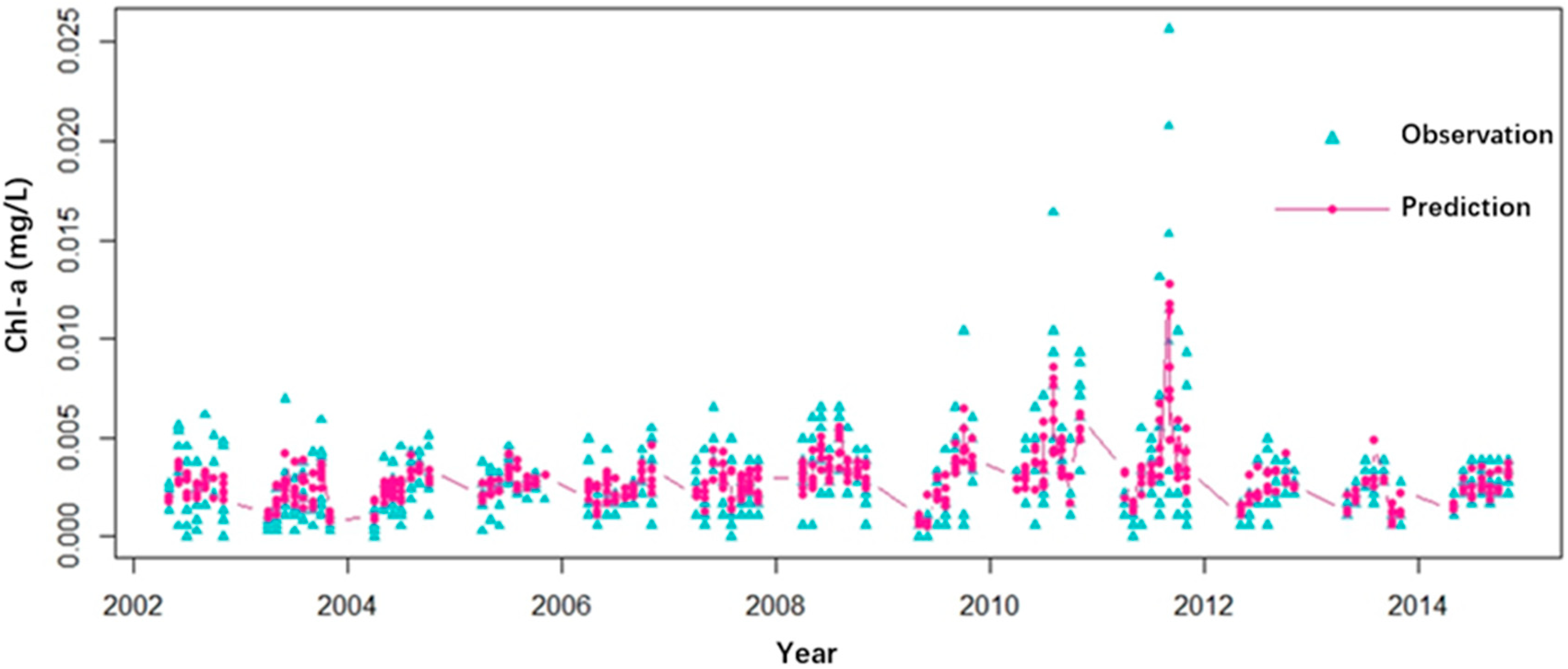
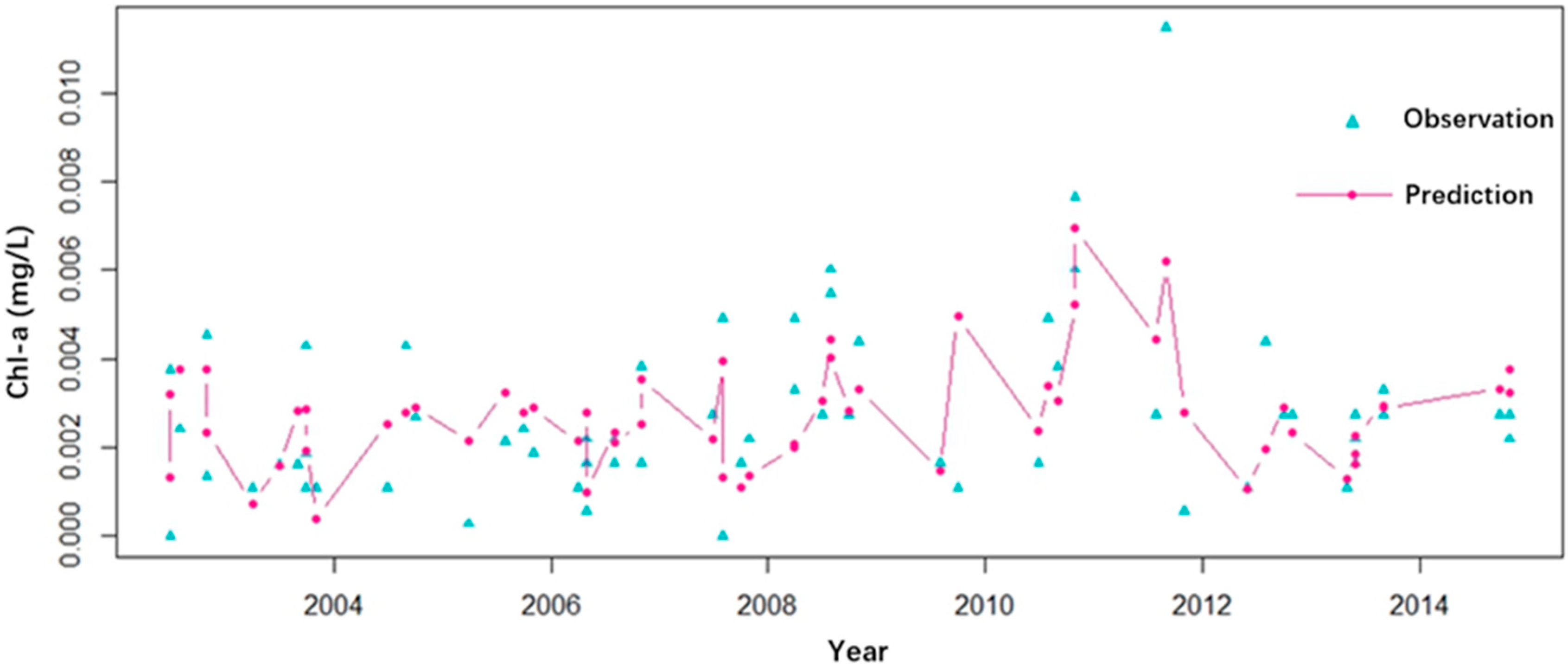
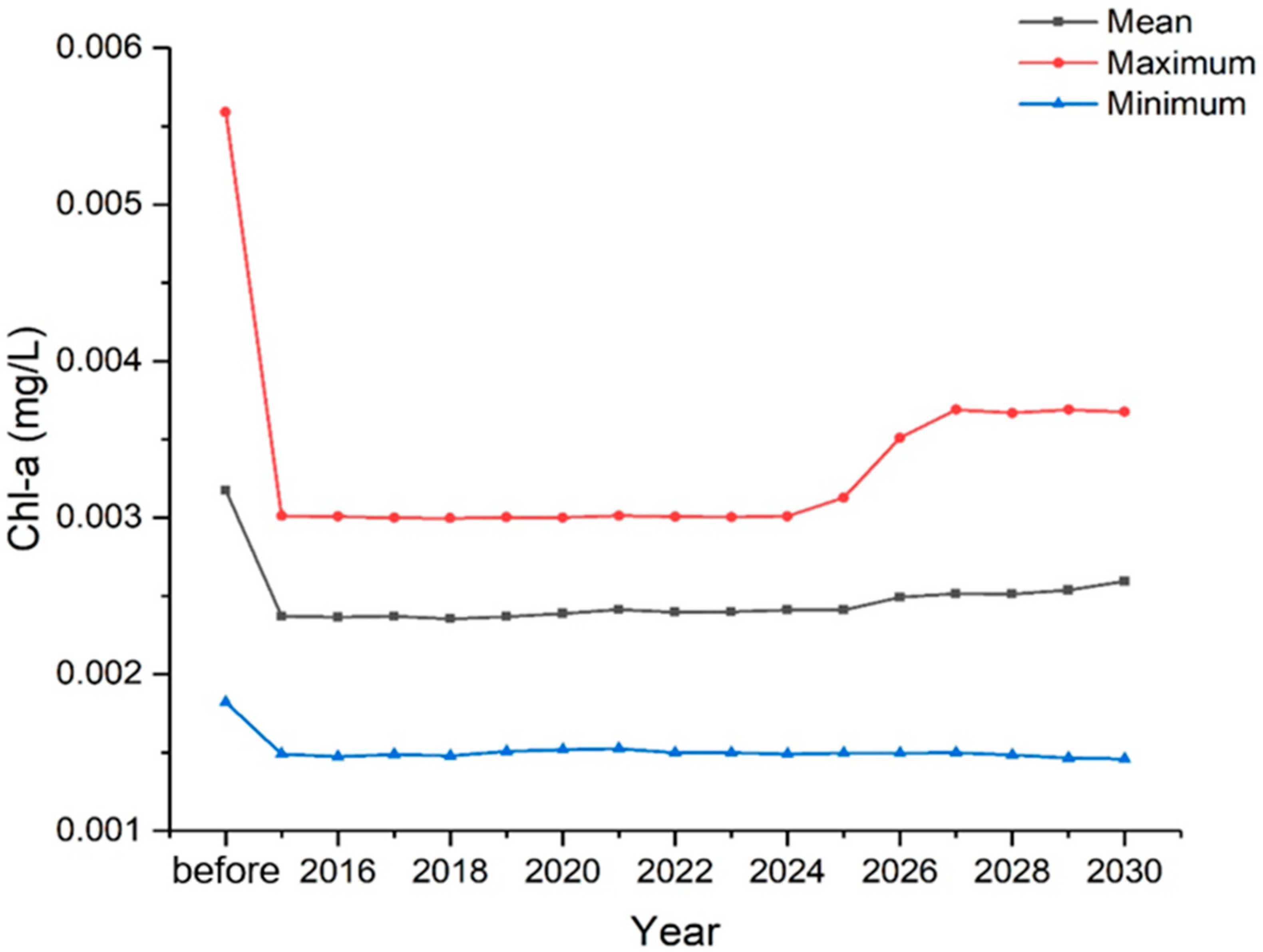
3.2. Prediction of Chl-a Concentration Variations
4. Discussion
4.1. Analysis on the Variation Trend of Chl-a Concentrations in the Miyun Reservoir
4.2. Performance Comparisons of Machine Learning Models and Other Models
5. Conclusions
- Compared with the SVM model, the RF model had higher prediction accuracy, more stable results, less overfitting, and more robust prediction ability when the data was missing or abnormal. Thus, the RF model was more suitable for predicting Chl-a variations in receiving reservoirs affected by the implementation of SNWTP.
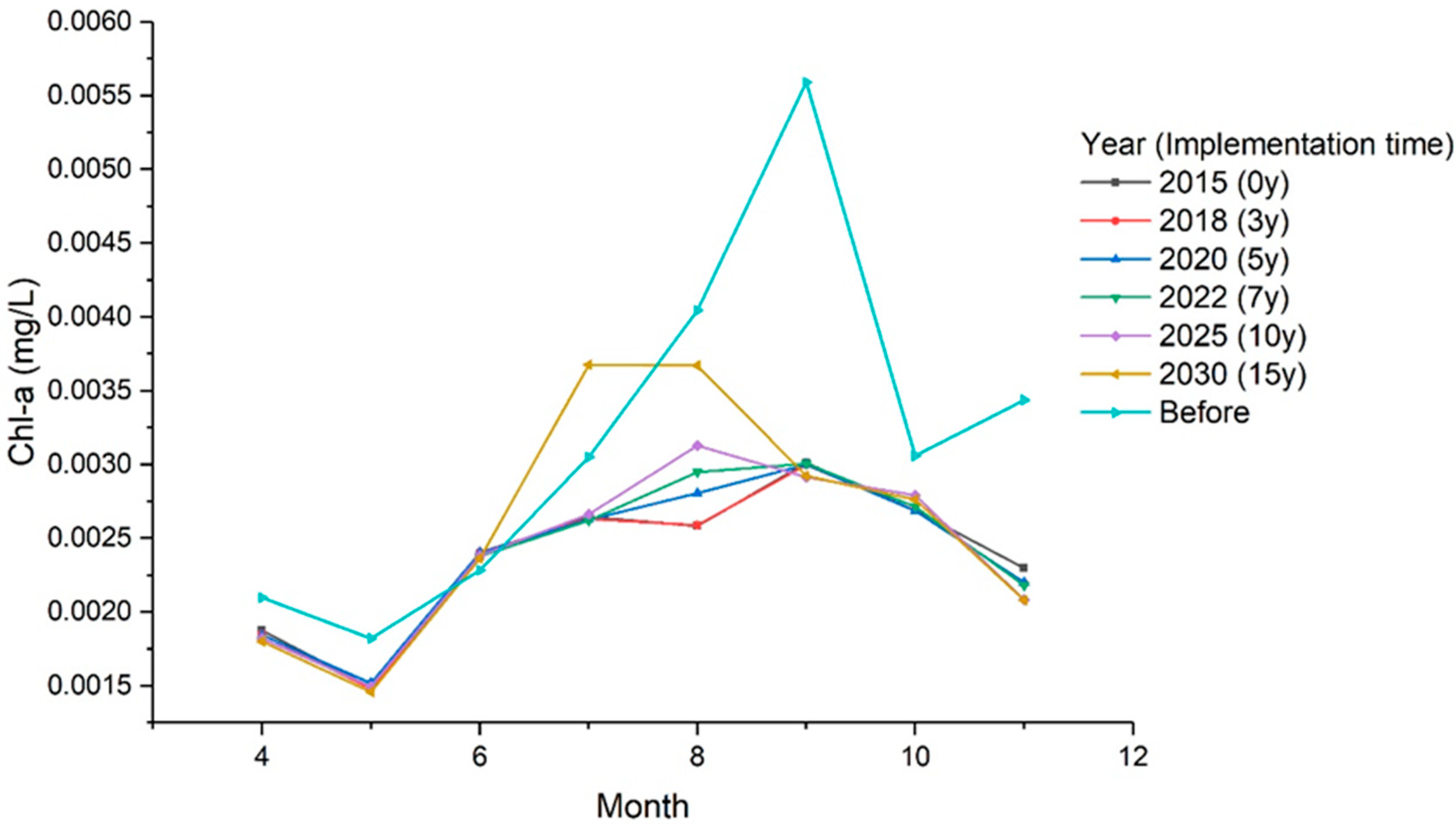
- The prediction results showed that short-term (within 3 years) implementation of SNWTP would not cause significant variations in Chl-a concentrations in the Miyun Reservoir.
- The proportion of transferred water in the reservoir would have gradually increased as the SNWTP implementation time increased, causing the impact of transferred water to increase. Ten years after implementation, the Chl-a concentrations of the Miyun Reservoir would significantly increase, especially from July to August/September, indicating that the reservoir may suffer more severe eutrophication. Therefore, the long-term implementation of SNWTP may have a potential negative impact on the receiving reservoir, indicating that reservoir managers need to take more actions to prevent changes in the waterbody’s trophic state, especially in July and August.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, Z.; Hu, W.; Zhang, Y.; Liu, G.; Zhang, H.; Gao, R. Modelling the effects of joint operations of water transfer project and lake sluice on circulation and water quality of a large shallow lake. J. Hydrol. 2021, 593, 125881. [Google Scholar] [CrossRef]
- Zhuang, W. Eco-environmental impact of inter-basin water transfer projects: A review. Environ. Sci. Pollut. Res. 2016, 23, 12867–12879. [Google Scholar] [CrossRef]
- Guo, C.; Chen, Y.; Gozlan, R.E.; Liu, H.; Lu, Y.; Qu, X.; Xia, W.; Xiong, F.; Xie, S.; Wang, L. Patterns of fish communities and water quality in impounded lakes of China’s south-to-north water diversion project. Sci. Total Environ. 2020, 713, 136515. [Google Scholar] [CrossRef]
- Dai, J.; Wu, S.; Wu, X.; Lv, X.; Sivakumar, B.; Wang, F.; Zhang, Y.; Yang, Q.; Gao, A.; Zhao, Y.; et al. Impacts of a large river-to-lake water diversion project on lacustrine phytoplankton communities. J. Hydrol. 2020, 587, 124938. [Google Scholar] [CrossRef]
- Varol, M. Spatio-temporal changes in surface water quality and sediment phosphorus content of a large reservoir in Turkey. Environ. Pollut. 2020, 259, 113860. [Google Scholar] [CrossRef]
- Wen, S.; Wang, H.; Wu, T.; Yang, J.; Jiang, X.; Zhong, J. Vertical profiles of phosphorus fractions in the sediment in a chain of reservoirs in North China: Implications for pollution source, bioavailability, and eutrophication. Sci. Total Environ. 2020, 704, 135318. [Google Scholar] [CrossRef]
- Hempel, C.G. Aspects of Scientific Explanation and Other Essays in the Philosophy of Science; Free Press: New York, NY, USA, 1965. [Google Scholar]
- Salmon, W. Scientific Explanation and the Causal Structure of the World; Princeton University: Princeton, NJ, USA, 1984. [Google Scholar]
- Zhang, P. Research on Hempel’s Theory of Scientific Explanation. Ph.D. Thesis, Jilin University, Changchun, China, 2005. (In Chinese). [Google Scholar]
- Tang, C.; Yi, Y.; Yang, Z.; Cheng, X. Water pollution risk simulation and prediction in the main canal of the South-to-North Water Transfer Project. J. Hydrol. 2014, 519, 2111–2120. [Google Scholar] [CrossRef]
- Thoe, W.; Gold, M.; Griesbach, A.; Grimmer, M.; Taggart, M.; Boehm, A. Predicting water quality at Santa Monica Beach: Evaluation of five different models for public notification of unsafe swimming conditions. Water Res. 2014, 67, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Penev, S.; Leonte, D.; Lazarov, Z.; Mann, R.A. Applications of MIDAS regression in analysing trends in water quality. J. Hydrol. 2014, 511, 151–159. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.; Li, S. Scale relationship between landscape pattern and water quality in different pollution source areas: A case study of the Fuxian Lake watershed, China. Ecol. Indic. 2021, 121, 107136. [Google Scholar] [CrossRef]
- Hajigholizadeh, M.; Melesse, A.M. Assortment and spatiotemporal analysis of surface water quality using cluster and dis-criminant analyses. Catena 2017, 151, 247–258. [Google Scholar] [CrossRef]
- Li, T.; Li, S.; Liang, C.; Bush, R.T.; Xiong, L.; Jiang, Y. A comparative assessment of Australia’s Lower Lakes water quality under extreme drought and post-drought conditions using multivariate statistical techniques. J. Clean. Prod. 2018, 190, 1–11. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, K.; Bagheri, M.; Burken, J.G.; Gu, A.; Li, B.; Ma, X.; Marrone, B.L.; Ren, Z.J.; Schrier, J.; et al. Machine learning: New ideas and tools in environ-mental science and engineering. Environ. Sci. Technol. 2021. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Kumari, N.; Dharpure, J.; Mokhtar, A.; Alsafadi, K.; Kumar, M.; Mehdinejadiani, B.; Etedali, H.R.; Brouziyne, Y.; Islam, A.T.; et al. Prediction of Combined Terrestrial Evapotranspiration Index (CTEI) over Large River Basin Based on Machine Learning Approaches. Water 2021, 13, 547. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of Variable-Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.; Liu, Y.; Zhao, H.; Sun, M.; Li, X. Comparison of models for predicting the changes in phytoplankton community composition in the receiving water system of an inter-basin water transfer project. Environ. Pollut. 2017, 223, 676–684. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Kim, J.-H.; Li, M.-H. Predicting stream water quality under different urban development pattern scenarios with an interpretable machine learning approach. Sci. Total Environ. 2021, 761, 144057. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.P.; Basant, N.; Gupta, S. Support vector machines in water quality management. Anal. Chim. Acta 2011, 703, 152–162. [Google Scholar] [CrossRef]
- Castrillo, M.; Garcia, A.L. Estimation of high frequency nutrient concentrations from water quality surrogates using ma-chine learning methods. Water Res. 2020, 172, 115490. [Google Scholar] [CrossRef] [Green Version]
- El Bilali, A.; Taleb, A.; Brouziyne, Y. Groundwater quality forecasting using machine learning algorithms for irrigation purposes. Agric. Water Manag. 2021, 245, 106625. [Google Scholar] [CrossRef]
- Kim, H.G.; Hong, S.; Chon, T.S.; Joo, G.J. Spatial patterning of chlorophyll a and water-quality measurements for determin-ing environmental thresholds for local eutrophication in the Nakdong River basin. Environ. Pollut. 2021, 268 Pt A, 115701. [Google Scholar] [CrossRef]
- Liang, Z.; Xu, Y.; Qiu, Q.; Liu, Y.; Lu, W.; Wagner, T. A framework to develop joint nutrient criteria for lake eutrophication management in eutrophic lakes. J. Hydrol. 2021, 594, 125883. [Google Scholar] [CrossRef]
- Zou, W.; Zhu, G.; Cai, Y.; Vilmi, A.; Xu, H.; Zhu, M.; Gong, Z.; Zhang, Y.; Qin, B. Relationships between nutrient, chloro-phyll a and Secchi depth in lakes of the Chinese Eastern Plains ecoregion: Implications for eutrophication management. J. Environ. Manag. 2020, 260, 109923. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Yang, D.; Tan, S.K.; Gao, B.; Hu, Q. Impact of climate variability and human activity on streamflow decrease in the Miyun Reservoir catchment. J. Hydrol. 2010, 389, 317–324. [Google Scholar] [CrossRef]
- Wang, X.; Hao, G.; Yang, Z.; Liang, P.; Cai, Y.; Li, C.; Sun, L.; Zhu, J. Variation analysis of streamflow and ecological flow for the twin rivers of the Miyun Reservoir Basin in northern China from 1963 to 2011. Sci. Total Environ. 2015, 536, 739–749. [Google Scholar] [CrossRef]
- Li, D.; Liang, J.; Di, Y.; Gong, H.; Guo, X. The spatial-temporal variations of water quality in controlling points of the main rivers flowing into the Miyun Reservoir from 1991 to 2011. Environ. Monit. Assess. 2016, 188, 42. [Google Scholar] [CrossRef]
- Wang, X.; Zang, N.; Liang, P.; Cai, Y.; Li, C.; Yang, Z. Identifying priority management intervals of discharge and TN/TP concentration with copula analysis for Miyun Reservoir inflows, North China. Sci. Total Environ. 2017, 609, 1258–1269. [Google Scholar] [CrossRef]
- Li, S.; Cheng, X.; Xu, Z.; Han, H.; Zhang, Q. Spatial and temporal patterns of the water quality in the Danjiangkou Reservoir, China. Hydrol. Sci. J. 2009, 54, 124–134. [Google Scholar] [CrossRef]
- Yin, D.; Zheng, L.; Song, L. Spatio-temporal distribution of phytoplankton in the Danjiangkou Reservoir, a water source area for the Southto-North Water Diversion Project (Middle Route), China. Chin. J. Oceanol. Limnol. 2011, 29, 531–540. [Google Scholar] [CrossRef]
- Xu, H.; Zhao, L.; Sun, H.; Ren, Y.; Ding, T.; Chang, S.; Wang, H.; Li, M.; Guo, Z. Water Quality Analysis of Beijing Segment of South-to-North Water Diversion Middle Route Project. Environ. Sci. 2017, 38, 1357–1365. (In Chinese) [Google Scholar] [CrossRef]
- Tao, L.; Huang, Z.; Lu, Y. Study on countermeasures and the nutrition of water in South-to-North water diversion project. Beijing Water 2017, 6, 15–21. (In Chinese) [Google Scholar]
- Tan, H.; He, W.; Han, H.; Zhang, X.; Ma, Y.; Zhang, S. Monitoring and analysis of Danjiangkou Reservoir water quality. Water Technol. 2015, 9, 1–5. (In Chinese) [Google Scholar]
- China Meteorological Data Service Center. Available online: http://data.cma.cn/ (accessed on 7 September 2017). (In Chinese).
- Cao, Z. Study on Optimization of Random Forests Algorithm. Ph.D. Thesis, Capital University of Economics and Business, Beijing, China, 2014. (In Chinese). [Google Scholar]
- Harrison, J.W.; Lucius, M.A.; Farrell, J.L.; Eichler, L.W.; Relyea, R.A. Prediction of stream nitrogen and phosphorus concen-trations from high-frequency sensors using Random Forests Regression. Sci. Total Environ. 2021, 763, 143005. [Google Scholar] [CrossRef] [PubMed]
- Karamouz, M.; Ahmadi, A.; Moridi, A. Probabilistic reservoir operation using Bayesian stochastic model and support vector machine. Adv. Water Resour. 2009, 32, 1588–1600. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000. [Google Scholar]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Catherine, A.; Mouillot, D.; Escoffier, N.; Bernard, C.; Troussellier, M. Cost effective prediction of the eutrophication status of lakes and reservoirs. Freshw. Biol. 2010, 55, 2425–2435. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, C.; Liu, Q.; Xi, B.; Qian, G.; Zhang, D.; Huo, S. Method to predict key factors affecting lake eutrophication—A new approach based on Support Vector Regression model. Int. Biodeterior. Biodegrad. 2015, 102, 308–315. [Google Scholar] [CrossRef]
- Park, Y.; Pachepsky, Y.A.; Cho, K.H.; Jeon, D.J.; Kim, J.H. Stressor–response modeling using the 2D water quality model and regression trees to predict chlorophyll-a in a reservoir system. J. Hydrol. 2015, 529, 805–815. [Google Scholar] [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. Technological Regulations for Surface Water Resources Quality Assessment (SL395-2007); China Water&Power Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Li, Y. Analysis on the water quality and dynamic trend of Miyun Reservoir. Beijing Water 2020, S1, 36–40. (In Chinese) [Google Scholar] [CrossRef]
- Lin, M.; Zhang, Q.; Li, Z.; Zhang, G.; Zhang, Z.; Yang, Z.; Si, S.; Niu, H.; Sun, J.; Fan, H.; et al. Characteristics of the variance of the water qualtiy and quantity in the middle route of South-to-North Water Diversion Project and corresponding measures for urban water supply. Water Wastewater Eng. 2016, 52, 9–13. (In Chinese) [Google Scholar]
- Wu, X.; Wu, G.; Pan, K.; Liu, L. Predicting analysis on impact of incoming water from South-to-North water transfer project on water quality and aquatic organisms in Miyun reservoir. Beijing Water 2015, 4–6. (In Chinese) [Google Scholar] [CrossRef]
- Zeng, Q.; Qin, L.; Li, X. The potential impact of an inter-basin water transfer project on nutrients (nitrogen and phospho-rous) and chlorophyll a of the receiving water system. Sci. Total Environ. 2015, 536, 675–686. [Google Scholar] [CrossRef] [PubMed]
- Kuo, J.-T.; Hsieh, M.-H.; Lung, W.-S.; She, N. Using artificial neural network for reservoir eutrophication prediction. Ecol. Model. 2007, 200, 171–177. [Google Scholar] [CrossRef]
- Deng, T.; Chau, K.-W.; Duan, H.-F. Machine learning based marine water quality prediction for coastal hydro-environment management. J. Environ. Manag. 2021, 284, 112051. [Google Scholar] [CrossRef]
- Wu, T.; Zhu, G.; Zhu, M.; Xu, H.; Yang, J.; Zhao, X. Effects of algae proliferation and density current on the vertical distribu-tion of odor compounds in drinking water reservoirs in summer. Environ. Pollut. 2021, 288, 117683. [Google Scholar] [CrossRef]
| Water Quality Indicators | Miyun Reservoir | Danjiangkou Reservoir | Daning Surge Tank | ||
|---|---|---|---|---|---|
| Mean ± SD * | Mean | References | Mean | References | |
| Water temperature (°C) | 19.75 ± 6.31 | 19.02 | [31] | — | |
| Water transparency (m) | 2.93 ± 1.46 | 4.32 | [32] | — | |
| pH | 8.35 ± 0.24 | 8.00 | [32] | 8.31 | [33] |
| DO (mg/L) | 8.99 ± 1.48 | 7.97 | [32] | 9.65 | [34] |
| CODMn (mg/L) | 2.51 ± 0.51 | 2.58 | [35] | 2.75 | [34] |
| TP (mg/L) | 0.02 ± 0.01 | 0.036 | [32] | 0.018 | [33] |
| TN (mg/L) | 1.05 ± 0.58 | 1.27 | [32] | 1.18 | [33] |
| Factors | Indicators | Coefficients | Factors | Indicators | Coefficients |
|---|---|---|---|---|---|
| Climate | Sunshine duration (h) | 0.0795 | Water quality | Water transparency (m) | 0.2813 |
| Percentage of sunshine (%) | 0.0094 | pH | 0.0085 | ||
| Precipitation (mm) | 0.0226 | DO (mg/L) | 0.0702 | ||
| Average wind speed (m/s) | 0.0928 | CODMn (mg/L) | 0.1076 | ||
| Average air temperature (°C) | 0.0193 | BOD5 (mg/L) | 0.0001 | ||
| Hydrology | Water temperature (°C) | 0.1355 | TP (mg/L) | 0.0943 | |
| Upstream inflow (m3/s) | 0.0745 | TN (mg/L) | 0.0531 | ||
| Downstream outflow (m3/s) | 0.0948 | ||||
| Average water level (m) | 0.0107 | ||||
| Model | Program Package | Parameters | r | RMSE | MAE | |||
|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |||
| RF | randomForest | mtry = 2 ntree = 1000 | 0.6557 | 0.6488 | 0.0018 | 0.0017 | 0.0011 | 0.0011 |
| SVM | e1071 | RBF nu-regression C = 1.9 Sigma = 0.14 | 0.8447 | 0.5875 | 0.0013 | 0.0018 | 0.0006 | 0.0012 |
| Parameters | Scenarios | r | RMSE | MAE | |||
|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | ||
| mtry = 2 ntree = 1000 | Normal | 0.6532 | 0.6414 | 0.0018 | 0.0017 | 0.0011 | 0.0011 |
| Program | 0.6146 | 0.6229 | 0.0018 | 0.0018 | 0.0011 | 0.0011 | |
| Random | 0.6527 | 0.6616 | 0.0017 | 0.0016 | 0.0011 | 0.0010 | |
| Filling | 0.6522 | 0.6654 | 0.0017 | 0.0016 | 0.0010 | 0.0010 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Z.; Zang, N.; Wang, X.; Li, C.; Liu, Q. Machine Learning-Based Prediction of Chlorophyll-a Variations in Receiving Reservoir of World’s Largest Water Transfer Project—A Case Study in the Miyun Reservoir, North China. Water 2021, 13, 2406. https://doi.org/10.3390/w13172406
Liao Z, Zang N, Wang X, Li C, Liu Q. Machine Learning-Based Prediction of Chlorophyll-a Variations in Receiving Reservoir of World’s Largest Water Transfer Project—A Case Study in the Miyun Reservoir, North China. Water. 2021; 13(17):2406. https://doi.org/10.3390/w13172406
Chicago/Turabian StyleLiao, Zhenmei, Nan Zang, Xuan Wang, Chunhui Li, and Qiang Liu. 2021. "Machine Learning-Based Prediction of Chlorophyll-a Variations in Receiving Reservoir of World’s Largest Water Transfer Project—A Case Study in the Miyun Reservoir, North China" Water 13, no. 17: 2406. https://doi.org/10.3390/w13172406
APA StyleLiao, Z., Zang, N., Wang, X., Li, C., & Liu, Q. (2021). Machine Learning-Based Prediction of Chlorophyll-a Variations in Receiving Reservoir of World’s Largest Water Transfer Project—A Case Study in the Miyun Reservoir, North China. Water, 13(17), 2406. https://doi.org/10.3390/w13172406








