Prediction of Surface Water Quality by Artificial Neural Network Model Using Probabilistic Weather Forecasting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data Description
2.2. Methodology
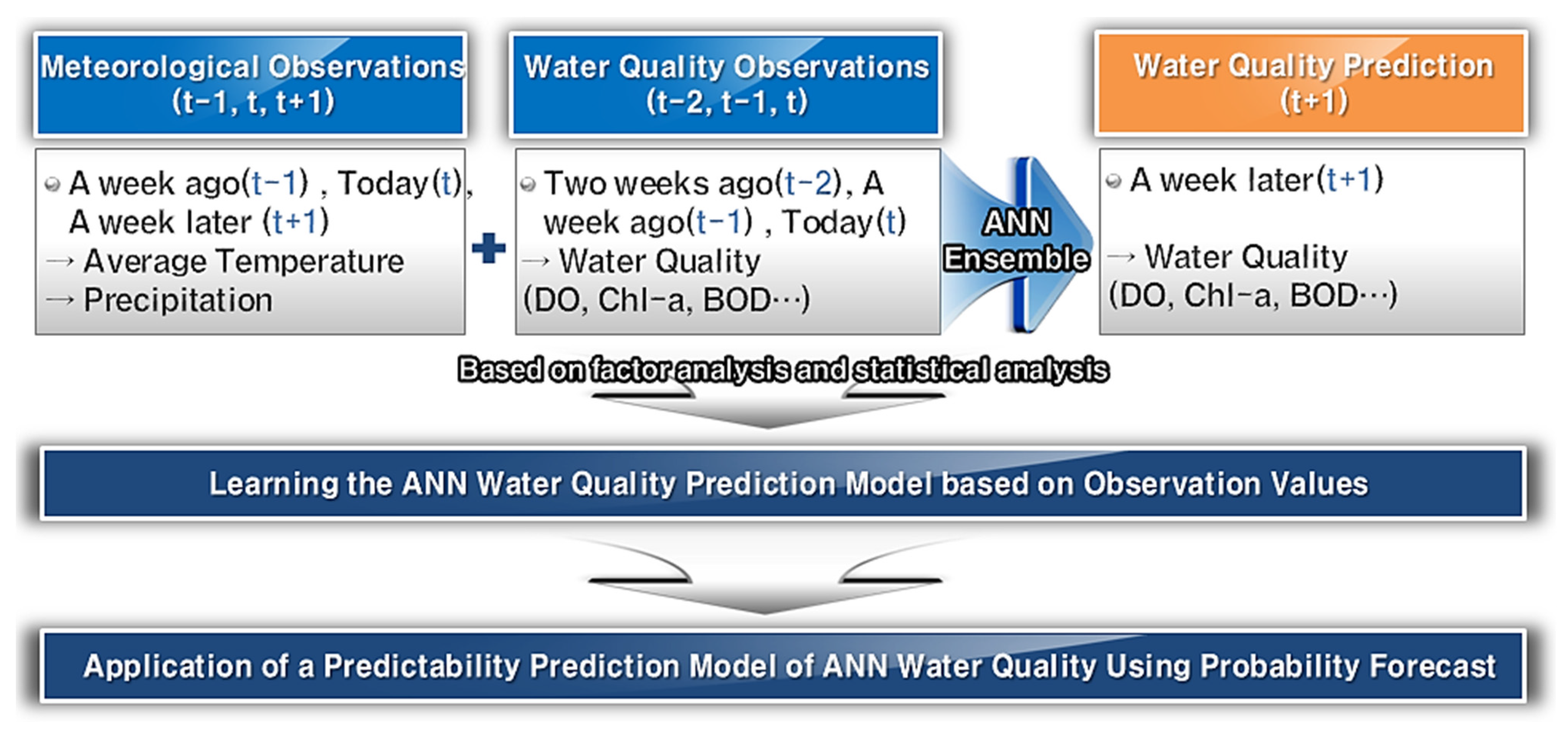
2.2.1. Probability Forecast System
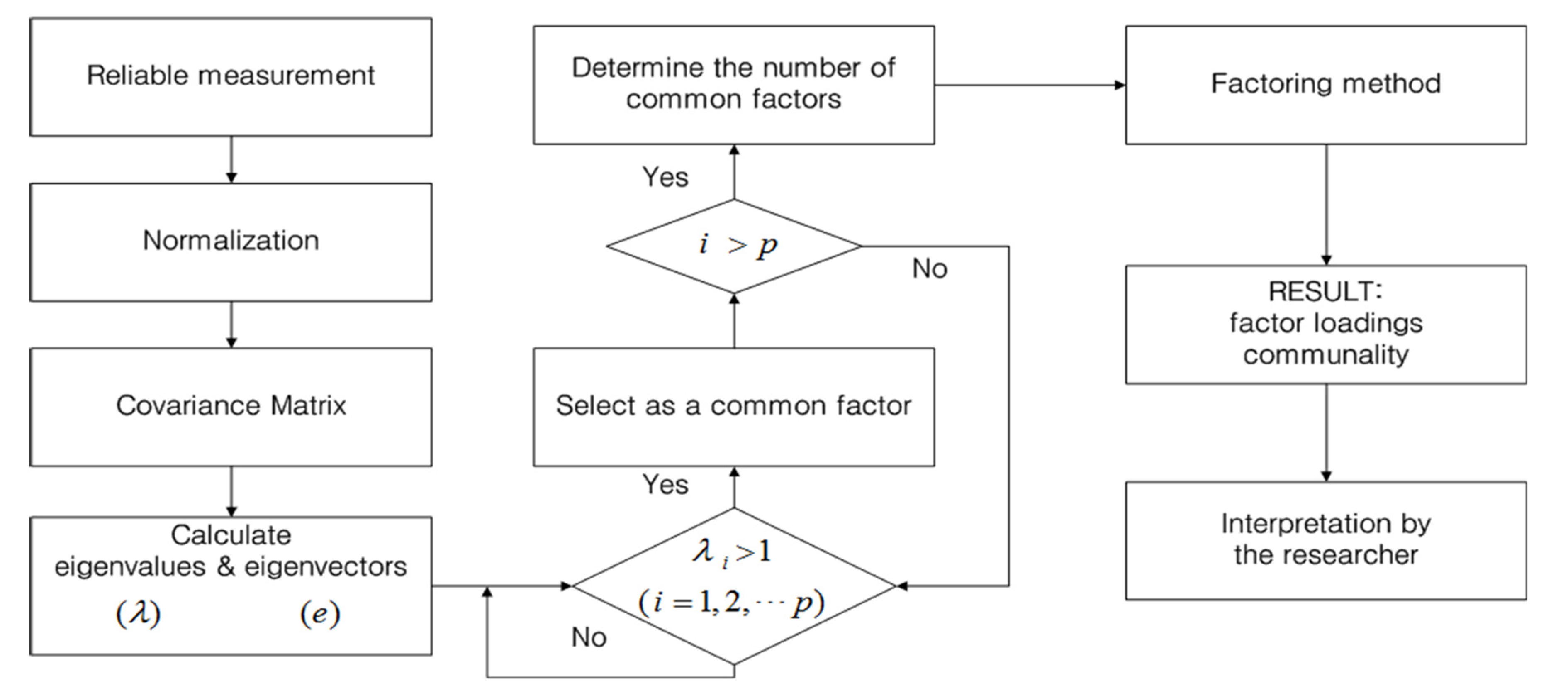
2.2.2. Exploratory Factor Analysis (EFA)
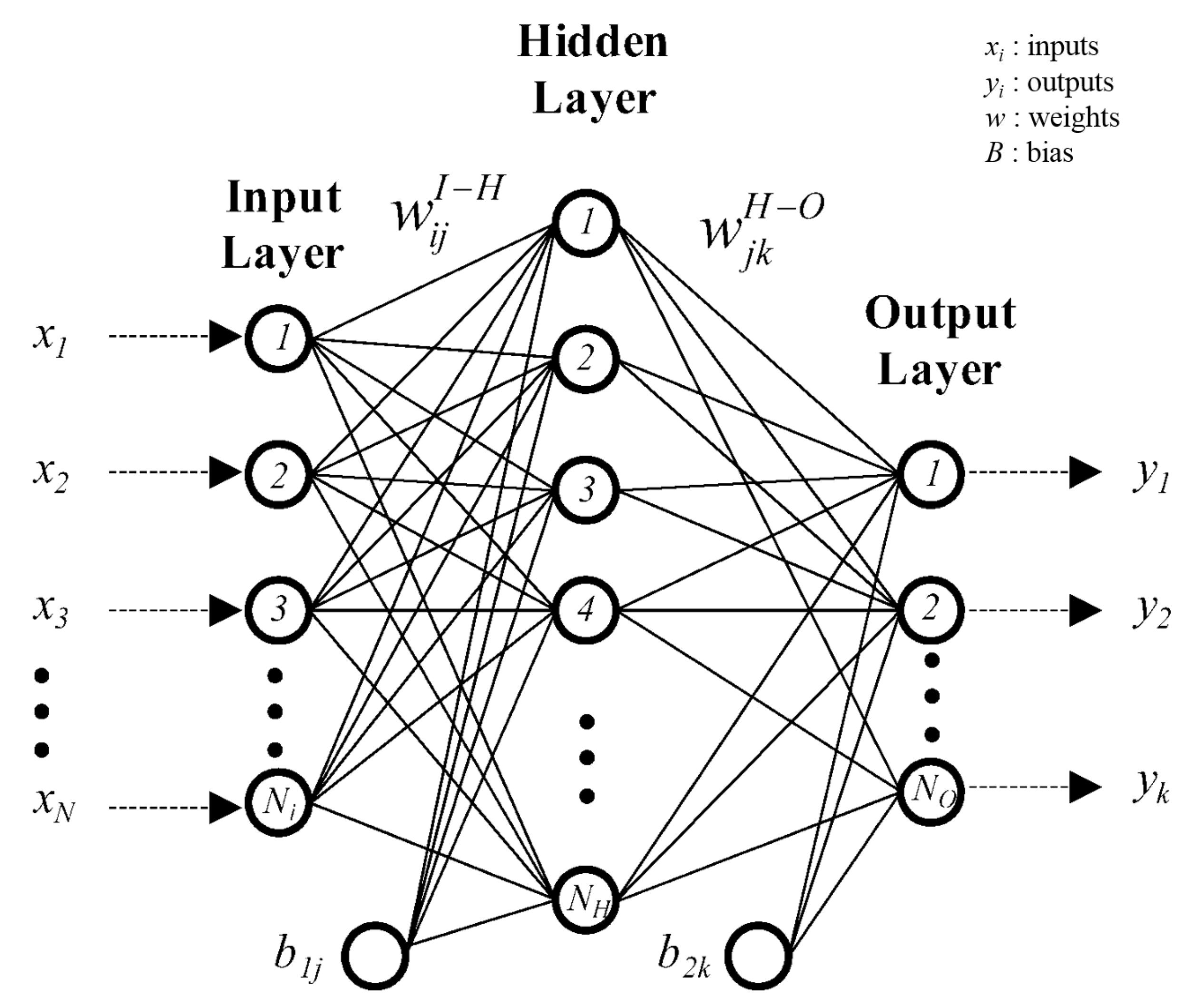
2.2.3. Artificial Neural Network (ANN)
2.2.4. Model Evaluation
3. Results
3.1. Exploratory Factor Analysis (EFA) Results
3.2. ANN Model Leaning
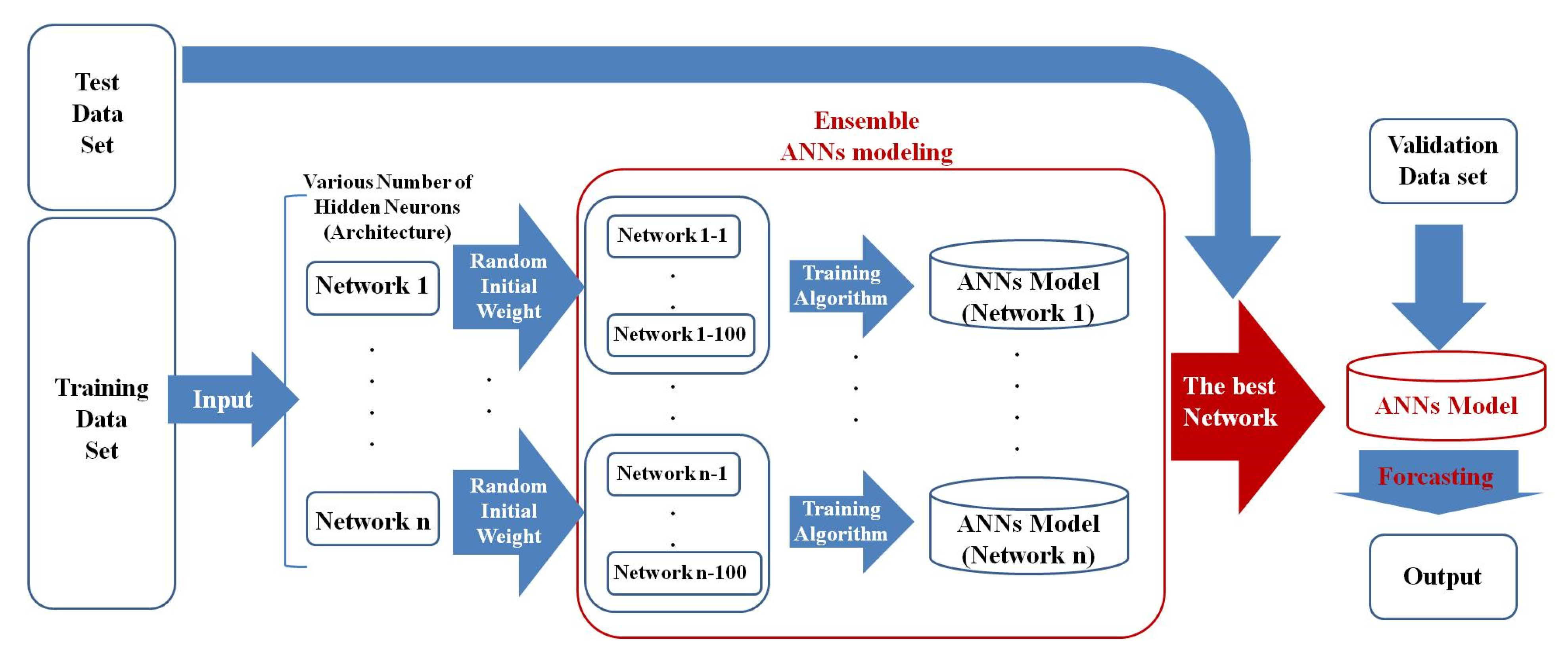
3.2.1. ANN Learning System
3.2.2. ANN Learning Results
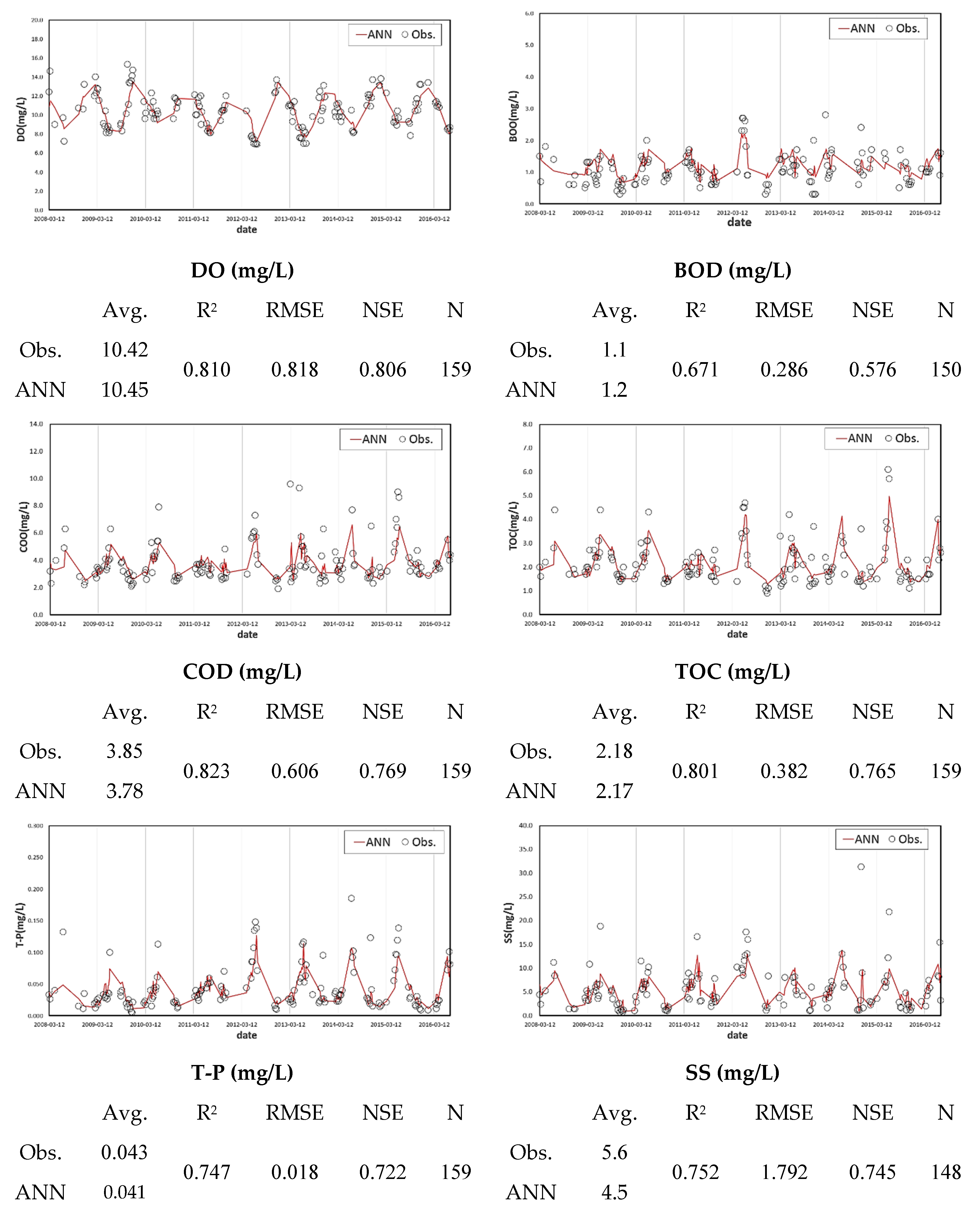
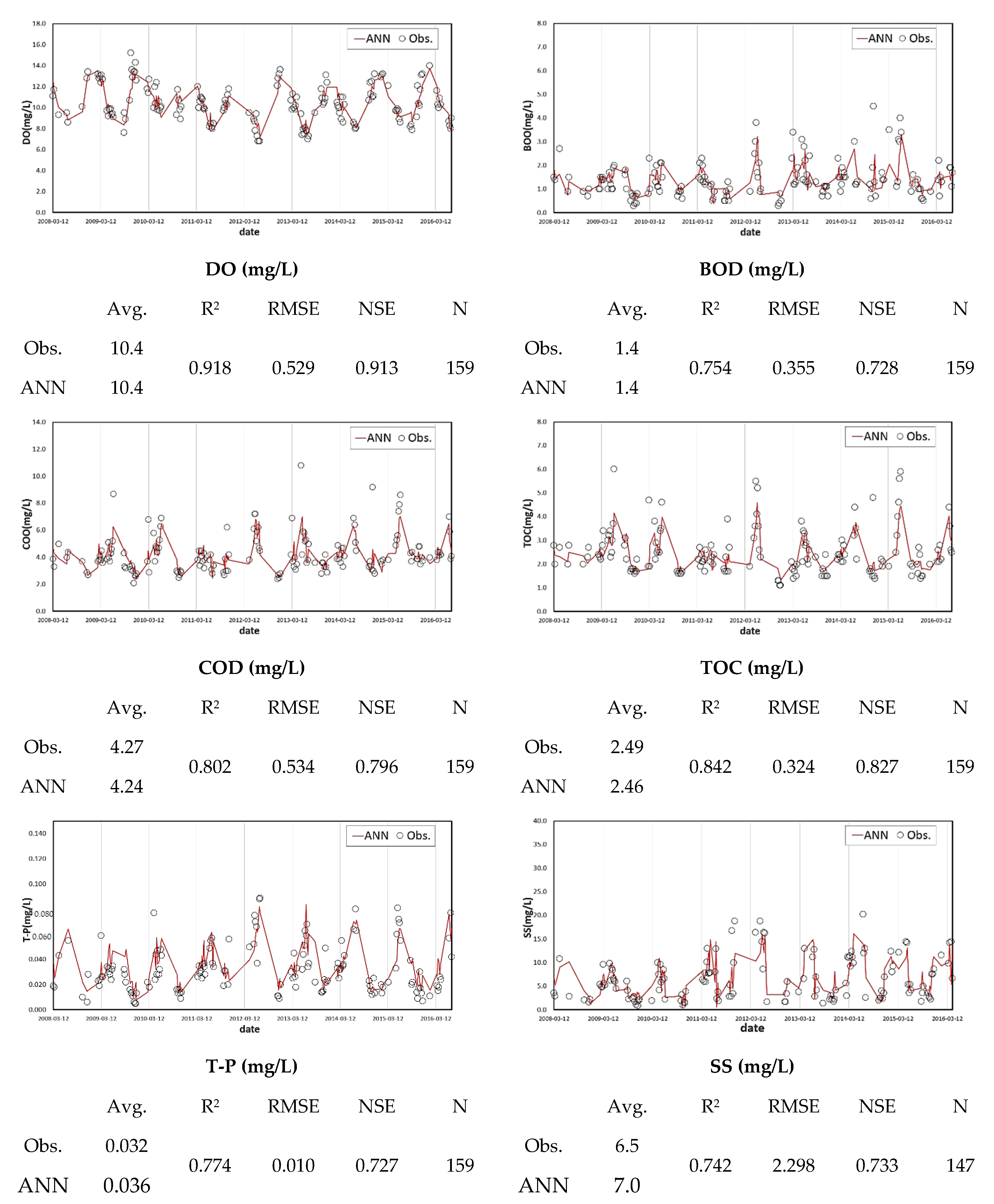
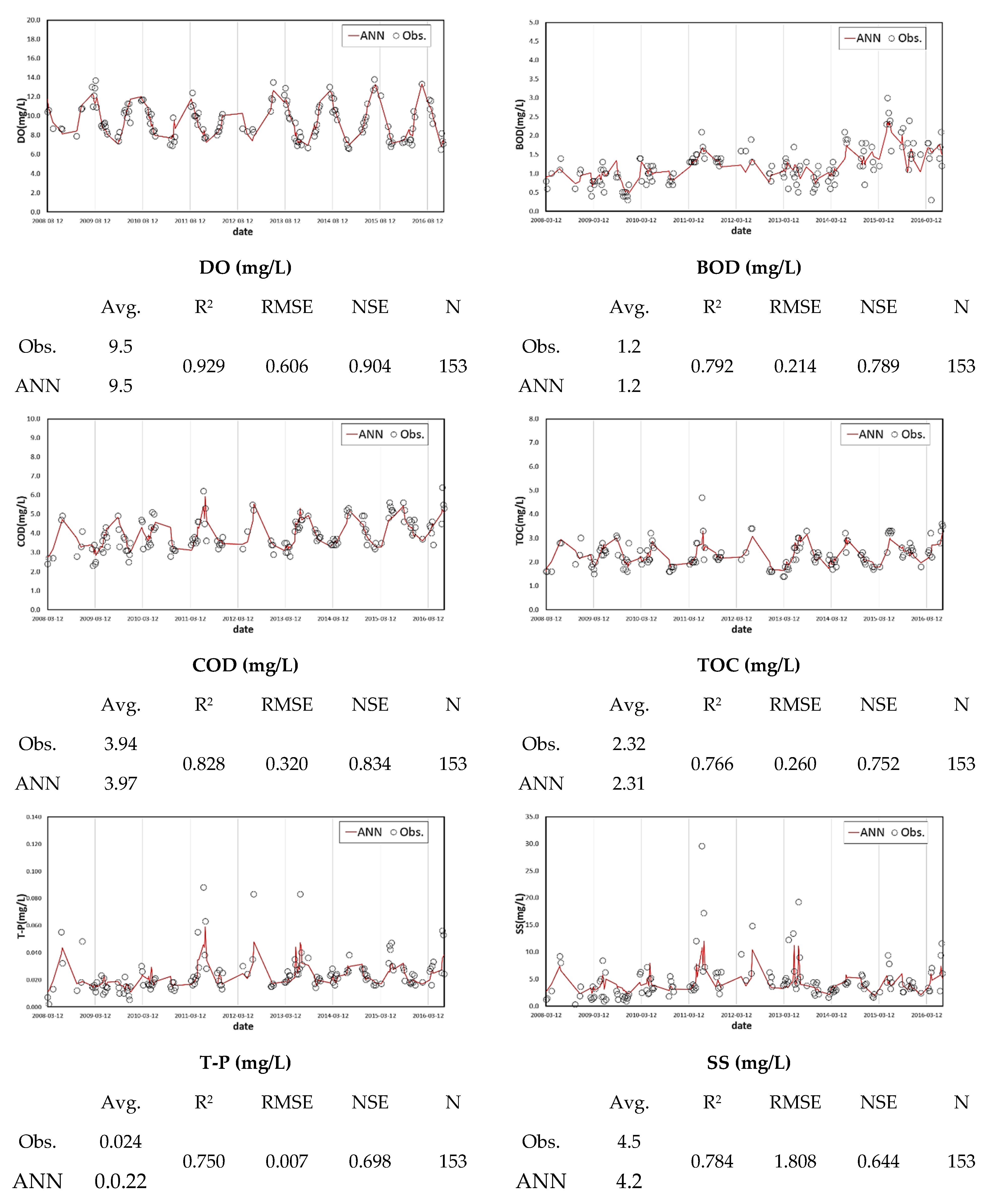
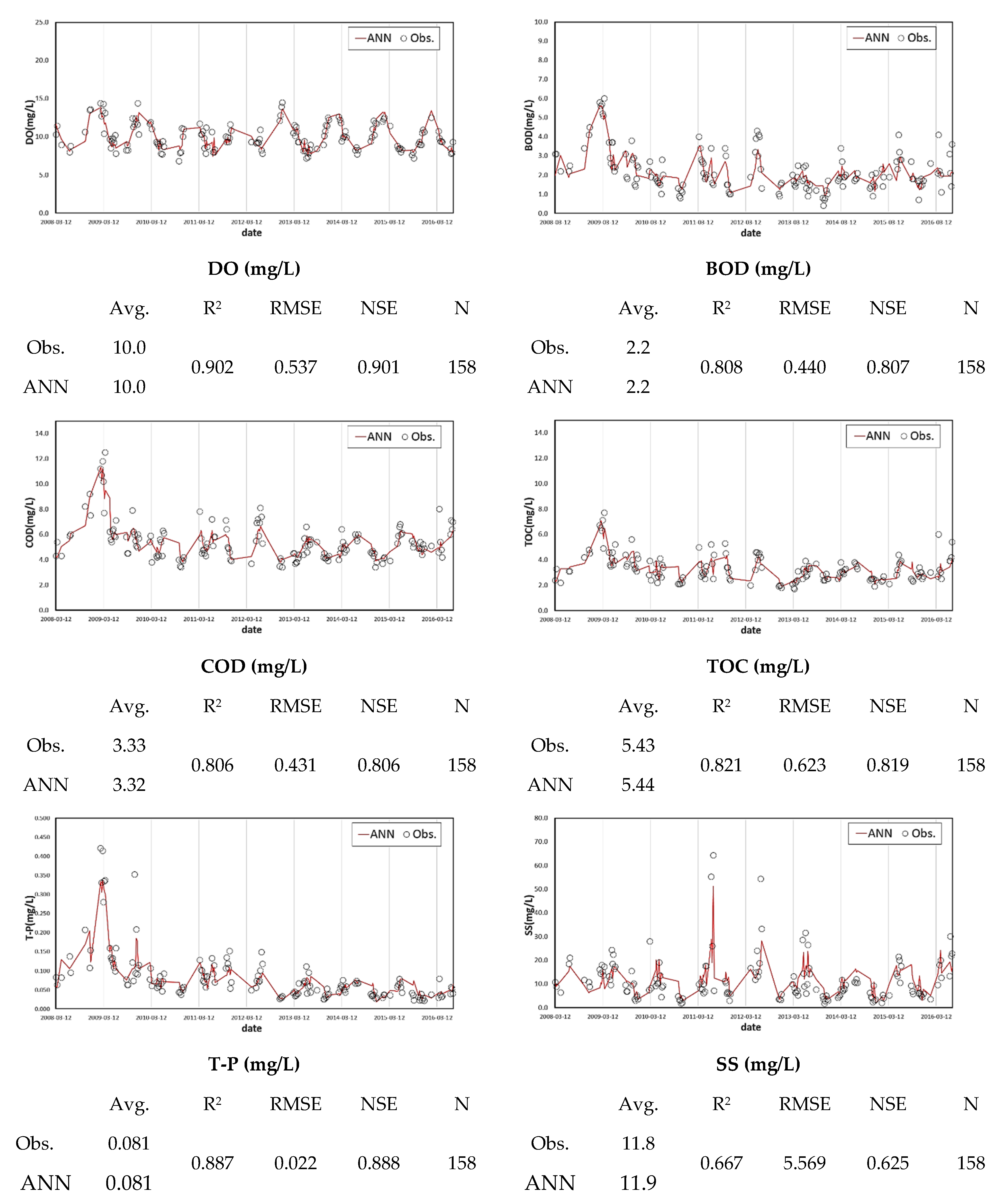
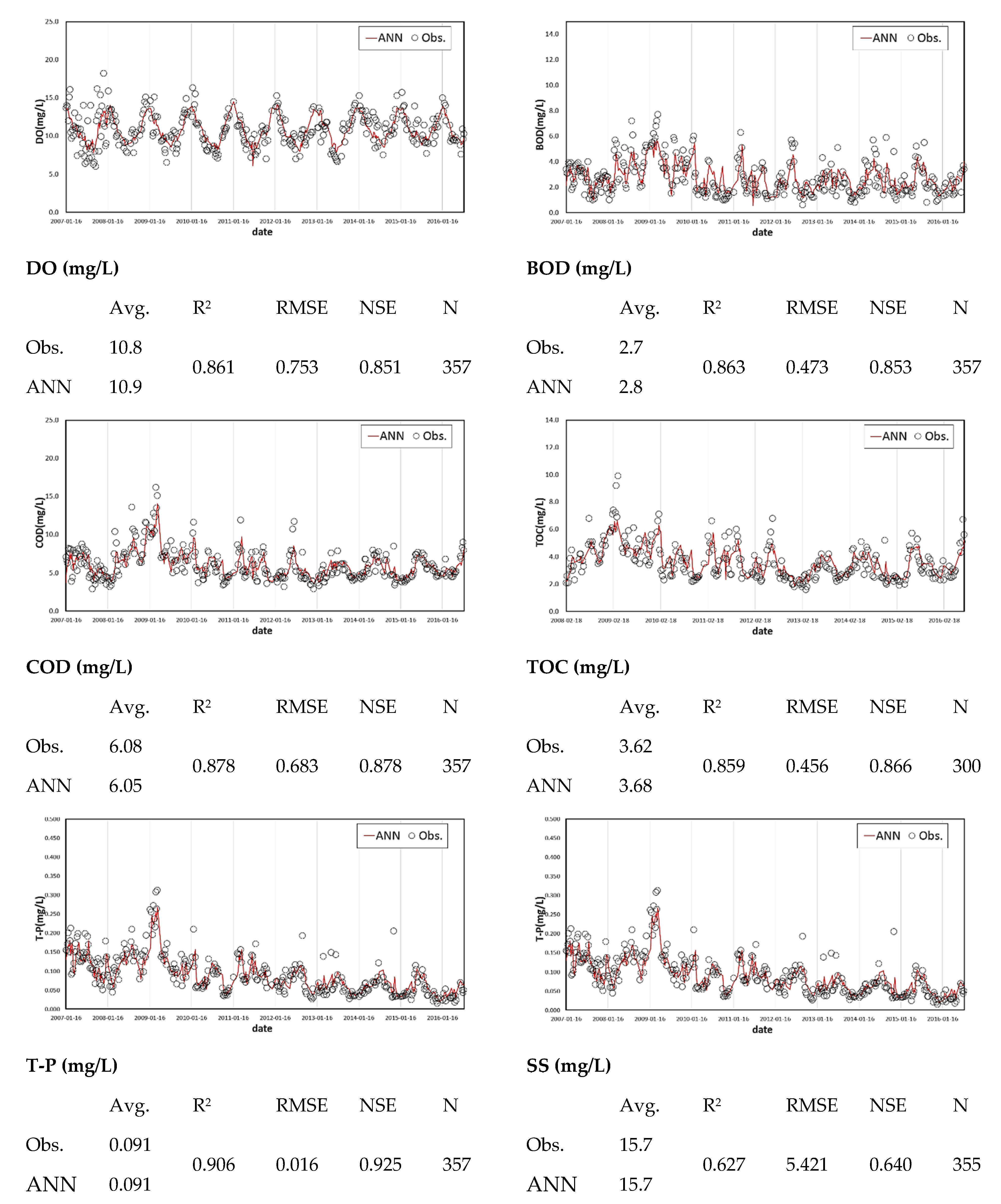
3.3. Evaluation of the ANN Model That Utilizes Probability Forecasts
4. Conclusions
- Based on the EFA results, the water temperature (W.T), temperature (T), and dissolved oxygen (DO) showed negative correlations at most locations and were classified as the same factor. This indicates that the characteristic of the decreasing dissolution rate of gas (oxygen) with decreasing W.T is reflected well. Immediately downstream of the Namgang Dam, water quality variables such as COD and nutrients were classified as the same factor. In Namgang E, BOD and Chl-a were classified as the same factor. This suggests that the native Chl-a and BOD have a high correlation owing to the hydraulically stagnant flow at the junction of the main stream and tributary.
- Most of the meteorological variables were not classified together with the water quality variables. This is because the meteorological variables did not exhibit large variability as they are not direct influencing factors for the water quality variables, but indirect factors related to the W.T or saturation. In other words, the nonlinear relationship between meteorological variables and water quality variables could not be statistically examined through EFA. However, we attempted to build a model that embodies the nonlinear correlation between the meteorological factors and water quality factors through ANN model learning.
- The coefficient of determination was determined, and the model was evaluated by building a water quality prediction model for each unit watershed, and the results were good for all water quality variables except for the SS. This seems to be attributable to the large changes in observation values due to changes in the watershed runoff characteristics caused by rainfall; moreover, the number of observations is extremely small to reflect the variation characteristics. It is expected that an enhanced model could be constructed if detailed ANN learning were performed through continuous accumulation of the water quality data of the existing water quality monitoring network. Significant quantitative model evaluation is difficult owing to the insufficient data of probabilistic weather forecasting, which started in 2014, and irregular water quality measurement dates. However, the improvement of accuracy through data accumulation in the future can be expected.
- The meteorological and water quality changes in the watershed have large spatiotemporal variability. Water quality data have strong nonlinear characteristics of the ecosystem due to very complex reaction mechanisms. Because the meteorological effects already contain some of the characteristics of water quality, the probabilistic forecasting of water quality will be possible through the ANN-based water quality forecast model in the future.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, S.Y.; Dunn, R.J.K.; Young, R.A.; Connolly, R.M.; Dale, P.E.R.; Dehayr, R.; Lemckert, C.J.; McKinnon, S.; Powell, B.; Teasdale, P.R.; et al. Impact of urbanization on coastal wetland structure and function. Austral. Ecol. 2006, 312, 149–163. [Google Scholar] [CrossRef]
- Freeman, L.A.; Corbett, D.R.; Fitzgerald, A.M.; Lemley, D.A.; Quigg, A.; Stepe, C.N. Impacts of Urbanization and Development on Estuarine Ecosystems and Water Quality. Estuaries Coasts 2019, 42, 1821–1838. [Google Scholar] [CrossRef]
- Wellen, C.; Kamran-Disfani, A.R.; Arhonditsis, G.B. Evaluation of the current state of distributed watershed nutrient water quality modeling. Environ. Sci. Technol. 2015, 49, 3278–3290. [Google Scholar] [CrossRef] [PubMed]
- Ji, Z.G. Hydrodynamics and Water Quality: Modeling Rivers, Lakes, and Estuaries; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Wenyan, W.; Graeme, C.D.; Holger, R.M. Protocol for developing ANN models and its application to the assessment of the quality of the ANN model development process in drinking water quality modelling. Environ. Model. Softw. 2014, 54, 108–127. [Google Scholar]
- Kim, S.E.; Seo, I.W. Artificial Neural Network ensemble modeling with conjunctive data clustering for water quality prediction in rivers. J. Hydro-Environ. Res. 2015, 9, 325–339. [Google Scholar] [CrossRef]
- Palani, S.; Liong, S.Y.; Tkalich, P. An ANN application for water quality forecasting. Mar. Pollut. Bull. 2008, 56, 1586–1597. [Google Scholar] [CrossRef] [PubMed]
- Patki, V.K.; Jahagirdar, S.; Patil, Y.M.; Karale, R.; Nadagouda, A. Prediction of water quality in municipal distribution system. Mater. Today Proc. 2021, in press. [Google Scholar] [CrossRef]
- Chang, F.J.; Tsai, Y.H.; Chen, P.A.; Alexandra, C.; Georges, V. Modeling water quality in an urban river using hydrological factors e Data driven approaches. J. Environ. Manag. 2015, 151, 87–96. [Google Scholar] [CrossRef] [PubMed]
- Dunn, R.J.K.; Teasdale, P.R.; Warnken, J.; Jordan, M.A.; Arthur, J.M. Evaluation of the in situ, time-integrated DGT technique by monitoring changes in heavy metal concentrations in estuarine waters. Environ. Pollut. 2007, 148, 213–220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeong, K.S.; Kim, D.K.; Shin, H.S.; Yoon, J.D.; Kim, H.W.; Joo, G.J. Impact of summer rainfall on the seasonal water quality variation (chlorophyll a) in the regulated Nakdong River. KSCE J. Civil. Eng. 2011, 15, 983–994. [Google Scholar] [CrossRef]
- Kim, S.E.; Seo, I.W.; Choi, S.Y. Assessment of water quality variation of a monitoring network using exploratory factor analysis and empirical orthogonal function. Environ. Model. Softw. 2017, 94, 21–35. [Google Scholar] [CrossRef]
- Rojas, R. The Backpropagation Algorithm. In Neural Networks; Springer: Berlin/Heidelberg, Germany, 1996; pp. 149–182. [Google Scholar] [CrossRef]
- ASCE. Criteria for evaluation of watershed models. J. Irrig. Drianage Eng. ASCE 1993, 119, 429–442. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydro climatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
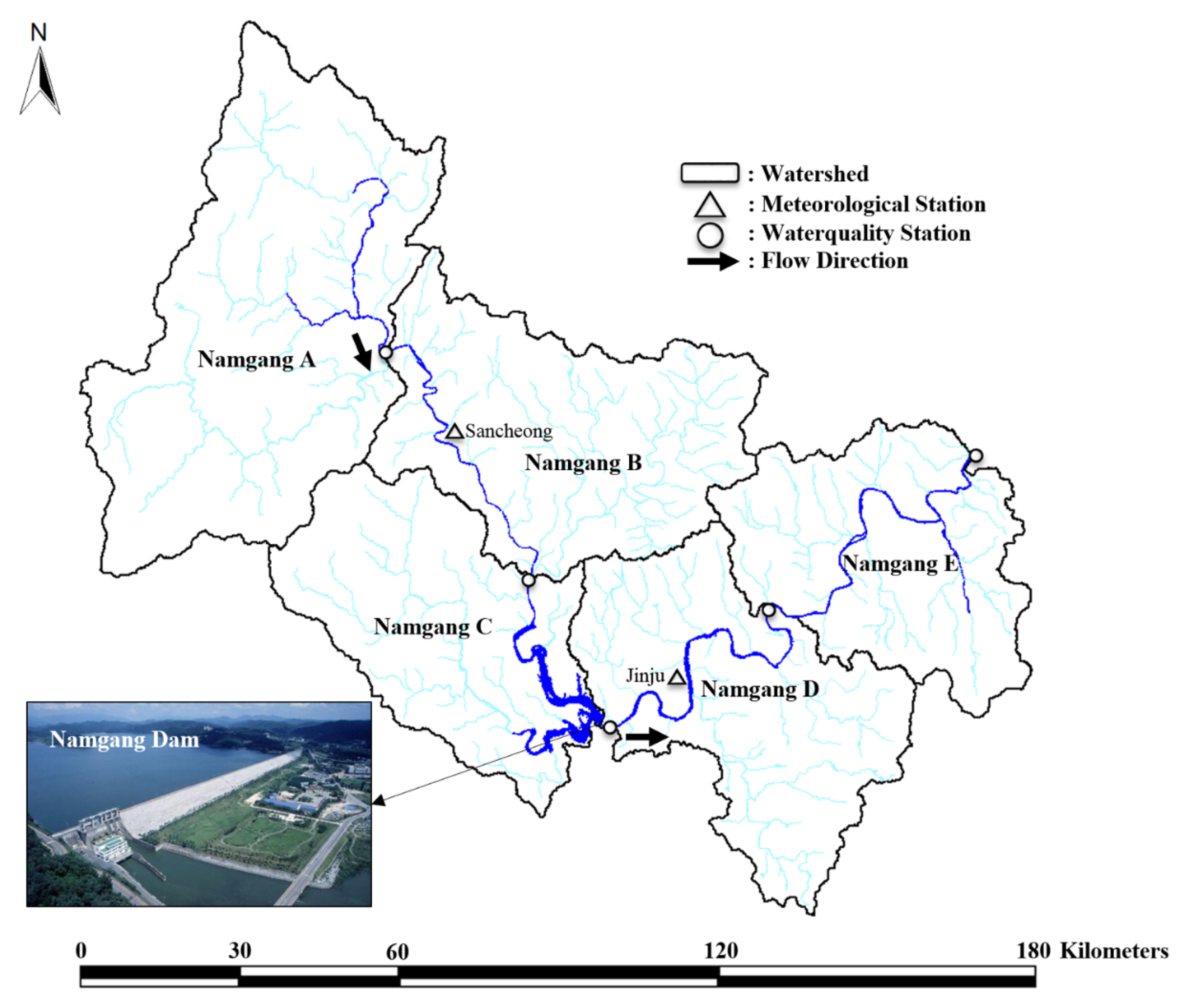
| Weather Station | Input Variables | Collection Period | Reference |
|---|---|---|---|
| Sancheong | Precipitation, Relative Humidity, Temperature, Solar Radiation, Wind Speed | 2007–2016 | KMA * |
| Jinju |
| Gauging Station | Input Variables | Collection Period | Reference |
|---|---|---|---|
| Namgang A | Water Temperature, EC, pH, DO, BOD, COD, SS, T-N, NH3-N, NO3-N, T-P, PO4-P, Chl-a, TOC, Flow | 2007–2016 | KWIS ** |
| Namgang B | |||
| Namgang C | |||
| Namgang D | |||
| Namgang E |
| Method | Basic Equation | Description of Variables |
|---|---|---|
| RMSE | = observed value, = simulated value, = mean observed value n = number of data | |
| NSE | ||
| R2 |
| Unit Watershed | Factor 1 | Factor 2 | Factor 3 | Factor 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Factor | Eigenvalue | Cumulative | Factor | Eigenvalue | Cumulative | Factor | Eigenvalue | Cumulative | Factor | Eigenvalue | Cumulative | |
| Namgang A | W.T, T, DO, T-N, NO3-N | 4.713 | 0.295 | Q, SS, Qs, COD, P | 2.671 | 0.462 | T-P, TOC, pH, BOD, Chl-a | 2.557 | 0.621 | Sun, R.H. | 1.534 | 0.717 |
| Namgang B | W.T, T, DO, T-N, NO3-N | 5.366 | 0.335 | COD, BOD, TOC, SS, T-P, Chl-a | 2.555 | 0.495 | Q, Qs, pH | 2.150 | 0.630 | Sun, R.H. | 1.455 | 0.720 |
| Namgang C | W.T, T, DO, EC | 6.246 | 0.347 | SS, COD, TOC, T-P, Q | 2.755 | 0.500 | Sun, Rad, R.H., P | 2.262 | 0.626 | pH, BOD, Chl-a | 1.266 | 0.696 |
| Namgang D | BOD, COD, TOC, T-P, Chl-a | 5.492 | 0.305 | W.T, T, EC, DO, T-N | 3.965 | 0.525 | Sun, R.H., P, Rad | 2.510 | 0.665 | pH, SS, Q. | 1.907 | 0.771 |
| Namgang E | W.T, T, EC, DO, T-N, NO3-N, NH3-N | 5.159 | 0.287 | BOD, COD, TOC, T-P, Chl-a | 4.008 | 0.509 | SS, Q, Qn, pH, PO4-P | 2.505 | 0.649 | Rad, R.H., Sun | 2.010 | 0.760 |
| Unit watershed | Water Quality Prediction Variable | Common Input Variable | Input Variable |
|---|---|---|---|
| Namgang A | DOt+1 | Temperaturet−1, Temperaturet, Temperaturet+1, Precipitationt−1, Precipitationt, Precipitationt+1 | DOt, DOt−1, DOt−2, T-Nt |
| BOOt+1 | BODt, BODt−1, BODt−2, TOCt, T-Pt, Chl-at | ||
| COOt+1 | CODt, CODt−1, CODt−2, SSt | ||
| TOCt+1 | TOCt, TOCt−1, TOCt−2, BODt, T-Pt, Chl-at | ||
| T-Pt+1 | T-Pt, T-Pt−1, T-Pt−2, BODt, TOCt, Chl-at | ||
| SSt+1 | SSt, SSt−1, SSt−2, CODt | ||
| Namgang B | DOt+1 | DOt, DOt−1, DOt−2, T-Nt | |
| BOOt+1 | BODt, BODt−1, BODt−2, TOCt, T-Pt, CODt, SSt, Chl-at | ||
| COOt+1 | CODt, CODt−1, CODt−2, BODt, TOCt, T-Pt, SSt, Chl-at | ||
| TOCt+1 | TOCt, TOCt−1, TOCt−2, BODt, T-Pt, CODt, SSt, Chl-at | ||
| T-Pt+1 | T-Pt, T-Pt−1, T-Pt−2, BODt, TOCt, CODt, SSt, Chl-at | ||
| SSt+1 | SSt, SSt−1, SSt−2, BODt, TOCt, T-Pt, CODt, Chl-at | ||
| Namgang C | DOt+1 | DOt, DOt−1, DOt−2 | |
| BOOt+1 | BODt, BODt−1, BODt−2, Chl-at | ||
| COOt+1 | CODt, CODt−1, CODt−2, TOCt, T-Pt, SSt | ||
| TOCt+1 | TOCt, TOCt−1, TOCt−2, CODt, T-Pt, SSt | ||
| T-Pt+1 | T-Pt, T-Pt−1, T-Pt−2, CODt, TOCt, SSt | ||
| SSt+1 | SSt, SSt−1, SSt−2, CODt, TOCt, T-P | ||
| Namgang D | DOt+1 | DOt, DOt−1, DOt−2, T-Nt | |
| BOOt+1 | BODt, BODt−1, BODt−2, TOCt, T-Pt, CODt, Chl-at | ||
| COOt+1 | CODt, CODt−1, CODt−2 BODt, TOCt, T-Pt, Chl-at | ||
| TOCt+1 | TOCt, TOCt−1, TOCt−2 BODt, T-Pt, CODt, Chl-at | ||
| T-Pt+1 | T-Pt, T-Pt−1, T-Pt−2 BODt, TOCt, CODt, Chl-at | ||
| SSt+1 | SSt, SSt−1, SSt−2 | ||
| Namgang E | DOt+1 | DOt, DOt−1, DOt−2, T-Nt | |
| BOOt+1 | BODt, BODt−1, BODt−2, TOCt, T-Pt, CODt, Chl-at | ||
| COOt+1 | CODt, CODt−1, CODt−2 BODt, TOCt, T-Pt, Chl-at | ||
| TOCt+1 | TOCt, TOCt−1, TOCt−2 BODt, T-Pt, CODt, Chl-at | ||
| T-Pt+1 | T-Pt, T-Pt−1, T-Pt−2 BODt, TOCt, CODt, Chl-at | ||
| SSt+1 | SSt, SSt−1, SSt−2, |
| Unit Watershed | R2 | RMSE | NSE | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DO | BOD5 | COD | TOC | T-P | SS | DO | BOD5 | COD | TOC | T-P | SS | DO | BOD5 | COD | TOC | T-P | SS | |
| Namgang A | 0.793 | 0.602 | 0.612 | 0.512 | 0.561 | 0.598 | 0.872 | 0.420 | 0.801 | 0.718 | 0.032 | 3.889 | 0.798 | 0.597 | 0.525 | 0.507 | 0.409 | 0.587 |
| Namgang B | 0.796 | 0.505 | 0.570 | 0.601 | 0.571 | 0.471 | 0.896 | 0.578 | 0.903 | 0.614 | 0.020 | 6.187 | 0.789 | 0.589 | 0.496 | 0.584 | 0.350 | 0.426 |
| Namgang C | 0.866 | 0.315 | 0.761 | 0.730 | 0.629 | 0.529 | 0.807 | 0.448 | 0.405 | 0.283 | 0.009 | 4.761 | 0.865 | 0.401 | 0.764 | 0.730 | 0.595 | 0.504 |
| Namgang D | 0.673 | 0.663 | 0.620 | 0.554 | 0.391 | 0.533 | 1.012 | 0.310 | 0.502 | 0.376 | 0.017 | 3.223 | 0.658 | 0.605 | 0.606 | 0.551 | 0.341 | 0.338 |
| Namgang E | 0.854 | 0.673 | 0.926 | 0.809 | 0.785 | 0.602 | 0.675 | 0.472 | 0.381 | 0.424 | 0.012 | 3.214 | 0.847 | 0.658 | 0.864 | 0.749 | 0.705 | 0.561 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, W.S.; Kim, S.E.; Kim, Y.D. Prediction of Surface Water Quality by Artificial Neural Network Model Using Probabilistic Weather Forecasting. Water 2021, 13, 2392. https://doi.org/10.3390/w13172392
Jung WS, Kim SE, Kim YD. Prediction of Surface Water Quality by Artificial Neural Network Model Using Probabilistic Weather Forecasting. Water. 2021; 13(17):2392. https://doi.org/10.3390/w13172392
Chicago/Turabian StyleJung, Woo Suk, Sung Eun Kim, and Young Do Kim. 2021. "Prediction of Surface Water Quality by Artificial Neural Network Model Using Probabilistic Weather Forecasting" Water 13, no. 17: 2392. https://doi.org/10.3390/w13172392






