Deriving Six Components of Reynolds Stress Tensor from Single-ADCP Data
Abstract
:1. Introduction
2. Method Description
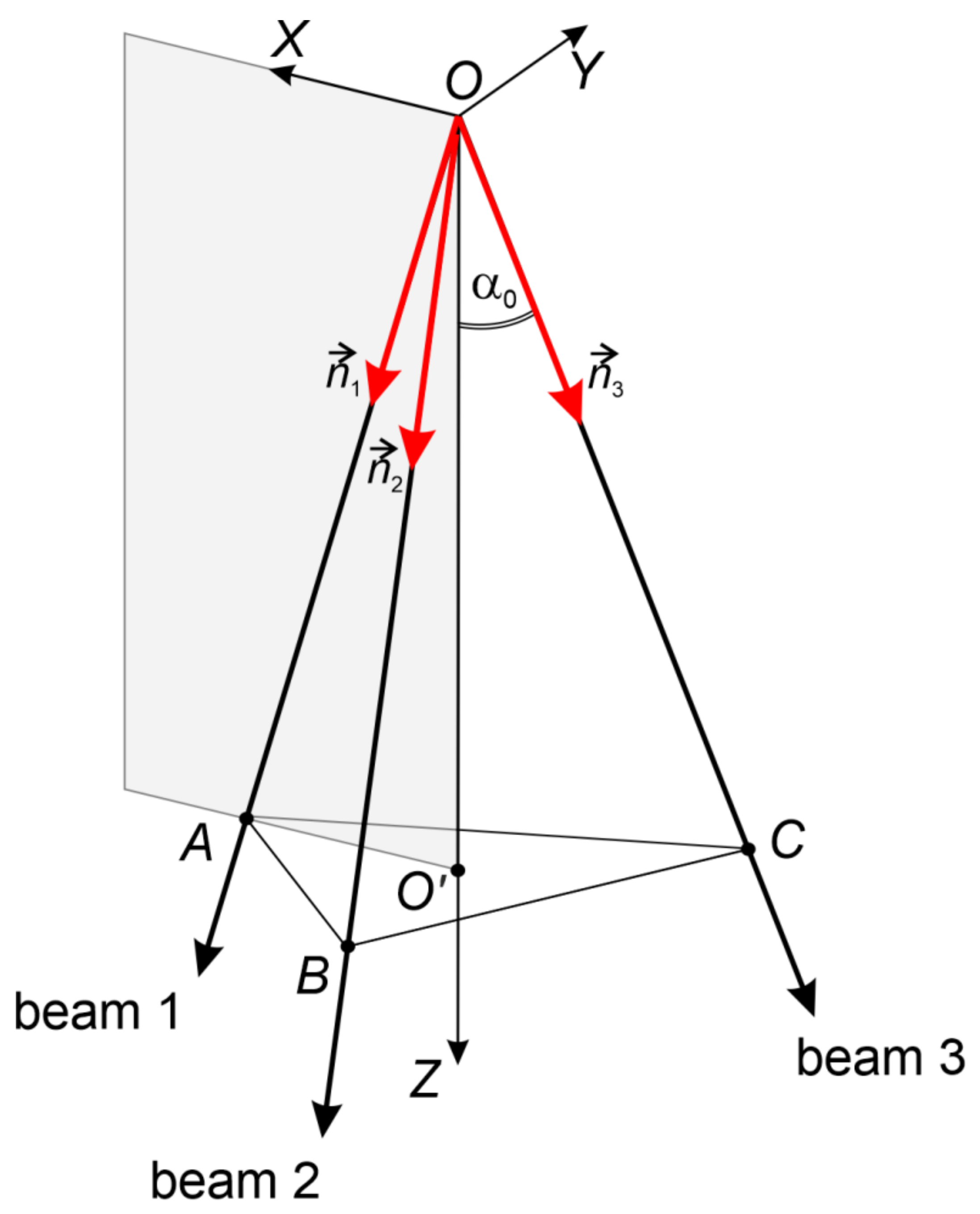
General Framework
- 1.
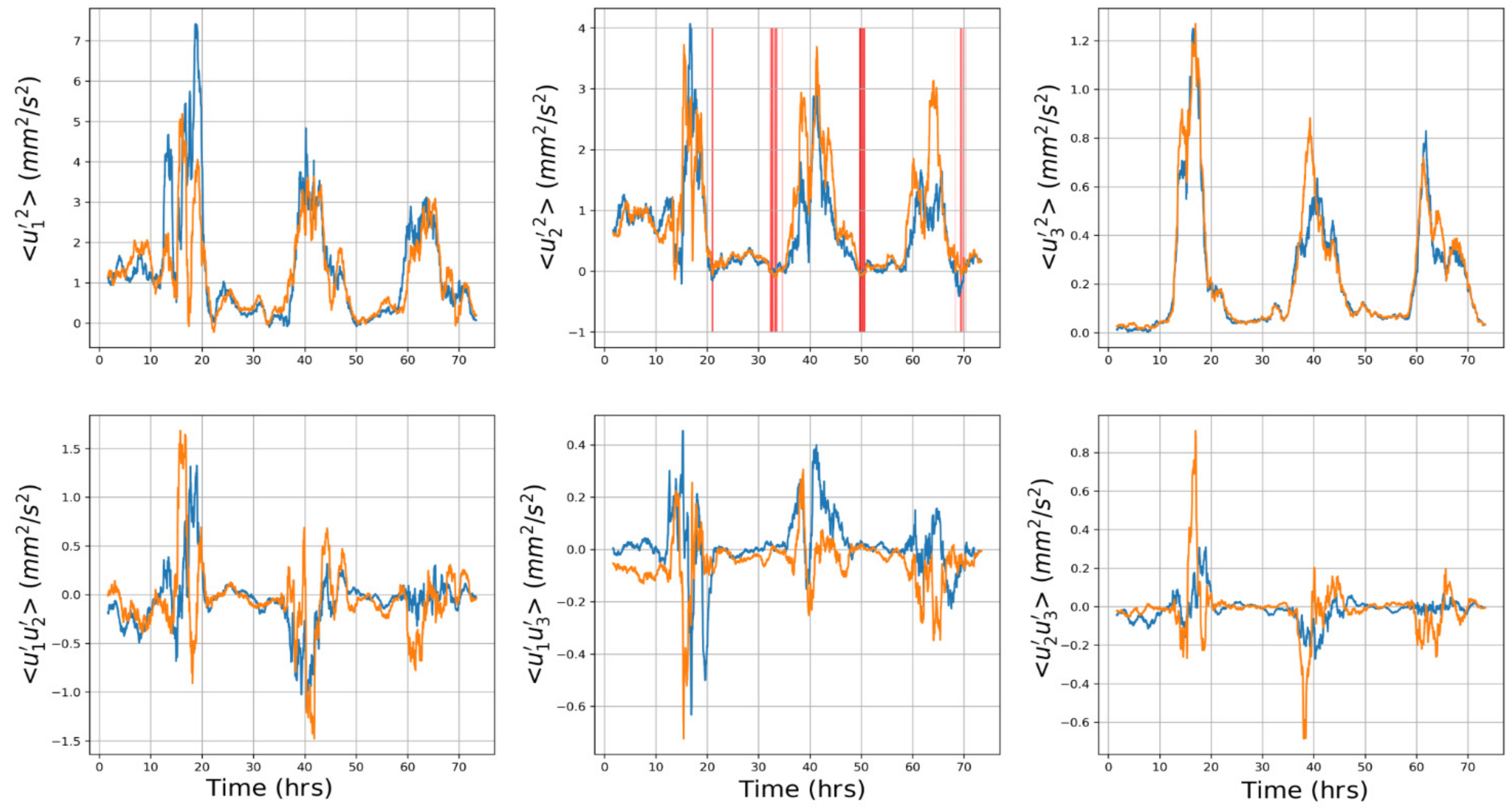
- After proper choice of time averaging interval, the mean beam velocities , pulsation intensities (Equation (2)) and correlations (Equation (5), i ≠ j) are calculated directly from experimental data.
- 2.
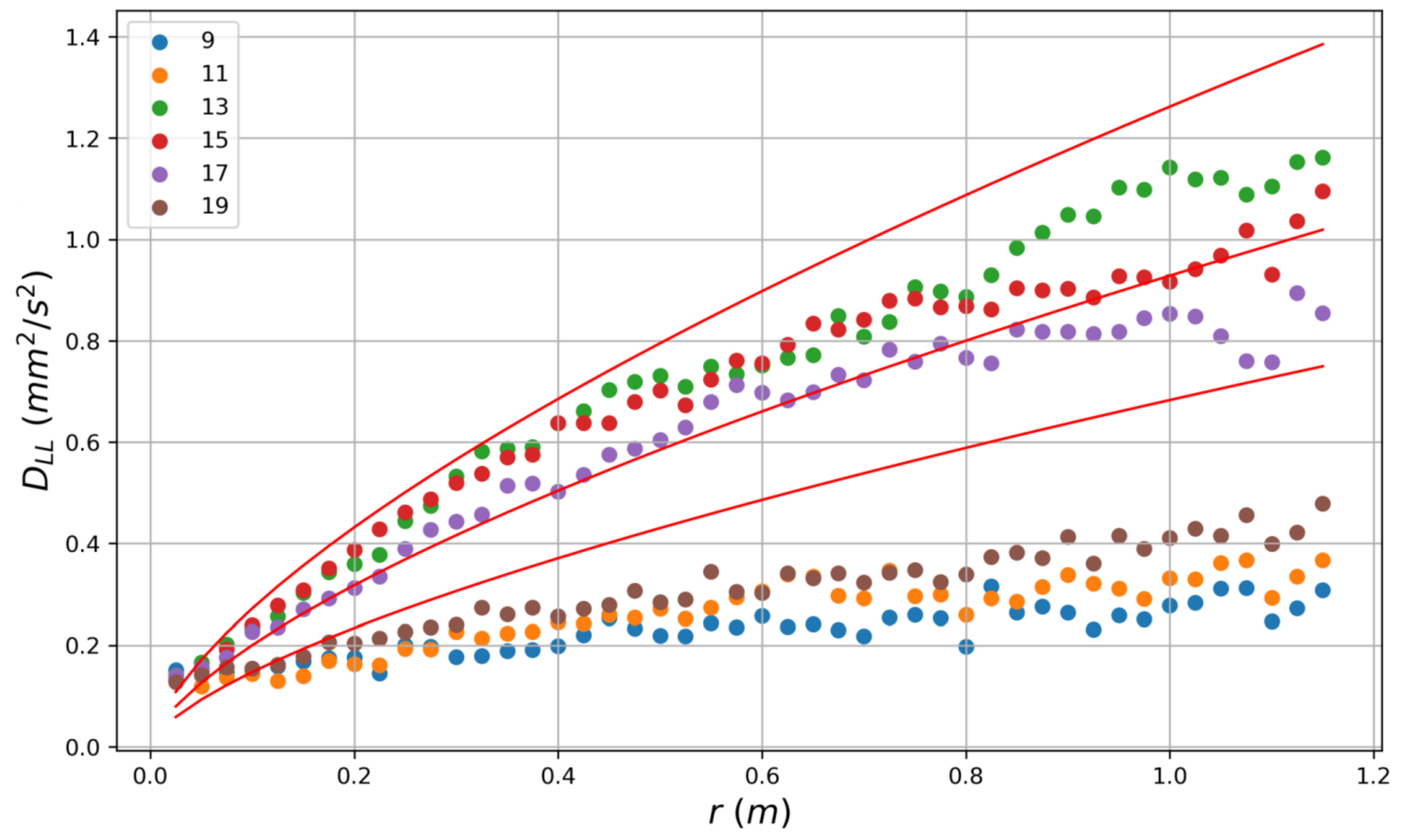
- For each beam the function is calculated. After revealing the inertial interval, its extent is estimated, with the special attention to its upper scale limit l.
- 3.
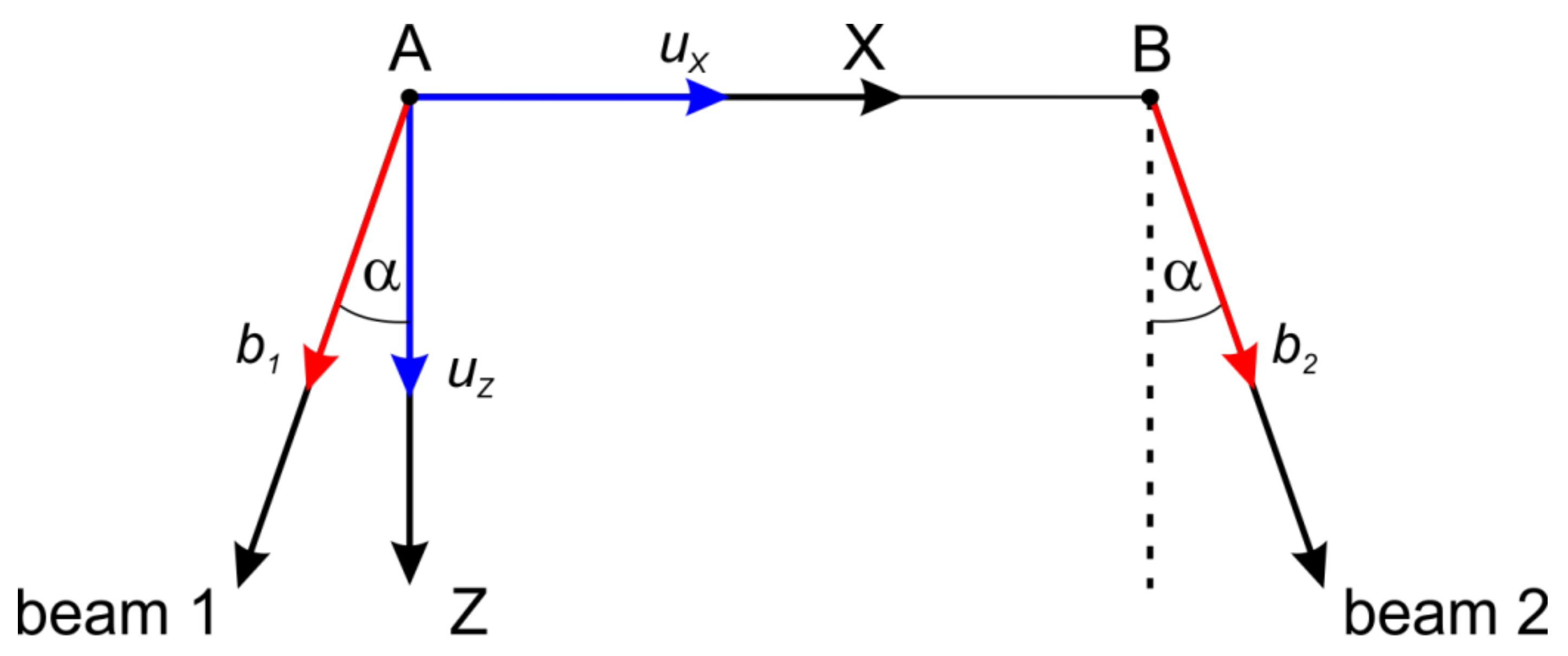
- The range of depths is chosen in such a way that the distance between beams does not exceed the scale l. The maximum depth h is derived from inequality AB < l (see Figure 1): .
- 4.
- For chosen depths, the turbulent stresses are calculated directly by solving the system (7):
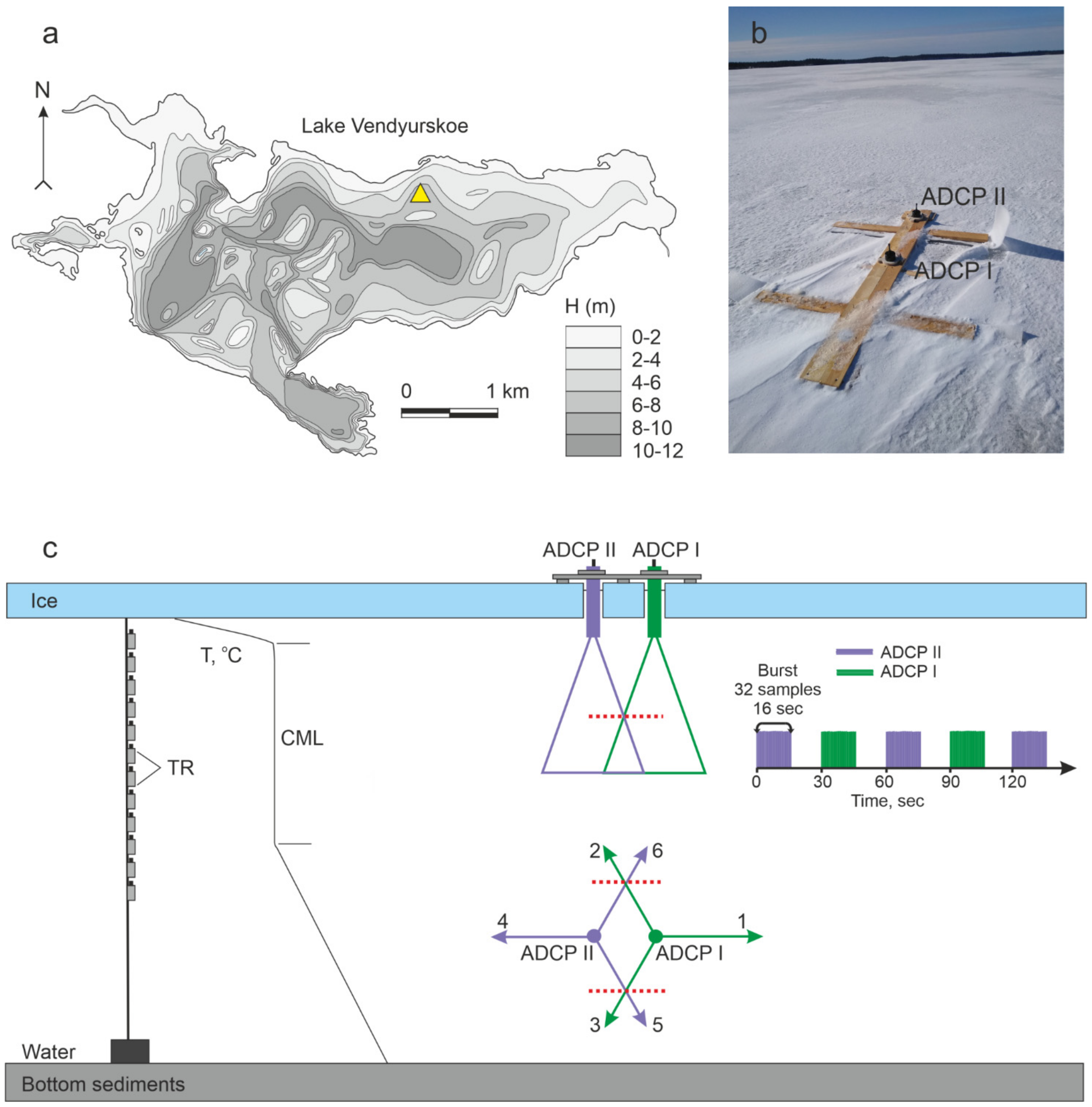
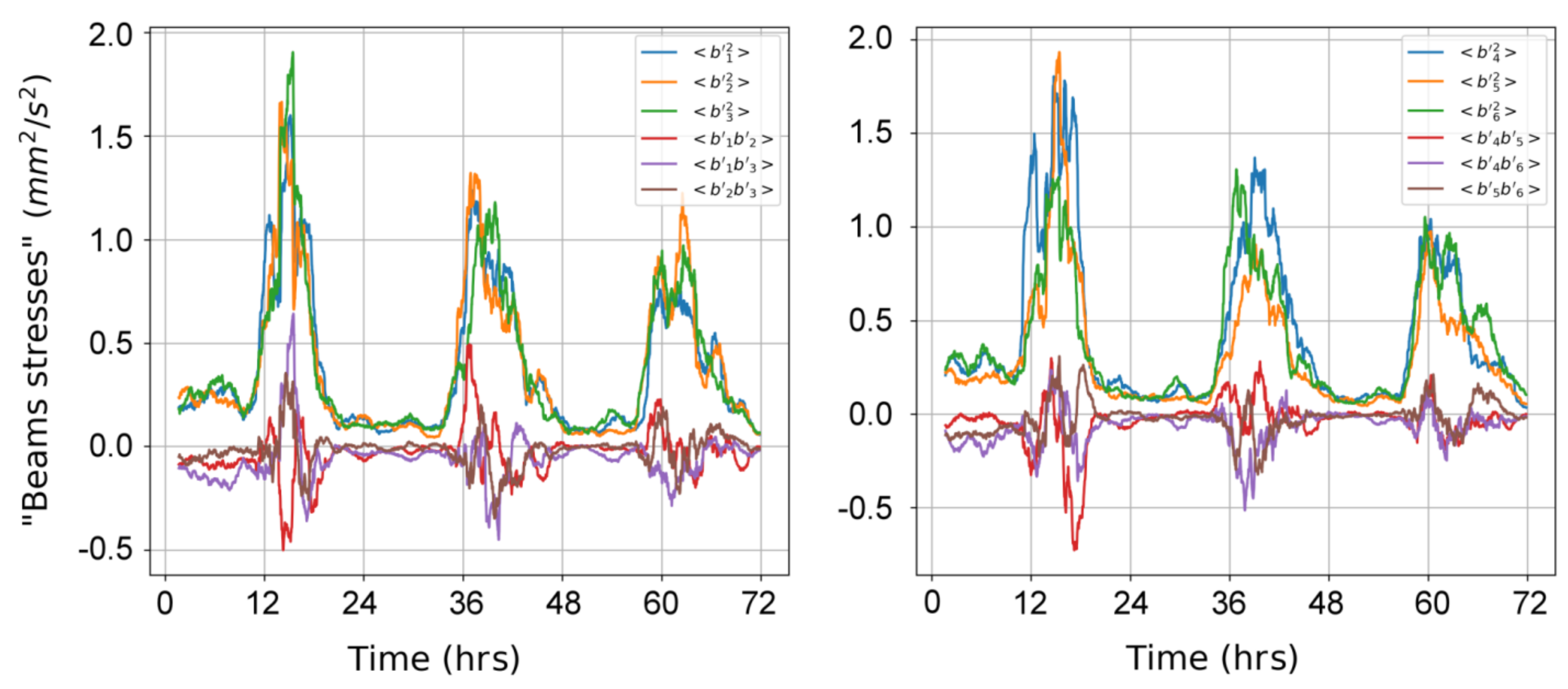
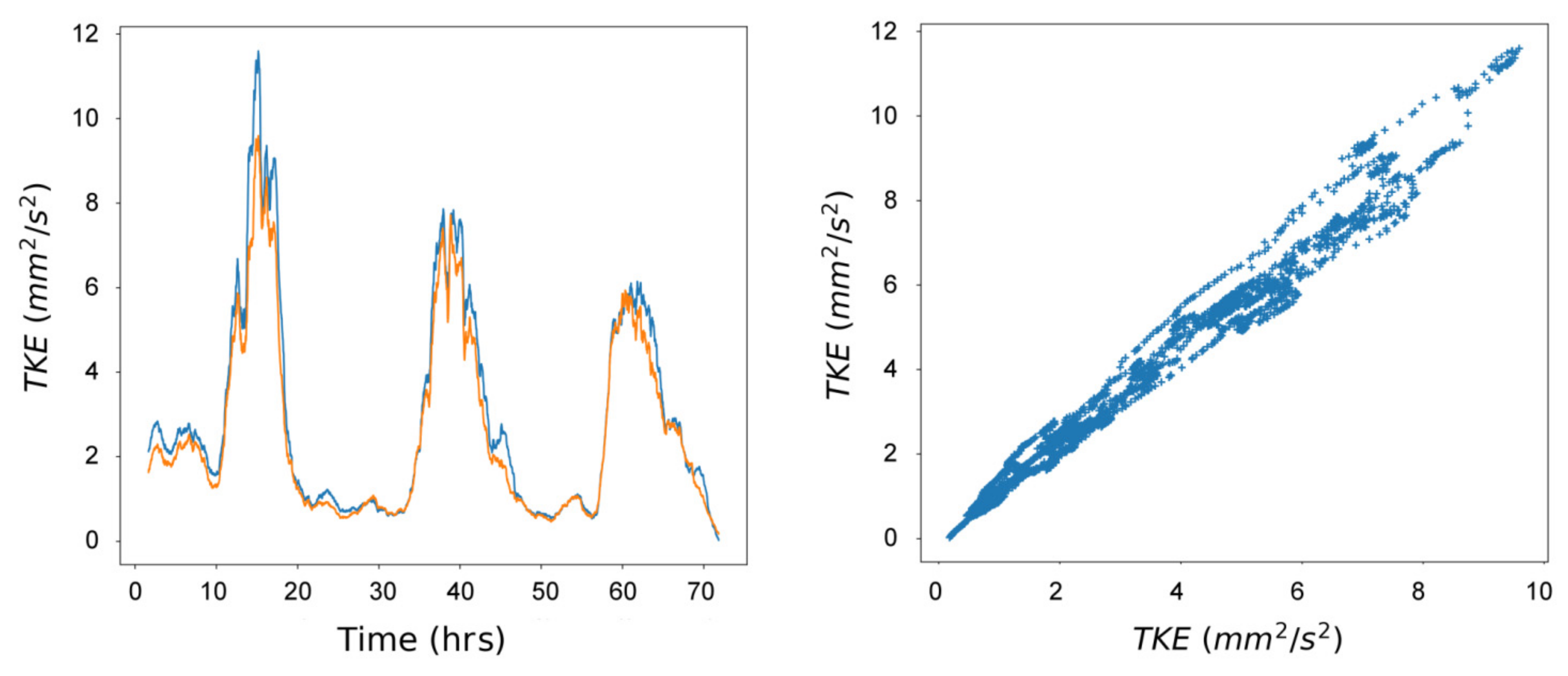
3. Experimental Setup and Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Relationships between Structure Functions
References
- Lhermitte, R. Turbulent air motion as observed by Doppler radar. In Proceedings of the 13th Conference on Radar Meteorology, Montreal, QC, Canada, 20–23 August 1968; American Meteorological Society: Boston, MA, USA, 1968; pp. 498–503. [Google Scholar]
- Lhermitte, R. Doppler sonar observation of tidal flow. J. Geophys. Res. 1983, 88, 725–742. [Google Scholar] [CrossRef]
- Lohrmann, A.; Hackett, B.; Roed, L. High-resolution measurements of turbulence, velocity, and stress using a pulse-to-pulse coherent sonar. J. Atmos. Ocean. Technol. 1990, 7, 19–37. [Google Scholar] [CrossRef] [Green Version]
- Guerra, M.; Thomson, J. Turbulence Measurements from Five-Beam Acoustic Doppler Current Profilers. J. Atmos. Ocean. Technol. 2017, 34, 1267–1284. [Google Scholar] [CrossRef]
- Bouffard, D.; Zdorovennova, G.; Bogdanov, S.; Efremova, T.; Lavanchy, S.; Palshin, N.; Terzhevik, A.; Vinnå, L.R.; Volkov, S.; Wüest, A.; et al. Under-ice convection dynamics in a boreal lake. Inland Waters 2019, 9, 142–161. [Google Scholar] [CrossRef]
- Bogdanov, S.; Zdorovennova, G.; Volkov, S.; Zdorovennov, R.; Palshin, N.; Efremova, T.; Terzhevik, A.; Bouffard, D. Structure and dynamics of convective mixing in Lake Onego under ice-covered conditions. Inland Waters 2019, 9, 177–192. [Google Scholar] [CrossRef] [Green Version]
- Wiles, P.J.; Rippeth, T.P.; Simpson, J.H.; Hendricks, P.J. A novel technique for measuring the rate of turbulent dissipation in the marine environment. Geophys. Res. Lett. 2006, 33, L21608. [Google Scholar] [CrossRef]
- Lucas, N.S.; Simpson, J.H.; Rippeth, T.P.; Old, C.P. Measuring Turbulent Dissipation Using a Tethered ADCP. J. Atmos. Ocean. Technol. 2014, 31, 1826–1837. [Google Scholar] [CrossRef] [Green Version]
- Volkov, S.; Bogdanov, S.; Zdorovennov, R.; Zdorovennova, G.; Terzhevik, A.; Palshin, N.; Bouffard, D.; Kirillin, G. Fine scale structure of convective mixed layer in ice-covered lake. Environ. Fluid Mech. 2019, 19, 751–764. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Lueck, R.G. Using a broadband ADCP in a tidal channel. Part II: Turbulence. J. Atmos. Ocean. Technol. 1999, 16, 1568–1579. [Google Scholar] [CrossRef]
- Stacey, M.T.; Monismith, S.G.; Burau, J.R. Measurements of Reynolds stress profiles in unstratified tidal flow. J. Geophys. Res. 1999, 104, 10933–10949. [Google Scholar] [CrossRef]
- Rippeth, T.P.; Simpson, J.H.; Williams, E.; Inall, M.E. Measurement of the rates of production and dissipation of turbulent kinetic energy in an energetic tidal flow: Red Wharf Bay revisited. J. Phys. Oceanogr. 2003, 33, 1889–1901. [Google Scholar] [CrossRef] [Green Version]
- Vermeulen, B.; Hoitink, A.J.F.; Sassi, M.G. Coupled ADCPs can yield complete Reynolds stress tensor profiles in geophysical surface flows. Geophys. Res. Lett. 2011, 38, L06406. [Google Scholar] [CrossRef]
- Bogdanov, S.R.; Zdorovennov, R.E.; Palshin, N.I.; Zdorovennova, G.E.; Terzhevik, A.Y.; Gavrilenko, G.G.; Volkov, S.Y.; Efremova, T.V.; Kuldin, N.A.; Kirillin, G.B. Deriving of turbulent stresses in a convectively mixed layer in a shallow lake under ice by coupling two ADCPs. Fundame. I Prikl. Gidrofiz. 2021, 14, 17–28. [Google Scholar] [CrossRef]
- Hinze, J.O. Turbulence; McGrawHill: New York, NY, USA, 1975. [Google Scholar]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics. Volume II: Mechanics of Turbulence, 1st ed.; Courier Corporation: Cambridge, UK; The MIT Press: Cambridge, MA, USA, 1971. [Google Scholar]
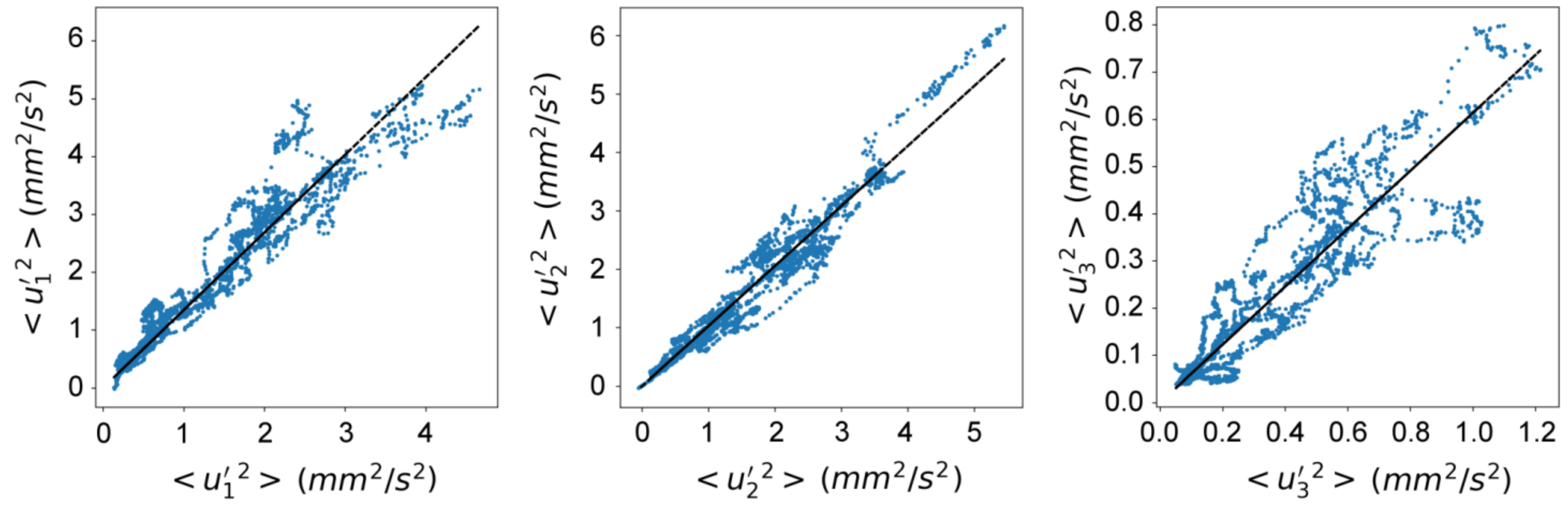
| Stress Component | Correlation Coefficient, r | Coefficient of Determination, R2 | Linear Regression Coefficient |
|---|---|---|---|
| 0.96 | 0.92 | 1.31 | |
| 0.98 | 0.96 | 1.03 | |
| 0.92 | 0.85 | 0.61 | |
| 0.99 | 0.98 | 1.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogdanov, S.; Zdorovennov, R.; Palshin, N.; Zdorovennova, G. Deriving Six Components of Reynolds Stress Tensor from Single-ADCP Data. Water 2021, 13, 2389. https://doi.org/10.3390/w13172389
Bogdanov S, Zdorovennov R, Palshin N, Zdorovennova G. Deriving Six Components of Reynolds Stress Tensor from Single-ADCP Data. Water. 2021; 13(17):2389. https://doi.org/10.3390/w13172389
Chicago/Turabian StyleBogdanov, Sergey, Roman Zdorovennov, Nikolay Palshin, and Galina Zdorovennova. 2021. "Deriving Six Components of Reynolds Stress Tensor from Single-ADCP Data" Water 13, no. 17: 2389. https://doi.org/10.3390/w13172389







