River Buffer Effectiveness in Controlling Surface Runoff Based on Saturated Soil Hydraulic Conductivity
Abstract
1. Introduction
2. Materials and Methods
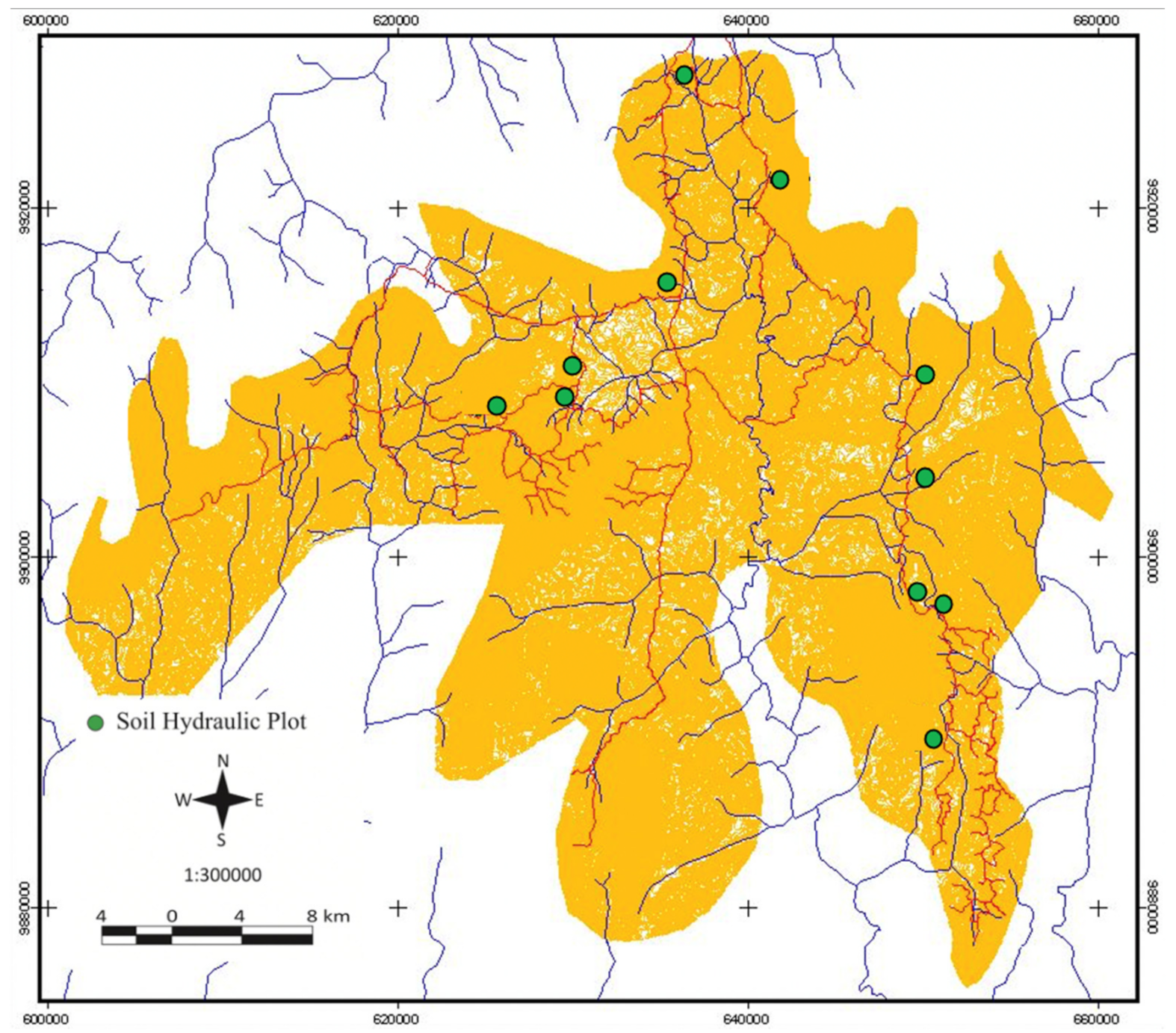
2.1. Study Area
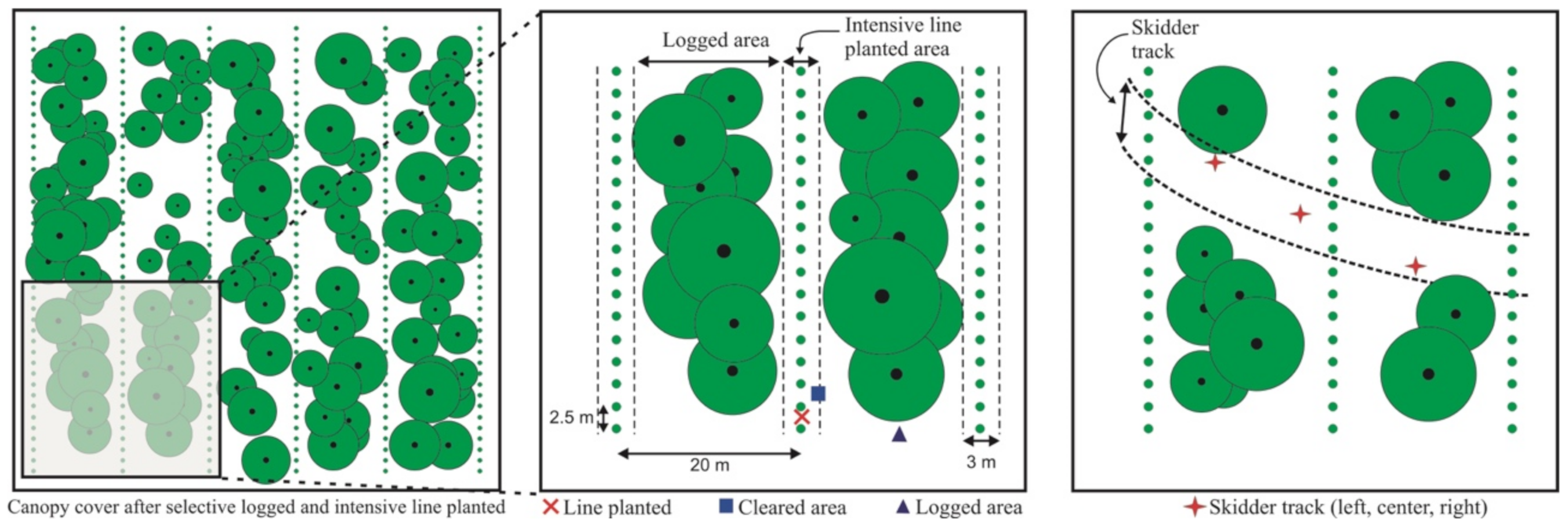
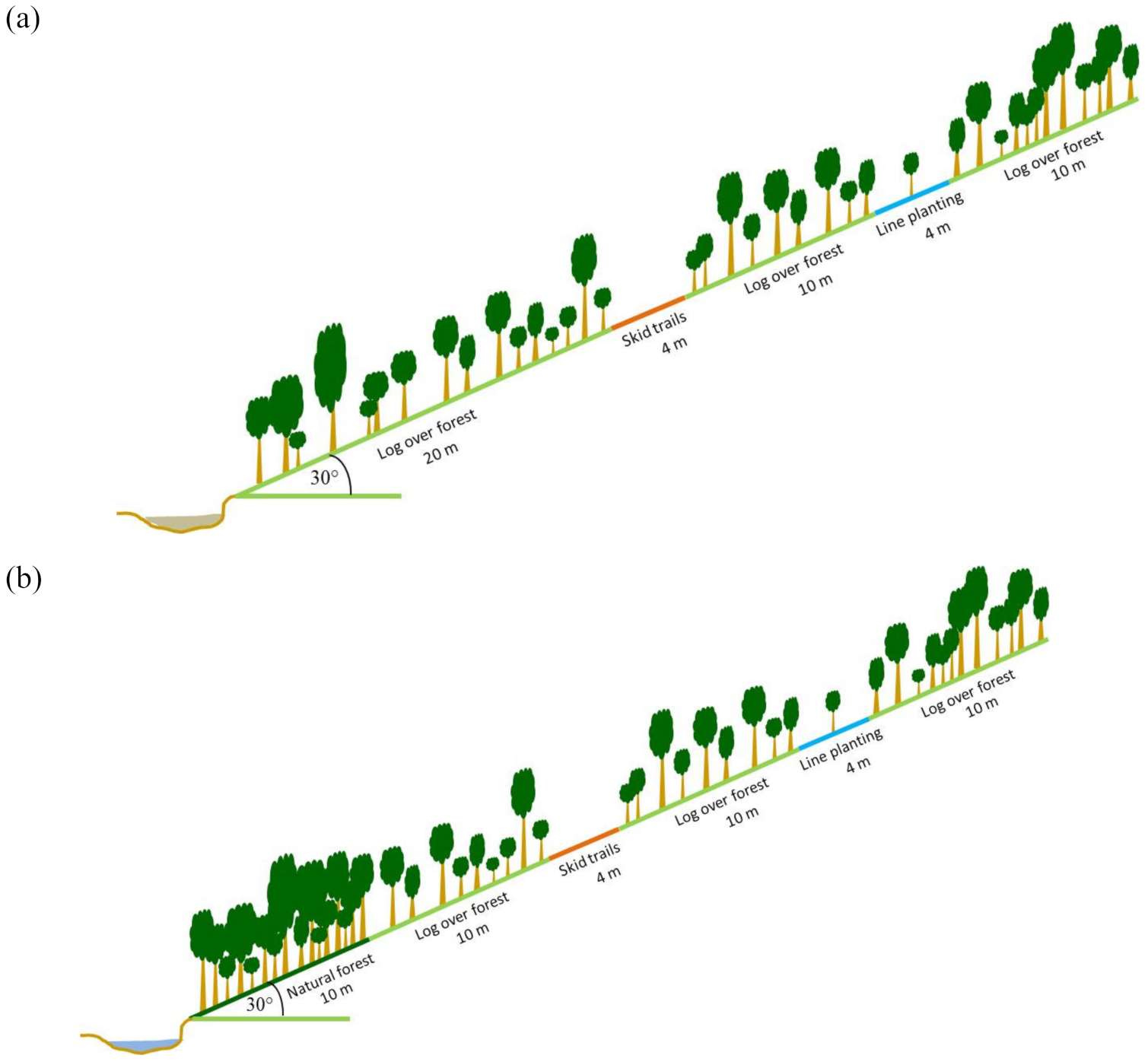
2.2. Experimental Plots
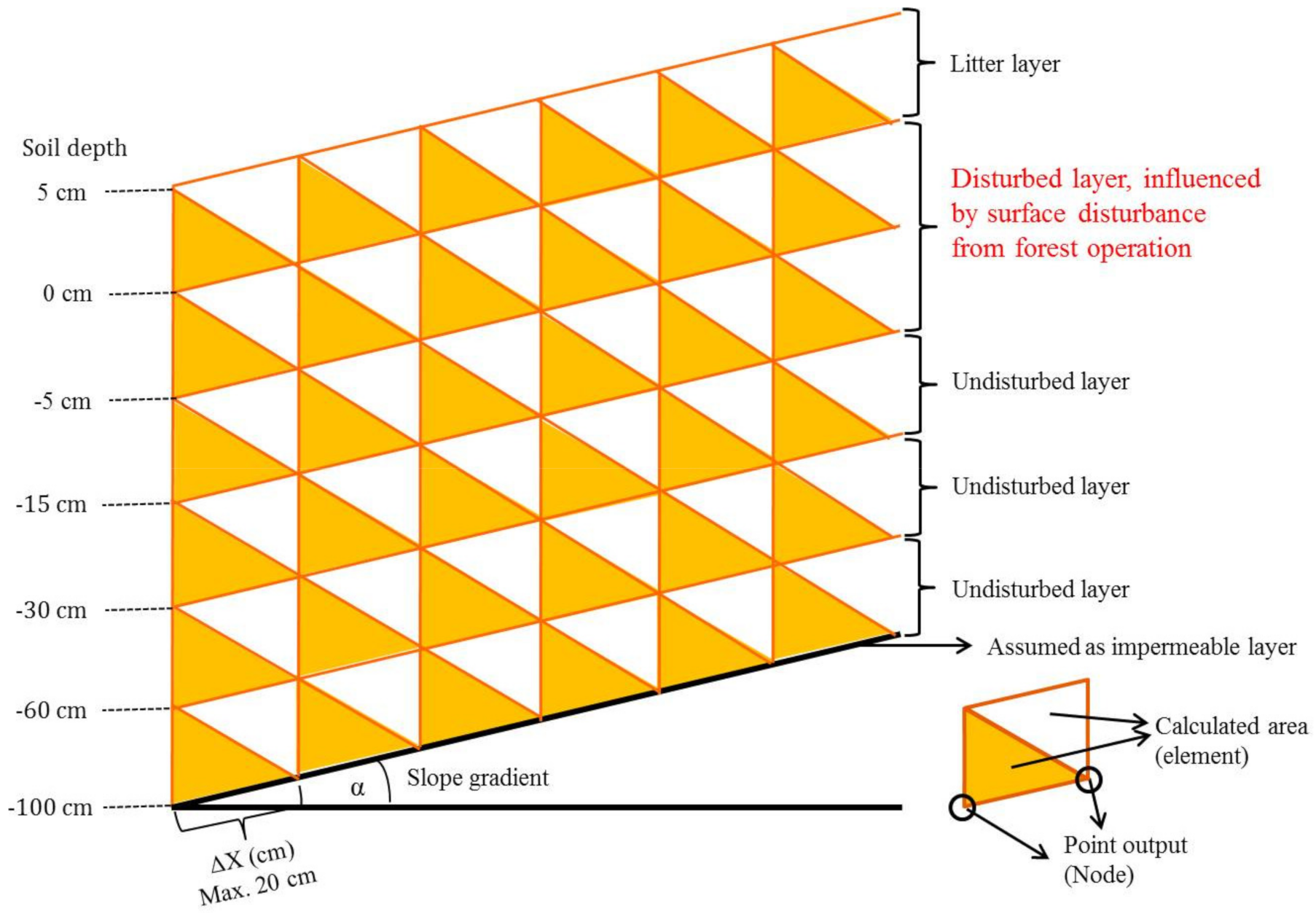
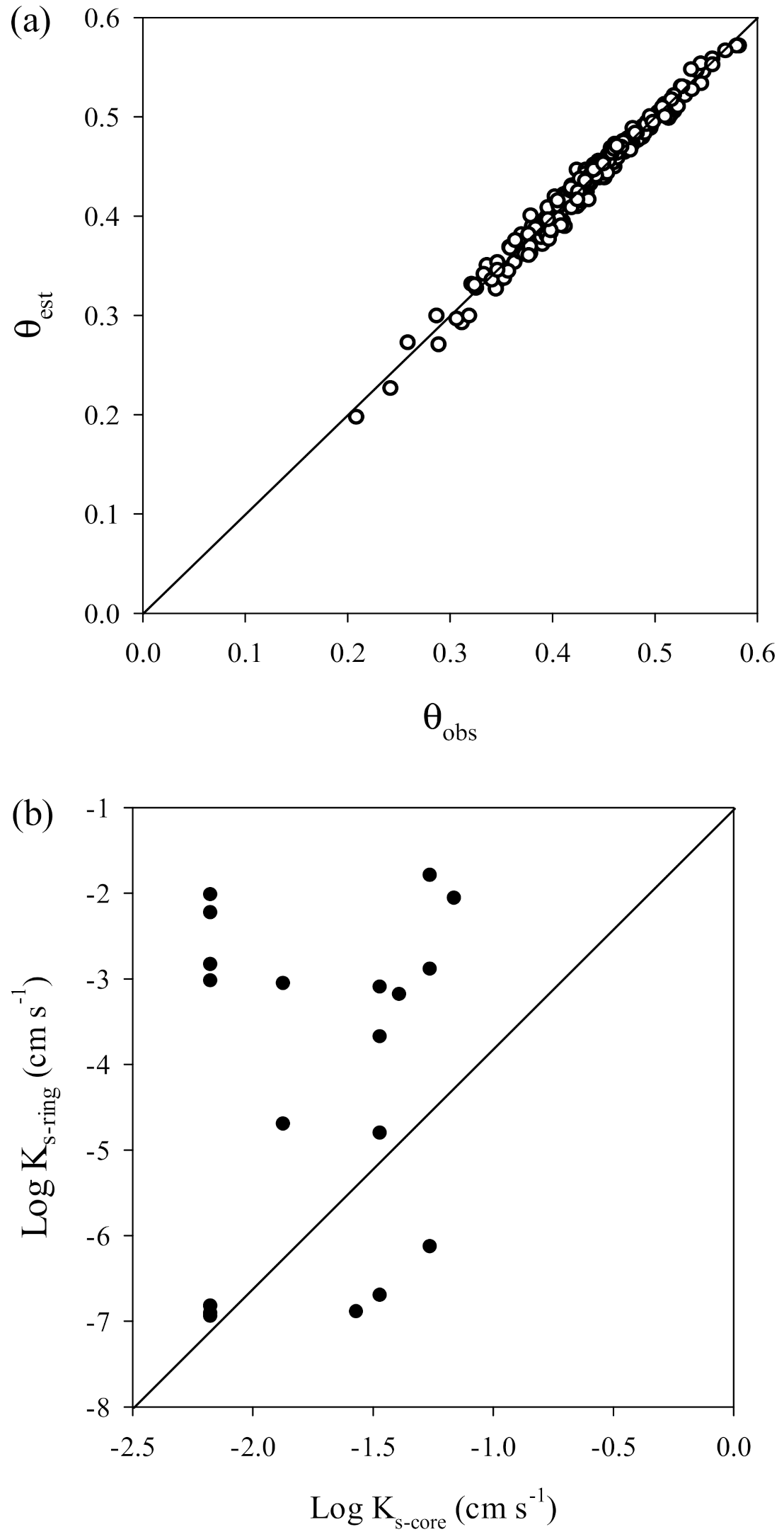
2.3. Saturated Hydraulic Conductivity
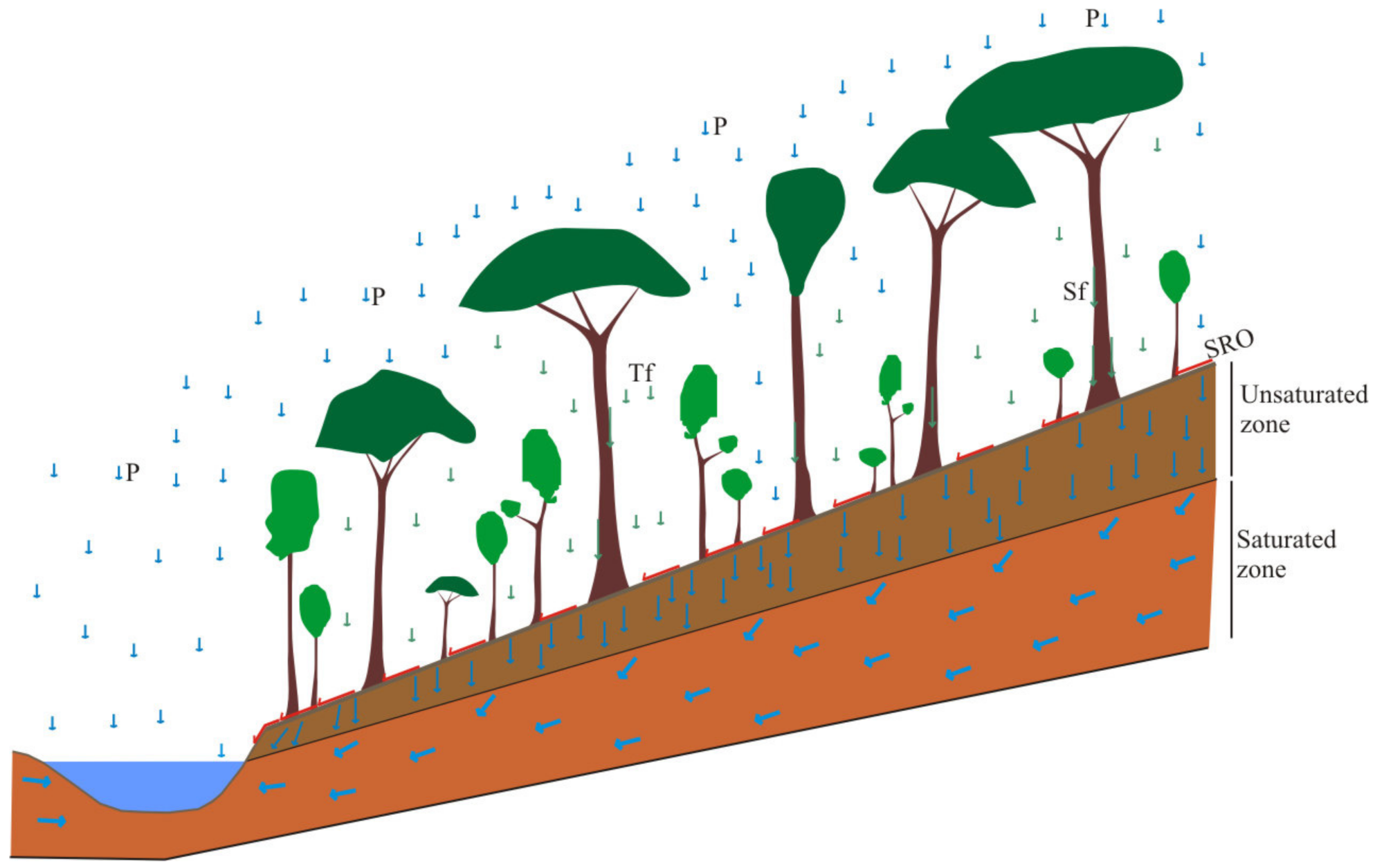
2.4. Surface Runoff Generation
3. Results and Discussion
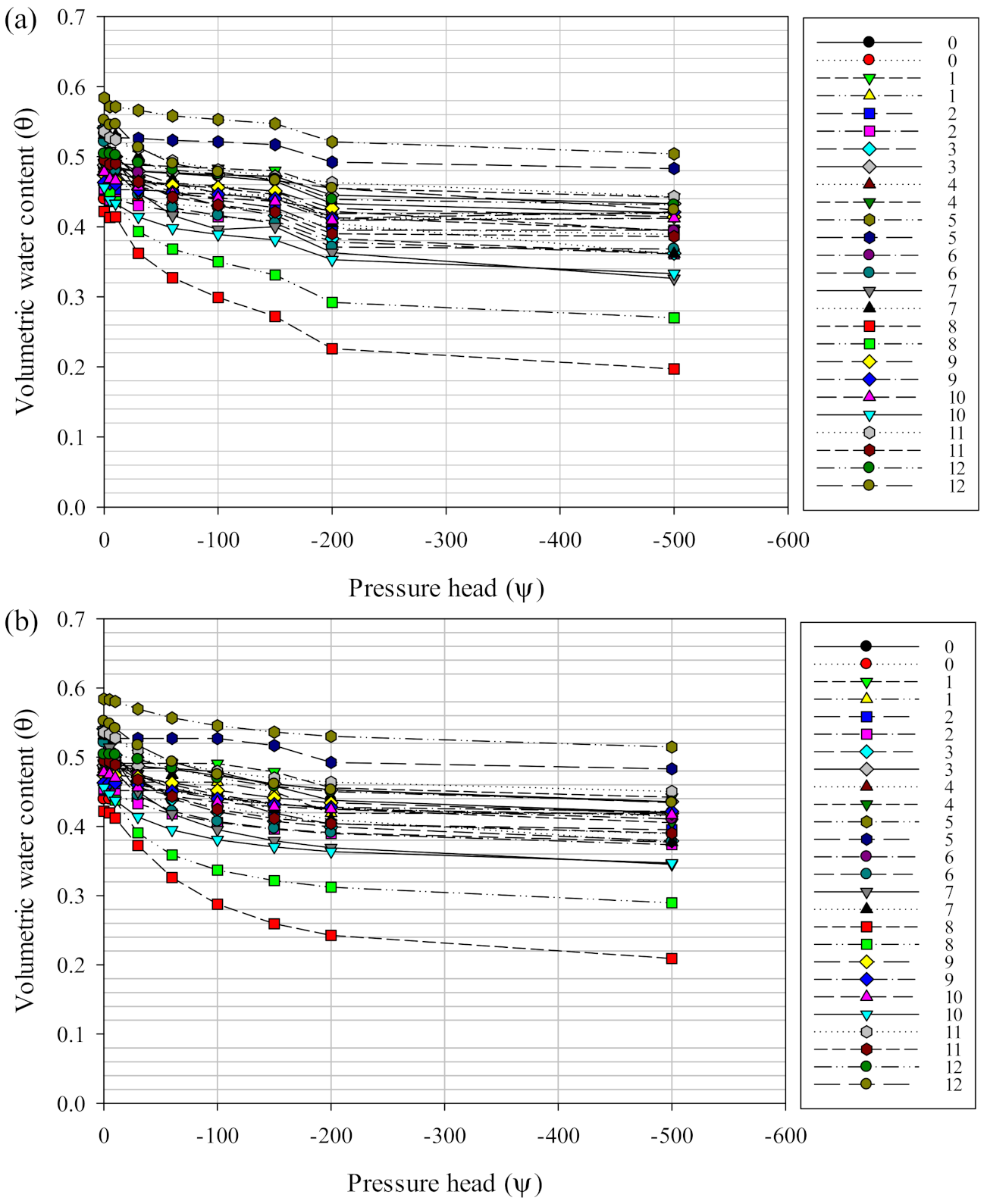
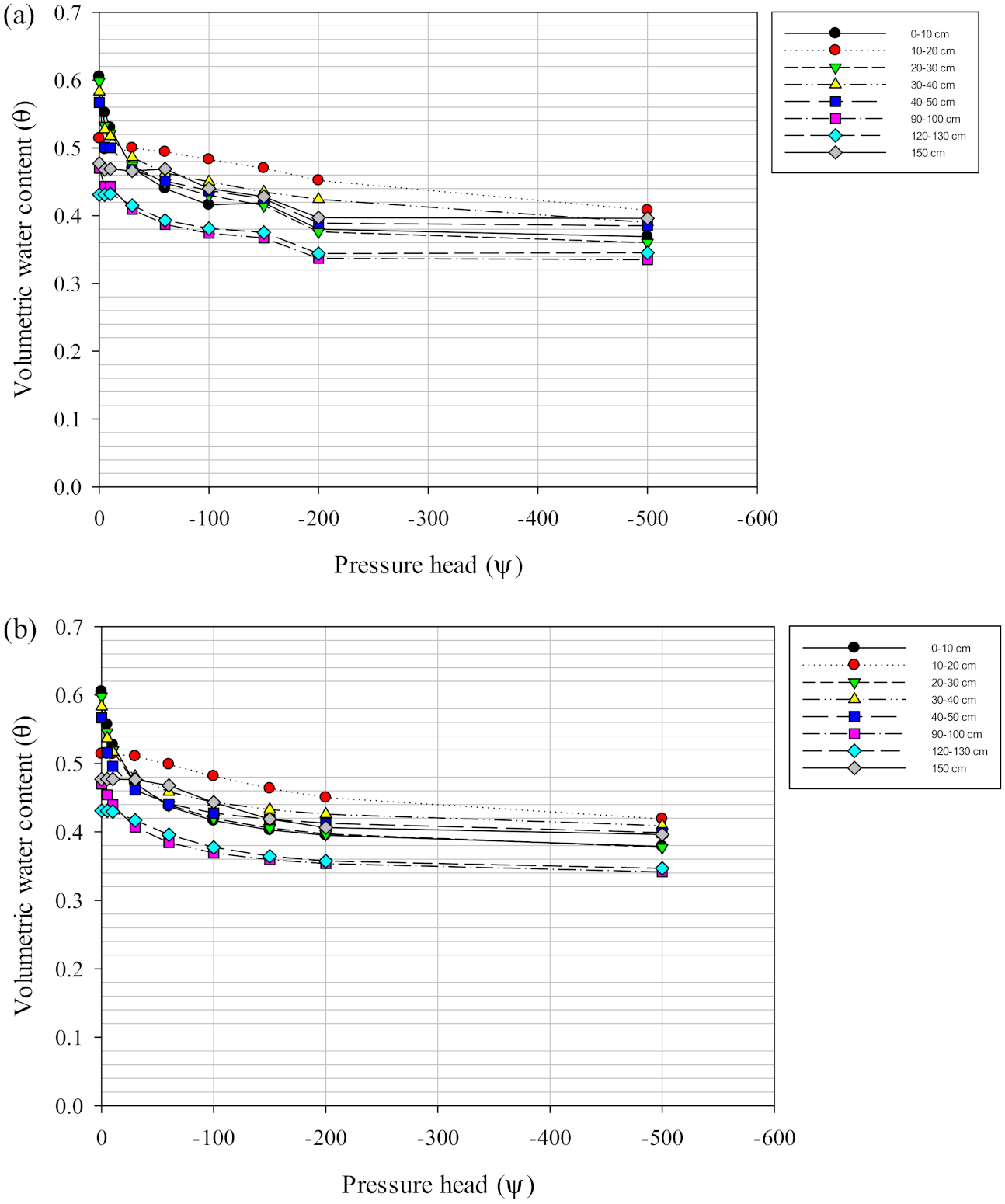
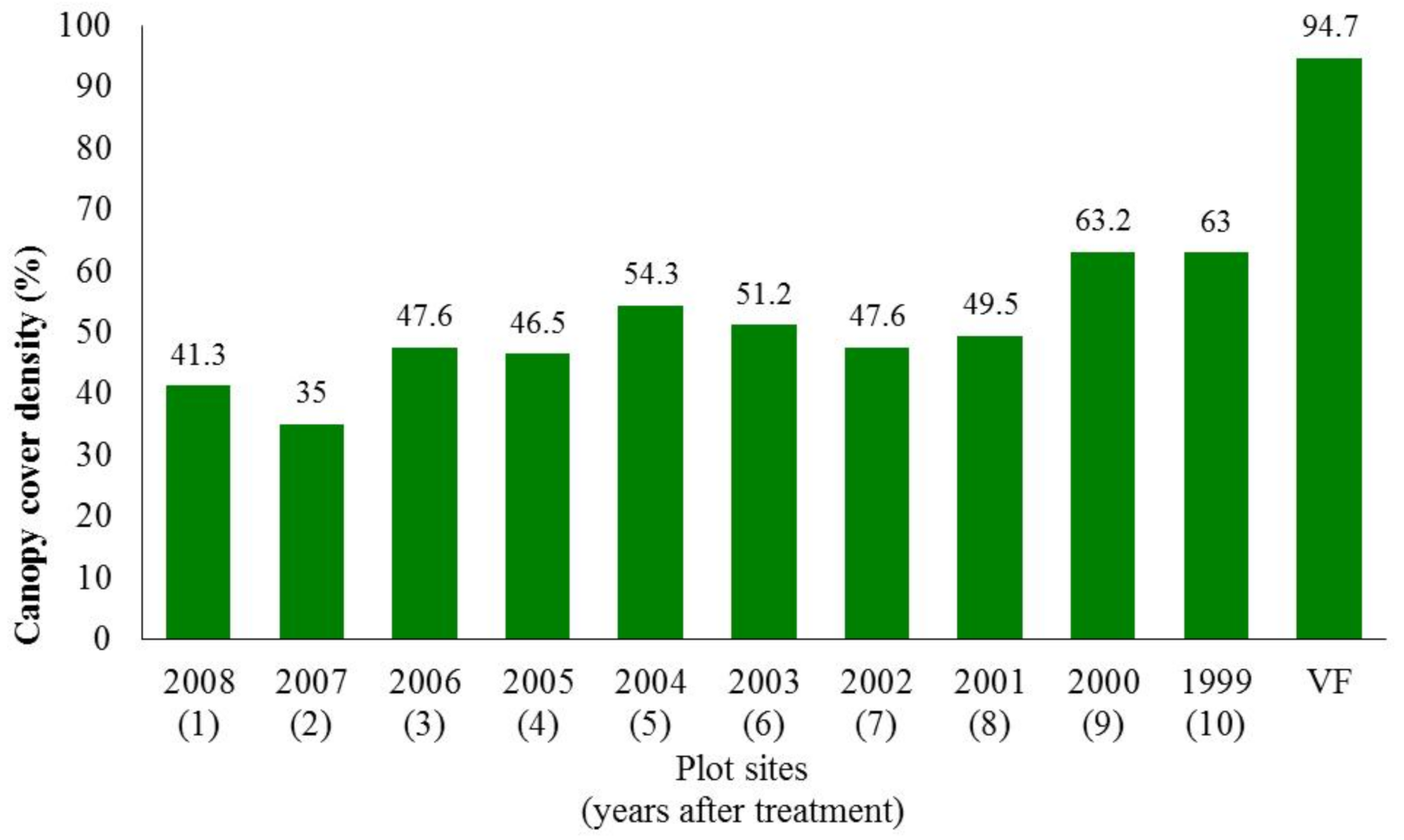
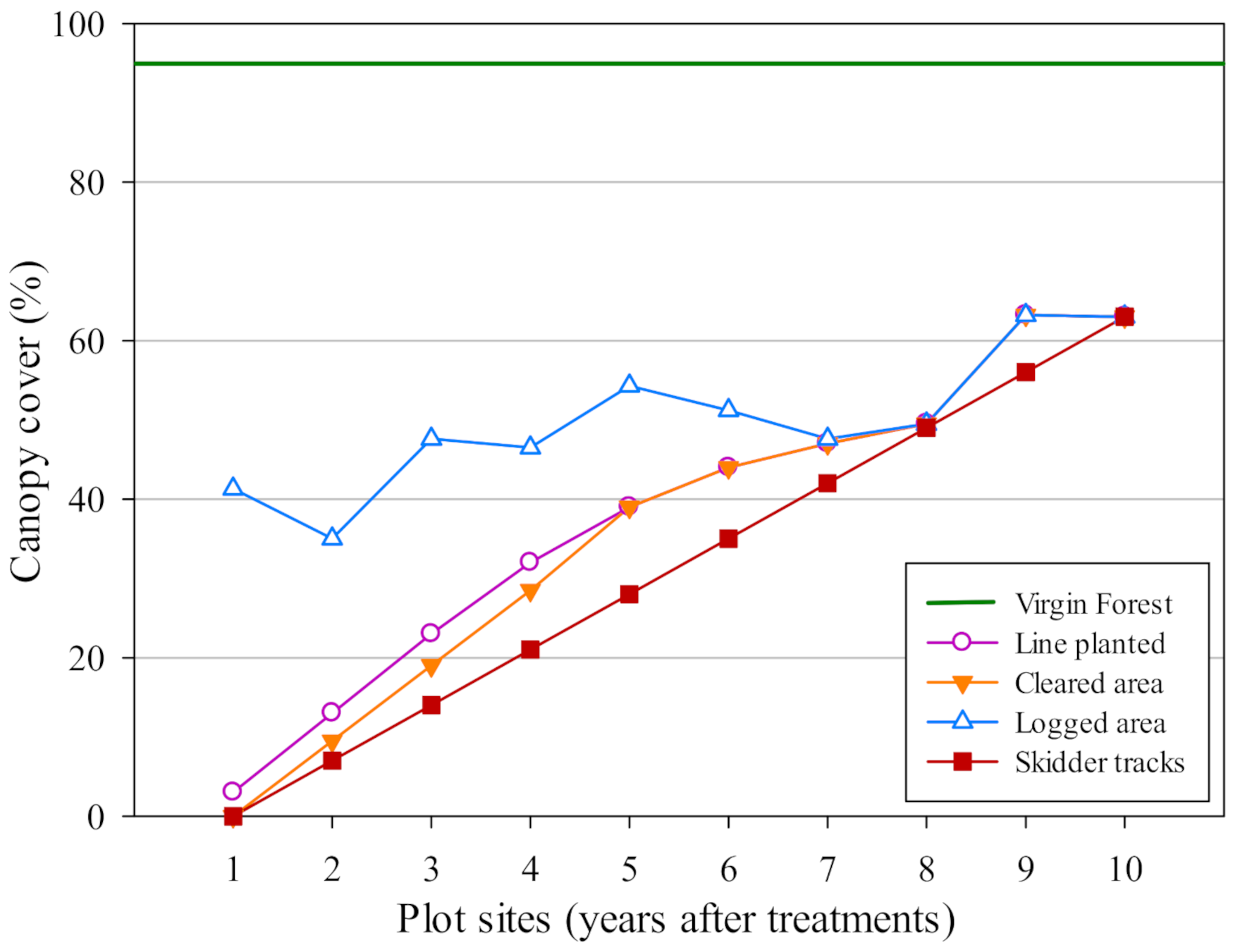
3.1. Soil Hydraulic Conductivity
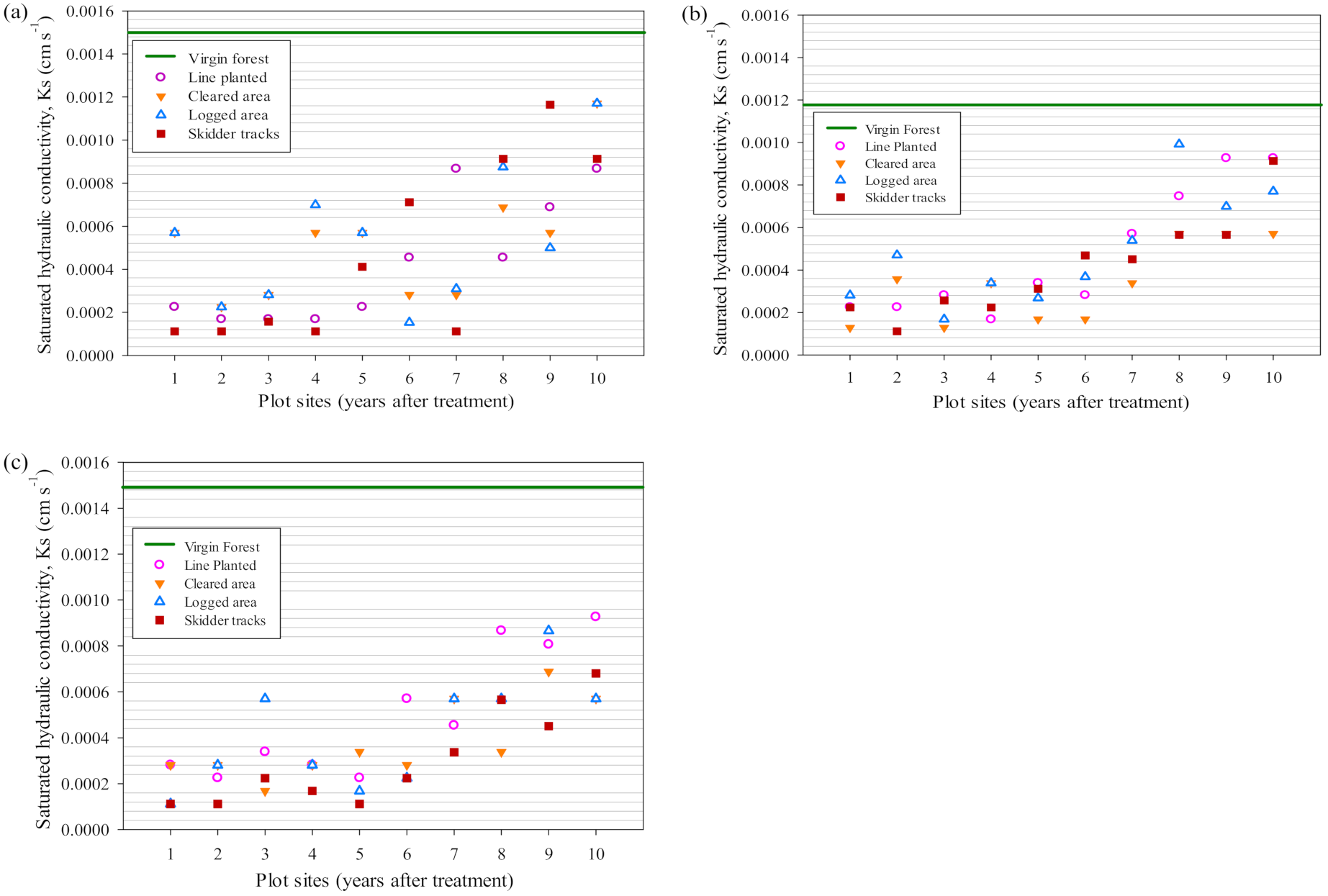
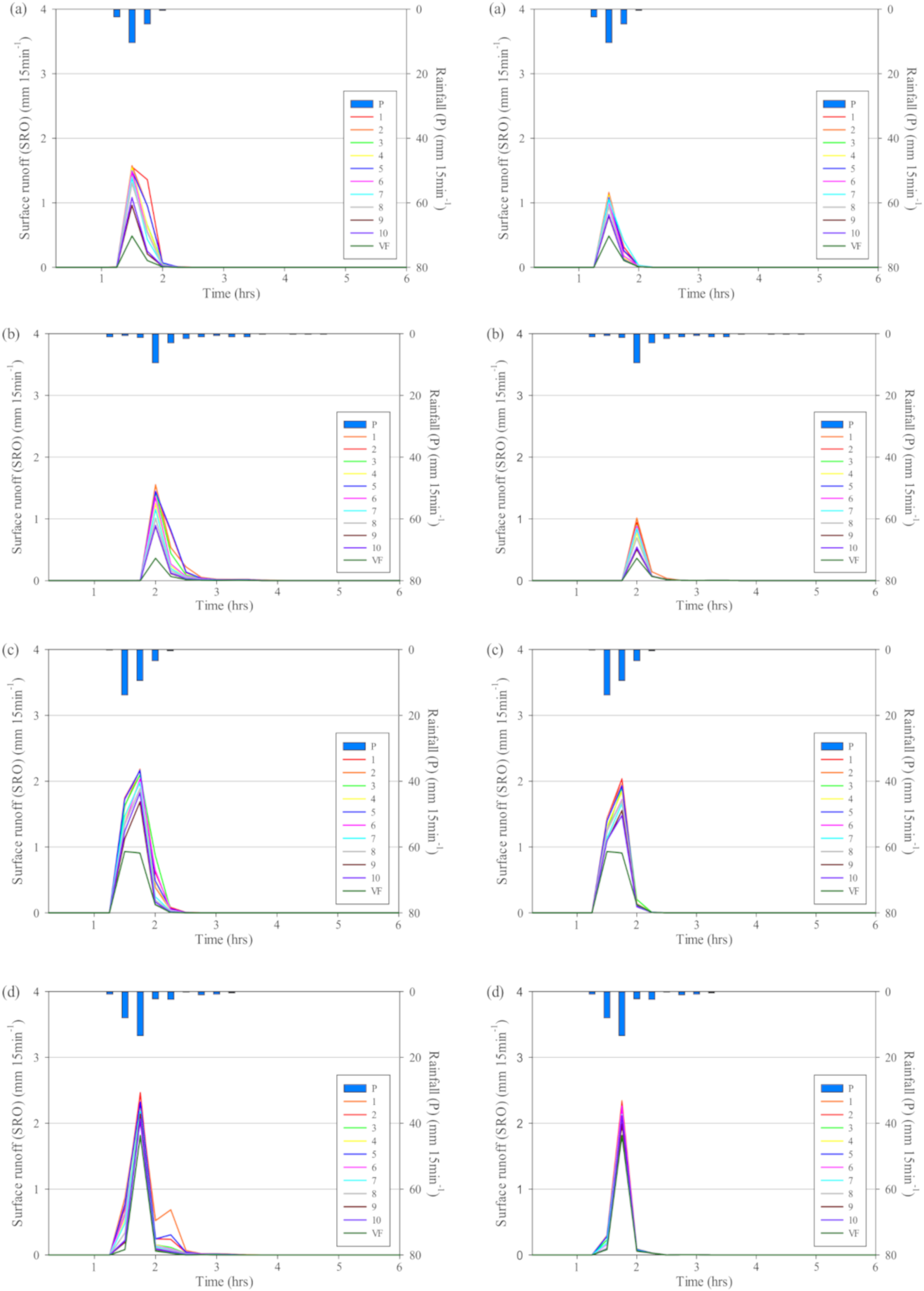
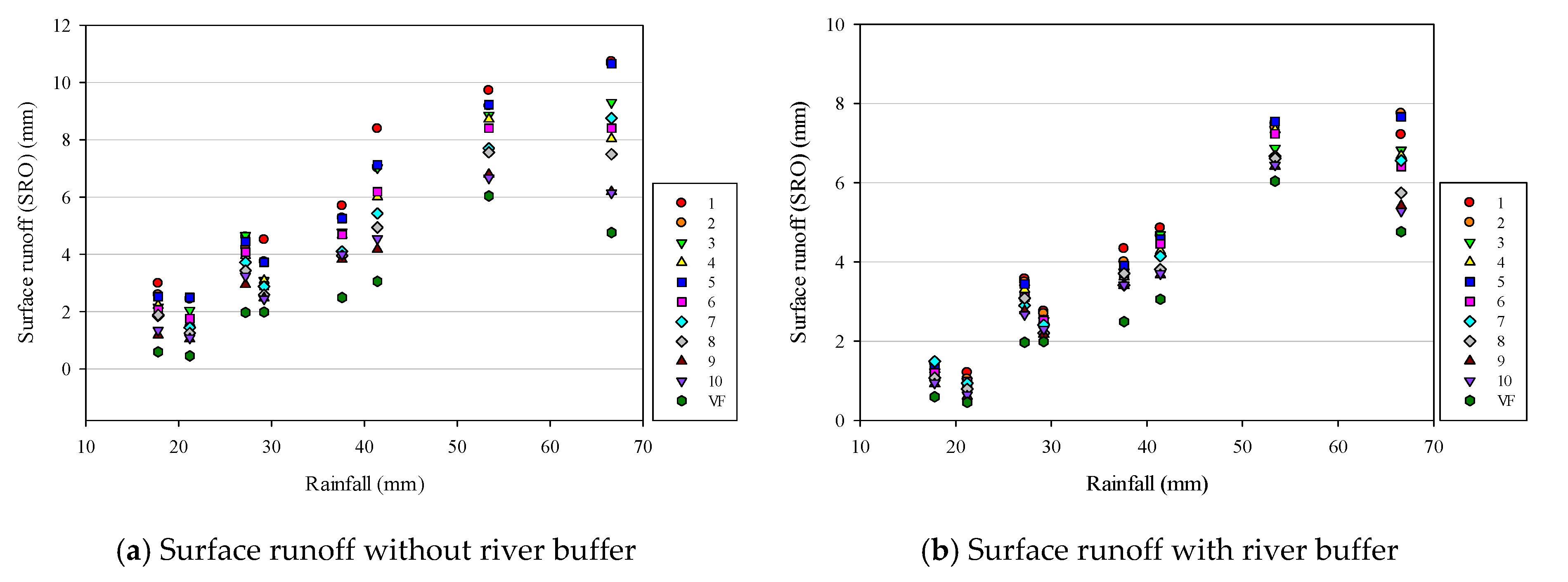
3.2. Saturated Hydraulic Conductivity to Generate Surface Runoff
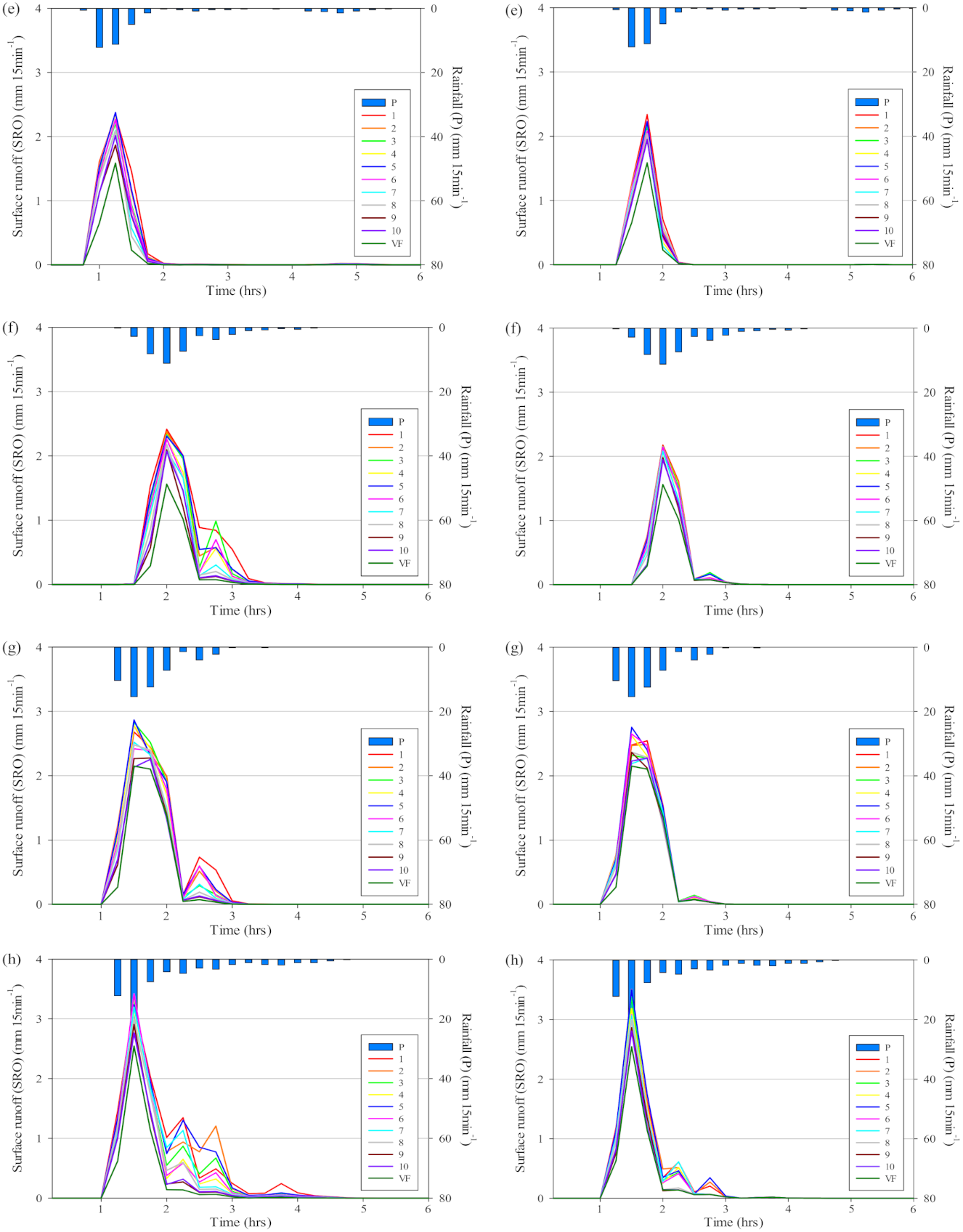
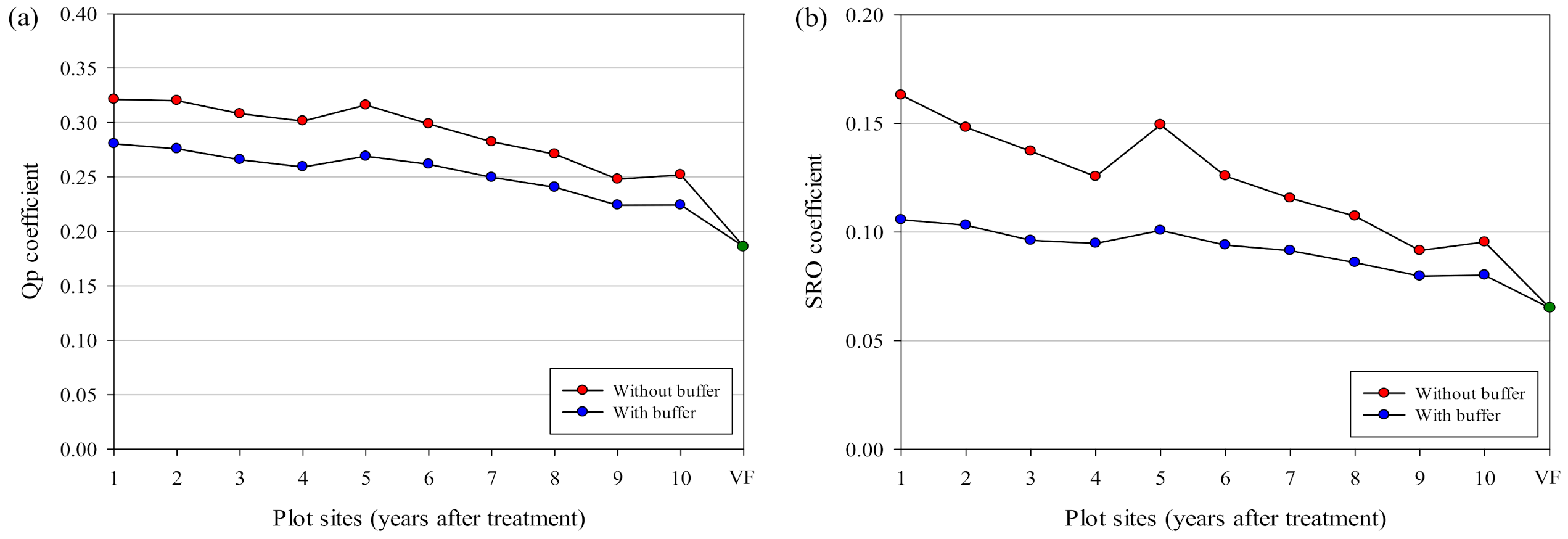
3.3. Effectiveness of a River Buffer on Surface Runoff Flow
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bruijnzeel, L.A. Hydrology of moist tropical forest and effects of conversion: A state knowledge review. In Hydrology of Moist Tropical Forests and Effects of Conversion: A State of Knowledge Review; UNESCO: Paris, France; Vrije Universiteit: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Beshta, R.L.; Pyles, M.R.; Skaugset, A.E.; Surfleet, C.G. Peakflow responses to forest practices in the western cascades of Oregon, USA. J. Hydrol. 2000, 233, 102–120. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Hydrological functions of tropical forests: Not seeing the soil for the tree? Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar] [CrossRef]
- Ziegler, A.D.; Negishi, J.N.; Sidle, R.C.; Noguchi, S.; Abdul Rahim, N. Impact of logging disturbance on hillslope saturated hydraulic conductivity in a tropical forest in Peninsular Malaysia. Catena 2006, 67, 89–104. [Google Scholar] [CrossRef]
- Suryatmojo, H.; Fujimoto, M.; Yamakawa, Y.; Kosugi, K.; Mizuyama, T. Runoff and soil erosion characteristics in different periods of an intensive forest management system in a tropical Indonesian rainforest. Int. J. Sustain. Dev. Plan. 2014, 9, 830–846. [Google Scholar] [CrossRef]
- Van Der Plas, M.C.; Bruijnzeel, L.A. Impact of Mechanized Selective Logging of Rainforest on Topsoil Infiltrability in the Upper Segama Area, Sabah, Malaysia. Hydrol. Warm Humid Regions IAHS Publ. 1993, 216, 203–211. [Google Scholar]
- Malmer, A. Hydrological effects and nutrient losses of forest plantation establishment on tropical rainforest land in Sabah, Malaysia. J. Hydrol. 1996, 174, 129–148. [Google Scholar] [CrossRef]
- Noguchi, S.; Abdul Rahim, N.; Yusop, Z.; Tani, M.; Toshiaki, S. Rainfall-runoff responses and roles of soil moisture variations to the response in Tropical Rain Forst, Bukit Tarek, Peninsular Malaysia. J. For. Res. 1997, 2, 125–132. [Google Scholar] [CrossRef]
- Williamson, J.R.; Neilsen, W.A. The influence of forest site on rate and extent of soil compaction and profile disturbance of skid trails during ground-based harvesting. Can. J. For. Res. 2000, 30, 1196–1205. [Google Scholar] [CrossRef]
- Ziegler, A.D.; Giambelluca, T.W.; Tran, L.T.; Vana, T.T.; Nullet, M.A.; Fox, J.; Pinthong, J.; Maxwell, J.F.; Evett, S. Hydrological consequences of landscape fragmentation in mountainous northern Vietnam: Evidence of accelerated surface runoff flow generation. J. Hydrol. 2004, 287, 124–146. [Google Scholar] [CrossRef]
- Zimmermann, B.; Elsenbeer, H.; De Moraes, J.M. The influence of land-use changes on soil hydraulic properties: Implications for runoff generation. For. Ecol. Manag. 2005, 222, 29–38. [Google Scholar] [CrossRef]
- Kosugi, K.I.; Uchida, T.; Matsuda, S.; Mizuyama, T. Spatial variability of soil hydraulic properties in forested hillslope. J. For. Res. 1999, 4, 107–114. [Google Scholar]
- Ziegler, A.D.; Giambelluca, T.W.; Plondke, D.; Leisz, S.; Tran, L.T.; Fox, J.; Nullet, M.A.; Vogler, J.B.; Troung, D.M.; Vien, T.D. Hydrological consequences of landscape fragmentation in mountainous nortern Vietnam: Buffering of Hortonian surface runoff flow. J. Hydrol. 2007, 337, 52–67. [Google Scholar] [CrossRef]
- Osuji, G.E.; Okon, M.A.; Chukwuma, M.C.; Nwarie, I.I. Infiltration Characteristics of Soils under Selected Land Use Practices in Owerri, Southeastern Nigeria. World J. Agric. Sci. 2010, 6, 322–326. [Google Scholar]
- Hassler, S.K.; Zimmermann, B.; Breugel, M.; Hall, J.S.; Elsenbeer, H. Recovery of saturated hydraulic conductivity under secondary succession on former pasture in the humid tropics. For. Ecol. Manag. 2011, 261, 1634–1642. [Google Scholar] [CrossRef]
- Zimmermann, A.; Schinn, D.S.; Francke, T.; Elsenbeer, H.; Zimmermann, B. Uncovering patterns of near surface saturated hydraulic conductivity in an overland flow-controlled landscape. Geoderma 2013, 195–196, 1–11. [Google Scholar] [CrossRef]
- Liang, W.-L.; Kosugi, K.; Mizuyama, T. Heterogeneous soil water dynamics around a tree growing on a steep hillslope. Vadose Zone J. 2007, 6, 879–889. [Google Scholar] [CrossRef]
- Nussbaum, R.; Hoe, A.L. Rehabilitation of Degraded Sites in Logged-Over Forest Using Dipterocarps. In Dipterocarps Forest Ecosystem. Towards Sustainable Management; Schulte, A., Schone, D., Eds.; World Publishing: Singapore, 1996; pp. 446–463. [Google Scholar]
- Nussbaum, R.; Anderson, J.; Spencer, T. Planting Dipterocarps for Rehabilitation of Log Landings and Skid Trails in Sabah, Malaysia. In Proceedings of the Fifth Round-Table Conference on Dipterocarps, Chiang Mai, Thailand, 7–10 November 1994; Appanah, S., Khoo, K.C., Eds.; Forest Research Institute Malaysia: Kuala Lumpur, Malaysia, 1994; pp. 299–315. [Google Scholar]
- Adam, K.L.; Bruijnzeel, L.A. Managing Tropical Forest Watersheds for Production: Where contra-dictionary theory and practice co-exist. In Wise Management of Tropical Forests; Oxford Forestry Institute: Oxford, UK, 1992; pp. 37–75. [Google Scholar]
- Bruijnzeel, L.A.; Chritchley, W.R. Environmental impacts of logging moist tropical forests. In International Hydrology Programme, Series 7; UNESCO: Paris, France, 1994. [Google Scholar]
- Ziegler, A.D.; Giambelluca, T.W. Importance of rural roads as source areas for runoff in mountainous areas of northern Thailand. J. Hydrol. 1997, 196, 204–229. [Google Scholar] [CrossRef]
- Wemple, B.C.; Swanson, F.J.; Jones, J.A. Forest roads and geomorphic process interactions, Cascade Range, Oregon. Earth Surf. Proc. Landf. 2001, 26, 191–204. [Google Scholar] [CrossRef]
- Chappell, N.A.; Douglas, I.; Hanapi, J.M.; Tych, W. Sources of suspended sediment within tropical catchment recovering from selective logging. Hydrol. Process. 2004, 18, 685–701. [Google Scholar] [CrossRef]
- Gholzom, E.H.; Gholami, V. A Comparison between Natural Forests and Reforested Lands in Terms of Runoff Generation Potential and Hydrologic Response (Case Study: Kasilian Watershed). Soil Water Res. 2012, 4, 166–173. [Google Scholar] [CrossRef]
- Schnorbus, M.; Alila, Y. Peak flow regime changes following forest harvesting in a snow-dominated basin: Effects of harvest area, elevation, and channel connectivity. Water Resour. Res. 2013, 49, 517–535. [Google Scholar] [CrossRef]
- Chandler, K.R.; Stevens, C.J.; Binley, A.; Keith, A.M. Influence of tree species and forest land use on soil hydraulic conductivity and implications for surface runoff generation. Geoderma 2018, 310, 120–127. [Google Scholar] [CrossRef]
- Hao, M.; Zhang, J.; Meng, M.; Chen, H.Y.; Guo, X.; Liu, S.; Ye, L. Impacts of changes in vegetation on saturated hydraulic con- ductivity of soil in subtropical forests. Sci. Rep. 2019, 9, 1–9. [Google Scholar]
- Zhao, M.; Boll, J.; Brooks, E.S. Evaluating the effects of timber harvest on hydrologically sensitive areas and hydrologic response. J. Hydrol. 2020, 593, 125805. [Google Scholar] [CrossRef]
- Fashi, F.H.; Gorji, M.; Shorafa, M. Estimation of soil hydraulic parameters for different land-uses. Model. Earth Syst. Environ. 2016, 2, 1–7. [Google Scholar] [CrossRef][Green Version]
- Suryatmojo, H.; Fujimoto, M.; Yamakawa, Y.; Kosugi, K.; Mizuyama, T. Water balance changes in the tropical rainforest with intensive forest management system. Int. J. Sustain. Future Hum. Secur. J.-SustaiN 2013, 1, 56–62. [Google Scholar] [CrossRef]
- Schmidt, F.H.; Ferguson, J.H.A. Rainfall types based on wet and dry period ratios for Indonesia with Western New Guinea. 1951. Available online: https://agris.fao.org/agris-search/search.do?recordID=US201300720509 (accessed on 21 November 2020).
- Tan, K.H. Soils in the Humid Tropics and Monsoon Region of Indonesia; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2008; pp. 77–90. [Google Scholar]
- Suryatmojo, H. Recovery of Forest Soil Disturbance in the Intensive Forest Management System. Procedia Environ. Sci. 2014, 20, 832–840. [Google Scholar] [CrossRef]
- Fodor, N.; Sandor, R.; Orfanus, T.; Lichner, L.; Rajkai, K. Evaluation method dependency of measured saturated hydraulic conductivity. Geoderma 2011, 165, 60–68. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Bowman, B.T.; Brunke, R.R.; Drudy, C.F.; Tan, C.S. Comparison of Tensio Infiltrometer, Pressure Infiltrometer, and Soil Core Estimates of Saturated Hydraulic Conductivity. J. Soil Sci. Soc. 2000, 64, 478–484. [Google Scholar] [CrossRef]
- Elsenbeer, H. Hydrologic flowpaths in tropical rainforest soilscapes: A review. Hydrol. Proces. 2001, 15, 1751–1759. [Google Scholar] [CrossRef]
- Jury, W.A.; Gardner, W.R.; Gardner, W.H. Soil Physics, 5th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991; pp. 77–87. [Google Scholar]
- Kluten, A.; Dirksen, C. Hydraulic conductivity and diffusivity: Laboratory methods. In Methods of Soil Analysis, Part. 1: Physical and Meneralogical Methods, Monograph No. 9; Klute, A., Ed.; American Society of Agronomy: Madison, WI, USA, 1986. [Google Scholar]
- Kosugi, K. Lognormal distribution model for unsaturated soil hydraulic properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar] [CrossRef]
- Kosugi, K. A new model to analyse water retention characteristics of forest soils based on soil pore radius distribution. J. For. Res. 1997, 2, 1–8. [Google Scholar] [CrossRef]
- Kosugi, K. New diagrams to evaluate soil pore radius distribution and saturated hydraulic conductivity of forest soil. J. For. Res. 1997, 2, 95–101. [Google Scholar] [CrossRef]
- Kosugi, K. Effect of pore radius distribution of forest soils on vertical water movement in soil profile. J. Jpn. Soc. Hydrol. Water Resour. 1997, 10, 226–237. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Kosugi, K.; Mori, K.; Yasuda, H. An inverse modelling approach for characterization of unsaturated water flow in an organic forest floor. J. Hydrol. 2001, 246, 96–108. [Google Scholar] [CrossRef]
- Suryatmojo, H.; Fujimoto, M.; Kosugi, K.; Mizuyama, T. Effects of Selective Logging Methods on Runoff Characteristics in Paired Small Headwater Catchment. Procedia Environ. Sci. 2013, 17, 221–229. [Google Scholar] [CrossRef][Green Version]
| Test Sites | Periods | Ks | Ψm | log (–Ψm) | θr | σ | θe |
|---|---|---|---|---|---|---|---|
| Line Planted | 1999 | 0.0009 | −41.0198 | 1.6130 | 0.3254 | 1.8264 | 0.1743 |
| 2000 | 0.0008 | −41.9226 | 1.6224 | 0.3275 | 1.8044 | 0.1722 | |
| 2001 | 0.0007 | −43.3268 | 1.6368 | 0.3308 | 1.7711 | 0.1689 | |
| 2002 | 0.0006 | −44.0213 | 1.6437 | 0.3324 | 1.7551 | 0.1673 | |
| 2003 | 0.0004 | −47.0335 | 1.6724 | 0.3389 | 1.6882 | 0.1608 | |
| 2004 | 0.0003 | −51.2237 | 1.7095 | 0.3474 | 1.6020 | 0.1523 | |
| 2005 | 0.0002 | −53.5833 | 1.7290 | 0.3519 | 1.5565 | 0.1479 | |
| 2006 | 0.0003 | −51.4185 | 1.7111 | 0.3478 | 1.5982 | 0.1519 | |
| 2007 | 0.0002 | −53.3802 | 1.7274 | 0.3515 | 1.5603 | 0.1482 | |
| 2008 | 0.0002 | −51.7840 | 1.7142 | 0.3485 | 1.5910 | 0.1512 | |
| Cleared Area | 1999 | 0.0007 | −42.6708 | 1.6301 | 0.3293 | 1.7865 | 0.1704 |
| 2000 | 0.0006 | −44.0285 | 1.6437 | 0.3324 | 1.7549 | 0.1673 | |
| 2001 | 0.0005 | −45.3997 | 1.6571 | 0.3354 | 1.7239 | 0.1643 | |
| 2002 | 0.0004 | −47.8510 | 1.6799 | 0.3406 | 1.6708 | 0.1591 | |
| 2003 | 0.0002 | −51.9810 | 1.7158 | 0.3488 | 1.5872 | 0.1509 | |
| 2004 | 0.0003 | −49.3260 | 1.6931 | 0.3437 | 1.6401 | 0.1561 | |
| 2005 | 0.0004 | −47.8510 | 1.6799 | 0.3406 | 1.6708 | 0.1591 | |
| 2006 | 0.0002 | −53.5833 | 1.7290 | 0.3519 | 1.5565 | 0.1479 | |
| 2007 | 0.0003 | −49.0211 | 1.6904 | 0.3430 | 1.6464 | 0.1567 | |
| 2008 | 0.0004 | −48.3744 | 1.6846 | 0.3417 | 1.6598 | 0.1580 | |
| Logged Area | 1999 | 0.0007 | −43.4338 | 1.6378 | 0.3311 | 1.7686 | 0.1687 |
| 2000 | 0.0007 | −42.7485 | 1.6309 | 0.3295 | 1.7847 | 0.1702 | |
| 2001 | 0.0005 | −45.1193 | 1.6544 | 0.3348 | 1.7302 | 0.1649 | |
| 2002 | 0.0005 | −45.9036 | 1.6618 | 0.3365 | 1.7128 | 0.1632 | |
| 2003 | 0.0004 | −47.6623 | 1.6782 | 0.3403 | 1.6748 | 0.1595 | |
| 2004 | 0.0003 | −50.5322 | 1.7036 | 0.3460 | 1.6157 | 0.1537 | |
| 2005 | 0.0004 | −47.0335 | 1.6724 | 0.3389 | 1.6882 | 0.1608 | |
| 2006 | 0.0003 | −48.8732 | 1.6891 | 0.3427 | 1.6494 | 0.1570 | |
| 2007 | 0.0003 | −49.8810 | 1.6979 | 0.3448 | 1.6288 | 0.1549 | |
| 2008 | 0.0002 | −52.6517 | 1.7214 | 0.3501 | 1.5742 | 0.1496 | |
| Skidder Tracks | 1999 | 0.0008 | −41.6762 | 1.6199 | 0.3270 | 1.8104 | 0.1727 |
| 2000 | 0.0007 | −43.3331 | 1.6368 | 0.3308 | 1.7710 | 0.1689 | |
| 2001 | 0.0007 | −43.3423 | 1.6369 | 0.3308 | 1.7708 | 0.1689 | |
| 2002 | 0.0003 | −51.2491 | 1.7097 | 0.3474 | 1.6015 | 0.1523 | |
| 2003 | 0.0003 | −51.2387 | 1.7096 | 0.3474 | 1.6017 | 0.1523 | |
| 2004 | 0.0001 | −59.3777 | 1.7736 | 0.3620 | 1.4528 | 0.1377 | |
| 2005 | 0.0003 | −51.2387 | 1.7096 | 0.3474 | 1.6017 | 0.1523 | |
| 2006 | 0.0004 | −47.0833 | 1.6729 | 0.3390 | 1.6871 | 0.1607 | |
| 2007 | 0.0001 | −59.3777 | 1.7736 | 0.3620 | 1.4528 | 0.1377 | |
| 2008 | 0.0001 | −56.9932 | 1.7558 | 0.3580 | 1.4942 | 0.1417 | |
| Virgin Forest | top soil | 0.0012 | −39.2047 | 1.5933 | 0.3209 | 1.8721 | 0.1788 |
| 20–30 cm | 0.0006 | −44.0910 | 1.6443 | 0.3325 | 1.7535 | 0.1672 | |
| 30–40 cm | 0.0005 | −44.9986 | 1.6532 | 0.3346 | 1.7329 | 0.1652 | |
| 40–50 cm | 0.0006 | −44.3201 | 1.6466 | 0.3331 | 1.7482 | 0.1667 | |
| 90–100 cm | 0.0008 | −41.8066 | 1.6212 | 0.3273 | 1.8072 | 0.1724 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suryatmojo, H.; Kosugi, K. River Buffer Effectiveness in Controlling Surface Runoff Based on Saturated Soil Hydraulic Conductivity. Water 2021, 13, 2383. https://doi.org/10.3390/w13172383
Suryatmojo H, Kosugi K. River Buffer Effectiveness in Controlling Surface Runoff Based on Saturated Soil Hydraulic Conductivity. Water. 2021; 13(17):2383. https://doi.org/10.3390/w13172383
Chicago/Turabian StyleSuryatmojo, Hatma, and Ken’ichirou Kosugi. 2021. "River Buffer Effectiveness in Controlling Surface Runoff Based on Saturated Soil Hydraulic Conductivity" Water 13, no. 17: 2383. https://doi.org/10.3390/w13172383
APA StyleSuryatmojo, H., & Kosugi, K. (2021). River Buffer Effectiveness in Controlling Surface Runoff Based on Saturated Soil Hydraulic Conductivity. Water, 13(17), 2383. https://doi.org/10.3390/w13172383





