1. Introduction
Tidal waves are a major hydrodynamic factor that influences the flooding, ecosystems, transport, and morphological evolution in estuaries. In contrast to tidal waves in deep oceans, which are driven by astronomical forces with a high degree of predictability, waves propagating along estuaries tend to adjust their amplitude, celerity, and shape during interactions with topography, friction, and other secondary factors such as wind stress and runoff. A tidal wave in a shallow estuary has the characteristics of amplification and damping, which alternate along the estuary. The tidal amplitude is influenced by two dominant processes: amplification due to convergent cross sections with a decrease in depth in the landward direction and damping due to bottom friction. If the former process dominates over the latter, the wave is amplified; otherwise, the wave is damped. The celerity of propagation is also influenced by the processes of tidal damping and amplification. If the tidal wave is damped, the celerity is decreased. Conversely, if the tidal wave is amplified, the celerity is increased [
1]. Moreover, the tidal wave can be strongly distorted as it propagates into the estuarine system [
2]. Therefore, tidal wave propagation in an estuary is an interesting but difficult issue to solve because of the nonlinear interaction resulting from the complex estuarine boundary lines and variably shallow topography.
To understand the mechanism of tidal wave propagation along an estuary, vast efforts have been made to induce and solve the estuary hydrodynamic model. Generally, these works can be divided into two methods: analytical solutions and numerical simulations. With advances in computational technology, tidal wave propagation can be accurately simulated by numerical models [
2,
3,
4,
5]. Compared with analytical solutions, numerical models are better at providing high-resolution data under various controlling conditions, which can be comparable with the measurements in a real estuary. However, the numerical results should be further investigated and extracted through the analytical solution to obtain a deeper understanding of the effect by multiple controlling factors with the respect of tidal wave propagation. Specifically, to figure out the relationship between hydrodynamics and the geometry of the estuary, we need the analytical solution not only to fit the data but also to extract some important parameters such as velocity number, damping number, celerity number, and their relationships with the geometry parameter of the estuary. Thus, an analytical solution is still an irreplaceable instrument in analyzing the properties of tidal waves propagating in an estuary. Thus far, a range of analytical solutions based on 1D Saint–Venant equations have been derived by Hunt [
6](1964), Ippen [
7], and Prandle [
8], which are all for a prismatic estuary and river. Meanwhile, the solutions for a more widely convergent estuary have been presented by Godin [
9], Jay [
10], Lanzoni and Seminara [
11], and VanRijn [
12]. Most of the above investigators linearized the equations by means of the perturbation method in an Eulerian framework. In contrast, Savenije [
13] derived a relatively simple solution in a Lagrangian framework. Furthermore, Savenije [
14] presented a fully explicit solution of the tidal equations by solving the set of four implicit equations derived from the Saint–Venant equations. With the advantage of considering the nonlinear effect of the bottom friction, Savenije’s analytical solution is constantly improved and widely used in analyzing the wave propagation on typical alluvial estuaries [
15,
16].
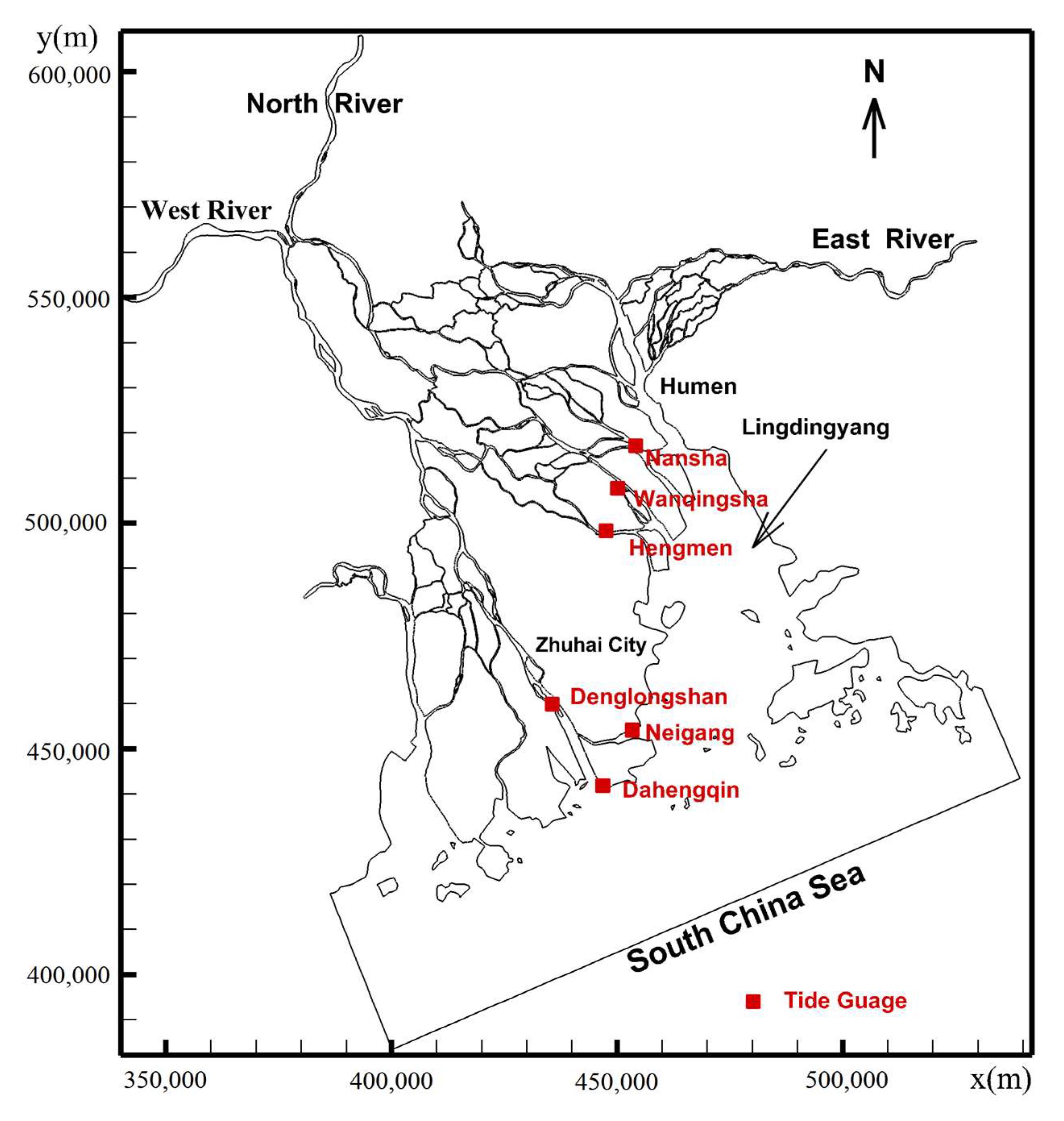
The Humen Estuary, one of the major accesses for a tidal wave from the South China Sea entering the Pearl River network, has a significant effect on flooding and inundation in Guangzhou city, which is the capital and economic center of Guangdong Province. However, limited measured data in the Humen Estuary restrict the understanding of tidal wave propagation along the Humen Estuary in the upstream direction. Although some previous numerical simulations have been performed [
17,
18], their results are not direct and clear enough to reflect the characteristics of how a certain controlling parameter affects other parameters. Another question is whether Savenije’s analytical solution can be applied to the situation under the interaction of tides and surges during typhoon landfall. If not, what are the changes in the hydrodynamic system and which parameters should be adjusted in the analytical solution?
With the questions mentioned above, the objectives of the study are as follows: 1. to compose and validate a method of analysis that combines a classical analytical solution and the numerical results and is able to correctly reflect the characteristics of tide propagation in the Humen Estuary; 2. to check and verify a way to adapt the method of analysis to the context of tidal wave and surge propagation associated with tropical cyclones; and 3. to extract insight into the hydrodynamic features and factors in the Humen Estuary. Thus, we apply Savenije’s analytical solution to the Humen Estuary in conjunction with numerical simulation results to describe and analyze the characteristics of the tidal wave in the Humen Estuary, Pearl River. A series of tests are conducted to answer the above questions in this paper.
The sections are organized as follows. First, some background information about the Humen Estuary in the Pearl River network is introduced in
Section 2, followed by a brief introduction of Savenije’s analytical solution in
Section 3. In
Section 4, the numerical model is verified. In
Section 5, calibration and verification for astronomic tides and storm surges are carried out. In
Section 6, the discussion focuses on the characteristics of tidal waves in the Humen Estuary. Finally, conclusions are drawn in
Section 7.
3. Analytical Solution
The tidal dynamics in an estuary can be described by the following Saint–Venant equations:
where
U is the tidal flow cross-sectional velocity,
is the acceleration due to gravity,
d is the flow depth,
is the bottom slope,
n is the Manning coefficient, and
Q is the tidal flow discharge.
is defined as the ratio between the storage width and the stream width, which is often more than unity in the river with shallow plains [
14] (Savenije, 2008).
After the scaling of Equations (4) and (5) and under the assumption of a harmonic wave traveling from the estuary mouth to the upstream reach, the following dimensionless parameter can be obtained:
where
c0 is the classical wave celerity of a frictionless progressive wave,
is the frequency of the wave,
is the dimensionless tidal amplitude, and
is the dimensionless friction factor defined as
Using the above dimensionless parameters in Equations (6)–(11), the scaling form of Equations (4) and (5) can be solved on the basis of the equations for the phase lag:
where
is the phase difference between high water and high water slack. It is clear that, for a progressive wave,
and that, for a standing wave,
. The above equations should be applied to the following conditions: (1) the ratio between the tidal amplitude and the water depth is less than unity, (2) the runoff is much less than the tidal influx and outflux, and (3) the incident wave can be simplified as a harmonic wave. Equations (12)–(15) can be solved by an iteration process when
and
have been determined.
4. Numerical Model and Verification
The Finite Volume Community Ocean Model (FVCOM), an unstructured-grid finite-volume, three-dimensional primitive equation coastal ocean model developed originally by Chen et al. [
19] and upgraded by the UMASS-D/WHOI model development team [
20,
21], is applied to simulate the tide and surge propagation process in the Pearl River network. As shown in
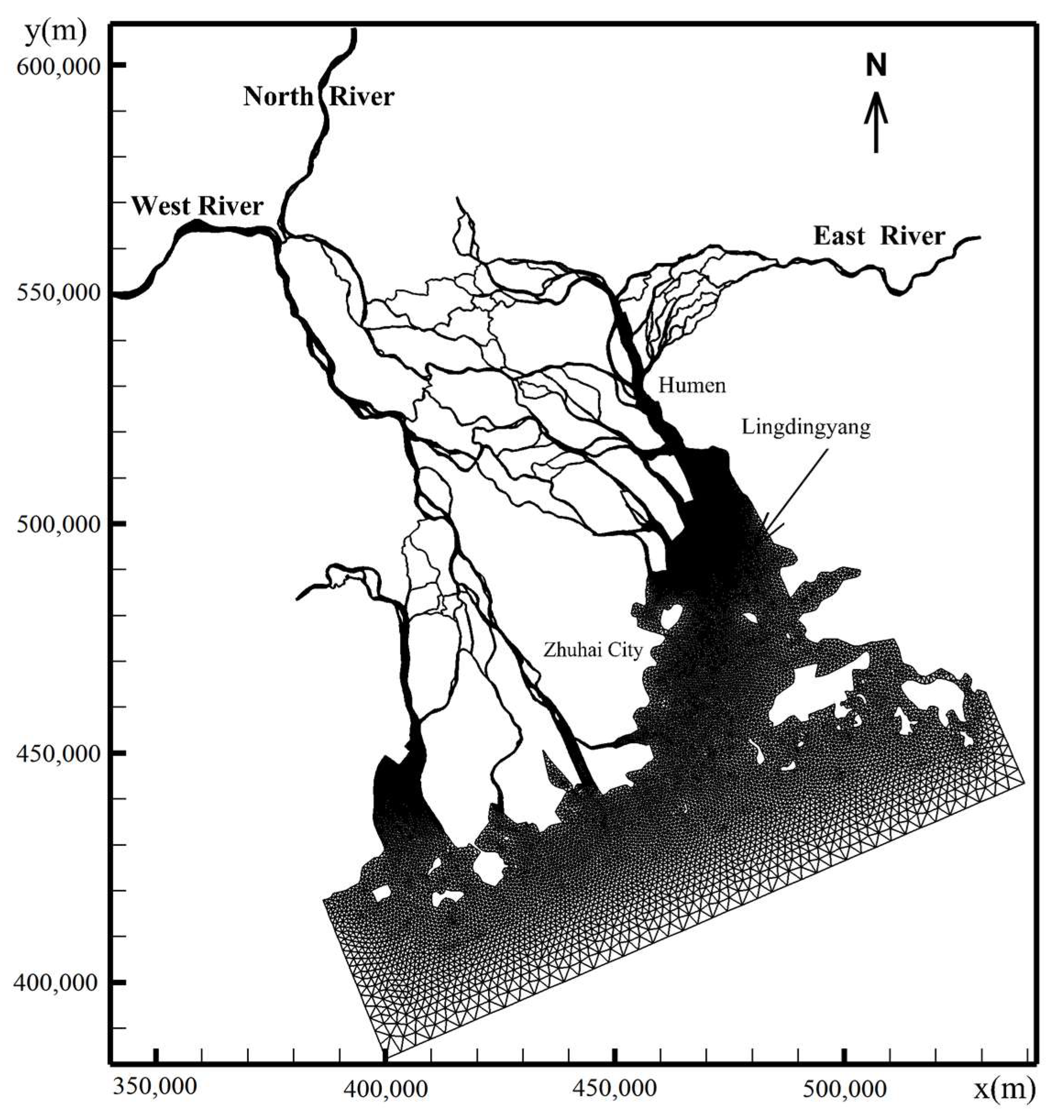
Figure 4, the model domain covers the entire region of the Pearl River network, eight estuaries, and the nearshore. The model contains 58,564 nodes and 91,572 elements. Horizontally, the spatial resolution varies from 40 to 50 m within the river network and from 600 to 1000 m near the estuarine mouth and bay to 5 km at the offshore open boundary. To model the surge under various approaching cyclones in summer days, the Pearl River network model is nested at the open boundary with the South China Sea model, which is also based on the spherical coordinate version of the FVCOM. Vertically, the model contains five uniform sigma layers to capture the process of turbulence momentum transferring upwards from the bottom.
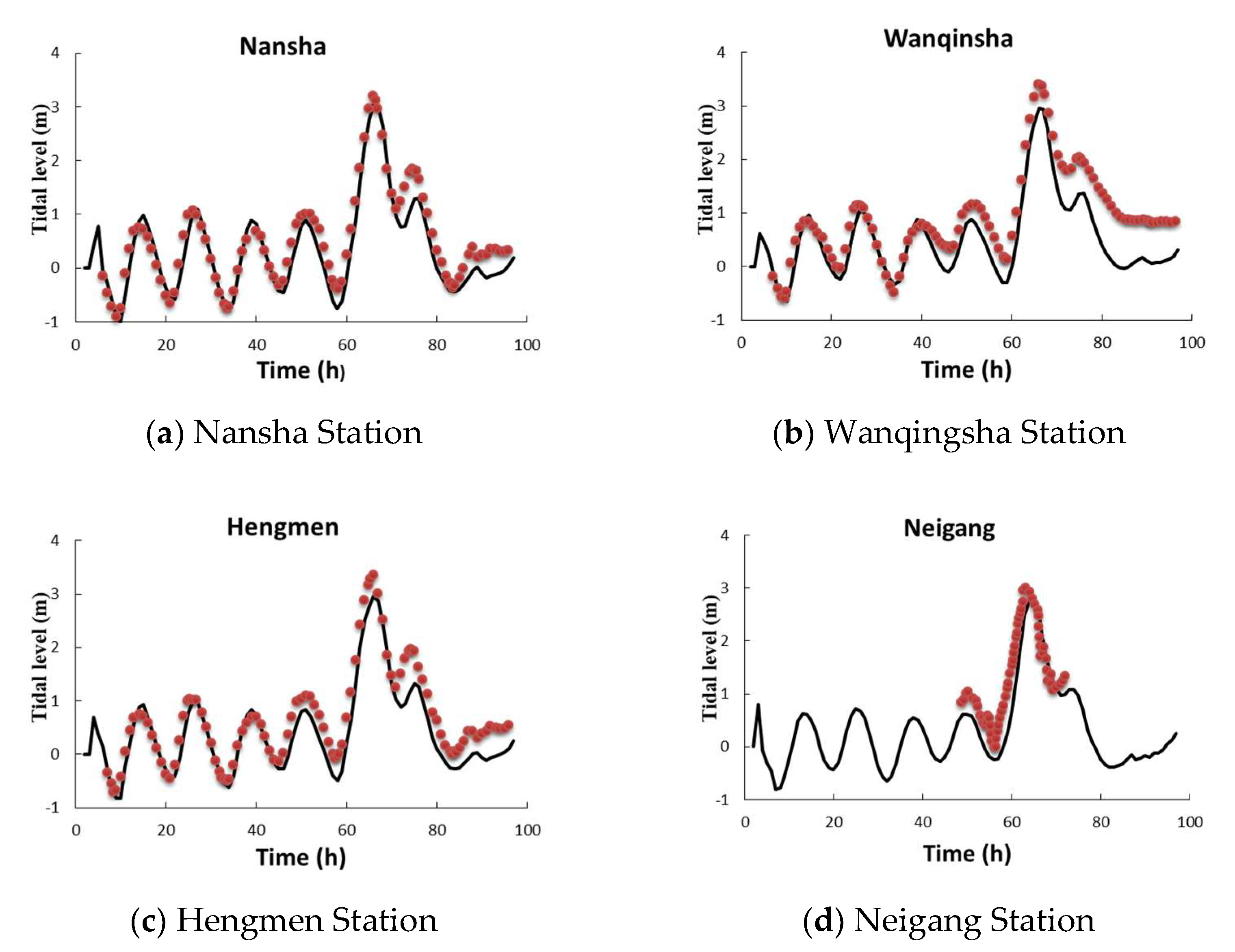
The forces driving the model include tidal waves from the South China Sea and surges caused by meteorological forces such as storms, cyclones, and rainfalls. In this paper, we consider only tropical cyclone. The semi-empirical parametric cyclone model is integrated into the ocean model to drive the surge. The advantage of the parametric cyclone model is that it does not require as much meteorological data as the dynamic model to drive the model. The only data needed contain the track of the cyclone, the center pressure drop, the forward speed, and the maximum wind radius, most of which are available on weather forecast websites except for the maximum wind radius, which should be obtained using a statistical formula and then adjusted according to the surge results. Here, the cyclone No.1822 (
Table 2), well known as the Super Typhoon Mangosteen (2018), is used as an example to simulate the storm surge in conjunction with the astronomical tide. The numerical results are compared with the measurements and demonstrate good agreement in the high surge level between them in
Figure 5.
5. Results
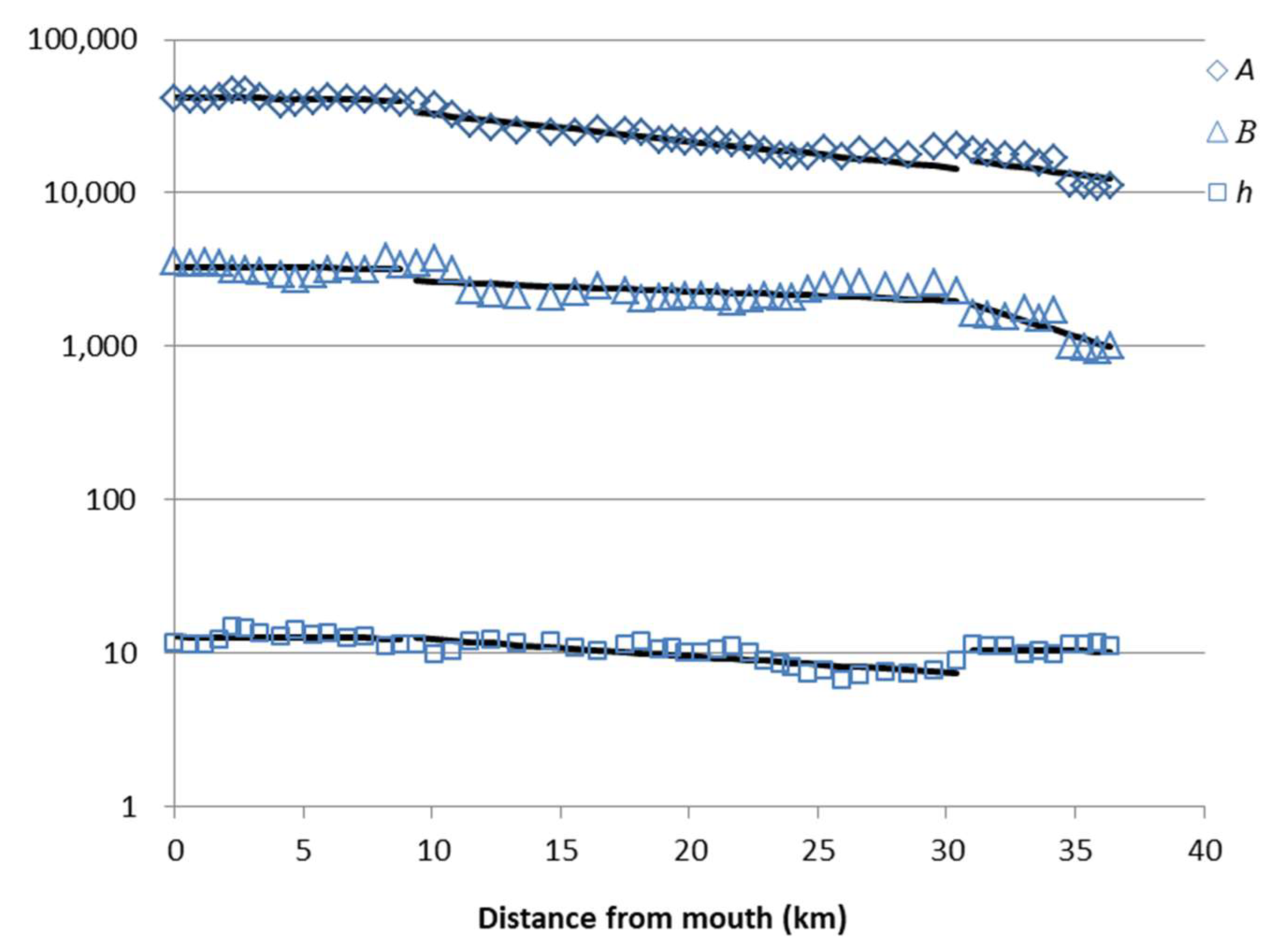
We used the Humen Estuary geometry presented in
Table 1 and the numerical results on 8–9 September 2018 (about one week before the typhoon landfall) to calibrate the analytical model. The calibration process are as follows: we first divided the parameter range into small subareas with an increment of 0.1 for
and 0.001 for
n with their ranges listed in
Table 3. The range of
and
n were referred to Savenije et al. (2005; 2008) [
1,
14]. Then, we used these parameters to obtain the tidal results. Lastly, we compare the analytical solutions with the numerical results and compute the RMSE (root mean square error) for every analytical solution corresponding to the parameters. The one with the least RMSE is considered the best fit solution, and its parameters are the optimal ones. The calibration parameters are presented in
Table 3. In general, the analytical solution fits the numerical result very well (
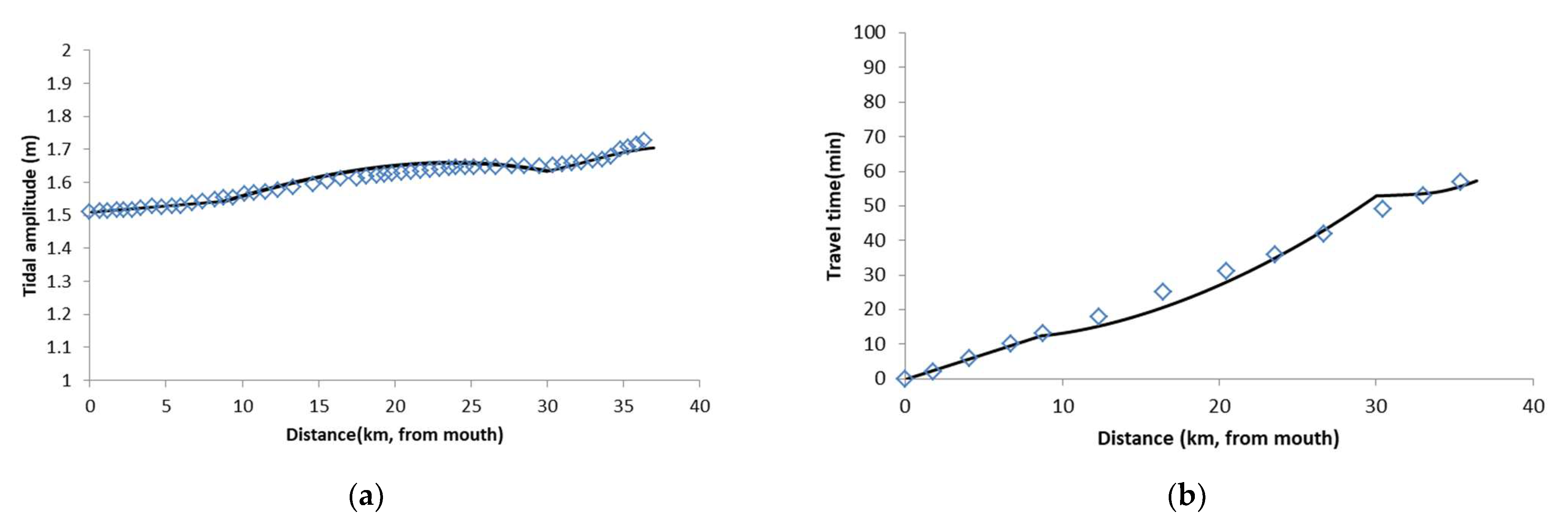
Figure 6), and the calibrated parameters are within the physically proper range. In contrast, in the upstream section, there appears to be more deviation than in the other two sections. The reason is probably that the length of this section is too short to match a more reasonable convergent length.
The model was further verified with the numerical results on 16–17 September 2018. The reason for choosing this period is that Super Typhoon Mangosteen approached and made landfall on the coast of Guangdong Province during this time. Thus, at first, we only simulated the astronomical tide without exerting a wind force in the numerical model. Through this simulation, the analytical result was compared with the numerical result assuming no cyclone landfall. From
Figure 7, it can be seen that the correspondence with the numerical result is good for the tidal amplitude. However, the deviation for the travel time shows that the analytical model tends to overestimate the celerity compared with the numerical model. A similar problem concerning the distinct accuracies between the tidal amplitude and the travel time was also encountered by others using Savenije’s analytical model, who attributed this deviation to the effect of the storage width ratio
at different tidal amplitudes (Cai et al., 2012).
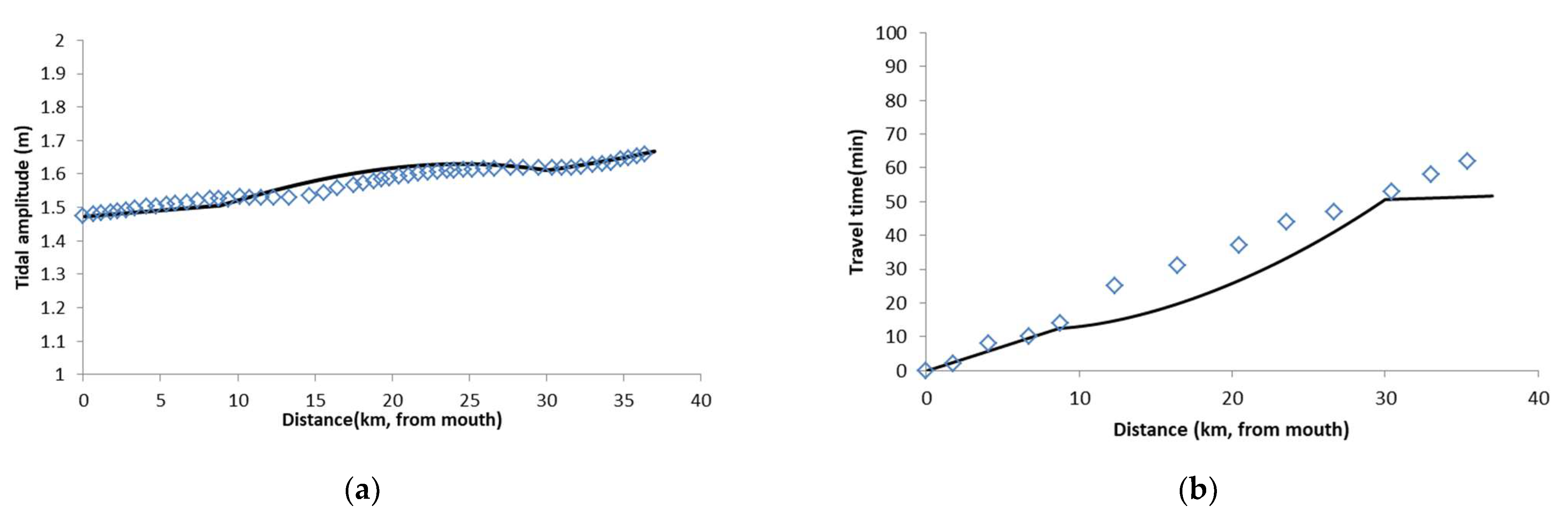
Then, we simulated the typhoon-surge scenario by setting the cyclone model and by exerting the wind and pressure forces on the surface of the tidal flow. The analytical result was compared with the numerical result. It is shown in
Figure 8 that the difference between them can reach a maximum of as much as 0.6 m. This result is unsurprising because the original scope of the analytical model does not include storm surges. With respect to the equation, a wind stress term should be supplemented in the momentum equation as follows:
where
is the wind stress along the x-coordinate direction with a positive direction from the mouth to the upstream.
From Equation (16), we can find that the effect of the positive wind stress term, which caused a maximum surge, is equivalent to a reduction in the Manning coefficient:
where
is considered the reduced version of the original Manning coefficient
n under the cyclone surge scenarios.
Therefore, we can make the analytical solution close to the numerical result by tuning Manning’s coefficient to be less. The analytically calculated tidal amplitudes before and after tuning the coefficient are shown in
Figure 8, and all of the parameters are listed in
Table 3. The Manning coefficient considering the cyclone surge is significantly less than that only considering the astronomical tide. Some are even below the lower limit of the physically reasonable range. This means that the effect of the storm surge on the tidal damping is similar to the reduction in the bottom friction. In other words, the wind that blew in the upstream direction before landfall of the cyclone counteracted part of the friction when the tidal wave traveled upstream along the river. For an application of the solution in a surge scenario and a physically reasonable estimate of the Manning coefficient in the meantime, a new solution based on Savenije’s analytical model, which contains the wind stress term, should be derived in the future.
7. Conclusions
In this study, Savenije’s solution was applied for the first time to the Humen Estuary. Due to the scarcity and low resolution of the measured data, we used the numerical results to calibrate and verify the analytical model. The merit of using an analytical model is that it can provide direct insight into relationships among the tidal properties, such as velocity amplitude, the tidal damping rate, and wave celerity; the geometry indicator; friction; and the tidal forces. This analytical model demonstrated good accuracy when it was applied to an estuary where the tide dominates in comparison with the river discharge. The results indicate that the analytical model can predict the astronomical tide well in the Humen Estuary after calibration. However, it cannot predict the tide well when a tropical cyclone-induced surge is superimposed onto the astronomical tide. The reason may lie in the fact that Savenije’s solution does not take the wind forces into account. After reducing Manning’s coefficient, we found that the analytical result could be close to the numerical results. This means that the loss of the wind forcing can partly be compensated by adjusting the friction.
By analyzing the tidal wave propagation along the Humen Estuary, we found that the characteristics of the three sections—the mouth section (0–8.7 km), the middle section (8.7–30.4 km), and the upstream section (30.4–36 km)—are not alike at all. The mouth section is a typical riverine estuary with a nearly constant cross section. The tidal wave traveling there is in the form of a progressive wave and with a nearly classical celerity in a frictionless state. In contrast, the upstream section is a typical oceanic estuary with a short convergence length. The tidal wave there is in the form of a standing wave with a nearly infinite celerity. The middle section is in the intermediate zone of the two solution families. The tidal wave is first amplified and then damped, with a transition point that is the location of the maximum tidal amplitude. Finally, a comparison was conducted between the Humen Estuary and other estuaries.