Apron and Cutoff Wall Scour Protection for Piano Key Weirs
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. PK Weir Hydraulics
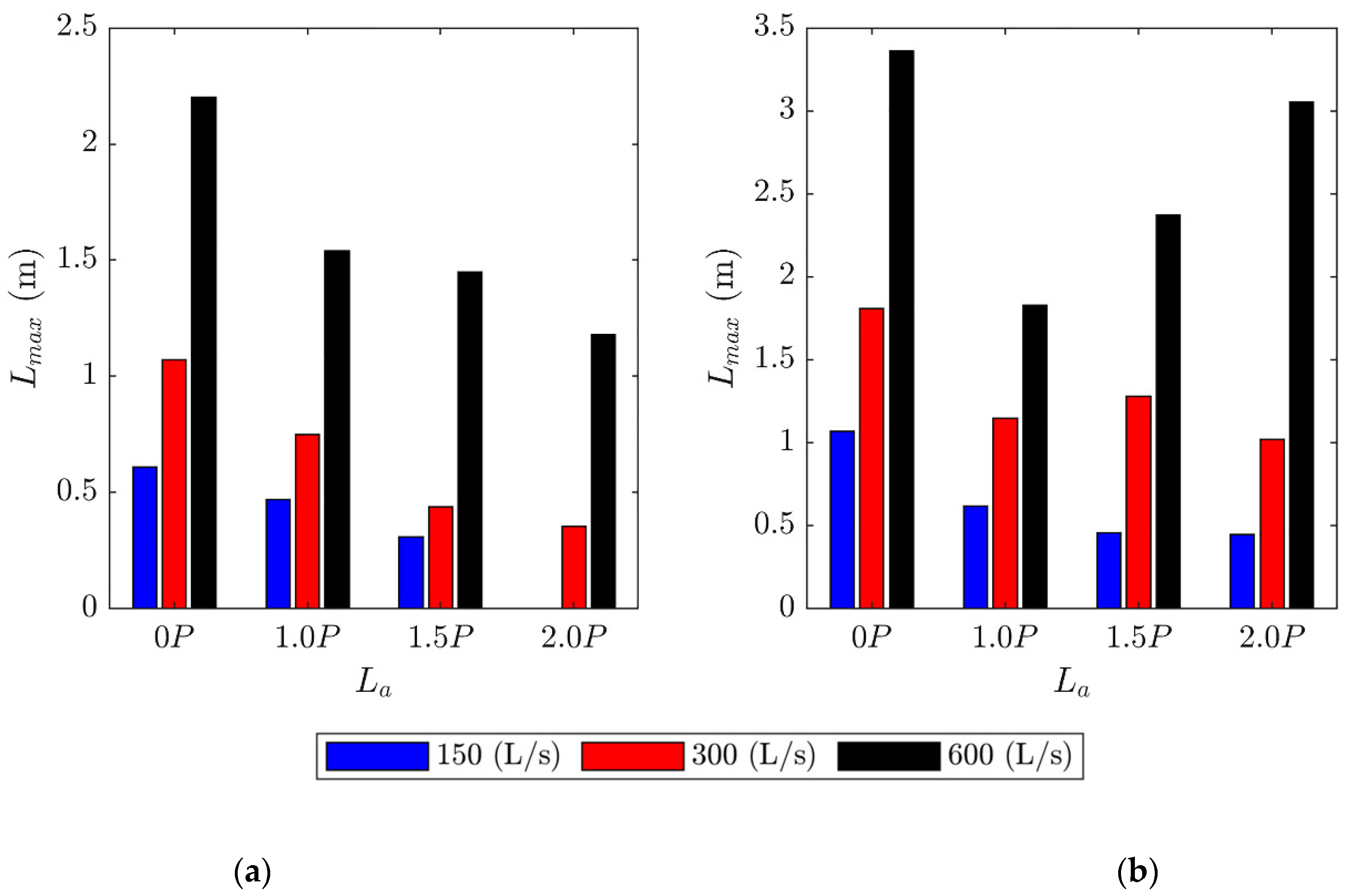
3.2. Analysis of Scour Processes
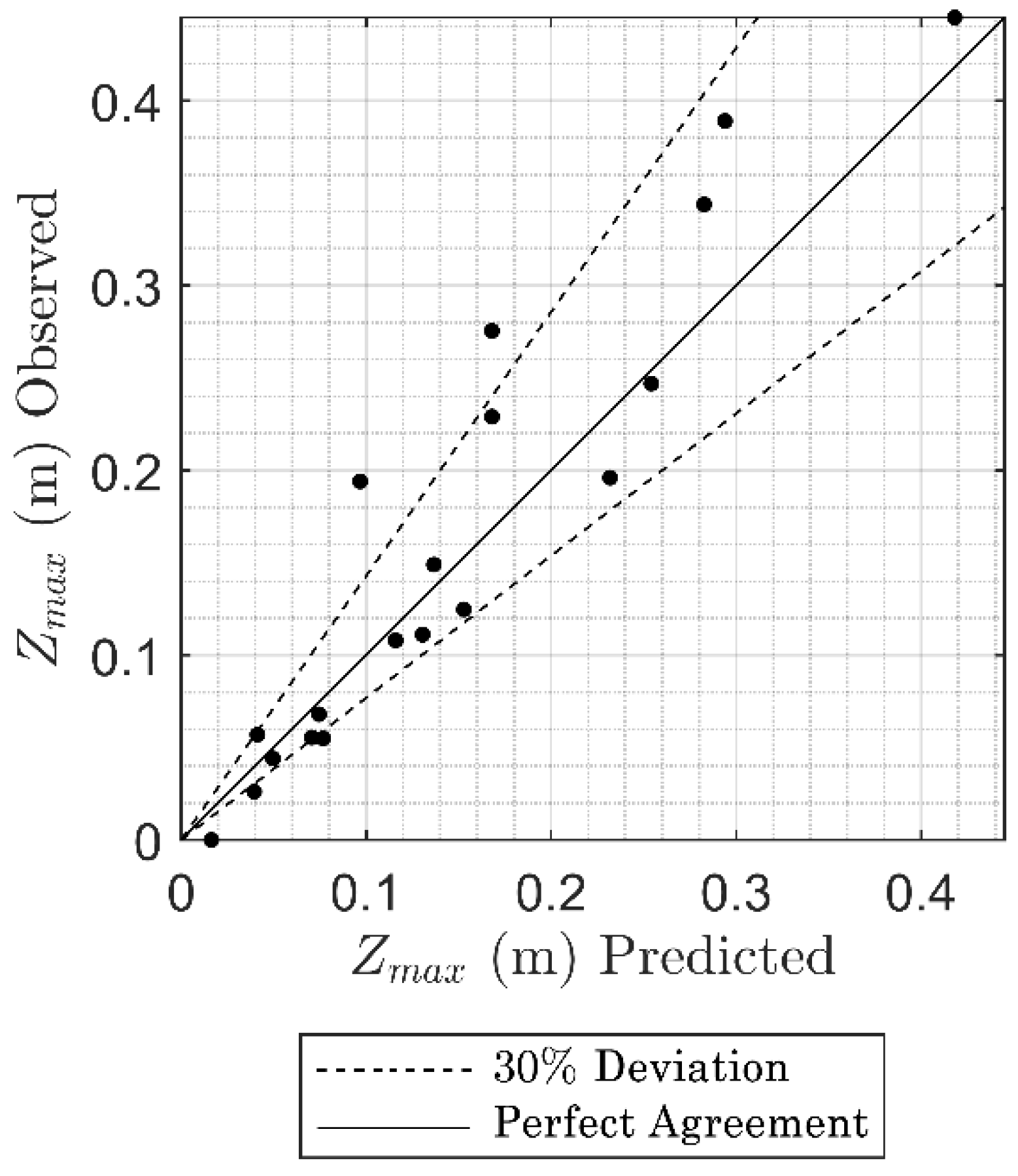
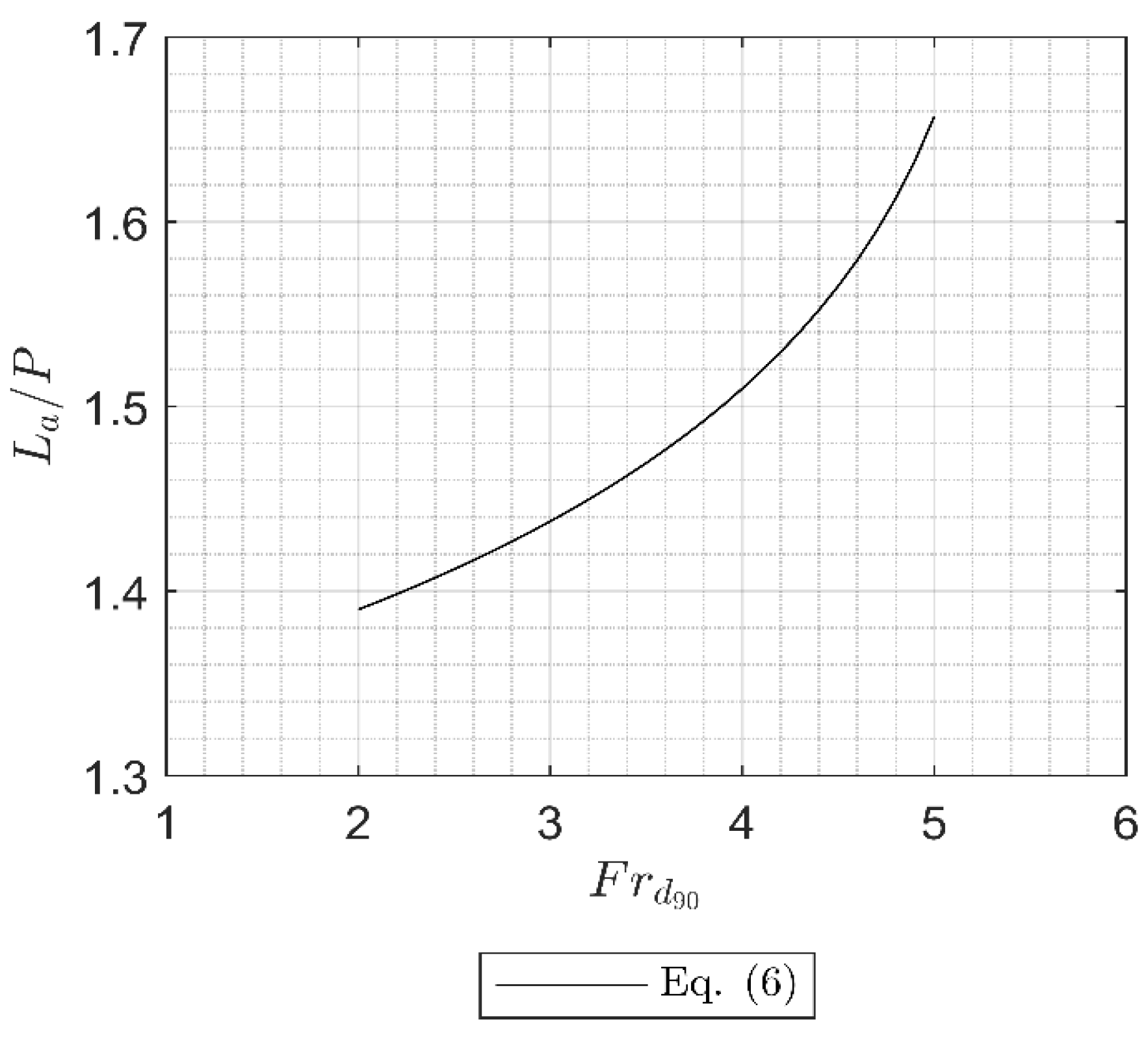
3.3. Apron and Cutoff Wall Design Guidance
4. Conclusions
- Scour depths in the two tested noncohesive gravel materials without an apron and cutoff wall were significant.
- Jets ensuing from the PK weir structure diffused over the apron and cause horizontal jet scour downstream of the apron.
- Adding a 1.0P long apron can reduce scour by an average of 61%, adding a 1.5P long apron can reduce scour by an average of 75%, and adding a 2.0P apron can reduce scour by an average of 83%. Thus, apron length La can be optimized considering PK weir hydraulics and geometry with geologic conditions at PK weir toe.
- Equations (3) and (6) were created to estimate La, Zmax downstream of an apron along with Equation (4), and Equation (7) was created to estimate Lc to protect the structure from scour undermining. Note that Equations (3) and (6) are considered valid for 2.4 ≤ Frd90 ≤ 5.3, 0 ≤ La/P ≤ 2, 0.11 ≤ H/P ≤ 0.36, and 0.24 ≤ hd/P ≤ 1.03. All proposed equations should be validated using field data.
- For this study, it was determined that there was an 8% difference in the reduction of scour from a 1.5P apron length to a 2.0P apron length, and a 1.5P apron may be an adequate and cost-effective length to minimize scour. Note that as the substrate diameter decreases the potential for scour depth and length downstream of the apron will increase.
- Although the facility tested at USU was quite large and might be considered a 1:5 to 1:10 scaled model, quantification of any scale effects requires additional investigation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laursen, E.M. Observations on the Nature of Scour. In Proceedings 5th Hydraulics Conference Bulletin; University of Iowa: Iowa City, IA, USA, 1952; pp. 179–197. [Google Scholar]
- Ettema, R.; Yoon, B.; Nakato, T.; Muste, M. A review of scour conditions and scour-estimation difficulties for bridge abutments. Water Eng. 2004, 8, 643–650. [Google Scholar] [CrossRef]
- Zehe, E.; Becker, R.; Bárdossy, A.; Plate, E. Uncertainty of simulated catchment runoff response in the presence of threshold processes: Role of initial soil moisture and precipitation. J. Hydrol. 2005, 315, 183–202. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Palermo, M.; Pagliara, S. Temporal evolution of jet induced scour depth in cohesionless granular beds and the phenomenological theory of turbulence. Phys. Fluids 2018, 30, 085109. [Google Scholar] [CrossRef]
- Palermo, M.; Pagliara, S.; Bombardelli, F.A. Theoretical Approach for Shear-Stress Estimation at 2D Equilibrium Scour Holes in Granular Material due to Subvertical Plunging Jets. J. Hydraul. Eng. 2020, 146, 04020009. [Google Scholar] [CrossRef]
- Hoffmans, G.J.C.M.; Verheij, H.J. Scour Manual; Balkema, A.A., Ed.; Taylor and Francis Group: Rotterdam, The Netherlands, 1997. [Google Scholar]
- Adduce, C.; Sciortino, G. Scour due to a horizontal turbulent jet: Numerical and experimental investigation. J. Hydraul. Res. 2006, 44, 663–673. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R. Scour below a High Vertical Drop. J. Hydraul. Eng. 2007, 133, 564–568. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. New Approach to Predicting Local Scour Downstream of Grade-Control Structure. J. Hydraul. Eng. 2020, 146, 04019058. [Google Scholar] [CrossRef]
- Lantz, W.; Crookston, B.M.; Palermo, M. Flood Infrastructure: Localized Scour at Piano Key Weirs. In Dam Safety 2020: Conference Proceedings; Association of State Dam Safety Officials: Lexington, KY, USA, 2020. [Google Scholar]
- United States Department of the Interior Bureau of Reclamation (USBR). Engineering Monograph No. 25: Hydraulic Design of Stilling Basins and Energy Dissipators; U.S Bureau of Reclamation: Denver, CO, USA, 1984.
- Thompson, P.; Kilgore, R. Hydraulic Design of Energy Dissipators for Culverts and Channels. In Federal Highway Administration; National Highway Institute: Washington, DC, USA, 2006. [Google Scholar]
- United States Department of Agriculture (USDA). The SAF Stilling Basin; U.S. Government Printing Office: Washington, DC, USA, 1959.
- Peterka, J. Hydraulic Design of Stilling Basins and Energy Dissipators; Bureau of Reclamation: Denver, CO, USA, 1958.
- Vischer, D.L.; Hager, W.H. Energy Dissipators: IAHR Hydraulic Structures Design Manuals 9; Taylor and Francis: Abingdon, UK, 1995. [Google Scholar]
- Novak, P.; Moffat, A.; Nalluri, C.; Narayanan, R. Hydraulic Structures, 4th ed.; E & FN Spon: Abingdon, UK, 1995. [Google Scholar]
- Khatsuria, R.M. Hydraulics of Spillways and Energy Dissipators; Marcel Decker: New York, NY, USA, 2005. [Google Scholar]
- Hager, W.H.; Schleiss, A.J.; Boes, R.M.; Pfister, M. Hydraulic Engineering of Dams; CRC Press: London, UK, 2020. [Google Scholar]
- Ho Ta Khanh, M.; Truong, C.H.; Nguyen, T.H. Main Results of the P.K Weir Model Tests in Vietnam (2004–2010); Labyrinth and Piano Key Weirs: PKW 2011; Taylor and Francis Group: London, UK, 2011; pp. 191–198. [Google Scholar]
- Crookston, B.M.; Erpicum, S.; Tullis, B.P.; Laugier, F. Hydraulics of Labyrinth and Piano Key Weirs: 100 Years of Prototype Structures, Advancements, and Future Research Needs. J. Hydraul. Eng. 2019, 145, 02519004. [Google Scholar] [CrossRef]
- Urban and Environmental Engineering (UEE). World Register of Piano Key Weirs Prototypes. Liege Universite. 2021. Available online: https://www.uee.uliege.be/cms/c_5026433/en/world-register-of-piano-key-weirs-prototypes (accessed on 11 March 2021).
- Schleiss, A.J. From Labyrinth to Piano Key Weirs—A Historical Review; Labyrinth and Piano Key Weirs: PKW 2011; Taylor and Francis Group: London, UK, 2011; pp. 3–16. [Google Scholar]
- Ribeiro, M.L.; Pfister, M.; Schleiss, A.J.; Boillat, J.L. Hydraulic design of A-Type Piano Key Weirs. J. Hydraul. Res. 2012, 50, 400–408. [Google Scholar] [CrossRef] [Green Version]
- Machiels, O.; Pirotton, M.; Pierre, A.; Dewals, B.; Erpicum, S. Experimental parametric study and design of Piano Key Weirs. J. Hydraul. Res. 2014, 52, 326–335. [Google Scholar] [CrossRef]
- López-Soto, J.; Wibowo, J.; Molina-Bas, O. Cost Reduction in Dam Infrastructure Using Arced Labyrinth Spillways. In Construction Research Congress 2016; San Juan, Puerto Rico, American Society of Civil Engineers (ASCE): Reston, VA, USA, 2016. [Google Scholar] [CrossRef]
- Laugier, F.; Vermeulen, J.; Lefebvre, V. Overview of Piano Key Weirs Experience Developed at EDF during the Past Few Years; Labyrinth and Piano Key Weirs II: PKW 2013; Taylor and Francis Group: London, UK, 2013; pp. 213–226. [Google Scholar]
- Jüstrich, S.; Pfister, M.; Schleiss, A.J. Mobile Riverbed Scour Downstream of a Piano Key Weir. J. Hydraul. Eng. 2016, 142, 04016043. [Google Scholar] [CrossRef]
- Pfister, M.; Jüstrich, S.; Schleiss, A.J. Toe-Scour Formation at Piano Key Weirs; Labyrinth and Piano Key Weirs III—PKW 2017; Taylor and Francis Group: London, UK, 2017; pp. 147–156. [Google Scholar]
- Palermo, M.; Crookston, B.; Pagliara, S. Analysis of Equilibrium Morphologies Downstream of a PK Weir Structure. In World Environmental and Water Resources Congress 2020; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2020; pp. 43–51. [Google Scholar] [CrossRef]
- Lantz, W. A Laboratory Study on the Geometric Effects of Piano Key Weirs on Scour for Non-Cohesive Substrates and Simple Mitigation Techniques. Master’s Thesis, Utah State University, Logan, UT, USA, 2021. [Google Scholar] [CrossRef]
- Yazdi, A.M.; Hoseini, S.A.; Nazari, S.; Amanian, N. Effects of weir geometry on scour development in the downstream of Piano Key Weirs. Water Supply 2021, 21, 289–298. [Google Scholar] [CrossRef]
- Hassan, N.M.K.N.; Narayanan, R. Local Scour Downstream of an Apron. J. Hydraul. Eng. 1985, 111, 1371–1384. [Google Scholar] [CrossRef]
- Chatterjee, S.S.; Ghosh, S.N.; Chatterjee, M. Local Scour due to Submerged Horizontal Jet. J. Hydraul. Eng. 1994, 120, 973–992. [Google Scholar] [CrossRef]
- Sarkar, A.; Dey, S. Scour downstream of aprons caused by sluices. Proc. Inst. Civ. Eng. Water Manag. 2005, 158, 55–64. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, A. Scour Downstream of an Apron Due to Submerged Horizontal Jets. J. Hydraul. Eng. 2006, 132, 246–257. [Google Scholar] [CrossRef]
- Erpicum, S.; Laugier, F.; Boillat, J.L.; Pirotton, M.; Reverchon, B.; Schleiss, A.J. Labyrinth and Piano Key Weirs—PKW 2011; CRC Press: London, UK, 2011. [Google Scholar]
- Microsonic. “mic+ 130/IU/TC.” mic+ Ultrasonic Sensors. 2021. Available online: https://www.microsonic.de/en/distance-sensors/cylindrical/micplus/standard-sensors/standard-sensors/micplus130iutc.htm (accessed on 4 March 2021).
- Zhang, G.; Valero, D.; Bung, D.; Chanson, H. On the estimation of free-surface turbulence using ultrasonic sensors. Flow Meas. Instrum. 2018, 60, 171–184. [Google Scholar] [CrossRef] [Green Version]
- Intel. “Depth Camera D435.” Intel RealSense. 2021. Available online: https://www.intelrealsense.com/depth-camera-d435/ (accessed on 4 March 2021).
- Bung, D.B.; Crookston, B.M.; Valero, D. Turbulent free-surface monitoring with an RGB-D sensor: The hydraulic jump case. J. Hydraul. Res. 2020, 1–12. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal Evolution of Clear-Water Pier and Abutment Scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Neill, C.R. Note on Initial Movement Of Coarse Uniform Bed-Material. J. Hydraul. Res. 1968, 6, 173–176. [Google Scholar] [CrossRef]
- Julien, P.Y. Erosion and Sedimentation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Pagliara, S.; Palermo, M. Scour control and surface sediment distribution downstream of block ramps. J. Hydraul. Res. 2008, 46, 334–343. [Google Scholar] [CrossRef]
- Pagliara, S.; Roy, D.; Palermo, M. 3D plunge pool scour with protection measures. J. Hydro-Environ. Res. 2010, 4, 225–233. [Google Scholar] [CrossRef]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Annandale, G.W. Erodibility. J. Hydraul. Res. 1995, 33, 471–494. [Google Scholar] [CrossRef]
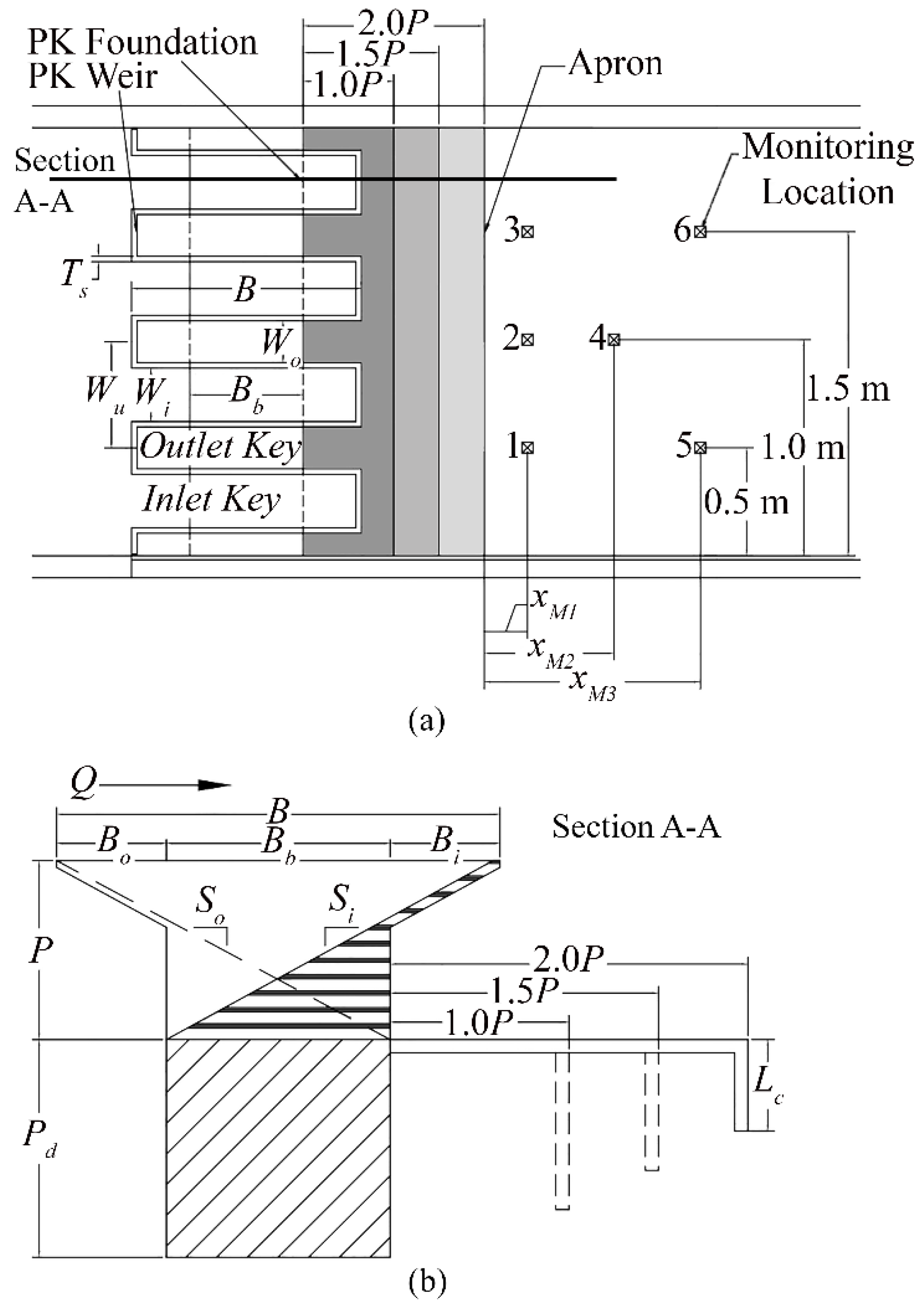
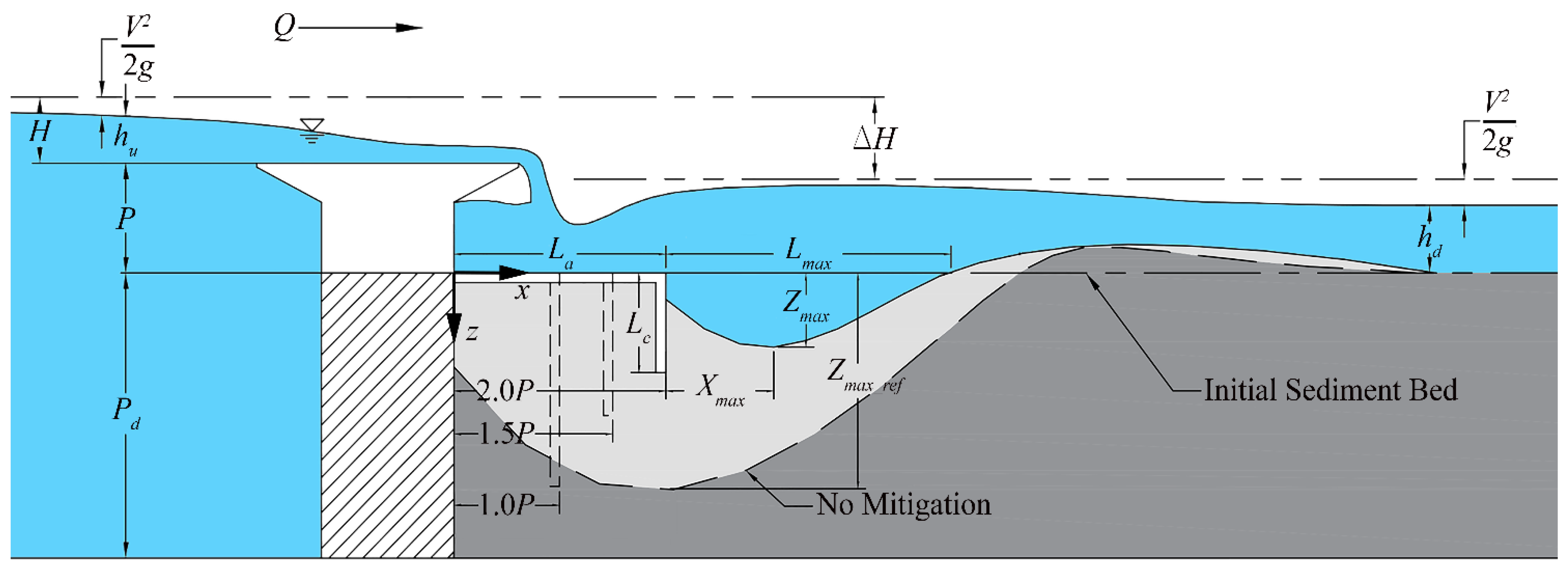


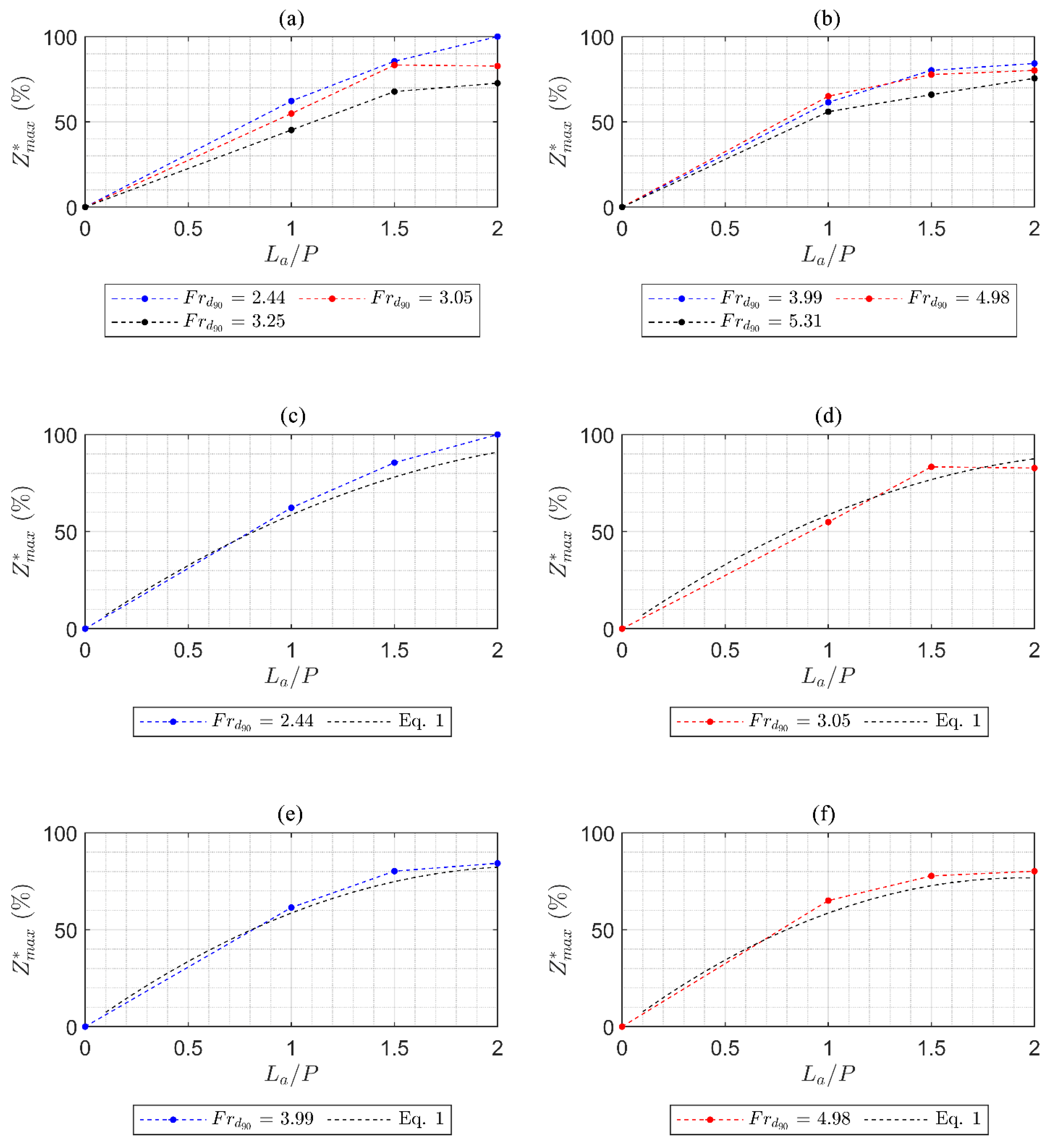
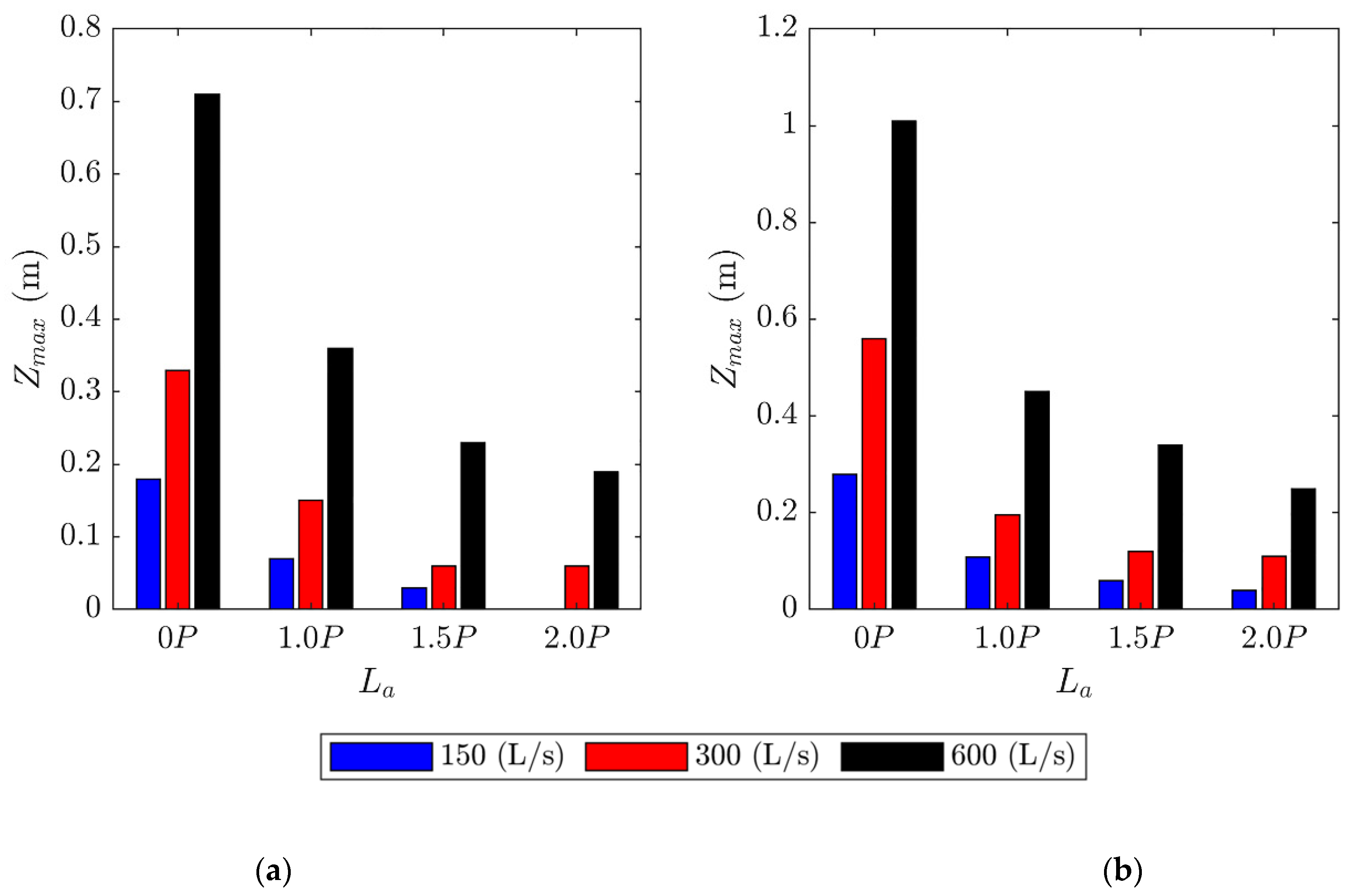
| Parameter | Value |
|---|---|
| B | 1.04 m |
| Bb | 0.52 m |
| Bi = Bo | 0.26 m |
| N | 4 |
| P | 0.42 m |
| Pd | 1.09 m |
| Si = So | 0.55 |
| Ts | 0.025 m |
| Wi | 0.248 m |
| Wo | 0.194 m |
| Wi/Wo | 1.280 m |
| Wu | 0.49 m |
| Feature | Detail |
|---|---|
| Global Shutter | 3 μm × 3 μm pixel size |
| IR Stereo: FOV | 86° × 57° (±3°) |
| IR Stereo: Resolution | 1280 × 720 |
| RGB: FOV | 64°×41° × 77° (±3°) |
| RGB: Resolution | 1920 × 1080 |
| Substrate Type | Discharge Q | Headwater Ratio | Tailwater † hd | Apron Length La |
|---|---|---|---|---|
| Substrate 1 d50 = 13 mm d90 = 20 mm σ = 1.54 Substrate 2 d50 = 6.5 mm d90 = 9.1 mm σ = 1.30 | 150 L/s | H/P = 0.11 | 16 cm = 0.38P | 2.0P = 0.84 m |
| 1.5P = 0.63 m | ||||
| 1.0P = 0.42 m | ||||
| 0.0P = 0.00 m * | ||||
| 300 L/s | H/P = 0.18 | 17 cm = 0.41P | 2.0P = 0.84 m | |
| 1.5P = 0.63 m | ||||
| 1.0P = 0.42 m | ||||
| 0.0P = 0.00 m * | ||||
| 600 L/s | H/P = 0.35 | 22 cm = 0.52P | 2.0P = 0.84 m | |
| 1.5P = 0.63 m | ||||
| 1.0P = 0.42 m | ||||
| 0.0P = 0.00 m * |
| Run (#) | Substrate (-) | t (min) | La/P (-) | Q (L/s) |
|---|---|---|---|---|
| 1 * | 1 | 180 | 0.0 | 150 |
| 2 * | 1 | 240 | 0.0 | 300 |
| 3 * | 1 | 900 | 0.0 | 600 |
| 4 | 1 | 360 | 1.0 | 150 |
| 5 | 1 | 360 | 1.0 | 300 |
| 6 | 1 | 870 | 1.0 | 600 |
| 7 | 1 | 360 | 1.5 | 150 |
| 8 | 1 | 360 | 1.5 | 300 |
| 9 | 1 | 360 | 1.5 | 600 |
| 9R | 1 | 360 | 1.5 | 600 |
| 10 | 1 | no scour | 2.0 | 150 |
| 11 | 1 | 120 | 2.0 | 300 |
| 12 | 1 | 360 | 2.0 | 600 |
| 13 * | 2 | 450 | 0.0 | 150 |
| 14 * | 2 | 1050 | 0.0 | 300 |
| 15 * | 2 | 1170 | 0.0 | 600 |
| 16 | 2 | 840 | 1.0 | 150 |
| 17 | 2 | 780 | 1.0 | 300 |
| 18 | 2 | 720 | 1.0 | 600 |
| 19 | 2 | 240 | 1.5 | 150 |
| 20 | 2 | 840 | 1.5 | 300 |
| 21 | 2 | 990 | 1.5 | 600 |
| 22 | 2 | 480 | 2.0 | 150 |
| 23 | 2 | 600 | 2.0 | 300 |
| 24 | 2 | 720 | 2.0 | 600 |
| Run (#) | hd (m) | Zmax (m) | Xmax (m) | Lmax (m) | V (m3) |
|---|---|---|---|---|---|
| 1 * | 0.16 | 0.18 | 0.25 | 0.61 | 0.12 |
| 2 * | 0.17 | 0.33 | 0.42 | 1.07 | 0.36 |
| 3 * | 0.22 | 0.71 | 0.73 | 2.20 | 1.49 |
| 4 | 0.09 | 0.07 | 0.00 | 0.47 | 0.03 |
| 5 | 0.16 | 0.15 | 0.00 | 0.75 | 0.12 |
| 6 | 0.21 | 0.39 | 0.00 | 1.54 | 0.50 |
| 7 | 0.10 | 0.03 | 0.00 | 0.31 | 0.00 |
| 8 | 0.17 | 0.06 | 0.00 | 0.44 | 0.03 |
| 9 | 0.22 | 0.28 | 0.00 | 1.54 | 0.37 |
| 9R | 0.23 | 0.23 | 0.00 | 1.45 | 0.37 |
| 10 | 0.09 | No Scour | No Scour | No Scour | No Scour |
| 11 | 0.15 | 0.06 | 0.00 | 0.36 | 0.02 |
| 12 | 0.22 | 0.19 | 0.00 | 1.18 | 0.27 |
| 13 * | 0.10 | 0.28 | 0.40 | 1.07 | 0.39 |
| 14 * | 0.14 | 0.56 | 0.52 | 1.81 | 1.03 |
| 15 * | 0.22 | 1.01 | 1.16 | 3.19 | 3.36 |
| 16 | 0.11 | 0.11 | 0.00 | 0.61 | 0.07 |
| 17 | 0.16 | 0.20 | 0.00 | 1.15 | 0.26 |
| 18 | 0.24 | 0.45 | 0.00 | 1.83 | 0.74 |
| 19 | 0.11 | 0.06 | 0.00 | 0.47 | 0.03 |
| 20 | 0.15 | 0.12 | 0.00 | 1.28 | 0.15 |
| 21 | 0.25 | 0.34 | 0.00 | 2.37 | 0.56 |
| 22 | 0.10 | 0.04 | 0.00 | 0.45 | 0.02 |
| 23 | 0.15 | 0.11 | 0.00 | 1.02 | 0.12 |
| 24 | 0.24 | 0.25 | 0.00 | 3.05 | 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lantz, W.; Crookston, B.M.; Palermo, M. Apron and Cutoff Wall Scour Protection for Piano Key Weirs. Water 2021, 13, 2332. https://doi.org/10.3390/w13172332
Lantz W, Crookston BM, Palermo M. Apron and Cutoff Wall Scour Protection for Piano Key Weirs. Water. 2021; 13(17):2332. https://doi.org/10.3390/w13172332
Chicago/Turabian StyleLantz, Wyatt, Brian Mark Crookston, and Michele Palermo. 2021. "Apron and Cutoff Wall Scour Protection for Piano Key Weirs" Water 13, no. 17: 2332. https://doi.org/10.3390/w13172332








