Spatial Prediction of Groundwater Potentiality in Large Semi-Arid and Karstic Mountainous Region Using Machine Learning Models
Abstract
:1. Introduction
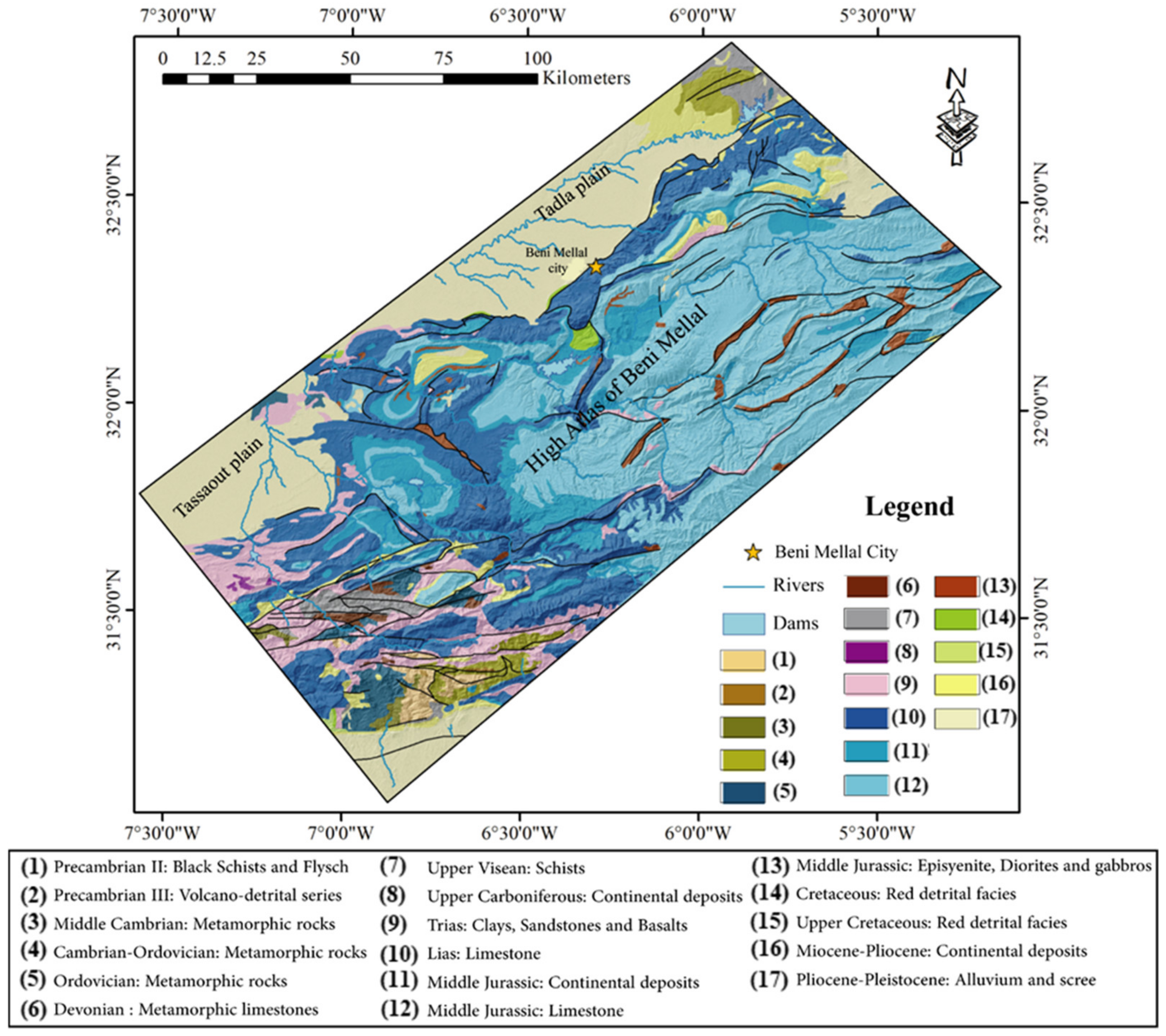
2. Study Area
2.1. Geographic and Climatic Context
2.2. Geological and Hydrogeological Setting
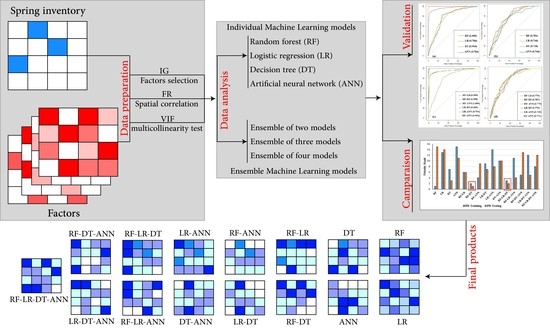
3. Materials and Methods
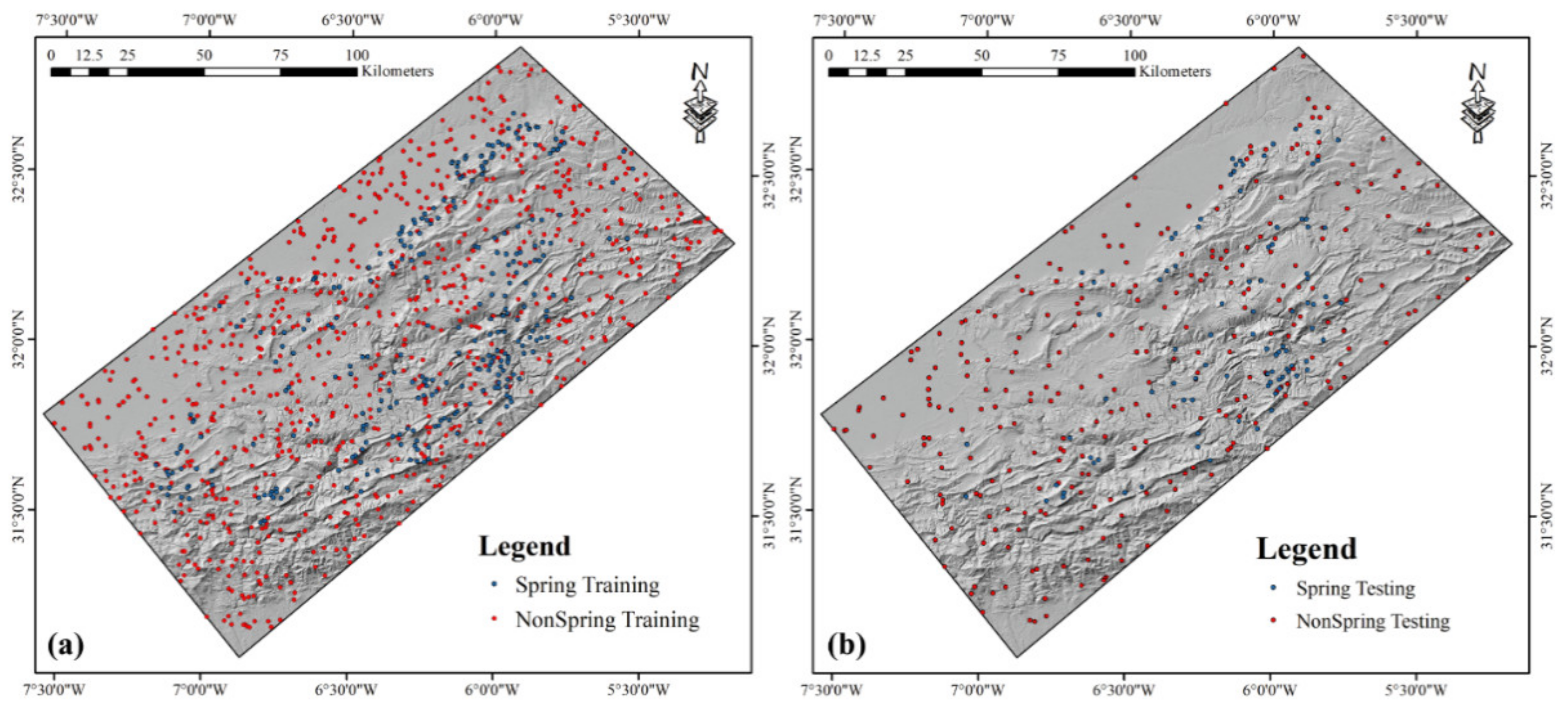
3.1. Groundwater Springs Inventory (SI)
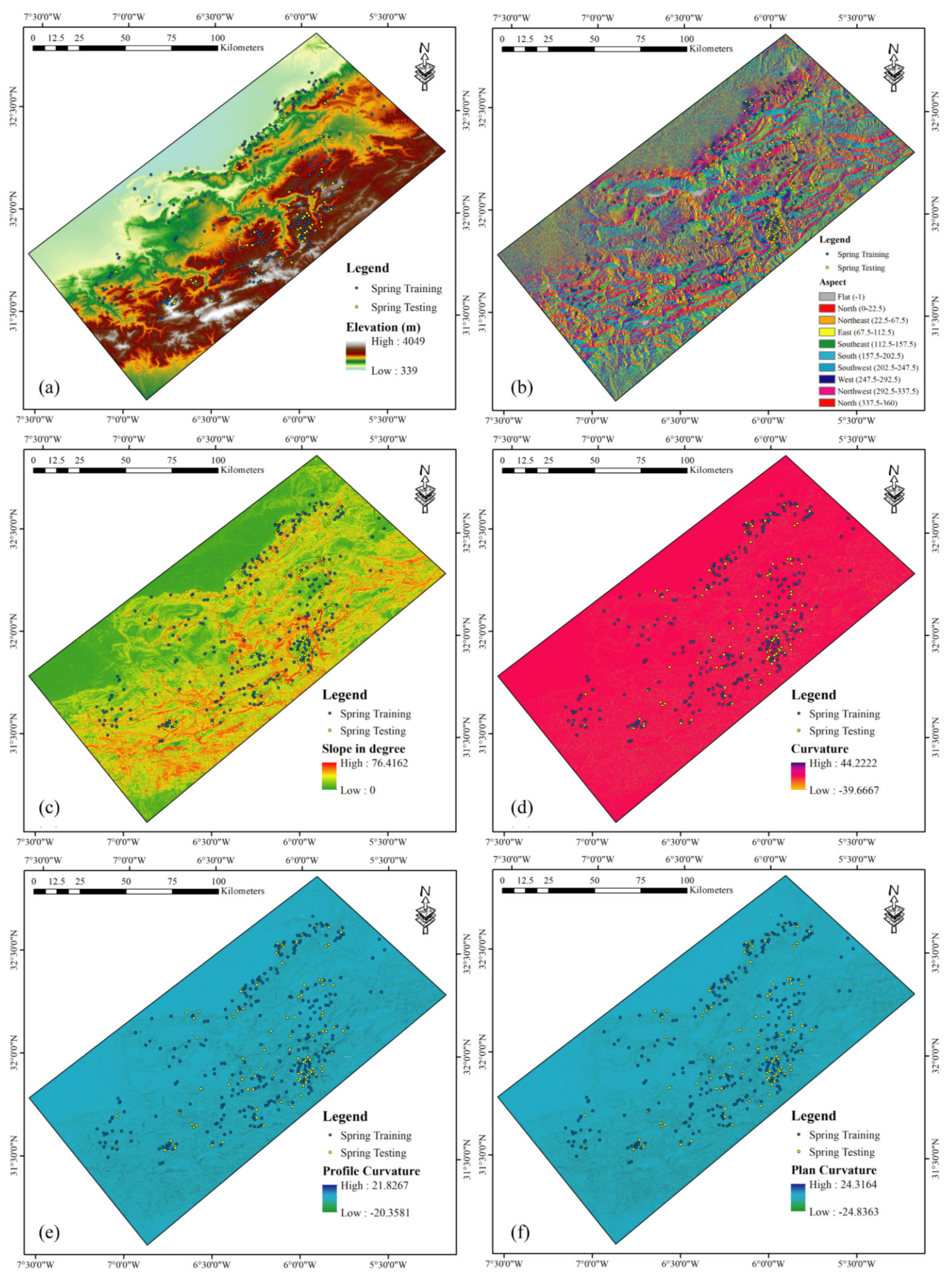
3.2. Groundwater Influencing Factors (GIFs)
3.2.1. Climatic Factors
3.2.2. Hydrological Factors
3.2.3. Geological Factors
3.2.4. Topographic Factors
3.2.5. Land Use/Cover Factors
3.3. Groundwater Influencing Factors (GIFs) Analysis
3.3.1. Multicollinearity Analysis and Confusion Matrix
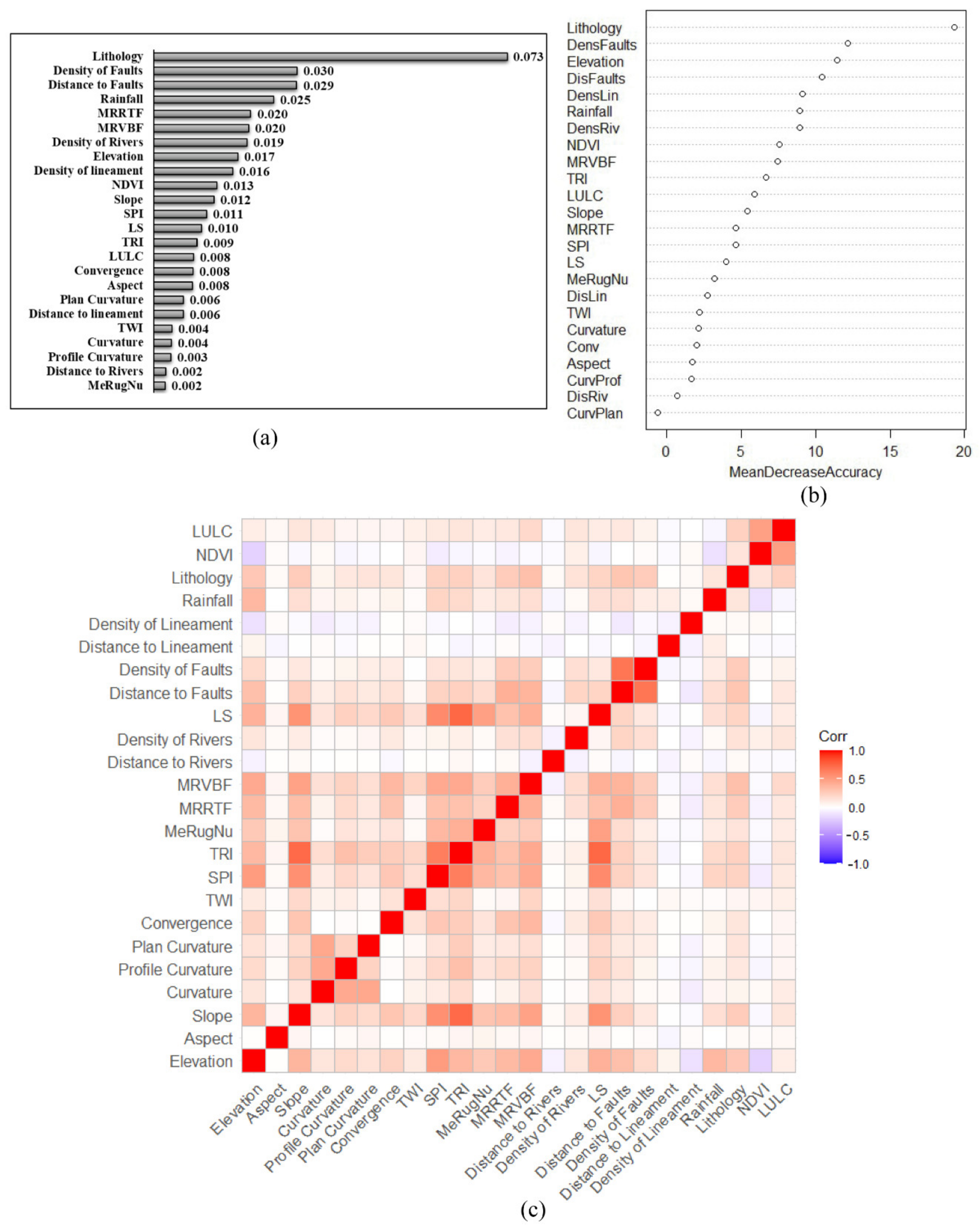
3.3.2. Selection of Groundwater Influencing Factors
3.3.3. Weight of the Groundwater Influencing Factors
3.4. Methods
3.4.1. Random Forest (RF) Model
3.4.2. Logistic Regression (LR) Model
3.4.3. Decision Tree (DT) Model (C 5.0)
3.4.4. Artificial Neural Network (ANN) Model
3.5. Ensembles of Models
3.6. Performance Metrics and Comparison
3.6.1. Statistical Metrics
3.6.2. ROC Curve
3.6.3. Model Prioritization Using Compound Factor
4. Results
4.1. GIF Selection and Analysis
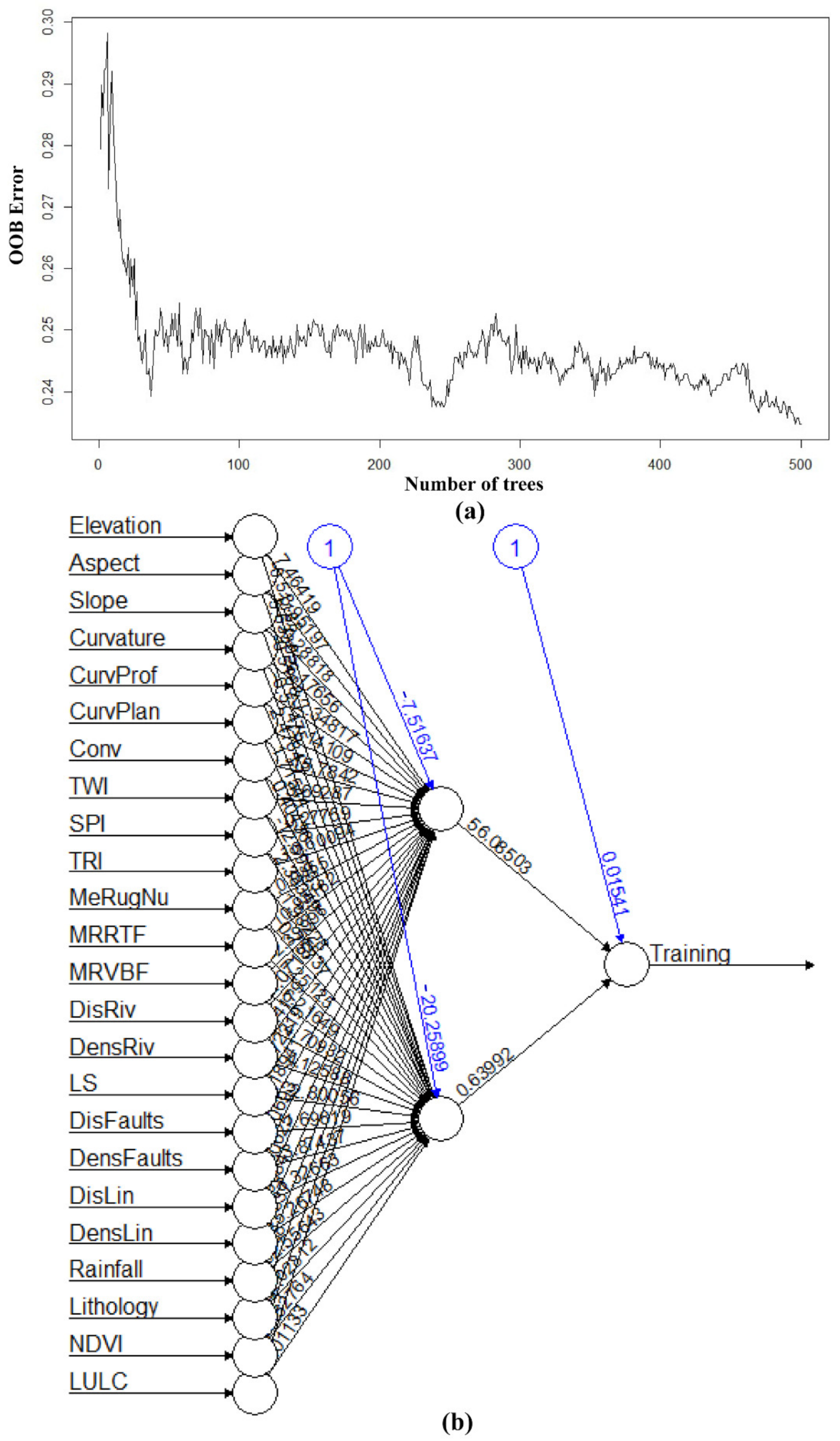
4.2. Models Building and Hyperparameters Tuning
4.3. Groundwater Potential Mapping
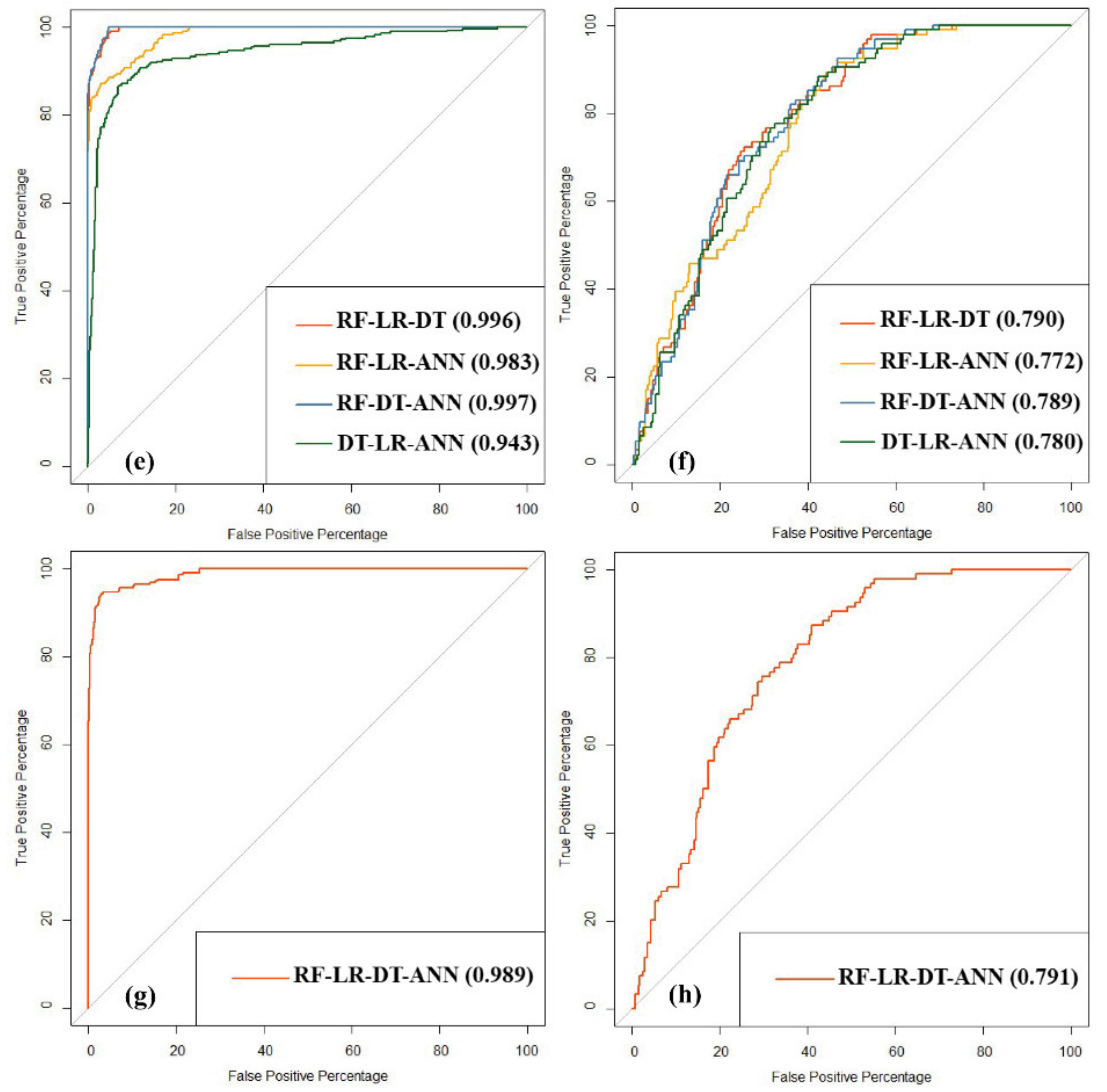
4.4. Performance Metrics and Comparison
5. Discussion
5.1. GIF Selection and Analysis
5.2. Role of Factors in the Occurrence of Karst Springs
5.3. Machine Learning Algorithm Performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Price, M.F.; Byers, A.C.; Friend, D.A.; Kohler, T.; Price, L.W. (Eds.) Mountain Geography: Physical and Human Dimensions; University of California Press: Berkeley, CA, USA, 2013. [Google Scholar]
- Kohler, T.; Giger, M.; Hurni, H.; Ott, C.; Wiesmann, U.; Von Dach, S.W.; Maselli, D. Mountains and Climate Change: A Global Concern. Mt. Res. Dev. 2010, 30, 53–55. [Google Scholar] [CrossRef] [Green Version]
- FAO. State of the World’s Forests 2003; FAO: Rome, Italy, 2003. [Google Scholar]
- Bouchaou, L.; Michelot, J.; Qurtobi, M.; Zine, N.; Gaye, C.; Aggarwal, P.; Marah, H.; Zerouali, A.; Taleb, H.; Vengosh, A. Origin and residence time of groundwater in the Tadla basin (Morocco) using multiple isotopic and geochemical tools. J. Hydrol. 2009, 379, 323–338. [Google Scholar] [CrossRef]
- Bouchaou, L.; Michelot, J.; Vengosh, A.; Hsissou, Y.; Qurtobi, M.; Gaye, C.; Bullen, T.; Zuppi, G. Application of multiple isotopic and geochemical tracers for investigation of recharge, salinization, and residence time of water in the Souss–Massa aquifer, southwest of Morocco. J. Hydrol. 2008, 352, 267–287. [Google Scholar] [CrossRef]
- Bouimouass, H.; Fakir, Y.; Tweed, S.; Leblanc, M. Groundwater recharge sources in semiarid irrigated mountain fronts. Hydrol. Process. 2020, 34, 1598–1615. [Google Scholar] [CrossRef]
- Rathay, S.; Allen, D.; Kirste, D. Response of a fractured bedrock aquifer to recharge from heavy rainfall events. J. Hydrol. 2018, 561, 1048–1062. [Google Scholar] [CrossRef] [Green Version]
- Voeckler, H.; Allen, D.M. Estimating regional-scale fractured bedrock hydraulic conductivity using discrete fracture network (DFN) modeling. Hydrogeol. J. 2012, 20, 1081–1100. [Google Scholar] [CrossRef]
- Shenga, Z.D.; Baroková, D.; Šoltész, A. Numerical modeling of groundwater to assess the impact of proposed railway construction on groundwater regime. Pollack Period. 2018, 13, 187–196. [Google Scholar] [CrossRef]
- Ozdemir, A. Using a binary logistic regression method and GIS for evaluating and mapping the groundwater spring potential in the Sultan Mountains (Aksehir, Turkey). J. Hydrol. 2011, 405, 123–136. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Madani, A.; Niyazi, B. Groundwater potential mapping using remote sensing techniques and weights of evidence GIS model: A case study from Wadi Yalamlam basin, Makkah Province, Western Saudi Arabia. Environ. Earth Sci. 2015, 74, 5129–5142. [Google Scholar] [CrossRef]
- Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using C5.0, random forest, and multivariate adaptive regression spline models in GIS. Environ. Monit. Assess. 2018, 190, 149. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, K.K.; Nahar, N.; Hossain, B.M.M. A machine learning-based prediction and analysis of flood affected households: A case study of floods in Bangladesh. Int. J. Disaster Risk Reduct. 2019, 34, 283–294. [Google Scholar] [CrossRef]
- Rizeei, H.M.; Pradhan, B.; Saharkhiz, M.A.; Lee, S. Groundwater aquifer potential modeling using an ensemble multi-adoptive boosting logistic regression technique. J. Hydrol. 2019, 579, 124172. [Google Scholar] [CrossRef]
- Hssaisoune, M.; Bouchaou, L.; Sifeddine, A.; Bouimetarhan, I.; Chehbouni, A. Moroccan Groundwater Resources and Evolution with Global Climate Changes. Geosciences 2020, 10, 81. [Google Scholar] [CrossRef] [Green Version]
- Milewski, A.; Seyoum, W.M.; Elkadiri, R.; Durham, M. Multi-Scale Hydrologic Sensitivity to Climatic and Anthropogenic Changes in Northern Morocco. Geosciences 2019, 10, 13. [Google Scholar] [CrossRef] [Green Version]
- Ouatiki, H.; Boudhar, A.; Ouhinou, A.; Arioua, A.; Hssaisoune, M.; Bouamri, H.; Benabdelouahab, T. Trend analysis of rainfall and drought over the Oum Er-Rbia River Basin in Morocco during 1970–2010. Arab. J. Geosci. 2019, 12, 128. [Google Scholar] [CrossRef]
- Barakat, A.; Hilali, A.; El Baghdadi, M.; Touhami, F. Assessment of shallow groundwater quality and its suitability for drinking purpose near the Béni-Mellal wastewater treatment lagoon (Morocco). Hum. Ecol. Risk Assess. Int. J. 2020, 26, 1476–1495. [Google Scholar] [CrossRef]
- Barakat, A.; Mouhtarim, G.; Saji, R.; Touhami, F. Health risk assessment of nitrates in the groundwater of Beni Amir irrigated perimeter, Tadla plain, Morocco. Hum. Ecol. Risk Assess. Int. J. 2019, 26, 1864–1878. [Google Scholar] [CrossRef]
- Barakat, A.; Meddah, R.; Afdali, M.; Touhami, F. Physicochemical and microbial assessment of spring water quality for drinking supply in Piedmont of Béni-Mellal Atlas (Morocco). Phys. Chem. Earth Parts A/B/C 2018, 104, 39–46. [Google Scholar] [CrossRef]
- Bouchaou, L.; Chauve, P.; Mudry, J.; Mania, J.; Hsissou, Y. Structure et fonctionnement d’un hydrosystème karstique de montagne sous climat semi-aride: Cas de l’Atlas de Beni-Mellal (Maroc). J. Afr. Earth Sci. 1997, 25, 225–236. [Google Scholar] [CrossRef]
- Bouchaou, L.; Michelot, J.L. Contribution Des Isotopes à l’étude de La Recharge Des Aquifères de La Région de Béni Mellal (Tadla, Maroc). IAHS-AISH Publ. 1997, 244, 37–44. [Google Scholar]
- Ettazarini, S. Incidences of water-rock interaction on natural resources characters, Oum Er-Rabia Basin (Morocco). Environ. Geol. 2004, 47, 69–75. [Google Scholar] [CrossRef]
- Ettazarini, S. Groundwater pollution risk mapping for the Eocene aquifer of the Oum Er-Rabia basin, Morocco. Environ. Geol. 2006, 51, 341–347. [Google Scholar] [CrossRef]
- Archambault, C.; Combe, M.; Ruhard, J.P. The Phosphates Plateau. Water Resources. Notes Mém. Sér. Géol. Rabat 1975, 231, 239–258. [Google Scholar]
- Brede, R. Structural aspects of the Middle and the High Atlas (Morocco) phenomena and causalities. Geologische Rundschau 1992, 81, 171–184. [Google Scholar] [CrossRef]
- Boudhar, A.; Ouatiki, H.; Bouamri, H.; Lebrini, Y.; Karaoui, I.; Hssaisoune, M.; Arioua, A.; Benabdelouahab, T. Hydrological Response to Snow Cover Changes Using Remote Sensing over the Oum Er Rbia Upstream Basin, Morocco. In Mapping and Spatial Analysis of Socio-Economic and Environmental Indicators for Sustainable Development; Springer: Cham, Switzerland, 2020; pp. 95–102. [Google Scholar]
- Kordestani, M.D.; Naghibi, S.A.; Hashemi, H.; Ahmadi, K.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using a novel data-mining ensemble model. Hydrogeol. J. 2019, 27, 211–224. [Google Scholar] [CrossRef] [Green Version]
- Ouatiki, H.; Boudhar, A.; Tramblay, Y.; Jarlan, L.; Benabdelouhab, T.; Hanich, L.; El Meslouhi, M.R.; Chehbouni, A. Evaluation of TRMM 3B42 V7 Rainfall Product over the Oum Er Rbia Watershed in Morocco. Climate 2017, 5, 1. [Google Scholar] [CrossRef]
- Shaban, A.; Khawlie, M.; Abdallah, C. Use of remote sensing and GIS to determine recharge potential zones: The case of Occidental Lebanon. Hydrogeol. J. 2005, 14, 433–443. [Google Scholar] [CrossRef]
- Yeh, H.-F.; Cheng, Y.-S.; Lin, H.-I.; Lee, C.-H. Mapping groundwater recharge potential zone using a GIS approach in Hualian River, Taiwan. Sustain. Environ. Res. 2016, 26, 33–43. [Google Scholar] [CrossRef] [Green Version]
- Botzen, W.J.W.; Aerts, J.C.J.H.; Bergh, J.V.D. Individual preferences for reducing flood risk to near zero through elevation. Mitig. Adapt. Strat. Glob. Chang. 2013, 18, 229–244. [Google Scholar] [CrossRef] [Green Version]
- Gokceoglu, C.; Sonmez, H.; Nefeslioglu, H.A.; Duman, T.Y.; Çan, T. The 17 March 2005 Kuzulu landslide (Sivas, Turkey) and landslide-susceptibility map of its near vicinity. Eng. Geol. 2005, 81, 65–83. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. Index that quantifies topographic heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Juliev, M.; Mergili, M.; Mondal, I.; Nurtaev, B.; Pulatov, A.; Hübl, J. Comparative analysis of statistical methods for landslide susceptibility mapping in the Bostanlik District, Uzbekistan. Sci. Total Environ. 2019, 653, 801–814. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Knoll, L.; Breuer, L.; Bach, M. Large scale prediction of groundwater nitrate concentrations from spatial data using machine learning. Sci. Total Environ. 2019, 668, 1317–1327. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Bourenane, H.; Guettouche, M.S.; Bouhadad, Y.; Braham, M. Landslide hazard mapping in the Constantine city, Northeast Algeria using frequency ratio, weighting factor, logistic regression, weights of evidence, and analytical hierarchy process methods. Arab. J. Geosci. 2016, 9, 1–24. [Google Scholar] [CrossRef]
- Saito, H.; Nakayama, D.; Matsuyama, H. Comparison of landslide susceptibility based on a decision-tree model and actual landslide occurrence: The Akaishi Mountains, Japan. Geomorphology 2009, 109, 108–121. [Google Scholar] [CrossRef]
- Tseng, C.-J.; Lu, C.-J.; Chang, C.-C.; Chen, G.-D.; Cheewakriangkrai, C. Integration of data mining classification techniques and ensemble learning to identify risk factors and diagnose ovarian cancer recurrence. Artif. Intell. Med. 2017, 78, 47–54. [Google Scholar] [CrossRef]
- Quinlan, R.C. 4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Kawabata, D.; Bandibas, J. Landslide susceptibility mapping using geological data, a DEM from ASTER images and an Artificial Neural Network (ANN). Geomorphology 2009, 113, 97–109. [Google Scholar] [CrossRef]
- Song, Y.; Niu, R.; Xu, S.; Ye, R.; Peng, L.; Guo, T.; Li, S.; Chen, T. Landslide Susceptibility Mapping Based on Weighted Gradient Boosting Decision Tree in Wanzhou Section of the Three Gorges Reservoir Area (China). ISPRS Int. J. Geo-Inf. 2018, 8, 4. [Google Scholar] [CrossRef] [Green Version]
- Demir, G.; Aytekin, M.; Akgun, A. Landslide susceptibility mapping by frequency ratio and logistic regression methods: An example from Niksar–Resadiye (Tokat, Turkey). Arab. J. Geosci. 2014, 8, 1801–1812. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Avand, M.; Janizadeh, S.; Bui, D.T.; Pham, V.H.; Ngo, P.T.T.; Nhu, V.-H. A tree-based intelligence ensemble approach for spatial prediction of potential groundwater. Int. J. Digit. Earth 2020, 13, 1408–1429. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Ha, D.H.; Avand, M.; Jaafari, A.; Nguyen, H.D.; Al-Ansari, N.; Van Phong, T.; Sharma, R.; Kumar, R.; Van Le, H.; et al. Soft Computing Ensemble Models Based on Logistic Regression for Groundwater Potential Mapping. Appl. Sci. 2020, 10, 2469. [Google Scholar] [CrossRef] [Green Version]
- Nampak, H.; Pradhan, B.; Manap, M.A. Application of GIS based data driven evidential belief function model to predict groundwater potential zonation. J. Hydrol. 2014, 513, 283–300. [Google Scholar] [CrossRef]
- Karami, G.H.; Bagheri, R.; Rahimi, F. Determining the groundwater potential recharge zone and karst springs catchment area: Saldoran region, western Iran. Hydrogeol. J. 2016, 24, 1981–1992. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Chatterjee, C. Development of an accurate and reliable hourly flood forecasting model using wavelet–bootstrap–ANN (WBANN) hybrid approach. J. Hydrol. 2010, 394, 458–470. [Google Scholar] [CrossRef]




| Factors | Data Layers | Data Provider |
|---|---|---|
| Spring inventory | Previous studies Field investigation Topographic maps | |
| Topographic factors | Elevation Aspect Slope Curvature Profile curvature Plan curvature Convergence TWI SPI TRI MeRugNu MRRTF MRVBF LS | SRTM-DEM from (http://gdex.cr.usgs.gov/gdex/ (accessed on 10 January 2020)) pixel size of 30 m × 30 m. |
| Geologic factors | Lithology | Geological map of Morocco at the scale 1:500,000 Geological map of Morocco at the scale 1:500,000 LANDSAT satellite image at 30 m from (https://earthexplorer.usgs.gov/ (accessed on 10 January 2020)) |
| Distance to Faults Faults Density Distance to lineaments Lineaments density | ||
| Hydrologic factors | Distance to rivers Rivers density | DEM at 30 m |
| Land cover factors | NDVI LULC | LANDSAT satellite image at 30 m from (https://earthexplorer.usgs.gov/ (accessed on 10 January 2020)) |
| Climatic factors | Rainfall | Climatic stations data from hydraulic basin agency of Oum Erabia Tropical Rainfall Measuring Mission |
| Information Gain | Collinearity Statistics | LR Model | ||
|---|---|---|---|---|
| Influencing Factors | Average Merit | Tolerance | VIF | β |
| Elevation | 0.017 | 0.530 | 1.886 | 0.967 |
| Aspect | 0.008 | 0.983 | 1.017 | 2.758 |
| Slope | 0.012 | 0.411 | 2.434 | 0.021 |
| Curvature | 0.004 | 0.667 | 1.499 | −0.751 |
| Profile Curvature | 0.003 | 0.696 | 1.436 | −0.116 |
| Plan Curvature | 0.006 | 0.773 | 1.294 | 0.389 |
| Convergence | 0.008 | 0.754 | 1.327 | −2.774 |
| TWI | 0.004 | 0.907 | 1.103 | −0.081 |
| SPI | 0.011 | 0.471 | 2.122 | 0.522 |
| TRI | 0.009 | 0.231 | 4.323 | −0.965 |
| MeRugNu | 0.002 | 0.707 | 1.414 | −0.947 |
| MRRTF | 0.020 | 0.615 | 1.625 | 1.687 |
| MRVBF | 0.020 | 0.546 | 1.832 | 1.232 |
| Distance to Rivers | 0.002 | 0.977 | 1.024 | 1.971 |
| Density of Rivers | 0.019 | 0.899 | 1.112 | 2.136 |
| LS | 0.010 | 0.330 | 3.034 | 0.749 |
| Distance to Faults | 0.029 | 0.407 | 2.456 | 0.510 |
| Density of Faults | 0.030 | 0.503 | 1.988 | 1.380 |
| Distance to lineament | 0.006 | 0.975 | 1.026 | 1.962 |
| Density of lineament | 0.016 | 0.949 | 1.054 | 2.979 |
| Rainfall | 0.025 | 0.829 | 1.207 | 1.836 |
| Lithology | 0.073 | 0.741 | 1.350 | 1.519 |
| NDVI | 0.013 | 0.681 | 1.469 | 2.313 |
| LULC | 0.008 | 0.681 | 1.469 | −0.540 |
| Constant | −12.0977 | |||
| Accuracy | Kappa | Resample | |
|---|---|---|---|
| 1 | 0.7321429 | 0.21052632 | Fold02 |
| 2 | 0.6785714 | 0.10000000 | Fold01 |
| 3 | 0.7017544 | 0.17637059 | Fold04 |
| 4 | 0.7079646 | 0.12196845 | Fold03 |
| 5 | 0.6902655 | 0.09309791 | Fold06 |
| 6 | 0.6696429 | −0.01369863 | Fold05 |
| 7 | 0.7232143 | 0.19480519 | Fold08 |
| 8 | 0.7678571 | 0.31578947 | Fold07 |
| 9 | 0.7142857 | 0.20000000 | Fold10 |
| 10 | 0.7232143 | 0.25301205 | Fold09 |
| 25/75% of Overall Sample | 50/50% of Overall Sample | 75/25% Of Overall Sample | Elimination of Redundant Factors | |||||
|---|---|---|---|---|---|---|---|---|
| Models | Success Rate | Prediction Rate | Success Rate | Prediction Rate | Success Rate | Prediction Rate | Success Rate | Prediction Rate |
| RF | 1.000 | 0.719 | 1.000 | 0.767 | 1.000 | 0.786 | 1.000 | 0.780 |
| LR | 0.729 | 0.780 | 0.780 | 0.755 | 0.784 | 0.744 | 0.781 | 0.746 |
| DT | 0.939 | 0.612 | 0.911 | 0.596 | 0.964 | 0.738 | 0.946 | 0.609 |
| ANN | 0.788 | 0.693 | 0.776 | 0.743 | 0.784 | 0.744 | 0.782 | 0.743 |
| RF-LR | 0.999 | 0.773 | 0.999 | 0.775 | 0.999 | 0.779 | 0.999 | 0.773 |
| RF-DT | 0.996 | 0.722 | 0.997 | 0.742 | 0.998 | 0.787 | 0.997 | 0.725 |
| RF-ANN | 0.999 | 0.722 | 1.000 | 0.760 | 1.000 | 0.775 | 1.000 | 0.770 |
| LR-DT | 0.920 | 0.759 | 0.904 | 0.739 | 0.949 | 0.779 | 0.931 | 0.702 |
| LR-ANN | 0.783 | 0.753 | 0.796 | 0.750 | 0.794 | 0.749 | 0.784 | 0.746 |
| DT-ANN | 0.922 | 0.697 | 0.919 | 0.714 | 0.954 | 0.771 | 0.933 | 0.700 |
| RF-LR-DT | 0.995 | 0.757 | 0.995 | 0.758 | 0.996 | 0.790 | 0.995 | 0.732 |
| RF-LR-ANN | 0.985 | 0.757 | 0.981 | 0.766 | 0.983 | 0.772 | 0.980 | 0.765 |
| RF-DT-ANN | 0.995 | 0.723 | 0.995 | 0.748 | 0.997 | 0.789 | 0.996 | 0.730 |
| LR-DT-ANN | 0.915 | 0.745 | 0.905 | 0.739 | 0.943 | 0.780 | 0.920 | 0.713 |
| RF-LR-DT-ANN | 0.987 | 0.750 | 0.984 | 0.756 | 0.989 | 0.791 | 0.985 | 0.738 |
| Training | Rank Total | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ac | R | Sen | R | Sp | R | Pr | R | FPR | R | MCC | R | Ka‘1 | R | AUC | R | MAE | R | RMSE | R | RT | CF | PR | |
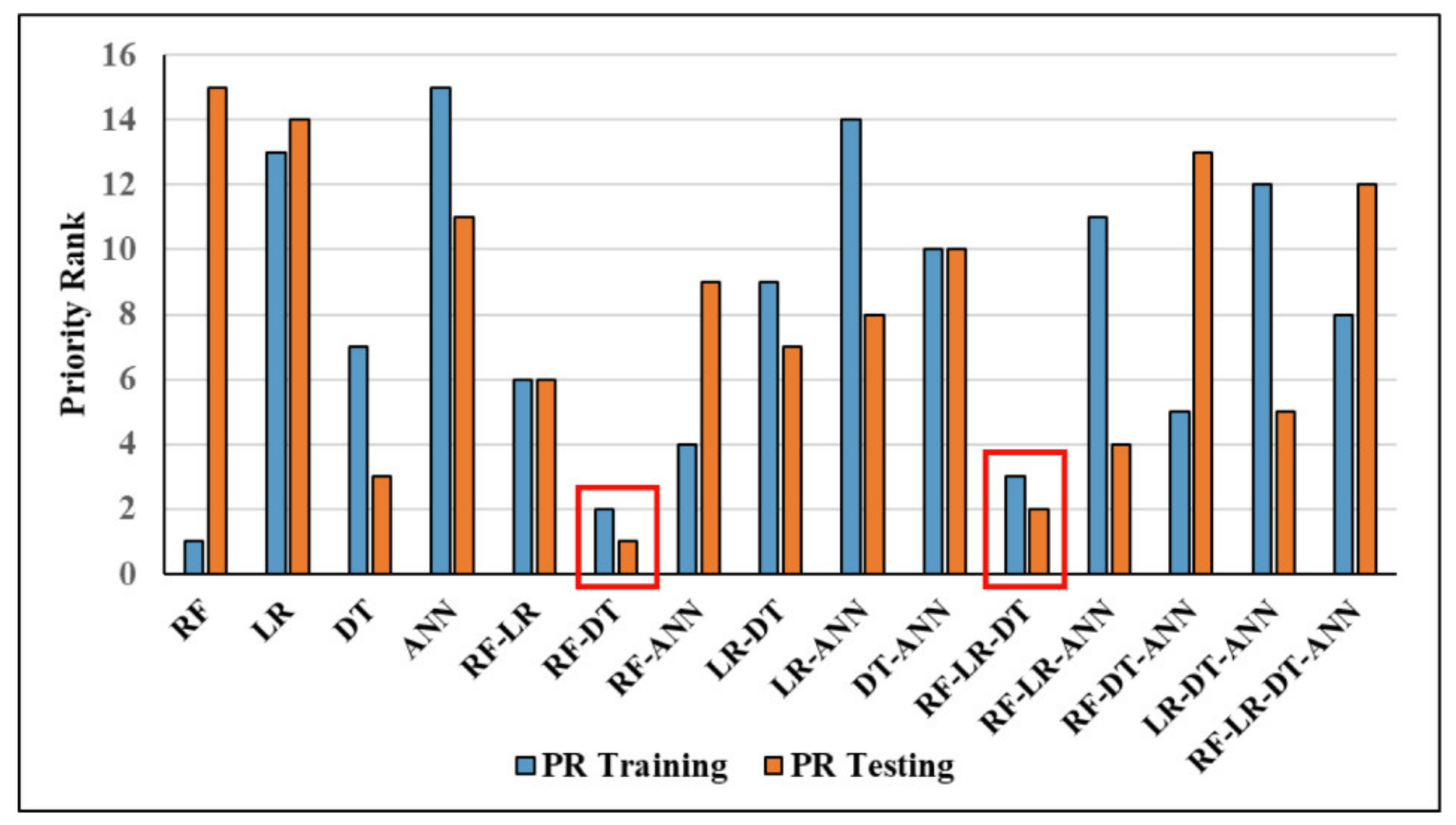
| RF | 1.000 | 1 | 1.000 | 1 | 1.000 | 1 | 1.000 | 1 | 0.334 | 1 | 1.000 | 1 | 1.000 | 1 | 1.000 | 1 | 0.000 | 1 | 0.000 | 1 | 10 | 1 | 1 |
| LR | 0.765 | 13 | 0.257 | 15 | 0.935 | 13 | 0.567 | 13 | 0.086 | 15 | 0.262 | 13 | 0.234 | 14 | 0.784 | 14 | 0.137 | 15 | 0.485 | 13 | 138 | 13.8 | 13 |
| DT | 0.942 | 8 | 0.861 | 5 | 0.969 | 11 | 0.903 | 12 | 0.287 | 5 | 0.843 | 8 | 0.843 | 8 | 0.964 | 9 | 0.012 | 2 | 0.241 | 9 | 77 | 7.7 | 7 |
| ANN | 0.754 | 15 | 0.512 | 13 | 0.797 | 15 | 0.311 | 15 | 0.092 | 13 | 0.256 | 15 | 0.244 | 13 | 0.784 | 14 | 0.098 | 13 | 0.496 | 15 | 141 | 14.1 | 15 |
| RF-LR | 0.956 | 6 | 0.825 | 7 | 1.000 | 1 | 1.000 | 1 | 0.275 | 7 | 0.883 | 6 | 0.876 | 6 | 0.999 | 3 | 0.044 | 10 | 0.209 | 7 | 54 | 5.4 | 6 |
| RF-DT | 0.968 | 2 | 0.886 | 2 | 0.995 | 6 | 0.984 | 6 | 0.295 | 2 | 0.914 | 2 | 0.911 | 2 | 0.998 | 4 | 0.025 | 3 | 0.179 | 2 | 31 | 3.1 | 2 |
| RF-ANN | 0.963 | 5 | 0.850 | 6 | 1.000 | 1 | 1.000 | 1 | 0.283 | 6 | 0.900 | 5 | 0.895 | 5 | 1.000 | 1 | 0.038 | 7 | 0.194 | 5 | 42 | 4.2 | 4 |
| LR-DT | 0.929 | 9 | 0.793 | 9 | 0.974 | 9 | 0.910 | 9 | 0.264 | 10 | 0.804 | 9 | 0.801 | 9 | 0.949 | 11 | 0.038 | 8 | 0.194 | 6 | 89 | 8.9 | 9 |
| LR-ANN | 0.763 | 14 | 0.264 | 14 | 0.929 | 14 | 0.552 | 14 | 0.088 | 14 | 0.257 | 14 | 0.233 | 15 | 0.794 | 13 | 0.130 | 14 | 0.487 | 14 | 140 | 14 | 14 |
| DT-ANN | 0.929 | 10 | 0.793 | 10 | 0.974 | 9 | 0.910 | 9 | 0.264 | 10 | 0.804 | 10 | 0.801 | 10 | 0.954 | 10 | 0.032 | 6 | 0.267 | 10 | 94 | 9.4 | 10 |
| RF-LR-DT | 0.967 | 3 | 0.882 | 3 | 0.995 | 6 | 0.984 | 6 | 0.294 | 3 | 0.911 | 3 | 0.909 | 3 | 0.996 | 6 | 0.026 | 4 | 0.182 | 3 | 40 | 4 | 3 |
| RF-LR-ANN | 0.910 | 11 | 0.646 | 11 | 0.998 | 4 | 0.989 | 5 | 0.215 | 11 | 0.754 | 11 | 0.728 | 11 | 0.983 | 8 | 0.087 | 12 | 0.300 | 11 | 95 | 9.5 | 11 |
| RF-DT-ANN | 0.966 | 4 | 0.871 | 4 | 0.998 | 4 | 0.992 | 4 | 0.290 | 4 | 0.909 | 4 | 0.906 | 4 | 0.997 | 5 | 0.030 | 5 | 0.184 | 4 | 42 | 4.2 | 5 |
| LR-DT-ANN | 0.893 | 12 | 0.639 | 12 | 0.977 | 8 | 0.904 | 11 | 0.213 | 12 | 0.700 | 12 | 0.683 | 12 | 0.943 | 12 | 0.073 | 11 | 0.327 | 12 | 114 | 11.4 | 12 |
| RF-LR-DT-ANN | 0.950 | 7 | 0.814 | 8 | 0.955 | 12 | 0.983 | 8 | 0.271 | 8 | 0.865 | 7 | 0.859 | 7 | 0.989 | 7 | 0.043 | 9 | 0.224 | 8 | 81 | 8.1 | 8 |
| Testing | Rank Total | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ac | R | Sen | R | Sp | R | Pr | R | FPR | R | MCC | R | Ka | R | AUC | R | MAE | R | RMSE | R | RT | CF | PR | |
| RF | 0.753 | 7 | 0.213 | 14 | 0.933 | 5 | 0.513 | 6 | 0.071 | 14 | 0.207 | 15 | 0.181 | 15 | 0.786 | 5 | 0.141 | 9 | 0.497 | 8 | 98 | 9.8 | 15 |
| LR | 0.756 | 5 | 0.223 | 11 | 0.933 | 6 | 0.525 | 5 | 0.074 | 11 | 0.220 | 13 | 0.193 | 14 | 0.744 | 13 | 0.143 | 10 | 0.494 | 6 | 94 | 9.4 | 14 |
| DT | 0.737 | 11 | 0.511 | 2 | 0.813 | 13 | 0.475 | 8 | 0.170 | 1 | 0.316 | 1 | 0.316 | 2 | 0.738 | 15 | 0.019 | 3 | 0.512 | 12 | 68 | 6.8 | 3 |
| ANN | 0.756 | 6 | 0.520 | 1 | 0.792 | 15 | 0.277 | 15 | 0.080 | 9 | 0.245 | 8 | 0.227 | 7 | 0.744 | 14 | 0.117 | 8 | 0.494 | 6 | 89 | 8.9 | 11 |
| RF-LR | 0.761 | 3 | 0.234 | 10 | 0.936 | 4 | 0.550 | 4 | 0.078 | 10 | 0.240 | 10 | 0.211 | 10 | 0.779 | 7 | 0.143 | 11 | 0.489 | 3 | 72 | 7.2 | 6 |
| RF-DT | 0.737 | 12 | 0.468 | 4 | 0.827 | 11 | 0.473 | 9 | 0.155 | 3 | 0.296 | 3 | 0.296 | 4 | 0.787 | 4 | 0.003 | 1 | 0.512 | 12 | 63 | 6.3 | 1 |
| RF-ANN | 0.761 | 4 | 0.213 | 14 | 0.943 | 2 | 0.556 | 3 | 0.071 | 15 | 0.230 | 11 | 0.197 | 12 | 0.775 | 9 | 0.154 | 13 | 0.489 | 3 | 86 | 8.6 | 9 |
| LR-DT | 0.735 | 13 | 0.500 | 3 | 0.813 | 14 | 0.470 | 11 | 0.166 | 2 | 0.306 | 2 | 0.306 | 3 | 0.779 | 7 | 0.154 | 14 | 0.489 | 3 | 72 | 7.2 | 7 |
| LR-ANN | 0.764 | 2 | 0.223 | 11 | 0.943 | 3 | 0.568 | 2 | 0.074 | 12 | 0.243 | 9 | 0.209 | 11 | 0.749 | 12 | 0.151 | 12 | 0.486 | 2 | 76 | 7.6 | 8 |
| DT-ANN | 0.729 | 15 | 0.436 | 5 | 0.827 | 12 | 0.456 | 14 | 0.145 | 4 | 0.267 | 4 | 0.267 | 5 | 0.771 | 11 | 0.010 | 2 | 0.520 | 15 | 87 | 8.7 | 10 |
| RF-LR-DT | 0.748 | 8 | 0.351 | 7 | 0.880 | 8 | 0.493 | 7 | 0.117 | 6 | 0.261 | 5 | 0.255 | 6 | 0.790 | 2 | 0.072 | 6 | 0.502 | 9 | 64 | 6.4 | 2 |
| RF-LR-ANN | 0.767 | 1 | 0.223 | 11 | 0.947 | 1 | 0.583 | 1 | 0.074 | 13 | 0.251 | 6 | 0.215 | 9 | 0.772 | 10 | 0.154 | 15 | 0.483 | 1 | 68 | 6.8 | 4 |
| RF-DT-ANN | 0.735 | 14 | 0.340 | 8 | 0.866 | 9 | 0.457 | 13 | 0.113 | 7 | 0.229 | 12 | 0.225 | 8 | 0.789 | 3 | 0.064 | 5 | 0.515 | 14 | 93 | 9.3 | 13 |
| LR-DT-ANN | 0.740 | 9 | 0.362 | 6 | 0.866 | 10 | 0.472 | 10 | 0.120 | 5 | 0.250 | 7 | 0.339 | 1 | 0.780 | 6 | 0.058 | 4 | 0.510 | 10 | 68 | 6.8 | 5 |
| RF-LR-DT-ANN | 0.740 | 10 | 0.277 | 9 | 0.894 | 7 | 0.464 | 12 | 0.092 | 8 | 0.208 | 14 | 0.197 | 13 | 0.791 | 1 | 0.101 | 7 | 0.510 | 10 | 91 | 9.1 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Namous, M.; Hssaisoune, M.; Pradhan, B.; Lee, C.-W.; Alamri, A.; Elaloui, A.; Edahbi, M.; Krimissa, S.; Eloudi, H.; Ouayah, M.; et al. Spatial Prediction of Groundwater Potentiality in Large Semi-Arid and Karstic Mountainous Region Using Machine Learning Models. Water 2021, 13, 2273. https://doi.org/10.3390/w13162273
Namous M, Hssaisoune M, Pradhan B, Lee C-W, Alamri A, Elaloui A, Edahbi M, Krimissa S, Eloudi H, Ouayah M, et al. Spatial Prediction of Groundwater Potentiality in Large Semi-Arid and Karstic Mountainous Region Using Machine Learning Models. Water. 2021; 13(16):2273. https://doi.org/10.3390/w13162273
Chicago/Turabian StyleNamous, Mustapha, Mohammed Hssaisoune, Biswajeet Pradhan, Chang-Wook Lee, Abdullah Alamri, Abdenbi Elaloui, Mohamed Edahbi, Samira Krimissa, Hasna Eloudi, Mustapha Ouayah, and et al. 2021. "Spatial Prediction of Groundwater Potentiality in Large Semi-Arid and Karstic Mountainous Region Using Machine Learning Models" Water 13, no. 16: 2273. https://doi.org/10.3390/w13162273
APA StyleNamous, M., Hssaisoune, M., Pradhan, B., Lee, C.-W., Alamri, A., Elaloui, A., Edahbi, M., Krimissa, S., Eloudi, H., Ouayah, M., Elhimer, H., & Tagma, T. (2021). Spatial Prediction of Groundwater Potentiality in Large Semi-Arid and Karstic Mountainous Region Using Machine Learning Models. Water, 13(16), 2273. https://doi.org/10.3390/w13162273