Water Distribution in a Socio-Technical System: Resilience Assessment for Critical Events Causing Demand Relocation

Abstract

This study presents an exploratory, historically-informed approach to assessing resilience for critical events that cause demand relocation within a water distribution system (WDS). Considering WDS as an interdependent socio-technical system, demand relocation is regarded as a critical factor that can affect resilience similarly to the more commonly analyzed component failures such as pipe leaks and pump failures. Critical events are modeled as events during which consumer nodes are evacuated within a perimeter varying in size according to a typical length scale in the studied network. The required demand drops to zero in the evacuated area, and the equivalent demand is relocated according to three sheltering schemes. Results are presented for analyzing the effect of the size of the evacuated area, the feasibility of sheltering schemes, vulnerability of particular parts of the city as well as the suitability of network nodes to accommodate relocated demand using a suitable resilience metric. The results provided by this metric are compared with those drawn from common graph-based metrics. The conclusions are critically discussed under the consideration of historical knowledge to serve as a basis for future research to refine resilience assessment of socio-technical systems.

1. Introduction

Cities and the infrastructure systems that permeate them are historically evolved socio-technical systems. It is common to regard infrastructures as purely technical system from an engineering perspective. However, water being a vital resource for human life and activity there is a connection between the urban population with its demand for fresh water and the water distribution system (WDS) that supplies it. Together, these two sub-systems constitute an interdependent socio-technical system. First conceived and implemented in western European countries in the 19th century due to considerations of hygiene and sanitation [1,2], WDSs evolved jointly with the society that constructed and maintained them in their own image. An infrastructure network maps the demands, needs and economic possibilities of the society which conceives and constructs them. More so: historians have pointed out that infrastructure systems can carburize power relations. The scope of action of later generations thus can be limited by the durability of the systems [3].

In spite of their interdependence, the two sub-systems are disparate in nature. In cities of the industrialized Global North, the topology of WDS is generally static, since they are typically subterranean. Once built, it is often too expensive to change their shape, furthering so-called path dependency and cementing their configuration. Nevertheless, this also implies that they are comparatively safe against external threats. Even after heavy bombing in World War II, Berlin water infrastructures for instance remained more or less intact [4].

By contrast, the social system which populates the WDS may be more volatile and behave more dynamically. Daily routines of people engaged in labour lead to demand peaks in the mornings and evenings as well as shifts in demand from residential to commercial or industrial areas of a city. These temporal and spatial variations of demand are foreseeable and the WDS may be designed to match the supply to them. However, if a critical event occurs, large numbers of people may be forced to leave their neighbourhoods and relocate to different parts of the city (e.g., bomb disposals that require evacuations in Frankfurt am Main [5], Beirut explosion in 2020 [6], Texas weather crisis [7], or in case of floods, extreme weather events, natural catastrophes, attacks, chemical leaks). In consequence, the demand for water moves with them whereas the WDS remains unchanged. How well the WDS is able to fulfill its functionality as a technical system of satisfying demand for water in the face of sudden unexpected changes in conditions is a question of resilience. In the presented work, the effect of the described disparities within the interdependent socio-technical WDS on water service availability (WSA) are studied and the system’s resilience is assessed using a suitable metric.

1.1. Research Questions

In order to further detail the research questions, the following section will briefly introduce the approach of the study and state five concrete questions to which the focus is narrowed. In Section 2, the modeling approaches are more thoroughly illustrated.

As stated above, the effect of demand relocation in an urban WDS associated with the displacement of citizens caused by critical events is investigated. In this scenario, an area of the city is evacuated meaning that demand moves within the network while the water infrastructure remains intact. Different factors come into play here, such as the size of the evacuated area as well as how and where relocated citizens seek shelter. As the evacuated area can occur in any part of the city, vulnerable parts of the network need to be identified. Furthermore, as relocated demand is accommodated in different parts of the city varying degrees of suitability may be identified throughout the network. Finally, different approaches to assessing resilience of WDS entail computationally expensive or less expensive analysis. The equivalence of these approaches needs to be examined. Consequently, the following research questions are posed:

(i)

What effect does the size of evacuated area have?

(ii)

With which sheltering scheme can demand be best fulfilled?

(iii)

Which part of the city is most vulnerable?

(iv)

Which areas are best suited for accommodating relocated demand?

(v)

How do the results of the resilience assessment compare to graph-theoretical resilience metrics?

The remainder of the presented work is structured in the following way. After reviewing the relevant existing work, the system analysis and methodology for the modeling of the water network and the critical events is outlined. The results of the study are then presented and discussed.

1.2. Related Work

The concept of resilience has a long and iridescent past, being used in such diverse fields as psychology, anthropology, sociology, philosophy and environmental sciences [8]. It has been adopted by the United Nations (UN) as a desirable attribute of societies and communities to “resist, absorb, accommodate to and recover from the effects of a hazard in a timely and efficient manner” [9]. This concept is not however uncontroversial and under close scrutiny it has been noted to incorporate elements of contemporary ideology [8]. Holling first applied it for describing complex systems in the context of ecosystems [10]. It was introduced to the discipline of engineering by Hollnagel constituting a new sub-discipline Resilience Engineering [11,12] albeit one which is closely related to systems engineering. The importance of conceiving technical systems as socio-technical systems when studying resilience in engineering has been stressed [13]. In mechanical engineering, resilience was identified as a strategy for coping with uncertainty [14]. Altherr et al. give the following definition of a resilient technical system:

“A resilient technical system guarantees a predetermined minimum of functional performance even in the event of disturbances or failure of system components, and a subsequent possibility of recovering at least the setpoint function. Resilience can be increased by adjusting the system state via monitoring, responding, learning and/or anticipating, as well as by systematically designing the system topology.”

[14]

From this, two characteristics of a technical system come to play during a disturbance: withstanding to a degree which allows to fulfill the minimum functional performance as well as recovering from the disturbance. In the presented work, the focus is limited to the former characteristic.

When studying resilience of WDS it is necessary to quantify this ambiguous concept. There is a wide range of different resilience metrics as four recent reviews of measures of resilience for infrastructure systems show [15,16,17,18]. Core principles of the relevant approaches will briefly be mentioned here. A common approach to modeling WDSs is to describe them as mathematical graphs [19]. In consequence, graph-based resilience metrics make up a substantial portion of resilience measures. They focus on water network topology considering the two aspects, redundancy and connectivity [15]. This is a generalized approach which refrains from studying specific failure scenarios and considers the uncertain nature of failures. This approach is in line with common conceptualizations of resilience as opposed to robustness where a given set of possible failures is used to fortify a technical system [19,20,21]. Some examples of this type of metric simply use statistical and spectral measures in graph theory, e.g., betweenness or closeness centrality spectral gap and algebraic connectivity [15]. Others take into account water network specific characteristics, such as pipe friction and the ensuing head loss, and connect these with the above mentioned measures based on graph theory [19,22]. However, it has been pointed out that the validity of the assumption that measures of topology can assess resilience has not been justified [23]. A second group of resilience measures focus on the functional performance of a system under conditions of failure. When studying the functional performance of a WDS for resilience assessment, perturbations are often introduced such as pipe failures, additional demand or pollution [20,24]. In this approach, it is again important to avoid studying certain predefined failure scenarios so as not to remain in the limits of robustness analysis. Todini [25] proposes a measure based on the energy surplus in a looped water distribution network. This has given rise to similar measures with some variations and adaptations (e.g., [26,27]). While the measures mentioned so far consider the static WDS, a third approach has been explored which takes into account the dynamic behaviour of the water network. On approach here is to relate probabilities of recovery of the WDS and of it remaining in an unsatisfactory state [28,29]. Zhuang et al. [30] chose to evaluate resilience in terms of the ratio of satisfied water demand to required water demand. For the purpose of the presented work, this last metric proves the most useful as it directly measures the functional performance of the studied WDS.

The problem of demand uncertainty in WDS has been the subject of several publications in the past which focus on demand uncertainty under normal operating conditions rather than during critical events [31,32,33]. Lu et al., consider demand for life-supporting resources including water under an emergency in a game-theoretical equilibrium model that contains a multi-layer infrastructure network [34]. Their approach provides an interesting insight into interdependencies between the infrastructures as well as of the response of the citizens but proves too complex for the assessment of resilience of the WDS as a socio-technical system only. To the best of the authors’ knowledge, so far no study has been proposed that (i) perceives the WDS as a socio-technical system that may be peturbed solely by its interdependence with the society populating it rather than component failure, (ii) models critical events informed by historical knowledge of relocation of citizens within a city during such events, (iii) measures resilience of a WDS by assessing minimum functional performance during operation while maintaining the uncertain nature of critical events, (iv) relates the results to topological resilience metrics for comparison and validation. The presented work aims to fill this gap.

2. Materials and Methods

This section describes the methods used to assess the resilience of a benchmark WDS in order to answer the research questions posed in Section 1.1 and specifies the terminology used throughout the paper. It starts by providing a general description of modeling WDS as mathematical graphs and justifies the choice of the selected benchmark WDS. Methods introduced in Section 2.2 show how the critical events are modeled. Sheltering schemes are presented in Section 2.3. Section 2.4 shows the resilience metric used to assess the resilience of the WDS. A further metric evaluating the number of under-serviced nodes as well as a brief overview of two graph-based metrics are given in Section 2.5 and Section 2.6, respectively.

2.1. Modelling WDSs

The WDS is modeled as a planar mathematical graph. The vertices represent junctions, tanks and reservoirs and will be referred to as nodes. The edges represent pipes and pumps and will be referred to as links. The WDS is modeled using the Water Network Tool for Resilience (WNTR), a Python package designed to simulate and analyze resilience of WDSs that is based on EPANET [35]. In order to analyze the performance of the WDS in critical events, pressure dependent simulations are run using the EPANET solver (version 2.2) implemented in WNTR. Pressure dependent simulation accounts for pressure–demand relationships in the WDS [16] and allows us to express the delivered demand depending on the pressure while relying on empirical equations, see Section 2.5.

Each node in the WDS graph has a fixed base demand that is multiplied by a demand multiplier which can vary in time. Demand multipliers allow for applying demand patterns to the WDS. Base demand and the demand patterns determine the required demand D, i.e., the demand that the WDS should satisfy in order to perfectly service all nodes. The available flowrate d is obtained by running the pressure dependent simulations. Water service availability (WSA) A at time t for node n can then be expressed as a ratio of the available flowrate and the required demand:

$$A_{n,t}=\frac{d_{n,t}}{D_{n,t}}.$$

(1)

This study uses the C-Town WDS. C-Town is a benchmark WDS with 396 nodes and 444 links. In total, 334 nodes have base demand higher than zero and can be considered consumer nodes. C-Town is supplied from one reservoir and contains seven water tanks with a total capacity of 9501 m${}^3$, 11 water pumps and average daily required demand of approximately 15,500 m${}^3$ [24]. As such, it represents a local scale WDS modeled with a high resolution. Considering average daily required demand per capita of 130 liters per day, the WDS supplies a population of about 120,000 if other than residential use is not considered.

2.2. Modelling Critical Events

In the context of this study, the term critical event describes an event of strong demand relocation within the WDS as a result of perturbations in the socio-technical system. A critical event does not cause failures in the WDS directly. Instead, it is characterized by perturbations that have an influence on the social system, motivating or forcing people to relocate. In contrast to the term disruptive event, critical events do not have to include a disruption of services and can include emergency situations such as bomb disposals when evacuation is necessary even though the infrastructure system is intact. In Germany, such evacuations happen regularly, especially in cities that were heavily bombed during World War II such as Frankfurt am Main, and lead to the relocation of tens of thousands of people (25,000 in Frankfurt am Main in 2021 [5]). Other examples when people relocate despite the WDS staying intact have been mentioned in Section 1. Moreover, the term critical event does not have a strong normative character like the term disruptive event or catastrophic event. Resulting in altered demand patterns, the perturbation that such significant changes on the social side of the socio-technical system cause can influence the functioning of the WDS as a whole.

During the critical event, required demand from nodes in the evacuation area is relocated onto shelter nodes outside of the evacuation area so that for each time step, the overall required demand in the WDS under normal operating conditions is equal to the overall required demand in the WDS with demand relocation during the critical event. This means that the evacuated population keeps relying on the WDS rather than using mobile and network-independent solutions. This approach was selected based on the experiences reported by German Federal agencies since the 1960s when experts recommended the deployment of mobile and network-independent water supply systems. These were envisaged to serve in case of a possible Atomic War as well as in case of natural disasters and network failure. Over time, it became apparent that these substitutes were extremely cost intensive. In addition, they did not really meet the needs of rapid, demand-oriented and efficient distribution [36,37,38,39]. Our approach of continuing to use the existing network is the result of these experiences.

Evacuation area can be expressed as a set of nodes within the distance of the evacuation radius r from the origin of the evacuation area, node o:

$$E=\{n\in N:|no|\le r\},$$

(2)

where N is a set of all consumer nodes in the WDS: $N=\{n\in \widehat{N}:D_n>0\}$ with $\widehat{N}$ being the set of all nodes in the WDS. Since consumer nodes are of primary focus here, the terms nodes and consumer nodes will be considered synonymous below.

It is assumed that in each critical event, there is only one evacuation area the origin of which is any consumer node in the WDS. Higher density of nodes reflects higher densities of population and thus higher risk of the occurrence of a critical event in the social system. Moreover, since the density of nodes in the C-Town WDS is relatively homogeneous, selecting nodes as origins of the evacuation area is a sensible approach. Nodes in the central parts of the WDS as well as nodes at the edge of the WDS can equally serve as origins of evacuation areas. While this results in evacuation areas with their origins at the edge of the WDS having less nodes than if the origin is centrally located, past experiences show that critical events can occur at the margins of the WDS as well and thus should not be excluded from the analysis (e.g., the Beirut explosion in 2020 [40]).

The critical events are assumed to start just before the first peak in the required demand, at time t = 4 h. 48 h are simulated, reflecting real-world experiences that show that after 2 days, the critical event is either overcome or batch solutions are set up to provide water supply [6,24].

2.3. Sheltering Schemes

During critical events, the population relocated from the evacuated area must be accommodated elsewhere. In this study, it is assumed that the population relocates to shelter areas outside of the evacuation area but within the urban area serviced by the WDS, relying on the WSA provided by the WDS as discussed in Section 2.2. Relocating the required demand from the evacuation area is modeled along three sheltering schemes:

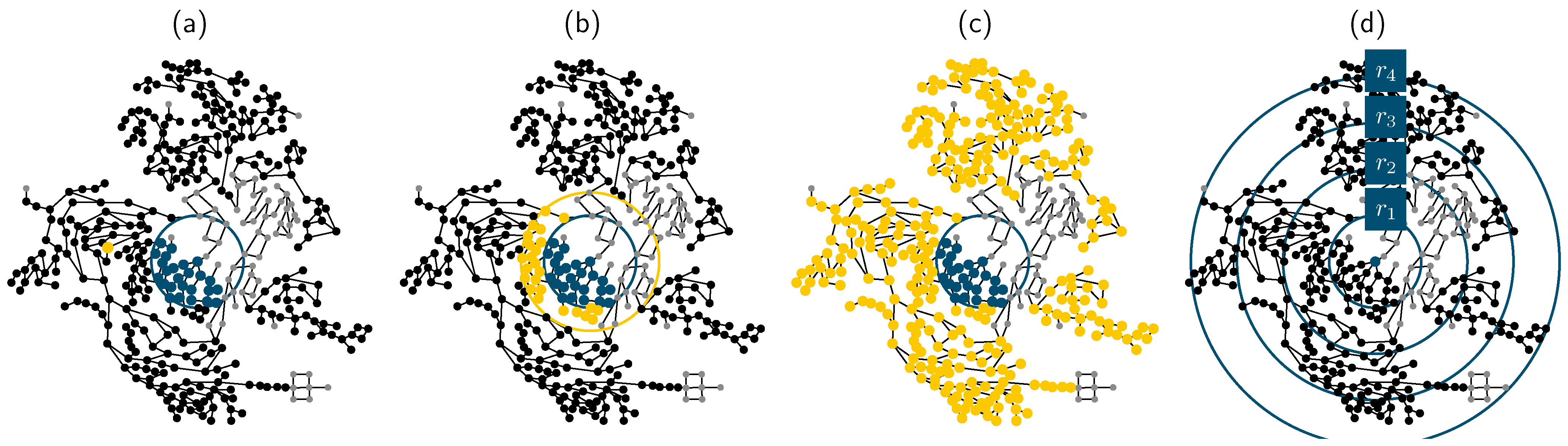
• centralized sheltering
  In the centralized sheltering scheme, the set of shelter nodes is a singleton consisting of precisely one node, n, see Figure 1:

  $$S_{\mathrm{cen}}=\{\exists n:n\in N\backslash E\}$$

  (3)
  The required demand from the evacuation area E is summed for each time step t and transferred onto a single pre-defined central shelter node from the set of shelter nodes, $c\in S_{\mathrm{cen}}$:

  $$D_{c,t}=\sum _{n\in E}{D}_{n,t}.$$

  (4)
  While in reality, multiple sheltering locations are often dedicated to accommodate evacuated population, selecting a single shelter node represents the most critical case. Hence, centralized schemes with more than one shelter node have not been considered in the scope of this work but might be the subject of future research.
• near-at-hand sheltering
  In the near-at-hand sheltering, demand from the evacuated area is distributed onto the immediate annulus around the evacuation area, with the width $0.5r$ (Figure 1). Shelter nodes can then be expressed as a set of nodes $S_{\mathrm{nah}}$:

  $$S_{\mathrm{nah}}=\{n\in N:r<|no|\le 3r/2\}.$$

  (5)

  where N is the set of all consumer nodes and $\left|no\right|$ is the distance between a consumer node n and the origin of the evacuation area o.
  A probability p for each node in $S_{\mathrm{nah}}$ is generated using the truncated normal distribution function from the Python package scipy so that

  $$\sum _{n\in S_{\mathrm{nah}}}{p}_n=1.$$

  (6)
  The required demand on a shelter node after demand relocation is then

  $$D_{n,t}=p_n\sum _{n^{\prime }\in E}{D}_{n^{\prime },t}\mathrm{for}n\in S_{\mathrm{nah}}.$$

  (7)
• diffuse sheltering
  During the diffuse sheltering, demand from the evacuated area is distributed onto the remaining nodes in the city (Figure 1). The set of shelter nodes, $S_{\mathrm{dif}}$, can thus be expressed as

  $$S_{\mathrm{dif}}=N\backslash E$$

  (8)

  and the required demand is relocated on the shelter nodes with the same strategy as in the near-at-hand scheme, i.e., using the truncated normal distribution.

2.4. Resilience Assessment

In order to answer the research questions posed in the Introduction, sets of simulations were run using the Epanet simulator implemented in the WNTR package. All three schemes were simulated with four evacuation radii each. The radii were de-dimensionalized with relation to the radius of a circumcircle of the area of the WDS, as shown in

Table 1. Dimensionless evacuation radii and their magnitude.

Name	Magnitude
$r_1$	$1/4$
$r_2$	$1/2$
$r_3$	$3/4$
$r_4$	1

.

Each consumer node was selected as the origin of the evacuation area. For the centralized sheltering, each consumer node from the remaining set $N\backslash E$ was selected as the shelter node. For the near-at-hand and the diffuse sheltering scheme, 100 and 300 runs with varying probability distributions were run, ensuring that nodes in the shelter node set have a sufficient variety of required demand.

For the evaluation, the resilience index proposed by Zhuang et al. [30] is used, which expresses the relation between the actual flow d and the required demand D for a given time period T:

$$\rho =\frac{{\displaystyle \sum _{t=0}^T}{\displaystyle \sum _{n\in N}}{d}_{n,t}}{{\displaystyle \sum _{t=0}^T}{\displaystyle \sum _{n\in N}}{D}_{n,t}}$$

(9)

Originally, this metric was proposed for evaluating the resilience of a water network faced with link failures and stochastically defined shifts in demand. For a single evacuation area characterized by an origin node o and radius r, the value of the resilience index $\rho$ was obtained as the mean value over all simulations that were performed for that origin node. In the centralized sheltering scheme, the mean value was obtained from the values of all shelter node simulations:

$${{\displaystyle \overline{\rho }}}^{\left(o\right)}=\frac{1}{|N\backslash E^{\left(o\right)}|}{\displaystyle \sum _{n\in N\backslash E^{\left(o\right)}}}{\rho }_n^{\left(o\right)},$$

(10)

where $N\backslash E^{\left(o\right)}$ is a set of all nodes that were not in the set of evacuated nodes for the origin o, $E^{\left(o\right)}$, and could thus be selected as shelter nodes.

From the perspective of a shelter node s, an equivalent expression could be obtained:

$${\overline{\rho }}^{\left(s\right)}=\frac{1}{|N^{\left(s\right)}|}\sum _{n\in N^{\left(s\right)}}{\rho }_n^{\left(s\right)},$$

(11)

where $N^{\left(s\right)}$ is a set of all nodes that are in a sufficient distance from the shelter node s to serve as origins of an evacuation area.

For the near-at-hand and diffuse sheltering, the mean was obtained from M simulation runs, with $M=100$ and $M=300$, respectively:

$${\overline{\rho }}^{\left(o\right)}=\frac{1}{M}{\displaystyle \sum _{m=1}^M}{\rho }_n^{\left(o\right)}$$

(12)

The mean resilience index for the entire WDS could be expressed as a mean of the resilience indices for each origin o:

$$\overline{\rho }=\frac{1}{\left|N\right|}{\displaystyle \sum _{o\in N}}{\overline{\rho }}^{\left(o\right)}$$

(13)

2.5. Evaluation of Under-Serviced Nodes

Another useful metric is the number of under-serviced nodes (USN). These are consumer nodes outside of the evacuation area that have insufficient pressure and thus cannot deliver sufficient flowrate in order to satisfy the required demand. In the pressure-driven simulation in WNTR, actual flow is calculated based on pressure as

$$d=\left\{\begin{array}{cc}0\hfill & h\le H_0\hfill \\ D{\left(\frac{h-H_0}{H_f-H_0}\right)}^{1/e}\hfill & H_0\le h\le H_f\hfill \\ D\hfill & h\ge H_f\hfill \end{array}\right.$$

(14)

where $H_0$ is the minimum pressure and $H_f$ the required pressure [35]. Demand is fully satisfied (WSA $A=1$) if the pressure h is greater than the required pressure $H_f$. If the pressure lies between $H_f$ and $H_0$, demand is partially satisfied (WSA $0<A<1$), and if the pressure lies below $H_0$, the available flowrate will be zero (WSA $A=0$). In the present paper, $H_0$ was set to 0 and $H_f=15\mathrm{m}$. The number of USN at time t for origin node o is the size of a set of all nodes that were not in the evacuation set E and had a pressure lower than $H_f$:

$${\eta }_{\mathrm{sim},t}^{\left(o\right)}=\left|U_t\right|\mathrm{with}{U}_t=\{n\in N\backslash E^{\left(o\right)}:h_{n,t}<H_f\}$$

(15)

${\eta }_{\mathrm{sim},t}$ is obtained from a simulation with relocated demand. In order to determine whether there was a change in the number of USNs between normal (reference) operating conditions and operating conditions with relocated demand, a new variable ${\eta }_t^{\left(o\right)}$ was introduced to express the difference between the number of USN resulting from the simulation with relocated demand, ${\eta }_{\mathrm{sim}}$, and the number of USN of the WDS under normal operating conditions, ${\eta }_{\mathrm{ref}}$:

$${\eta }_t^{\left(o\right)}={\eta }_{\mathrm{sim},t}^{\left(o\right)}-{\eta }_{\mathrm{ref},t}^{\left(o\right)}.$$

(16)

A value of $\eta \left(t\right)$ characteristic for the entire WDS could be obtained from the mean value of ${\eta }^{\left(o\right)}\left(t\right)$ of each origin of the evacuation area, o:

$${\overline{\eta }}_t=\frac{1}{\left|N\right|}{\displaystyle \sum _{o\in N}}{\eta }_t^{\left(o\right)}.$$

(17)

2.6. Basic Graph-Based Resilience Metrics

In addition to the evaluation of the resilience index according to Zhuang [30], two graph-based metrics that are commonly used for resilience assessment have been evaluated: betweenness centrality and the shortest path length. To compute these, the WNTR package relies on methods from the Network X package [41,42].

Betweenness centrality of a node n is the sum of the fraction of all-pairs shortest paths that pass through n:

$$c_B\left(n\right)={\displaystyle \sum _{s,t\in N}}\frac{\sigma (s,t|n)}{\sigma (s,t)},$$

(18)

with N being the set of all nodes, $\sigma (s,t)$ the number of shortest paths between s and t and $\sigma (s,t|n)$ the number of shortest paths between s and t that pass through the node n (other than s and t) [43].

The shortest path length metric computes the shortest hydraulic path length between the closest source and all other reachable nodes for a weighted graph using the Dijkstra algorithm implemented in the method single_source_dijkstra from the Network X package [44]. The weighing was performed with the head loss $\Delta H$ averaged over the time of the simulation on each link in the WDS simulated under normal operating conditions (without demand relocation).

3. Results

This section will present and discuss the results of the study with regard to the research questions posed in Section 1. Accordingly, it will be structured in the same order.

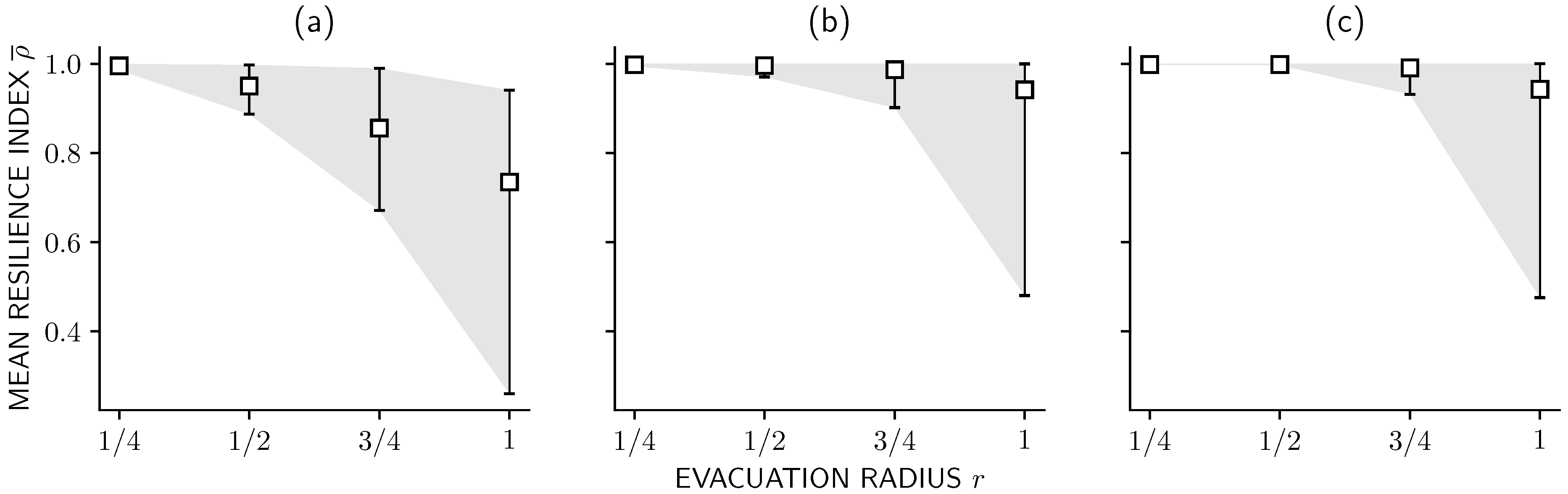
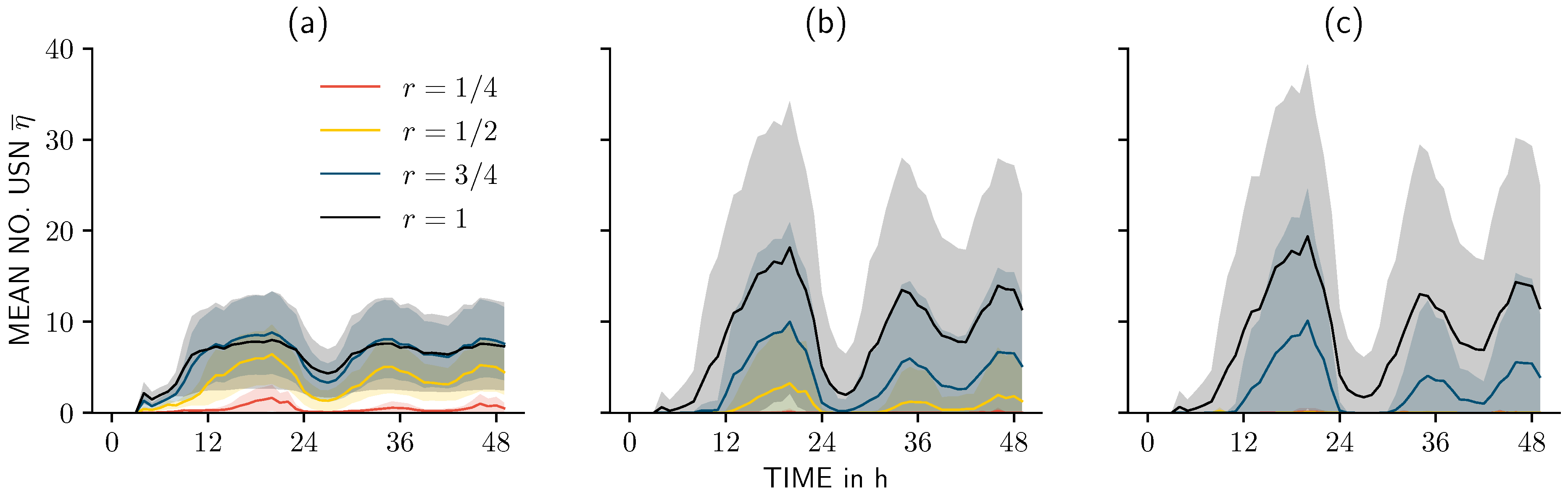
3.1. Effect of Evacuation Radius

In order to answer the first research question, the results for all simulation runs were aggregated to calculate the mean resilience index $\overline{\rho }$ for each evacuation radius. The values are plotted over evacuation radius for all three sheltering schemes as depicted in Figure 2. Additionally, error bars are added to depict the spread of values of ${\overline{\rho }}^{\left(o\right)}$ for all nodes in the network. The size of the error bar is determined by the maximum and minimum values of ${\overline{\rho }}^{\left(o\right)}$ for $o\in N$. As illustrated in Section 2, the spread of evacuation radii was chosen to range from minimal detectable impact to a critical event encompassing the entire network. The results in Figure 2 showed close to maximum values for resilience index $\overline{\rho }\approx 1$ for the smallest evacuation radius $r_1$. In all three sheltering schemes it can be observed that $\overline{\rho }$ decreased quadratically, with increasing values of r. Closer inspection shows that this decrease of $\overline{\rho }$ scaled with the square of the evacuation radius for the centralized sheltering scheme $\overline{\rho }\propto -r^2$. As the nodes that may be evacuated were fairly evenly distributed and required demands did not vary greatly between nodes this behaviour was consistent with the expectations. This did not hold true for near-at-hand and diffuse sheltering schemes. Here, additional influences of differing number of available shelter nodes for different evacuation radii came into play.

Figure 3 shows the mean and standard deviation of USN over time for all evacuation radii in the case of each sheltering scheme. In all schemes the number of USN varied with time depending on the required demand in the network. For the centralized scheme, roughly equal numbers of nodes were under-serviced for evacuation radii $r_4$ and $r_3$, the mean never exceeding 10 nodes. For the evacuation radius $r_2$, a reduced number of nodes was under-serviced, though from the onset of the critical event to the end of the run time there were USNs in the network. Only at times of high required demand in the network were there USNs for $r_1$. This suggests that especially if the relocated demand reached high values, a distinct increase in the number of USN could be observed. Nodes other than the shelter node were thus also under-serviced. It may also be attributable to the fact that with growing evacuation radius the remaining nodes were similarly affected. Both the near-at-hand and diffuse sheltering schemes showed much higher numbers of USN with a maximum of 20, though the deviation from full service was much lower in absolute terms as shown in Figure 2. In the near-at-hand sheltering scheme no nodes were under-serviced for $r_1$ while for $r_2$ only at times of high required demand. For $r_4$ the same amount of nodes was under-serviced in the diffuse sheltering scheme as in the near-at-hand scheme while for $r_3$ during times of low required demand, full service was available.

3.2. Effect of Sheltering Scheme

Addressing the second research question, the sub-figures in Figure 2 and Figure 3 are now compared to assess the effectiveness of the three sheltering schemes.

For the lowest value of r, $\overline{\rho }$ for all three schemes was close to the maximum of 1. As the radius increased, the resilience index decreased significantly for the centralized sheltering scheme, the mean reaching the lowest value of $0.735$ for $r_4$ while the minimum value for any node in the network was $0.26$ for a critical event with this expanse. The effect of relocation was already noticeable at evacuation radii $r_2$ and $r_3$. This shows serious under-servicing of demand in the network. By comparison, the near-at-hand scheme only showed a marginal decrease of $\overline{\rho }$ at $r_3$ while at $r_4$ the lowest value was just under $0.95$. Here, mainly the minimum values for any node in the network show that there were areas in the network where demand relocation could cause reduced service with a reduction of $10\%$ for the origin with the worst effect and $\overline{\rho }=0.48$ at $r_4$. The diffuse sheltering scheme showed no reduction of $\overline{\rho }$ for $r_1$ and $r_2$. For evacuation radii $r_3$ and $r_4$, the values of the centralized and near at hand sheltering schemes overlapped. This can be explained by the fact that the set of available shelter nodes for these schemes and evacuation radii largely corresponded to one another.

When regarding the number of under-serviced nodes this phenomenon could also be detected. As has already been remarked in the previous section, the number of nodes was smaller in the centralized scheme than in the other two for radii $r_3$ and $r_4$, but greater for radii $r_1$ and $r_2$. It can be seen that the number exceeds 1 in this scheme for the three larger radii, implying that not only the shelter node was under-serviced. This means that centralized sheltering may also reduce water service in other parts of the network, though only at a limited number of nodes. In the case of the near-at-hand and diffuse schemes some nodes suffered reduced service which could mean that the accommodating population at shelter nodes had to reduce their own consumption as a result of sheltering the relocated population, testing the social cohesion and cooperation in the population. During past events, the authorities and the public were able to successfully appeal to the cooperativeness of those not affected [45].

In summary, from a technological perspective, the diffuse sheltering scheme was best suited for maintaining water service in the case of a critical event. However, other considerations played a significant role here such as efficiency for supplying aid from the authorities’ perspective and the willingness of the population in the sheltering area to accommodate the citizens from the evacuated area.

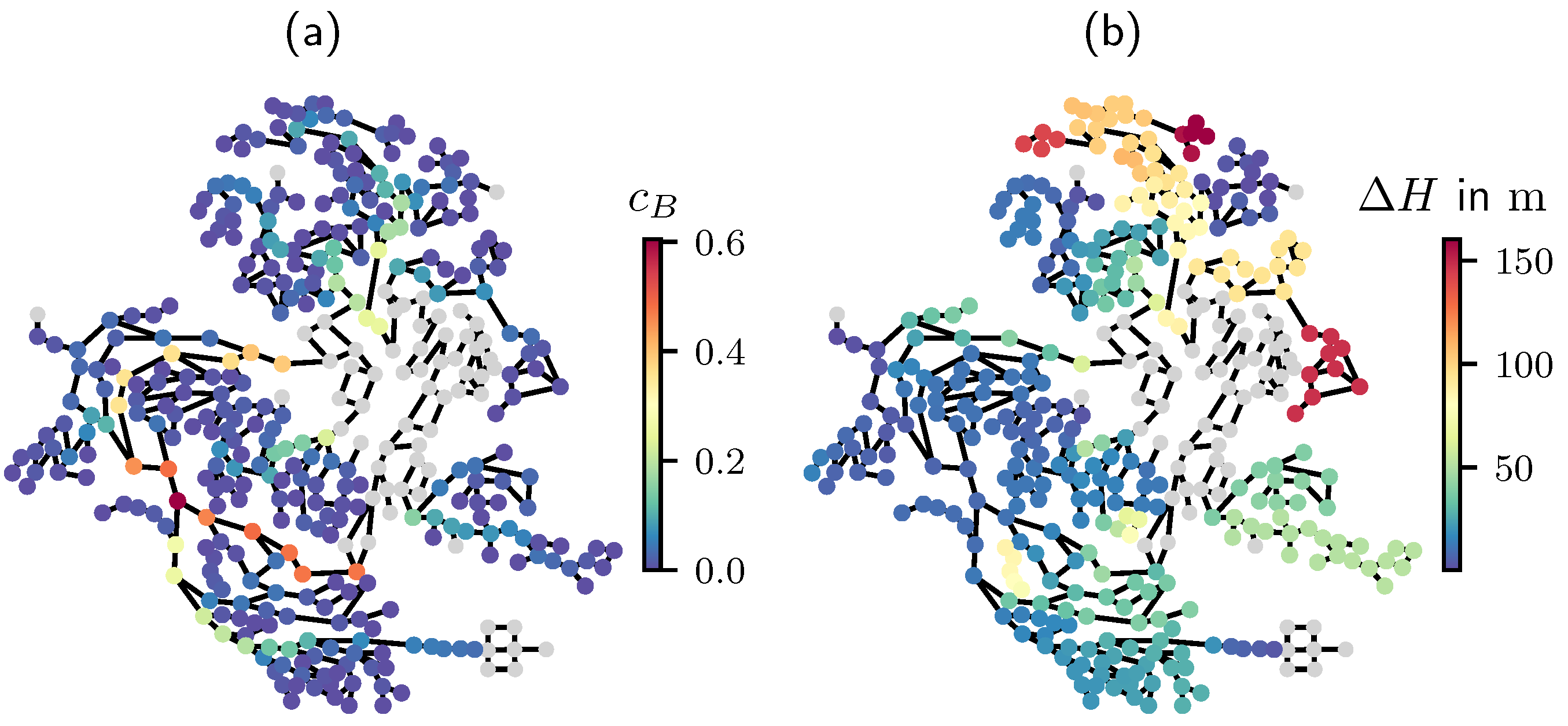
3.3. Vulnerable Areas

Figure 4 shows the WDS for all sheltering schemes and all evacuation radii where the node attribute was the average resilience index ${\overline{\rho }}^{\left(o\right)}$ for that node when it was the evacuation origin. The spread of values was between the minimum and maximum values of ${\overline{\rho }}^{\left(o\right)}$ and is represented by the error bars in Figure 2. For the centralized sheltering scheme at $r_1$, low values of ${\overline{\rho }}^{\left(o\right)}$ could be observed at the centre of each of the two main clusters of consumer nodes with demand while the edges had higher values of ${\overline{\rho }}^{\left(o\right)}$. This was consistent with the fact that when origins lay at edges of the WDS, less demand needed to be relocated. As the evacuation radius increased the evacuation area was no longer on the scale of the two clusters and so the areas with low values for the resilience index merged into one at the core of the entire network. A viable interpretation of this phenomenon is that it was (i) easier to maintain water service when less demand was relocated and (ii) easier to service relocated demand in the centre of the city than at the edges. A vivid example of this are the two small peripheral clusters in the eastern part of the city. When these were evacuated and the demand relocated to the centre high values of resilience index were achieved. Regarding the near-at-hand and diffuse sheltering schemes, the differences for radii $r_1$ and $r_2$ were too insignificant to draw compelling conclusions. Nevertheless, the cluster of nodes with higher resilience indices in the centre of the network were remarkable. This may be explained by the fact that to the northeast there was an uninhabited area that could not accommodate relocated demand forcing it instead south and southwest which was closer to the main supply line from the reservoir in the network. Furthermore, for $r_2$ in the near-at-hand sheltering scheme two vulnerable areas could be detected to the north and west. Here it appears that the shelter area was such that it forced normally well connected demand to relocate to more remote areas in the network.

As previously noted, for radii $r_3$ and $r_4$ both near-at-hand and diffuse schemes approximately coincided. This is also reflected in Figure 4. However, for the near-at-hand scheme at radius $r_3$ there was an area with lower values of ${\overline{\rho }}^{\left(o\right)}$ at the main line. The interpretation offered here is that the population on the main line relocated to areas in the periphery with significantly lower connectivity to tanks or reservoirs. This is further illustrated by the fact that nodes removed from the centre to the southwest showed lower values of ${\overline{\rho }}^{\left(o\right)}$ than towards the north and east. As this area was closer to the supplying reservoir, this phenomenon shows that when demand was relocated downstream, it was harder to service than when it was moved upstream, implying a general inequality depending on the proximity to the reservoir which was generally alleviated by supply tanks distributed throughout the network. Nonetheless, in the critical events studied here it was still noticeable.

The results shown here for vulnerable areas reflect to a certain degree the methods utilized here for modeling the critical events. However, disparities between the periphery and centre as well as between upstream and downstream were still recognizable in the network.

3.4. Identifying Shelter Nodes

Figure 5 depicts values of the mean resilience index ${\overline{\rho }}^{\left(s\right)}$ for each node of the WDS if it was chosen as a shelter node in the centralized sheltering scheme (Figure 1a). The values were computed using Equation (11). Higher values of ${\overline{\rho }}^{\left(s\right)}$ suggest the respective node was better suited to serve as a rescue node. For the evacuation radius $r_1$, big clusters of shelter nodes with high values of ${\overline{\rho }}^{\left(s\right)}$ could be observed, despite the values of betweenness centrality $c_B$ being low in the same areas, see Figure 6a. Shelter nodes with low ${\overline{\rho }}^{\left(s\right)}$ were usually cul-de-sacs and tended to have higher values of shortest path length $\Delta H$, see Figure 6b. Especially in the North of the WDS, the value of ${\overline{\rho }}^{\left(s\right)}$ dropped for a significant number of nodes when considering the evacuation radius $r_2$. The nodes with the highest $\Delta H$ were among the nodes with the lowest ${\overline{\rho }}^{\left(s\right)}$ in the north of the WDS. In the centre of the WDS, the proportion of nodes with maximum ${\overline{\rho }}^{\left(s\right)}$ also decreased, even though $\Delta H$ was comparatively low in this area. For the remaining radii $r_3$ and $r_4$, two clusters of high ${\overline{\rho }}^{\left(s\right)}$ could be identified in the south and the west of the WDS. Both of these areas had a relatively low $\Delta H$, but also a low betweenness centrality $c_B$. To answer the research question (iv), two clusters could be identified that provided high values of ${\overline{\rho }}^{\left(s\right)}$ regardless of the size of the evacuation area. These were best suited to serve as shelter nodes during a critical event with demand relocation. The suitability of the southern cluster was justified by its location in the immediate vicinity of the main reservoir of the WDS, equipped with large diameter pipes to supply the entire system. The western cluster was supplied by two tanks in the very west and in the middle of the WDS, providing for low values of $\Delta H$. Moreover, ${\overline{\rho }}^{\left(s\right)}$ was high for all four cases along the main supply line, which was easily recognizable as the line with high values of $c_B$ in Figure 6a.

4. Discussion

This study has introduced a historically-informed method of assessing resilience for critical events that cause demand relocation within a WDS. The WDS has thus been considered to be an interdependent, socio-technical system in which the social and the technical system interact: the technical system has to maintain its service during a critical event despite the social system accounting for strong changes in demand distribution. The WDS has been modeled as a planar graph with consumer nodes representing residential areas characterized by required demand. The critical event has been modeled as an event during which population leaves consumer nodes within the evacuation area, where required demand drops to zero, and subsequent demand relocation according to three sheltering schemes: (a) centralized sheltering, (b) near-at-hand sheltering, (c) diffuse sheltering.

To answer the research question (i) stated in Section 1.1, four evacuation radii have been compared. The results in Section 3.1 show that the mean resilience index $\overline{\rho }$ is inversely proportional to the square of the evacuation radius, $\overline{\rho }\propto -r^2$, i.e., decreases linearly with growing evacuation area. For the near-at-hand and the diffuse sheltering scheme, a similar relationship could not be observed. The evacuation radius had a decisive influence on the number of under-serviced nodes for the near-at-hand and the diffuse sheltering scheme, where radii $r_3$ and $r_4$ causes significantly more nodes to remain under-serviced than the radii $r_1$ and $r_2$. When assessing the effect of the sheltering schemes to answer the research question (ii), it has been demonstrated that the centralized sheltering scheme resulted in the most serious under-servicing. This was an expected result because the centralized scheme causes the most drastic change in required demand distribution in the network. In reality, relocating the evacuated population to a single node is unlikely, and as such, it is to be interpreted as a worst case. In the near-at-hand and the diffuse sheltering scheme, the WDS could provide nearly full service for the smaller radii $r_1$ and $r_2$. The number of under-serviced nodes is significantly higher for the near-at-hand and the diffuse sheltering scheme. This shows that even if the diffuse sheltering scheme can provide best overall service, social factors would play an important role in determining the acceptance of this scheme. With regard to the vulnerability, a strong disparity between the central and the peripheral nodes has been identified, answering the research question (iii). The peripheral nodes are less vulnerable by causing the demand to relocate towards the better-serviced centre of the WDS. To determine suitable shelter nodes and address the research question (iv), two clusters in the south and the west of the WDS have been identified that deliver high values of mean resilience index ${\overline{\rho }}^{\left(s\right)}$, as well as the nodes along the main pipeline. This is in good agreement with the results delivered by the evaluation of betweenness centrality (identification of the main pipeline) and the shortest path lengths (identification of the clusters in the south and west). While each of the graph-based metrics provides insight into specific phenomena observed in the simulation results, neither of them is capable to reproduce the simulation results sufficiently alone (research question (v)).

The presented results show limitations which need to be acknowledged and which will be presented in the following. A first limitation to the approach is that the system boundary is restricted to the WDS and the embeddedness of the system in another system on a larger scale is neglected. Thus, flux of citizens or goods over the system boundary are not considered. Furthermore, only a very simplified model of the social system is used which is linked to the WDS. Each sheltering scheme is considered separately where in reality mixed forms would always appear and dynamic changes in relocation during an ongoing critical event are also possible, taking on chaotic forms in some cases [46]. Historical examples show that the population did not always react in the way relief authorities had planned. The fact that centralized accommodation is offered does not automatically mean that citizens also use it as planned. Inhabitants of the evacuated area returned to their homes during the day after spending the night in centralized shelter in order to secure property, necessitating checks along the perimeter of the evacuated area [47]. Instead of using accommodation centres (centralized scheme), a huge number of the evacuated population preferred independent accommodation with family members or friends (diffuse or near-at-hand scheme), especially if the disturbance lasted longer (e.g., when residential neighbourhoods are flooded). This can be explained by the lack of comfort and limited privacy in the emergency shelters. Furthermore, the authorities called for the provision of private shelters during large-scale situations. As central accommodation for tens of thousands of people affected, in addition to the actual handling of the critical event, also means an enormous logistical effort [48]. Other groups, however, which lacked this option, stayed for long periods in emergency shelters, e.g., [49,50]. It can be concluded from this that a combination of centralized, near-at-hand and diffuse demand would develop during a critical event.

While simple stochastic methods are used to relocate demand in the near-at-hand and diffuse sheltering schemes a more refined model will incorporate socio-economic data, including income, household size and living spaces as well as other social factors, e.g., social ties and cohesion in neighbourhoods, the sense of solidarity and historical experience if not routine. The latter could be researched in neighbourhoods that are regularly affected by river floods in cities like Cologne, Passau, Dresden. Incorporating these parameters will enable us to determine indicators for the spatial mobility of city dwellers in the case of critical events. While it may appear that some critical events investigated within this study are too extreme to be realistic it needs to be emphasized that this is in accordance with the uncertain nature of critical events where none should be excluded, especially since there is historical precedence for close to entire cities becoming uninhabitable. Different cities may also respond differently to critical events. As the presented study was carried out using just one WDS, the results cannot yet be generalized for all networks. It has been remarked that in some results the method of modeling critical events is reflected. Further methods for generalized models and subsequent analysis need to be explored to meet this limitation. Finally, only two graph-based metrics were chosen to compare to the results of the hydraulic simulations. More detailed methods for evaluating correlations between graph-based and simulation-based metrics may yield deeper insights which holds true for the vulnerability assessment of the network. As an exploratory study of interdependence between WDS and the social system populating it, the presented work shows promising results that compel future research of this topic.

Future work should further investigate the interdependence of technical with social systems. When evaluating resilience of technical systems, metrics should be refined to consider the influence of the social system. Thus, the understanding of a critical event should be broadened to include factors other than component failure within the considered technical system. In order to study interdependencies in WDS as socio-technical systems adequately, validated modeling approaches to modeling social systems, e.g., agent-based modeling, may be leveraged and coupled with hydraulic models so as to arrive at a socio-technical model of WDS. Finally, further research into the scales of critical events and the dependence of the impact on them may give a deeper understanding of risks WDSs are faced with.

5. Conclusions

This study has presented an exploratory, historically-informed approach to assessing resilience for critical events that cause demand relocation within a WDS. The WDS has been considered to be an interdependent, socio-technical system in which the social and the technical systems interact. Demand relocation has been considered as a critical factor that can affect resilience similarly to the more commonly analyzed component failures such as pipe leaks and pump failures. The WDS has been modeled as a planar graph in which consumer nodes represent residential areas characterized by required demand. The critical event has been modeled as an event during which population leaves consumer nodes within the evacuation area, where required demand drops to zero, and subsequent demand relocation according to three sheltering schemes. Five research questions have been addressed, analyzing the effect of the size of the evacuated area, the feasibility of sheltering schemes, vulnerability of particular parts of the city, the the suitability of nodes to serve as shelter nodes and last but not least, the comparison of the approach to graph-based metrics.

It has been shown that the size of the evacuation area has a decisive influence on the resilience of the city, with the resilience index being inversely proportional to the size of the evacuation area in the centralized sheltering scheme. The diffuse sheltering scheme has been identified as the scheme that can provide the highest value of resilience index while also negatively affecting the number of under-serviced nodes. A noticeable disparity between the central and the peripheral nodes has been identified when analyzing the vulnerability of the areas of the city, showing that peripheral nodes are less vulnerable by causing the demand to relocate towards the better-serviced centre of the WDS. Moreover, it has been shown that nodes along the supply line as well as in the area of two clusters in the West and South of the WDS are best suited to serve as shelter nodes, comparing the present approach to graph-based metrics (betweenness centrality and shortest paths length).

The results have been critically discussed under the consideration of historical knowledge, recognizing possible limitations of the work. The most severe limitation is that in real-world scenarios, the sheltering schemes generally do not occur in their pure form. This provides scope for future work that should investigate the interdependence of technical with social systems further, using more refined models.