Propagation from Meteorological to Hydrological Drought and Its Influencing Factors in the Huaihe River Basin
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
3. Methodology
3.1. Drought Characterizing
3.1.1. Drought Indices
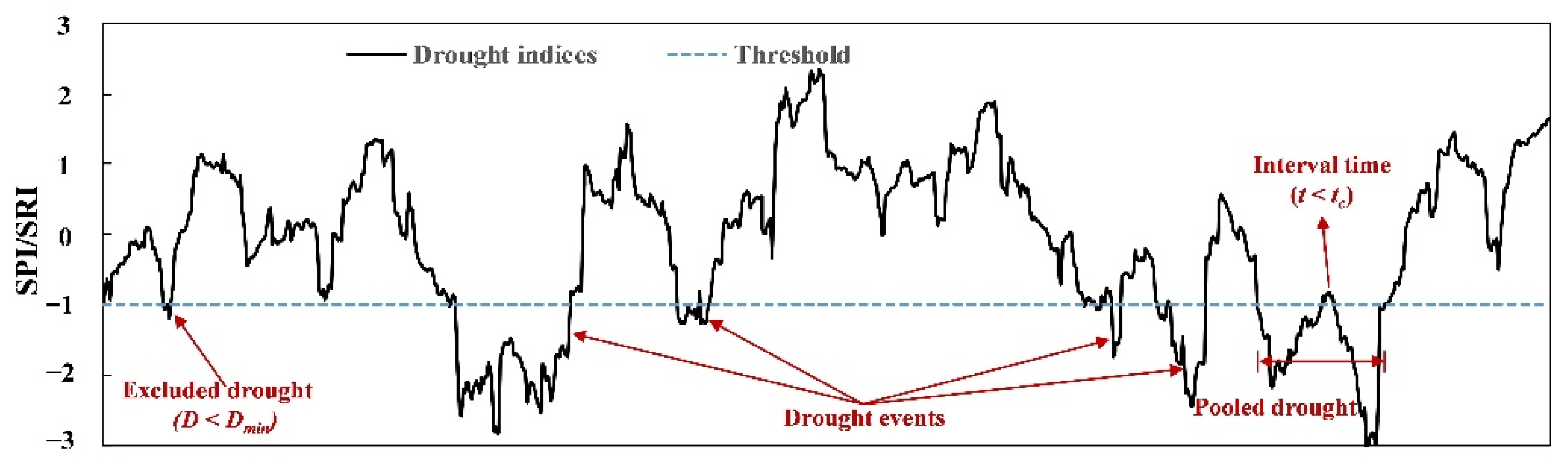
3.1.2. Drought Identification
- (1)
- Initial identification. Set threshold τ = −1 to capture drought events;
- (2)
- Pooling adjacent droughts. Interval time criteria (tc) was selected to pool mutually dependent droughts. If the interval time t between two adjacent droughts is less than the predefined tc and the drought index between two droughts is less than 0, then two adjacent droughts can be pooled to form a new drought event. Repeat the procedure until the interval time between all the droughts is greater than tc. Then, tc is predefined as 10 days for both meteorological and hydrological drought identification;
- (3)
- Excluding minor droughts. Minor droughts with a short duration have little impact on hydrological conditions but large impacts on drought characterization. If the duration of a drought event is less than the predefined minimum duration Dmin, then the event is excluded. The Dmin is predefined as 10 and 30 days for meteorological and hydrological drought identification, respectively.
3.1.3. Estimation of Drought Characteristics
- Drought duration (D) is the period from the onset time to end time of a drought event;
- Drought severity (S) is the sum of SPI/SRI values during a drought;
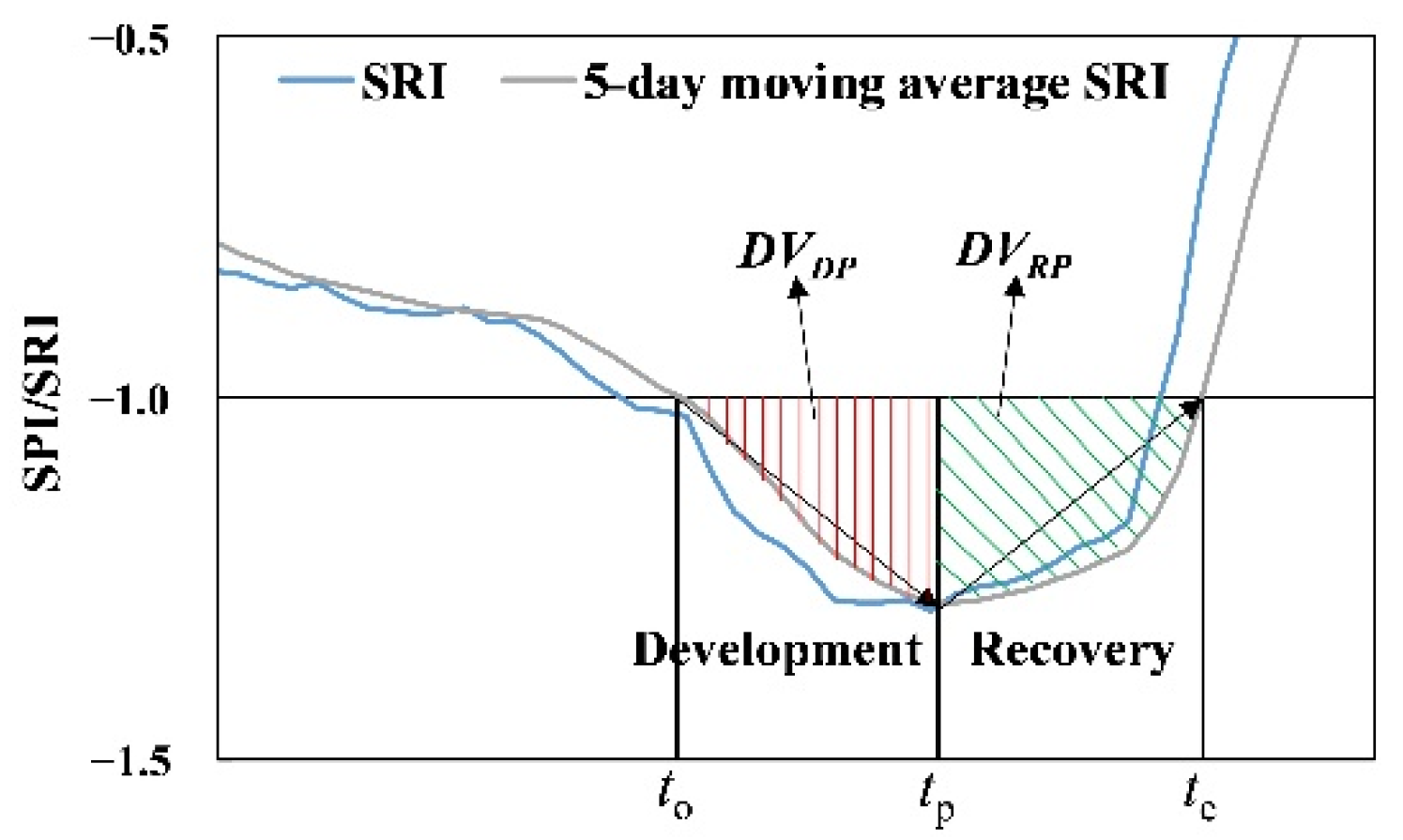
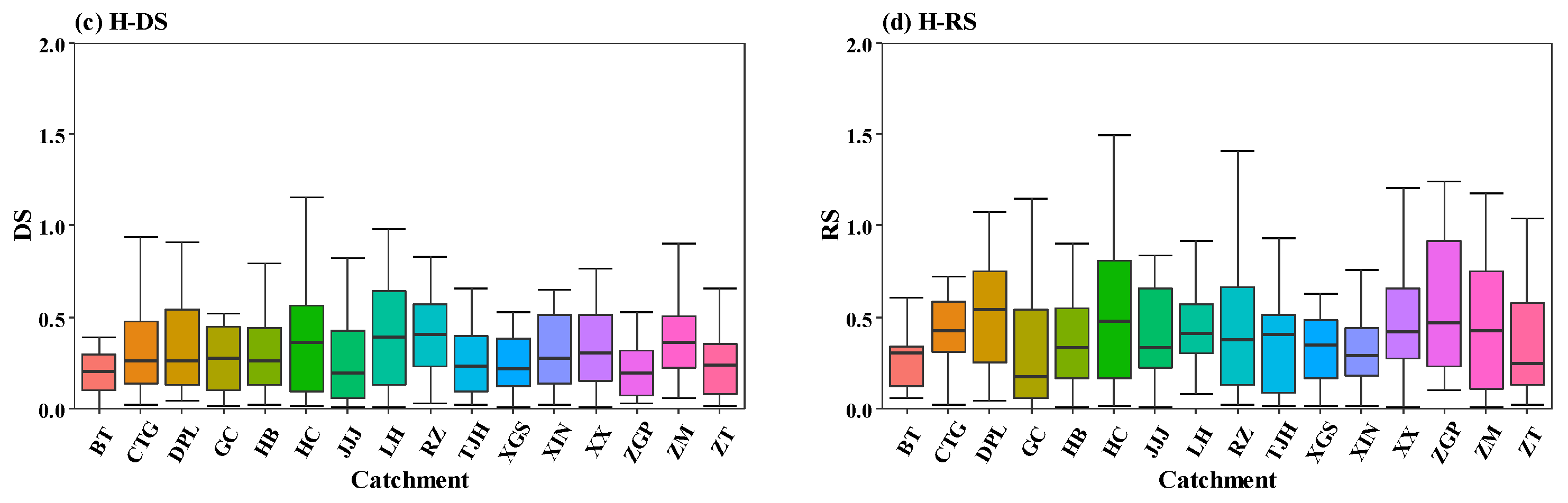
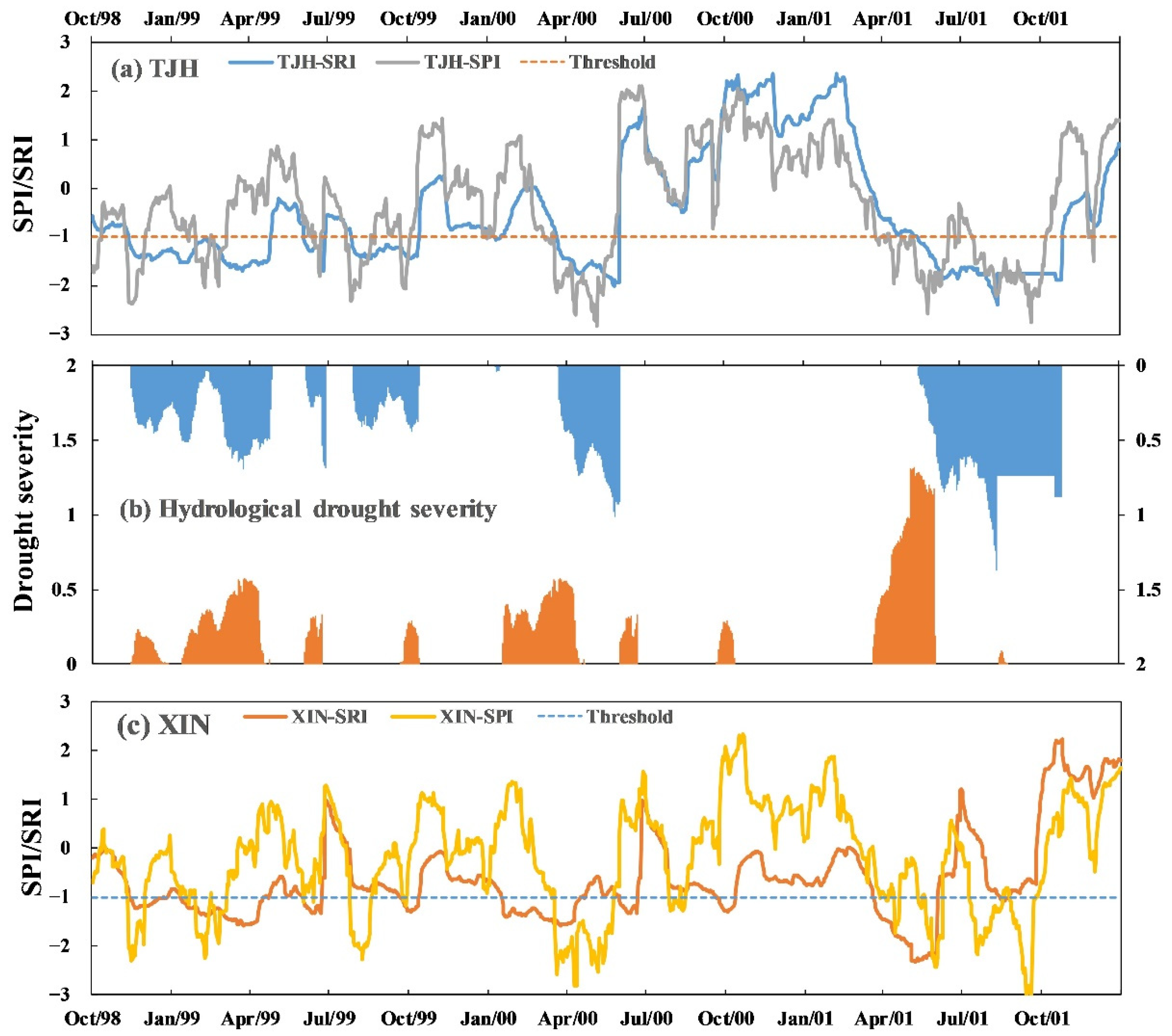
- Drought development speed (DS) is the change rate of the drought index from the onset time (to) to the peak time (tp) during the drought development stage and recovery speed (RS) [29] is the change rate of the drought index from the peak time (tp) to the end time (te) at the drought recovery stage. To reduce the fluctuation of daily series without significantly changing the onset and end time of drought events, the 5-day moving average process is first employed to the daily SPI/SRI series (Figure 3). Then, DS and RS are calculated as follows:where DVDP and DVRP are the deficit volumes of rainfall/streamflow in terms of the 5-day moving average drought index in the development and recovery period, respectively. Additionally, to, tp, and te are the onset, peak, and end time of a drought event. For a pooled drought event, DS (RS) refers to the development (recovery) speed of the first (last) drought.
3.2. Propagation Relationship Analysis
3.2.1. Matching Meteorological and Hydrological Drought Events
3.2.2. Quantification of Propagation Relationship
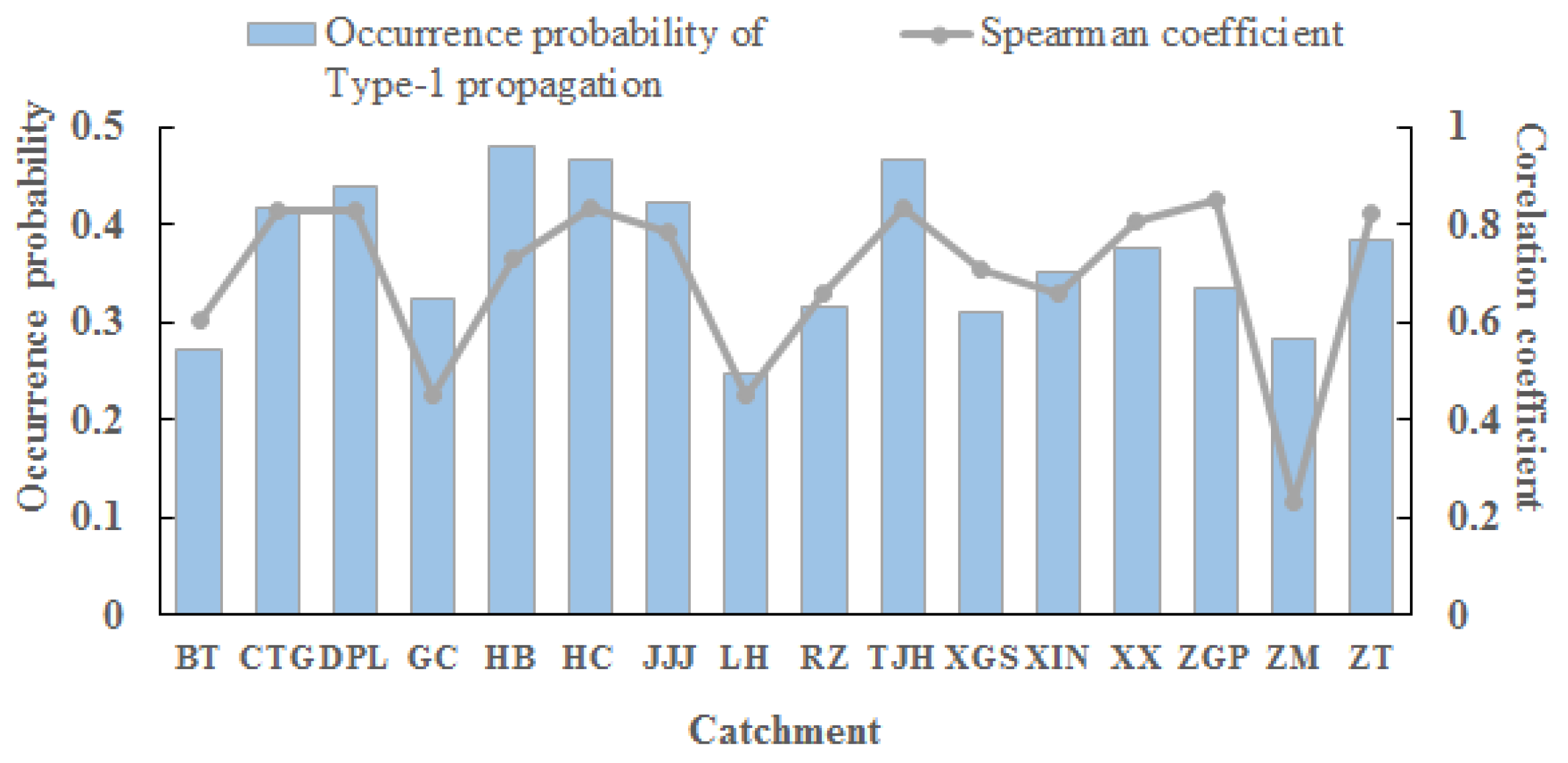
- Occurrence probability of Type-1 propagation (PH|M) is defined as the probability that a hydrological drought (referred to as H) is triggered when a meteorological drought (referred to as M) occurs. Conditional probability is widely used in studies of probabilistic drought prediction [31,32] and probabilistic links between matched meteorological and hydrological drought characteristics [23,24]. Here, we apply the bivariate conditional probability based on the copula function to estimate PH|M. Assuming that X and Y are random variables with marginal distributions and , the bivariate conditional probability is given by:
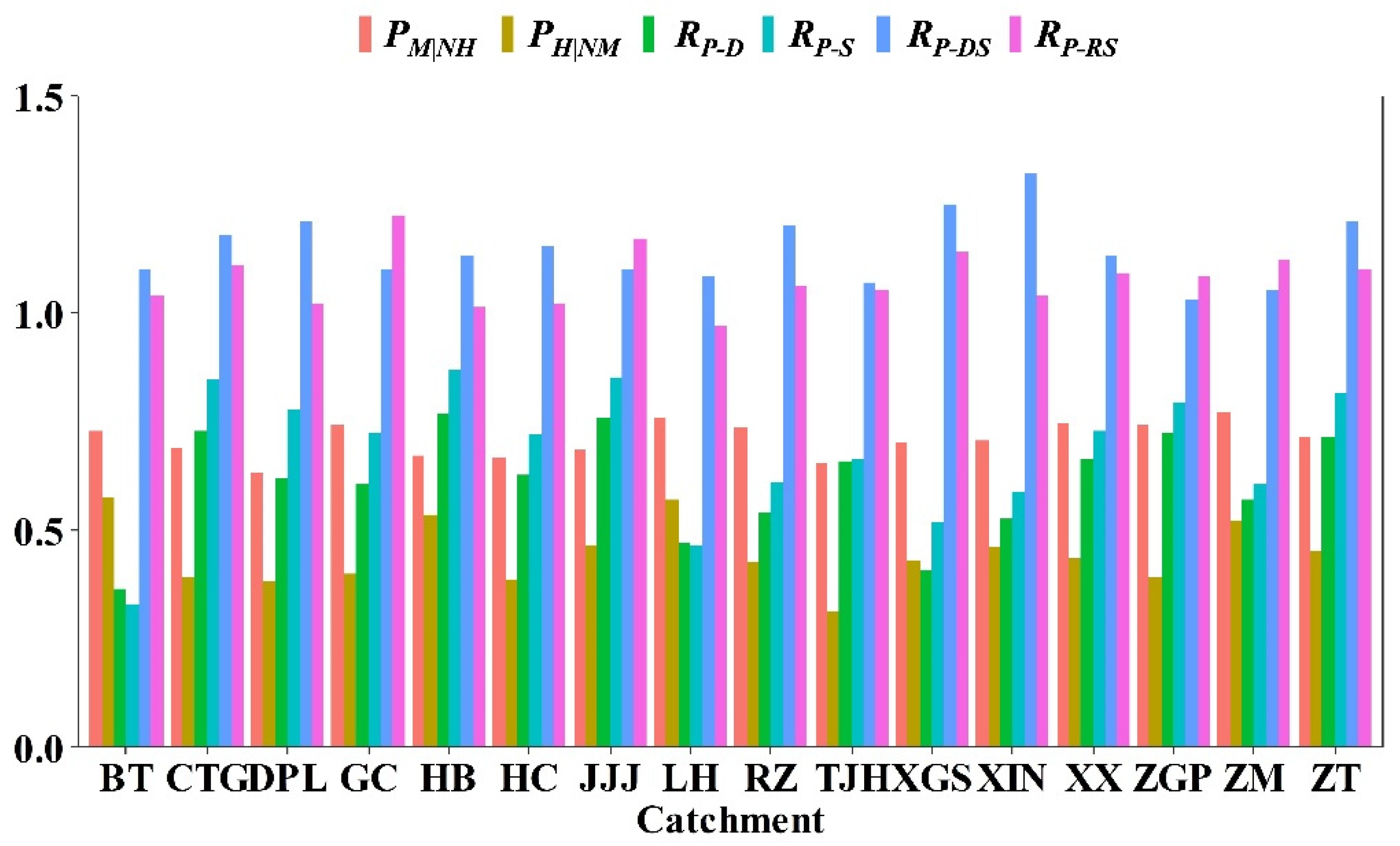
- Occurrence probability of Type-2 propagation (PM|NH) is defined to describe the situation that a meteorological drought (M) occurs but no hydrological drought occurs (referred to as NH). PM|NH equals the bivariate conditional probability , given by:PM|NH is calculated as the ratio of the number of meteorological drought events triggering hydrological drought events to the total number of meteorological drought events in the record period, given by:where is the number of meteorological drought events that trigger hydrological drought events and nm is the total number of meteorological drought events.
- Occurrence probability of Type-3 (PH|NM) is defined to quantify the situation that a hydrological drought event occurs without a proceeding meteorological drought event (referred to as NM). PH|NM equals the bivariate conditional probability of , given by:
- Propagation time (TP) is the time difference between the onset of matched meteorological and hydrological drought events.where Mo and Ho are the onset time of matched meteorological and hydrological drought events. For the many-to-one situation, Mo refers to the onset time of the first meteorological drought event.
- Propagation ratio of drought characteristics (RP) is the ratio of matched meteorological to hydrological drought event characteristics, given by:where CM,i and CH,i are the characteristics (duration, severity, and development/recovery speed) of matched meteorological and hydrological drought events, respectively; n is the number of hydrological drought events triggered by meteorological drought events. The drought characteristics considered here include the duration, severity, and development/recovery speed, and consequently we have RP-D, RP-S, RP-DS, and RP-RS to represent the propagation ratio of duration, severity, development speed, and recovery speed, respectively. For the many-to-one situation, when calculating RP-D or RP-S, the CM,i should be the sum of duration or severity of all meteorological drought events that triggers the ith hydrological drought event; when calculating RP-DS (RP-RS), the CM,i should be the development (recovery) speed of the first (last) meteorological drought event that triggers the ith hydrological drought event.
3.3. Influence of Climate, Catchment Properties, and Human Activities on Drought Propagation
3.3.1. Selected Influencing Factors
3.3.2. Analyze the Influence with the Correlation Analysis
4. Results
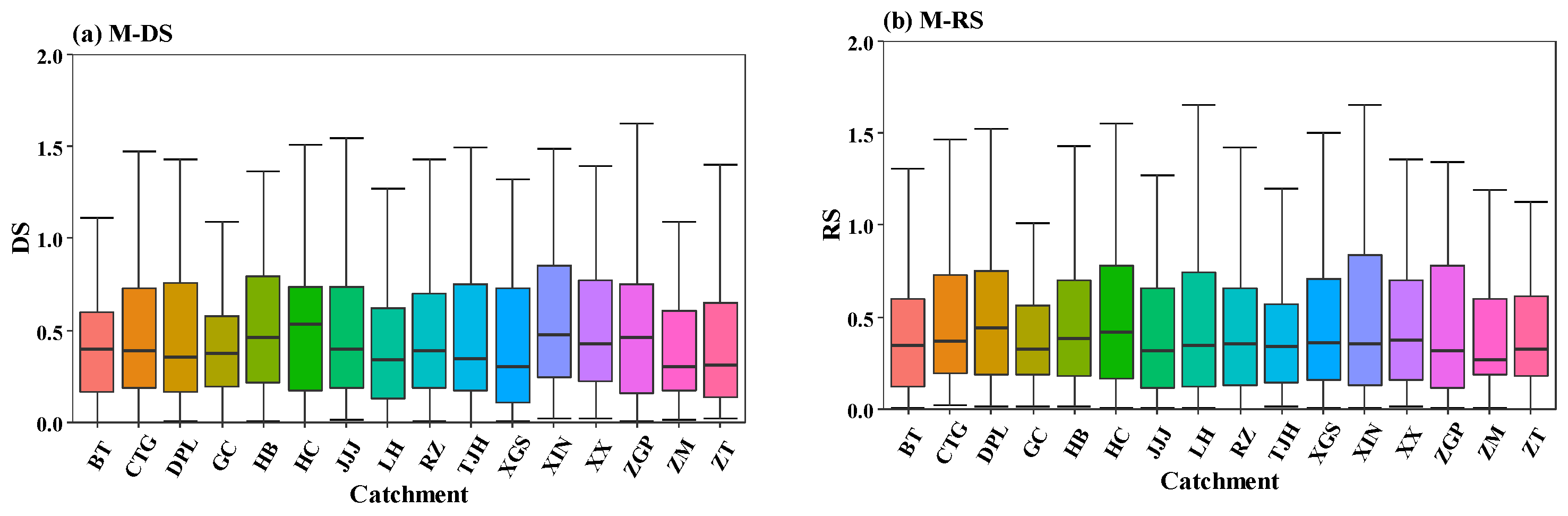
4.1. Characteristics of Meteorological and Hydrological Drought Events
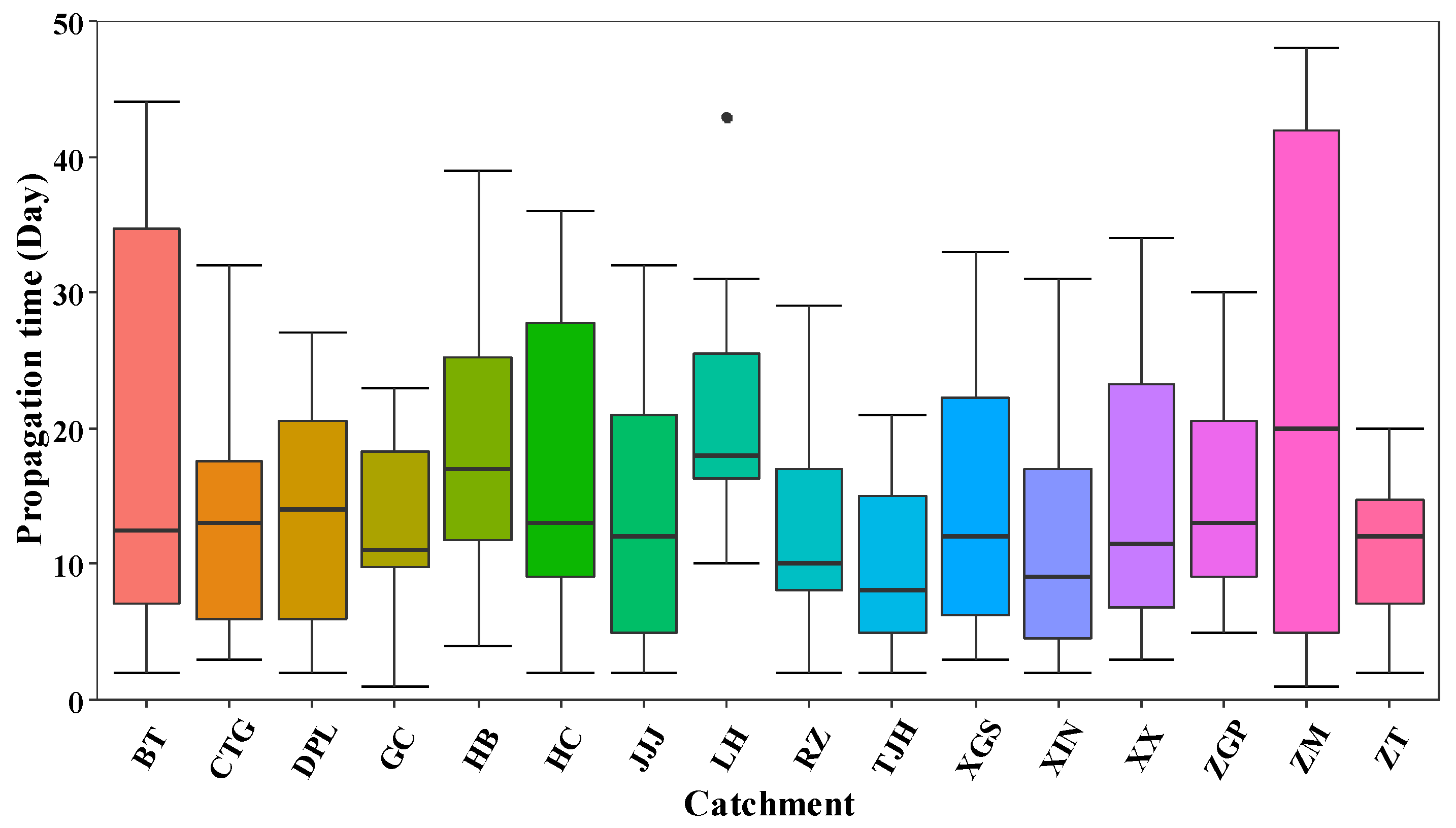
4.2. Propagation Features from Meteorological to Hydrological Droughts
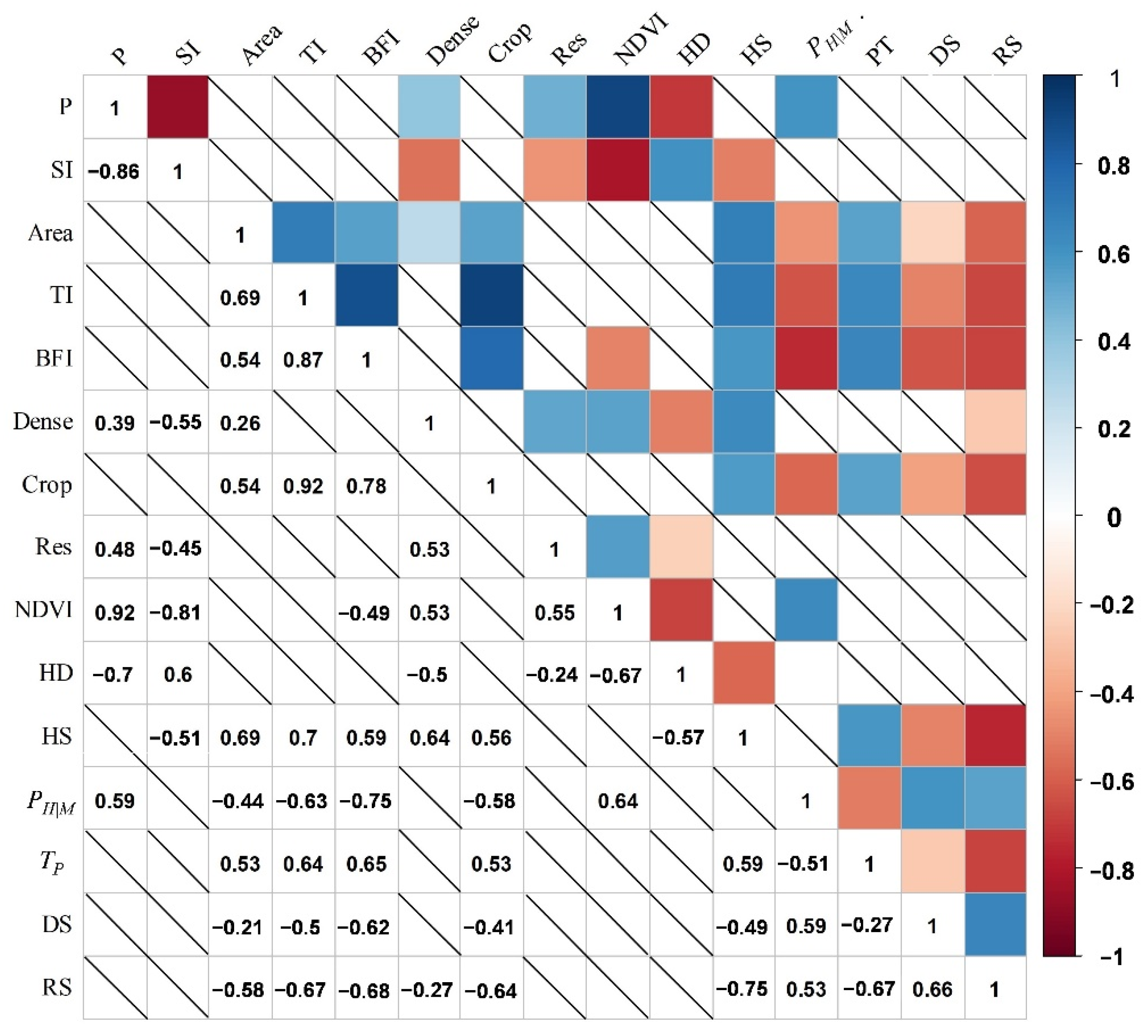
4.3. Impacts of Climate and Catchment Properties on Drought Propagation
4.4. Impacts of Reservoir on Hydrological Drought and Drought Propagation
5. Discussion
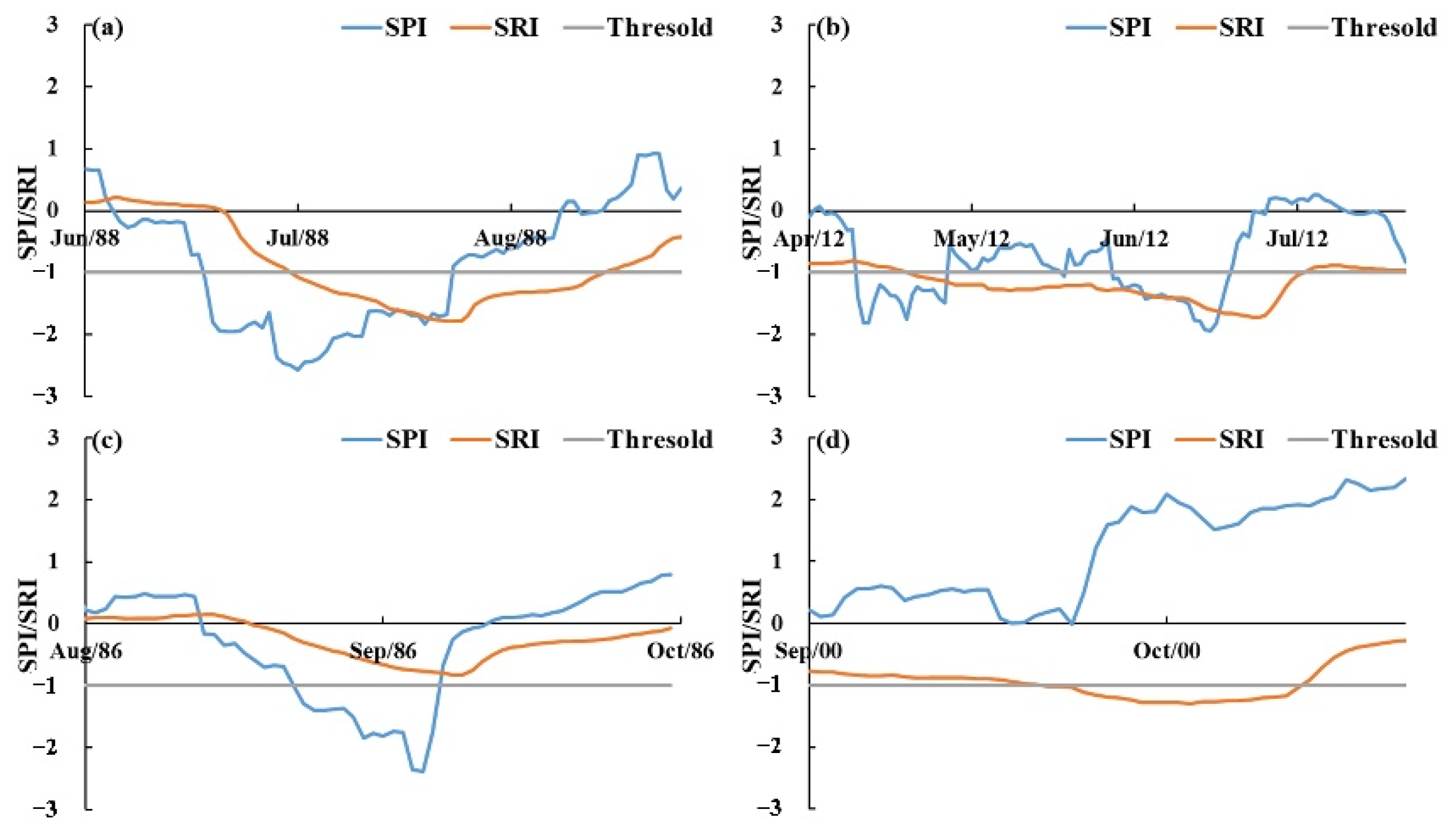
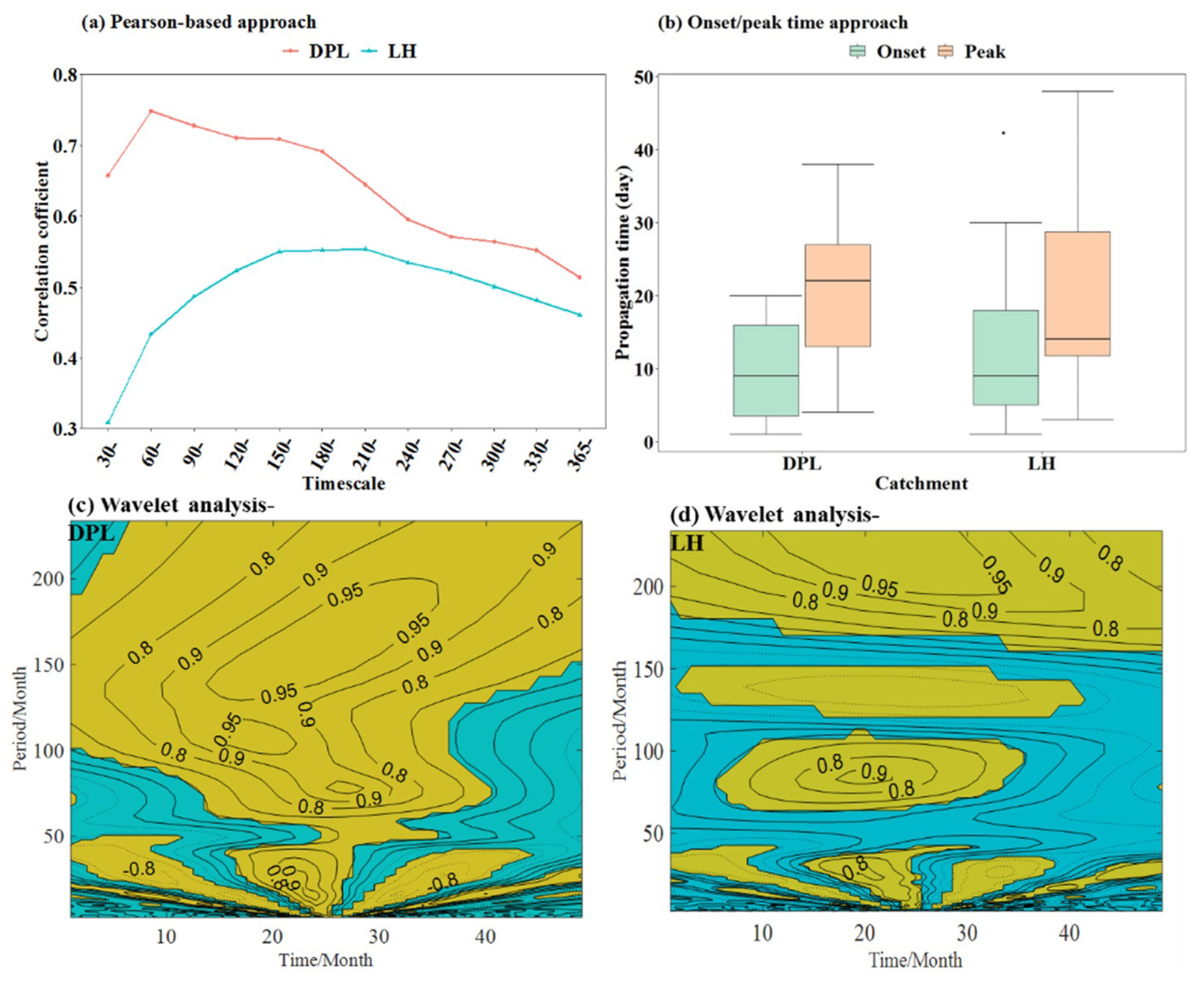
5.1. How to Quantify Propagation Time from Meteorological to Hydrological Drought?
5.2. Which One Performs Better in Representing the Effect of Catchment Properties on Drought Propagation, Base Flow Index or Topographic Index?
5.3. How Does Irrigation Affect Hydrological Drought?
6. Conclusions
- (1)
- The occurrence probability of Type-1 propagation varies from 0.25 to 0.48 among all catchments. The propagation time ranges from 1 to 47 days in study catchments. Catchments with low occurrence probability of Type-1 propagation is found in LH, BT, and ZM, which also have a longer propagation time. Features of Type-1 propagation include the lengthening of duration, amplification of severity, lag of onset time, and reduction of speed.
- (2)
- Climate factors have a significant effect on hydrological drought duration, while the topographic index (TI) from TOPMODEL representing catchment properties significantly correlates with hydrological drought severity. The base flow index (BFI) and TI indicating catchment storage show the strongest relationship with propagation time, probability, and development/recovery speed. Partial correlation analyses show that the impact of crop land on hydrological drought is far less than that of TI, indicating that the impact of irrigation on hydrological drought is less than that of catchment properties.
- (3)
- Reservoir operation has a significant effect on alleviating the duration and severity of extreme hydrological drought. However, it also increases the occurrence of Type-3 propagation due to the impoundment of reservoir upstream at the end of flood season. The off-set of two sides of effect on hydrological drought may be the reason that the average hydrological drought characteristics of paired-catchment is very close.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Ertsen, M.W.; Svoboda, M.D.; Hafeez, M. Propagation of Drought: From Meteorological Drought to Agricultural and Hydrological Drought. Adv. Meteorol. 2016, 2016, 6547209. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological drought explained. WIREs Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Ren, L.; Singh, V.P.; Yong, B.; Jiang, S.; Yuan, F.; Yang, X. Understanding the Spatiotemporal Links Between Meteorological and Hydrological Droughts From a Three-Dimensional Perspective. J. Geophys. Res. Atmos. 2019, 124, 3090–3109. [Google Scholar] [CrossRef]
- Yang, Y.; McVicar, T.R.; Donohue, R.J.; Zhang, Y.; Roderick, M.L.; Chiew, F.H.S.; Zhang, L.; Zhang, J. Lags in hydrologic recovery following an extreme drought: Assessing the roles of climate and catchment characteristics. Water Resour. Res. 2017, 53, 4821–4837. [Google Scholar] [CrossRef]
- Van Loon, A.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2014, 526, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Valiya Veettil, A.; Mishra, A.K. Multiscale hydrological drought analysis: Role of climate, catchment and morphological variables and associated thresholds. J. Hydrol. 2020, 582, 124533. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A. Quantifying Climate and Catchment Control on Hydrological Drought in the Continental United States. Water Resour. Res. 2020, 56, e2018WR024620. [Google Scholar] [CrossRef]
- Huang, S.; Li, P.; Huang, Q.; Leng, G.; Hou, B.; Ma, L. The propagation from meteorological to hydrological drought and its potential influence factors. J. Hydrol. 2017, 547. [Google Scholar] [CrossRef]
- Bhardwaj, K.; Shah, D.; Aadhar, S.; Mishra, V. Propagation of Meteorological to Hydrological Droughts in India. J. Geophys. Res. Atmos. 2020, 125, e2020JD033455. [Google Scholar] [CrossRef]
- Apurv, T.; Sivapalan, M.; Cai, X. Understanding the Role of Climate Characteristics in Drought Propagation. Water Resour. Res. 2017, 53, 9304–9329. [Google Scholar] [CrossRef] [Green Version]
- Barker, L.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardised indicators. Hydrol. Earth Syst. Sci. 2016, 20, 2483–2505. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Zhang, X.; Wang, X.; Hao, Z.; Singh, V.P.; Hao, F. Propagation from meteorological drought to hydrological drought under the impact of human activities: A case study in northern China. J. Hydrol. 2019, 579, 124147. [Google Scholar] [CrossRef]
- Ma, F.; Luo, L.; Ye, A.; Duan, Q. Drought Characteristics and Propagation in the Semiarid Heihe River Basin in Northwestern China. J. Hydrometeorol. 2018, 20, 59–77. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, X.; Zhang, Z.; Shi, P. Evolution of hydrological drought under the regulation of two reservoirs in the headwater basin of the Huaihe River, China. Stoch. Environ. Res. Risk Assess. 2015, 29, 487–499. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.H.; Wanders, N.; Bierkens, M.F.P. Human water consumption intensifies hydrological drought worldwide. Environ. Res. Lett. 2013, 8, 34036. [Google Scholar] [CrossRef] [Green Version]
- Yu, M.; Liu, X.; Li, Q. Responses of meteorological drought-hydrological drought propagation to watershed scales in the upper Huaihe River basin, China. Environ. Sci. Pollut. Res. 2020, 27, 17561–17570. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, Y.; Wang, W.; Singh, V.; Ma, X.; Yu, Z. Three dimensional characterization of meteorological and hydrological droughts and their probabilistic links. J. Hydrol. 2019, 578, 124016. [Google Scholar] [CrossRef]
- Fleig, A.K.; Tallaksen, L.M.; Hisdal, H.; Hannah, D.M. Regional hydrological drought in north-western Europe: Linking a new Regional Drought Area Index with weather types. Hydrol. Process. 2011, 25, 1163–1179. [Google Scholar] [CrossRef]
- Li, Q.; He, P.; He, Y.; Han, X.; Zeng, T.; Lu, G.; Wang, H. Investigation to the relation between meteorological drought and hydrological drought in the upper Shaying River Basin using wavelet analysis. Atmos. Res. 2020, 234, 104743. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Q.; Wang, L.; Lei, L.; Huang, M.; Xiang, J.; Feng, W.; Zhao, Y.; Xue, D.; Liu, C.; et al. Impact of Climate Change and Land-Use on the Propagation from Meteorological Drought to Hydrological Drought in the Eastern Qilian Mountains. Water 2019, 11, 1602. [Google Scholar] [CrossRef] [Green Version]
- Wong, G.; van Lanen, H.A.J.; Torfs, P.J.J.F. Probabilistic analysis of hydrological drought characteristics using meteorological drought. Hydrol. Sci. J. 2013, 58, 253–270. [Google Scholar] [CrossRef] [Green Version]
- Sattar, M.N.; Lee, J.-Y.; Shin, J.-Y.; Kim, T.-W. Probabilistic Characteristics of Drought Propagation from Meteorological to Hydrological Drought in South Korea. Water Resour. Manag. 2019, 33, 2439–2452. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Leng, G.; Fang, W.; Wang, L.; Wang, H. Propagation thresholds of meteorological drought for triggering hydrological drought at various levels. Sci. Total Environ. 2020, 712, 136502. [Google Scholar] [CrossRef]
- McKee, T.B.; Nolan, J.; Kleist, J. The relationship of drought frequency and duration to time scales. Prepr. Eighth Conf. Appl. Climatol. Amer. Meteor Soc. 1993, 17, 179–183. [Google Scholar]
- Shukla, S.; Wood, A. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Svoboda, M.; Hayes, M.; Wood, D. Standardized Precipitation Index User Guide; World Meteorological Organization: Geneva, Switzerland, 2012. [Google Scholar]
- Fleig, A.K.; Tallaksen, L.M.; Hisdal, H.; Demuth, S. A global evaluation of streamflow drought characteristics. Hydrol. Earth Syst. Sci. 2006, 10, 535–552. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Chen, X.; Yao, H.; Liu, Z.; Zhang, D. Hydrological Drought Instantaneous Propagation Speed Based on the Variable Motion Relationship of Speed-Time Process. Water Resour. Res. 2018, 54, 9549–9565. [Google Scholar] [CrossRef]
- Li, J.; Guo, Y.; Wang, Y.; Lu, S.; Chen, X. Drought Propagation Patterns under Naturalized Condition Using Daily Hydrometeorological Data. Adv. Meteorol. 2018, 2018, 2469156. [Google Scholar] [CrossRef]
- Khedun, C.P.; Mishra, A.K.; Singh, V.P.; Giardino, J.R. A copula-based precipitation forecasting model: Investigating the interdecadal modulation of ENSO’s impacts on monthly precipitation. Water Resour. Res. 2014, 50, 580–600. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Hwang, Y. Improving drought predictability in Arkansas using the ensemble PDSI forecast technique. Stoch. Environ. Res. Risk Assess. 2015, 29, 79–91. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J.; Freer, J.E.; Lamb, R. A history of TOPMODEL. Hydrol. Earth Syst. Sci. 2021, 25, 527–549. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Muttiah, R.; Bernhardt, G. Automated Base Flow Separation and Recession Analysis Techniques. Groundwater 1995, 33, 1010–1018. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Wang, H.; Leng, G.; Wang, L. Identifying drought propagation by simultaneously considering linear and nonlinear dependence in the Wei River basin of the Loess Plateau, China. J. Hydrol. 2020, 591, 125287. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Rangecroft, S.; Coxon, G.; Breña Naranjo, J.A.; Van Ogtrop, F.; Van Lanen, H.A.J. Using paired catchments to quantify the human influence on hydrological droughts. Hydrol. Earth Syst. Sci. 2019, 23, 1725–1739. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Xu, J.; Wang, X.; Cai, H.; Zhou, Z.; Sun, Y.; Shi, H. Propagation of meteorological to hydrological drought for different climate regions in China. J. Environ. Manag. 2021, 283, 111980. [Google Scholar] [CrossRef]
- Gevaert, A.I.; Veldkamp, T.I.E.; Ward, P.J. The effect of climate type on timescales of drought propagation in an ensemble of global hydrological models. Hydrol. Earth Syst. Sci. 2018, 22, 4649–4665. [Google Scholar] [CrossRef] [Green Version]
- Bloomfield, J.P.; Allen, D.J.; Griffiths, K.J. Examining geological controls on baseflow index (BFI) using regression analysis: An illustration from the Thames Basin, UK. J. Hydrol. 2009, 373, 164–176. [Google Scholar] [CrossRef] [Green Version]
- Koskelo, A.I.; Fisher, T.R.; Utz, R.M.; Jordan, T.E. A new precipitation-based method of baseflow separation and event identification for small watersheds (<50 km2). J. Hydrol. 2012, 450–451, 267–278. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, M.; He, X.; Ren, L.; Pan, M.; Yu, X.; Wei, Z.; Sheffield, J. Contrasting Influences of Human Activities on Hydrological Drought Regimes Over China Based on High-Resolution Simulations. Water Resour. Res. 2020, 56, e2019WR025843. [Google Scholar] [CrossRef]
- Wan, W.; Zhao, J.; Li, H.-Y.; Mishra, A.; Ruby Leung, L.; Hejazi, M.; Wang, W.; Lu, H.; Deng, Z.; Demissisie, Y.; et al. Hydrological Drought in the Anthropocene: Impacts of Local Water Extraction and Reservoir Regulation in the U.S. J. Geophys. Res. Atmos. 2017, 122, 313–328. [Google Scholar] [CrossRef]
- De Graaf, I.E.M.; Van Beek, L.P.H.; Wada, Y.; Bierkens, M.F.P. Advances in Water Resources Dynamic attribution of global water demand to surface water and groundwater resources: Effects of abstractions and return flows on river discharges. Adv. Water Resour. 2014, 64, 21–33. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Ghazavi, R.; Karimi, H. Estimation of Groundwater Recharge from the Rainfall and Irrigation in an Arid Environment Using Inverse Modeling Approach and RS. Water Resour. Manag. 2016, 30, 1939–1951. [Google Scholar] [CrossRef]
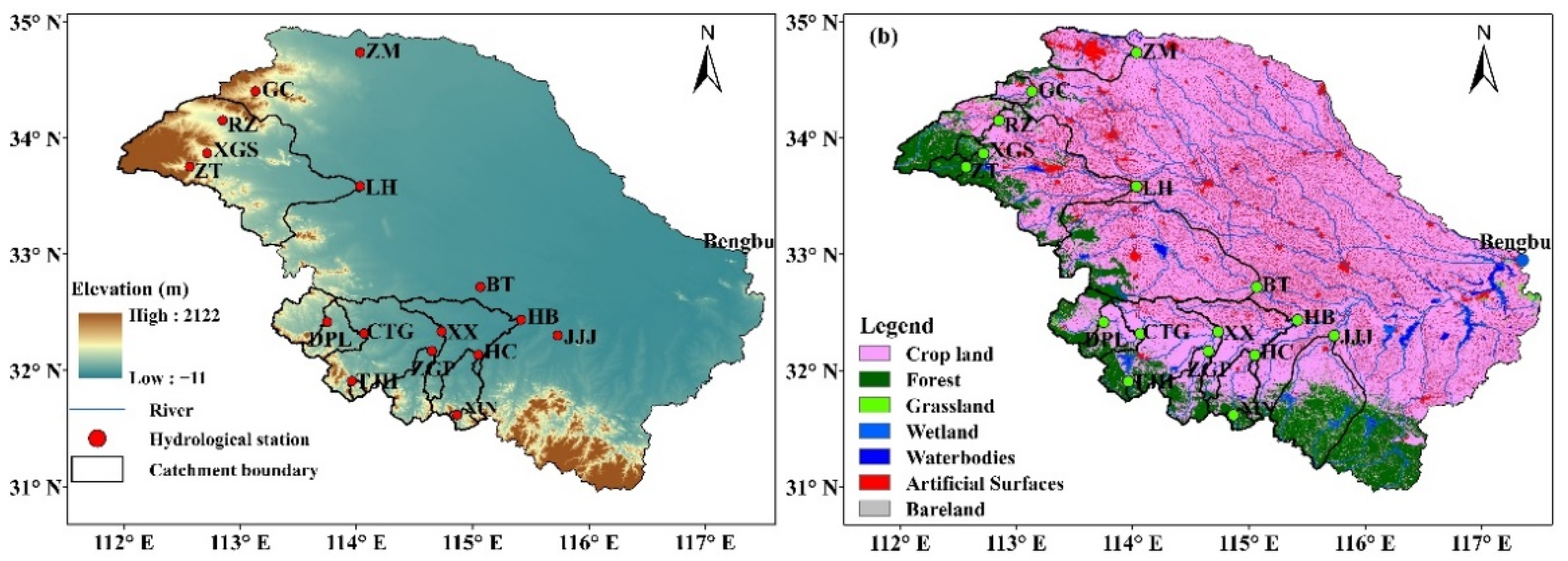

| Catchments | Longitude (°) | Latitude (°) | Area (km2) | Annual Precipitation (mm) |
|---|---|---|---|---|
| Dapoling (DPL) | 113.75 | 32.42 | 1640 | 997 |
| Changtaiguan (CTG) | 114.07 | 32.32 | 3090 | 1005 |
| Xixian (XX) | 114.73 | 32.33 | 10,230 | 1020 |
| Huaibin (HB) | 115.42 | 32.43 | 15,780 | 1034 |
| Tanjiahe (TJH) | 113.88 | 31.90 | 173 | 1232 |
| Zhuganpu (ZGP) | 114.65 | 32.17 | 1639 | 1128 |
| Xinxian (XIN) | 114.87 | 31.62 | 274 | 1319 |
| Huangchuan (HC) | 115.05 | 32.13 | 2050 | 1202 |
| Ruzhou (RZ) | 112.85 | 34.15 | 2912 | 628 |
| Xiagushan (XGS) | 112.72 | 33.87 | 359 | 802 |
| Zhongtang (ZT) | 112.57 | 33.75 | 467 | 928 |
| Luohe (LH) | 114.03 | 33.58 | 12,150 | 767 |
| Gaocheng (GC) | 113.13 | 34.40 | 631 | 670 |
| Zhongmou (ZM) | 114.03 | 34.73 | 2132 | 634 |
| Bantai (BT) | 115.07 | 32.72 | 11,104 | 972 |
| Jiangjiaji (JJJ) | 115.73 | 32.30 | 5631 | 1246 |
| Index Name | Abbreviation | Details | Units |
|---|---|---|---|
| Average annual precipitation | P | Average annual precipitation is calculated using Thiessen polygon based on station observational data. | mm |
| Seasonality index | SI | The index represents the degree of variability in monthly precipitation within a year [11]. | |
| Drainage area | Area | The total drainage area of catchment. | Km2 |
| Drainage density | Dense | The total length of all the streams and rivers in a drainage basin divided by the total area of catchment. | Km/Km2 |
| Base flow index | BFI | The ratio of base flow and total runoff. Base flow was separated from the total streamflow using the digital filter method [34]. | - |
| Topographic index | TI | ln (α/tanβ) from TOPMODEL [33], α is the cumulative upslope area draining through the per contour length to a pixel and tanβ is the local slope angle of the cell. | - |
| NDVI | NDVI | NDVI quantifies vegetation by measuring the difference between near-infrared (which vegetation strongly reflects) and red light. | - |
| Ratio of reservoir capacity | Res | The ratio of the reservoir storage capacity to the annual average runoff of the catchment, reflecting the impact of reservoir on runoff (only the large- and medium-sized reservoir are considered). | % |
| Ratio of crop land | Crop | The ratio of catchment covered by crop land derived from GlobeLand30 to catchment area, reflecting the proportion of agricultural irrigation consumption in total runoff. | % |
| Area | P | TI | BFI | |
|---|---|---|---|---|
| HD | −0.431 | −0.684 (*) | −0.140 | 0.225 |
| HS | 0.460 | 0.722 (*) | 0.156 | 0.410 |
| PH|M | −0.198 | 0.502 | 0.037 | −0.395 |
| TP | 0.205 | 0.117 | 0.028 | 0.307 |
| Catchment | Area (km2) | Precipitation (mm) | ET (mm) | BFI | TI | Land Cover | |
|---|---|---|---|---|---|---|---|
| Crop Land | Forests | ||||||
| TJH (no reservoir) | 173 | 1232 | 64.2 | 0.140 | 7.811 | 17.80% | 82.10% |
| XIN (reservoir) | 274 | 1319 | 64.0 | 0.165 | 7.538 | 13.80% | 81.60% |
| Catchment | HD (Day) | HS | TP (Day) | PH|M | PH|NM | ||
|---|---|---|---|---|---|---|---|
| Average | Maximum | Average | Maximum | ||||
| TJH (no reservoir) | 64.6 | 169 | −121 | −277 | 10.7 | 0.48 | 0.31 |
| XIN (reservoir) | 62.5 | 163 | −108 | −255 | 11.0 | 0.45 | 0.46 |
| Difference (%) | −3.3 | −3.6 | −10.7 | −7.9 | 2.8 | 6.3 | 48.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, W.; Cheng, H.; Wang, H.; Zhu, Y. Propagation from Meteorological to Hydrological Drought and Its Influencing Factors in the Huaihe River Basin. Water 2021, 13, 1985. https://doi.org/10.3390/w13141985
Wang J, Wang W, Cheng H, Wang H, Zhu Y. Propagation from Meteorological to Hydrological Drought and Its Influencing Factors in the Huaihe River Basin. Water. 2021; 13(14):1985. https://doi.org/10.3390/w13141985
Chicago/Turabian StyleWang, Jingshu, Wen Wang, Hui Cheng, Hongjie Wang, and Ye Zhu. 2021. "Propagation from Meteorological to Hydrological Drought and Its Influencing Factors in the Huaihe River Basin" Water 13, no. 14: 1985. https://doi.org/10.3390/w13141985







